Multimodal Optimization of Permutation Flow-Shop Scheduling Problems Using a Clustering-Genetic-Algorithm-Based Approach

Abstract

Though many techniques were proposed for the optimization of Permutation Flow-Shop Scheduling Problem (PFSSP), current techniques only provide a single optimal schedule. Therefore, a new algorithm is proposed, by combining the k-means clustering algorithm and Genetic Algorithm (GA), for the multimodal optimization of PFSSP. In the proposed algorithm, the k-means clustering algorithm is first utilized to cluster the individuals of every generation into different clusters, based on some machine-sequence-related features. Next, the operators of GA are applied to the individuals belonging to the same cluster to find multiple global optima. Unlike standard GA, where all individuals belong to the same cluster, in the proposed approach, these are split into multiple clusters and the crossover operator is restricted to the individuals belonging to the same cluster. Doing so, enabled the proposed algorithm to potentially find multiple global optima in each cluster. The performance of the proposed algorithm was evaluated by its application to the multimodal optimization of benchmark PFSSP. The results obtained were also compared to the results obtained when other niching techniques such as clearing method, sharing fitness, and a hybrid of the proposed approach and sharing fitness were used. The results of the case studies showed that the proposed algorithm was able to consistently converge to better optimal solutions than the other three algorithms.

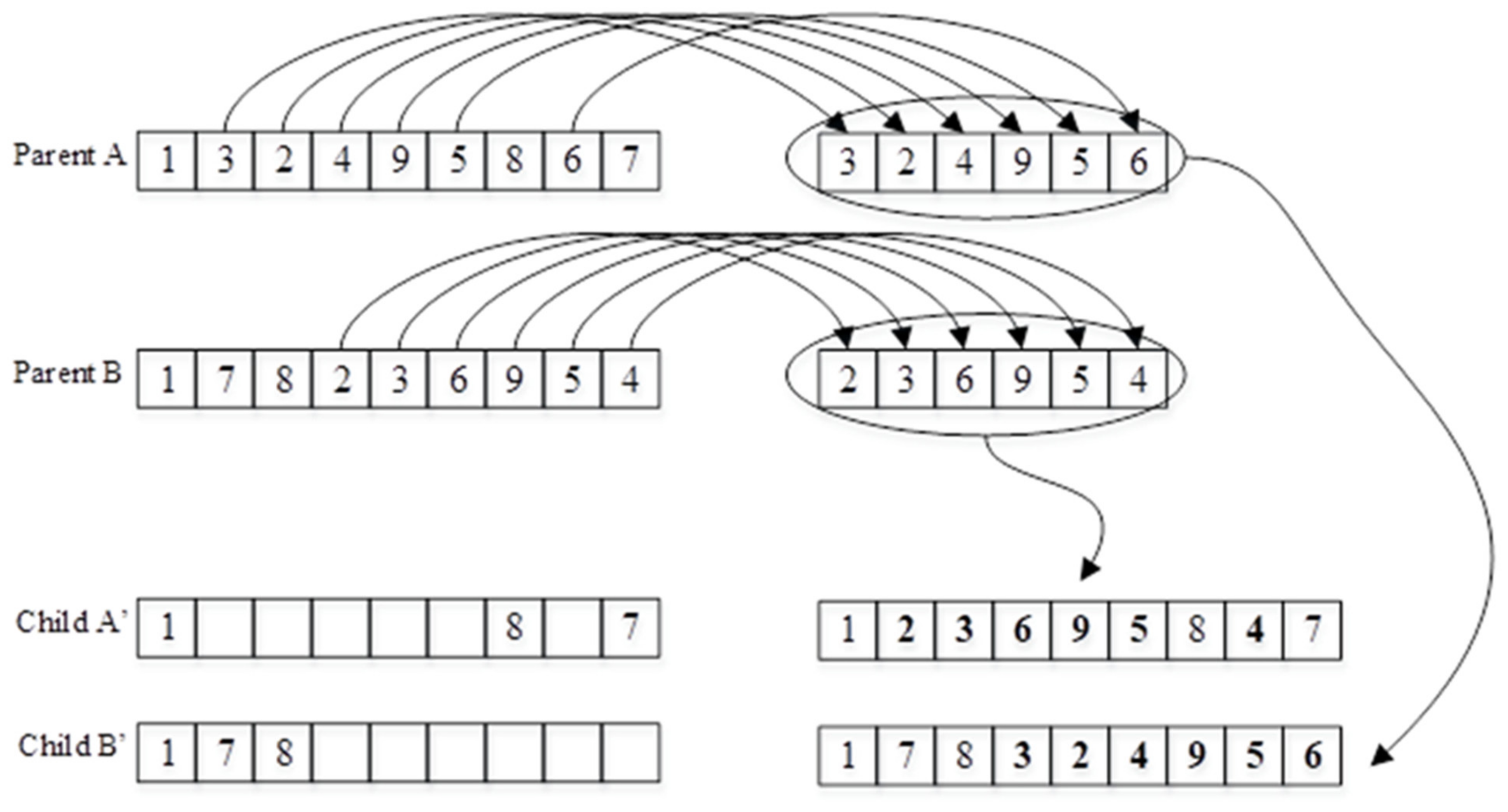
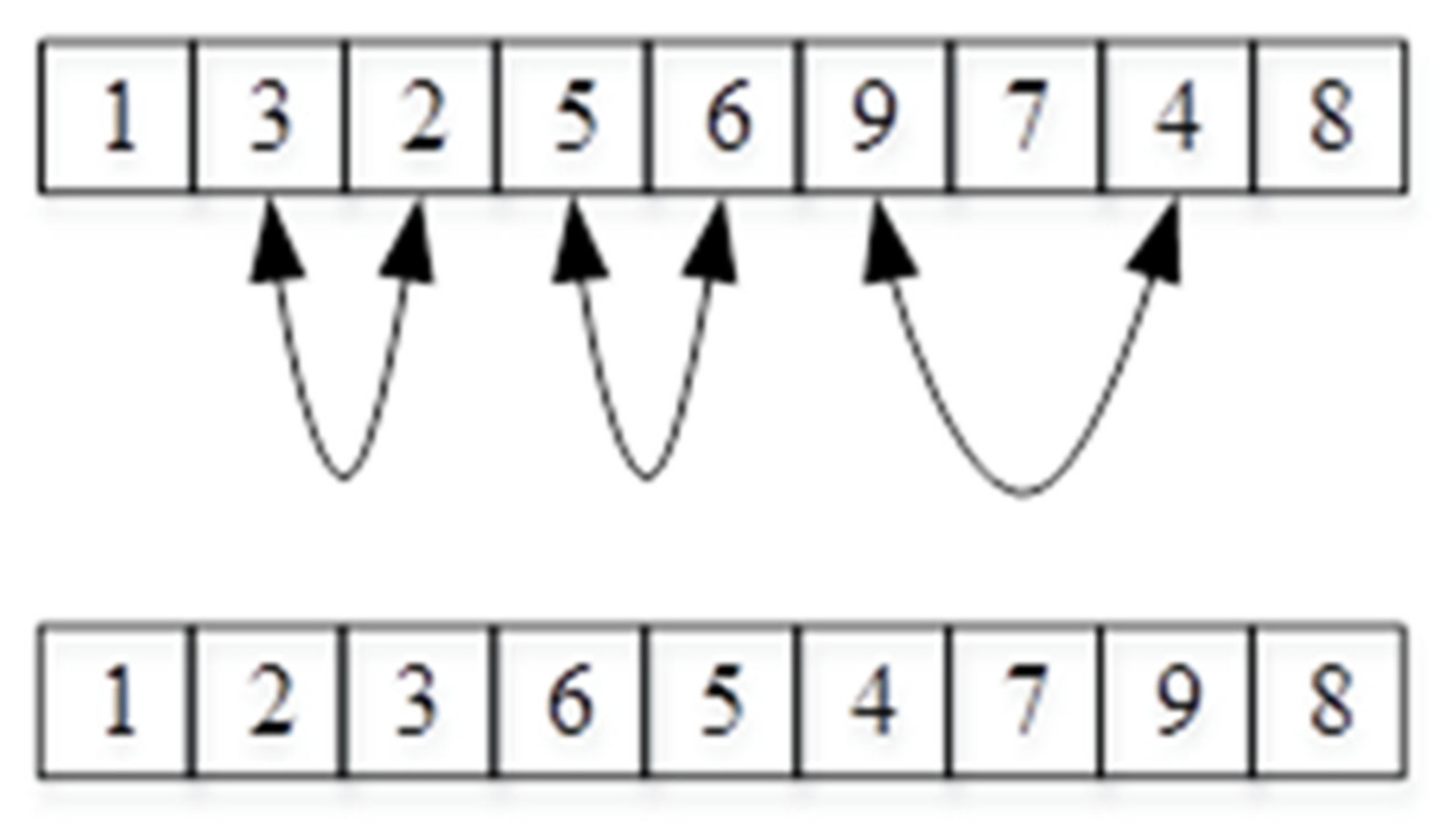
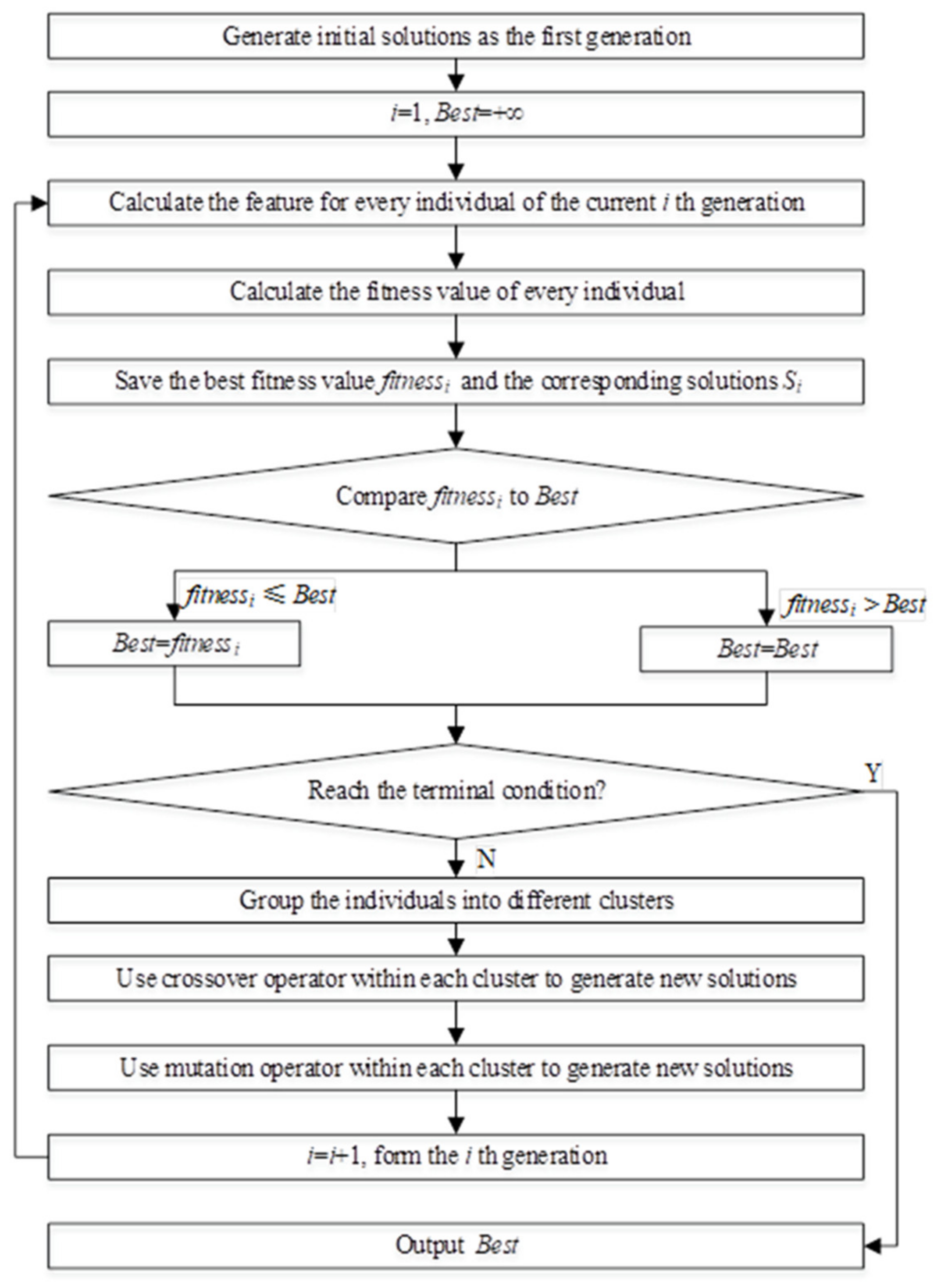
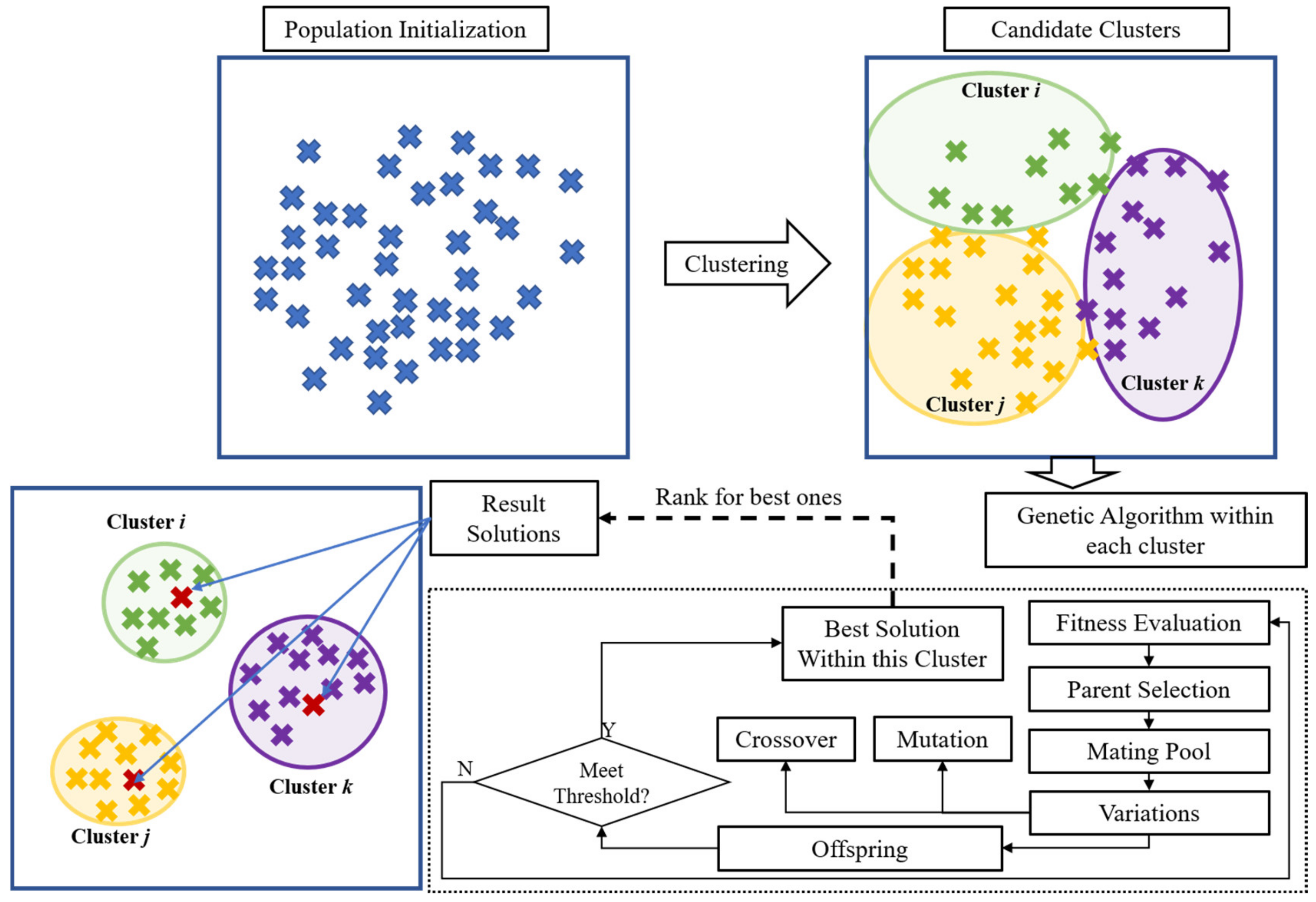
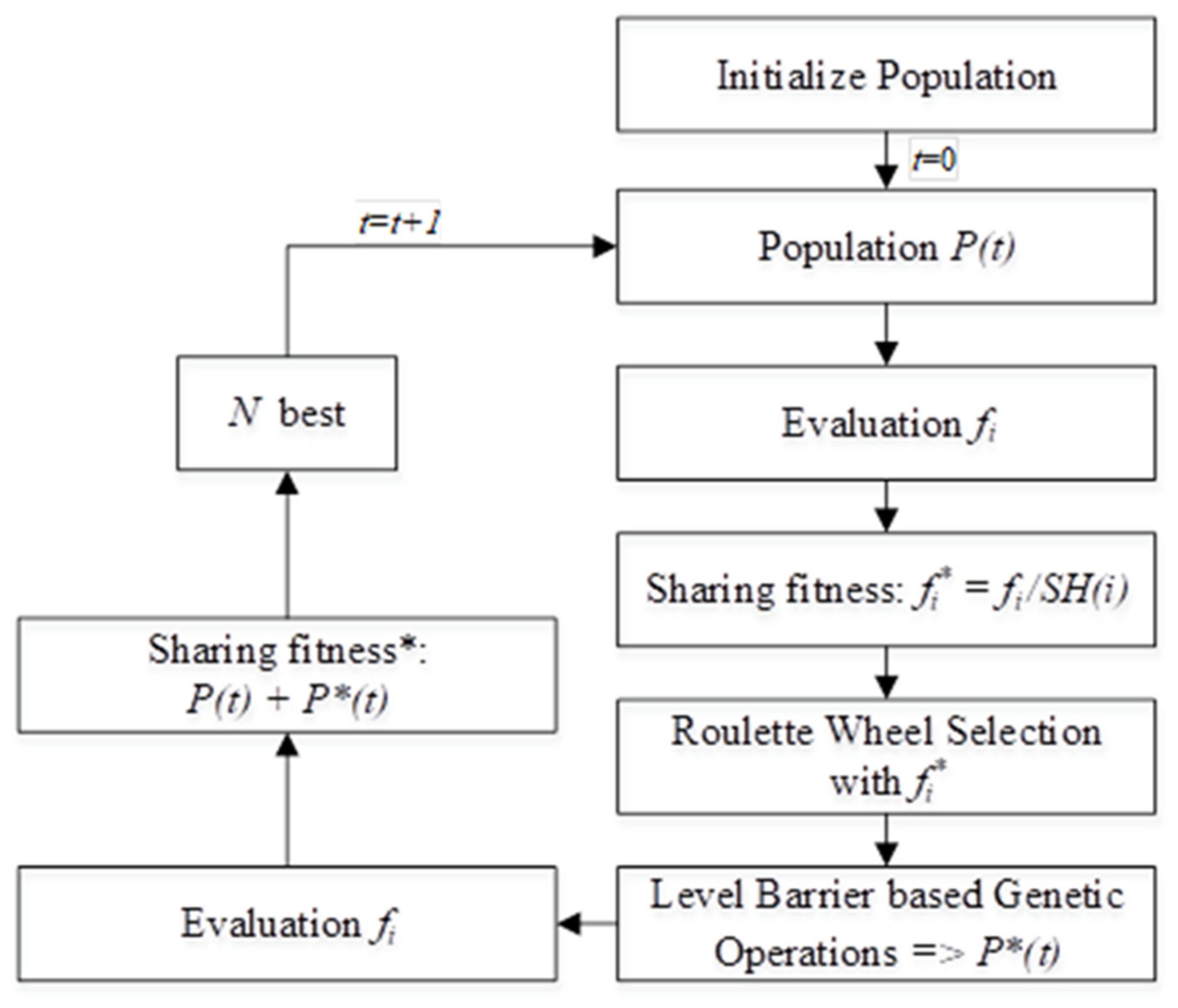
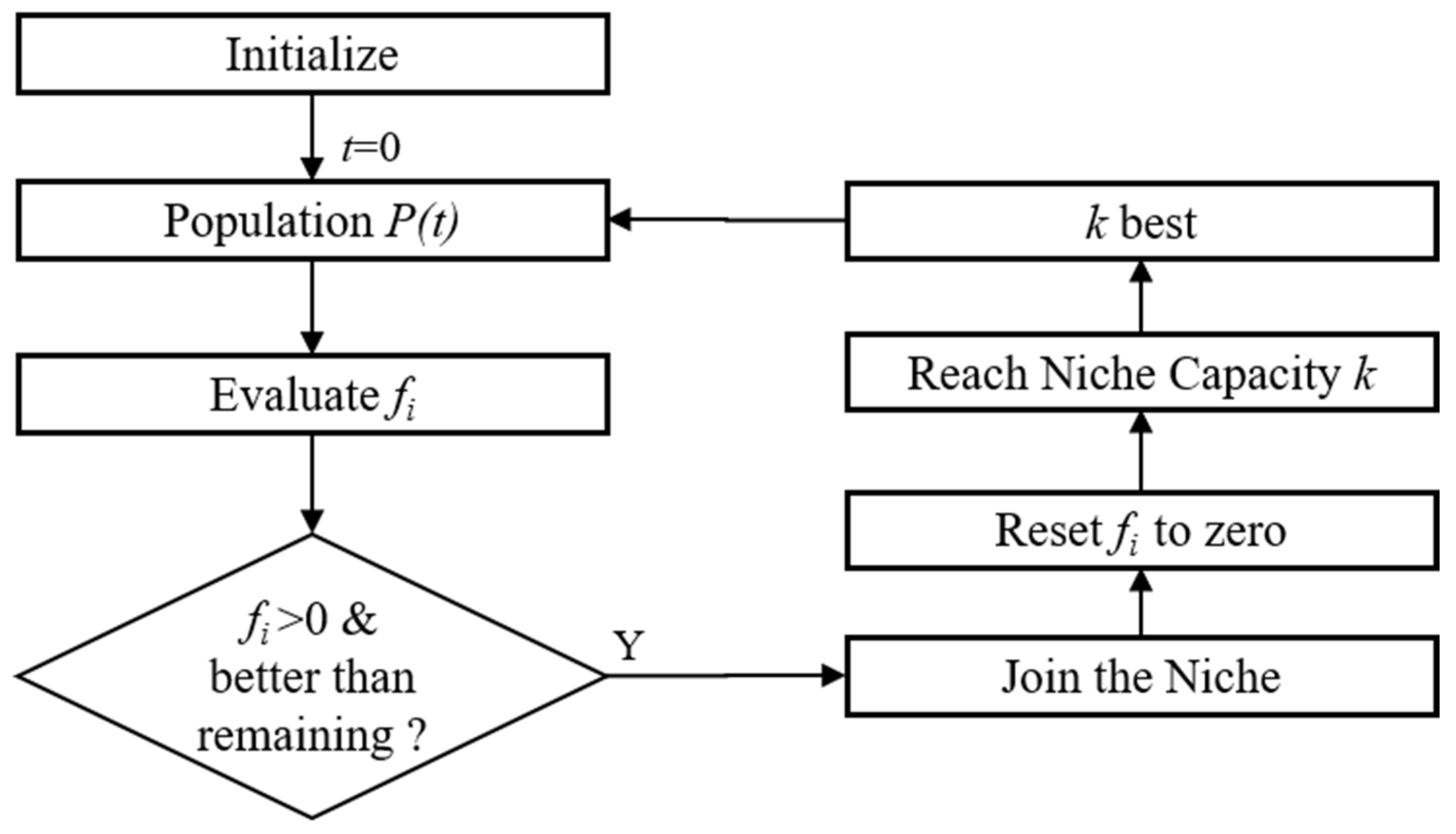
1. Introduction

Scheduling problems such distribution, transportation, management, construction, engineering and manufacturing, are omnipresent in real-world applications [1]. These scheduling problems are complex and very difficult to solve using conventional techniques. The complexity of these scheduling problems arises due to the presence of a large number of constraints. Due to these reasons, there was ample research conducted in the past few decades that focused on developing different techniques for the optimization of these scheduling problems. Permutation flow-shop scheduling problem (PFSSP), a variation of the classical flow-shop scheduling problem (FSSP), is a problem in operation research in which n ideal jobs, J1, J2, …, Jn, of varying processing times are assigned to m resources (usually machines). The objective is to allocate the available resources to the jobs to maximize (or minimize) performance indicators, such as makespan, tardiness, etc. In classical FSSP, for n jobs on m machines, there are (n!)m different alternatives for sequencing jobs on machines, while in permutation problems, the search space is reduced to n!. Like any scheduling problem, there are constraints and assumptions associated with PFSSP. In this paper, these constraints and assumptions are as follows.

(1)

On the shop floor, all machines are independent from each other.

(2)

The operation of all jobs have deterministic processing times.

(3)

No pre-emption of job operation is permitted.

(4)

The set-up times are not considered in these problems.

(5)

No machine down-time or maintenance time is considered.

(6)

The machine used for each operation of a job is known and fixed.

(7)

A job cannot revisit a machine group for more than one operation.

(8)

Operation constraints must always be followed.

(9)

All jobs must enter the machines in the same order.

Since PFSSP are commonly encountered in various industries, researchers developed many methods to optimize the key performance indicators (KPIs) of PFSSP. Liu and Liu [2] used a hybrid discrete artificial bee colony algorithm for minimizing the makespan in PFSSP. They utilized Greedy Randomized Adaptive Search Procedure (GRASP) to create the initial population and operators such as insert, swap, path relinking to generate new solutions. The authors also improved the local search by further optimizing the best solution. When applied to PFFP, their algorithm had superior performance compared to other algorithms like particle sawm optimization (PSO) algorithm, hybrid GA (HGA), etc. Govindan et al. [3] combined decision tree (DT) and scatter search (SS) algorithms to solve PFSSP. DT was used initially to convert the problem into a tree structure using the entropy function, followed by SS, to do an extensive investigation of the solution space. Simulation results and statistical test comparisons showed the advantage of the authors’ proposed algorithm. Ancău [4] proposed two algorithms for solving PFSSP. (1) A constructive greedy heuristic (CG) and (2) stochastic greedy heuristic (SG). The CG was based on a greedy selection, while the SG was a modified version of CG with iterative stochastic start. The authors validated the proposed algorithms by using them to solve benchmark problems, and the results showed that the algorithm was able to come within 6% of the best-known solution. Zobolas et al. [5] created a hybrid algorithm by combining greedy heuristic, GA, and variable neighborhood search (VNS) algorithm. The hybrid algorithm was able to take advantage of both GA and VNS, and obtain the best-known makespan for the benchmark problems in a short computational time.

Zhang et al. [6] proposed an enhanced GA to solve the distributed assembly permutation flow shop scheduling problems (DAPFSP). The authors used a greedy mating pool to select better candidates. They also updated the crossover strategy and incorporated local search strategies to improve local convergence. Andrade et al. [7] minimized the total flowtime of PFFSP by using a Biased Random-Key Genetic Algorithm (BRKGA). Their proposed technique used a shaking strategy to perturb individuals from the elite population, while resetting the remainder of the population. The authors validated their proposed approach by its application to 120 benchmark problems and comparing the results to those obtained by Iterative Greedy Search and Iterated Local Search. The results showed that the proposed approach was more efficient and was able to identify new bounds as well as optimal solutions for the problems. Ruiz et al. [8] used the iterated Greedy (IG) search algorithm to solve the distributed permutation flow shop scheduling problems. The authors improved the initialization, construction, and deconstruction procedures, and improved the local search (ILS) to obtain better results. A big advantage of the proposed technique was that it required very little problem-specific knowledge to be implemented. Pan et al. [9] proposed three constructive heuristics, DLR (inspired by LR heuristic), DNEH (inspired by NEH heuristic), a hybrid DLR-DNEH heuristic, and four metaheuristics—Discrete Artificial Bee Colony (DABC), Scatter Search (SS), ILS, & IG—for minimizing the total flowtime criterion of the distributed permutation flow shop scheduling problem (DPFSP). Both the heuristics and metaheuristic were able to significantly improve upon the existing results in literature. Their results also showed that the trajectory-based metaheuristics were considerably better than the population-based metaheuristics.

Though ample work is done in solving PFSSP, the current techniques only provide a single optimal schedule upon execution. Furthermore, real-life operators and schedulers have preferences that cannot be modeled and added to the fitness function of optimization algorithms. The single optimal schedule found using these techniques might theoretically satisfy the objective function. However, it might not be able to satisfy the aforementioned complexities. Although multimodal optimization provides multiple similar solutions for the same problem under consideration, it cannot handle complex situations such as machine breakdowns, delayed supply chain, etc., without changing the fitness function and constraints. However, having multiple similar solutions for the same problem could make it possible to provide opportunity for the operators to have the flexibility to handle emergency using their experience, while waiting to solve the underlying problem. Therefore, it is important to obtain multiple optimal schedules that satisfy the objective function, i.e., perform multimodal optimization (MMO). Over the years, many different techniques were developed to accomplish MMO, such as niching techniques [10,11,12,13,14,15,16], differential evolutionary strategies [17,18,19,20,21,22,23,24], use of GA [25,26,27,28] etc. However, these techniques were only tested on benchmark mathematical problems. Furthermore, the aim of these techniques was to find both global and local optima, which increases their computational complexity. Additionally, it is possible for local optima to have much worse objective value than global optima, which is undesirable in scheduling problems.

Therefore, in this study, a new algorithm is proposed for the MMO of PFSSP. This is accomplished by using the k-means clustering algorithm with GA. In each iteration of the proposed algorithm, first, solutions are clustered together, using k-means clustering algorithm. Next, the operators of GA are utilized within each cluster to generate solutions for the next generation. Various techniques used by Perez et al. were also modified and utilized for the MMO of PFSSP and the performance of the algorithms was tested on benchmark PFSSP. The rest of the paper is organized as follows. Section 2 presents information about the modified GA operators used in the proposed algorithm to represent a solution and create new solutions during the iterations of the algorithm. Section 3 provides detailed information about the proposed algorithm, the clearing method (CM), and the sharing fitness methods used for the MMO of PFSSP, as well as the features used to cluster the solutions. Section 4 presents information about the benchmark problems used to test the proposed algorithm and presents the results obtained by utilizing various algorithms. Section 5 draws upon conclusions based on the results obtained from the case studies and mentions the future direction of the proposed technique.

2. Modeling of PFSSP

2.1. Encoding Method and Initial Solution Creation

In this study, the optimization objective was to find the sequence of operations on each machine that would lead to a minimization of the makespan. An important task in any optimization problem is to determine the encoding method. Over the years, many different methods were used to encode the solutions of scheduling problems, such as the direct method [29], the binary method [30], the circular method [31], and the permutation with repetition [32] method. As the jobs must be processed in the same order on each machine in PFSSP, a solution is created using permutation encoding for a single machine. The length of the chromosome (solution) can be determined by the size of the problem. For example, for a 9 × 3 problem (9 jobs with 3 operations each) the chromosome length would be 9. An example of permutation for the 9 × 3 problem is shown in Figure 1. According to Figure 1, the order of operations on any machine will be job 3, 1, 2, 9, 5, 4, 6, 8 and 7. By utilizing permutation encoding, only feasible initial solutions would be created, which would reduce the computational cost of the algorithm.

2.2. Adaption of Genetic Operators

In the optimization process, GA operators are utilized to produce the initial population, as well as the population belonging to the next generations. To create only feasible solutions for the iterations of the algorithm, appropriate crossover and mutation operator must be developed. In the crossover operator, half the number of jobs of the problem under consideration were randomly selected and the corresponding genes were switched on in both the parents. An example of the crossover process is shown in Figure 2 for a PFSSP with nine jobs. In the example, jobs 2, 3, 4, 5, 6, and 9 were randomly chosen and the corresponding genes (3,2,4,9,5,6) in Parent A and (2,3,6,9,5,4) in Parent B were switched on. The crossover operator was limited to solutions belonging to the same cluster, in order to preserve some features of the cluster. Similarly, in the mutation operator, half the jobs were randomly chosen and their corresponding location within the solution was switched on. An example of the mutation operator is shown in Figure 3 for a PFSSP with nine jobs. As can be seen from Figure 2 and Figure 3, using the crossover and mutation operator only creates feasible solution.

3. Multimodal Optimization Methodologies

As stated earlier, an algorithm is proposed for the MMO of PFSSP. To accomplish this, the GA is combined with the k-means clustering algorithm, in order to converge to multiple optimal solutions. Additionally, GA is also combined with niching techniques, such as sharing fitness and CM, and the performance of the three algorithms is compared. Sharing fitness and CM were used as these were shown to have good performance when utilized for the MMO of JSSP [33,34]. The steps of the three different algorithms are outlined below.

3.1. Clustering-Optimization Approach

In traditional GA, the elite population survives each generation as they represent the best solution. Majority of the offspring are generated using crossover which has a high probability of selecting individuals with better fitness values. Though these operations ensure that the population would converge towards an optimal solution, they also reduce the diversity of the population significantly. This strategy is applicable when the objective is to obtain a single optimal solution. However, it is severely lacking when multiple optimal or near optimal solutions are required.

To achieve MMO, the diversity of the elite population and the remainder of the population must be maintained throughout the iterations of GA. In the proposed approach, this is achieved by splitting the population of GA in multiple niches, based on similarity and dissimilarities. Since cluster algorithms maximize the distance between different clusters and by assuming that different optimal solutions have high dissimilarity, we can utilize the cluster algorithms to split the search space into different clusters and find multiple optimal solution in each cluster. By limiting crossover and optimization within each niche, we can maintain the high diversity of the population, as we can avoid exposure from other clusters. Finally, to search the solution space more effectively, mutation is performed after every iteration. The basic procedure of the proposed algorithm is given below and is also shown in Figure 4.

• Define the fitness function of the specific case study. In this study, the maximum completion time (makespan) was used as the fitness value.
• Define the parameters for the k-means clustering algorithm (k value) as well as population size, crossover rate, mutation rate, generation limit, and initialize the best solution set.
• Generate the initial population.
• Evaluate the current population, calculate the feature matrix of every solution, and update the best solution set.
• Using the k-means clustering algorithm, divide the current population into k clusters, based on the features calculated in step 4.
• Within each cluster, select elite individuals that would be a part of the next generations population.
• Within each cluster, select individuals for crossover using roulette wheel selection to produce offspring for the next generation.
• Randomly select individuals (based on mutation probability) and mutate them.
• Repeat Steps 4–8 until the generation limit is reached. Output the final population and the best solution set.

To cluster solutions together, a feature matrix must be defined. Typically, in MMO, the distance between two individuals is used as a feature to cluster the solutions together. However, in PFSSP, a distance cannot be defined using the proposed encoding method, therefore, the feature matrix used to cluster the solutions together in the proposed algorithm is defined as the sequence of jobs on a particular machine. For example, the feature matrix for Parent A shown in Figure 2 would be (1,3,2,4,9,5,8,6,7). An example of applying the proposed algorithm is shown in Figure 5. It should be noted that clustering would not improve the algorithm efficiency. However, that is not the top priority in this study. The focus is to obtain multiple and different solutions with the same objective value.

3.2. Sharing Fitness

In the sharing fitness method, the fitness of an individual decreases in accordance with the number of similar individuals in the population. Figure 6 shows the overall flow chart of the sharing fitness method.

After evaluating the individuals of the current population, their shared fitness is calculated according to Equation (1):

$$f_i^{*}=\frac{f_i}{{{\displaystyle \sum }}_{j=1}^{N}Sh\left(d\left(i,j\right)\right)}$$

(1)

where, f_i is the fitness of individual i, and SH(d(i,j)) is the sharing function. Here, the sharing function depends on the distance (d(i,j)) between individuals i and j. The sharing function can be calculated using Equation (2).

$$Sh\left(d\left(i,j\right)\right)=\left\{\begin{array}{c}1-{\left(\frac{d\left(i,j\right)}{{\sigma }_{share}}\right)}^{\alpha }\mathrm{If} d\left(i,j\right)<{\sigma }_{share}\\ 0\hspace{1em}\hspace{1em}\mathrm{Otherwise}\end{array}\right.$$

(2)

where ${\sigma }_{share}$ is the maximum distance of a niche and α is the slope of the sharing fitness function. A value of 1 is most commonly used for the slope, while ${\sigma }_{share}$ depends on the problem under consideration. Next, based on the new fitness $f_i^{*}$, parents are selected for crossover and mutation, using the roulette-wheel selection method. Once offspring are generated using modified crossover and mutation operators, their fitness is evaluated. Next, the fitness of the parents and offspring are updated to $f_i^{**}$ using Equation (3).

$$f_i^{*}=\beta \ast \frac{f_i}{{{\displaystyle \sum }}_{j=1}^{2N}{f}_i}+\left(1-\beta \right)\ast \frac{\frac{1}{2 \ast N \ast SH\left(i\right)}}{\frac{1}{2 \ast N}{{\displaystyle \sum }}_{j=1}^{2N}\frac{1}{SH\left(i\right)}}$$

(3)

where

$$SH\left(i\right)={\displaystyle \sum }_{j=1}^{2N}Sh\left(d\left(i,j\right)\right)$$

(4)

The distance in Equations (1)–(4) is problem dependent and for the sharing fitness and CM, it was defined as the number of operations situated in different places for each machine. For example, the distance between Parents A and B shown in Figure 2 would be 8 (only job 1 is located in the same place for the two solutions). The above definition of distance was used for CM and the sharing fitness method, as it was shown to provide a large number of optimal solutions when used by Perez et al. for the MMO of JSSP.

3.3. Clearing Method

CM is similar to sharing fitness but is based on the concept of limited resources of the environment. CM is applied after evaluating all individuals but before the selection process. In CM, the individuals are ordered according to their fitness, from best to worst. The first individual is called the dominant (and belongs to the first niche) and it is compared with the remaining n−1 individuals. The comparison is done to determine whether the remaining individuals belong to the first niche. Only k individuals from each move forward to the next generation as elite individuals, while the rest of the individuals belonging to that niche have their fitness reset to zero. The above procedure is repeated for individuals whose fitness is greater than zero. A pseudocode of the CM is given below, and a flowchart is given in Figure 7.

Sort P(t)

FOR (i = 1 to N)

IF (f_i > 0)

NicheCapacityi = 1

   FOR (j = i + 1 to N)

   IF (f_j > 0 AND d(i,j)) < σ share

IF (NicheCapacityi < k)

     NicheCapacityi = NicheCapacityi + 1

     ELSE

     f_j = 0

     ENDIF

      ENDIF

    ENDFOR

  ENDIF

ENDFOR

4. Experimental Study and Performance Benchmarking

To measure the performance of the algorithms outlined above, these were used for the MMO of multiple PFSSP. Eighteen benchmark problems from various datasets were taken for experiments. The first nine problems were proposed by Carlier [35], the next eight were proposed by Reeves [36] and the last one was proposed by Heller [37]. To better assess the algorithms, 10 independent simulations were performed for each test problems. The performance of the algorithms used was then measured on the basis of four indicators. (1) The best solution found in the 10 simulations. (2) The mean value and the standard deviation of the optimal solution found for the 10 simulations. (3) The number of times the algorithms converged to the best optimal solution. (4) The average number of best optimal solutions found for the 10 simulations. For indicator number 4, only simulations in which the algorithm converged to the best solution from (1) were taken into consideration i.e., if the algorithm only converged to the best solution in 4 out of 10 simulations, then the average number of optimal solutions found was calculated using those 4 simulations. The parameters used for the three algorithms were determined after numerous simulations and are given in

Table 1. Parameters used for the three algorithms.

	Generations	Population Size	Algorithm Specific Parameters
Proposed Algorithm	1000	200	Number of clusters = 3
Sharing Fitness	1000	200	${\sigma }_{share}$ = 0	$\beta$ = 1
CM	1000	200	${\sigma }_{share}$ = 50	Maximum niche size = 1

. Additionally, the performance of the three algorithms was also compared to the performance of Improved Efficient Genetic Algorithm (IEGA) and the Hybrid IEGA (HIEGA) proposed by Basset et al. [38], when applicable. These algorithms were selected as they showed promising results when used for the optimization of benchmark PFSSPs.

4.1. The Best Solution Found

As mentioned above, 10 independent simulations were ran for each test problem using the three algorithms. The first method used to compare the performance of these algorithms included observing the best solution obtained during 10 simulations. The results obtained by these algorithms were also compared to the best-known solution, as well as the best-known solutions obtained using different algorithms in the available literature. These results are shown in

Table 2. Best optimal solution obtained by the different algorithms.

Problem	Best-Known Solution	Proposed Algorithm	HIEGA	IEGA	Sharing Fitness	CM
Rec-01	1247	1249	1247	1312	1249	1379
Rec-03	1109	1111	1109	1111	1114	1187
Rec-05	1242	1245	1245	1257	1245	1307
Rec-07	1566	1566	1566	1622	1589	1733
Rec-09	1537	1537	1537	1616	1600	1706
Rec-11	1431	1431	1431	1565	1475	1614
Rec-13	1930	1954	1930	2020	1980	2145
Rec-15	1950	1962	1959	2043	2007	2156
Rec-17	1902	1919	1935	2030	1989	2178
Car-01	7038	7038	7038	7038	7038	7038
Car-02	7166	7166	7166	7166	7166	7565
Car-03	7312	7312	7312	7366	7312	7399
Car-04	8003	8003	8003	8003	8003	8410
Car-05	7720	7720	7720	7720	7720	7720
Car-06	8505	8505	8505	8505	8505	8505
Car-07	6590	6590	6590	6590	6590	6590
Car-08	8366	8366	8366	8366	8366	8366
Hel-02	136	137	136	140	139	154

.

According to Table 2, the proposed algorithm, sharing fitness algorithm, and HIEGA were able to find the best-known solutions for all Carlier benchmark problems. IEGA was able to converge to the best-known solution for all Carlier problems besides Car-03, while CM was able to find the best-known solution for Car-01, 05, 06, 07, and 08. For the Reeves problems, the HIEGA had the best performance, as it was able to converge to the best-known solution for 6 out of the 9 problems. The proposed algorithm was able to obtain the best-known solution for Rec-07, Rec-09, and Rec-11, and was able to obtain a better solution than HEIGA for Rec-17. It was also able to converge within 1% of the best-known solution for the remainder of the problems. Sharing fitness, IEGA, and CM were unable to converge to any of the best-known solutions for the Reeves problems and were within 4% and 15% of the best-known solutions. Similarly, only HIEGA converged to the best-known solution of the Heller problem. However, the proposed algorithm was within 0.7% of the best solution, while sharing fitness, IEGA, and CM were unable to do so.

4.2. Mean Value and Standard Deviation of the Optimal Solution

Next, to evaluate the stability of the algorithms, the mean value and the standard deviation of the optimal solution found in the 10 simulations was calculated. Since these were 10 independent simulations, the starting points were randomized in each simulation. These results are shown in

Table 3. Mean value and standard deviation of the optimal solution found after 10 independent simulations using the algorithms.

Problem	Proposed Algorithm	HIEGA	IEGA	Sharing Fitness	CM
Rec-01	1249.00 ± 0.00	1250.33 ± 4.83	1335.26 ± 14.53	1302.30 ± 30.65	1429.40 ± 29.14
Rec-03	1111.00 ± 0.00	1111.40 ± 4.64	1153.93 ± 13.92	1136.4 ± 15.61	1246.50 ± 29.01
Rec-05	1245.00 ± 0.00	1250.00 ± 5.48	1284.93 ± 11.74	1266.20 ± 39.63	1360.90 ± 25.59
Rec-07	1579.00 ± 8.07	1578.00 ± 8.48	1655.17 ± 20.45	1622.20 ± 25.21	1771.20 ± 24.48
Rec-09	1567.70 ± 16.54	1559.70 ± 21.51	1673.93 ± 22.15	1625.40 ± 12.29	1767.60 ± 30.15
Rec-11	1440.80 ± 11.78	1451.40 ± 17.78	1598.47 ± 18.99	1505.2 ± 21.82	1669.00 ± 29.45
Rec-13	1956.90 ± 2.28	1960.23 ± 15.68	2076.93 ± 29.53	2029.50 ± 30.87	2218.70 ± 38.50
Rec-15	1974.30 ± 6.31	1997.36 ± 35.10	2084.50 ± 19.42	2026.80 ± 12.92	2189.30 ± 20.34
Rec-17	1944.30 ± 11.62	1968.90 ± 25.98	2079.47 ± 24.35	2024.60 ± 20.67	2219.13 ± 21.71
Car-01	7038.00 ± 0.00	7038.00 ± 0.00	7038.00 ± 0.00	7038.00 ± 0.00	7468.50 ± 276.02
Car-02	7166.00 ± 0.00	7166.00 ± 0.00	7289.60 ± 94.77	7166.00 ± 0.00	7862.30 ± 163.70
Car-03	7312.00 ± 0.00	7338.30 ± 28.71	7516.17 ± 85.49	7351.40 ± 43.06	7832.50 ± 266.94
Car-04	8803.00 ± 0.00	8803.00 ± 0.00	8012.13 ± 22.40	8813.40 ± 32.89	8468.30 ± 70.84
Car-05	7720.00 ± 0.00	7743.07 ± 33.40	7802.87 ± 49.14	7759.70 ± 38.77	7731.20 ± 16.48
Car-06	8505.00 ± 0.00	8528.83 ± 31.23	8684.50 ± 147.22	8550.50 ± 31.40	8511.50 ± 20.55
Car-07	6590.00 ± 0.00	6591.77 ± 0.00	6602.37 ± 22.42	6600.60 ± 22.37	6590.00 ± 0.00
Car-08	8366.00 ± 0.00	8366.00 ± 0.00	8366.00 ± 0.00	8366.00 ± 0.00	8366.00 ± 0.00
Hel-02	137.00 ± 0.00	136.87 ± 0.72	143.66 ± 1.77	143.00 ± 1.89	155.90 ± 1.45

.

Even though HIEGA had a better performance than the proposed algorithm when converging to the best-known solution, the proposed algorithm was able to consistently converge to a better solution than HEIGA, as indicated by the mean value and standard deviation. For the Reeves problems, the proposed algorithm had a better performance than HEIGA. For 7 out of 9 problems, its average optimal value was much closer to the best-known solution than that of HEIGA, IEGA, sharing fitness, and CM. The standard deviation varied between 0.00 and 16.54 for the proposed algorithm, while it varied between 4.64 and 35.10 for HEIGA, 11.74 and 29.53 for IEGA, 15.61 and 39.63 for sharing fitness and 20.34 and 30.15 for CM. The proposed algorithm had the best results for all Carlier problems, as it always converged to the best-known solution. HEIGA had a 100% convergence rate for 4 out of the 8 problems, sharing fitness had a 100% convergence rate to the best-known solutions of problems 1, 2, and 8, while CM and IEGA had a 100% convergence rate to the best-known solutions for 2 out of 8 problems. Lastly, for Heller, the proposed algorithm consistently converged to within 0.7% of the best-known solution. However, HIEGA converged to a better average. These results show the robustness of the proposed algorithm i.e., its ability to consistently converge to a better optimal solution.

4.3. Number of Times the Algorithm Converged to the Optimal Solution

To ensure that the algorithms could find multiple solutions consistently, the number of simulations in which the algorithm converged to the best-known solution (N_C) was also recorded. Since none of the algorithms converged to majority of the best-known solution for the Reeves problems, the best optimal solution found was used instead. For example, the best-known solution for Rec-01 was 1247, while the best optimal solution found by the algorithms was 1249, therefore, 1249 was used to calculate N_C. The results for N_C are given in

Table 4. Number of simulations in which the algorithms were able to converge to the best optimal solution (N_C).

Problem	Proposed Algorithm	HEIGA	IEGA	Sharing Fitness	CM
Rec-01	2	NA	NA	1	0
Rec-03	8	NA	NA	0	0
Rec-05	1	NA	NA	0	0
Rec-07	10	NA	NA	0	0
Rec-09	10	NA	NA	0	0
Rec-11	4	NA	NA	0	0
Rec-13	1	NA	NA	0	0
Rec-15	2	NA	NA	0	0
Rec-17	1	NA	NA	0	0
Car-01	10	10	10	10	2
Car-02	10	10	NA	10	0
Car-03	10	NA	NA	4	0
Car-04	10	10	NA	9	0
Car-05	10	NA	NA	3	6
Car-06	10	NA	NA	3	9
Car-07	10	0	NA	8	10
Car-08	10	10	10	10	10
Hel-02	10	NA	NA	0	0

. A complete analysis for HEIGA and IEGA could not be done for this metric as these results were not reported by the authors (this is indicated by ‘NA’ in Table 4). However, some inferences could be made based on the results reported. For example, we could assume that both HEIGA and IEGA always converged to the best-known solution for Car-01 and Car-02, as the mean values were equal to the best-known solution and the standard deviations were zero.

Since CM had the worst optimal solution of the three algorithms for the Reeves problems, its N_C’s were 0. Similarly, sharing fitness was unable to find the best optimal solution for all but problem 1, and therefore, its N_C for those problems was 0. The proposed algorithm had the best performance of all algorithms (where results were available). It had a N_C of 10 for problems 7 and 9, 1 for problems 5, 13, and 17, 2 for problems 1 and 15, 4 for problem 11, and 8 for problem 3.

The proposed algorithm had an N_C of 10 for all Carlier problems, indicating that it had a 100% converge rate to the best-known solution for those problems. Sharing fitness also had an N_C of 10 for problems, 1, 2, and 8, and had an N_C of 4, 9, 3, 3, and 8 for the remaining problems. CM had the worst performance as it was unable to converge to the best-known solution for problems 2, 3, and 4. It had an N_C of 2, 6, and 9 for problems 1, 5, and 6, respectively, and had an N_C of 10 for problems 7 and 8. Lastly, for the Heller problem, the proposed algorithm had an N_C of 10 while the other two algorithms had an N_C of 0. These results further solidified the argument that the proposed algorithm had the best performance of the three algorithms, as it was able to consistently converge to the best optimal solution.

4.4. Average Number of Best Optimal Solutions Found

Lastly, the average number of best optimal solutions found for each test problem using the different algorithms was compared. For this index, only simulations that had an N_C greater than 0 were used. For example, since the proposed algorithm had an N_C of two for Rec-01, N_O was calculated using the results of those two simulations. N_O for the different test problems using the different algorithms are given in

Table 5. Average number of best optimal solutions found (N_O) using different algorithms.

Problem	Proposed Algorithm	Sharing Fitness	CM
Rec-01	6.60	18.00	0.00
Rec-03	6.80	0.00	0.00
Rec-05	4.20	0.00	0.00
Rec-07	3.00	0.00	0.00
Rec-09	4.00	0.00	0.00
Rec-11	3.00	0.00	0.00
Rec-13	3.00	0.00	0.00
Rec-15	2.00	0.00	0.00
Rec-17	3.00	0.00	0.00
Car-01	37.90	40.00	58.50
Car-02	30.40	9.89	0.00
Car-03	6.20	1.25	0.00
Car-04	13.5	8.67	0.00
Car-05	1.90	1.00	1.00
Car-06	1.00	1.00	1.00
Car-07	1.00	1.00	1.00
Car-08	1.00	1.00	1.00
Hel-02	6.30	0	0.00

. Since the purpose of HIEGA and IEGA was to only find a single optimal solution, these were excluded for the purpose of this metric.

Like the previous three indicators, the proposed algorithm had a significantly better performance than the sharing fitness and CM. Though the sharing fitness found 18 solutions for Rec-01, it was unable to find multiple best optimal solutions for rest of the Reeves problems. The proposed algorithm was able to find 2–6.8 best optimal solutions for all Reeves. CM was unable to find multiple best optimal solutions for any of the Reeves problems, as it never converged to the best optimal solution.

Thought both CM and sharing fitness found more optimal solutions compared to the proposed algorithm for Car-01, their performance was worse for problems 2, 3, 4, and 5. The proposed algorithm found 30.40, 6.20, 13.50, and 1.90 different best-known solutions on average for those problems, while sharing fitness only obtained 9.89, 1.25, 8.67, and 1.00 and the CM obtained 0.00 for all. All algorithms were only able to find 1.00 different optimal solutions for problems 6–8, indicating that the global optimal solution is a unique one. Lastly, for the Heller problem, the proposed algorithm again had the best performance, as it was able to obtain 6.30 different optimal solutions on average, while both sharing fitness and CM obtained 0.00. These results indicate that the proposed algorithm was able to consistently converge to the best optimal solution for all test problems, while finding multiple best optimal solutions.

An attempt was also made to combine the proposed algorithm with sharing fitness, to take advantage of both algorithms, i.e., the ability of the proposed algorithm to consistently converge to the best optimal solution and the ability of sharing fitness to find multiple best optimal solutions. The above task was accomplished by calculating the distance used in the sharing fitness method using the feature matrix of the proposed method. This distance could be calculated using Equation (5).

$$d\left(i,j\right) = \Vert F_i-F_j\Vert$$

(5)

where F_i is the feature matrix of individual i and F_j is the feature matrix of individual j. For the hybrid algorithm, the value of ${\sigma }_{share}$ was changed to 10. The performance of the hybrid algorithm was then compared to the performances of sharing fitness. The proposed algorithm and the results for the four indicators are given in

Table 6. Comparison of the best optimal solution found using the new hybrid algorithm and the previous three algorithms.

Problem	Best Optimal Solution Found Using the New Hybrid Algorithm	Best Optimal Solution Found Using Previous Three Algorithms
Rec-01	1280	1249
Rec-03	1124	1111
Rec-05	1249	1245
Rec-07	1584	1566
Rec-09	1590	1537
Rec-11	1457	1431
Rec-13	2003	1954
Rec-15	2012	1962
Rec-17	2008	1919
Car-01	7038	7038
Car-02	7166	7166
Car-03	7312	7312
Car-04	8803	8803
Car-05	7720	7720
Car-06	8505	8505
Car-07	6590	6590
Car-08	8366	8366
Hel-02	139	137

,

Table 7. Comparison of the mean value and standard deviation of the optimal solutions found using the new hybrid algorithm and from the previous three algorithms.

Problem	Best Mean Value and Standard Deviation of the Optimal Solution Found Using the New Hybrid Algorithm	Best Mean Value and Standard Deviation of the Optimal Solution Found Using the Previous Three Algorithms
Rec-01	1310.60 ± 17.66	1249.00 ± 0.00
Rec-03	1139.80 ± 13.10	1111.00 ± 0.00
Rec-05	1269.60 ± 11.28	1245.00 ± 0.00
Rec-07	1623.90 ± 29.44	1579.00 ± 8.07
Rec-09	1617.70 ± 18.60	1567.70 ± 16.54
Rec-11	1457.20 ± 17.76	1440.80 ± 11.78
Rec-13	2042.20 ± 21.90	1956.90 ± 2.28
Rec-15	2047.60 ± 30.31	1974.30 ± 6.31
Rec-17	2028.00 ± 13.72	1944.30 ± 11.62
Car-01	7038.00 ± 0.00	7038.00 ± 0.00
Car-02	7187.00 ± 66.41	7166.00 ± 0.00
Car-03	7382.10 ± 27.89	7312.00 ± 0.00
Car-04	8803.00 ± 0.00	8803.00 ± 0.00
Car-05	7745.70 ± 18.37	7720.00 ± 0.00
Car-06	8561.20 ± 71.27	8505.00 ± 0.00
Car-07	6605.90 ± 25.60	6590.00 ± 0.00
Car-08	8366.00 ± 0.00	8366.00 ± 0.00
Hel-02	143.10 ± 1.66	137.00 ± 0.00

,

Table 8. Comparison of the N_c found using the new hybrid algorithm and the previous three algorithms.

Problem	NC Obtained Using the New Hybrid Algorithm	Best NC Obtained Using the Previous Three Algorithms
Rec-01	0	2
Rec-03	0	8
Rec-05	0	1
Rec-07	0	10
Rec-09	0	10
Rec-11	0	10
Rec-13	0	1
Rec-15	0	2
Rec-17	0	1
Car-01	10	10
Car-02	9	10
Car-03	1	10
Car-04	10	10
Car-05	2	10
Car-06	4	10
Car-07	7	10
Car-08	10	10
Hel-02	0	10

and

Table 9. Comparison of the N_O using the new hybrid algorithm and the previous three algorithms.

Problem	NO Obtained Using the New Hybrid Algorithm	Best NO Obtained Using the Previous Three Algorithms
Rec-01	0.00	18.00
Rec-03	0.00	4.20
Rec-05	0.00	3.00
Rec-07	0.00	4.00
Rec-09	0.00	3.00
Rec-11	0.00	3.00
Rec-13	0.00	2.00
Rec-15	0.00	3.00
Rec-17	0.00	6.80
Car-01	33.80	58.50
Car-02	17.11	30.40
Car-03	1.00	6.20
Car-04	12.20	13.5
Car-05	1.00	1.90
Car-06	1.00	1.00
Car-07	1.00	1.00
Car-08	1.00	1.00
Hel-02	0.00	6.30

.

As can be seen from the results above, the new hybrid algorithm was able to achieve the same best optimal makespan for the Carlier problems but not for the Reeves and Heller problems. In terms of the mean value and standard deviation of the optimal solution found, the new hybrid algorithm had a similar performance to the proposed algorithm for the Carlier problems 1, 4, and 8, while it had a higher mean value and standard deviation for rest of the benchmark problems. When comparing N_c, the new hybrid algorithm was able to converge to the best optimal solutions in all 10 simulations for Carlier problems 1, 4, and 8, but was unable to achieve similar results for the remaining problems. In terms of N_O, the new hybrid algorithm was unable to obtain more optimal solutions for any benchmark problem. These results indicate that the new hybrid algorithm did not have a superior performance compared to sharing fitness or the proposed algorithm. The reason that the proposed algorithm was able to achieve better performance than sharing fitness, CM, and the hybrid algorithm, was its utilization of a feature vector to separate the individuals into different clusters rather than a single value.

In this section, the performance of the three algorithms was measured by their application to 18 benchmark PFSSP. Four indicators were used to measure the performance—(1) best optimal found, (2) mean value and standard deviation of the optimal solution found in 10 simulations, (3) number of simulations in which the algorithm converged to the best optimal solution, and (4) average number of best optimal solution found. The results indicated that the proposed algorithm had a better performance than the sharing fitness and CM, and also a hybrid algorithm created by combining the proposed algorithm and sharing fitness.

5. Conclusions

In this study, a new algorithm is proposed for the MMO of PFSSP, i.e., provide multiple solutions with the same objective value. The proposed algorithm utilizes GA for the optimization procedure with the k-means clustering algorithm being used to cluster the individuals of each generation. Unlike standard GA, where all individuals belong to the same cluster, the individuals in the proposed approach were split into multiple clusters and crossover operator is restricted to individuals belonging to the same cluster. Doing so enabled the possibility of the proposed algorithm to find multiple global optima in each cluster. Sharing fitness and CM utilized by Perez et al. for the MMO of JSSP were also modified and used for the MMO of PFSSP. The performance of the three algorithms was tested on various benchmark PFSSP and the results indicated that the proposed algorithm had a better performance than CM and sharing fitness, in terms of its ability to find the best-known optimal solution, consistently provide a better optimal solution, and converge to multiple optimal solutions.

As the sharing fitness method had a better performance on a few problems in terms of finding more optimal solutions, an attempt was made to combine the sharing fitness method with the proposed algorithm. This was done by using the feature matrix of the proposed algorithm in the sharing fitness method. When applied for MMO of benchmark PFSSP, the new hybrid algorithm was unable to outperform or equal the proposed algorithm.

Though the proposed algorithm had the best performance of the algorithms tested, further research needs to be performed in the following areas:

• Introduction of more rigorous similarity measure metrics for a more efficient clustering.
• Comparison of the performance of the proposed approach to algorithms specifically developed for optimization of PFSSP.
• Embedding the proposed approach in algorithms specifically developed for optimization of PFSSP and use it to achieve the MMO of PFFSP.
• Applying the proposed approach to real-life operational environment, testing the robustness of the proposed algorithms and its parameters, and measuring its performance under different criteria.