EPTlib: An Open-Source Extensible Collection of Electric Properties Tomography Techniques
Abstract
Featured Application
Abstract
1. Introduction
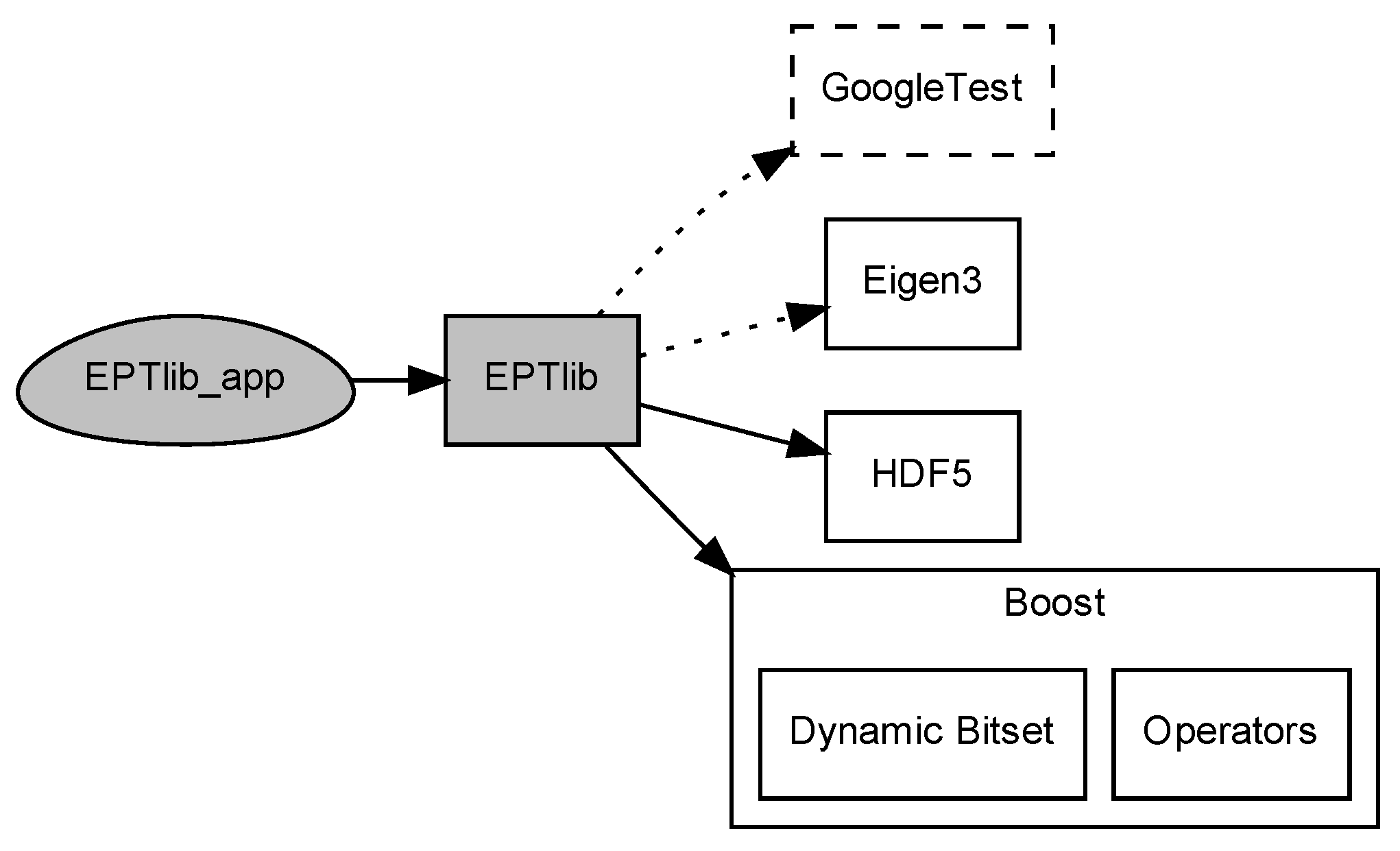
2. Software Architecture
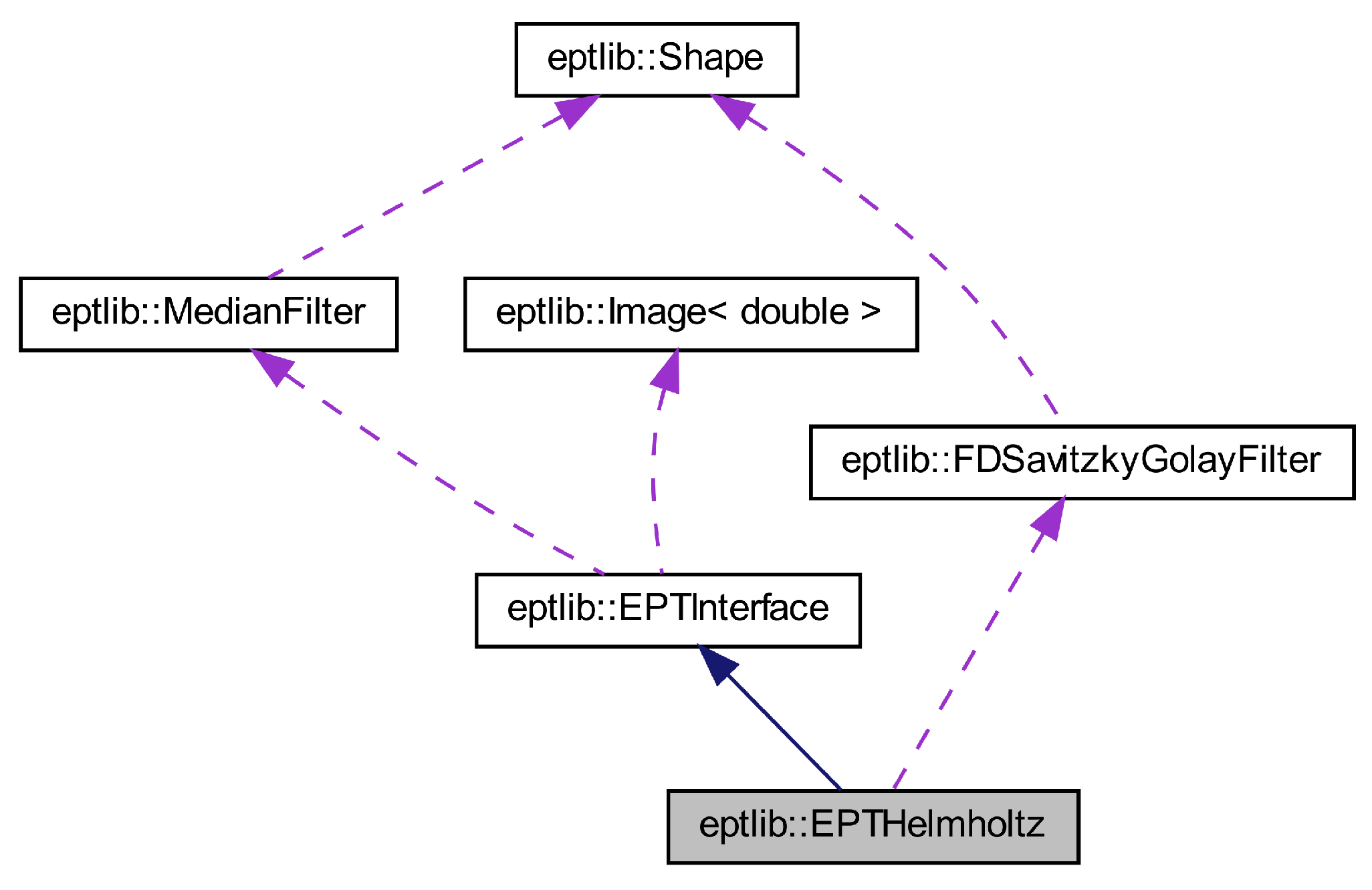
2.1. Library
2.2. Terminal Application
| Configuration File 1 Common settings for EPTlib_app |
|
- title and description provide a brief description of the case study.
- method is an integer value that selects the EPT technique to use according to the following list: 0 for Helmholtz-EPT, 1 for convection-reaction-EPT and 2 for gradient-EPT.
- size is the number of voxels of the input data in the three dimensions.
- step is the length in meters of the voxels in the three dimensions.
- frequency is the Larmor frequency in hertz of the input data.
- tx-channels and rx-channels are the number of Tx and Rx channels in the input data, respectively. They must assume values in certain ranges depending on the adopted EPT technique.
- tx-sensitivity and trx-phase are the addresses of the Tx sensitivity and the TRx phase datasets in suitable HDF5 files. The address is provided as a string in which the HDF5 file address is separated from the internal dataset identifier by a colon. Moreover, in case of multiple Tx channels, the wildcard character ’>’ can be used to distinguish the data from each channel. It will be replaced by an increasing integer number from zero up to the number of Tx channels minus one. Similarly, the wildcard character ’<’ is used for multiple Rx channels. Thus, the string “in.h5:/trx_phase><” denotes the datasets “/trx_phase00”, “/trx_phase10”, “/trx_phase01”, “/trx_phase11”, “/trx_phase02” and so on in the file “in.h5”.
- wrapped-phase is true if the input TRx phase maps are wrapped. This setting is optional and false by default.
- tx-character and rx-character are the above-mentioned wildcard character. By default ’>’ and ’<’, respectively.
- start-from is the integer number from which the wildcard character replacement starts. By default 0.
- step is the integer step in the wildcard character replacement. By default it is 1.
- electric-conductivity and relative-permittivity are the addresses of the datasets in HDF5 files in which the electric conductivity and the relative permittivity estimated by the EPT technique will be stored, respectively. The address is provided as a string in which the HDF5 file address is separated from the internal dataset identifier by a colon. Thus, the string “out.h5:/sigma” denotes the dataset “/sigma” in the file “out.h5”.
3. EPT Techniques
3.1. Helmholtz-EPT
| Configuration File 2 Helmholtz-EPT specific settings for EPTlib_app |
|
3.2. Convection-Reaction-EPT
| Configuration File 3 Convection-reaction-EPT specific settings for EPTlib_app |
|
- electric-conductivity is the electric conductivity in siemens per meter forced at the domain boundary. By default 0. It is worth noting that this condition is used also by the phase-based approximated convection-reaction-EPT (22), in which case the assigned value must be different from zero in order to allow the correct definition of the resistivity .
- relative-permittivity is the relative permittivity forced at the domain boundary. By default 1.
- volume-tomography is false if the two-dimensional approximation is selected. By default false.
- imaging-slice is the index of the slice selected for the two-dimensional tomography. This setting is ignored if volume-tomography is true. The mid-plane of the input data is selected by default. If the number of slices is even, then the lower of the two planes in the middle is selected by default.
- artificial-diffusion is true if the artificial diffusion regularization is adopted. By default false.
- artificial-diffusion-coefficient is the value of the artificial diffusion coefficient . This setting is ignored if artificial-diffusion is false. By default 0.
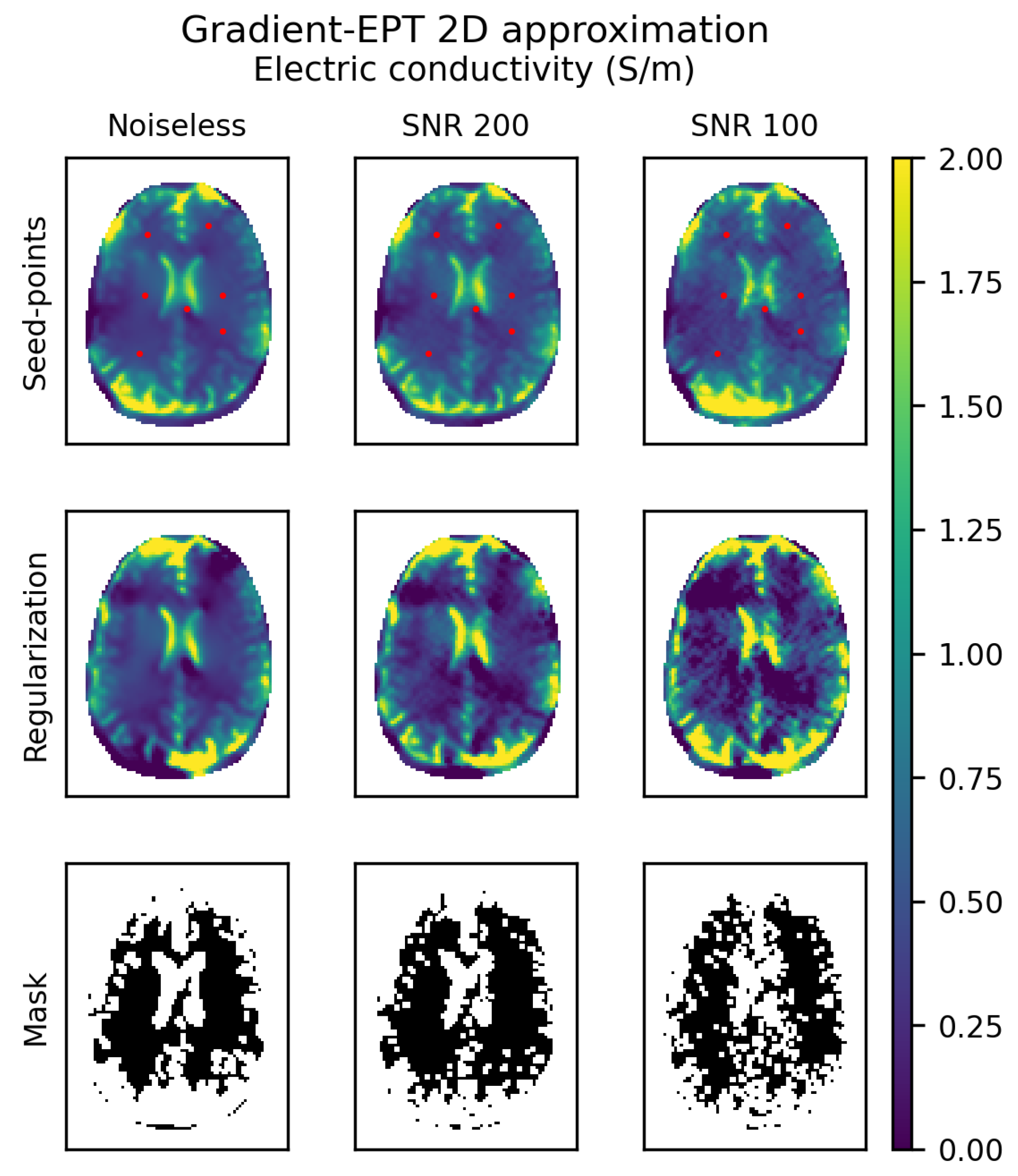
3.3. Gradient-EPT
| Configuration File 4 Gradient-EPT specific settings for EPTlib_app |
|
- use-seed-point is true if the seed point constraint is selected. By default false.
- coordinates is the list of the integer coordinates of the seed points in the mesh of voxels (index 0 is used for the first voxel). This setting is mandatory if use-seed-point is true, otherwise it is ignored.
- electric-conductivity is the list of the electric conductivity in siemens per meter forced in each seed point. This setting is mandatory if use-seed-point is true, otherwise it is ignored.
- relative-permittivity is the list of the relative permittivity forced in each seed point. This setting is mandatory if use-seed-point is true, otherwise it is ignored.
- regularization-coefficient is the value of the regularization coefficient . By default 1.
- gradient-tolerance is the value of the tolerance k for determining the sub-domain . By default 0.
- output-mask is the address of the dataset in HDF5 file in which the characteristic function of will be stored. The address is provided as a string in which the HDF5 file address is separated from the internal dataset identifier by a colon. Thus, the string “out.h5:/mask” denotes the dataset “/mask” in the file “out.h5”. If this setting is omitted, the data will not be stored.
- volume-tomography is false if the two-dimensional approximation is selected. By default false.
- imaging-slice is the index of the slice selected for the two-dimensional tomography. This setting is ignored if volume-tomography is true. The mid-plane of the input data is selected by default.
- full-run is false if the execution must stop after the local step. By default true.
3.4. Summary of the Implemented Techniques
- Helmholtz-EPT assumes that the EPs are locally homogeneous, leading to large systematic errors at the tissue boundaries.
- The complete versions of both Helmholtz-EPT and convection-reaction-EPT estimate the Tx phase as half of the measurable TRx phase . This is a reasonable estimation when the same RF coil is used both in transmission and in reception with a polarization switch [5], or when special care is taken in the phase acquisition, like for example adopting a CLEAR reconstruction [46].
- Both convection-reaction-EPT and gradient-EPT assume that the longitudinal component of has a negligible gradient. This assumption limits the applicability of these techniques around the mid-plane of longitudinally symmetric sources, which are usually adopted for volume coils.
- Gradient-EPT requires acquisitions performed with a pTx system with at least five Tx channels. Currently, this kind of equipment is mainly employed in the research of ultra high field scanners.
4. Examples of Application
4.1. Body-Coil
4.1.1. Helmholtz-EPT
4.1.2. Convection-Reaction-EPT
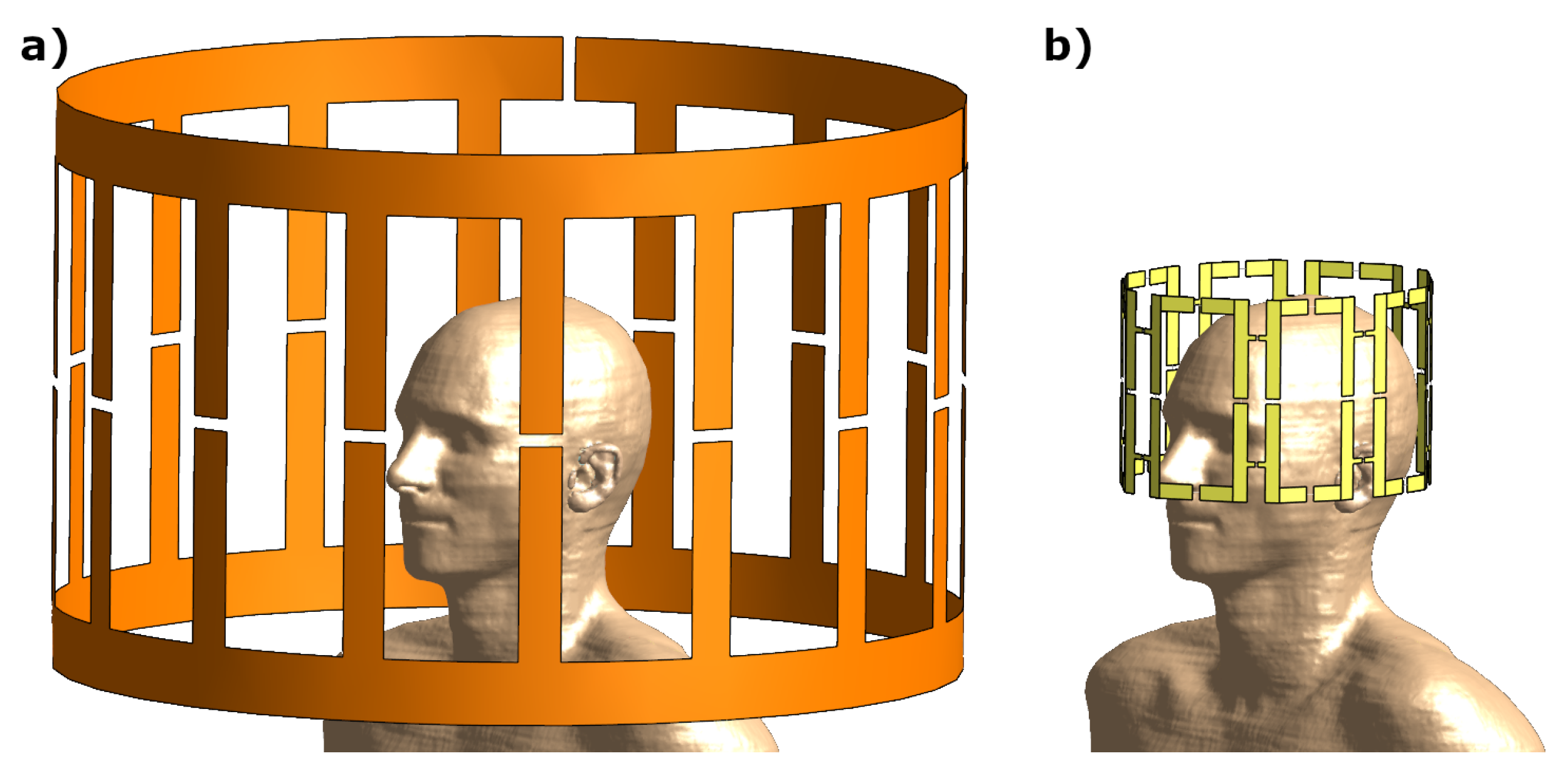
4.2. 7 8-Channel Head-Coil
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, D.; Gulani, V.; Seiberlich, N.; Liu, K.; Sunshine, J.L.; Duerk, J.L.; Griswold, M.A. Magnetic resonance fingerprinting. Nature 2013, 495, 187–192. [Google Scholar] [CrossRef]
- Venkatesh, S.K.; Yin, M.; Ehman, R.L. Magnetic resonance elastography of liver: Technique, analysis, and clinical applications. J. Magn. Reson. Imaging 2013, 37, 544–555. [Google Scholar] [CrossRef]
- Hiscox, L.V.; Johnson, C.L.; Barnhill, E.; McGarry, M.D.J.; Huston, J.; Van Beek, E.J.R.; Starr, J.M.; Roberts, N. Magnetic resonance elastrography (MRE) of the human brain: Technique, findings and clinical applications. Phys. Med. Biol. 2016, 61, R401–R437. [Google Scholar] [CrossRef]
- Haacke, E.M.; Petropoulos, L.S.; Nilges, E.W.; Wu, D.H. Extraction of conductivity and permittivity using magnetic resonance imaging. Phys. Med. Biol. 1991, 36, 723–734. [Google Scholar] [CrossRef]
- Katscher, U.; Kim, D.-H.; Seo, J.K. Recent progress and future challenges in MR electric properties tomography. Comput. Math. Methods Med. 2013, 2013, 546562. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Katscher, U.; He, B. Electrical properties tomography based on B1 maps in MRI: Principles, applications, and challenges. IEEE Trans. Biomed. Eng. 2017, 64, 2515–2530. [Google Scholar] [CrossRef]
- Leijsen, R.; Brink, W.; van den Berg, C.A.T.; Webb, A.; Remis, R. Electrical properties tomography: A methodological review. Diagnostics 2021, 11, 176. [Google Scholar] [CrossRef]
- Kim, S.Y.; Shin, J.; Kim, D.H.; Kim, M.J.; Kim, E.-K.; Moon, H.J.; Yoon, J.H. Correlation between conductivity and prognostic factors in invasive breast cancer using magnetic resonance electric properties tomography (MREPT). Eur. Radiol. 2016, 26, 2317–2326. [Google Scholar] [CrossRef]
- Tha, K.K.; Katscher, U.; Yamaguchi, S.; Stehning, C.; Teresaka, S.; Fujima, N.; Kudo, K.; Kazumata, K.; Yamamoto, T.; van Cauteren, M.; et al. Noninvasive electrical conductivity measurement by MRI: A test of its validity and the electrical conductivity characteristics of glioma. Eur. Radiol. 2018, 28, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Balidemaj, E.; Kok, H.P.; Schooneveldt, G.; van Lier, A.L.H.M.W.; Remis, R.F.; Stalpers, L.J.A.; Westerveld, H.; Nederveen, A.J.; van den Berg, C.A.T.; Crezee, J. Hyperthermia treatment planning for cervical cancer patients based on electrical conductivity tissue properties acquired in vivo with EPT at 3 T MRI. Int. J. Hyperth. 2016, 32, 558–568. [Google Scholar] [CrossRef]
- Gavazzi, S.; van Lier, A.L.H.M.W.; Zachiu, C.; Jansen, E.; Lagendijk, J.J.W.; Stalpers, L.J.A.; Crezee, H.; Kok, H.P. Advanced patient-specific hyperthermia treatment planning. Int. J. Hyperth. 2020, 37, 992–1007. [Google Scholar] [CrossRef] [PubMed]
- Michel, E.; Hernandez, D.; Lee, S.Y. Electrical conductivity and permittivity maps of brain tissues derived from water content based on T1-weighted acquisition. Magn. Reson. Med. 2017, 77, 1094–1103. [Google Scholar] [CrossRef]
- Han, J.; Gao, Y.; Nan, X.; Liu, F.; Xin, S.X. Statistical analysis of the accuracy of water content-based electrical properties tomography. NMR Biomed. 2020, 33, 4273. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Gao, Y.; Nan, X.; Yu, X.; Liu, F.; Xin, S.X. Effect of radiofrequency inhomogeneity on water-content based electrical properties tomography and its correction by flip angle maps. Magn. Reson. Imaging 2021, 78, 25–34. [Google Scholar] [CrossRef]
- Yarnykh, V.L. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 2007, 57, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Sacolick, L.I.; Wiesinger, F.; Hancu, I.; Vogel, M. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 2010, 63, 1315–1322. [Google Scholar] [CrossRef]
- Katscher, U.; Voigt, T.; Findeklee, C.; Vernickel, P.; Nehrke, K.; Doessel, O. Determination of electric conductivity and local SAR via B1 mapping. IEEE Trans. Med. Imaging 2009, 28, 1365–1374. [Google Scholar] [CrossRef]
- Voigt, T.; Katscher, U.; Doessel, O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn. Reson. Med. 2011, 66, 456–466. [Google Scholar] [CrossRef]
- Hafalir, F.S.; Oran, O.F.; Gurler, N.; Ider, Y.Z. Convection-reaction equation based magnetic resonance electrical properties tomography (cr-MREPT). IEEE Trans. Med. Imaging 2014, 33, 777–793. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, X.; Schmitter, S.; van de Moortele, P.-F.; He, B. Gradient-based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn. Reson. Med. 2015, 74, 634–646. [Google Scholar] [CrossRef]
- Lee, S.-K.; Bulumulla, S.; Wiesinger, F.; Sacolick, L.; Sun, W.; Hancu, I. Tissue electrical property mapping from zero echo-time magnetic resonance imaging. IEEE Trans. Med. Imaging 2015, 34, 541–550. [Google Scholar] [CrossRef]
- Schmidt, R.; Webb, A. A new approach for electrical properties estimation using a global integral equation and improvements using high permittivity materials. J. Magn. Reson. 2016, 262, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Gurler, N.; Ider, Y.Z. Gradient-based electrical conductivity imaging using MR phase. Magn. Reson. Med. 2017, 77, 137–150. [Google Scholar] [CrossRef]
- Balidemaj, E.; van den Berg, C.A.T.; Trinks, J.; van Lier, A.L.H.M.W.; Nederveen, A.J.; Stalpers, L.J.A.; Crezee, H.; Remis, R.F. CSI-EPT: A contrast source inversion approach for improved MRI-based electric properties tomography. IEEE Trans. Med. Imaging 2015, 34, 1788–1796. [Google Scholar] [CrossRef]
- Ropella, K.M.; Noll, D.C. A regularized, model-based approach to phase-based conductivity mapping using MRI. Magn. Reson. Med. 2017, 78, 2011–2021. [Google Scholar] [CrossRef]
- Hong, R.; Li, S.; Zhang, J.; Zhang, Y.; Liu, N.; Yu, Z.; Liu, Q.H. 3-D MRI-based electrical properties tomography using the volume integral equation method. IEEE Trans. Microw. Theory Tech. 2017, 65, 4802–4811. [Google Scholar] [CrossRef]
- Rahimov, A.; Litman, A.; Ferrand, G. MRI-based electric properties tomography with a quasi-Newton approach. Inverse Probl. 2017, 33, 105004. [Google Scholar] [CrossRef]
- Arduino, A.; Bottauscio, O.; Chiampi, M.; Zilberti, L. Magnetic resonance-based imaging of human electric properties with phaseless contrast source inversion. Inverse Probl. 2018, 34, 084002. [Google Scholar] [CrossRef]
- Serrallés, J.E.C.; Giannakopoulos, I.I.; Zhang, B.; Ianniello, C.; Cloos, M.A.; Polimeridis, A.G.; White, J.K.; Sodickson, D.K.; Daniel, L.; Lattanzi, R. Non-invasive estimation of electrical properties from magnetic resonance measurements via global maxwell tomography and match regularization. IEEE Trans. Biomed. Eng. 2020, 67, 3–15. [Google Scholar] [CrossRef]
- Mandija, S.; Meliadò, E.F.; Huttinga, N.R.F.; Luijten, P.R.; van den Berg, C.A.T. Opening a new window on MR-based electrical properties tomography with deep learning. Sci. Rep. 2019, 9, 8895. [Google Scholar] [CrossRef]
- Gavazzi, S.; den Berg, C.A.T.; Savenije, M.H.F.; Kok, H.P.; Boer, P.; Stalpers, L.J.A.; Lagendijk, J.J.W.; Crezee, H.; Lier, A.L.H.M.W. Deep learning-based reconstruction of in vivo pelvis conductivity with a 3D patch-based convolutional neural network trained on simulated MR data. Magn. Reson. Med. 2020, 84, 2772–2787. [Google Scholar] [CrossRef] [PubMed]
- Adler, A.; Lionheart, W.R.B. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, S25–S42. [Google Scholar] [CrossRef]
- Borcea, L. Electrical impedance tomography. Inverse Probl. 2002, 18, R99–R136. [Google Scholar] [CrossRef]
- Sajib, S.Z.K.; Katoch, N.; Kim, H.J.; Kwon, O.I.; Woo, E.J. Software toolbox for low-frequency conductivity and current density imaging using MRI. IEEE Trans. Biomed. Eng. 2017, 64, 2505–2514. [Google Scholar]
- Woo, E.J.; Seo, J.K. Magnetic resonance electrical impedance tomography (MREIT) for high-resolution conductivity imaging. Physiol. Meas. 2008, 29, R1–R26. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Collins, C.M.; Yang, B.; Yang, Q.X.; Smith, M.B. Numerical calculations of the static magnetic field in three-dimensional multi-tissue models of the human head. Magn. Reson. Imaging 2002, 20, 413–424. [Google Scholar] [CrossRef]
- Hoult, D.I. The principle of reciprocity in signal strength calculations—A mathematical guide. Concepts Magn. Reson. 2000, 12, 173–187. [Google Scholar] [CrossRef]
- Van Lier, A.L.H.M.W.; Raaijmakers, A.; Voigt, T.; Lagendijk, J.J.W.; Luijten, P.R.; Katscher, U.; van den Berg, C.A.T. Electrical properties tomography in the human brain at 1.5, 3 and 7T: A comparison study. Magn. Reson. Med. 2014, 71, 354–363. [Google Scholar] [CrossRef]
- Lee, J.; Shin, J.; Kim, D.-H. MR-based conductivity imaging using multiple receiver coils. Magn. Reson. Med. 2016, 76, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jin, J.; Guo, L.; Li, M.; Tesiram, Y.; Chen, H.; Liu, F.; Xin, X.; Crozier, S. MR-based electrical property tomography using a modified finite difference scheme. Phys. Med. Biol. 2018, 63, 145013. [Google Scholar] [CrossRef]
- Sun, X.; Lu, L.; Qi, L.; Mei, Y.; Liu, X.; Chen, W. MR-based electrical conductivity imaging using second-order total generalized variation regularization. Appl. Sci. 2020, 10, 7910. [Google Scholar] [CrossRef]
- Li, C.; Yu, W.; Huang, S.Y. An MR-based viscosity-type regularization method for electrical properties tomography. Tomography 2017, 3, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Shao, Q.; Wang, Y.; Adriany, G.; Bischof, J.; van de Moortele, P.-F.; He, B. In vivo imaging of electrical properties of an animal tumor model with an 8-channel transceiver array at 7T using electrical properties tomography. Magn. Reson. Med. 2017, 78, 2157–2169. [Google Scholar] [CrossRef]
- Wang, Y.; van de Moortele, P.-F.; He, B. CONtrast Conformed Electrical Properties Tomography (CONCEPT) based on multi-channel transmission and alternating direction method of multipliers. IEEE Trans. Med. Imaging 2019, 38, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Voigt, T.; Homann, H.; Katscher, U.; Doessel, O. Patient-individual local SAR determination: In vivo measurements and numerical validation. Magn. Reson. Med. 2012, 68, 117–1126. [Google Scholar] [CrossRef] [PubMed]
- Seifert, F.; Pfeiffer, H.; Mekle, R.; Waxmann, P.; Ittermann, B. 7T 8-channel pTx head coil with high B1+ efficiency optimized for MRS. Proc. Int. Soc. Mag. Reson. Med. 2016, 24, 3545. [Google Scholar]
- Christ, A.; Kainz, W.; Hahn, E.G.; Honegger, K.; Zefferer, M.; Neufeld, E.; Rascher, W.; Janka, R.; Bautz, W.; Chen, J.; et al. The Virtual Family—Development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol. 2010, 55, N23–N38. [Google Scholar] [CrossRef]
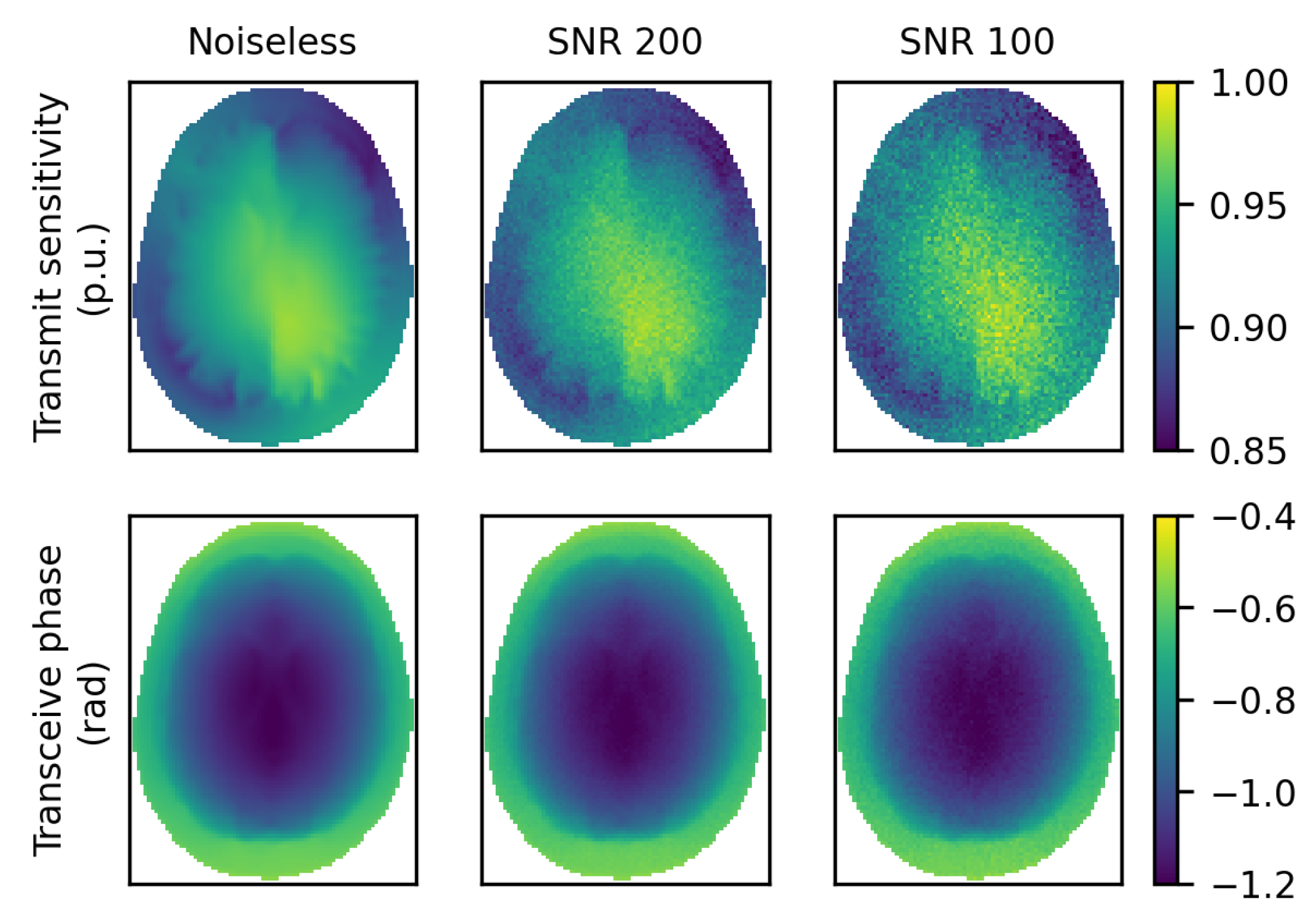
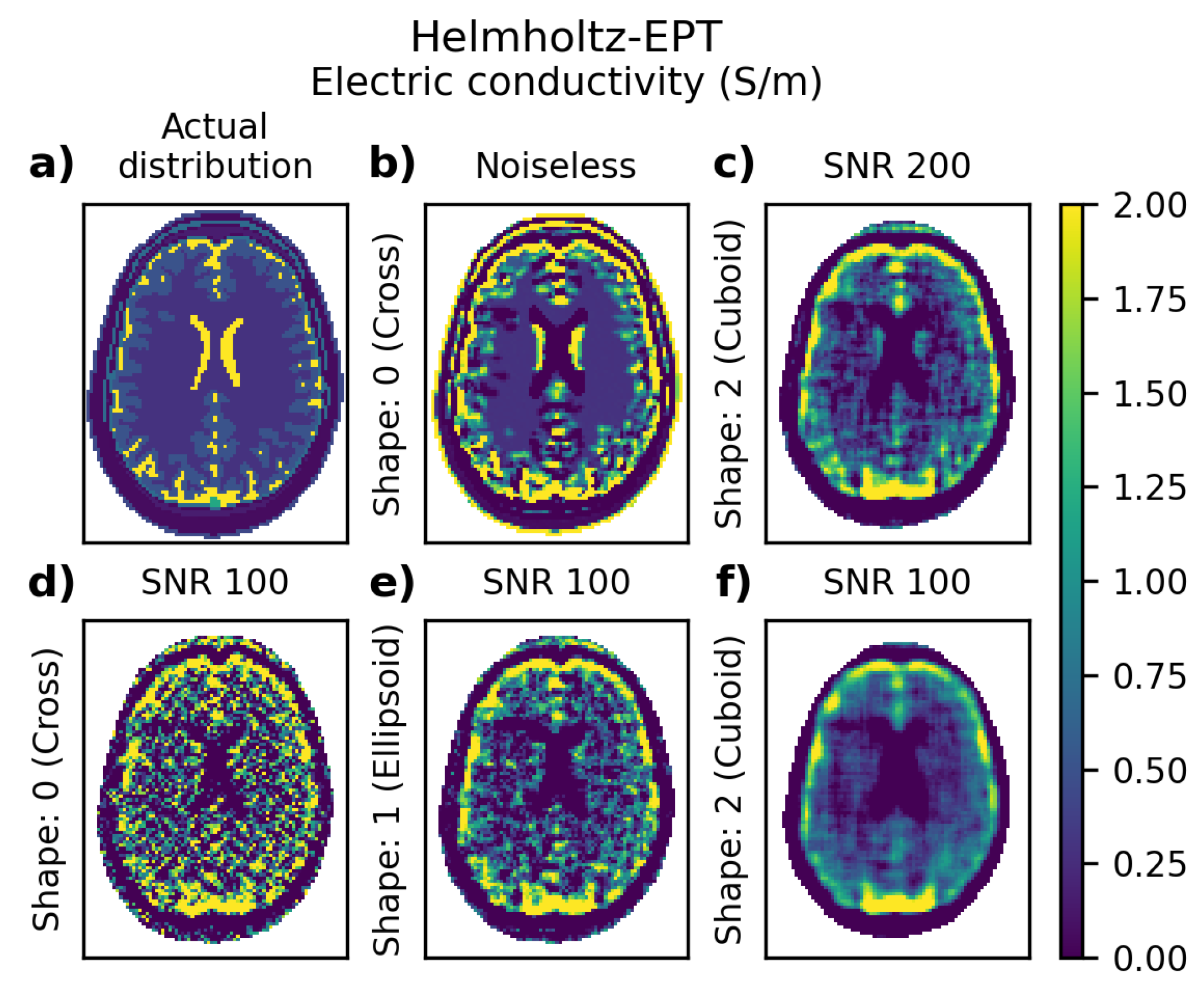
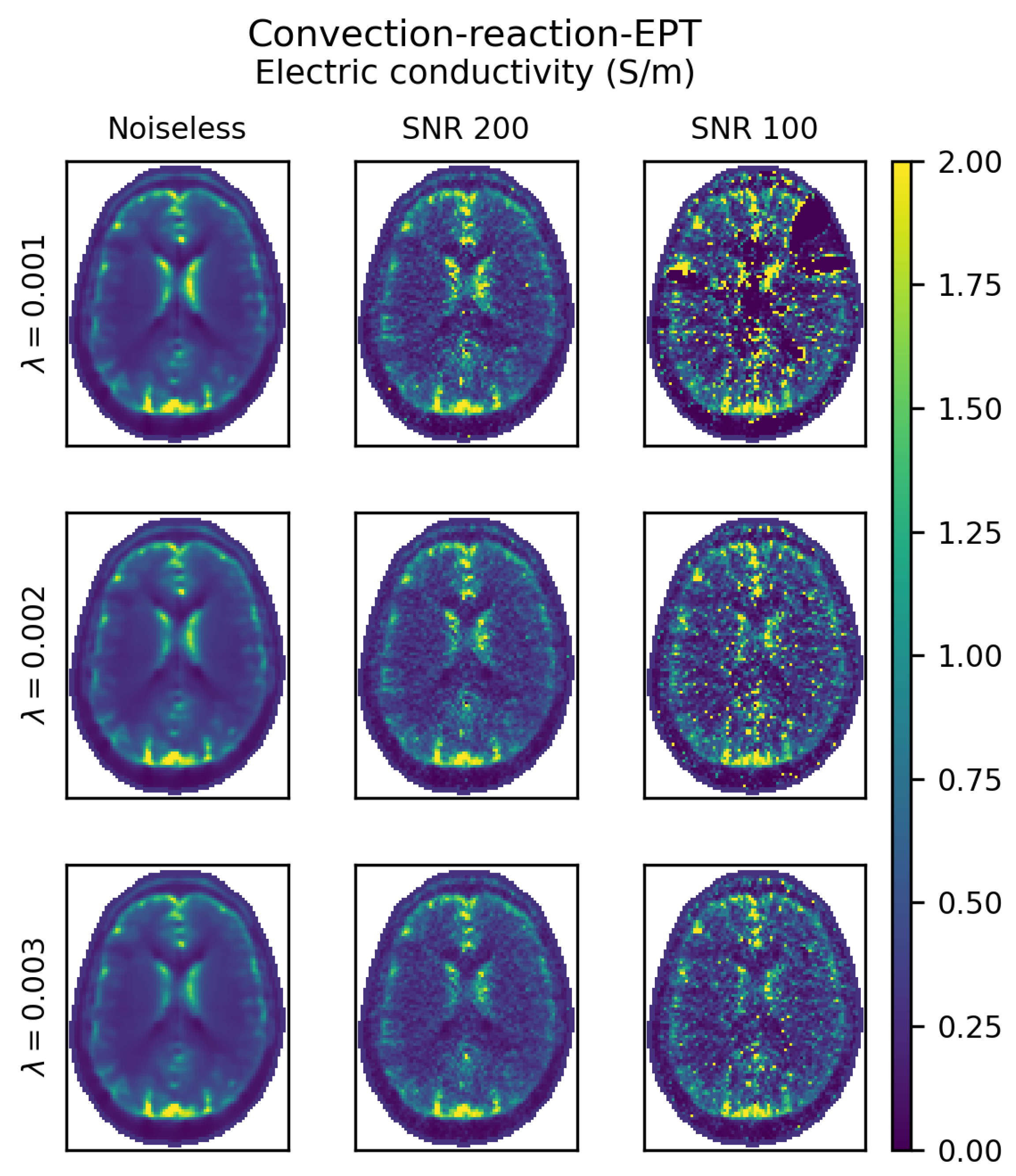
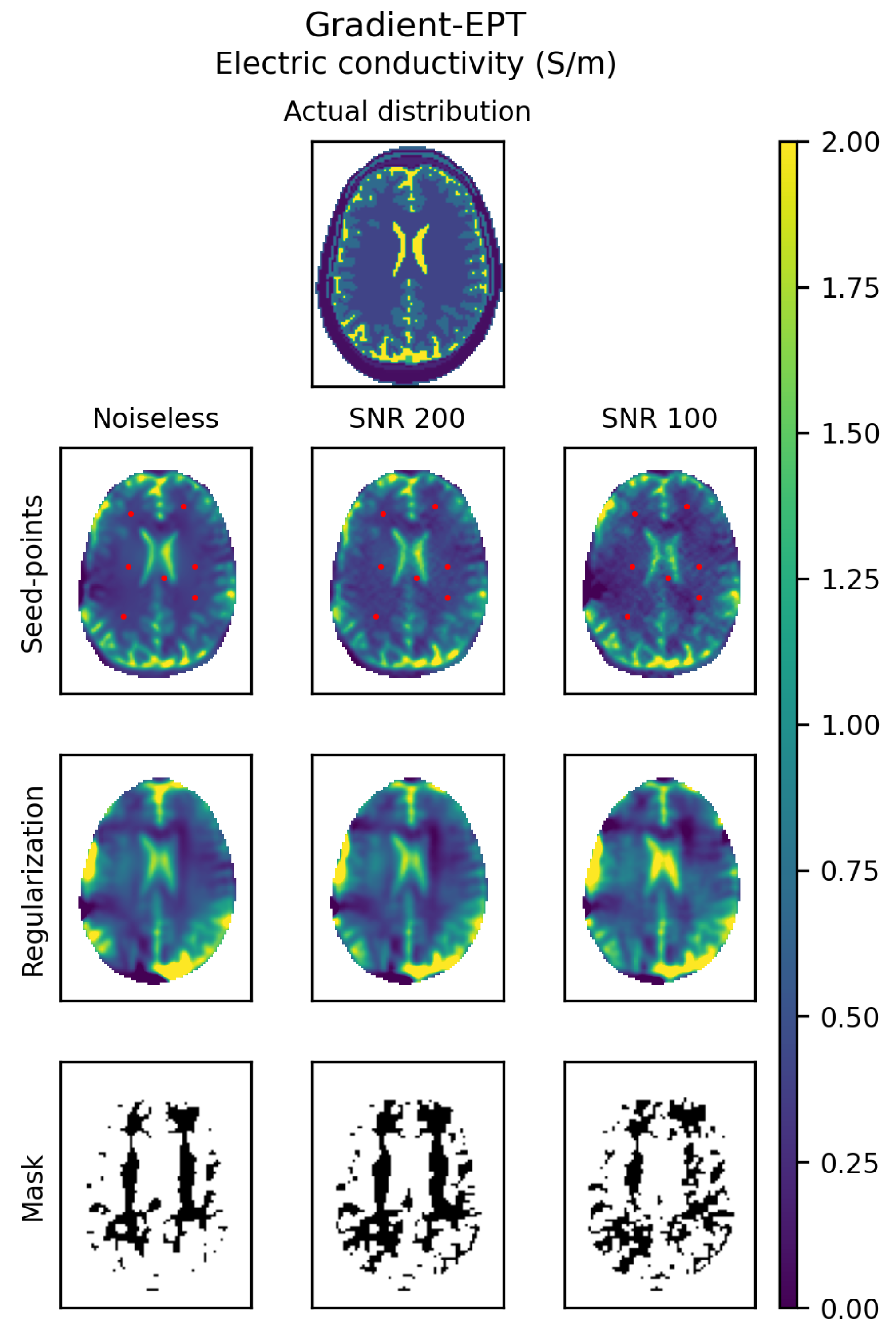
| Input | Output | |||||
|---|---|---|---|---|---|---|
| Tx Chan. | Rx Chan. | Tx Sens. | TRx Phase | |||
| Helmholtz-EPT: | ||||||
| Complete | 1 | 1 | ✓ | ✓ | ✓ | ✓ |
| Phase-based | 1 | 1 | ✗ | ✓ | ✓ | ✗ |
| Magnitude-based | 1 | 1 | ✓ | ✗ | ✗ | ✓ |
| Convection-reaction-EPT: | ||||||
| Complete | 1 | 1 | ✓ | ✓ | ✓ | ✓ |
| Phase-based | 1 | 1 | ✗ | ✓ | ✓ | ✗ |
| Gradient-EPT: | ||||||
| Complete | ≥5 | 1 | ✓ | ✓ | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arduino, A. EPTlib: An Open-Source Extensible Collection of Electric Properties Tomography Techniques. Appl. Sci. 2021, 11, 3237. https://doi.org/10.3390/app11073237
Arduino A. EPTlib: An Open-Source Extensible Collection of Electric Properties Tomography Techniques. Applied Sciences. 2021; 11(7):3237. https://doi.org/10.3390/app11073237
Chicago/Turabian StyleArduino, Alessandro. 2021. "EPTlib: An Open-Source Extensible Collection of Electric Properties Tomography Techniques" Applied Sciences 11, no. 7: 3237. https://doi.org/10.3390/app11073237
APA StyleArduino, A. (2021). EPTlib: An Open-Source Extensible Collection of Electric Properties Tomography Techniques. Applied Sciences, 11(7), 3237. https://doi.org/10.3390/app11073237






