Modeling Dendritic Cell Pulsed Immunotherapy for Mice with Melanoma—Protocols for Success and Recurrence

Abstract

Nowadays, immunotherapy has become an important alternative to fight cancer. One way in which biologists and medics use immunotherapy is by injecting antigen-incubated Dendritic Cells (DCs) into mice to stimulate an immune response. The DCs optimal quantities and infusion times for a successful cancer eradication are often unknown to the therapists; usually, these quantities are obtained by testing various protocols. The article shows a model of five differential equations which represents some interactions between some cells of the immune system and tumor cells which is used to test different infusion protocols of Dendritic Cells. This study aims to find operation ranges to DCs quantities and injection times for which the therapy reduces the tumor significantly. To that end, an exhaustive search of operative protocols is performed using simulations of a mathematical model. Furthermore, nonlinear analysis of the model reveals that without the DC therapy tumor cells cannot stay under non-lethal bounds. Finally, we show that a pulsed periodic therapy can prevent tumor relapsing when the doses and period times lie within a certain range.

1. Introduction

In recent years, new developments in cancer immunotherapy have made great progress such as the immunotherapy via Dendritic cells (DCs) by melanoma, which uses the DCs properties to begin the immune response against cancer [1,2]. The understanding of human Dendritic biology and its potential in immunotherapeutic approaches (e.g., cell-based vaccines) is nowadays limited. However, due to the recent advancements in cell culture systems that allow for the generation of functional DCs from CD34+ hematopoietic stem and progenitor cells (HSPC), studying DCs has become easier [3], in addition to many other related studies see for instance [4]. Besides, recent advances in single-cell sequencing have begun to streamline this process. This protocol synthesizes and expands upon methodologies to generate, isolate, and engineer human T cells with tumor-reactive TCRs for adoptive cell therapy [5]. Immunotherapies have even been suggested as an adjunct therapy in severe Coronavirus Disease 2019 (COVID-19) cases. Such immunotherapies are based on inflammatory cytokine neutralization, immunomodulation, and passive viral neutralization [6]. The above shows that the development of immunotherapies has had and continues to have a great advance in our days.

Before starting the immunotherapy, bone marrow DCs from mice are activated and maturated using melanoma MAGE antigen (Melanoma-associated antigen). The process roughly consists of curating the DCs with MAGE-AX and GK-1 peptide (an 18 amino-acid peptide derived from the Helminth Taenia crassiceps [7]). Such peptide serves as an immunoadjuvant to increase the production of cytokine IL2 and costimulatory signal by CD80 [8]; and the MAGE-AX serves to activate the DCs against the melanoma. Then, the maturated-activated DCs are stored for eventual use as a vaccine. Subsequently, the DC vaccine is injected into groups of mice injected with melanoma cells. The vaccine DCs that reach the lymph nodes now can present melanoma-specific antigen to immature T cells which evolve into matured T cells (helper T cells or cytotoxic T cells). Now Cytotoxic T cells (CTLs) can recognize melanoma-specific antigen through MHC I and induce death of the tumor cell [9,10].

Effective immunotherapy via DCs requires an adequate DCs schedule, which depends on the dose and frequency of vaccine administration [11]. An example of a protocol is shown in

Table 1. Induction of melanoma in mouse protocols.

Protocol	Type of Cancer	Infusion	Size	Type of Mice
Subcutaneous melanoma	B16 melanoma	${10}^5$ cells/mouse	1 cm${}^3$ from 14 to 21 days	$C57BL/6$

. This protocol consists of an infusion of ${10}^5$ melanoma cells and test immunotherapy models in mice; they observed the growth of subcutaneous B16 melanoma [12].

The success of immunotherapy protocol depends on the complex interactions of a large number of factors, for example, the administration route, minimum immunogenic dose, effects on higher doses, vaccination schedule (weekly, monthly, or multiple times in a week or month), immunological adjuvant type, and the existing state of host immunological competence [13]. Until now, it has been a challenge of the cancer vaccine to define a standardized protocol, and to minimize the cost and time required for such treatments [13,14,15].

Currently, these immunotherapies has been studied and tested in mouse models by a group of immunologist in the faculty of medicine in the National Autonomous University of Mexico (UNAM, acronym in Spanish). They are looking for immunotherapy that could reduce the size of melanoma tumors in mice along with extending survival time [8].

Concerning the finding of operating ranges for injected DCs (dose and schedule) which have the feasibility of success. The model and parameter are adjusted for the immunotherapy developed by the research group in the UNAM (National University of Mexico) [8]. The model consists of ODE system that considers interactions between melanoma cells (T), cytotoxic T cells (CTLs), dendritic cells (immunotherapy), and the immune suppression via the Transforming Growth Factor Beta ($TGF-\beta$) cytokine [16]. The ODE (Ordinary Differential Equations) model assists in testing several hypothetical protocols which produced a respective tumor growth.

It is worthwhile to mention some limitations that the study protocol has, the first is that some parameters had been obtained from literature and others had been calculated using the model and based on in vivo experimental results of immunotherapy developed by the research group. To evaluate the model, the growth rate and carrying capacity parameters reported by Castillo-Montiel et al. [17] were used and after was evaluated again with the values of the growth rate and carrying capacity used by Kronik et al. [18], obtaining optimal immunotherapies results in the same ranges. To know which parameters affect the model outcome a local parametric sensitivity analysis (LPSA) was performed. Additionally, we think that other important limitation result from the fact that the hypothetical protocols are not experimental feasible due to the expensive cost of them. So it will be hard to prove its efficacy experimentally.

Furthermore, we analyzed the model fixed points stability and proved that there are no periodic orbits between infusion periods. Next, we transformed our system to a periodically pulsed system to account for the multiple intravenous bolus injections over fixed periods of time. We used those results to find a stability condition for a fixed point when $T=0$ using periodically pulsed immunotherapy.

2. Mathematical Model

The mathematical model was built considering the biological experiments reported by Piñon-Zárate et al. [8] (It is important to notice that in a previous paper [17] the authors validate a similar model with the experimental results given by Piñon-Zarate et al.). Then in our case, the model consists of four ordinary differential equations which represent the simplified interactions between melanoma cells, immune system and DCs injected in bolus doses to melanoma-induced mice. In these interactions melanoma cells, Dendritic cells, Cytotoxic T lymphocyte cells (CTLs) and $TGF-\beta$ cytokine, are given by variables T, D, $C_a$ and $F_{\beta }$ respectively.

To model the growth of melanoma tumor cells we used a logistic equation, whereas the death of tumor cells only occurs by activated CTLs and the cytokine $TGF-\beta$ acting as an inhibitor of the immune system (1). Equation (2) considers only the death rate of DCs after the hypothetical infusion of DCs in the mouse. A modification was performed of this equation to analyze multiple injections. For this model, it was considered that CTLs are activated and replicated by DCs injections whereas the death of CTLs occurs by a death rate given in (3). The model takes into account the number of inactivated cells as constant in the initial conditions. Finally, the production of the cytokine $TGF-\beta$ by the tumor cells acting as an inhibitor of the immune system is represented in (4).

2.1. Growth of Tumor Cells

In Equation (1), the first term on the right side of the equation describes the growth as a logistic function, where $r_T$ is the rate of cell growth and K is the limit growth of tumor cells. The second term describes the eradication of tumor cells by the activated CTLs. The parameter $a_T$ is the maximum efficiency with which the CTLs kill tumor cells by lysis; the term $\frac{T}{T+h_T}$ defines the accessibility of CTLs cells to tumor cells using a term saturation with a Michaelis-Menten constant $h_T$. The last term on the right side of Equation (1) represents the inhibition effect on the immune system by $TGF-\beta$. It is also considered a reverse saturation function of Michaelis-Menten. The maximum reduction effect of $TGF-\beta$ on CTLs efficiency is represented by the $a_{T,\beta }$ Kronik et al. [18,19].

$$\frac{dT}{dt}=r_T·T\left(1-\frac{T}{K}\right)-a_T·C_a\left(\frac{T}{T+h_T}\right)$$

$$\left(a_{T\beta }+\frac{e_{T,\beta }(1-a_{T,\beta })}{F_{\beta }+e_{T,\beta }}\right).$$

(1)

2.2. Growth of Dendritic Cells

Equation (2), describes infusion of immunotherapy using Dendritic cells. It is considered that the number of DCs, $d_0$ decays at a constant rate ${\mu }_D$ taking into account the infusion protocol of DCs proposed by Piñon-Zarate et al. [8]. If the time simulation t is less than 168 h, the number of DCs is given by

$$D(t)=d_0{e}^{-{\mu }_{D}t}\mathrm{if}\mathrm{t}<168$$

when $t_n=n\times 168$ with $n=1\cdots 3$, are infused ${10}^6$ DCs

$$D(t)=\sum _{n=0}^3{d}_n(t)e^{-{\mu }_D(t-168n)}\mathrm{if}\mathrm{t}>0,$$

where $d_n(t)={10}^6{\chi }_{168n}(t)$ for ${\chi }_{168n}(t)=0$, if $t<168n$ and ${\chi }_{168n}(t)=1$ in another case.

Note that the growth of DCs in the time interval $(168(n-1),168n)$ with $n=1\cdots 6$ is shown in the next equation;

$$\frac{dD}{dt}=-{\mu }_{D}Dt\in (168(n-1),168n)\mathrm{for} n=1\cdots 3.$$

(2)

2.3. Dynamic of Activated CTLs

Equation (3), describes the dynamics of activated CTLs. The first term on the right side of (3) represents the expansion of the activated cytotoxic cells. This expansion shows a rate of $r_e$, given for the contact between the DCs and the activated cytotoxic cells (described as a saturation function of type Michaelis-Menten). The next term on the right side of the equation represents the cytotoxic cells activation. It is considered that the contact between the DCs and the inactive cytotoxic cells $C_{naive}$ produces the activation of these (this last term is similar to that use in Reference [20]). It is proposed that the activation is made before the death of the tumor cells and gives a rate $r_a$. This term is performed when injecting Dendritic cells (new CTLs are not allowed in the absence of DCs). Finally, a death term of CTLs is introduced.

$$\frac{d{C}_a}{dt}=r_e·C_a·\left(\frac{D}{D+{\theta }_D}\right)+r_a·C{}_{naive}·D_{on}-{\mu }_{C{}_a}·C{}_a,$$

(3)

where

$${\displaystyle D_{on}=\left\{\genfrac{}{}{0pt}{}{0,if D(t)=0}{1,if D(t)>0}.\right.}$$

2.4. Dynamic of $TGF-\beta$ Cytokine

The first term of (4), represents the production of $TGF-\beta$ by tumor cells. This model takes into account that tumor cells produce $TGF-\beta$ by constant rate $r_{T\beta }$ and that cytokine $TGF-\beta$ is degraded naturally using a constant rate ${\mu }_{\beta }$ in the model.

$$\frac{d{F}_{\beta }}{dt}=r_{T\beta }·T-{\mu }_{\beta }·F_{\beta }.$$

(4)

3. Computer Simulation and Results

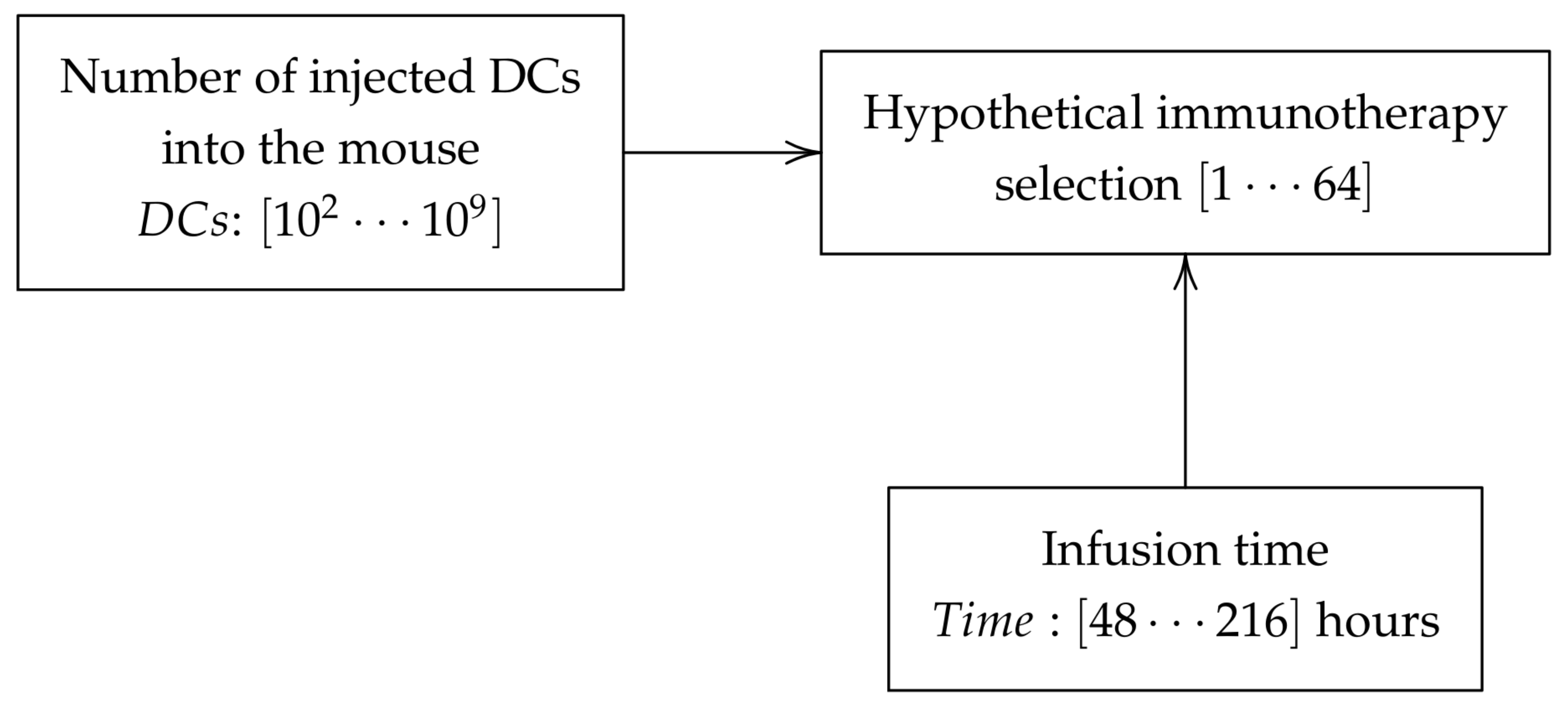
To begin, the numerical experiments was proposed that every hypothetical immunotherapy was testing with 100 different initial conditions, randomly choosing the parameters of tumor growth r in a range between $0.001$ to $0.1$ and the initial tumor cells $t_0$ in a range between $5\times {10}^4$ and $2\times {10}^5$ (See diagram in Figure 1).

For this work 64 immunotherapies were proposed, where each immunotherapy is a combination injected into the mouse and the time of application. In this case, the DCs used for therapy proposals are of the order of ${10}^2$, ${10}^3$, ${10}^4$, ${10}^5$, ${10}^6$, ${10}^7$, ${10}^8$ and ${10}^9$ DCs infused ($D_{inf}$), whereas infusion time considered was 48, 72, 96, 120, 144, 168, 192 and 216 h (see Figure 2), performing more than 1200 experiments. Following the protocol to induce melanoma in mice described by Zhiya et al. [14] the first infusion of DCs is injected 168 h after initiated simulation.

Once the initial conditions for the growth of the tumor and the number of initial cells are chosen, the simulation of the tumor growth with and without immunotherapy is performed, using a classical Runge-Kutta method (4th Order) for solving the ODE system numerically.

To determine the success of a hypothetical protocol three attributes were suggested: the population tumor cells without immunotherapy, the population tumor cell with immunotherapy, and the average population growth of tumor cells. The average population growth of tumor cells was calculated between the difference of both populations in terms of a percentage of the population tumor cell without immunotherapy.

If the average population growth is greater than $70\%$ it is considered that immunotherapy is not successful because there is no response and tumor cells continue to grow. However, if the average is between $30\%$ and $69\%$ it is considered that the growth is stable. On the other hand, if the population growth is less than $30\%$ compared to the tumor cell population without immunotherapy it is considered that therapy is successful. We also use the protocol RECIST (Response evaluation criteria in solid tumors) to evaluate the response of the therapy [21]. The value of the model constants is shown in greater detail in

Table A2. Parameters used in the model.

Parameter	Name	Value	Observations
$r_T$	Maximum rate of tumor growth	$0.001$$h^{-1}$	Kronik et al. [18] and Castillo-Montiel E. et al. [17].
K	carrying capacity of tumor	$6.754\times {10}^{15}$$cell$${10}^{11}$$cell$	Observing the biological results, the mice is sacrified when the tumor reached a diameter of 4.3 cm Castillo-Montiel E. et al. [17]; Kronik et al. [18]
$a_T$	Maximum efficiency of cytotoxic cells	$0.12$$h^{-1}$	[19,30] and
$h_T$	Saturation efficiency of CTLs to a large tumor size	$5\times {10}^{8}cell$	[19,31] and
$a_{T\beta }$	Maximum effect of reduction of the cytokine $TGF-\beta$ in the efficiency of CTLs	$0.69$ none	and [18,32]
$e_{T\beta }$	Dependence of CTLs the efficiency in the efficiency of $TGF-\beta$	${10}^4$$pg$	and [18,33]
$r_e$	Rate of expansion of CTLs by CD	$3.5416$$h^{-1}$	[34]
${\theta }_D$	Limit the density of the CD by the maximum rate of proliferation of CTLs	212 $cells$	[34]
$r_a$	Activation rate of CTLs by CD	$0.00004$${(cell*h)}^{-1}$	[34]
${\mu }_{C_a}$	Death rate of CLTs activated at the tumor site	$0.01925$$h^{-1}$	[20]
$r_{T\beta }$	Production rate TGF $TGF-\beta$ by a single tumor cell	$5.57\times {10}^{-6}$$pg{(cell\times h)}^{-1}$	[18]
${\mu }_{\beta }$	Degradation rate of $TGF-\beta$	$7h^{-1}$	[18]
$C_{naive}$	Number of naive CTL cells contributing to primary clonal expansion	370 $cells$	[20] (ah doc)
${\mu }_D$	Rate death of D cells	$0.009625$$h^{-1}$	[34] (ah doc)

and in the Supplementary Materials file.

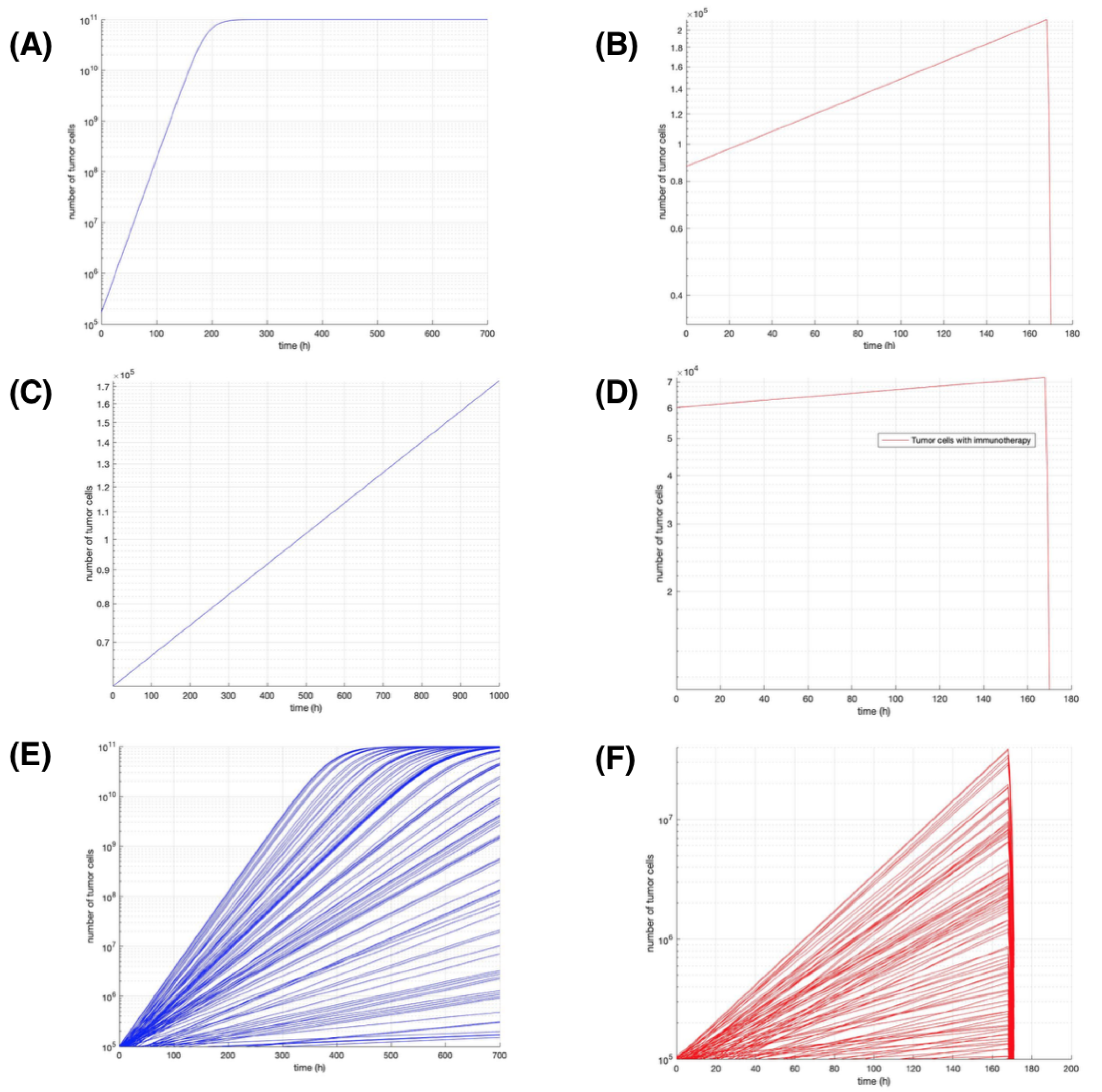
Figure 3, presents the results obtained by applying 100 different initial conditions randomly chosen between the tumor growth rate $r_T$ and the initial tumor cell $T_0$ taking into account infusions of ${10}^9$ DCs injected every 168 h. The red curves represent the tumor growth with DC immunotherapy treatment and blue curves represent the growth of tumor cells without treatment. Figure 3A shows only one simulation without immunotherapy treatment likewise, Figure 3B shows the result applying the immunotherapy treatment using the same initial conditions and parameters of growth rate and carrying capacity reported by Kronik [18]. The Figure 3C,D show the results of the same initial conditions but with the parameters of growth rate and carrying capacity obtained from the biological experiment reported by Castillo-Montiel E [17]. Figure 3E,F show the results of 100 different simulations setting random initial conditions but using the same scheme of immunotherapy treatment, see

Table 2. Hypothetical immunotherapy for ODEs model with different number of Dendritic cells (DCs) injected and different periods of infusion.

HM	NDC	PI	%G	RT	ST	SuT	RECIST
1	${10}^3$	48	0.99	100	0	0	PD
2	${10}^3$	96	0.99	100	0	0	PD
3	${10}^3$	144	0.99	100	0	0	PD
4	${10}^3$	192	0.99	100	0	0	PD
5	${10}^7$	48	0.49	50	0	50	PR
6	${10}^7$	96	0.53	54	0	46	PR
7	${10}^7$	144	0.55	56	0	44	PR
8	${10}^7$	192	0.50	51	0	49	PR
9	${10}^9$	48	0.011	0	0	100	CR
10	${10}^9$	96	0.007	0	0	100	CR
11	${10}^9$	144	0.010	0	0	100	CR
12	${10}^9$	192	0.009	0	0	100	CR

HM = Hypothetical immunotherapy, NDC = Number of DCs injected, PI = Period of infusion, $\%G$ = Percentage of growth, RT = Response tests, ST = Stable tests, SuT = Success tests, RECIST = Response evaluation criteria in solid tumors [21] (Complete Response: CR, Partial response: PR, Progressive Disease: PD, and Stable Disease: SE).

for numerical results. As can be seen in image A, the growth of tumor cells remains fixed after reaching a maximum of ${10}^{11}$ tumor cells at approximately 200 h, on the other hand, in image C, growth continues after 200 h because it has not yet the maximum size of 6754 × ${10}^{15}$ tumor cells is reached, however when applying the infused cell therapy every 72 h for 3 weeks, the same successful result is obtained on the growth of the tumor cells by presenting its decrease at 170 h (see Figure 3B,D).

The results shown in Table 2 use the values of growth rate and tumor carrying capacity reported by Kronik et al. [18] identified in the Table A2 and shows some results of 24 proposed hypothetical treatments, which consists in simulating the injection of ${10}^3$, ${10}^7$ and ${10}^9$ DCs into a mouse, each one tested with 100 different initial conditions. In Table 2 in the first four rows, the hypothetical treatments do not generate any response in the growth of tumor cells. Testing therapies with ${10}^7$ DCs injected show that about $50\%$ of the therapies are successful (see the fifth to eighth rows in the table). In the last rows are the results of applying hypothetical treatments equal or greater than ${10}^9$ DCs with different infusion periods; these therapies are successful. The percentage of tumor cells growth is less than $3\%$ as shown in Table 2.

The results of the computer simulations show that a major reduction in the growing tumor cell population is obtained when the infusions are ${10}^7$ and ${10}^9$ DCs regardless of the chosen period of infusion; however, these DCs are difficult to cultivate in vitro. If we choose to simulate ${10}^6$ DCs infusions, we have fewer possibilities to reduce the growth of tumor cells, although those quantities of DCs are more feasible to cultivate in vitro.

In the next section to find operable protocols for the therapies, we are going to change our approach to non-linear analysis instead of an exhaustive search. Then we use this analysis to find conditions in which a periodic therapy can prevent relapsing of tumor growth.

Sensitivity Analysis

For this model, a local analysis of sensitivity was performed, to identify the parameters that are more sensitive to the model.

Table 3. Parameter Sensitivity Analysis.

Param	PR1	S1	PR2	S2
r	$2.10\times {10}^{-15}$	2	$9.99\times {10}^{10}$	$2.44\times {10}^{-4}$
K	$4.99\times {10}^{10}$	$1.00$	$1.49\times {10}^{11}$	$1.00$
${\mu }_D$	$9.95\times {10}^{10}$	$0.008$	$9.99\times {10}^{10}$	$6.07\times {10}^{-4}$
$D_{inf}$	$9.99\times {10}^{10}$	$-0.0034$	$9.99\times {10}^{10}$	$0.0034$
${\mu }_{Ca}$	$9.98\times {10}^{10}$	$0.003$	$9.99\times {10}^{10}$	$3.41\times {10}^{-4}$
$a_{T,\beta }$	$9.99\times {10}^{10}$	$-3.34\times {10}^{-4}$	$9.99\times {10}^{10}$	$-3.34\times {10}^{-4}$

HM = Hypothetical immunotherapy, NDC = Number of DCs injected, PI = Period of infusion, $\%G$ = Percentage of growth, RT = Response tests, ST = Stable tests, SuT = Success tests, RECIST = Response evaluation criteria in solid tumors [21] (Complete Response: CR, Partial response: PR, Progressive Disease: PD, and Stable Disease: SE).

are shown the results of changing $\pm 50\%$ the value of the parameters was considered the decrease in tumor cell population for observing the behavior of the model parameters. It is noted that change values by $\pm 50\%$ the most sensitive parameter is K, however, decreasing the value parameters in $-50\%$ are r with major changes in the population of tumor cells.

It can be seen from Table 3, that the most sensitive parameters of the model are $r_T$, K, ${\mu }_D$ and $D_{inf}$. Additionally, it is worth mentioning that, when performing experiments by changing the CD number from ${10}^7$ to ${10}^9$, the sensitivity is around $200\%$, showing that the decrease of tumor cell population depends strongly on the number of Dendritic cells infused, even when we use random conditions.The other parameters have a sensitivity of less than 0.3 percent, so they are not reported.

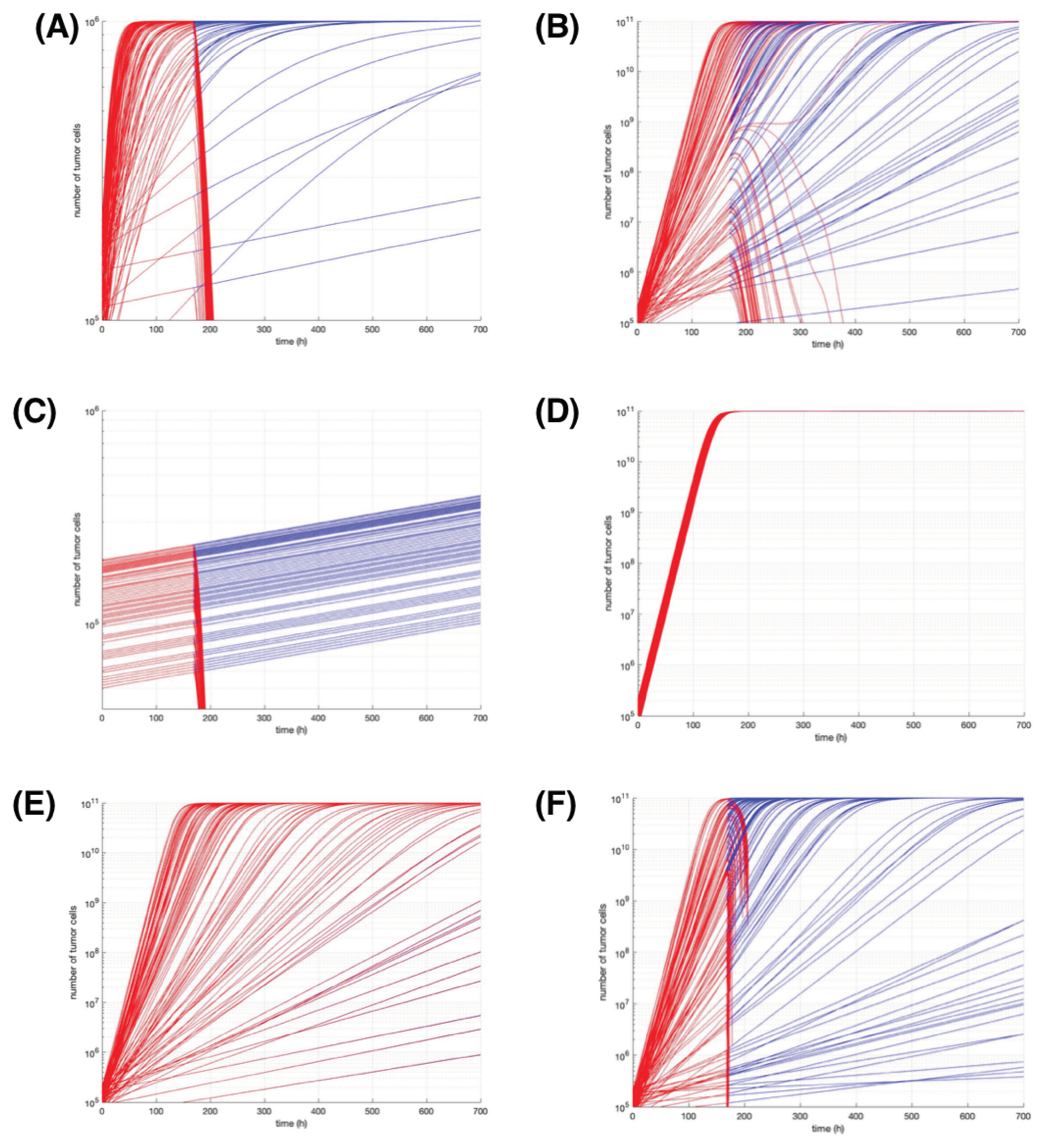
In Figure 4 the results from varying the most sensitive model parameters are shown. In all simulations we infused ${10}^7$ DCs every 168 h; except Figure 4E,F where the number of Dendritic cells injected varies.

Figure 4A,B modify the value of parameter K in ${10}^6$ and ${10}^{11}$ respectively, it can be seen the larger the value of K, the less response there is from applied immunotherapy.

In the case of Figure 4C,D the varied parameter now is $r_T$, the rate of tumor growth with values of $0.001$ and $0.1$ respectively, observing that when using smaller values, the immunotherapy can be more effective. Finally, for graphs Figure 4E,F the number of dendritic cells injected is varied in ${10}^3$ and ${10}^9$ every 168 h. It can be seen that by increasing the amount of DCs, the success of the therapy increases dramatically having a sensitivity of $200\%$ when ${10}^9$ DCs is infused.

4. From Exhaustive Search to Non-Linear Analysis

In the former sections simulations of the model were made. By trying different quantities for the injected DCs, periods of hypothetical successful treatments can be inferred. Table 2 shows that therapies with ${10}^3$ are not sufficient for a successful therapy. Table 2 shows that a reasonable period of infusion ${10}^9$ is enough for successful treatment. The result of Table 2 shows that injections of ${10}^7$ during smaller periods have a better reduction of tumor growth percentage. Nevertheless, for the Department of Tissue and Cellular Biology in UNAM to create doses greater than ${10}^8$ is not feasible. The main objective of the computer simulation, then, was to find operation ranges to DCs quantities and injection times for which the therapy reduces the tumor significantly. To that end, an exhaustive search of operative protocols was performed.

Now to confirm the numerical results a non-linear analysis of the model was performed. It reveals that without the DC therapy tumor cells cannot stay under non-lethal bounds. The latter was done analyzing the stability of fixed points of the Equations (1)–(4) and showing the existence of periodic orbits, as it is shown in the following. Then, we show that a pulsed periodic therapy can prevent tumor relapsing when the doses and period times lie within a certain range. For this purpose, we transformed to a periodically pulsed system to account for the multiple bolus injections over fixed periods of time. We used those results to find a condition of stability for a fixed point when $T=0$ using periodically pulsed immunotherapy. This fixed point ($T=0$) could be used to analyze the success of the immunotherapy after a surgery in which the tumor is extracted. That is, we give conditions in which the immunotherapy is effective for the remaining tumor cells after such a procedure.

4.1. Non-Dimensionalization

To make the analysis easier we reduced the number of parameters using non-dimensionalization. Thus, the rescalings:

$$\tilde{T}=\frac{T}{h_T},\widetilde{C_a}=\frac{C_a}{C_{naive}}\widetilde{F_{\beta }}=\frac{F_{\beta }}{e_{T,\beta }},\tilde{D}=\frac{D}{{\theta }_D},\tilde{t}=\frac{t}{r_e}$$

and the introduction of parameters:

$$\begin{array}{c}\hfill r_1=\frac{r_T}{r_e},r_2=\frac{h_T}{K},r_3=\frac{a_T{C}_{naive}}{r_e},\\ \hfill r_4=\frac{r_a}{r_e},r_5=\frac{{\mu }_{Ca}}{r_e},r_6=\frac{r_{T\beta }{h}_T}{r_e{e}_{T,\beta }},\\ \hfill r_7=\frac{{\mu }_{\beta }}{r_e},r_8=\frac{{\mu }_D}{r_e}\end{array}$$

give us the non-dimensionalization of the system (1)–(4). We omit the tilde notation in the rescaling equations. Therefore, the system becomes

$$\begin{array}{cc}\hfill \frac{dT}{dt}& =r_{1}T(1-r_{2}T)-r_3{C}_a\left(\frac{T}{T+1}\right)\left(\frac{a_{T,\beta }{F}_{\beta }+1}{F_{\beta }+1}\right)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \frac{d{C}_a}{dt}& =C_a\left(\frac{D}{D+1}\right)+r_4{D}_{on}-r_5{C}_a\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{d{F}_{\beta }}{dt}& =r_{6}T-r_7{F}_{\beta }\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \frac{dD}{dt}& =-r_{8}D.\hfill \end{array}$$

(8)

4.2. Recurrence and Periodic Orbits Without Pulsed Immunotherapy

We shall continue the analysis using the system (5)–(8), which has the Jacobian matrix

$$\begin{array}{cc}\hfill & \left(\begin{array}{cccc}{\zeta }_3& {\zeta }_2& {\zeta }_1& 0\\ 0& \frac{D}{D+1}-r_5& 0& r_4+\frac{C_a}{D+1}-\frac{C_{a}D}{{(D+1)}^2}\\ r_6& 0& -r_7& 0\\ 0& 0& 0& -r_8\end{array}\right)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\zeta }_1& =\frac{C_a(a_{T_{\beta }}{F}_{\beta }+1)T{r}_3}{{(F_{\beta }+1)}^2(T+1)}-\frac{a_{T_{\beta }}{C}_{a}T{r}_3}{(F_{\beta }+1)(T+1)}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\zeta }_2& =-\frac{(a_{T_{\beta }}{F}_{\beta }+1)T{r}_3}{(F_{\beta }+1)(T+1)}\hfill \end{array}$$

(11)

$${\zeta }_3=-r_{2}T{r}_1+(1-r_{2}T)r_1+\frac{(a_{T_{\beta }}{F}_{\beta }+1)T{r}_3{C}_a}{(F_{\beta }+1){(T+1)}^2}-\frac{C_a(a_{T_{\beta }}{F}_{\beta }+1)r_3}{(F_{\beta }+1)(T+1)}.$$

(12)

The system (5)–(8) has two fixed points: $E_1=(0,0,0,0)$ and $E_2=(\frac{1}{r_2},0,\frac{r_6}{r_2{r}_7},0)$. The eigenvalues of (9) evaluated in $E_1$ give us the eigenvalues ${\lambda }_1=-r_7$, ${\lambda }_2=r_1$, ${\lambda }_3=-r_5$, ${\lambda }_4=r_8$ which implies that $E_1$ is a saddle point since all parameters are strictly positive. The eigenvalues in $E_2$ are ${\lambda }_1=-r_7$,${\lambda }_2=-r_1$,${\lambda }_3=-r_5$,${\lambda }_4=-r_8$, therefore, $E_2$ is asymptotically stable. We now proceed to show that for our parameter configuration there are no periodic orbits in this system (5)–(8). The instability of the fixed point $E_1$ shows that it is not likely to prevent a relapse of tumor population without pulsed immunotherapy. On the contrary, the stability of $E_2$ exhibits the tendency of the tumor population to go to its carry capacity: $\frac{1}{r_2}=\frac{K}{h_T}$. Another option is to observe if the tumor can stay in a periodic orbit where a threshold of lethality is not surpassed. For instance, a tumor mass of ${10}^5-{10}^9$ cells is clinically not detectable; with ${10}^9-{10}^{12}$ cells it is detectable, and over ${10}^{12}$ it is lethal [22]. The next result shows that without pulsed immunotherapy it is not expected that the tumor stays in a periodic orbit under a non-lethal threshold because periodic orbits do not exist for our set of parameters. To show this, we used Dulac’s criterion which can be consulted in reference [23].

Proposition 1.

The system (5)–(8) has no periodic orbit if ${\mu }_{\beta }+{\mu }_D{\theta }_D+2\frac{r_T{h}_T}{K}T>r_T$.

Proof. 

We proceed using Dulac’s criterion in the region $G=\{(T,C_a,F_{\beta },D)|T\ge 0,C_a>0,F_{\beta }\ge 0,D\ge 0\}$. Let $g=\frac{1}{C_a}$ and $x=(\frac{dT}{dt},\frac{d{C}_a}{dt},\frac{d{F}_{\beta }}{dt},\frac{dD}{dt})$ in (5)–(8) then

$$\begin{array}{c}\hfill \nabla ·(gx)=-\left(\frac{r_4}{C_a^2}+\frac{r_7+r_8-r_1+2r_{2}T{r}_1}{C_a}+\frac{(1+a_{T,\beta }{F}_{\beta })r_3}{(1+F_{\beta }){(1+T)}^2}\right).\end{array}$$

So if $r_7+r_8-r_1+2r_{2}T{r}_1>0$ then $\nabla ·(gx)<0$ on G. This in the original parameters is ${\mu }_{\beta }+{\mu }_D{\theta }_D+2\frac{r_T{h}_T}{K}T>r_T$. □

Using the parameters of

Table 4. Specific numerical results for the stable zone using Equation (25).

$\mathit{\tau }$	d	Stability
20	50,000	Unstable
20	200,000	Stable
20	150,000	Stable
50	100,000	Unstable
50	600,000	Stable
50	100,000,000	Stable
100	50,000	Unstable
100	600,000	Stable
100	1,000,000	Stable
144	1000	Unstable
144	100,000,000	Stable
150	100,000	Unstable
150	200,000	Stable
150	100,000,000	Stable
168	10,000,000	Stable

gives us ${\mu }_{\beta }=2.7$ and $r_T=0.001060289$ then the condition of (13) is consummate for this paper.

5. A Model with Periodically Pulsed Immunotherapy

If we apply an external dose of d Dendritic cells each period of time $\tau$ the behavior when $t\to \infty$ of the system (5)–(8) is greatly affected by the sizes of d and $\tau$. So we redefined system (5)–(8) to account for the periodically pulsed immunotherapy. Equation (8) is then redefined as,

$$\frac{dD}{dt}=-r_{8}D+\sum _k^{\infty }d\delta (t-k\tau ).$$

(13)

The second term at the right applies an impulse of size d at $t=n\tau n=0,1,2,\dots$ which corresponds to periodically bolus doses of d Dendritic cells each period of time $\tau$. The system (5)–(7) and (13) can be solved numerically integrating (5)–(8) applying $D(t)+d$ as new initial conditions on each $t=n\tau n=0,1,2,\dots$. For example, to solve it $[0,2\tau )$, first (5)–(8) must be integrated on $[0,\tau ]$ with initial conditions $(T(0),C_a(0),F_{\beta }(0),D(0)+d)$. Then again (5)–(8) should be integrated from $[\tau ,2\tau )$ with new initial conditions $(T(\tau ),C_a(\tau ),F_{\beta }(\tau ),D(\tau )+d)$. This lets us handle the Dirac delta functions. Now we explicitly define this notion of inserting new initial conditions at $t=n\tau n=0,1,2,\dots$. Defining,

$$D(n{\tau }^{+})=D(n{\tau }^{-})+d,$$

(14)

where ${\tau }^{-}$ and ${\tau }^{+}$ denote the time just before, and just after the impulse given by $\delta$. Observe that the system (5)–(7) and (13) is equivalent to (5)–(8) defined at $(n\tau ,(n+1)\tau )$ with (14) to deal with the impulsive periodically immunotherapy.

A diversity of research in periodically pulsed models used in cancer-fighting has been made. Previous work by Panetta [24] used periodically pulsed chemotherapy in a competition model to study the parameter conditions needed to prevent tumor regression following a tumor removal procedure. Also, an early work by Cojocaru [25] shows the importance of interval size in treatment efficacy using a cancer drug called cytosine arabinoside. Concerning numerical approaches, in [26] a periodically pulsed therapy is proposed for a model given in [27], with a numerical method to find the fixed points. Bifurcation curves of fixed points can be obtained numerically with the method proposed in [28].

Recurrence with Pulsed Immunotherapy

After removing the tumor with any surgical procedure, remaining cancer cells from the extirpated tumor could re-emerge as tumor mass. In this section, we will analyze the fixed points of the system (5)–(7) and (13) when $T=0$, and give conditions to make fixed points stable under small perturbations. Since the variable D is the one immediately affected by the immunotherapy we will look at its behavior under the periodically pulsed injections. The analysis shall be made discretizing (13) with the aid solution (8) and (14).

Proposition 2.

Equation (13) has the steady-state periodic solution

$$D_s(t)=D^{*}exp(-r_8(t-n\tau )),n\tau <t<(n+1)\tau$$

(15)

where

$$D^{*}=\frac{d}{1-exp(-r_8\tau )}.$$

Proof. 

The solution of (8) is $D(t)=C_{1}exp(-r_{8}t)$ then $D(n{\tau }^{-})=D((n-1){\tau }^{+})exp(r_8\tau )$ and (14) give $D(n{\tau }^{+})=d+D((n-1){\tau }^{+})exp(r_8\tau )$. Defining $D_n=D(n{\tau }^{+})$ gives us the difference equation $D_n=f(D_n)=D_{n-1}exp(-r_8\tau )+d$ which will approach the fixed point $D^{*}=\frac{d}{1-exp(-r_8\tau )}$ as $n\to \infty$. It is stable since $|f^{\prime }(D_n)|=|exp(-r_8\tau )|<1$. Thus, $D_s(t)$ is obtained substituting $D^{*}$ in the solution of (8) as an initial condition for the interval $n\tau <t<(n+1)\tau$. □

Proposition 3.

Let $F_{\beta }(n{\tau }^{+})=F_{\beta }(n{\tau }^{-})$ then (7) has the steady-state periodic solution

$$F_s(t)=0.$$

(16)

when $T=0$.

Proof. 

From (7) we have $\frac{d{F}_{\beta }}{dt}=r_7{F}_{\beta }$ with solution

$$F_{\beta }(t)=C_{1}exp(-r_{7}t).$$

(17)

Since $r_7>0$, $F_{\beta }(t)\to 0$ as $t\to \infty$ $(n\to \infty )$ then a difference equation defined on intervals $n\tau$ from $F_{\beta }$ like the procedure in (2) would tend to 0. So $F_s(t)=0.$ □

Since the tumor cells were the only producer of cytokine $TGF-\beta$, $F_s(t)=0$ is required to happen. Now, if we substitute (15) on (6) we obtain

$$\frac{d{C}_a}{dt}=C_a\left(\frac{D^{*}exp(-r_{8}t)}{D^{*}exp(-r_{8}t)+1}\right)+r_4-r_5{C}_a,$$

(18)

which has a solution

$$\begin{array}{cc}\hfill C_a(t)& =e^{t-r_{5}t}{\left(d{e}^{r_8\tau }+e^{r_8(t+\tau )}-e^{r_{8}t}\right)}^{\frac{-1}{r_8}}\left({\gamma }_1+C_1\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\gamma }_1& ={\int }_1^t{r}_4{e}^{\xi \left(r_5-1\right)}\left(d{e}^{r_8\tau }+e^{\xi r_8}\left(e^{r_8\tau }-1\right)\right){}^{\frac{1}{r_8}}d\xi ,\hfill \end{array}$$

(20)

where $C_1$ is a constant.

Proposition 4.

$$\begin{array}{c}\hfill C_{as}(t)=\left(\frac{e^{t-r_{5}t}{\left(d{e}^{r_8\tau }+e^{r_8(t+\tau )}-e^{r_{8}t}\right)}^{-\frac{1}{r_8}}}{1}\right)\left(\frac{{\alpha }_1\left({\gamma }_1-{\gamma }_2\right)+{\alpha }_2\left({\gamma }_3-{\gamma }_1\right)}{{\alpha }_1-{\alpha }_2}\right)\end{array}$$

$$\begin{array}{cc}\hfill {\gamma }_2& ={\int }_1^0{r}_4{e}^{\xi \left(r_5-1\right)}\left(d{e}^{r_8\tau }+e^{\xi r_8}\left(e^{r_8\tau }-1\right)\right){}^{\frac{1}{r_8}}d\xi \hfill \\ \hfill {\gamma }_3& ={\int }_1^{\tau }{r}_4{e}^{\xi \left(r_5-1\right)}\left(d{e}^{r_8\tau }+e^{\xi r_8}\left(e^{r_8\tau }-1\right)\right){}^{\frac{1}{r_8}}d\xi \hfill \\ \hfill {\alpha }_1& =e^{r_5\tau }\left(e^{r_8\tau }\left(d+e^{r_8\tau }-1\right)\right){}^{\frac{1}{r_8}}\hfill \\ \hfill {\alpha }_2& =e^{\tau }\left((d+1)e^{r_8\tau }-1\right){}^{\frac{1}{r_8}}.\hfill \end{array}$$

Proof. 

Taking $C_a(0)=C(n{\tau }^{+})$ in (19) and solving for $C_1$

$$C_1=C(n{\tau }^{+})\left(d{e}^{r_8\tau }+e^{r_8\tau }-1\right){}^{\frac{1}{r_8}}-{\gamma }_2.$$

(21)

Now substituting in (19) gives

$$C_a((n+1){\tau }^{+})=$$

$$e^{\tau -r_5\tau }\left(d{e}^{r_8\tau }-e^{r_8\tau }+e^{2r_8\tau }\right){}^{-\frac{1}{r_8}}$$

$$\left(\left({\gamma }_3-{\gamma }_1\right)+C(n{\tau }^{+})\left(d{e}^{r_8\tau }+e^{r_8\tau }-1\right){}^{\frac{1}{r_8}}\right),$$

(22)

this is a different equation to $C_a(n{\tau }^{+})$. Then (22) has the fixed point

$$\begin{array}{cc}\hfill C^{*}& =\frac{e^{\tau -r_5\tau }{\alpha }_3{\gamma }_3-e^{\tau -r_5\tau }{\alpha }_3{\gamma }_2}{1-e^{\tau -r_5\tau }\left(d{e}^{r_8\tau }+e^{r_8\tau }-1\right){}^{\frac{1}{r_8}}{\alpha }_3}\hfill \\ \hfill {\alpha }_3& =\left(d{e}^{r_8\tau }-e^{r_8\tau }+e^{2r_8\tau }\right){}^{-\frac{1}{r_8}}.\hfill \end{array}$$

The stability of $C^{*}$ is given by $|e^{\tau -r_5\tau }\left(d{e}^{r_8\tau }+e^{r_8\tau }-1\right){}^{\frac{1}{r_8}}\left(d{e}^{r_8\tau }-e^{r_8\tau }+e^{2r_8\tau }\right){}^{-\frac{1}{r_8}}|<1$. Thus, $C_{as}(t)$ is obtained substituting $C^{*}$ in solution (19) as an initial condition for the interval $n\tau <t<(n+1)\tau$. □

Proposition 5.

The fixed point $(0,C_s,F_s,D_s)$ of system (5)–(7) and (13) is stable if

$$r_1\tau -r_3{\int }_0^{\tau }{C}_{as}(t)dt<0.$$

Proof. 

Linearizing the system (5)–(8) around $(0,C_s,F_s,D_s)$ gives us;

$$\left(\begin{array}{c}{v}^{\prime }\\ v_2^{\prime }\\ v_3^{\prime }\\ v_4^{\prime }\end{array}\right)=\left(\begin{array}{c}v\\ v_2\\ v_3\\ v_4\end{array}\right)\left(\begin{array}{cccc}{r}_1-C_{as}{r}_3& 0& 0& 0\\ 0& \frac{D_s}{D_s+1}-r_5& 0& r_4+\frac{C_{as}}{D_s+1}-\frac{C_{as}{D}_s}{{(D_s+1)}^2}\\ r_6& 0& -r_7& 0\\ 0& 0& 0& -r_8\end{array}\right).$$

where $T=0+ϵv$, $C_{as}=C_s+ϵv_2$, $F_{\beta }=F_s+ϵv_3$,$D=D_s+ϵv_4$. If the system is stable in the perturbation v then the fix point $(0,C_s,F_s,D_s)$ is stable. The stability of v is given by solving

$$v^{\prime }=(r_1-C_{as}{r}_3)v,n\tau <t<(n+1)\tau$$

(23)

and deriving a different equation such as in the proof on Proposition 2. Integrating (23) on $n\tau <t<(n+1)\tau$ gives us

$${\int }_{v(n{\tau }^{+})}^{v((n+1){\tau }^{-})}\frac{dv}{v}={\int }_{n{\tau }^{+}}^{(n+1){\tau }^{-}}(r_1-r_3{C}_{as}(t))dt$$

$$v((n+1){\tau }^{+})v{(n{\tau }^{-})}^{-1}=exp\left({\int }_{n{\tau }^{+}}^{(n+1){\tau }^{-}}(r_1-r_3{C}_{as}(t))dt\right)$$

$$v_{n+1}=v_{n}exp\left(r_1\tau -r_3{\int }_0^{\tau }{C}_{as}(t)dt\right).$$

(24)

□

Then (24) tends to zero if the argument of exponential is negative:

$$r_1\tau -r_3{\int }_0^{\tau }{C}_{as}(t)dt<0.$$

(25)

It is possible to perform a bifurcation diagram (25) using the parameters from

Table A1. Initial condition of the model.

Variable of the Model	Value	Time Interval	Reference
$T(t)$	$6\times {10}^4$	$[-\tau ,0]$	Piñon-Zárate et al. [8]
$D(t)$	0	$[-\tau ,0]$
$C_a(t)$	0	$[-\tau ,0]$
$F_{\beta }$	0	$[-\tau ,0]$

, but computationally it is hard to obtain it. Taking into account the latter we developed some specific computations in a region that we called “the stable zone” which is a region of dose and period where hypothetical immunotherapy prevents regression of remaining tumor cells after tumor removal. Numerical searching of fixed points was performed in the stable zone and we obtain the following results:

Furthermore, when solved with $d={10}^9$ and $\tau =144$ the Newton method converged to the fixed point $(0,C_s,F_s,D_s)$ which explains the tendency of the system to decay to $T=0$ when a strong immunotherapy is performed.

6. Discussion and Concluding Remarks

Nowadays, one of the most successful therapies in cancer has been immunotherapy. In many laboratories around the world, scientists have observed how lethal tumors such as melanoma or lung cancer seem to shrink after the use of these therapies. Promising immunotherapy used in some laboratories is the infusion of Dendritic cells which have had good results in patients. Furthermore, there are some unanswered questions that must be addressed to have better results; for example, the number of the DCs injected into the patient or the period of the infusion time.

With this in mind, we proposed a model with four ODEs that simulate some interactions between DCs, CTLs, $TGF-\beta$, and tumor cells which allows us to test different hypothetical immunotherapies to find successful operating ranges in the quantities of injected DCs and periods of infusion. The model was evaluated using parameters reported by Kronik et al. [18] and those calculated by the experimental results of Piñon-Zárate et al. [8] and reported by Castillo-Montiel et al. [17]. Although the model is poorly validated with experimental results, in both evaluations and testing the same experiments, the results are very similar, obtaining operating ranges where successful therapies are found and similar sensitivity parameters.

Our results show that the average population growth is between $30\%$ and $69\%$ which is considered as a stable growth, that is, the tumor cells do not grow exponentially and then the cancer is controlled resulting in an increased survival rate. Moreover, the ranges of DCs injected where the therapy is stable are between ${10}^6$ and ${10}^9$, which corresponds to a period of infusion between 168 and 256 h. These results have a good coincidence with experimental results found by Piñon-Zárate et al. [8].

Performing the analysis of sensitivity, it is observed that a change of $\pm 50\%$ in the value of the parameters, we show that the most sensitive parameter is the K (carrying capacity). However, by decreasing the value parameters at $-50\%$, the r (Production rate of tumor cells) presents the greatest change in the population of tumor cells, with a sensitivity value of 2. However, changing the amount of injected DCs from ${10}^7$ to ${10}^9$, the measured sensitivity was $200\%$, so we consider that this term plays a very important role in the model, since its increase causes a considerable decrease in tumor cells. The other parameters present small changes in the population this means that the model presents a low sensitivity.

One of the most sensitive parameter, the maximum rate of tumor growth $r_T=0.1$ per hour, which translates to 2.4 times per day, this is about 2.5 times faster than most experiments suggest. Some authors have noticed that most mammalian cells have evolved to follow the circadian rhythm with doubling times of 24 h, this seems to be also true for melanoma cells [29].

In order to gain insights for the different values of injected DCs and the period of infusion we decided to take a different strategy; instead of using computer simulations, we analyzed the ODE mathematical model proposed using a dynamical system approach. When we consider the system without immunotherapy we obtain two fixed points; the instability of the first fixed-point $E_1$ shows that it is not possible to prevent a relapse of tumor population without pulsed immunotherapy. On the contrary, the stability of $E_2$ exhibits the tendency of the tumor population to go to its caring capacity: $\frac{1}{r_2}=\frac{K}{h_T}$. Another option is to observe if the tumor can stay in a periodic orbit where a threshold of lethality is not surpassed. For instance, a tumor mass of ${10}^5-{10}^9$ cells is clinically not detectable; with ${10}^9-{10}^{12}$ cells it is detectable and over ${10}^{12}$ it is lethal [22]. Besides, we can show that without pulsed immunotherapy it is not expected that the tumor stays in a periodic orbit under a non-lethal threshold because periodic orbits do not exist for our set of parameters.

On the other hand, we studied the possibility of recurrence after removing the tumor with any surgical procedure. This was made analyzing the stability of the fixed point $(0,C_s,F_s,D_s)$ when the immunotherapy is active. The condition of stability of such point is given by Equation (25). This gives us a range of values in the size of injected DCs and the period of injection where the fixed point $(0,C_s,F_s,D_s)$ is stable. This condition can be visualized in Table A1. If the injected DC (d) and the period of infusions ($\tau$) stay in the stable region the recurrence of the tumor can be prevented. For example, the Table A1 shows that it is enough to have periods of infusion of size $\tau =20$ with injections of $d=200,000$ to prevent a recurrence, among other possible protocols identified by the clinicians. Experimental confirmation of this condition is in our plans.

In summary, computational simulation and mathematical analysis can be taken both as a useful tool which provides some insights for the biologists and immunologists to develop new immunotherapy protocols based on DCs, reducing the number of possible therapies saving time and experimentation trials.