Uncertainty of the 2D Resistivity Survey on the Subsurface Cavities
Abstract
1. Introduction
2. Methodology
2.1. Forward-Inverse Modeling
2.2. Data Analysis
3. Results and Discussion
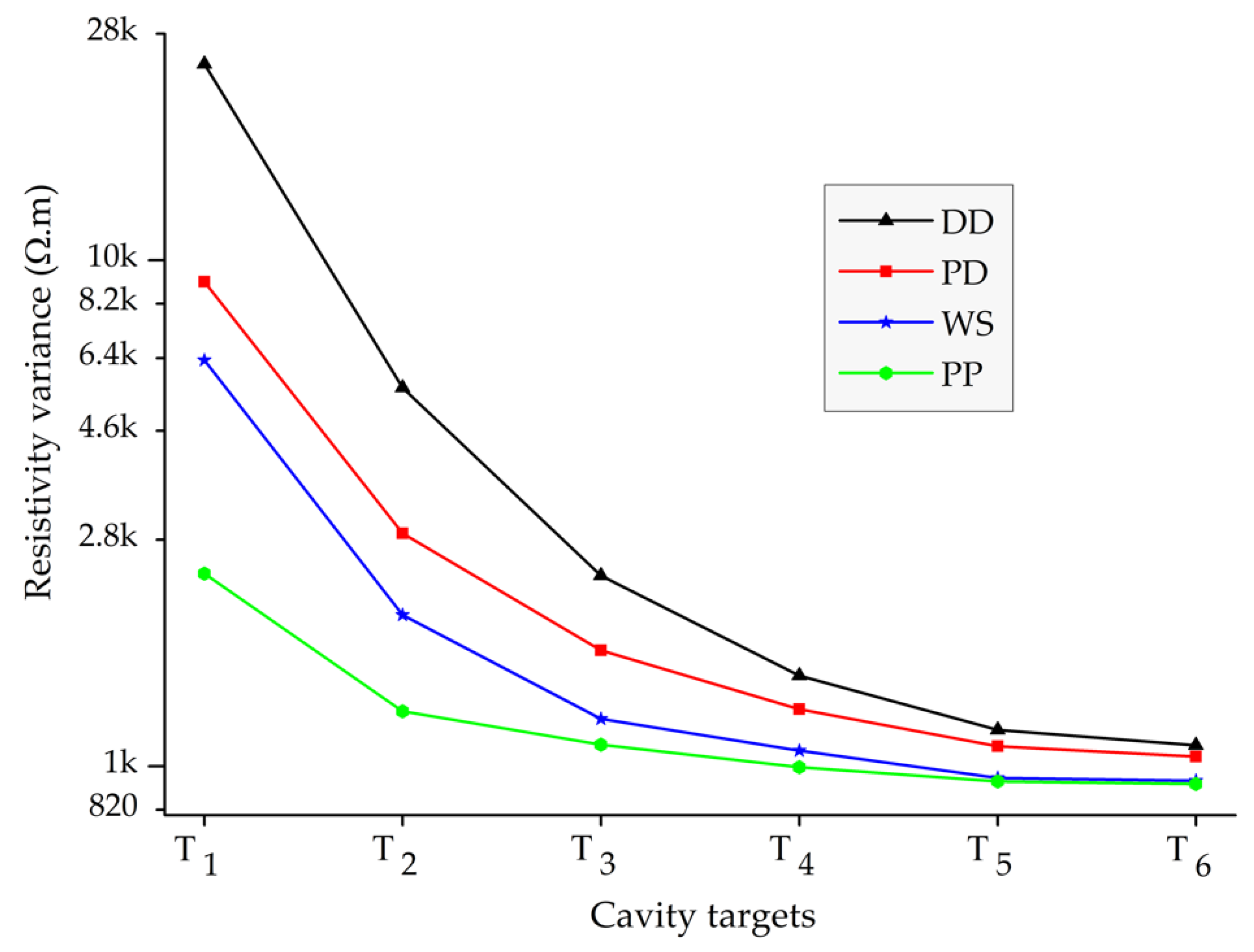
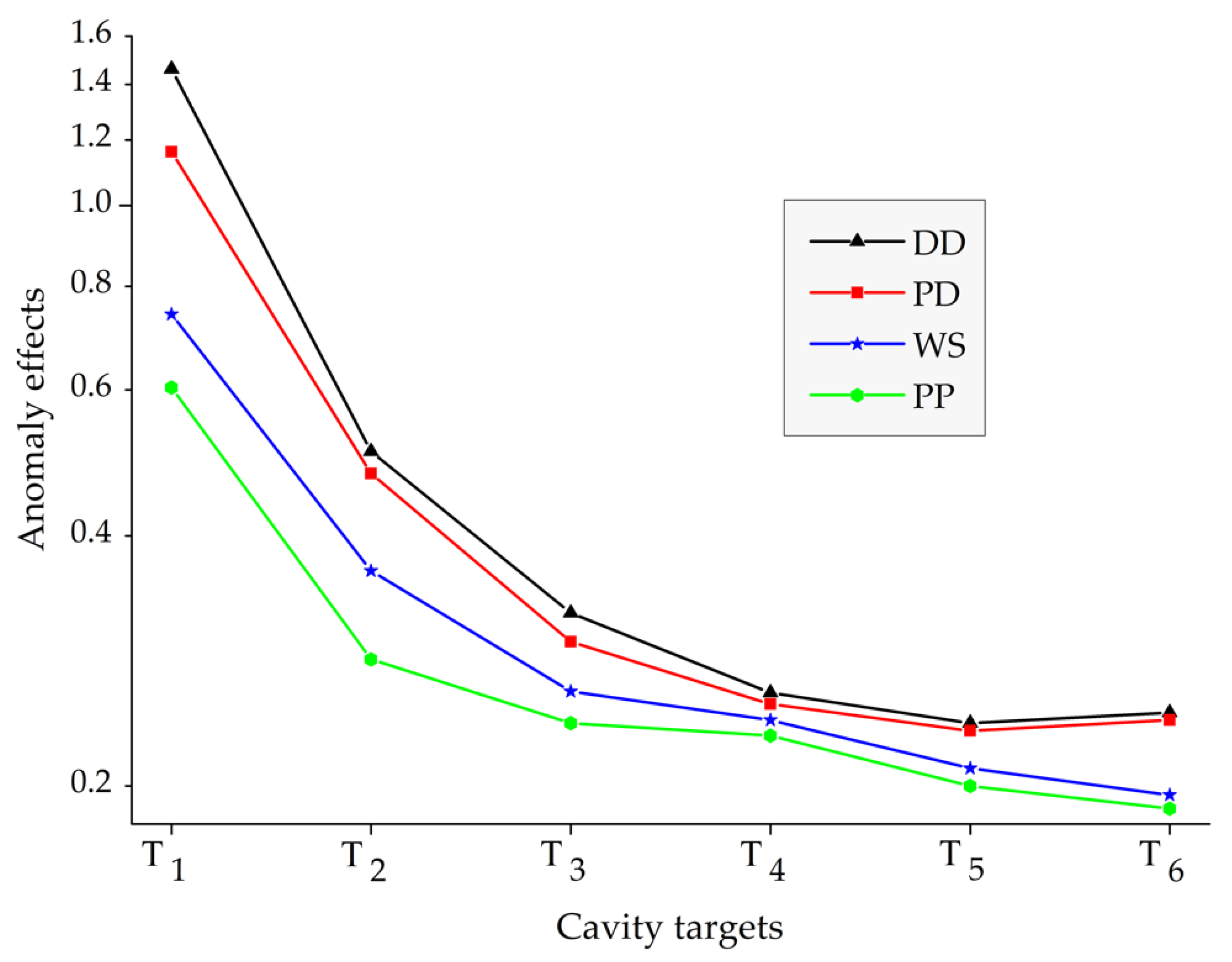
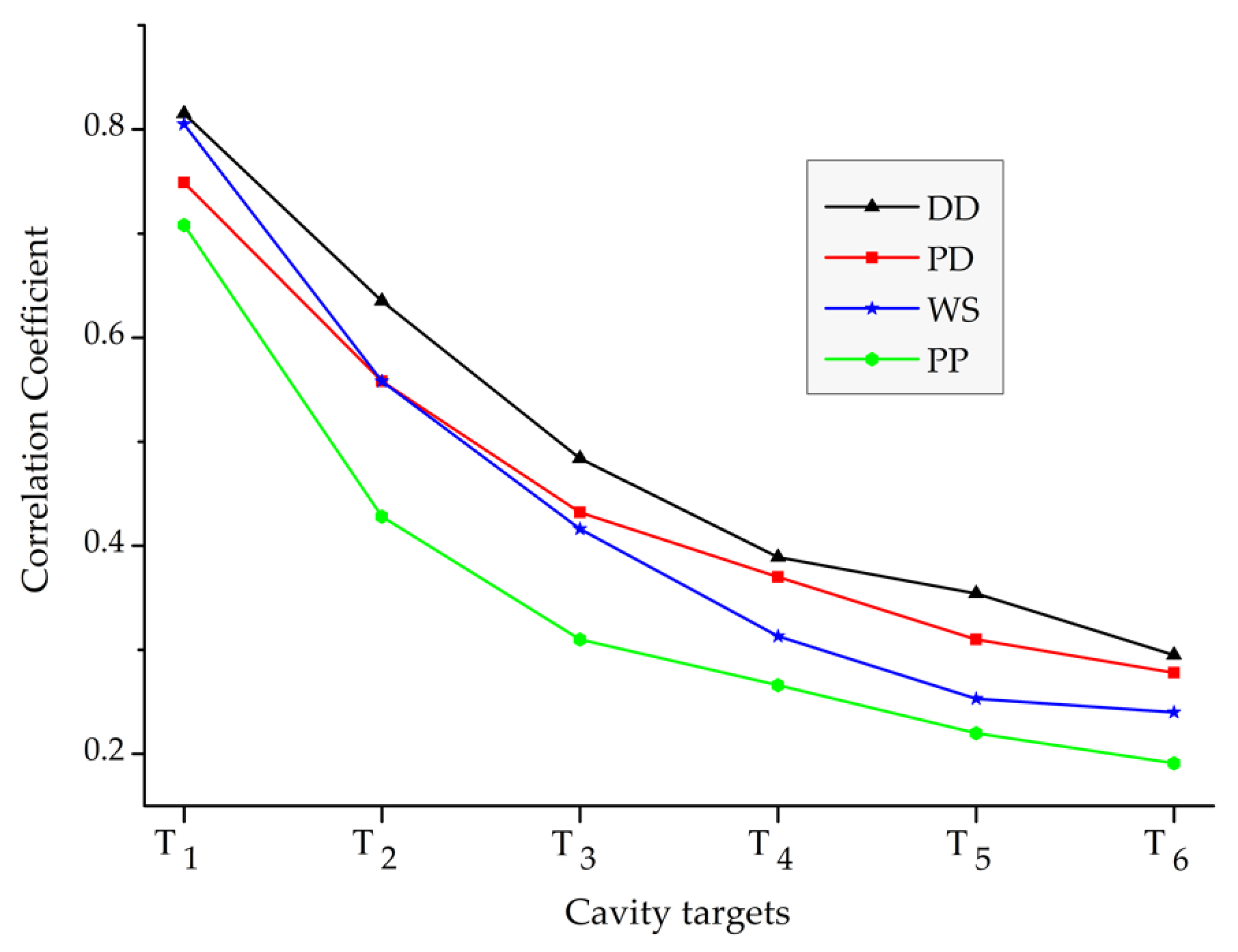
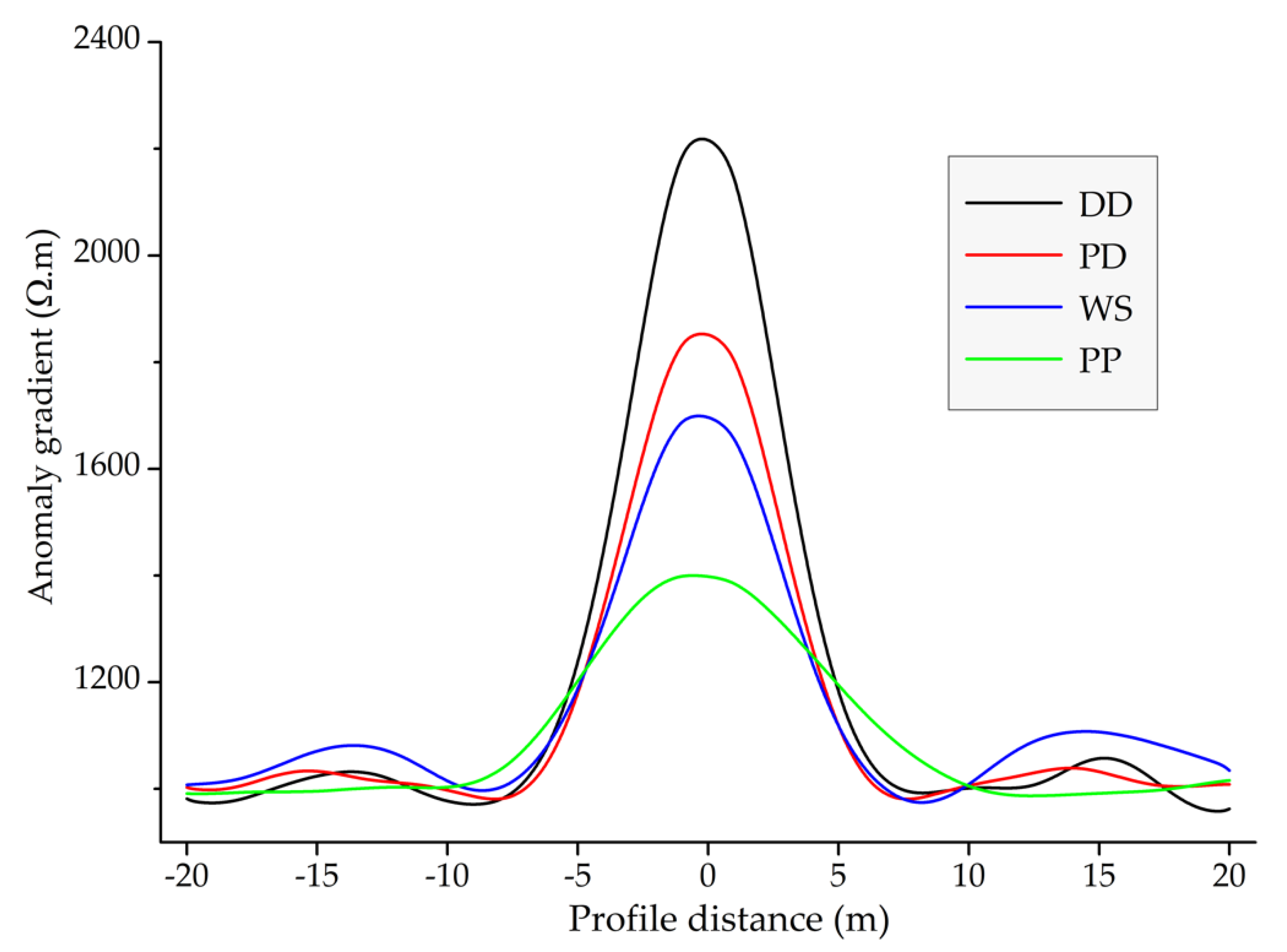
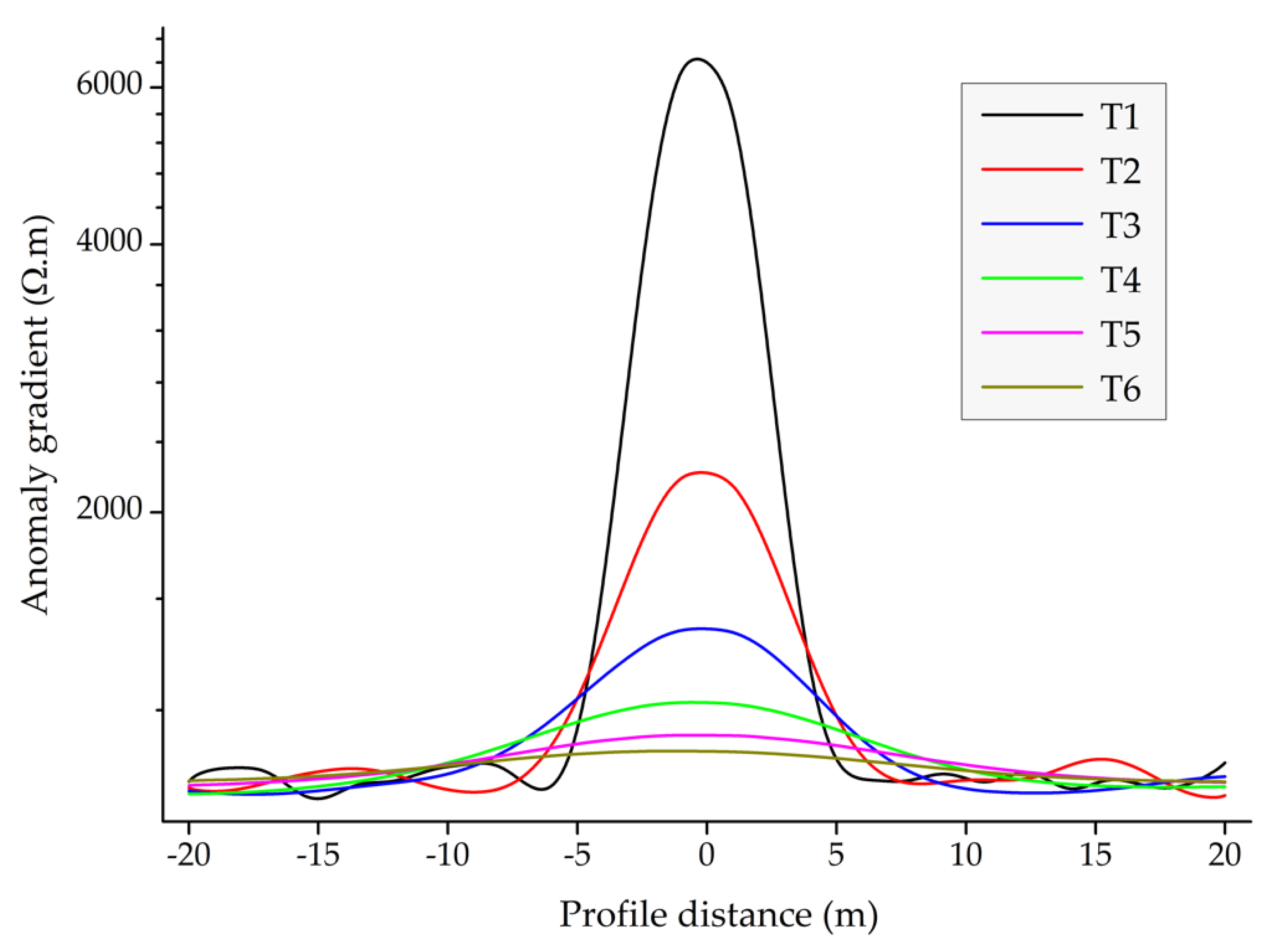
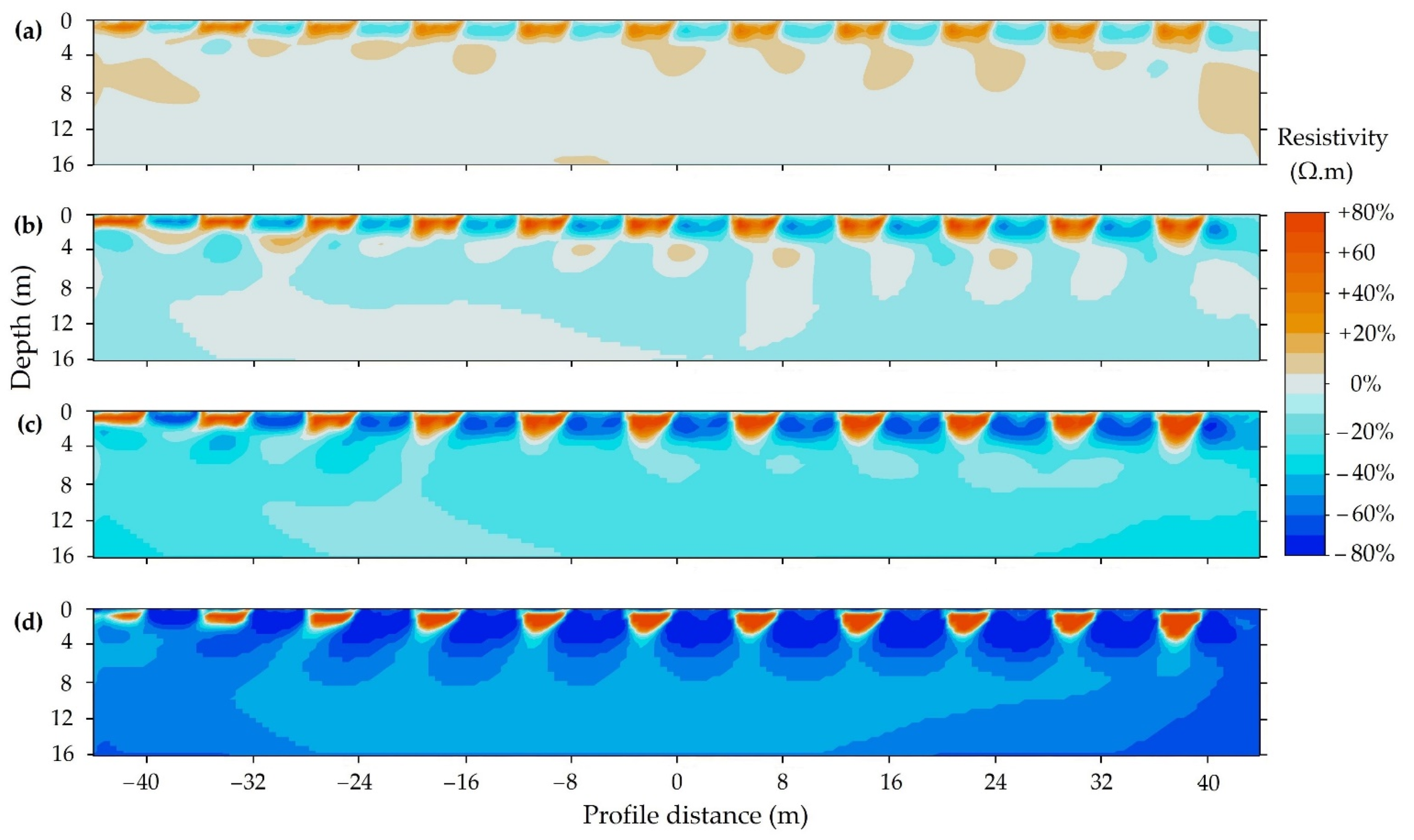
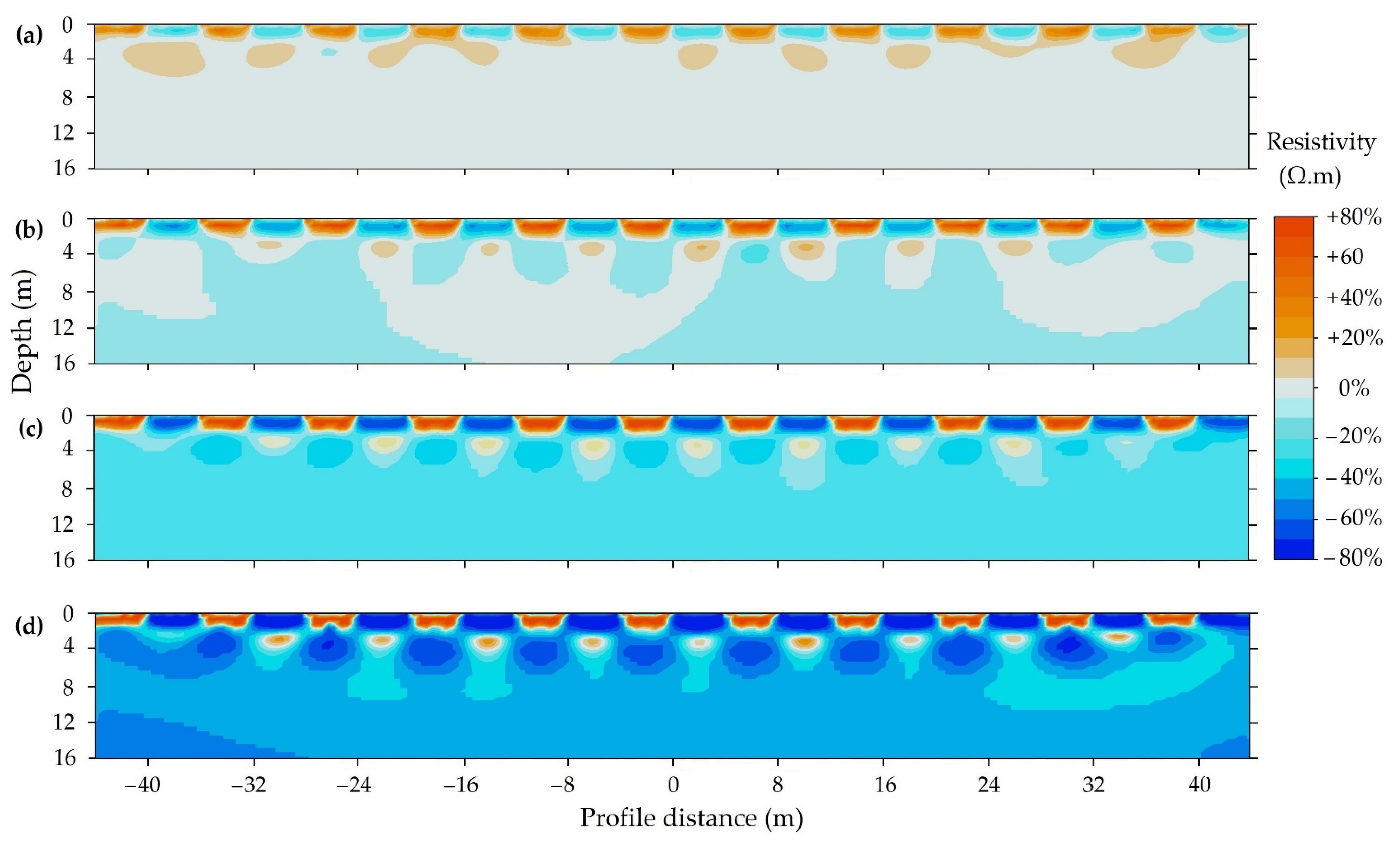
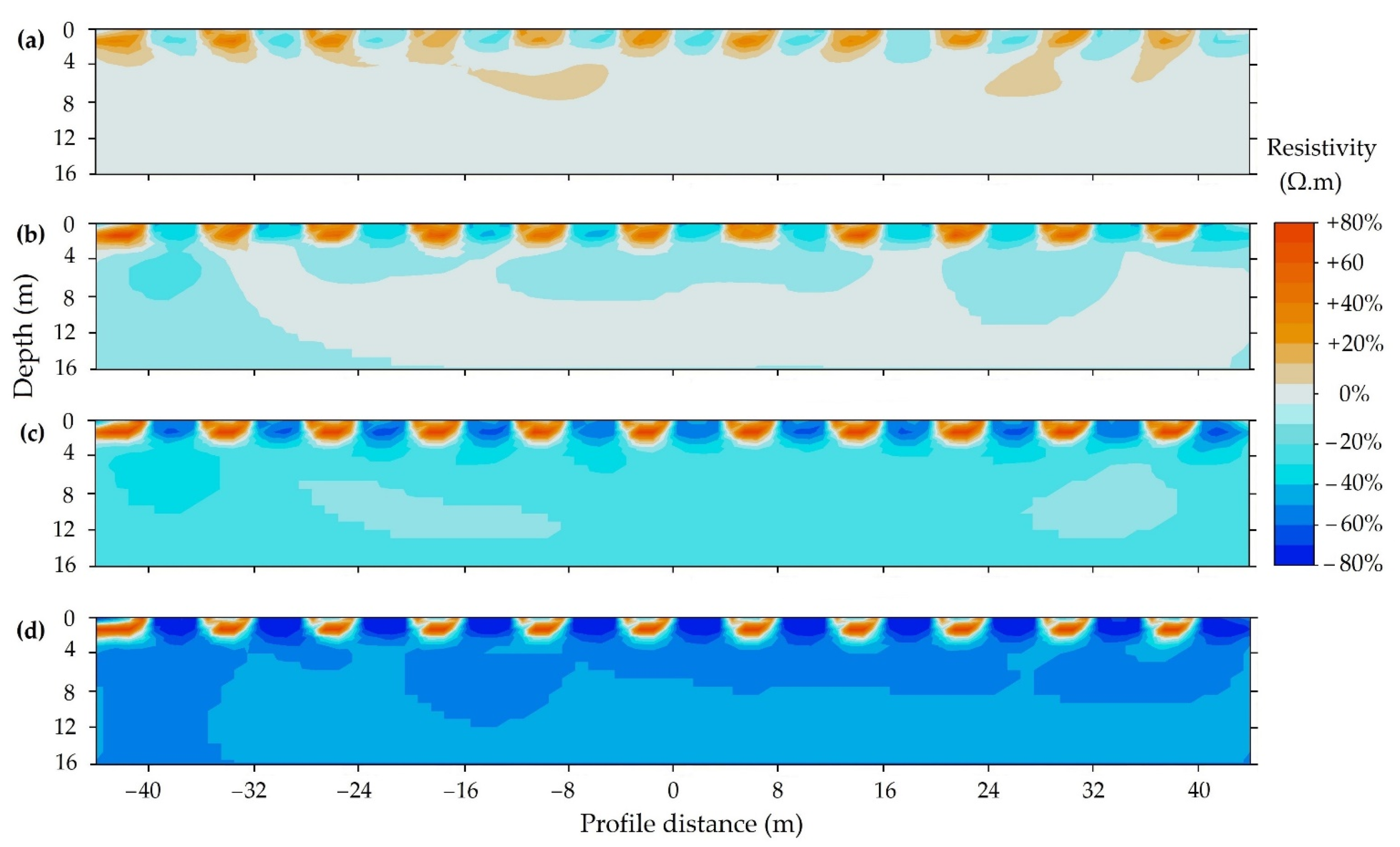
3.1. Array Detection Ability
3.2. Inversion Error
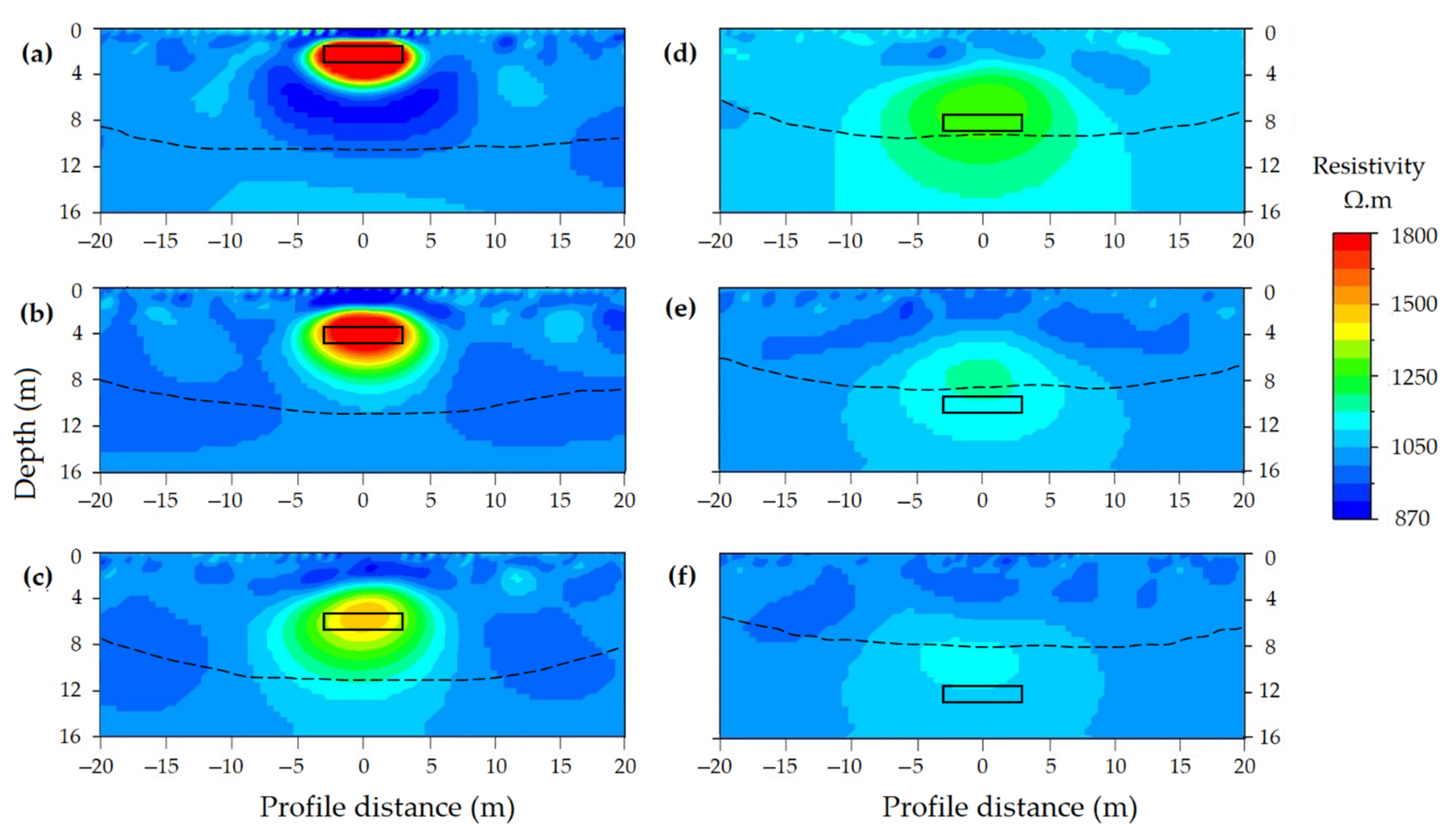
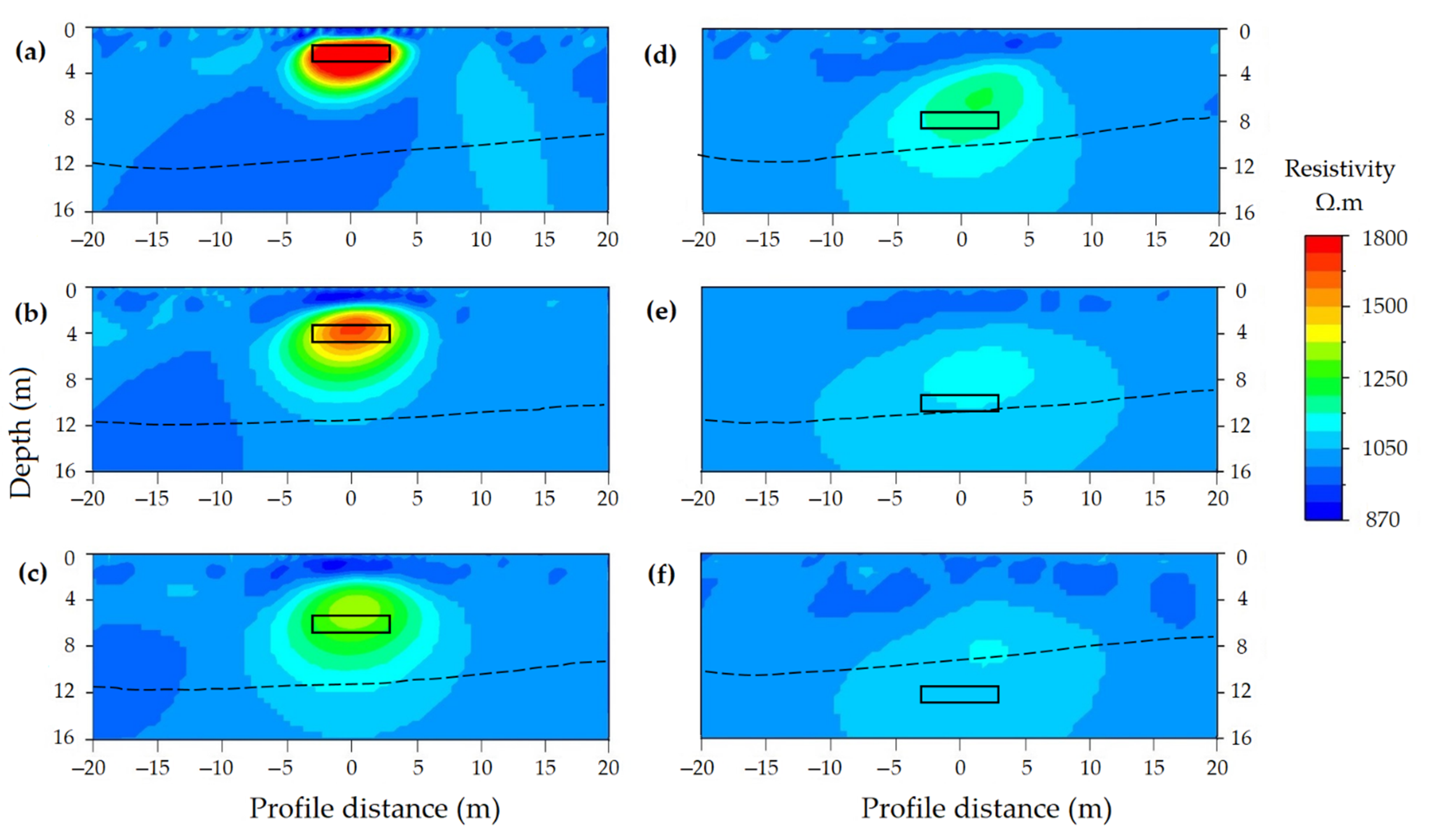
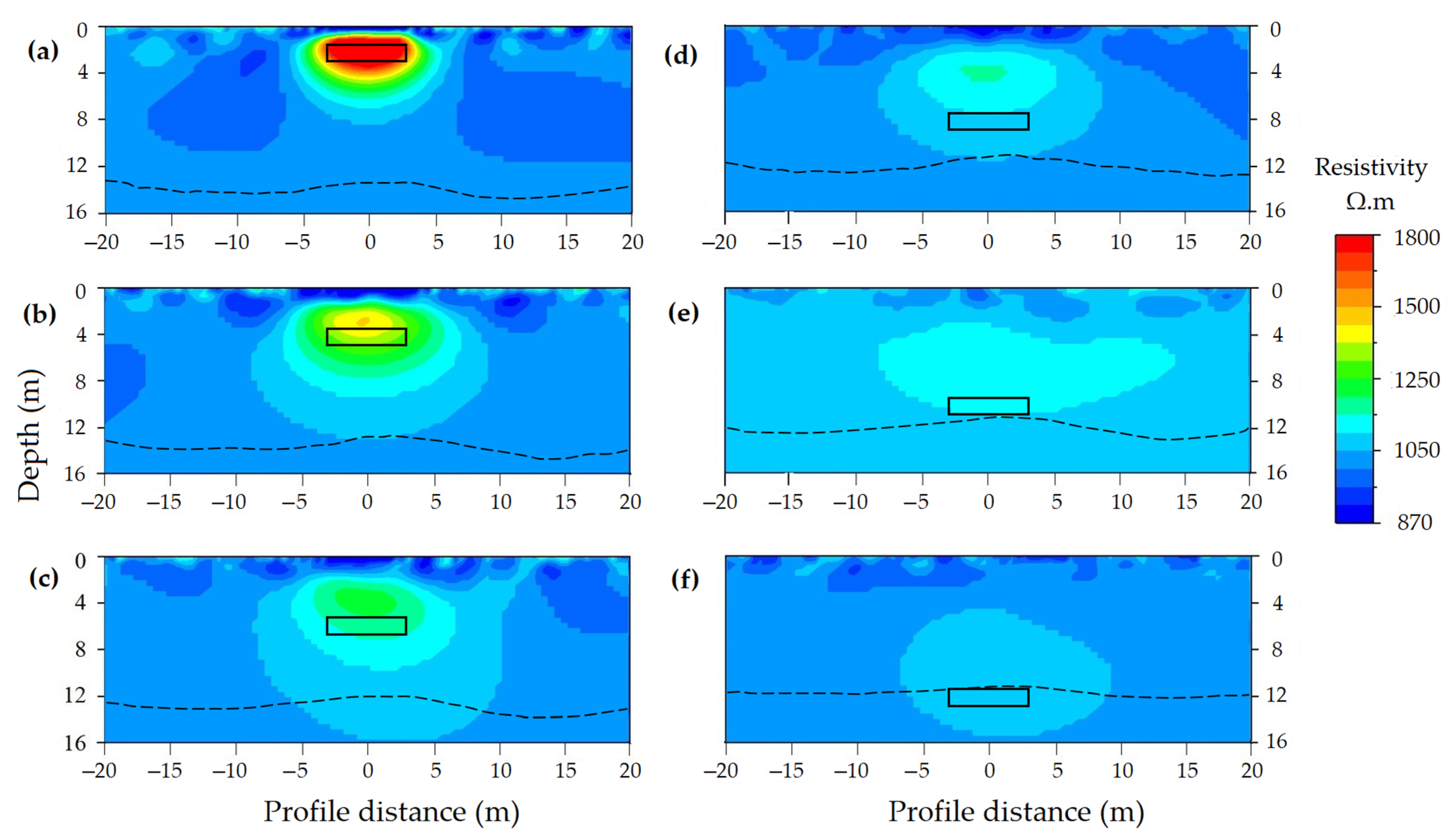
3.3. Model Accuracy, Resolution, and Sensitivity
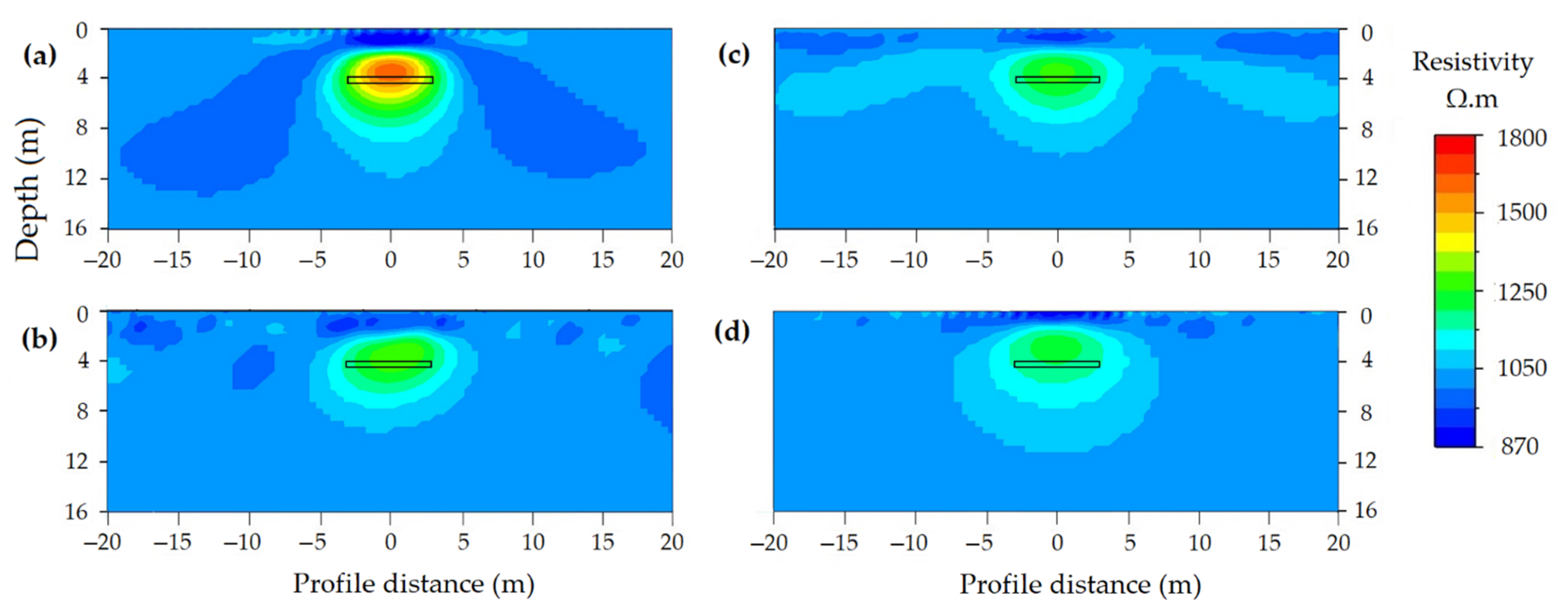
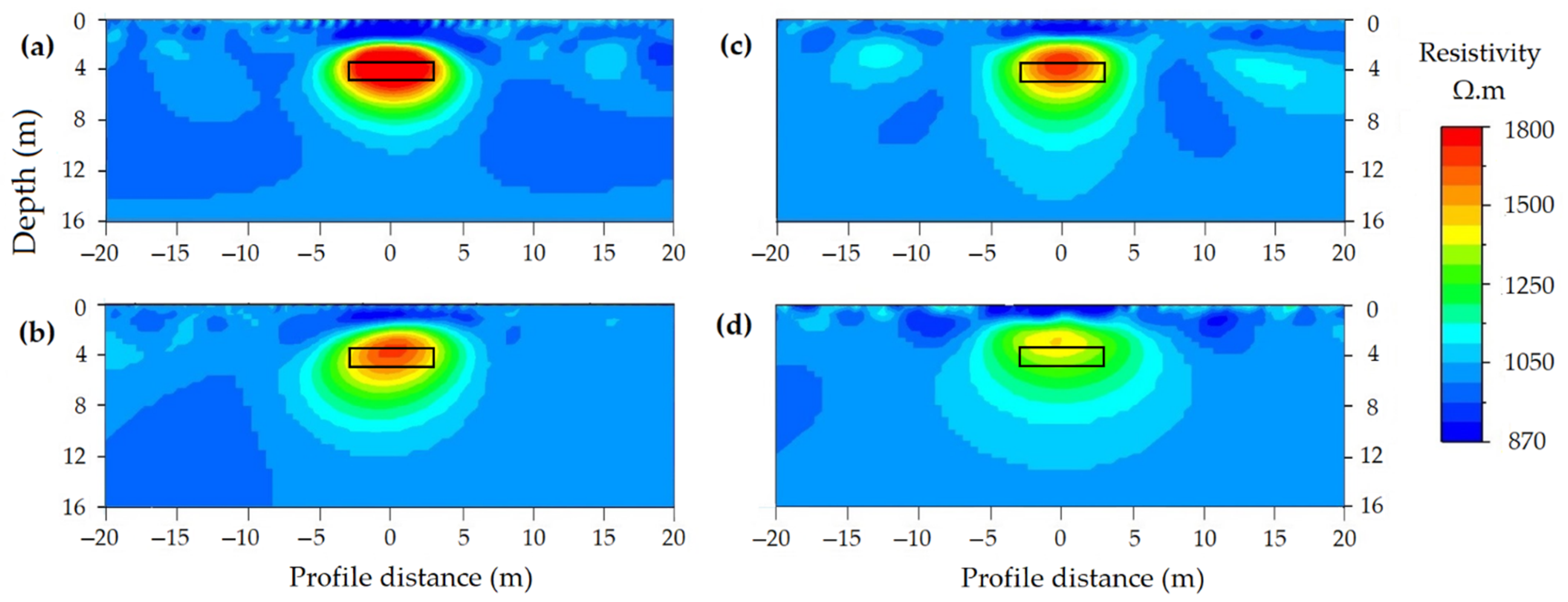
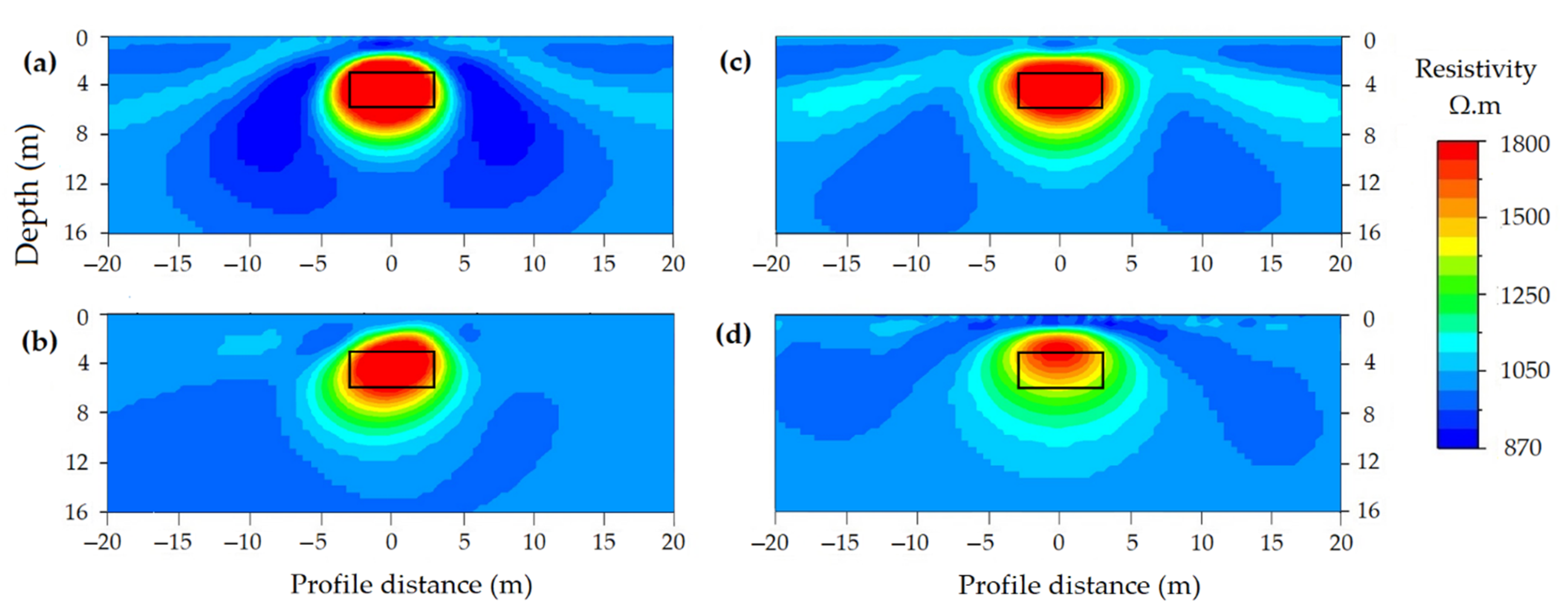
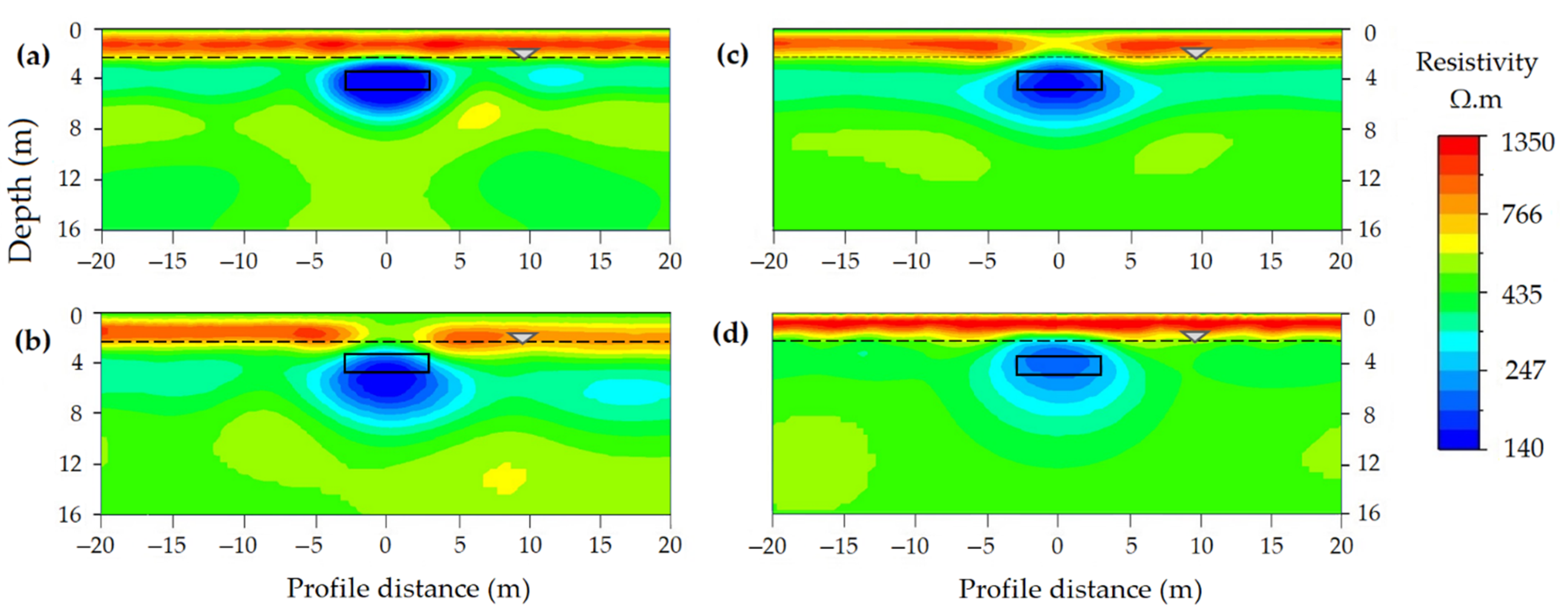
3.3.1. Model Accuracy
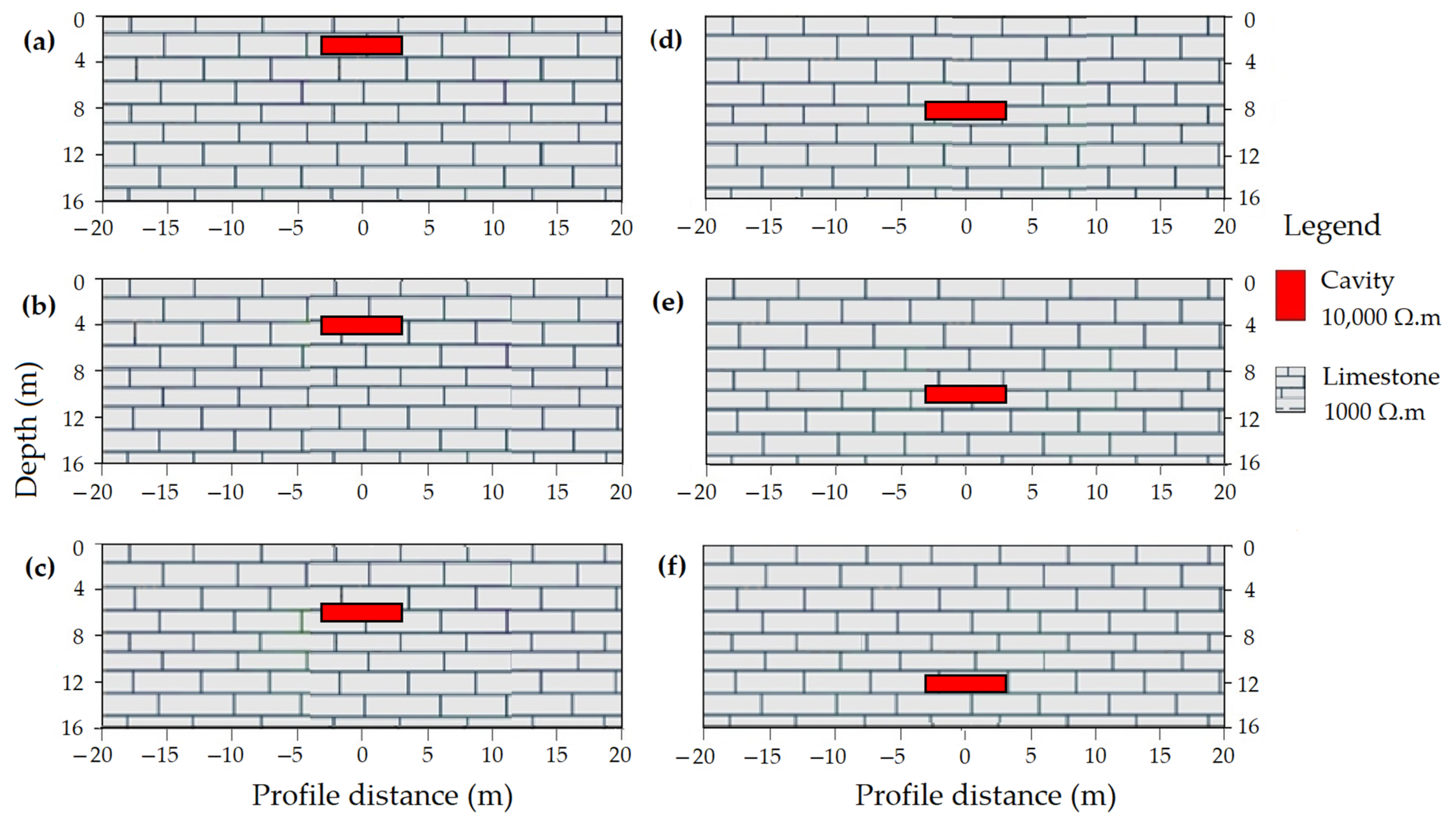
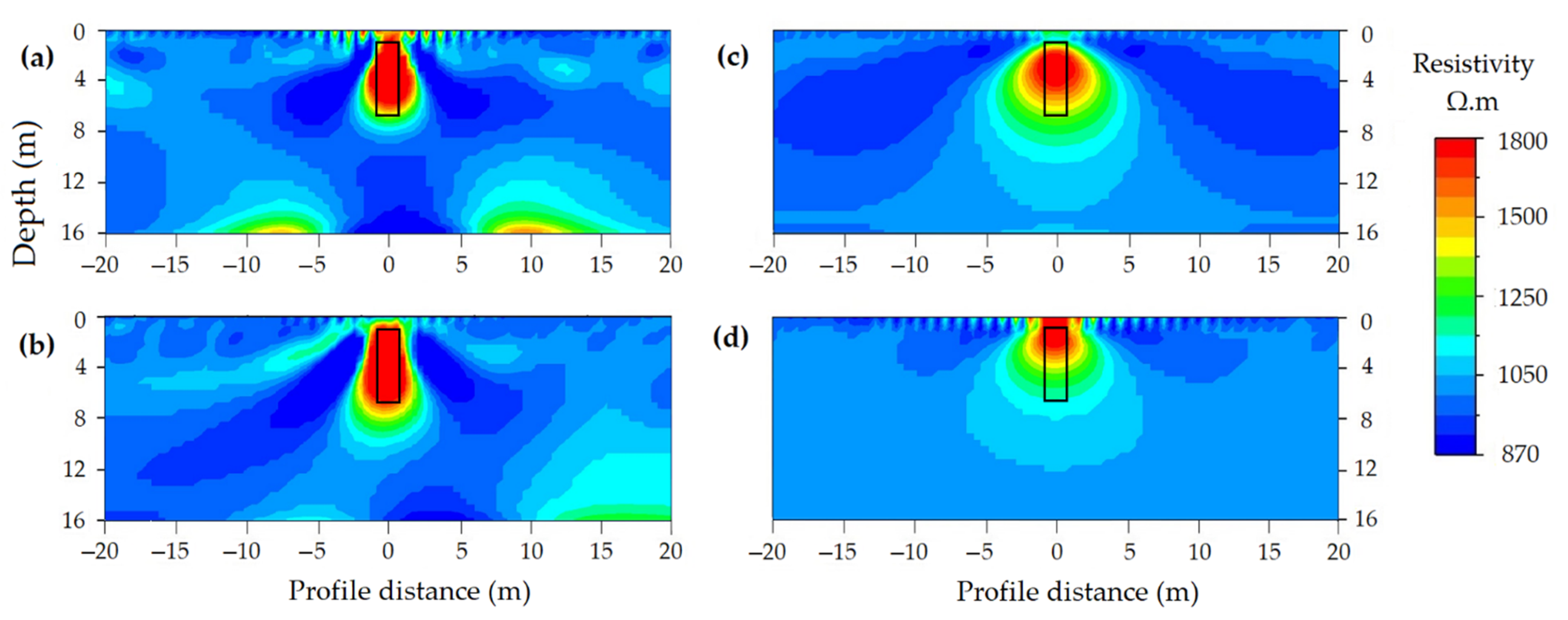
Depth of Cavity
Size of Cavity
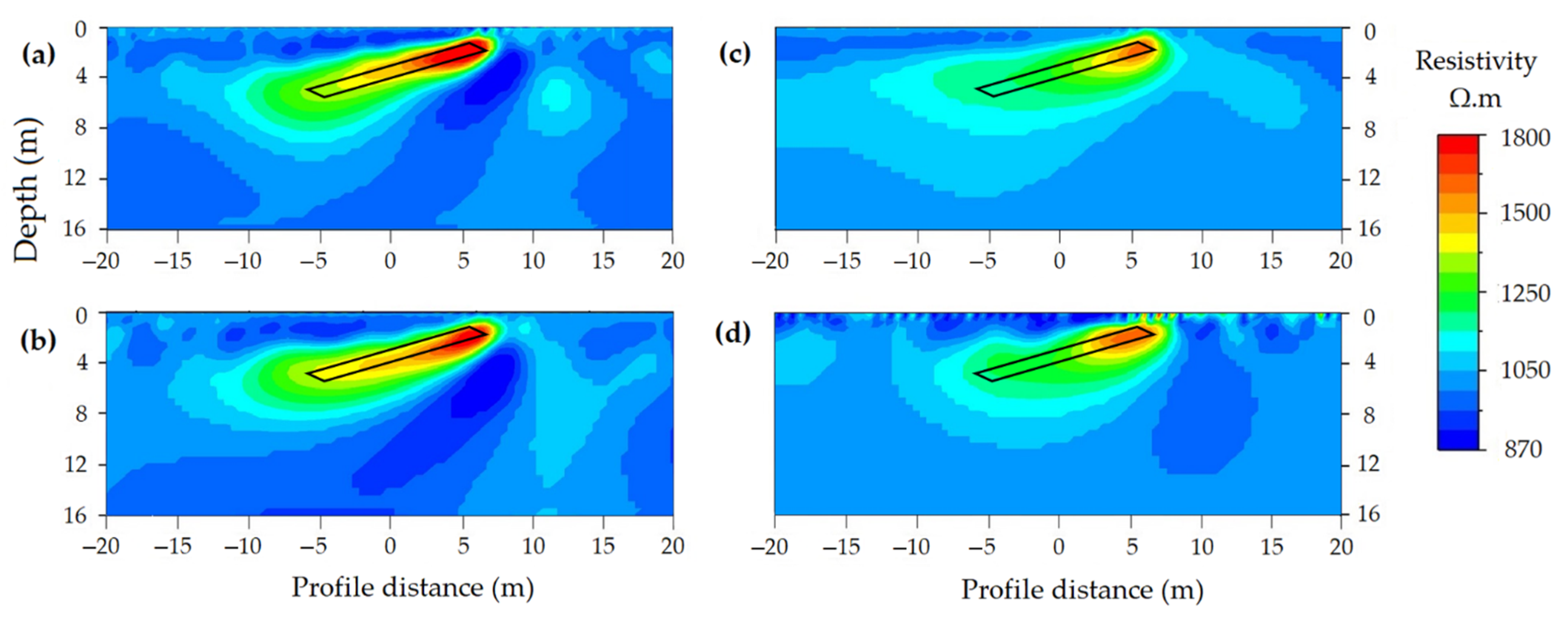
Orientation of Cavity
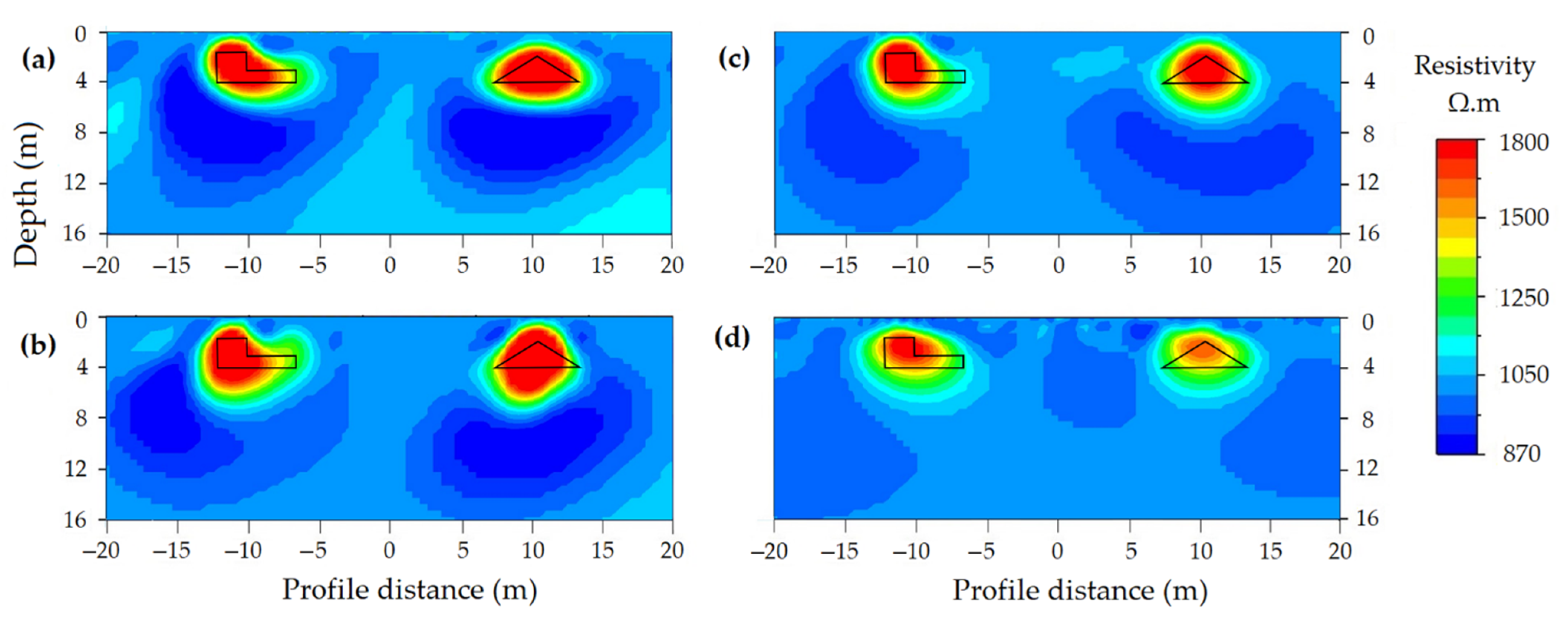
Geometry of Cavity
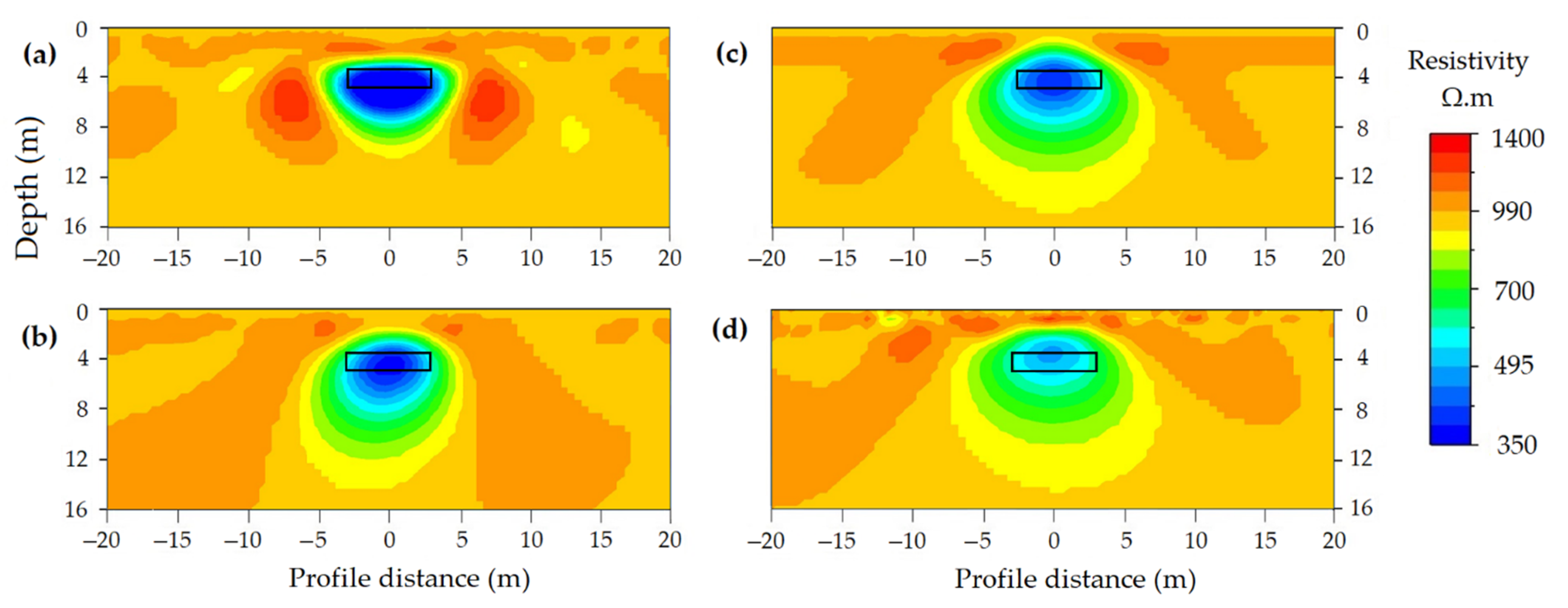
Conductive Cavity Modeling
Experimental Cavity Study
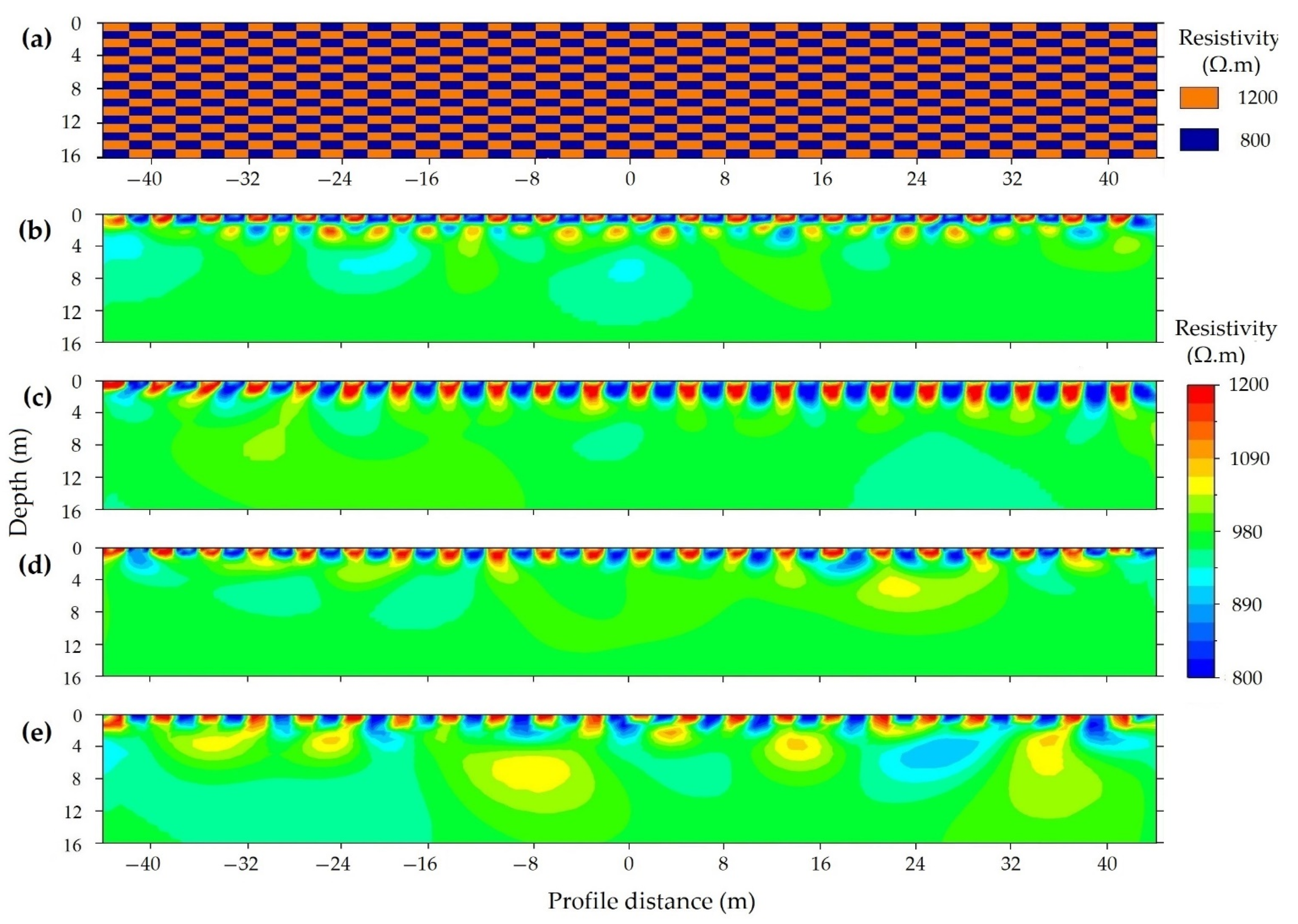
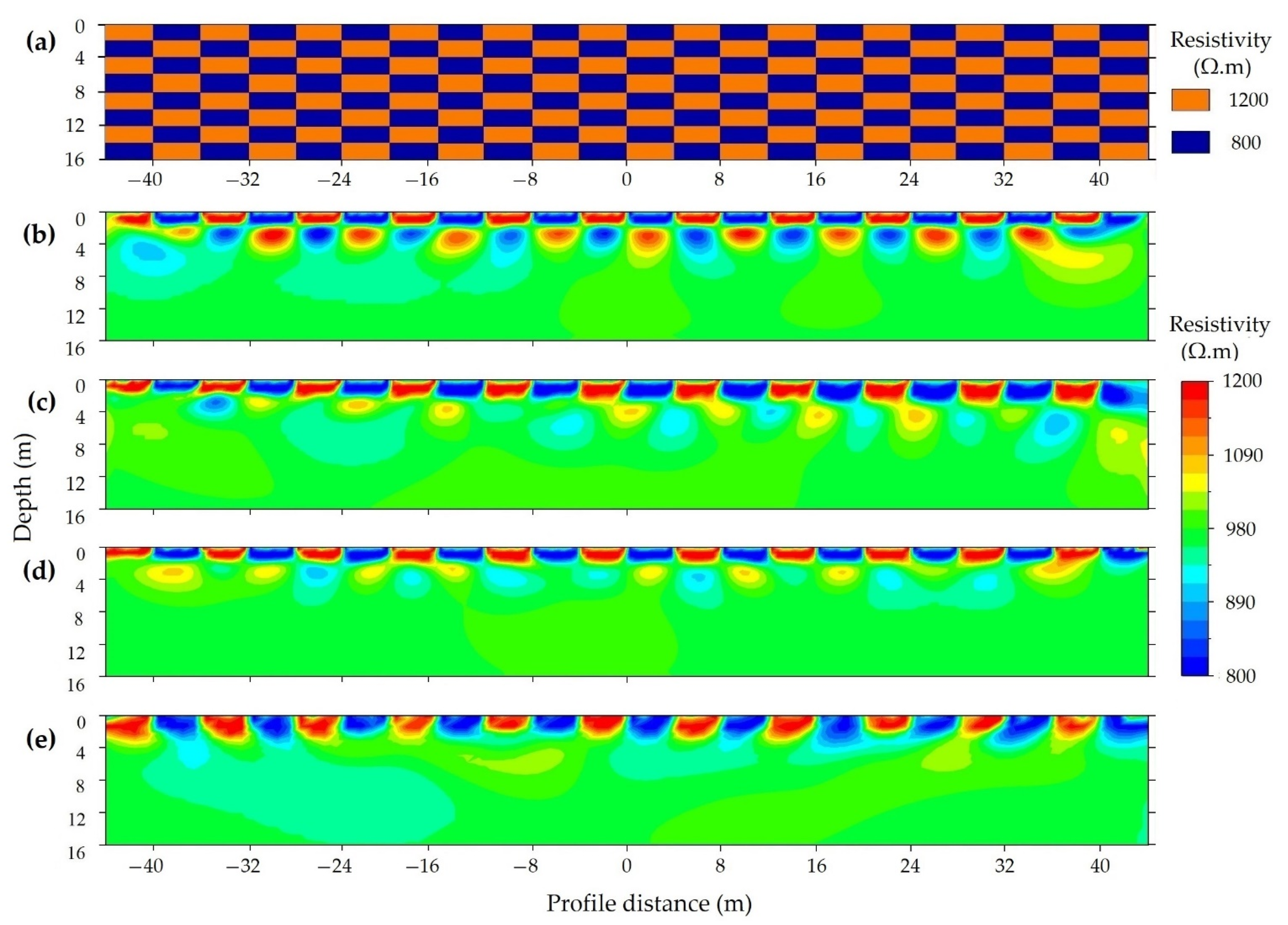
3.3.2. Spatial Resolution
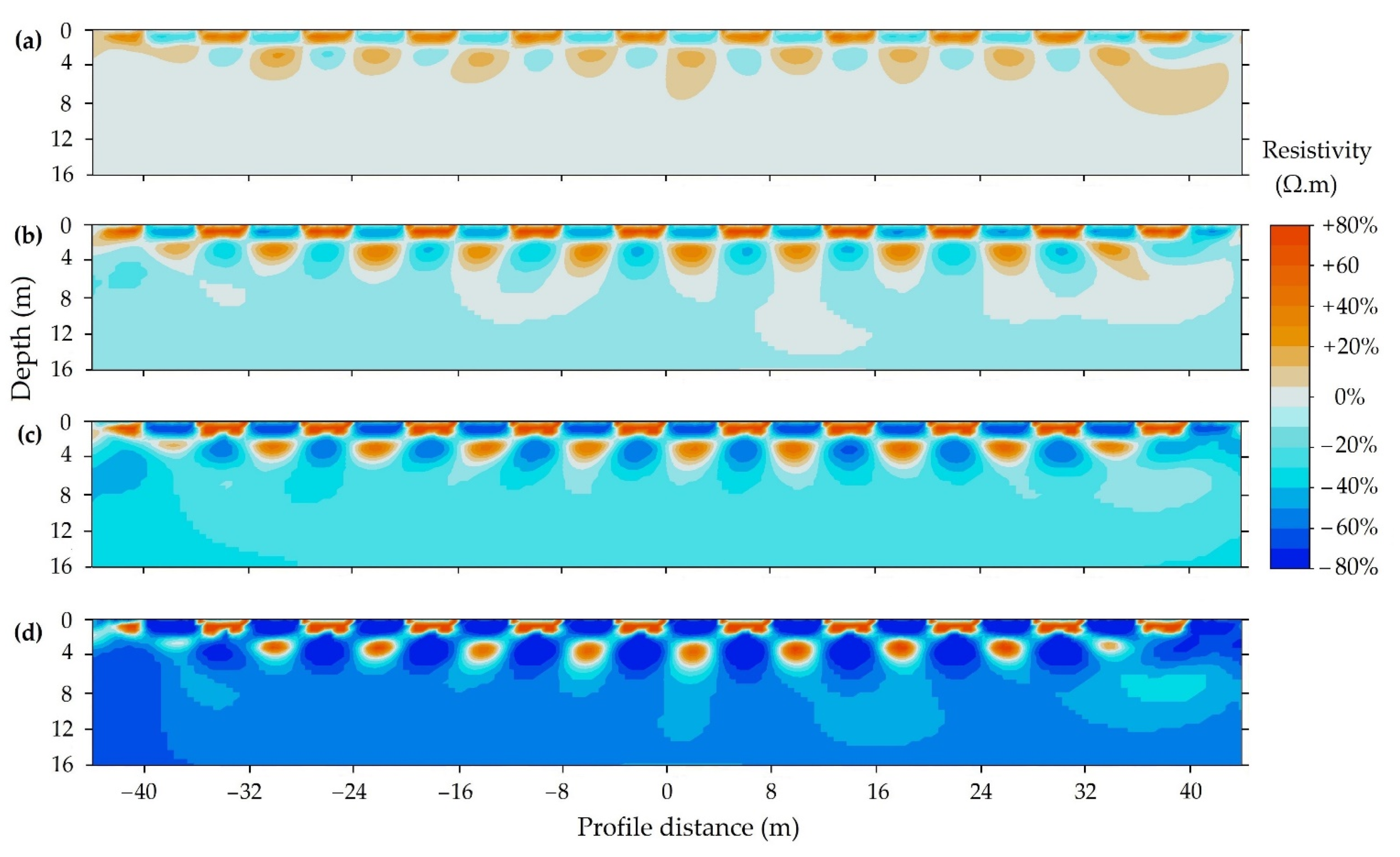
3.3.3. Sensitivity to Resistivity Contrasts
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, P.-Y.; Chang, L.-C.; LEE, T.-Q.; Chan, Y.-C.; Chen, H.-F. Examining Lake-bottom structures with the resistivity imaging method in Ilan’s Da-Hu Lake in Northeastern Taiwan. J. Appl. Geophy. 2015, 119, 170–177. [Google Scholar]
- Fazzito, S.Y.; Rapalini, A.E.; Cortés, J.M.; Terrizzano, C.M. Characterization of Quaternary faults by electric resistivity tomography in the Andean Precordillera of Western Argentina. J. S. Am. Earth Sci. 2009, 28, 217–228. [Google Scholar] [CrossRef]
- Ho, G.-R.; Chang, P.Y.; Lo, W.; Liu, C.-M.; Song, S.-R. New evidence of regional geological structures inferred from reprocessing and resistivity data interpretation in the Chingshui-Sanshing-Hanchi area of Southwestern Ilan County, NE Taiwan. Terr. Atoms. Ocean Sci. 2014, 25, 491. [Google Scholar] [CrossRef][Green Version]
- Tsai, J.P.; Chang, P.Y.; Yeh, T.C.J.; Chang, L.C.; Hsiao, C.T. Constructing the Apparent Geological Model by Fusing Surface Resistivity Survey and Borehole Records. J. Groundw. 2019, 57, 590–601. [Google Scholar] [CrossRef]
- Caputo, R.; Piscitelli, S.; Oliveto, A.; Rizzo, E.; Lapenna, V. The use of electrical resistivity tomographies in active tectonics: Examples from the Tyrnavos Basin, Greece. J. Geodyn. 2003, 36, 19–35. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Chang, L.-C.; Hsu, S.-Y.; Tsai, J.-P.; Chen, W.-F. Estimating the hydrogeological parameters of an unconfined aquifer with the time-lapse resistivity-imaging method during pumping tests: Case studies at the Pengtsuo and Dajou sites, Taiwan. J. Appl. Geophy. 2017, 144, 134–143. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, G.-B.; Chen, C.-C.; Chang, P.-Y.; Wang, T.-P.; Yen, H.-Y.; Dong, J.-J.; Ni, C.-F.; Chen, S.-C.; Chen, C.-W. Imaging rainfall infiltration processes with the time-lapse electrical resistivity imaging method. Pure Appl. Geophys. 2016, 173, 2227–2239. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Chen, C.-c.; Chang, S.-K.; Wang, T.-B.; Wang, C.-Y.; Hsu, S.-K. An investigation into the debris flow induced by Typhoon Morakot in the Siaolin Area, Southern Taiwan, using the electrical resistivity imaging method. Geophys. J. Int. 2012, 188, 1012–1024. [Google Scholar] [CrossRef]
- Drahor, M.G.; Göktürkler, G.; Berge, M.A.; Kurtulmuş, T.Ö. Application of electrical resistivity tomography technique for investigation of landslides: A case from Turkey. J. Environ. Geol. 2006, 50, 147–155. [Google Scholar] [CrossRef]
- Gómez-Ortiz, D.; Martín-Velázquez, S.; Martín-Crespo, T.; De Ignacio-San José, C.; Lillo, J. Application of electrical resistivity tomography to the environmental characterization of abandoned massive sulphide mine ponds (Iberian Pyrite Belt, SW Spain). Near Surf. Geophys. 2010, 8, 65–74. [Google Scholar] [CrossRef]
- Cardarelli, E.; Cercato, M.; Cerreto, A.; Di Filippo, G. Electrical resistivity and seismic refraction tomography to detect buried cavities. Geophys. Prospect. 2010, 58, 685–695. [Google Scholar] [CrossRef]
- Van Schoor, M. Detection of sinkholes using 2D electrical resistivity imaging. J. Appl. Geophy. 2002, 50, 393–399. [Google Scholar] [CrossRef]
- Gabarrón, M.; Martínez-Pagán, P.; Martínez-Segura, M.A.; Bueso, M.C.; Martínez-Martínez, S.; Faz, Á.; Acosta, J.A.J.M. Electrical resistivity tomography as a support tool for physicochemical properties assessment of near-surface waste materials in a mining tailing pond (El Gorguel, SE Spain). Minerals 2020, 10, 559. [Google Scholar] [CrossRef]
- Batayneh, A.T. Archaeogeophysics–archaeological prospection–A mini review. J. King Saud Univ. Sci. 2011, 23, 83–89. [Google Scholar] [CrossRef]
- Mochales, T.; Casas, A.; Pueyo, E.; Pueyo, O.; Román, M.; Pocoví, A.; Soriano, M.; Ansón, D. Detection of underground cavities by combining gravity, magnetic and ground penetrating radar surveys: A case study from the Zaragoza area, NE Spain. Environ. Geol. 2008, 53, 1067–1077. [Google Scholar] [CrossRef]
- Das, P.; Mohanty, P.R. Resistivity imaging technique to delineate shallow subsurface cavities associated with old coal working: A numerical study. Environ. Earth Sci. 2016, 75, 661. [Google Scholar] [CrossRef]
- Loke, M.; Barker, R. Practical techniques for 3D resistivity surveys and data inversion. Geophys. Prospect. 1996, 44, 499–523. [Google Scholar] [CrossRef]
- Sharma, S.; Verma, S. Solutions of the inherent problem of the equivalence in direct current resistivity and electromagnetic methods through global optimization and joint inversion by successive refinement of model space. Geophys. Prospect. 2011, 59, 760–776. [Google Scholar] [CrossRef]
- Orlando, L. GPR to constrain ERT data inversion in cavity searching: Theoretical and practical applications in archeology. J. Appl. Geophy. 2013, 89, 35–47. [Google Scholar] [CrossRef]
- Narayan, S.; Dusseault, M.B.; Nobes, D.C. Inversion techniques applied to resistivity inverse problems. Inverse Probl. 1994, 10, 669. [Google Scholar] [CrossRef]
- Zhou, W.; Beck, B.F.; Adams, A.L. Effective electrode array in mapping karst hazards in electrical resistivity tomography. J. Environ. Geol. 2002, 42, 922–928. [Google Scholar] [CrossRef]
- Loke, M. Tutorial: 2-D and 3-D Electrical Imaging Surveys; Geotomo Software: Penang, Malaysia, 2004. [Google Scholar]
- Yang, X.; Lagmanson, M.B. Planning resistivity surveys using numerical simulations. In Proceedings of the 16th EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems, San Antonio, TX, USA, 6–10 April 2003; p. cp-190-00047. [Google Scholar]
- Santos, F.A.M.; Afonso, A.R.A. Detection and 2D modelling of cavities using pole–dipole array. J. Environ. Geol. 2005, 48, 108–116. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. A numerical comparison of 2D resistivity imaging with 10 electrode arrays. Geophys. Prospect. 2004, 52, 379–398. [Google Scholar] [CrossRef]
- Amini, A.; Ramazi, H. CRSP, numerical results for an electrical resistivity array to detect underground cavities. Open Geosci. 2017, 9, 13–23. [Google Scholar] [CrossRef]
- Martinez-Lopez, J.; Rey, J.; Duenas, J.; Hidalgo, C.; Benavente, J. Electrical Tomography Applied to the Detection of Subsurface Cavites. J. Caves Karst Stud. 2013, 75, 28–37. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Estimating depth of investigation in dc resistivity and IP surveys. Geophysics 1999, 64, 403–416. [Google Scholar] [CrossRef]
- Martorana, R.; Fiandaca, G.; Casas Ponsati, A.; Cosentino, P. Comparative tests on different multi-electrode arrays using models in near-surface geophysics. J. App. Geophy. 2009, 6, 1–20. [Google Scholar] [CrossRef]
- Hassan, A.A.; Kadhim, E.H.; Ahmed, M.T. Performance of Various Electrical Resistivity Configurations for Detecting Buried Tunnels Using 2D Electrical Resistivity Tomography Modelling. Diyala J. Eng. Sc. 2018, 11, 14–21. [Google Scholar] [CrossRef]
- Rezaei, S.; Shooshpasha, I.; Rezaei, H. Reconstruction of landslide model from ERT, geotechnical, and field data, Nargeschal landslide, Iran. Bull. Eng. Geol. Environ. 2019, 78, 3223–3237. [Google Scholar] [CrossRef]
- Eissa, R.; Cassidy, N.; Pringle, J.; Stimpson, I. Electrical resistivity tomography array comparisons to detect cleared-wall foundations in brownfield sites. Q. J. Eng. Geol. 2020, 53, 137–144. [Google Scholar] [CrossRef]
- Park, M.K.; Park, S.; Yi, M.-J.; Kim, C.; Son, J.-S.; Kim, J.-H.; Abraham, A.A. Application of electrical resistivity tomography (ERT) technique to detect underground cavities in a karst area of South Korea. Environ. Earth Sci. 2014, 71, 2797–2806. [Google Scholar] [CrossRef]
- Neyamadpour, A.; Wan Abdullah, W.; Taib, S.; Neyamadpour, B. Comparison of Wenner and dipole–dipole arrays in the study of an underground three-dimensional cavity. J. App. Geophy. 2010, 7, 30–40. [Google Scholar] [CrossRef]
- Boschi, L. Measures of resolution in global body wave tomography. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Mewes, B.; Hilbich, C.; Delaloye, R.; Hauck, C. Resolution capacity of geophysical monitoring regarding permafrost degradation induced by hydrological processes. Cryosphere 2017, 11, 2957–2974. [Google Scholar] [CrossRef]
- Butler, D.J.N.-S.G.; Activity, H. Detection and characterization of subsurface cavities, tunnels and abandoned mines. Near Surf. Geophys. Hum. Act. 2008, 578–584. [Google Scholar]
- Satitpittakul, A.; Vachiratienchai, C.; Siripunvaraporn, W. Factors influencing cavity detection in Karst terrain on two-dimensional (2-D) direct current (DC) resistivity survey: A case study from the western part of Thailand. Eng. Geol. 2013, 152, 162–171. [Google Scholar] [CrossRef]
- Smith, R.C.; Sjogren, D.B. An evaluation of electrical resistivity imaging (ERI) in Quaternary sediments, southern Alberta, Canada. Geosphere 2006, 2, 287–298. [Google Scholar] [CrossRef][Green Version]
- Keller, G.V.; Carmichael, R. Electrical properties of rocks and minerals. CRC Handb. Phys. Prop. Rocks 1982, 1, 217–293. [Google Scholar]
- Lowrie, W.; Fichtner, A. Fundamentals of Geophysics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Zhao, D.; Hasegawa, A.; Kanamori, H. Deep structure of Japan subduction zone as derived from local, regional, and teleseismic events. J. Geophys. Res. Solid Earth 1994, 99, 22313–22329. [Google Scholar] [CrossRef]
- Zhao, D.; Yanada, T.; Hasegawa, A.; Umino, N.; Wei, W. Imaging the subducting slabs and mantle upwelling under the Japan Islands. Geophys. J. Int. 2012, 190, 816–828. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B.; Lin, G.; Ouyang, Y.; Wang, T.; Xu, S.; Song, L.; Wang, R. Three-Dimensional P-wave Velocity Structure of the Zhuxi Ore Deposit, South China Revealed by Control-Source First-Arrival Tomography. Minerals 2020, 10, 148. [Google Scholar] [CrossRef]
- Athanasiou, E.; Tsourlos, P.; Papazachos, C.; Tsokas, G. Combined weighted inversion of electrical resistivity data arising from different array types. J. App. Geophy. 2007, 62, 124–140. [Google Scholar] [CrossRef]
- Günther, T. Inversion Methods and Resolution Analysis for the 2D/3D reconstRuction of Resistivity Structures from DC Measurements; Universitätsbibliothek der TU BAF: Freiberg, Germany, 2005. [Google Scholar]
- Okpoli, C.C. Sensitivity and resolution capacity of electrode configurations. Geophys. J. Int. 2013, 2013, 608037. [Google Scholar] [CrossRef]
- Oldenborger, G.A.; Routh, P.S.; Knoll, M.D. Sensitivity of electrical resistivity tomography data to electrode position errors. Geophys. J. Int. 2005, 163, 1–9. [Google Scholar] [CrossRef]
- AGI. Instruction Manual for EarthImager™ 2D Version 2.4. 0.; Advanced Geosciences, Inc.: Austin, TX, USA, 2009. [Google Scholar]
- Rubin, Y.; Hubbard, S.S. Hydrogeophysics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 50. [Google Scholar]
- Wolke, R.; Schwetlick, H. Iteratively reweighted least squares: Algorithms, convergence analysis, and numerical comparisons. SIAM J. Sci. Comput. 1988, 9, 907–921. [Google Scholar] [CrossRef]
- Degroot-Hedlin, C.; Constable, S. Occam’s inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics 1990, 55, 1613–1624. [Google Scholar] [CrossRef]
- Ren, Z.; Kalscheuer, T. Uncertainty and resolution analysis of 2D and 3D inversion models computed from geophysical electromagnetic data. Surv. Geophys. 2020, 41, 47–112. [Google Scholar] [CrossRef]
- Militzer, H.; Rösler, R.; Lösch, W. Theoretical and experimental investigations for cavity research with geoelectrical resistivity methods. Geophys. Prospect. 1979, 27, 640–652. [Google Scholar] [CrossRef]
- Aizebeokhai, A.; Olayinka, A. Anomaly effects of arrays for 3d geoelectrical resistivity imaging using orthogonal or parallel 2d profiles. Afr. J. Environ. Sci. Technol. 2010, 4, 446–454. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Hilbich, C.; Marescot, L.; Hauck, C.; Loke, M.; Mäusbacher, R. Applicability of electrical resistivity tomography monitoring to coarse blocky and ice-rich permafrost landforms. Permafr. Periglac. Process. 2009, 20, 269–284. [Google Scholar] [CrossRef]
- Yang, X.; Chen, X.; Carrigan, C.R.; Ramirez, A.L. Uncertainty quantification of CO2 saturation estimated from electrical resistance tomography data at the Cranfield site. Int. J. Greenh. Gas Control. 2014, 27, 59–68. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Hauck, C.; Mühll, D.V. Inversion and interpretation of two-dimensional geoelectrical measurements for detecting permafrost in mountainous regions. Permafr. Periglac. Process. 2003, 14, 305–318. [Google Scholar] [CrossRef]
- Olayinka, A.; Yaramanci, U.; Geophysics, E. Choice of the best model in 2-D geoelectrical imaging: Case study from a waste dump site. Eur. J. Environ. Sci. 1999, 3, 221–244. [Google Scholar]
- Carey, A.M.; Paige, G.B.; Carr, B.J.; Dogan, M.J. Forward modeling to investigate inversion artifacts resulting from time-lapse electrical resistivity tomography during rainfall simulations. J. Appl. Geophy. 2017, 145, 39–49. [Google Scholar] [CrossRef]
- Caterina, D.; Beaujean, J.; Robert, T.; Nguyen, F. A comparison study of different image appraisal tools for electrical resistivity tomography. Near Surf. Geophys. 2013, 11, 639–658. [Google Scholar] [CrossRef]
- Seaton, W.J.; Burbey, T.J. Evaluation of two-dimensional resistivity methods in a fractured crystalline-rock terrane. J. Appl. Geophy. 2002, 51, 21–41. [Google Scholar] [CrossRef]
- Kim, J.-H.; Yi, M.-J.; Hwang, S.-H.; Song, Y.; Cho, S.-J.; Synn, J.-H. Integrated geophysical surveys for the safety evaluation of a ground subsidence zone in a small city. J. Geophys. Eng. 2007, 4, 332–347. [Google Scholar] [CrossRef]
- Festa, V.; Fiore, A.; Parise, M.; Siniscalchi, A.; Studies, K. Sinkhole evolution in the Apulian karst of southern Italy: A case study, with some considerations on sinkhole hazards. J Caves Karst Stud. 2012, 74, 137–147. [Google Scholar] [CrossRef]
- Muhammad, F.; Samgyu, P.; Young, S.S.; Ho Kim, J.; Mohammad, T.; Adepelumi, A.A. Subsurface cavity detection in a karst environment using electrical resistivity (er): A case study from yongweol-ri, South Korea. Earth Sci. Res. J. 2012, 16, 75–82. [Google Scholar]
- Saribudak, M.; Hawkins, A.; Stoker, K. Do air-filled caves cause high resistivity anomalies? A six-case study from the Edwards Aquifer Recharge Zone in San Antonio, Texas. Houst. Geol. Soc. Bull. 2012, 54, 41–49. [Google Scholar]
- Gourdol, L.; Clément, R.; Juilleret, J.; Pfister, L.; Hissler, C. Large-scale ERT surveys for investigating shallow regolith properties and architecture. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–39. [Google Scholar]
- Nimmer, R.E.; Osiensky, J.L.; Binley, A.M.; Williams, B.C. Three-dimensional effects causing artifacts in two-dimensional, cross-borehole, electrical imaging. J. Hydrol. 2008, 359, 59–70. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A. Electrical resistance tomography during in-situ trichloroethylene remediation at the Savannah River Site. J. Appl. Geophy. 1995, 33, 239–249. [Google Scholar] [CrossRef]
- Verdet, C.; Anguy, Y.; Sirieix, C.; Clément, R.; Gaborieau, C. On the effect of electrode finiteness in small-scale electrical resistivity imaging. Geophysics 2018, 83, EN39–EN52. [Google Scholar] [CrossRef]
- Rucker, D.F.; Loke, M.H.; Levitt, M.T.; Noonan, G.E. Electrical-resistivity characterization of an industrial site using long electrodes. Geophysics 2010, 75, WA95–WA104. [Google Scholar] [CrossRef]
- Hermawan, O.R.; Putra, D.P.E. the effectiveness of wenner-schlumberger and dipole-dipole array of 2d geoelectrical survey to detect the occurring of groundwater in the gunung kidul karst aquifer system, Yogyakarta, Indonesia. J. Appl. Geol. 2016, 1, 71–81. [Google Scholar] [CrossRef]
- Andrej, M.; Uros, S.; Studies, K. Electrical Resistivity Imaging of Cave Divaska Jama, Solvania. J. Caves Karst. Stud. 2012, 74, 235–242. [Google Scholar] [CrossRef]
- Dahlin, T.; Loke, M.H. Resolution of 2D Wenner resistivity imaging as assessed by numerical modelling. J. Appl. Geophy. 1998, 38, 237–249. [Google Scholar] [CrossRef]
- Adepelumi, A.; Fayemi, O. Joint application of ground penetrating radar and electrical resistivity measurements for characterization of subsurface stratigraphy in Southwestern Nigeria. J. Geophys. Eng. 2012, 9, 397–412. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]






| Adequacy of Arrays for Cavity | DD | PD | WS | PP |
|---|---|---|---|---|
| Shallow depth (≲4 m) 1 | xxx | xxx | xxx | xx |
| Intermediate depth (≲8 m and >4 m) 1 | xx | x | x | x |
| Deeper depth (>8 m) 1 | x | x | x | - |
| Small size (≲0.5 m) 2 | x | - | - | - |
| Intermediate size (≲3 m and >0.5 m) 2 | xxx | xx | xx | x |
| Large size (>3 m) 2 | xxx | xxx | xxx | xx |
| Horizontal cavity 1,2 | xxx | xx | xx | x |
| Vertical cavity 1 | xx | xx | x | x |
| Inclined cavity 1 | xxx | xxx | x | x |
| Dry clay-filled cavity 1,2 | xxx | x | xx | x |
| Saturated clay-filled cavity 1,2 | xxx | xxx | xxx | xx |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doyoro, Y.G.; Chang, P.-Y.; Puntu, J.M. Uncertainty of the 2D Resistivity Survey on the Subsurface Cavities. Appl. Sci. 2021, 11, 3143. https://doi.org/10.3390/app11073143
Doyoro YG, Chang P-Y, Puntu JM. Uncertainty of the 2D Resistivity Survey on the Subsurface Cavities. Applied Sciences. 2021; 11(7):3143. https://doi.org/10.3390/app11073143
Chicago/Turabian StyleDoyoro, Yonatan Garkebo, Ping-Yu Chang, and Jordi Mahardika Puntu. 2021. "Uncertainty of the 2D Resistivity Survey on the Subsurface Cavities" Applied Sciences 11, no. 7: 3143. https://doi.org/10.3390/app11073143
APA StyleDoyoro, Y. G., Chang, P.-Y., & Puntu, J. M. (2021). Uncertainty of the 2D Resistivity Survey on the Subsurface Cavities. Applied Sciences, 11(7), 3143. https://doi.org/10.3390/app11073143








