International Airline Alliance Network Design with Uncertainty
Abstract
1. Introduction
2. Literature Review
3. Airline Alliance Network
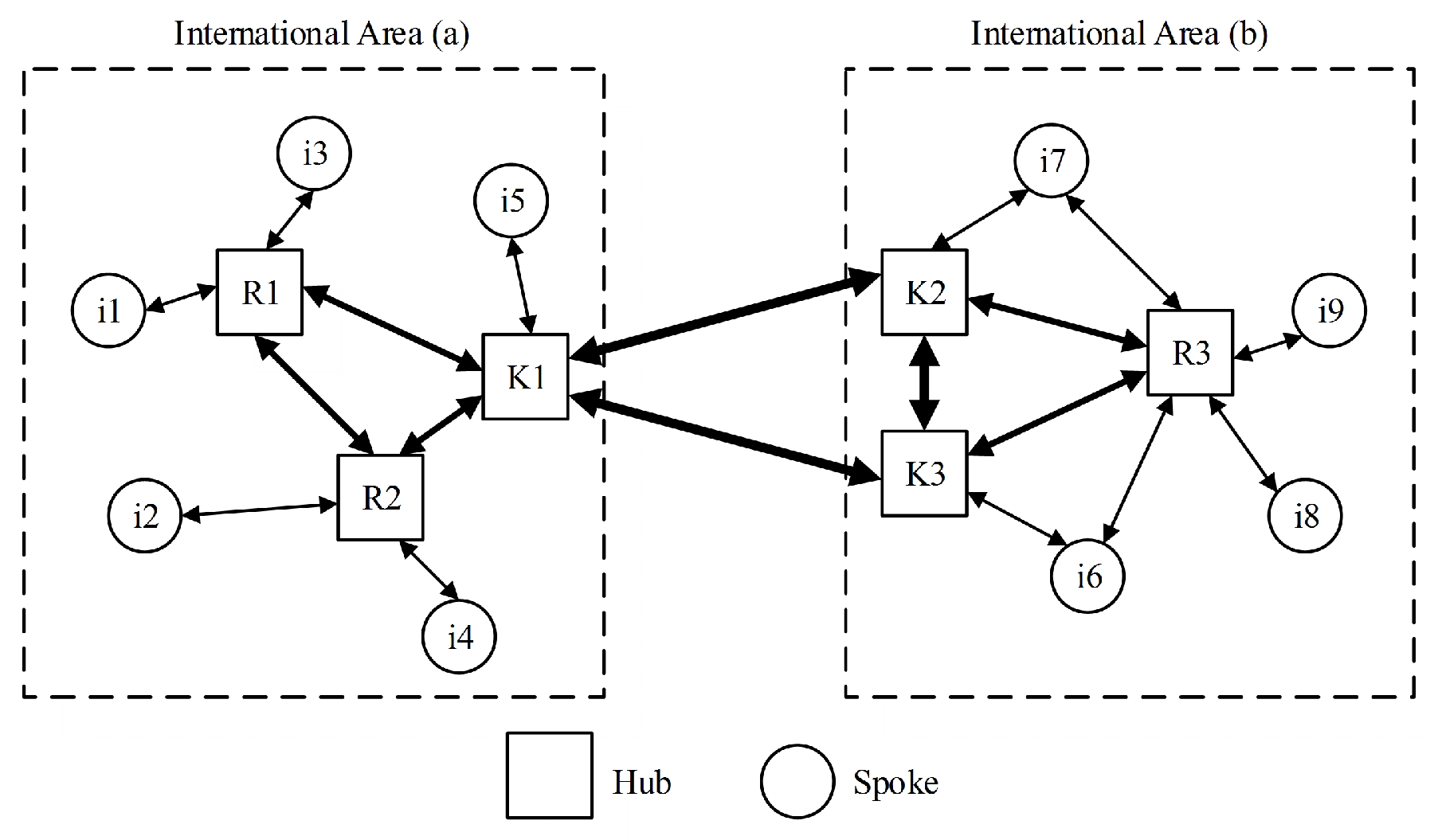
3.1. Problem Formulation
- The cooperation between alliance partners should meet the limitations of traffic rights.
- The round-trip passenger flow of international routes usually differs greatly and is asymmetric.
- Usually, the domestic network of an airline is relatively complete before the airline joins an alliance, and the regional hubs can be given. However, airlines need to choose their international gateways from the set of regional hubs through optimization.
- One or more international gateways coexist with each area for each airline, and all gateways are interconnected across international areas.
- All international gateways are interconnected across international areas. Due to the economy of scale in which passengers converge at gateway airports, a discount factor is incorporated into the cost between international gateways.
- According to the actual transportation situation, international transportation usually does not exceed two transits, so airports other than the international gateways are regarded as “spokes” of international routes. Multi-allocation connections between “spokes” and international gateways are adopted; is the discount factor from “spokes” to international gateways, and is the discount factor from international gateways to “spokes”. Generally, .
- The regional hubs within each area are given, and airlines choose their international gateways from this subset of regional hubs.
- Inter-area journeys are limited to three legs, that is, if both the origin and destination nodes are “spokes”, traveling across international areas will necessarily involve a three-leg journey. For example, to travel from i5 to i7 would involve one leg from i5 to K1, a second leg from K1 to K2, and, finally, a third leg from K2 to i7. On the other hand, inter-area journeys contain at least one leg, and this happens when both the originating and destination nodes are the international gateways.
- Inter-area traffic must all be transported from the originating node to the destination node.
- The round-trip passenger demand of international routes is usually asymmetric; .
3.2. Alliance Route Network Model
3.3. Optimal Solution
| Algorithm 1 An Iterative Optimization Algorithm for the Alliance Route Network |
|
4. Case Study
4.1. Data Settings
4.2. Computational Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oum, T.H.; Park, J.H. Airline alliances: Current status, policy issues, and future directions. J. Air Transp. Manag. 1997, 3, 133–144. [Google Scholar] [CrossRef]
- Adler, N.; Hanany, E. Regulating inter-firm agreements: The case of airline codesharing in parallel networks. Transp. Res. B Meth. 2016, 84, 31–54. [Google Scholar] [CrossRef]
- Park, J.H.; Zhang, A.Y. Analytical models of international alliances in the airline industry. Transp. Res. B Meth. 2001, 35, 865–886. [Google Scholar] [CrossRef]
- IATA International Traffic Statistics. Available online: https://www.iata.org (accessed on 1 December 2019).
- Snyder, L.V. Facility location under uncertainty: A review. IIE Trans. 2006, 38, 547–564. [Google Scholar] [CrossRef]
- Brueckner, J.K. The economics of international codesharing: An analysis of airline alliances. Int. J. Ind. Organ. 2001, 19, 1475–1498. [Google Scholar] [CrossRef]
- Zhang, A. Competition models of strategic alliances. Res. Transp. Econ. 2005, 13, 75–100. [Google Scholar] [CrossRef]
- Jie, J.; Yong, L. Flight frequency, congestion cost and complementary aviation alliance: Congestion analysis of hub and spoke network airports. Manag. Rev. 2012, 24, 164–170. [Google Scholar]
- Jiayue, L. Optimization design of airline route network. Electr. Technol. Softw. Eng. 2019, 20, 4–5. [Google Scholar]
- Alumur, S.; Kara, B.Y. Network hub location problems: The state of the art. Eur. J. Oper. Res. 2008, 190, 1–21. [Google Scholar] [CrossRef]
- Szűcs, G. Route planning based on uncertain information in transport networks. Transport 2012, 27, 79–85. [Google Scholar] [CrossRef]
- Adler, N.; Smilowitz, K. Hub-and-spoke network alliances and mergers: Price-location competition in the airline industry. Transp. Res. B Meth. 2007, 41, 394–409. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Oum, T.H.; Park, J.H.; Zhang, A. Globalization and Strategic Alliances: The Case of the Airline Industry; Elsevier: Oxford, UK, 2000. [Google Scholar]
- Oum, T.H.; Park, J.H.; Kim, K.; Yu, C. The effect of horizontal alliances on firm productivity and profitability: Evidence from the global airline industry. J. Bus Res. 2004, 57, 844–853. [Google Scholar] [CrossRef]
- Wen, Y.H.; Hsu, C.I. Interactive multiobjective programming in airline network design for international airline code-share alliance. Eur. J. Oper. Res. 2006, 174, 404–426. [Google Scholar] [CrossRef]
- Lordan, O.; Sallan, J.M.; Simo, P.; Gonzalez-Prieto, D. Robustness of airline alliance route networks. Commun. Nonlinear Sci. 2015, 22, 587–595. [Google Scholar] [CrossRef]
- Lordan, O.; Klophaus, R. Measuring the vulnerability of global airline alliances to member exits. Transp. Res. Proc. 2017, 25, 7–16. [Google Scholar] [CrossRef][Green Version]
- O’kelly, M.E. A quadratic integer program for the location of interacting hub facilities. Eur. J. Oper. Res. 1987, 32, 393–404. [Google Scholar] [CrossRef]
- Campbell, J.F. Integer programming formulations of discrete hub location problems. Eur. J. Oper. Res. 1994, 72, 387–405. [Google Scholar] [CrossRef]
- Campbell, J.F. Hub location and the p-hub median problem. Oper. Res. 1996, 44, 923–935. [Google Scholar] [CrossRef]
- Ernst, A.T.; Krishnamoorthy, M. Efficient algorithms for the uncapacitated single allocation p-hub median problem. Locat. Sci. 1996, 4, 139–154. [Google Scholar] [CrossRef]
- Ernst, A.T.; Krishnamoorthy, M. Exact and heuristic algorithms for the uncapacitated multiple allocation p-hub median problem. Eur. J. Oper. Res. 1998, 104, 100–112. [Google Scholar] [CrossRef]
- Fageda, X.; Flores-Fillol, R. A note on optimal airline networks under airport congestion. Econ. Lett. 2015, 128, 90–94. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, A. Airline network choice and market coverage under high-speed rail competition. Transp. Res. A Pol. 2016, 92, 248–260. [Google Scholar] [CrossRef]
- Babić, D.; Kalić, M. Modeling the selection of airline network structure in a competitive environment. J. Air Transp. Manag. 2018, 66, 42–52. [Google Scholar] [CrossRef]
- Averbakh, I. Minmax regret solutions for minimax optimization problems with uncertainty. Oper. Res. Lett. 2000, 27, 57–65. [Google Scholar] [CrossRef]
- Baohua, W.; Shiwei, H. Robust optimization model and algorithm for logistics center location and allocation under uncertain environment. J. Transp. Syst. Eng. Inform. Technol. 2009, 9, 69–74. [Google Scholar]
- Campbell, J.F.; O’Kelly, M.E. Twenty-five years of hub location research. Transp. Sci. 2012, 46, 153–169. [Google Scholar] [CrossRef]
- Shahabi, M.; Unnikrishnan, A. Robust hub network design problem. Transp. Res. E Log. 2014, 70, 356–373. [Google Scholar] [CrossRef]
- FAA Digital-Terminal Procedures Publication. Available online: http://www.gcmap.com (accessed on 1 December 2019).
- Adler, N.; Njoya, E.T.; Volta, N. The multi-airline p-hub median problem applied to the African aviation market. Transp. Res. A Pol. 2018, 107, 187–202. [Google Scholar] [CrossRef]
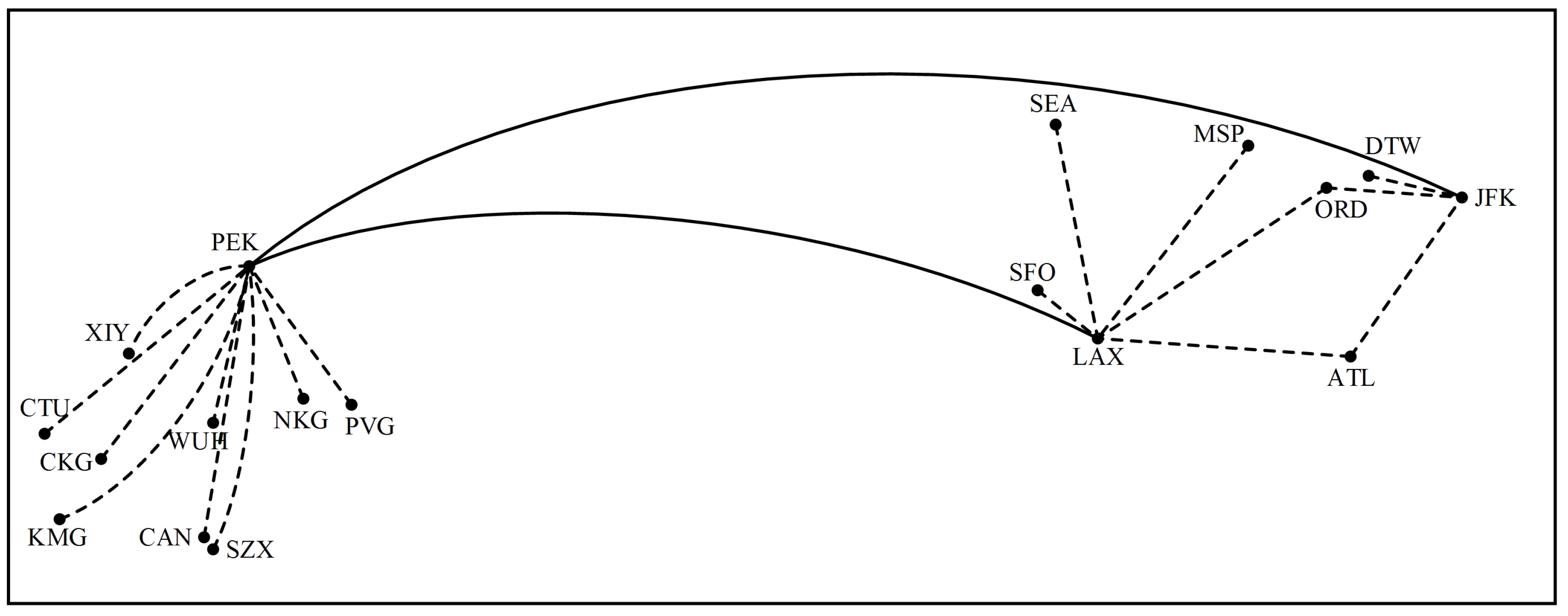
| Node | Airport | Node | Airport | Node | Airport |
|---|---|---|---|---|---|
| 1 | PEK*\Beijing | 7 | CKG\Chongqing | 13 | DTW*\Detroit |
| 2 | CAN\Guangzhou | 8 | XIY*\Xi’an | 14 | LAX*\Los Angeles |
| 3 | PVG*\Shanghai | 9 | WUH*\Wuhan | 15 | MSP*\Minneapolis |
| 4 | CTU\Chengdu | 10 | NKG\Nanjing | 16 | SFO\San Francisco |
| 5 | SZX\Shenzhen | 11 | ATL*\Atlanta | 17 | SEA\Seattle |
| 6 | KMG*\Kunming | 12 | JFK*\New York | 18 | ORD\Chicago |
| Short Haul | Medium Haul | Long Haul | |
|---|---|---|---|
| CNY per ASK | 0.3724 | 0.2894 | 0.2941 |
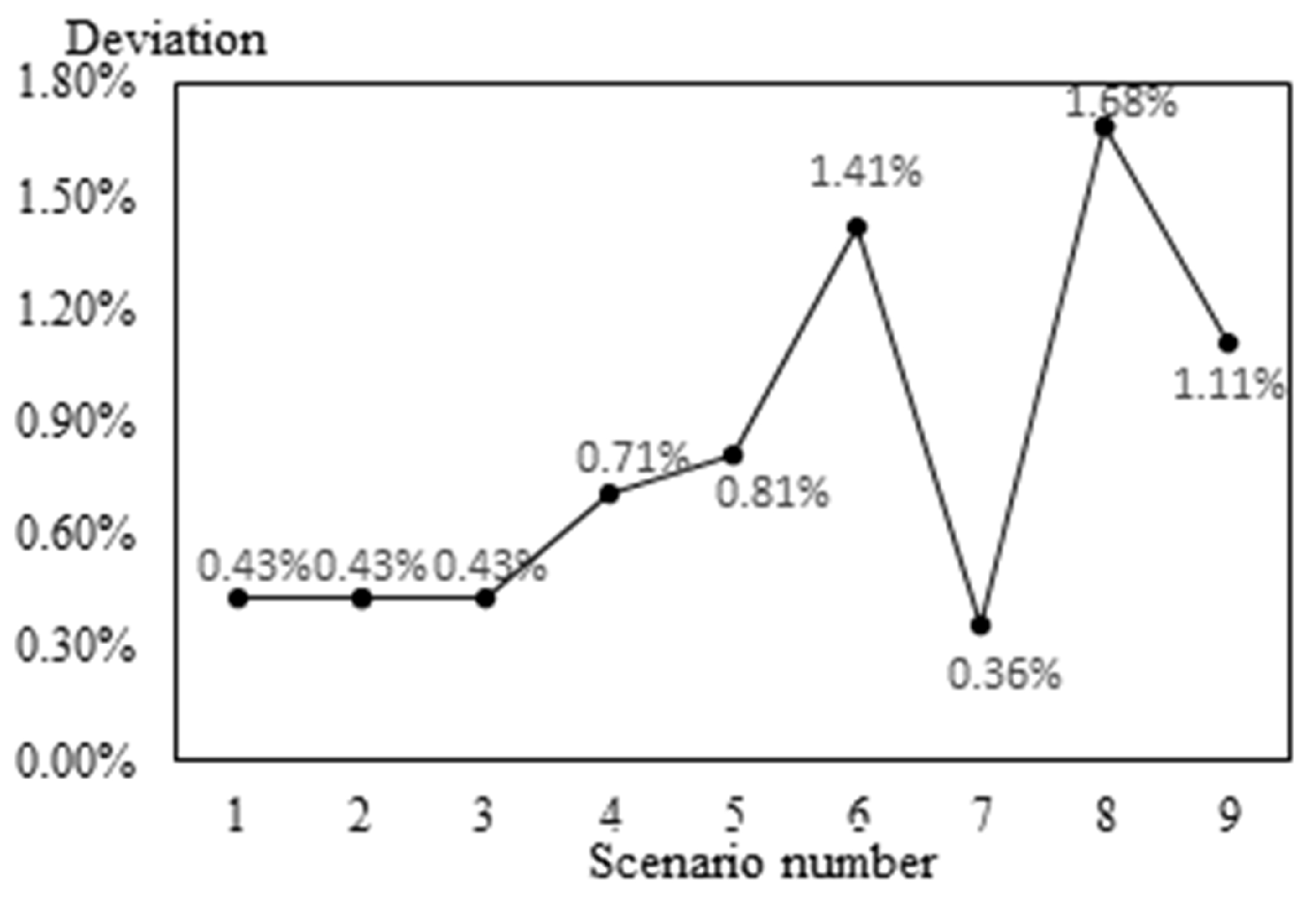
| Scenario Number | CASK-SH Deviation (%) | CASK-MH Deviation (%) | CASK-LH Deviation (%) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 20 | 20 | 20 |
| 3 | −20 | −20 | −20 |
| 4 | 20 | 20 | −20 |
| 5 | 20 | −20 | 20 |
| 6 | −20 | 20 | 20 |
| 7 | 20 | −20 | −20 |
| 8 | −20 | 20 | −20 |
| 9 | −20 | −20 | 20 |
| Intl. GL | Trans. Costs | Intl. GL | Trans. Costs | Intl. GL | Trans. Costs | Intl. GL | Trans. Costs | |
| s1 | 3, 12, 14 | 223,129,610 | 1, 12, 14 | 365,549,030 | 1, 12, 14 | 506,512,065 | 1, 13, 14 | 647,009,456 |
| s2 | 3, 12, 14 | 267,755,532 | 1, 12, 14 | 438,658,836 | 1, 12, 14 | 607,814,479 | 1, 13, 14 | 776,411,347 |
| s3 | 3, 12, 14 | 178,503,688 | 1, 12, 14 | 292,439,224 | 1, 12, 14 | 405,209,652 | 1, 13, 14 | 517,607,565 |
| s4 | 3, 12, 14 | 208,191,272 | 1, 12, 14 | 325,888,407 | 1, 12, 14 | 438,658,836 | 1, 12, 14 | 551,429,264 |
| s5 | 1, 12, 14 | 241,491,590 | 1, 12, 14 | 410,647,234 | 1, 12, 14 | 579,766,838 | 1, 14, 15 | 743,667,894 |
| s6 | 3, 13, 14 | 260,392,325 | 1, 13, 14 | 429,436,112 | 1, 13, 14 | 596,487,252 | 1, 13, 14 | 763,538,391 |
| s7 | 3, 12, 14 | 183,698,164 | 3, 12, 14 | 297,876,805 | 1, 12, 14 | 410,647,234 | 1, 12, 14 | 523,417,662 |
| s8 | 3, 13, 14 | 201,692,264 | 1, 13, 14 | 318,068,686 | 1, 13, 14 | 429,436,112 | 1, 13, 14 | 540,803,538 |
| s9 | 1, 12, 14 | 236,054,009 | 1, 12, 14 | 405,209,652 | 1, 14, 15 | 572,475,719 | 1, 14, 15 | 736,129,225 |
| RM | 3, 12, 14 | 1, 12, 14 | 1, 12, 14 | 1, 12, 14 | ||||
| p = 2 | p = 3 | p = 4 | p = 5 | |
|---|---|---|---|---|
| 3, 14 | 3, 12, 14 | 1, 3, 12, 14 | 1, 3, 12, 13, 14 | |
| 1, 14 | 1, 12, 14 | 1, 3, 12, 14 | 1, 3, 12, 13, 14 | |
| 1, 14 | 1, 12, 14 | 1, 3, 12, 14 | 1, 3, 12, 14, 15 | |
| 1, 14 | 1, 12, 14 | 1, 3, 12, 14 | 1, 3, 12, 14, 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Shao, J.; Jiang, Y.; Xu, Z.; Tsourdos, A. International Airline Alliance Network Design with Uncertainty. Appl. Sci. 2021, 11, 3065. https://doi.org/10.3390/app11073065
Yang W, Shao J, Jiang Y, Xu Z, Tsourdos A. International Airline Alliance Network Design with Uncertainty. Applied Sciences. 2021; 11(7):3065. https://doi.org/10.3390/app11073065
Chicago/Turabian StyleYang, Wendong, Jiajia Shao, Yun Jiang, Zhengjia Xu, and Antonios Tsourdos. 2021. "International Airline Alliance Network Design with Uncertainty" Applied Sciences 11, no. 7: 3065. https://doi.org/10.3390/app11073065
APA StyleYang, W., Shao, J., Jiang, Y., Xu, Z., & Tsourdos, A. (2021). International Airline Alliance Network Design with Uncertainty. Applied Sciences, 11(7), 3065. https://doi.org/10.3390/app11073065










