Network Analysis to Identify the Risk of Epidemic Spreading

Abstract

Several epidemics, such as the Black Death and the Spanish flu, have threatened human life throughout history; however, it is unclear if humans will remain safe from the sudden and fast spread of epidemic diseases. Moreover, the transmission characteristics of epidemics remain undiscovered. In this study, we present the results of an epidemic simulation experiment revealing the relationship between epidemic parameters and pandemic risk. To analyze the time-dependent risk and impact of epidemics, we considered two parameters for infectious diseases: the recovery time from infection and the transmission rate of the disease. Based on the epidemic simulation, we identified two important aspects of human safety with regard to the threat of a pandemic. First, humans should be safe if the fatality rate is below 100%. Second, even when the fatality rate is 100%, humans would be safe if the average degree of human social networks is below a threshold value. Nevertheless, certain diseases can potentially infect all nodes in the human social networks, and these diseases cause a pandemic when the average degree is larger than the threshold value. These results indicated that certain infectious diseases lead to human extinction and can be prevented by minimizing human contact.

1. Introduction

The emergence of a pandemic is one of the various scenarios frequently discussed as a human extinction event, and it is listed as one of the global catastrophic risks in studies regarding the future [1,2,3]. In particular, several pandemics, such as the Black Death [4,5], Spanish flu [6], and those caused by smallpox [7], severe acute respiratory syndrome (SARS) [8], and Ebola [9], have affected a large population throughout history. The risk of pandemics increases with an increase in population mobility between cities, nations, and continents, thereby threatening humankind [10,11,12]. It is essential to analyze the epidemic spread in society to minimize the damage from epidemic disasters; however, extinctive epidemic spreading experiments have limitations in real-world situations, as they predict stochastic effects on the spread without considering the structure of human society. Network-based approaches have been proposed to overcome these limitations and perform epidemic spreading simulations by considering the network structure of numerous real-world connections [13,14,15]. These methods use various models of epidemic spreading, such as the susceptible–infectious–susceptible (SIS) [16,17,18], susceptible–infectious–recovered (SIR) [19,20,21], and Watts threshold models [22]. While these methods are mathematically convenient, they are epidemiologically unrealistic for various infections because they require exponentially distributed incubation and infectious periods [23,24,25]. Moreover, previous epidemic studies did not perform quantitative assessment of the pandemic risk depending on the network connectivity in individuals and fatality rate of various diseases [26].

In the present study, we applied an SIR epidemic model to a scale-free network with Monte Carlo simulation to identify the quantitative relationship between infectious diseases and human existence. Our fundamental hypothesis states that when the epidemic spreads to all nodes of the network and the fatality rate is 100%, it can increase the pandemic risk. To address this, we initially constructed a scale-free network to simulate a society. Moreover, for the epidemic spreading simulation, an SIR model was applied to the network to describe the immune state of an individual after infection. From the simulation study, we found that the mean degree of a scale-free network was an essential factor in determining whether epidemics threaten humans. This approach provides important insights into epidemic spreading analysis by investigating the relationship between epidemic and scale-free network parameters. Furthermore, it highlights the necessity of determining information flow during an epidemic.

2. Materials and Methods

We designed an epidemic simulation process to identify the relationship between pandemic risk and network parameters. This study was performed in four steps (Figure 1): (i) generating a scale-free network model to reflect real-world conditions; (ii) applying an SIR model to the scale-free network for epidemic spreading simulations; (iii) adapting the Monte Carlo method to reflect the stochastic process in the node status of the SIR model; and (iv) iteratively performing simulation for every parameter set and analyzing the results. We have provided the source code and sample results of epidemic simulation in Supplementary Materials.

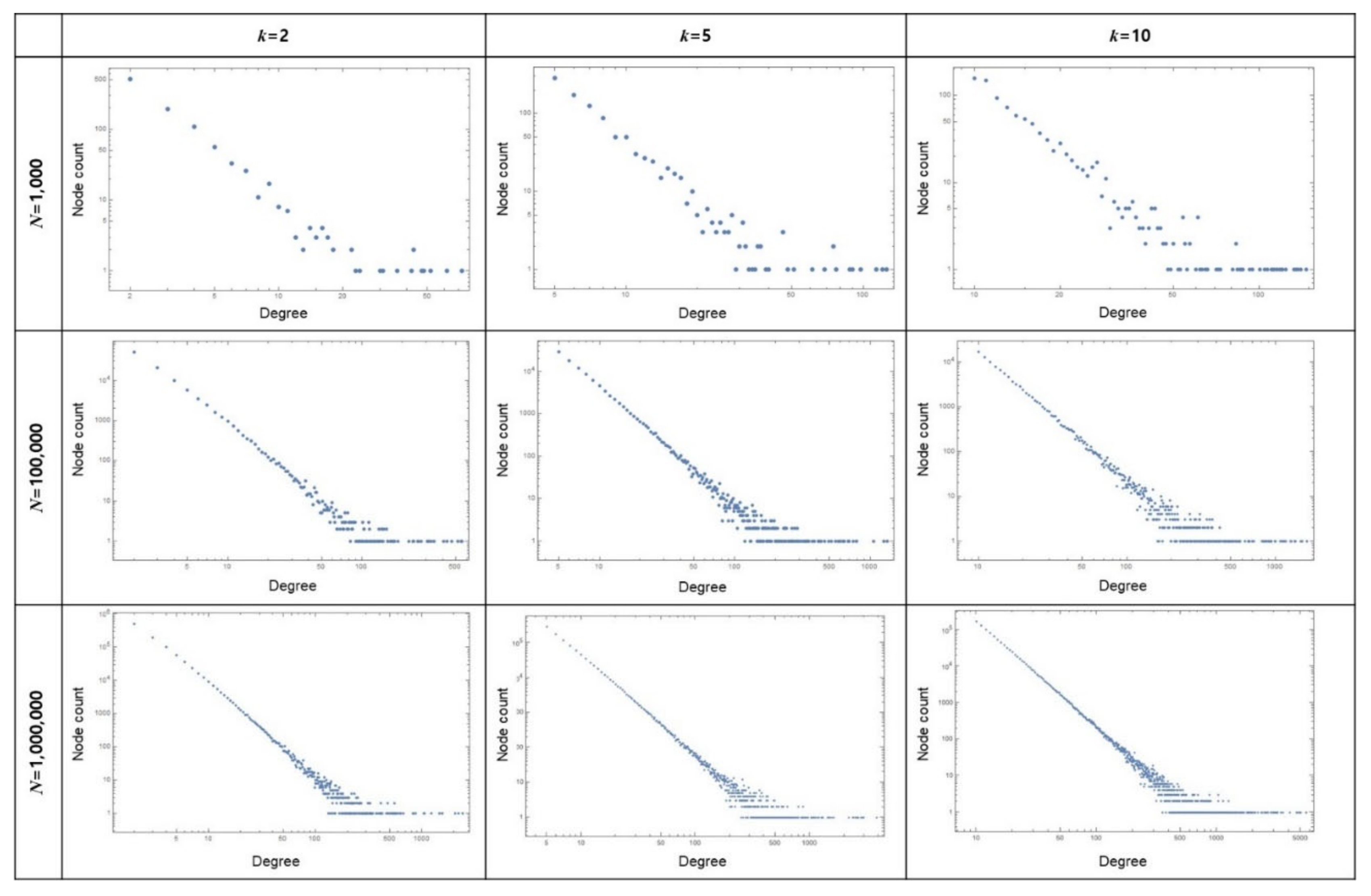
2.1. Network Generation Based on a Scale-Free Model

We constructed a network model for the epidemic spreading simulation (Figure 1). The nodes and edges of the network represent people in the society and their physical contacts, respectively. We used a scale-free network model, which follows the preferential attachment property observed in numerous real-world networks, such as social networks, physical systems, and economic networks [27,28,29]. In the scale-free network, when a node is added to the network, its likelihood of connecting to existing nodes increases with an increase in the node’s degree. Hub nodes, which lead to fast and vast spreading of epidemics, exist. Two characteristic parameters, including N and k, affect the form of scale-free networks. The parameter N denotes all nodes in the network. In the real world, N indicates the whole population size. The parameter k is the average degree of the network, which determines the degree of the newly attached node for each step during network generation. Following the characteristics of the network model, we generated scale-free networks representing human contacts for epidemic spread. The scale-free network was generated by the Barabasi–Albert graph distribution, in which the network is constructed from a cycle graph with three vertices, followed by the addition of k edges at each construction step [30]. The k edges are randomly attached to the vertex based on the degree distribution of the vertex. After network generation, we investigated the degree distribution properties of the network (Figure 2). The results indicate that the degree distributions have similar tendency for networks with varying number of nodes and edges. This study constructed scale-free networks with the largest number of nodes considering computational complexity (N = 1,000,000).

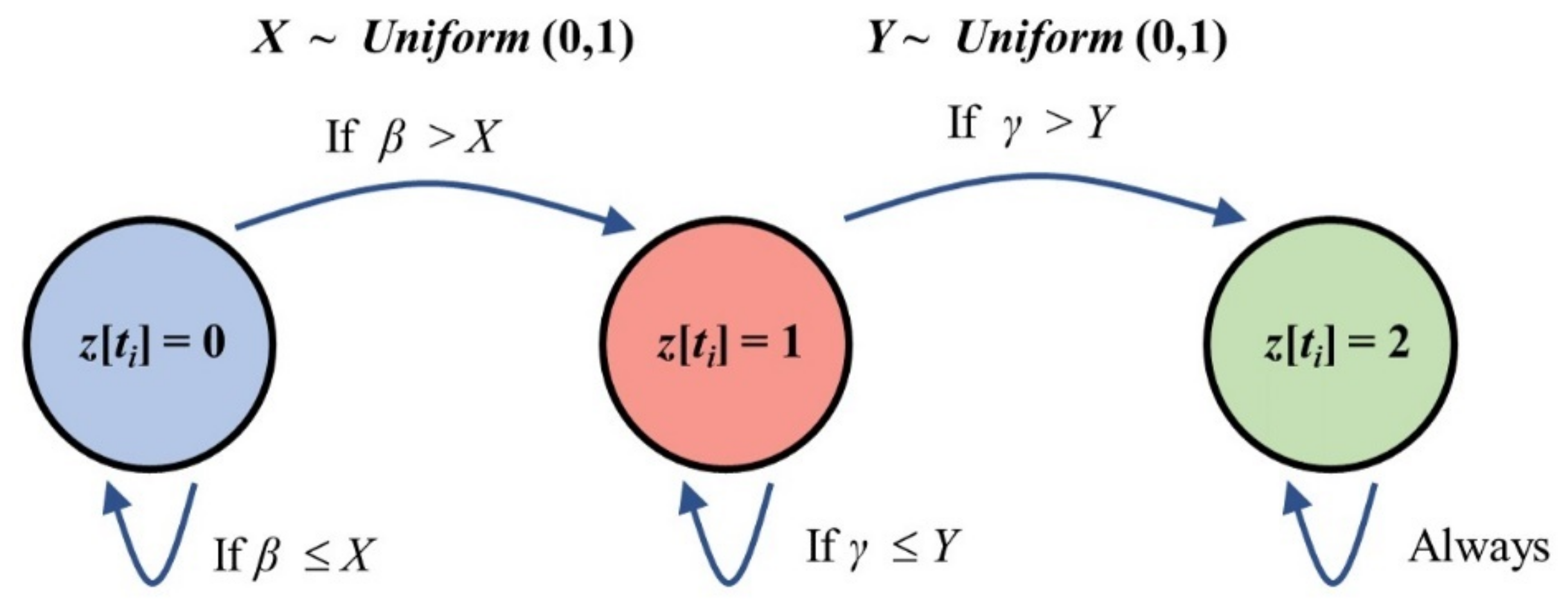
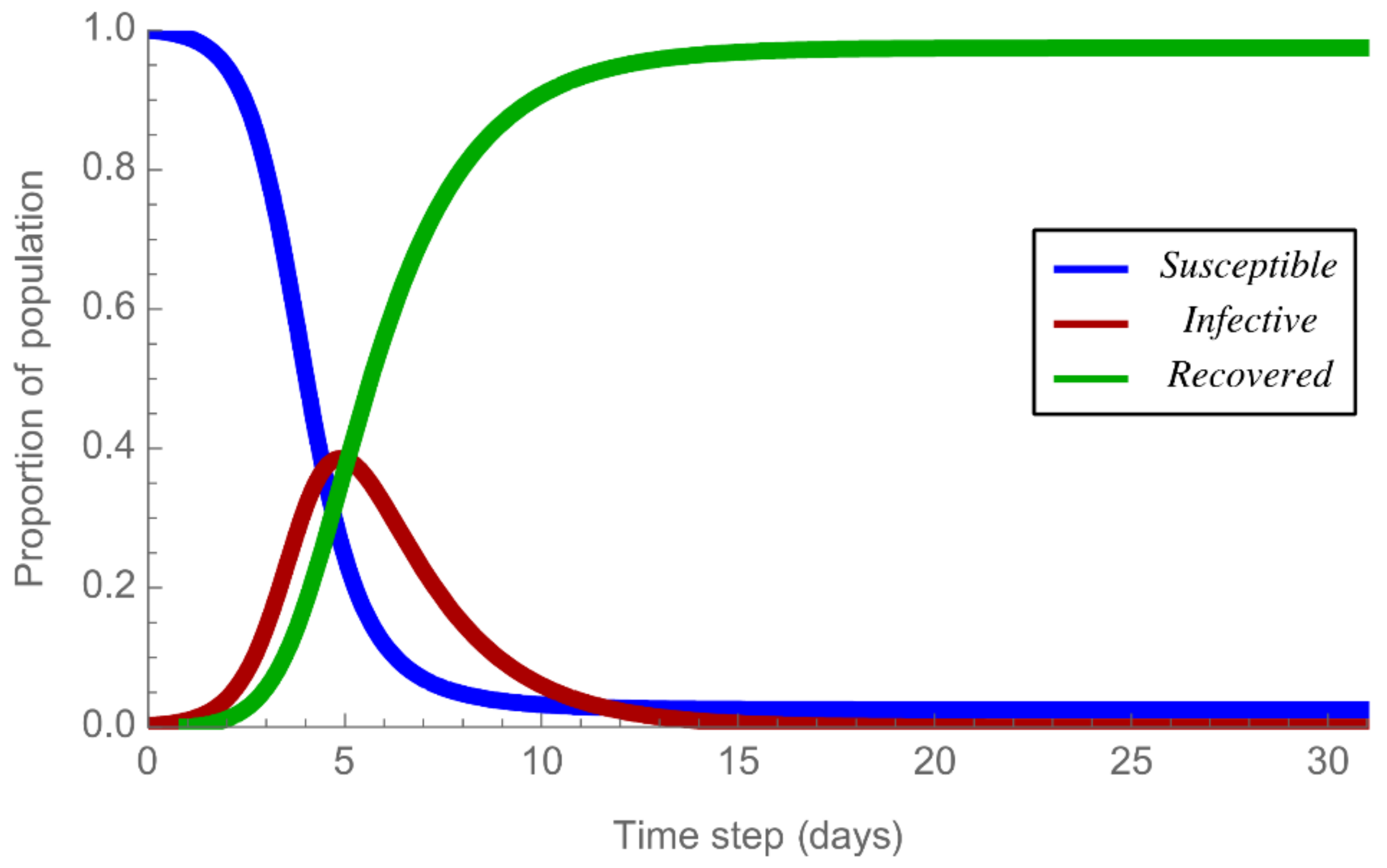
2.2. Epidemic Spreading Based on the SIR Model

For the epidemic spreading simulations, we applied an SIR model to the generated scale-free network. The classical SIR model can be expressed by the following nonlinear differential equations [21]:

$$\frac{dS}{dt}=-\beta SI,$$

(1)

$$\frac{dI}{dt}=\beta SI-\gamma I,$$

(2)

$$\frac{dR}{dt}=\gamma I,$$

(3)

S + I + R = N,

(4)

where S, I, and R represent susceptible, infected, and recovered compartments, respectively, in the whole population. S represents people who have not been infected yet but can be infected in future. I represents infected people who can spread the epidemic to susceptible people through physical contact. R denotes people who have recovered or died from the epidemic and who no longer participate in the epidemic spreading process. The sum of the S, I, and R values represents the whole population size N. Epidemics have two parameters in the SIR model, transmission rate (β) and recovery rate (γ), which arise from the basic reproduction number R₀ (Figure 1B). The basic reproduction number is the number of infections caused by one infective node [31,32,33]. If the R₀ is more than 1, the infection can spread in a population, whereas if R₀ is less than 1, the infection cannot spread. We express the basic reproduction number as R₀ = β/γ, where β represents the spreading rate of epidemics between infective nodes and adjacent susceptible nodes and γ represents the probability of recovery from infection [34]. We mainly used γ_d, which is the reciprocal of γ and reflects the time interval between infection and recovery.

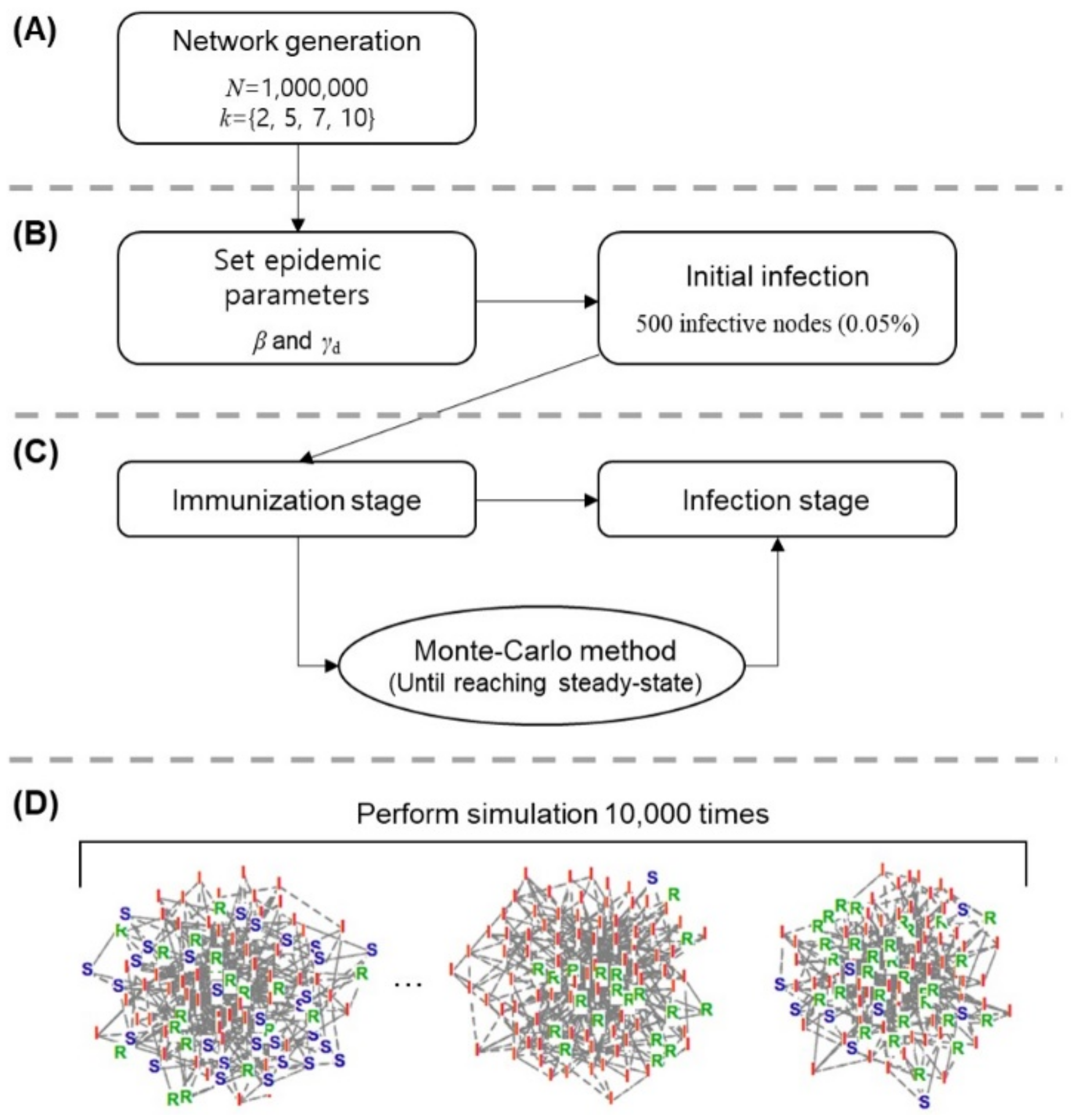
2.3. Investigation of Epidemic Status Based on the Monte Carlo Method

The epidemic simulation was performed for a time series event by constructing epidemic status matrix (z) to represent the status of the nth node at time step t. For each node, the value of epidemic status matrix at time step t can be 0, 1, or 2, indicating that a node is susceptible, infective, or recovered, respectively. We initially (t = 0) set every value of epidemic status matrix to 0 because all nodes are susceptible before the epidemic spreads. At the initial infection stage, randomly selected 0.05% of nodes were infected. At every time period, we performed immunization and observed the infection stages (Figure 3).

At the immunization stage, we identified infective nodes and determined whether these nodes would be recovered in the next time step. To calculate the transition probability of infected and recovered phenomena, the Monte Carlo method was applied [35,36]. When infection and recovery parameters are provided, it is possible to investigate whether a node transitions from an epidemic state to another state. To accomplish this, we compared the method revealing the change in each population in every compartment over time (Figure 4).

The final steady state of the epidemic spreading simulation model indicates the total number of casualties of the epidemic who either are dead or have recovered from the disease. Infective nodes at time t (z_n [t] = 1) are transformed to recovered nodes at time t + 1 (z_n [t + 1] = 2) when 1/γ_d is larger than a random real number between 0 and 1. We determined whether the neighbor nodes of the infection node would be infected by identifying susceptible nodes adjacent to the infective nodes at time t (z_n [t] = 0, with the adjacent infective node) (Figure 5). When β is larger than a random real number between 0 and 1, a susceptible node becomes an infective node at time t + 1 (z_n [t + 1] = 1); this scenario represents epidemic spread. For each time step, we recorded the number of susceptible, infective, and recovered nodes during epidemic spread.

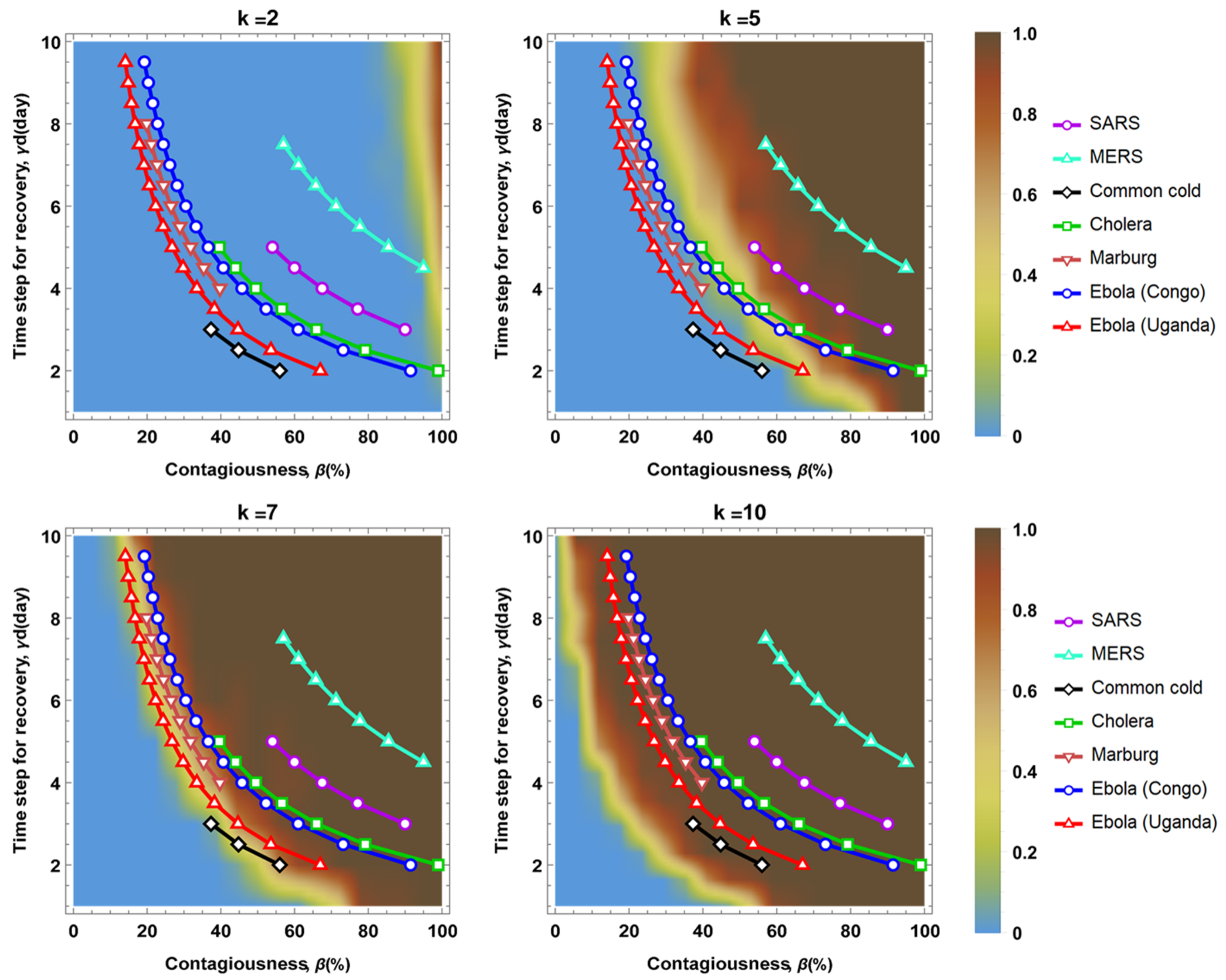
2.4. Simulation Parameters

We carried out simulation trials for various mean degrees of networks (k = 2, 5, 7, and 10). Each network considered the following epidemic parameters: β ranges from 0.05 to 0.95 and γ_d ranges from 1 to 10. The Monte Carlo model was repeatedly simulated to observe saturation of the recovery process. Considering that the simulation pipeline contains random processes such as initial infection and Monte Carlo trials, we performed the simulation iteratively until the status of nodes remained unchanged. After simulation, time series data from every simulation were interpolated in the time domain.

The fatality rate determines the ratio of deceased and recovered individuals in the final population [37,38,39]. If the fatality rate is below 100%, the recovered population contains both dead and recovered individuals. Such a situation does not always cause a pandemic. In this simulation, we assumed a 100% fatality rate. To accomplish this, we enumerated the recovered nodes as dead for considering the pandemic risk.

3. Results

Through our method, we obtained epidemic spreading data with various network and epidemic parameter sets. In the present study, we focused on the case where the epidemic infects all nodes and defined this phenomenon as “extinctive spread”. Diseases causing extinctive spread are potential candidates of high pandemic risk. In the real world, extinctive spreading indicates that the disease will infect every person in the society. From the simulation data, we calculated the extinctive spread score by dividing the total number of simulation trials by the number of extinctive spread cases. Thereafter, we identified that the number of extinctive spread cases is mainly influenced by spreading speed, which is determined by β, γ_d, and k (Figure 6).

The extinctive spread region (brown area in Figure 6) is expanded as the value of mean degree of network (k) is increased, thereby indicating that the area of extinctive spread becomes noticeably wider in a dense network than in a sparse network. Thus, the more contact between people, the higher the risk of epidemics. Moreover, high γ_d and high β cause extinctive spread across a large region, indicating that the high spreading rate and short time interval between infection and recovery are risk factors of epidemic diseases. In contrast, the infective nodes recover before they transmit the disease to their neighbors in low β and low γ_d scenarios, thus disconnecting the network and preventing extinctive spread. This occurs because the infective nodes need more time to transmit the disease in low β and high γ_d scenarios. Therefore, the disease begins to subside due to a lack of new infective nodes.

Furthermore, we investigated the range of β and γ_d for existing epidemics of the common cold [40,41] and fatal diseases, namely, cholera [42,43], Marburg [44,45], Ebola (Congo and Uganda) [46,47,48,49], SARS [50], and MERS [51] (

Table 1. Epidemic parameters of infectious diseases.

Epidemic Disease	Infectious Period (γd)	Basic Reproduction Number (R0)	Transmission Rate (β)
Common cold	3~7	1.12	0.16~0.37
Cholera	1~5	1.98	0.39~1.98
Marburg	3	1.59	0.53
Ebola (Congo)	6.5	1.83	0.28
Ebola (Uganda)	6.5	1.34	0.20
SARS	3~5	2.70	0.54~0.90
MERS	4.5~7.8	4.275	0.548~0.95

). We selected diseases with relatively well-known epidemic parameters, such as average duration of infection and basic number of reproductions from previous studies. Transmission rates were calculated using the mean duration of infectious periods and basic reproduction numbers of the epidemics. Different studies reveal multiple values of infectious period and transmission rate for some of these diseases; we considered these values separately [40,41,42,43,46,47,48,49]. For example, the infectious period of a common cold is from 3 to 7 days and that of Ebola is 6.5 days. Next, we placed the possible regions of these epidemics as a disease band for various k values (colored lines in Figure 6). When k > 5, fatal diseases have an opportunity to cause a pandemic. Even when k = 5, diseases such as cholera and Ebola (Congo) can be threatening in regions of low γ_d and high, thus demonstrating that the knowledge of network parameters of the society and the characteristics of epidemic diseases can aid in quantifying the risk of epidemics.

4. Discussion

Many previous studies have made stochastic SIR models to analyze the dynamics or stability of epidemic diseases. They investigated the distribution of susceptible, infected, and removed populations for specific epidemic disease spreading, such as cholera, SARS, Marburg, and MERS, based on mathematical modelling [52,53,54,55]. However, they did not conduct a quantitative assessment of pandemic risk taking into account physical contact between people. To solve this limitation, we performed epidemic spreading simulations by applying an SIR model to scale-free networks with Monte Carlo simulation. In the simulation, we consider various connectivity and disease characteristics on scale-free networks. For each network and epidemic parameter set, the probability of extinctive spread was calculated. The results revealed that certain infectious diseases can lead to extinction. Moreover, even if the disease band extends over the extinctive spread regions, it does not indicate that human extinction results from the disease, as the fatality rate is below 100%; however, in the case of 100% fatality, the disease can cause a human extinction event. The risk of infectious disease is influenced by the network structure. A dense network has a higher risk of spreading infectious disease than a sparse network, as we observed in the extinctive spreading maps. According to our results, when the average degree of human social networks is below the risk threshold, i.e., less than 4 in this study, human society is safe from an extinctive outbreak based on our knowledge regarding the epidemic parameters of the infectious disease. Nevertheless, in other cases, human extinction is possible. For example, if the population is 1,000,000 and there are 4 or more instances of physical contact between people, human extinction events may occur, depending on the fatality rate of the epidemics. Hence, physical contact between people is closely related to an extinction event of infectious diseases. Eventually, from a public health perspective, lowering the average contact level of society is an appropriate way to increase the robustness of strategies against the occurrence of extinction. In the real world, reducing network density can be accomplished by epidemic prevention activity, such as isolation and quarantine treatment. This action prevents epidemic risk to the society, thereby avoiding human extinction.

Additional considerations may improve our analysis. First, large population size and various proportions of initial infective nodes were not considered in the experiments. We have confirmed that the result was consistent when the proportion of initial infective nodes was 0.05% of the total population; however, this can vary depending on the distinct proportion of initial infective nodes in a different population. To achieve robust results, we need to perform additional experiments for various parameters; however, we could not address this issue due to computational complexity. Second, we did not consider numerous known epidemic diseases. We calculated the transmission rates of epidemic diseases using the known infectious periods and reproduction numbers of the epidemics from evidence in the literature. In the present study, we only considered five epidemic diseases, since the information on infectious periods and reproduction numbers of diseases was mostly unavailable for other epidemic diseases. Third, this study only considers the SIR model on scale-free networks in epidemic simulation. Since the dynamics of epidemic diseases can be varied in different models or networks, it is important to experiment in various simulation environments to confirm the robustness of the results. Nevertheless, these limitations can be considered in future experiments or using improved computational methods. With these further improvements, our approach can be used as a computational tool to analyze the risk of epidemic diseases.

5. Conclusions

In this study, we analyzed the risk of epidemic diseases by creating an epidemic simulation on a scale-free network. Based on the simulation results for various epidemic parameters, we confirmed that certain infectious diseases can lead to extinction and can be prevented by minimizing human contact. We believe that identifying potential candidate diseases that may lead to human extinction is crucial in addressing epidemic prevention activities such as quarantine.