Computational Study on Interfacial Interactions between Polymethyl Methacrylate-Based Bone Cement and Hydroxyapatite in Nanoscale
Abstract
1. Introduction
2. MD Simulation Model
2.1. BC Microstructures
2.2. HAp Substrate and HAp/BC Bilayer Models
3. Results and Discussion
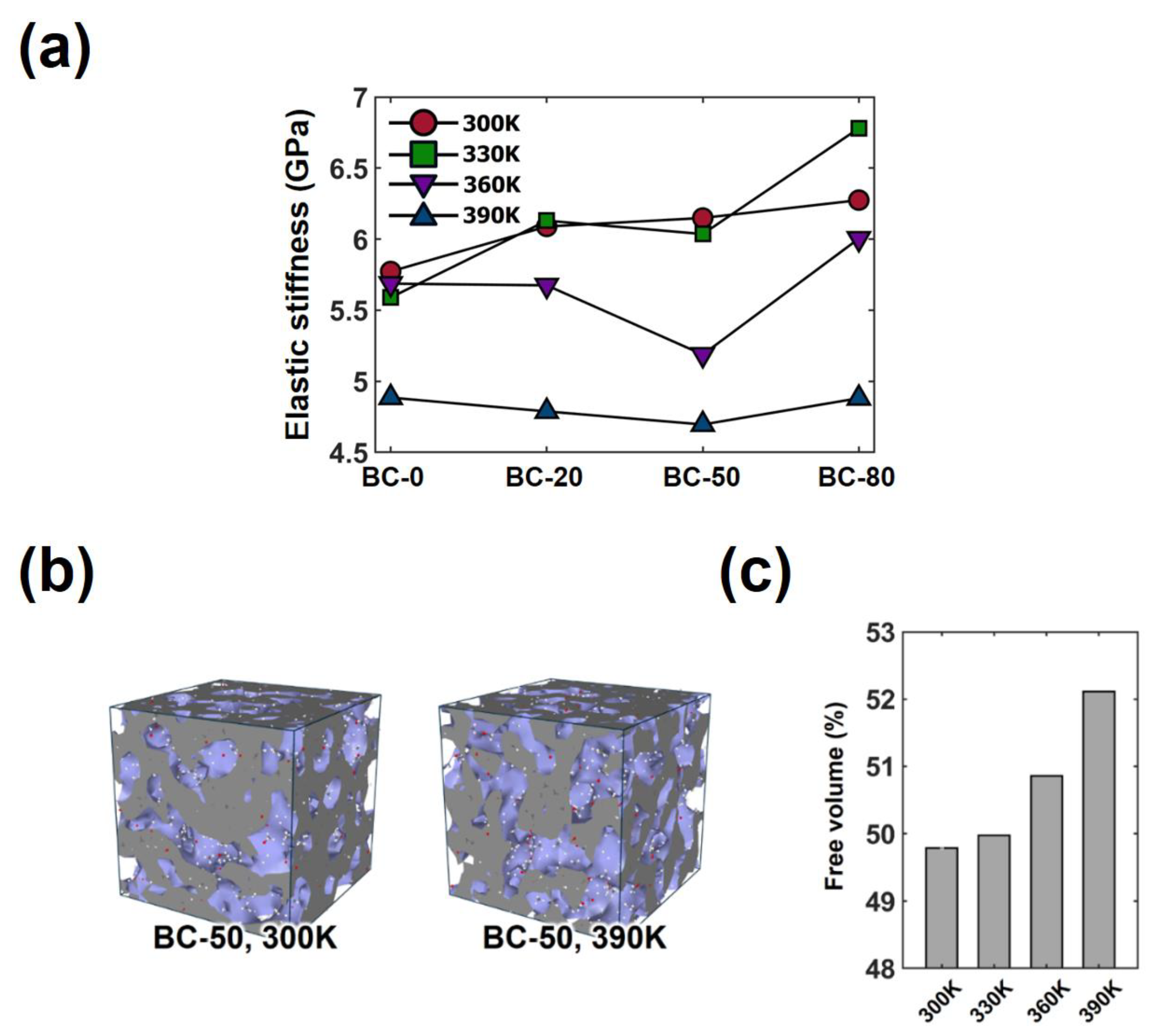
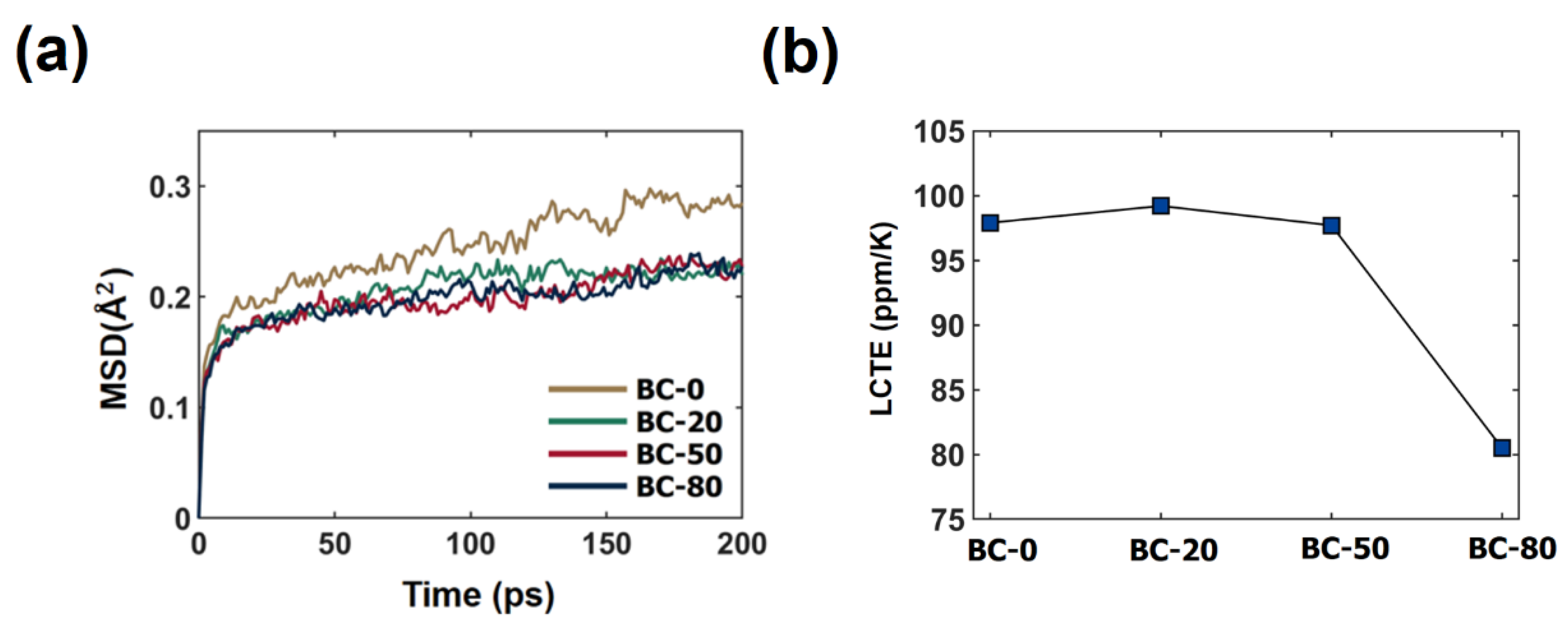
3.1. Effect of the Crosslinking Reaction on the Thermo-Mechanical Properties
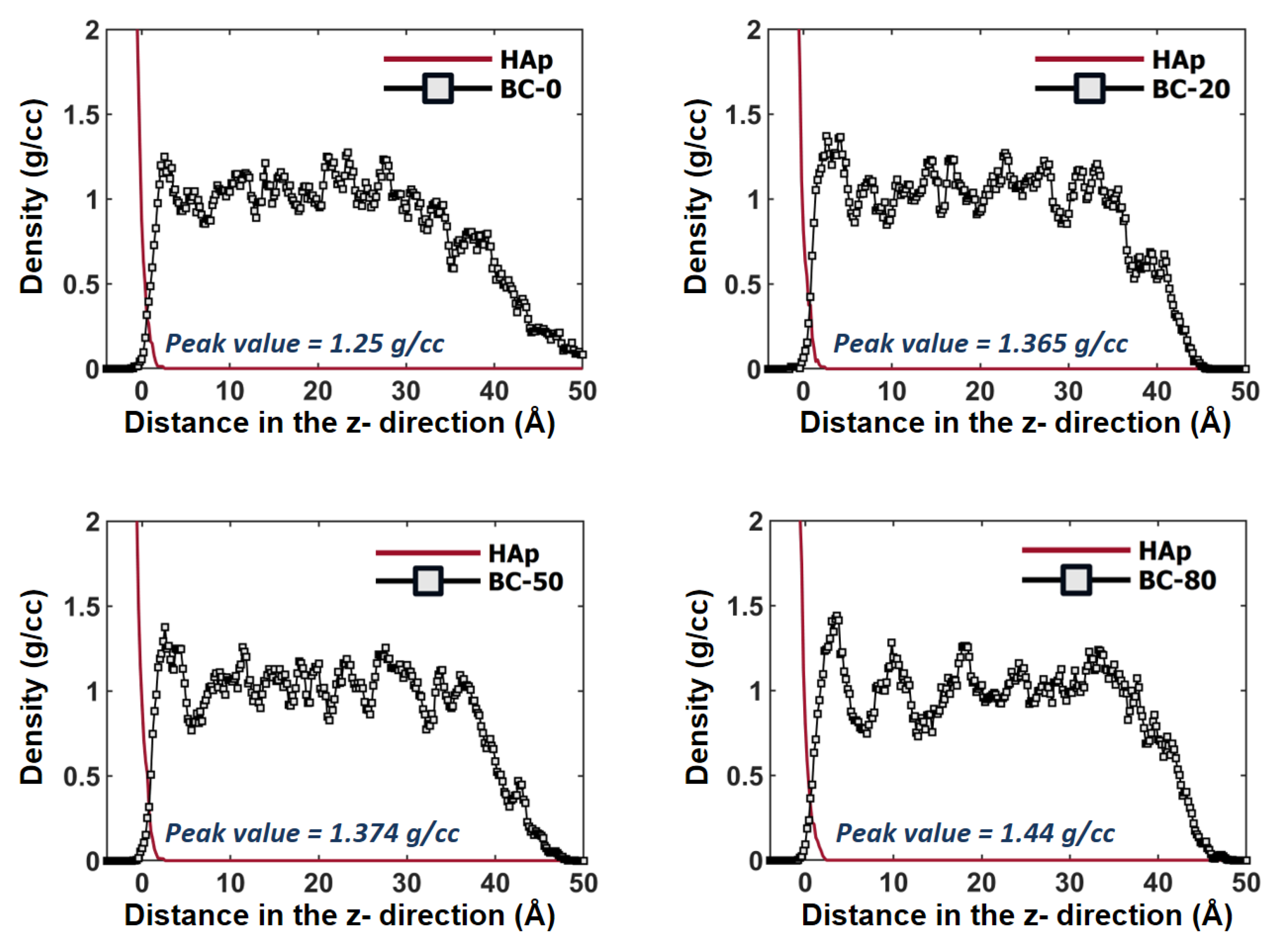
3.2. Density Distributions in the Interfacial Regions of HAp/BC Bilayer Models
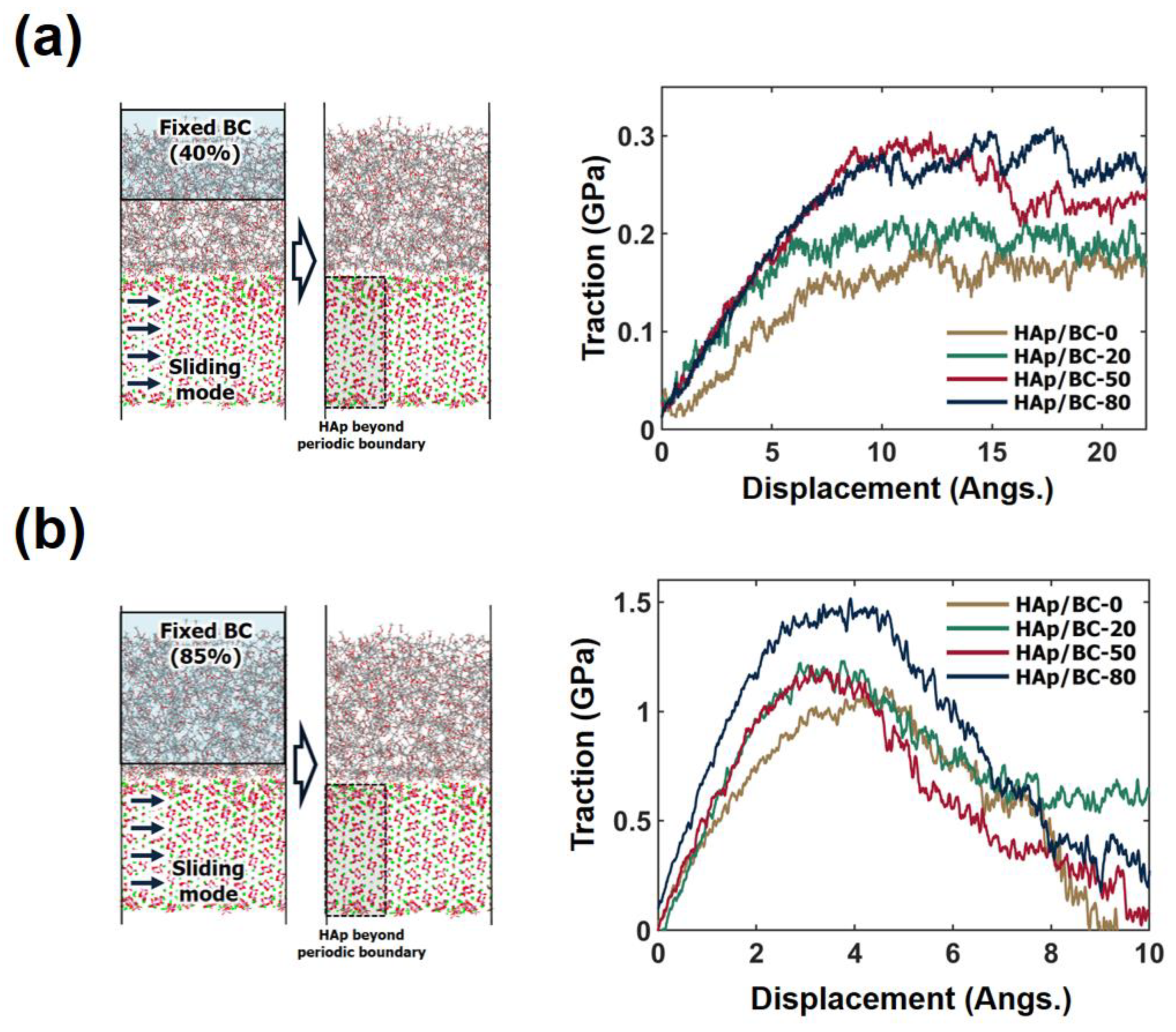
3.3. Cohesive Characteristics of the HAp/BC Bilayer Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bakhtiari, S.S.; Baksheshi-Rad, H.R.; Karbasi, S.; Tavakoli, M.; Razzaghi, M.; Ismail, A.F.; Krishna, S.R.; Betro, F. Polymethyl Methacrylate-Based Bone Cements Containing Carbon Nanotubes and Graphene Oxide: An Overview of Physical, Mechanical, and Biological Properties. Polymers 2020, 12, 1469. [Google Scholar] [CrossRef]
- Athans, V.; Veve, M.P.; Davis, S.L. Trowels and Tribulations: Review of Antimicrobial-Impregnated Bone Cements in Prosthetic Joint Surgery. Pharmacotherapy 2017, 37, 1565–1577. [Google Scholar] [CrossRef]
- Shahbaz, S.; Ayatollahi, M.R.; Torabi, A.R.; Cicero, S. Fracture Behavior of Two Biopolymers Containing Notches: Effects of Notch Tip Plasticity. Appl. Sci. 2020, 10, 8445. [Google Scholar] [CrossRef]
- Böker, K.O.; Richer, K.; Jäckle, K.; Taheri, S.; Grunwald, I.; Borcherding, K.; Byern, J.V.; Hartwig, A.; Wildemann, B.; Schilling, A.F.; et al. Current State of Bone Adhesives-Necessitiesand and Hurdles. Materials 2019, 12, 3975. [Google Scholar] [CrossRef]
- Tozzi, G.; Zhang, Q.; Tong, J. 3D Real-time Micromechanical Compressive Behaviour of Bone–cement Interface: Experimental and Finite Element Studies. J. Biomech. 2012, 45, 356–363. [Google Scholar] [CrossRef] [PubMed]
- Landgraf, R.; Ihlemann, J.; Kolmeder, S.; Lion, A.; Lebsack, H.; Kober, C. Modelling and Simulation of Acrylic Bone Cement Injection and Curing within the Framework of Vertebroplasty. Z. Angew. Math. Mech. 2015, 95, 1530–1547. [Google Scholar] [CrossRef][Green Version]
- Sasaki, T.; Uchida, T.; Sakurai, K. Effect of Crosslink on the Characteristic Length of Glass Transition of Network Polymers. J. Polym. Sci. B. Polym. Phys. 2006, 44, 1958–1966. [Google Scholar] [CrossRef]
- Shokuhfar, A.; Arab, B. The Effect of Cross linking Density on the Mechanical Properties and Structure of the Epoxy Polymers: Molecular Dynamics Simulation. J. Mol. Model. 2013, 19, 3719–3731. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Odegard, G.M. Molecular Modeling of Crosslink Distribution in Epoxy Polymers. Model. Simul. Mater. Sci. Eng. 2012, 20, 045018. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular Dynamics Predictions of Thermal and Mechanical Properties of Thermoset Polymer EPON862/DETDA. Polymer 2011, 52, 2920–2928. [Google Scholar] [CrossRef]
- Krumova, M.; Lopez, D.; Benavente, R.; Mijangos, C.; Perena, J.M. Effect of Crosslinking on the Mechanical and Thermal Properties of Poly(vinyl alcohol). Polymer 2000, 41, 9265–9272. [Google Scholar] [CrossRef]
- Kim, B.; Choi, J.; Yang, S.; Yu, S.; Cho, M. Multiscale Modeling of Interphase in Crosslinked Epoxy Nanocomposites. Compos. B Eng. 2017, 120, 128–142. [Google Scholar] [CrossRef]
- Aghadavoudi, F.; Golestanian, H.; Beni, Y.T. Investigating the Effects of Resin Crosslinking Ratio on Mechanical Properties of Epoxy-based Nanocomposites Using Molecular Dynamics. Polym. Compos. 2017, 38, E433–E442. [Google Scholar] [CrossRef]
- Hadden, C.M.; Jensen, B.D.; Bandyopadhyay, A.; Odegard, G.M.; Koo, A.; Liang, R. Molecular Modeling of EPON-862/graphite Composites: Interfacial Characteristics for Multiple Crosslink Densities. Compos. Sci. Technol. 2013, 76, 92–99. [Google Scholar] [CrossRef]
- Sun, H. Force Field for Computation of Conformational Energies, Structures, and Vibrational Frequencies of Aromatic Polyesters. J. Comput. Chem. 1994, 15, 752–768. [Google Scholar] [CrossRef]
- Ali, U.; Bt, K.J.; Karim, A.; Buang, N.A. A Review of the Properties and Applications of Poly (Methyl Methacrylate) (PMMA). Polym. Rev. 2015, 55, 678–705. [Google Scholar] [CrossRef]
- Goyal, R.K.; Katkade, S.S.; Mule, D.M. Dielectric, Mechanical and Thermal Properties of Polymer/BaTiO3 Composites for Embedded Capacitor. Compos. B Eng. 2013, 44, 128–132. [Google Scholar] [CrossRef]
- Pandey, A.K.; Nayak, K.C.; Mahapatra, S.S. Characterization of Friction Stir Spot Welding Between Copper and Poly-methyl-methacrylate (PMMA) Sheet. Mater. Today Commun. 2019, 19, 131–139. [Google Scholar] [CrossRef]
- Choi, J.; Shin, H.; Cho, M. A Multiscale Mechanical Model for the Effective Interphase of SWNT/Epoxy Nanocomposite. Polymer 2016, 89, 159–171. [Google Scholar] [CrossRef]
- Choi, J.; Shin, H.; Yang, S.; Cho, M. The Influence of Nanoparticle Size on the Mechanical Properties of Polymer Nanocomposites and the Associated Interphase Region: A Multiscale Approach. Compos. Struct. 2015, 119, 365–376. [Google Scholar] [CrossRef]
- Kim, H.; Choi, J. Interfacial and Mechanical Properties of Liquid Crystalline Elastomer Nanocomposites with Grafted Au Nanoparticles: A Molecular Dynamics Study. Polymer 2021, 218, 123525. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, Y.; Chai, W.; Zhang, Y.; Chen, X. Molecular Dynamics Simulation and Experimental Study of the Bonding Properties of Polymer Binders in 3D Powder Printed Hydroxyapatite Bioceramic Bone Scaffolds. Ceram. Int. 2017, 43, 13702–13709. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, X.; Leng, Y.; Fang, L.; Qu, S.; Feng, B.; Weng, J.; Wang, J. Molecular Dynamics Simulations on the Interaction Between Polymers and Hydroxyapatite with and without Coupling Agents. Acta Biomater. 2009, 5, 1169–1181. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, M.; Lu, X.; Wang, K.; Fang, L.; Ren, F.; Lu, G. Effects of Atomic-level Nanostructured Hydroxyapatite on Adsorption of Bone Morphogenetic Protein-7 and its Derived Peptide by Computer Simulation. Sci. Rep. 2017, 7, 15152. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Heinz, H. Accurate Force Field Parameters and pH Resolved Surface Models for Hydroxyapatite to Understand Structure, Mechanics, Hydration, and Biological Interfaces. J. Phys. Chem. C 2016, 120, 4975–4992. [Google Scholar] [CrossRef]
- Heyes, D.M. Pressure Tensor of Partial-charge and Point-dipole Lattices with Bulk and Surface Geometries. Phys. Rev. B 1994, 49, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Subramaniyan, A.K.; Sun, C.T. Continuum Interpretation of Virial Stress in Molecular Simulations. Int. J. Solids Struct. 2008, 45, 4340–4346. [Google Scholar] [CrossRef]
- Agrawal, S.; Patidar, D.; Dixit, M.; Sharma, K.; Saxena, N.S. Investigation of Thermo-mechanical Properties of PMMA. AIP Conf. Proc. 2010, 1249, 79. [Google Scholar]
- Abdel-Wahab, A.A.; Ataya, S.; Silberschmidt, V.V. Temperature-dependent Mechanical Behaviour of PMMA: Experimental Analysis and Modelling. Polym. Test 2017, 58, 86–95. [Google Scholar] [CrossRef]
- Choi, J.; Yu, S.; Yang, S.; Cho, M. The Glass Transition and Thermoelastic Behavior of Epoxy-based Nanocomposites: A Molecular Dynamics Study. Polymer 2011, 52, 5197–5203. [Google Scholar] [CrossRef]
- Gonzalez-Benito, J.; Castillo, E.; Cruz-Caldito, J.F. Determination of the Linear Coefficient of Thermal Expansion in Polymer Films at the Nanoscale: Influence of the Composition of EVA Copolymers and the Molecular Weight of PMMA. Phys. Chem. Chem. Phys. 2015, 17, 18495–18500. [Google Scholar] [CrossRef] [PubMed]
- Sahraei, A.A.; Mokarizadeh, A.H.; George, D.; Rodrigue, D.; Baniassadi, M.; Foroutan, M. Insights into Interphase Thickness Characterization for Graphene/epoxy Nanocomposites: A Molecular Dynamics Simulation. Phys. Chem. Chem. Phys. 2019, 21, 19890–19903. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, K.; Tang, Z.; Shinoda, W.; Okazaki, S. All-atom Molecular Dynamics Study of Impact Fracture of Glassy Polymers. I: Molecular Mechanism of Brittleness of PMMA and Ductility of PC. Polymer 2019, 178, 121570. [Google Scholar] [CrossRef]
- Minoia, A.; Chen, L.; Beljonne, D.; Lazzaroni, R. Molecular Modeling Study of the Structure and Stability of Polymer/carbon Nanotube Interfaces. Polymer 2012, 52, 5480–5490. [Google Scholar] [CrossRef]
- Jose, J.; Varkey, B.; Swaminathan, N. Insights into Traction-separation Phenomena of Graphene-cis-1,4-polyisoprene Interface Using Molecular Dynamics. Polymer 2017, 122, 280–295. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Rahimian-Koloor, S.M.; Karimzadeh, A.; Hamdi, M.; Petru, M.; Tamin, M.N. Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers 2019, 11, 1435. [Google Scholar] [CrossRef]
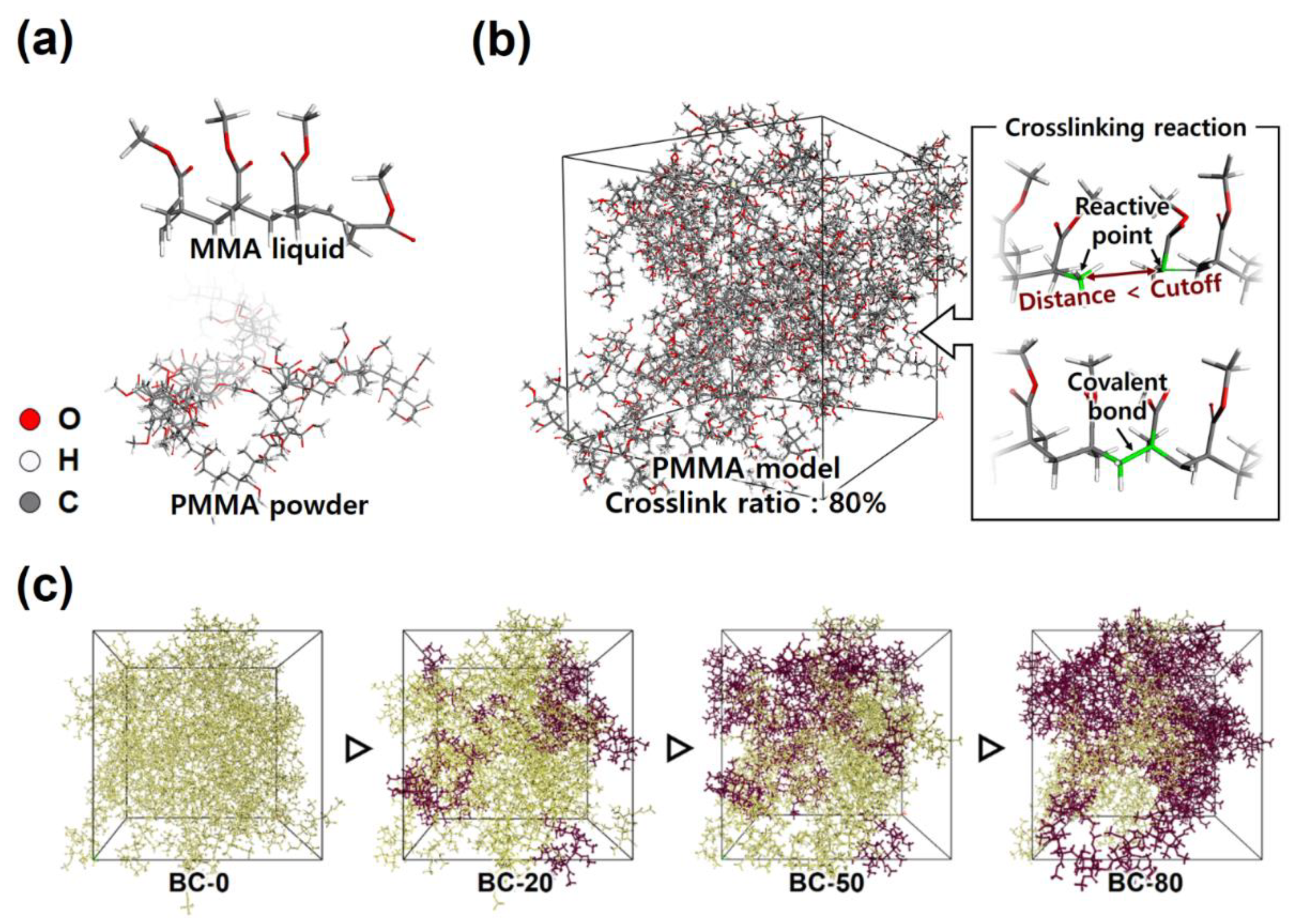
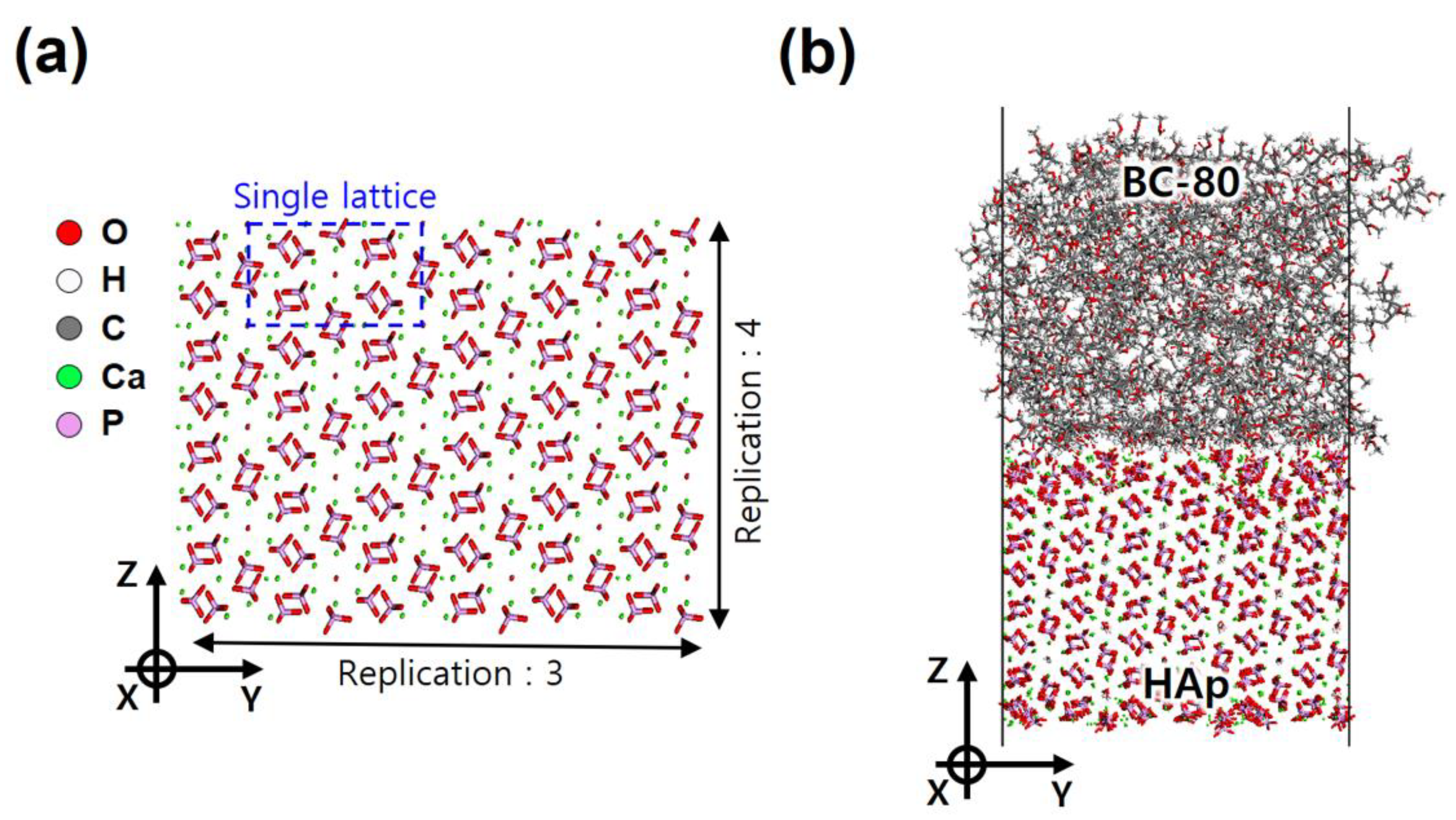

| Unit Cell Models | MMA Monomers | PMMA Chains | Crosslinking Ratio (%) | Cubic Unit Cell Length (Angs.) | Equilibrated Density (g/cc) |
|---|---|---|---|---|---|
| BC-80 | 50 | 8 | 81.81 | 45.04 | 1.080 |
| BC-50 | 50.00 | 45.11 | 1.075 | ||
| BC-20 | 20.45 | 45.17 | 1.071 | ||
| BC-0 | - | 45.14 | 1.073 |
| HAp/BC-0 | HAp/BC-20 | HAp/BC-50 | HAp/BC-80 | |
|---|---|---|---|---|
| (Å) | 0.92 | 0.95 | 0.8 | 0.85 |
| (Å) | 41.8 | 39.6 | 45.4 | 51.2 |
| (GPa/Å) | 0.2740 | 0.3044 | 0.434 | 0.3619 |
| (GPa Å) | 2.2278 | 2.5821 | 4.2952 | 4.4188 |
| HAp/BC-0 | HAp/BC-20 | HAp/BC-50 | HAp/BC-80 | |
|---|---|---|---|---|
| (Å) | 0.78 | 0.73 | 0.73 | 0.77 |
| (Å) | 6 | 6 | 6 | 6 |
| (GPa/Å) | 981.23 | 1177.1 | 1028.6 | 1116.1 |
| (GPa Å) | 2.7774 | 2.8453 | 2.9381 | 3.0163 |
| HAp/BC-0 | HAp/BC-20 | HAp/BC-50 | HAp/BC-80 | |
|---|---|---|---|---|
| (Å) | 7.44 | 5.93 | 8.79 | 9.48 |
| (GPa/Å) | 20.1 | 27.4 | 29.9 | 28.2 |
| HAp/BC-0 | HAp/BC-20 | HAp/BC-50 | HAp/BC-80 | |
|---|---|---|---|---|
| (Å) | 2.53 | 2.47 | 2.29 | 2.575 |
| (GPa/Å) | 16.2 | 24.5 | 22.6 | 27.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Goh, B.; Lee, S.; Lee, K.; Choi, J. Computational Study on Interfacial Interactions between Polymethyl Methacrylate-Based Bone Cement and Hydroxyapatite in Nanoscale. Appl. Sci. 2021, 11, 2937. https://doi.org/10.3390/app11072937
Kim H, Goh B, Lee S, Lee K, Choi J. Computational Study on Interfacial Interactions between Polymethyl Methacrylate-Based Bone Cement and Hydroxyapatite in Nanoscale. Applied Sciences. 2021; 11(7):2937. https://doi.org/10.3390/app11072937
Chicago/Turabian StyleKim, Hongdeok, Byeonghwa Goh, Sol Lee, Kyujo Lee, and Joonmyung Choi. 2021. "Computational Study on Interfacial Interactions between Polymethyl Methacrylate-Based Bone Cement and Hydroxyapatite in Nanoscale" Applied Sciences 11, no. 7: 2937. https://doi.org/10.3390/app11072937
APA StyleKim, H., Goh, B., Lee, S., Lee, K., & Choi, J. (2021). Computational Study on Interfacial Interactions between Polymethyl Methacrylate-Based Bone Cement and Hydroxyapatite in Nanoscale. Applied Sciences, 11(7), 2937. https://doi.org/10.3390/app11072937






