Bio-Inspired Morphing Tail for Flapping-Wings Aerial Robots Using Macro Fiber Composites
Abstract
Featured Application
Abstract
1. Introduction
1.1. UAS Actuation State of Art
1.2. Macro Fiber Composites
2. MFC Tail Actuator Characterization
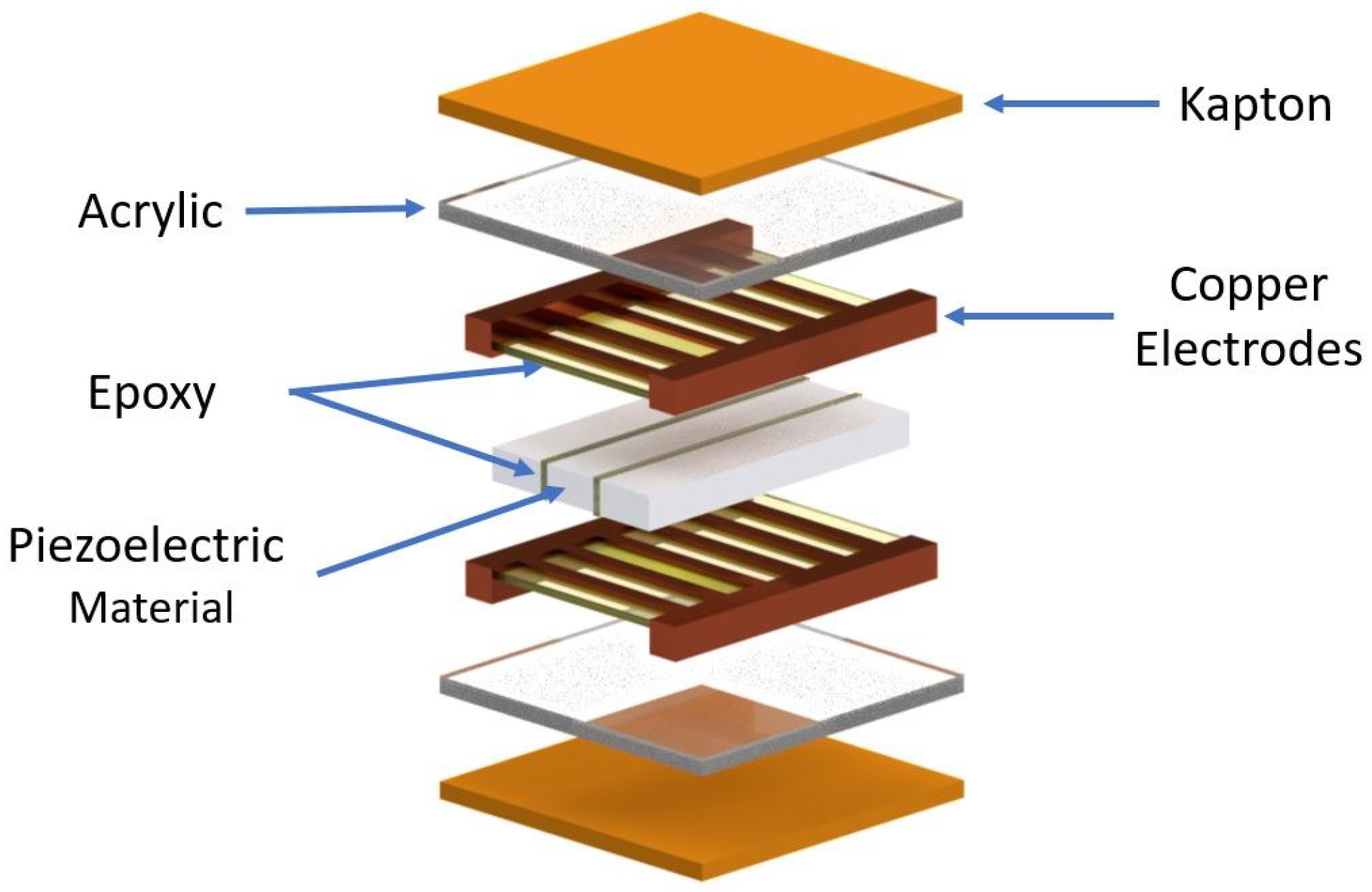
2.1. MFC Actuator Structure
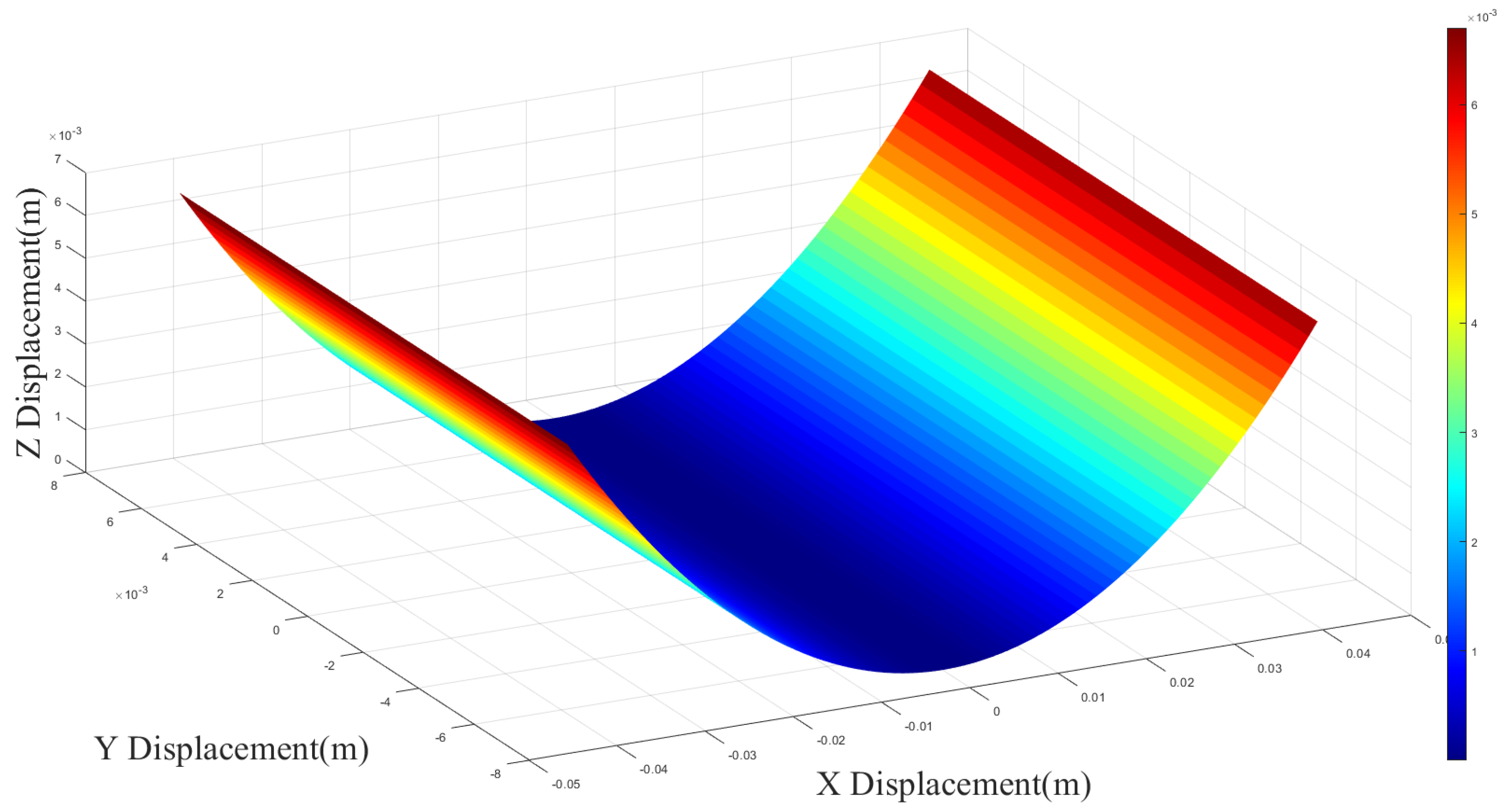
2.2. MFC Theoretical Displacement Model
Tail Actuators Comparison
3. Tail Concept and Design
3.1. Design and Development
3.2. Final Model
3.3. MFC Electronics Integration on the Ornithopter
4. Experimental Validation
4.1. Experimental Setup
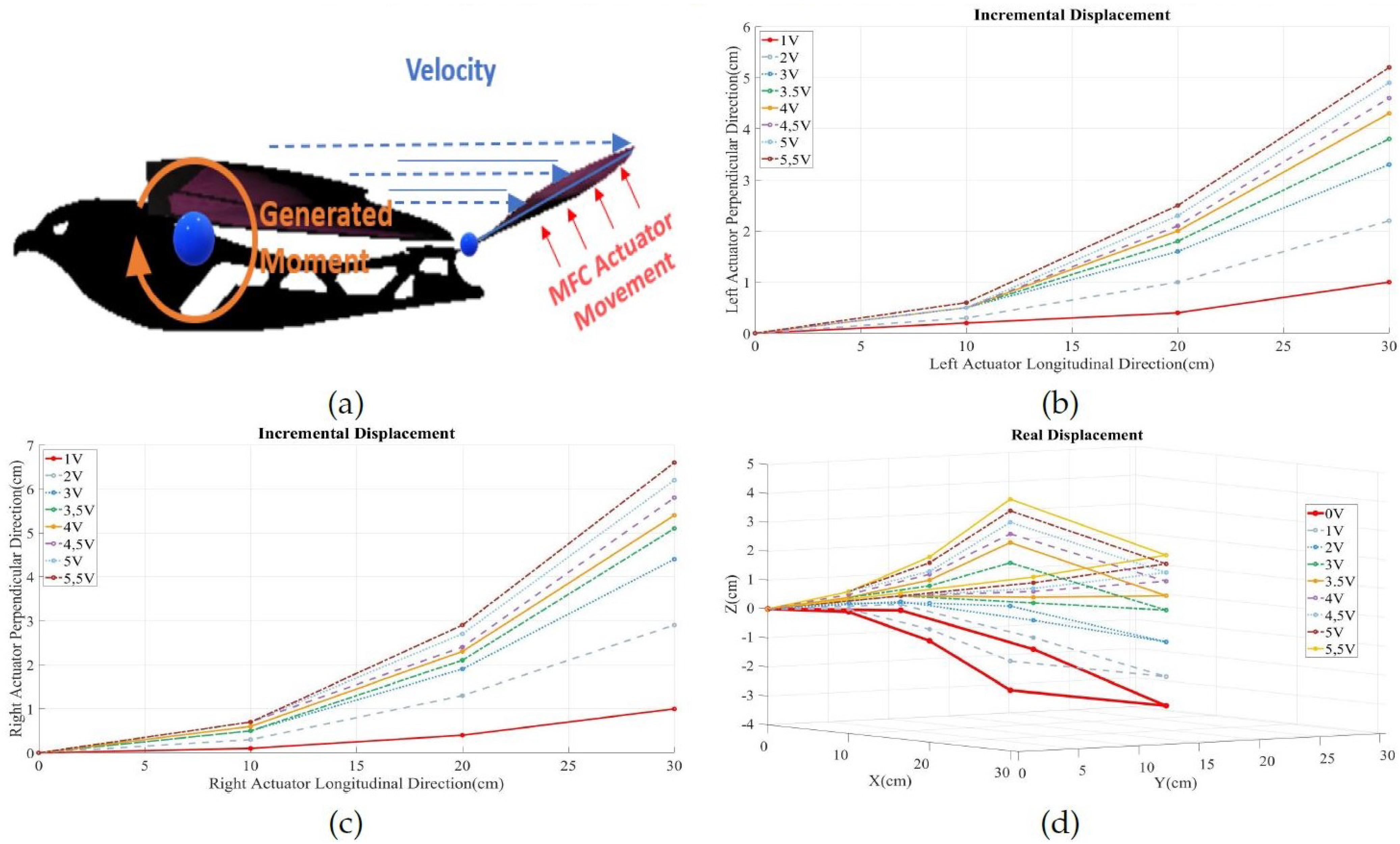
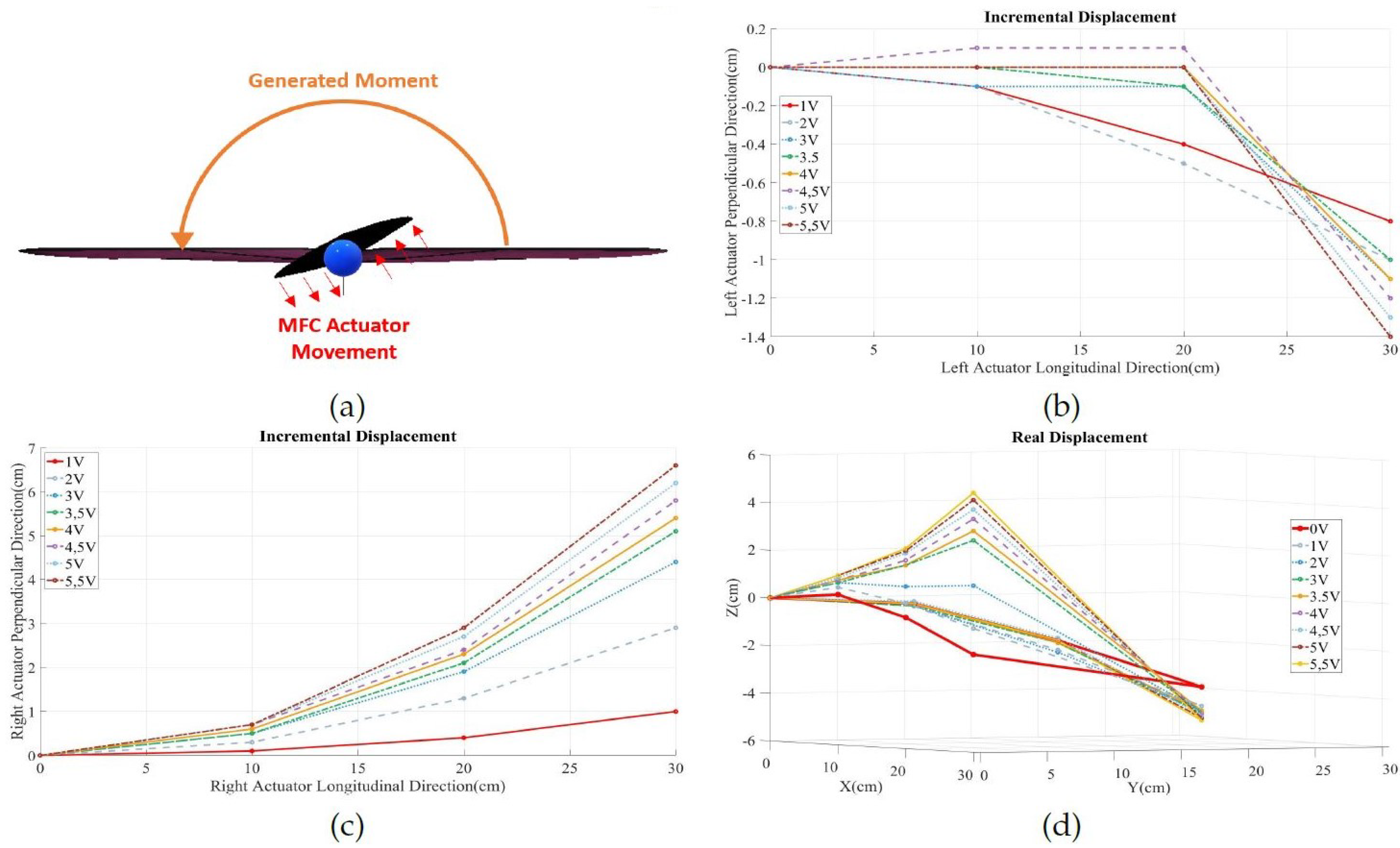
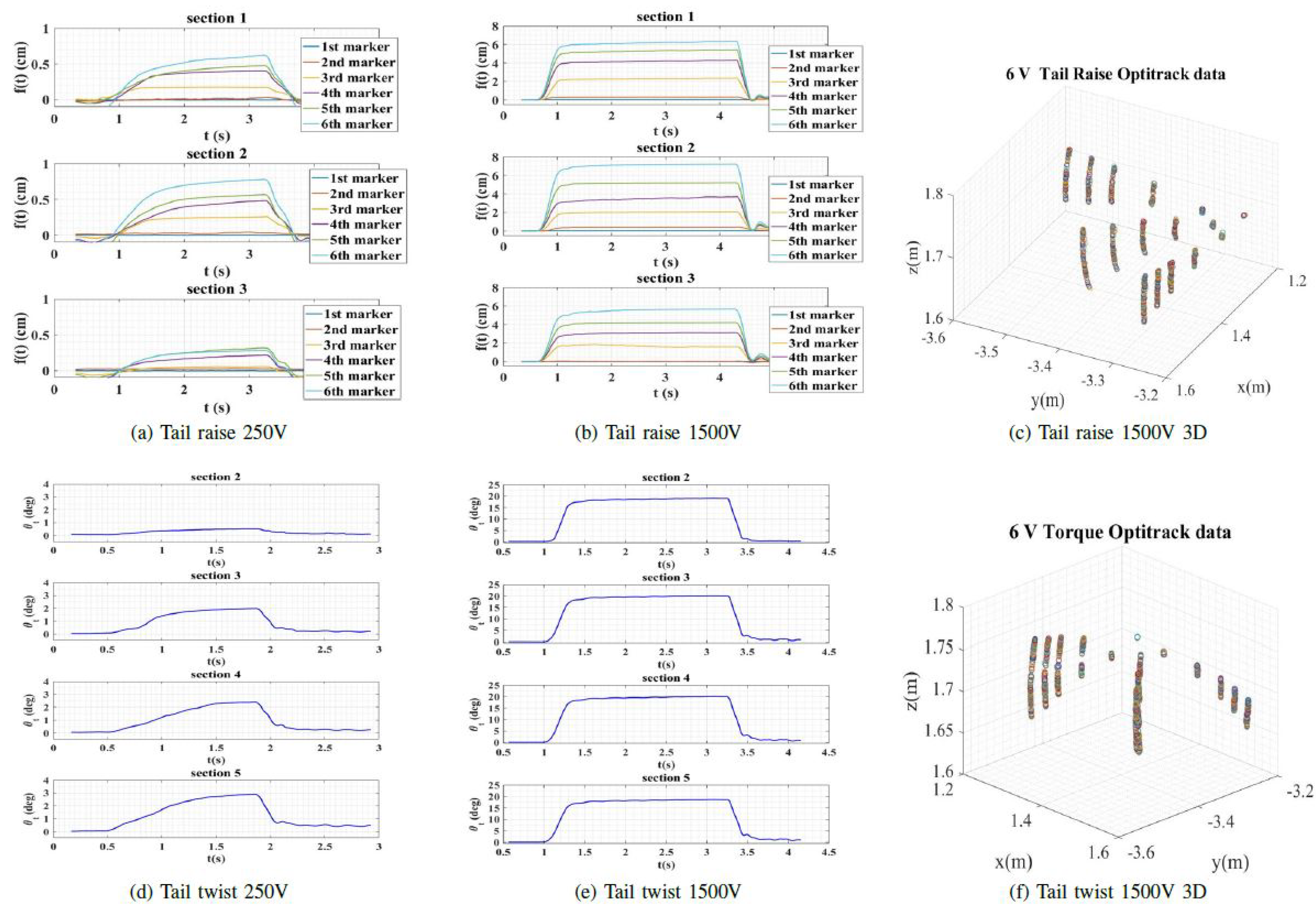
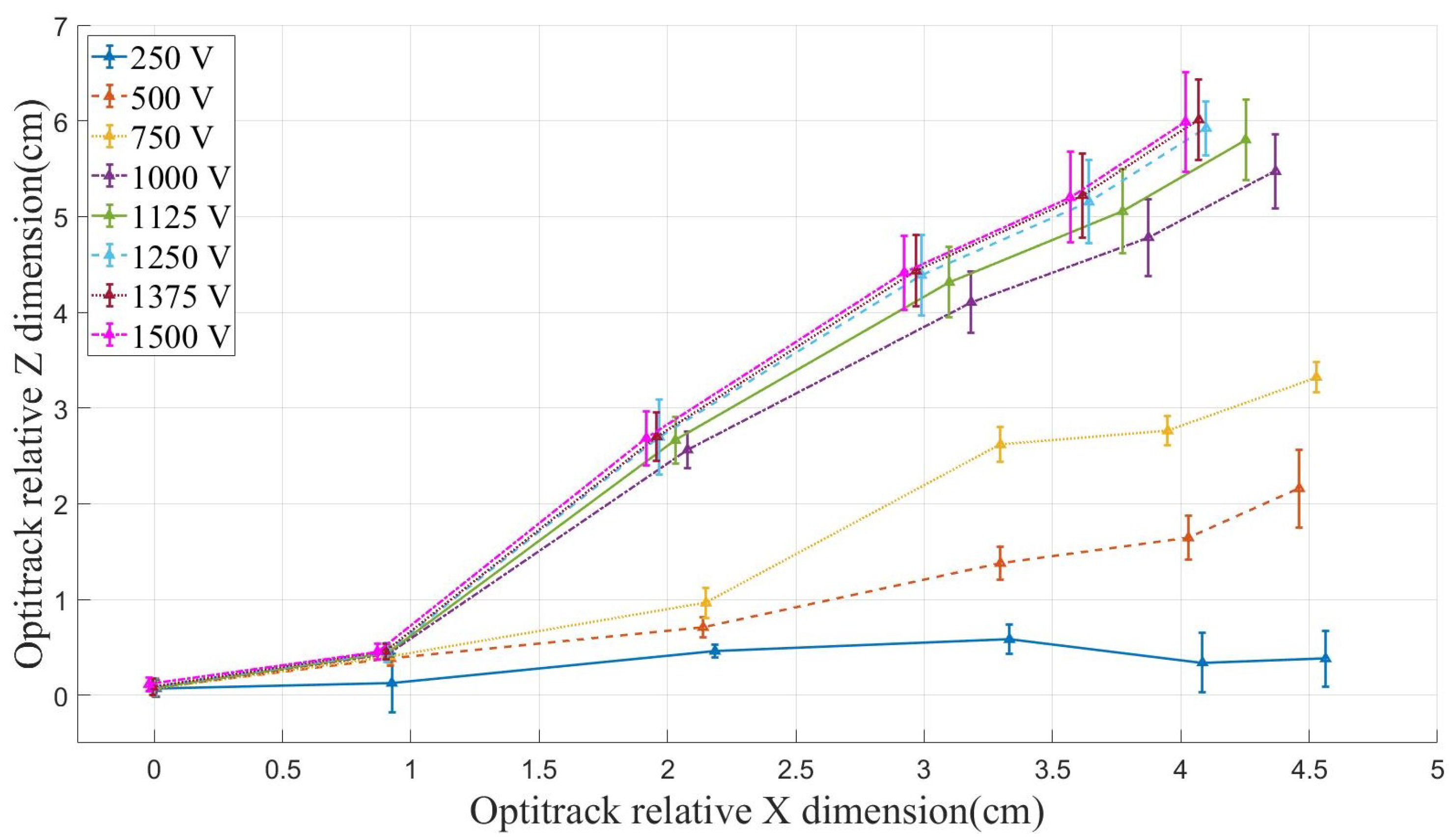
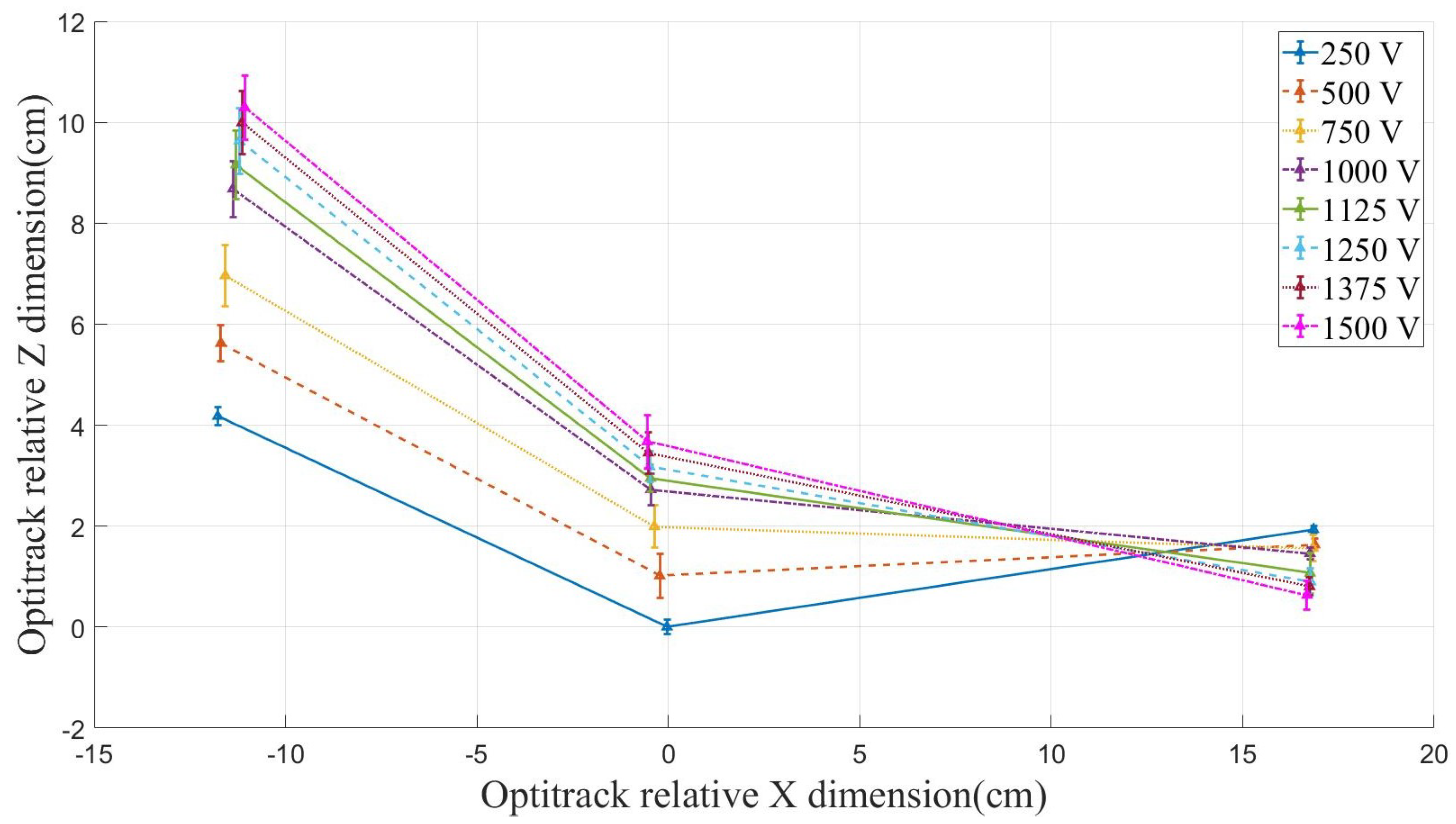
4.2. Kinematic Analysis
4.3. Repeatability and Control Study
4.4. Outdoors Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
| MFC | Macro Fiber Composites |
| UAS | Unmanned Aerial System |
| TCP | Twisted and Coiled Polimers |
| UAV | Unmanned Aerial Vehicle |
| MAV | Micro Aerial vehicles |
| CLT | Classical Lamination Theory |
| Mocap | Motion Capture System |
References
- Rakha, T.; Gorodetsky, A. Review of unmanned aerial system (uas) applications in the built environment: Towards automated building inspection procedures using drones. Autom. Constr. 2018, 93, 252–264. [Google Scholar] [CrossRef]
- Leva, S.; Aghaei, M.; Grimaccia, F. Pv power plant inspection by uas: Correlation between altitude and detection of defects on pv modules. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; IEEE: New York, NY, USA, 2015; pp. 1921–1926. [Google Scholar]
- Seo, J.; Duque, L.; Wacker, J.P. Field application of uas-based bridge inspection. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 72–81. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial manipulation: A literature review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.J.; Ramon-Soria, P.; Arrue, B.; Ollero, A.; Heredia, G. Robotic system for inspection by contact of bridge beams using uavs. Sensors 2019, 19, 305. [Google Scholar] [CrossRef] [PubMed]
- Ollero, A.; Siciliano, B. Aerial Robotic Manipulation; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Deng, C.; Wang, S.; Huang, Z.; Tan, Z.; Liu, J. Unmanned aerial vehicles for power line inspection: A cooperative way in platforms and communications. J. Commun. 2014, 9, 687–692. [Google Scholar] [CrossRef]
- Bircher, A.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Structural inspection path planning via iterative viewpoint resampling with application to aerial robotics. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: New York, NY, USA, 2015; pp. 6423–6430. [Google Scholar]
- You, D.I.; Jung, Y.D.; Cho, S.W.; Shin, H.M.; Lee, S.H.; Shim, D.H. A guidance and control law design for precision automatic take-off and landing of fixed-wing uavs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4674. [Google Scholar]
- Bellicoso, C.D.; Buonocore, L.R.; Lippiello, V.; Siciliano, B. Design, modeling and control of a 5-Dof light-weight robot arm for aerial manipulation. In Proceedings of the 2015 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; IEEE: New York, NY, USA, 2015; pp. 853–858. [Google Scholar]
- Suarez, A.; Heredia, G.; Ollero, A. Lightweight compliant arm for aerial manipulation. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: New York, NY, USA, 2015; pp. 1627–1632. [Google Scholar]
- Gomez-Tamm, A.E.; Ramon-Soria, P.; Arrue, B.; Ollero, A. Current state and trends on bioinspired actuators for aerial manipulation. In Proceedings of the 2019 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED UAS), Cranfield, UK, 25–27 November 2019; IEEE: New York, NY, USA, 2019; pp. 352–361. [Google Scholar]
- Gomez-Tamm, A.E.; Ramon-Soria, P.; Arrue, B.C.; Ollero, A. Tcp muscle tensors: Theoretical analysis and potential applications in aerial robotic systems. In Iberian Robotics Conference; Springer: Berlin/Heidelberg, Germany, 2019; pp. 40–51. [Google Scholar]
- Ramon-Soria, P.; Gomez-Tamm, A.; Garcia-Rubiales, F.; Arrue, B.; Ollero, A. Autonomous landing on pipes using soft gripper for inspection and maintenance in outdoor environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Garcia-Rubiales, F.J.; Ramon-Soria, P.; Arrue, B.; Ollero, A. Magnetic detaching system for modular uavs with perching capabilities in industrial environments. In Proceedings of the 2019 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED UAS), Cranfield, UK, 25–27 November 2019; IEEE: New York, NY, USA, 2019; pp. 172–176. [Google Scholar]
- Shyy, W.; Aono, H.; Chimakurthi, S.; Trizila, P.; Kang, C.-K.; Cesnik, C.; Liu, H. Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2010, 46, 284–327. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, C.; Chen, Y. Adaptive neural network control of a flapping wing micro aerial vehicle with disturbance observer. IEEE Trans. Cybern. 2017, 47, 3452–3465. [Google Scholar] [CrossRef]
- Keennon, M.; Klingebiel, K.; Won, H. Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 588. [Google Scholar]
- Peng, Y.; Cao, J.; Liu, L.; Yu, H. A piezo-driven flapping wing mechanism for micro air vehicles. Microsyst. Technol. 2016, 23, 967–973. [Google Scholar] [CrossRef]
- Ozaki, T.; Hamaguchi, K. Bioinspired flapping-wing robot with direct-driven piezoelectric actuation and its takeoff demonstration. IEEE Robot. Autom. Lett. 2018, 3, 4217–4224. [Google Scholar] [CrossRef]
- Rongfa, M.N.; Pantuphag, T.; Srigrarom, S. Analysis of kinematics of flapping wing uav using optitrack systems. Aerospace 2016, 3, 23. [Google Scholar] [CrossRef]
- Thomas, A.L.R. On the tails of birds. Bioscience 1997, 47, 215–225. [Google Scholar]
- Balmford, A.; Thomas, A.L.R.; Jones, I.L. Aerodynamics and the evolution of long tails in birds. Nature 1993, 361, 628–631. [Google Scholar] [CrossRef]
- Martin-Alcantara, A.; Grau, P.; Fernandez-Feria, R.; Ollero, A. A simple model for gliding and low-amplitude flapping flight of a bioinspired uav. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; IEEE: New York, NY, USA, 2019; pp. 729–737. [Google Scholar]
- Wilkie, W.K.; Bryant, R.G.; High, J.W.; Fox, R.L.; Hellbaum, R.F.; Jalink, A., Jr.; Little, B.D.; Mirick, P.H. Low-cost piezocomposite actuator for structural control applications. In Smart Structures and Materials 2000: Industrial and Commercial Applications of Smart Structures Technologies; International Society for Optics and Photonics: Bellingham, WA, USA, 2000; Volume 3991, pp. 323–334. [Google Scholar]
- Williams, R.B.; Park, G.; Inman, D.J.; Wilkie, W.K. An overview of composite actuators with piezoceramic fibers. Proceeding IMAC XX 2002, 4, 47. [Google Scholar]
- Sodano, H.A. Macro-Fiber Composites for Sensing, Actuation and Power Generation. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2003. [Google Scholar]
- Bilgen, O. Macro Fiber Composite Actuated Unmanned Air Vehicles: Design, Development, and Testing. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2007. [Google Scholar]
- Wang, D.; Yin, W.; Liu, Y.; Leng, J. Application of macro fibre composite in driving a tail of a biomimetic fish. In Active and Passive Smart Structures and Integrated Systems 2008; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6928, p. 69281H. [Google Scholar]
- Nagata, Y.; Park, S.; Ming, A.; Shimojo, M. Development of underwater robot using macro fiber composite. In Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; pp. 955–960. [Google Scholar]
- Ming, A.; Park, S.; Nagata, Y.; Shimojo, M. Development of underwater robots using piezoelectric fiber composite. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: New York, NY, USA, 2009; pp. 3821–3826. [Google Scholar]
- Hills, Z.P. Using Macro-Fiber Composite Actuators for Aquatic Locomotion. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2010. [Google Scholar]
- Bilgen, O.; Kochersberger, K.B.; Inman, D.J. Macrofiber composite actuators for a swept wing unmanned aircraft. Aeronaut. J. 2009, 113, 385–395. [Google Scholar] [CrossRef]
- Paradies, R.; Ciresa, P. Active wing design with integrated flight control using piezoelectric macro fiber composites. Smart Mater. Struct. 2009, 18, 035010. [Google Scholar] [CrossRef]
- Bilgen, O.; Kochersberger, K.B.; Inman, D.J.; Ohanian, O.J. Novel, bidirectional, variable-camber airfoil via macro-fiber composite actuators. J. Aircraft. 2010, 47, 303–314. [Google Scholar] [CrossRef]
- Butt, L.; Day, S.; Weaver, J.; Sossi, C.; Wolek, A.; Bilgen, O.; Mason, W.; Inman, D. Wing morphing design utilizing macro fiber composite smart materials. SAWE Pap. 2010, 3515-S, 1–61. [Google Scholar]
- Kancharala, A.K.; Philen, M.K. Enhanced hydrodynamic performance of flexible fins using macro fiber composite actuators. Smart Mater. Struct. 2014, 23, 115012. [Google Scholar] [CrossRef]
- LaCroix, B.W.; LaCroix, B.W.; Ifju, P.G.; Ifju, P.G. Macro fiber composites and substrate materials for mav wing morphing. In Experimental Mechanics of Composite, Hybrid, and Multifunctional Materials; Springer: Berlin/Heidelberg, Germany, 2014; Volume 6, pp. 89–101. [Google Scholar]
- Zou, C.; Li, B.; Liang, L.; Wang, W. Active vertical tail buffeting suppression based on macro fiber composites. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2016; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 9803, p. 98033A. [Google Scholar]
- Gamble, L.L.; Inman, D.J. Bioinspired pitch control using a piezoelectric horizontal tail for rudderless uavs. In Bioinspiration, Biomimetics, and Bioreplication VIII; hl International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10593, p. 1059303. [Google Scholar]
- Williams, R.B. Nonlinear Mechanical and Actuation Characterization of Piezoceramic Fiber Composites. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1999. [Google Scholar]
- Gamble, L. Bioinspired Control of Rudderless Morphing UAVs. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2018. [Google Scholar]
- Gamble, L.L.; Inman, D.J. A tale of two tails: Developing an avian inspired morphing actuator for yaw control and stability. Bioinspir. Biomimetics 2018, 13, 026008. [Google Scholar] [CrossRef] [PubMed]
- Optitrack System Cameras. Available online: https://optitrack.com/products/primex-13/ (accessed on 1 December 2020).
- Optitrack System. Available online: https://optitrack.com/ (accessed on 1 December 2020).
- Optitrack System Support. Available online: https://optitrack.com/support/ (accessed on 1 December 2020).
- Lopez-Lopez, R.; Perez-Sanchez, V.; Ramon-Soria, P.; Martin-Alcantara, A.; Fernandez-Feria, R.; Arrue, B.; Ollero, A. A Linearized Model for an Ornithopter in Gliding Flight: Experiments and Simulations. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–4 June 2020; pp. 7008–7014. [Google Scholar] [CrossRef]
- Perez-Sanchez, V. Movimiento y Desarrollo de un Controlador de Estabilidad para un Ornitóptero. Master’s Thesis, Universitario en Ingeniería Industrial, Universidad de Sevilla, Sevilla, Spain, 2019. [Google Scholar]





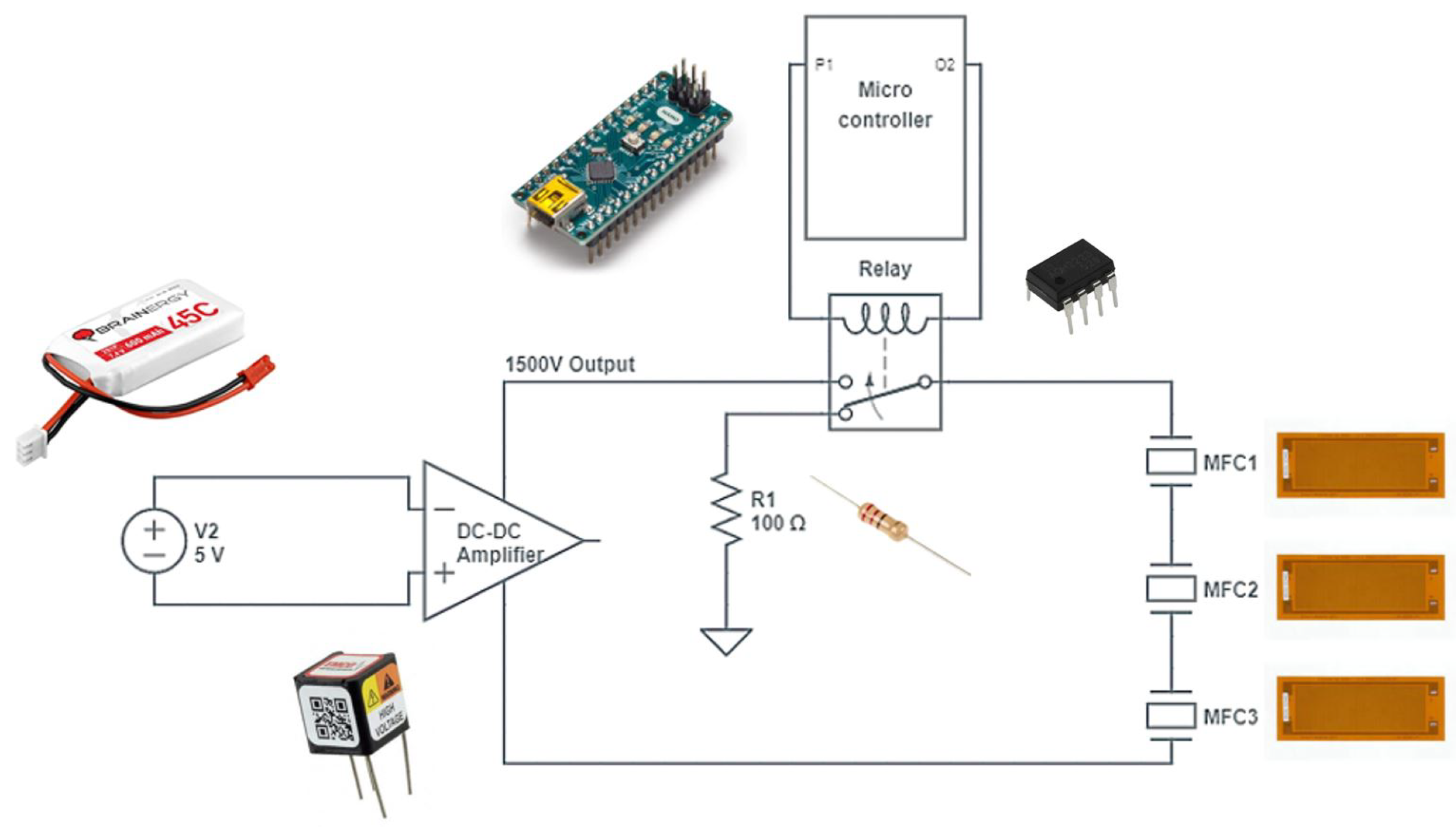





 |  | |
|---|---|---|
| Parameters | Servomotor | MFC |
| Dimensions (mm) | 22.8 × 12 × 29.4 | 101 × 20 × 0.5 |
| Weight (g) | 15.8 | 2 |
| Blocking Force (N) | 58.5 | 152 |
| Power consumption | 2 | ∼0 |
| Energy Efficiency | 85 | 100 |
| Speed | Medium | High |
| Dust and Water resistant | No | Yes |
 |  | |
|---|---|---|
| Parameters | V-Tail | Morphing Tail |
| Weight (g) | 67.1 | 51.8 |
| Surface (cm2) | 462 | 1190 |
| Weight/Surface Ratio (Kg/m2) | 1.45 | 0.44 |
| Improvement Ratio (%) | 100 | 330 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Sanchez, V.; Gomez-Tamm, A.E.; Savastano, E.; Arrue, B.C.; Ollero, A. Bio-Inspired Morphing Tail for Flapping-Wings Aerial Robots Using Macro Fiber Composites. Appl. Sci. 2021, 11, 2930. https://doi.org/10.3390/app11072930
Perez-Sanchez V, Gomez-Tamm AE, Savastano E, Arrue BC, Ollero A. Bio-Inspired Morphing Tail for Flapping-Wings Aerial Robots Using Macro Fiber Composites. Applied Sciences. 2021; 11(7):2930. https://doi.org/10.3390/app11072930
Chicago/Turabian StylePerez-Sanchez, Vicente, Alejandro E. Gomez-Tamm, Emanuela Savastano, Begoña C. Arrue, and Anibal Ollero. 2021. "Bio-Inspired Morphing Tail for Flapping-Wings Aerial Robots Using Macro Fiber Composites" Applied Sciences 11, no. 7: 2930. https://doi.org/10.3390/app11072930
APA StylePerez-Sanchez, V., Gomez-Tamm, A. E., Savastano, E., Arrue, B. C., & Ollero, A. (2021). Bio-Inspired Morphing Tail for Flapping-Wings Aerial Robots Using Macro Fiber Composites. Applied Sciences, 11(7), 2930. https://doi.org/10.3390/app11072930






