Prediction of Theoretical Derailments Caused by Cross-Winds with Frequency

Abstract

In this paper, theoretical derailment equations for cross-wind with frequency were derived to assess running safety. For a KTX (Korean high-speed train) unit, the wheel unloading ratios, which are the criteria for evaluating derailments in UIC (International union of railways) and TSI (Technical Specification for Interoperability) regulations, were calculated through the formula under the driving regulations according to cross-wind speeds, and the theoretical results were compared and evaluated through a multibody dynamics (MBD) simulation. In addition, the wheel unloading ratios were calculated for various frequencies of cross-winds. As a result of the formula and MBD, the wheel unloading ratios were shown to increase rapidly regardless of the dampers in suspension when the cross-wind frequency and the natural frequency of a vehicle were in agreement. Finally, we calculated the changes of wheel unloading ratio for different track gauges and found that these theoretical equations could calculate more accurate results than the existing Kunieda’s formula. The formula derived in this study has the advantage of considering various variables, such as fluctuant cross-winds, rail irregularities, and derailment behaviors, which were not considered in previous studies or Kunieda’s formula. It could be used for setting suspensions or railway vehicle specifications in the initial design stage.

1. Introduction

There are a lot of derailment causes for railway vehicles, such as improper wheel–rail interactions, track irregularities, and cross-winds. Recently, the speeds of railway vehicles including freight trains have increased but the weights of railway vehicles have decreased. For these reasons, cross-winds have increasingly become the cause of derailment accidents [1]. In addition, the strength of typhoons or gusts has increased due to climate change. So the risk of derailments by strong winds has increased [2,3]. Derailment accidents by cross-wind frequently occur all around the world, including Japan [4], China [5], and so forth, as shown in Figure 1.

Figure 1. Derailment accidents in Japan by strong cross-winds. [4].

As derailment accidents by strong winds have become serious, the risks of derailment by winds are evaluated by criteria given in standards like EN (European Standard), JIS (Japanese Industrial Standards) at the design stage of railway vehicles. In Europe, the safety of cross-winds by CWC (characteristic wind curves) in EN standard has usually been evaluated [6,7], and the EN and UIC regulations provide a model for wind forces acting on a vehicle under various conditions such as a wind force of Chinese hat type and wind pressure acting on a vehicle when entering a tunnel, as shown in Figure 2 [8,9].

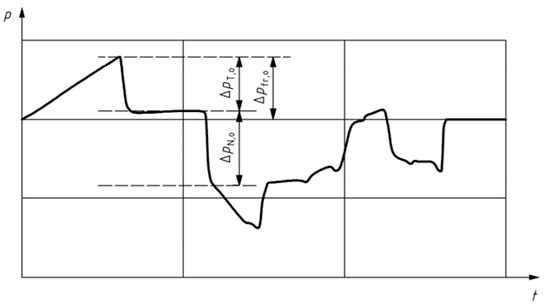
Figure 2. Tunnel pressure profile at a position just behind the nose of a train.

Since the 1970s in Japan, Masharu Kunieda [10] proposed Kunieda’s formula to evaluate the risk of derailment by cross-wind because derailment accidents had been frequently caused by strong cross-winds.

Since the shape of railway vehicles is a box type which can be severely affected by cross-wind, much research on derailment by cross-wind has been carried out.

The studies of cross-winds acting on railway vehicles can be divided into two fields: (1) aerodynamics, which considers the wind flow and force effects on vehicles, and (2) vehicle dynamics, which evaluates the risk of derailments of trains using the force effects derived from aerodynamics.

• Aerodynamics

Zhuang Sun measured the wind force acting on a train when it passed by a windbreak breach, and studied the effects according to the gap size of the windbreak breach through simulations [11]. Mulugeta Biadgo Asress carried out simulations on the ICE 2 high-speed train for a range of various yaw angles to compare with wind tunnel test data, and evaluated the changes of wind flows according to the yaw angles through simulation [12]. S. Giappino studied the aerodynamic coefficients through wind tunnel tests on down-scale models, which were on a lightweight train and a high-speed train, and evaluated rollover risks using the CWC based on static equilibrium [13].

Research on aerodynamics has been carried out through tests, using real or down scale models, and CFD (computational fluid dynamics) simulations. The tests using a real vehicle were carried out only in a special case because of cost and test bed problems. In many studies, down-scale tests and CFD simulations were performed in order to obtain wind force acting on a vehicle or aerodynamic characteristics of a vehicle. Whereas down-scale tests yield highly reliable values of the measured forces, CFD simulation reduces the cost of studies on phenomena, such as the pressure field and the wind flow [14].

• Vehicle dynamics

Takahiro Hosoi [15] used MBD (multibody dynamics) simulation to obtain the derailment coefficient for all wheels when cross-wind was applied in a curved track. In addition, the derailment coefficients according to vehicle speeds and wind speeds were analyzed. C. Baker [16] performed down-scale tests and CFD simulations to obtain the aerodynamic coefficients of a passenger car and a freight car. The wind forces were calculated based on the results and applied to the MBD simulation. The risk of derailment was assessed under various conditions reflecting wind forces and actual track conditions. Masaharu Kunieda studied the rollover derailment that could be caused by cross-wind and/or centrifugal force using physical parameters such as the center of gravity, aerodynamic coefficient, and the center of wind force on a vehicle body [10]. It was confirmed that the theoretical results obtained through the formula and the statical experimental ones obtained through the full-scale real tests were in good agreement [17]. The formula has been used in Japan to theoretically predict a rollover derailment by cross-winds until now [18]. S. W. Nam researched the rollover derailment safety of the KTX based on Kunieda’s formula, considering the wind forces generated by a train running from the opposite direction and the cross-wind on a curved track [19].

Research on derailments is carried out using MBD simulations and theoretical calculations. By the way, it is difficult to obtain accurate results through theoretical calculation because the behavior of a railway vehicle could be obtained through various variables and nonlinear equations. So, in many studies, the running safety has been evaluated using MBD simulation to obtain results similar to real situations. However, a theoretical derailment analysis is necessary to derive good estimations on suspensions at the initial design stage, because every detail of information on a vehicle must be prepared for MBD simulations, which give a better result.

Although a lot of studies on derailments by cross-wind were conducted, the derailment study on cross-winds with frequencies generated by geographical features or wayside structures is insufficient.

A cross-wind with exciting frequency can act on vehicles due to railside structures that are repeatedly placed, as in Figure 3, when running on a bridge. However, the theoretical derailment equations due to cross-wind in the previous studies could only statically evaluate the derailment risk under a constant wind speed condition [10,19], and the fluctuant wind or gust conditions have been evaluated using a multibody dynamics simulation [15,16,20].

Figure 3. Structures installed with regular intervals.

In this paper, a theoretical formula on the risk of derailment was derived considering cross-winds with varying wind forces generated by structures displaced at regular intervals on the trackside. Then, the relationship of the cross-wind frequency to the natural frequency of a vehicle was evaluated. The main content in this study is to predict the behavior of a railway vehicle using theoretical calculations, and the aerodynamic coefficients and cross-wind condition were referred to in previous studies [21,22,23] and the regulation [24] on driving conditions of high-speed trains in Korea.

To consider the dynamic effects of cyclic cross-winds and wheelsets running on tracks with irregularities, we combined this formulation with the single wheelset derailment formula derived by Koo and others in previous studies [25,26,27]. So, this derailment formula was improved for running train derailments, which is different from Kunieda’s formula or previous derailment theories for statically standing train derailments.

2. Vehicle Behaviors under a Constant Cross-Wind

2.1. Formula for a Constant Cross-Wind Acting on a Car Body

Since railway vehicles run on rails, the lateral and vertical forces applied to the rails can be used to assess derailment. When a cross-wind acts on a car body, the forces acting on suspensions of the vehicle must be known to evaluate its derailment. These forces are closely related to the data of the vertical and horizontal displacements and the roll angle of the body.

The free body diagram of a railway vehicle is shown in Figure 4 [28].

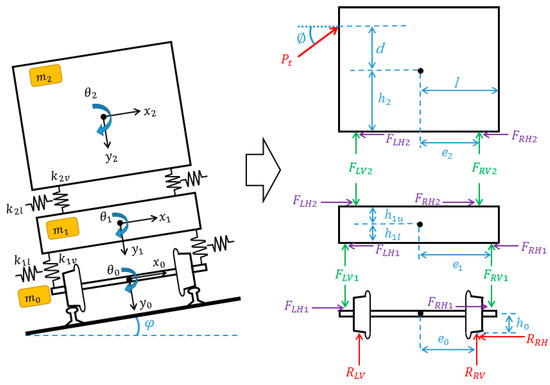
Figure 4. The free body diagram of a vehicle under a cross-wind.

The free body diagram is divided into a car body, a bogie, and a wheelset when a cross-wind force with an upper angle of φ is applied at a distance of “d” from the center of gravity of the body.

To take into account the equivalent amount to one wheelset, it is assumed that the mass and rotational inertias of the car body are 1/4 and those of the bogie are 1/2 [29].

For the primary suspension, the vertical and lateral stiffness values of rubber-metal springs installed at an axle box were denoted as k_1l and k_1v, respectively, because each axle box is directly connected with the bogie. For the secondary suspension, the vertical and lateral stiffness values of air springs connecting the bogie and the car body were denoted as k_2l and k_2v considering their half values to each wheelset.

The static equilibrium equation of a vehicle unit to predict the spring forces transmitted by the cross-wind can be summarized as follows.

• Static equilibrium equation for the car body:

$${{\displaystyle \sum }}^{}{F}_{x2}=P_t\cos \varnothing +m_2\left(\frac{v^2}{r}\cos \phi -g\sin \phi \right)-F_{RH2}-F_{LH2}=0$$

(1)

$${{\displaystyle \sum }}^{}{F}_{y2}=m_2\left(\frac{v^2}{r}\sin \phi +g\cos \phi \right)-P_t\sin \varnothing -F_{RV2}-F_{LV2}=0$$

(2)

$${{\displaystyle \sum }}^{}{M}_{G2}=P_t\left(d\cos \varnothing +l\sin \varnothing \right)+\left(F_{RH2}+F_{LH2}\right)h_2+\left(F_{LV2}-F_{RV2}\right)e_2=0$$

(3)

• Static equilibrium equation for the bogie:

$${{\displaystyle \sum }}^{}{F}_{x1}=m_1\left(\frac{v^2}{r}\cos \phi -g\sin \phi \right)+F_{RH2}+F_{LH2}-F_{RH1}-F_{LH1}=0$$

(4)

$${{\displaystyle \sum }}^{}{F}_{y1}=m_1\left(\frac{v^2}{r}\sin \phi +g\cos \phi \right)+F_{RV2}+F_{LV2}-F_{RV1}-F_{LV1}=0$$

(5)

$${{\displaystyle \sum }}^{}{M}_{G1}=\left(F_{RH2}+F_{LH2}\right)h_{1u}+\left(F_{RV2}-F_{LV2}\right)e_2+\left(F_{RH1}+F_{LH1}\right)h_{1l}+\left(F_{LV1}-F_{RV1}\right)e_1=0$$

(6)

• Static equilibrium equation for a wheelset:

$${{\displaystyle \sum }}^{}{F}_{x0}=F_{LH1}+F_{RH1}+m_0\left(\frac{v^2}{r}\cos \phi -g\sin \phi \right)-R_{RH}=0$$

(7)

$${{\displaystyle \sum }}^{}{F}_{y0}=m_0\left(\frac{v^2}{r}\sin \phi +g\cos \phi \right)+F_{LV1}+F_{RV1}-R_{RV}-R_{LV}=0$$

(8)

$${{\displaystyle \sum }}^{}{M}_{G0}=R_{RH}{h}_0+\left(F_{RV1}-F_{LV1}\right)e_1+\left(R_{LV}-R_{RV}\right)e_0=0$$

(9)

The forces of the secondary suspension springs generated by the relative displacements between the body and the bogie are as follows.

$$F_{RH2}=F_{LH2}=k_{2l}\left(x_2-x_1-h_2{\theta }_2+h_{1u}{\theta }_1\right)$$

(10)

$$F_{RV2}=k_{2v}\left(y_2-y_1+e_2{\theta }_2-e_2{\theta }_1\right)$$

(11)

$$F_{LV2}=k_{2v}\left(y_2-y_1-e_2{\theta }_2+e_2{\theta }_1\right)$$

(12)

The forces of the primary suspension springs generated by the relative displacements between the bogie and the wheelset are as follows.

$$F_{RH1}=F_{LH1}=k_{1l}\left(x_1-x_0-h_{1l}{\theta }_1\right)$$

(13)

$$F_{RV1}=k_{1v}\left(y_1-y_0+e_1{\theta }_1-e_1{\theta }_0\right)$$

(14)

$$F_{LV1}=k_{1v}\left(y_1-y_0-e_1{\theta }_1+e_1{\theta }_0\right)$$

(15)

The contact forces between the wheel and the rail can be calculated from the primary suspensions deformations as follows.

$$R_{RH}=k_{0l}\left(x_0-h_0{\theta }_0\right)$$

(16)

$$R_{RV}=k_{0v}\left(y_0+e_0{\theta }_0\right)$$

(17)

$$R_{LV}=k_{0v}\left(y_0-e_0{\theta }_0\right)$$

(18)

2.2. Dynamic Equations for a Cyclical Cross-Wind Acting on the Body

Winds in nature can generally blow at a constant speed but sometimes in the form of momentary gusts in the EN regulation. However, a cross-wind with various frequency components acts on railway vehicles by means of wayside structures repeatedly positioned or a cross-running train from the opposite direction.

In this study, we assumed that the cyclical cross-wind consists of one sine component. We evaluated how it affects derailment of a railway vehicle.

We can consider a wind force with frequency as the summation of a constant wind force of $P_t$ and an alternating wind force of $F_w\sin \omega t$ as shown in Figure 5.

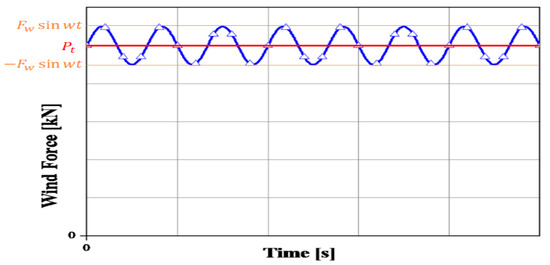
Figure 5. The wind force with a frequency component.

In order to derive the dynamic equations for the cross-wind with frequency, the free body diagram in term of a deformed shape is shown in Figure 6. In this step, the centrifugal force and gravity were not considered because their effects were considered in the previous step in Figure 4.

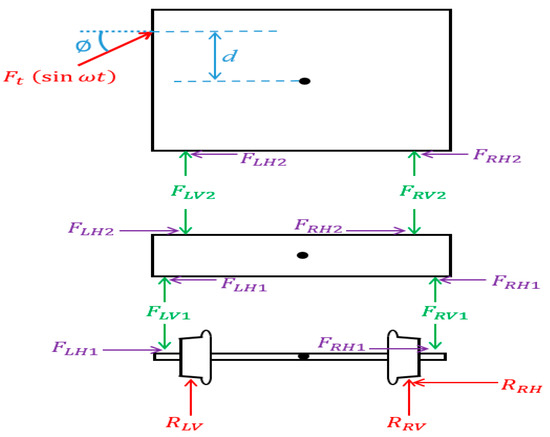
Figure 6. The free body diagram under the cyclic wind force with a specific frequency.

And then, the final forces of suspensions and the behavior of a train can be calculated by superimposing the two results obtained in the previous step (Figure 4) and this step (Figure 6). Here we assumed the cyclic effects are small compared to those of the constant force.

The equation of motion for the car body:

$${{\displaystyle \sum }}^{}{F}_{x2}=F_t\left(\sin \omega t\right)\cos \varnothing -F_{RH2}-F_{LH2}=m_2{\ddot{x}}_2$$

(19)

$${{\displaystyle \sum }}^{}{F}_{y2}=-F_t\left(\sin \omega t\right)\sin \varnothing -F_{RV2}-F_{LV2}=m_2{\ddot{y}}_2$$

(20)

$${{\displaystyle \sum }}^{}{M}_{G2}=F_t\left(d\cos \varnothing +l\sin \omega t\right)+h_2\left(F_{RH2}+F_{LH2}\right)+e_2\left(F_{LV2}-F_{RV2}\right)=I_2{\ddot{\theta }}_2$$

(21)

The forces of the secondary suspension springs generated by relative displacements between the body and the bogie can be obtained by the Equations (10)~(12), but the following assumptions are made to simplify these equations.

$$k_{1l}\gg k_{2l}, k_{1v}\gg k_{2v} \to x_2\gg x_1, y_2\gg y_1, {\theta }_2\gg {\theta }_1$$

From the Equations (19) and (21), the natural frequencies (ω_2a, ω_2b) for the lateral and rolling directions of the body are derived as the following Equations (22) and (23).

In general, since most of the cross-wind acting on a vehicle has low frequencies, the first natural frequency of the car body on suspensions becomes an important factor to assess derailment safety.

$$w_{2a}^2=\frac{1}{2}\left\{\begin{array}{c}\left(\frac{2k_{2l}}{m_2}+\frac{2k_{2l}{h}_2^2}{I_2}+\frac{2k_{2v}{e}_2^2}{I_2}\right)\\ -\sqrt{\left(\frac{2k_{2l}}{m_2}+\frac{2k_{2l}{h}_2^2}{I_2}+\frac{2k_{2v}{e}_2^2}{I_2}\right)-4\frac{2k_{2l}}{m_2}\frac{2k_{2v}{e}_2^2}{I_2}}\end{array}\right\}$$

(22)

$$w_{2b}^2=\frac{1}{2}\left\{\begin{array}{c}\left(\frac{2k_{2l}}{m_2}+\frac{2k_{2l}{h}_2^2}{I_2}+\frac{2k_{2v}{e}_2^2}{I_2}\right)\\ +\sqrt{\left(\frac{2k_{2l}}{m_2}+\frac{2k_{2l}{h}_2^2}{I_2}+\frac{2k_{2v}{e}_2^2}{I_2}\right)-4\frac{2k_{2l}}{m_2}\frac{2k_{2v}{e}_2^2}{I_2}}\end{array}\right\}$$

(23)

From the free body diagram of Figure 6, the equations of motion of the bogie and the wheelset can be derived as follows.

• The equation of motion for the bogie frame:

$${{\displaystyle \sum }}^{}{F}_{x1}=F_{RH2}+F_{LH2}-F_{RH1}-F_{LH1}=m_1{\ddot{x}}_1$$

(24)

$${{\displaystyle \sum }}^{}{F}_{y1}=F_{RV2}+F_{LV2}-F_{RV1}-F_{LV1}=m_1{\ddot{y}}_1$$

(25)

$${{\displaystyle \sum }}^{}{M}_{G1}=h_{1u}\left(F_{RH2}+F_{LH2}\right)+h_{1l}\left(F_{RH1}+F_{LH1}\right)+e_2\left(F_{RV2}-F_{LV2}\right)+e_1\left(F_{LV1}-F_{RV1}\right)=I_1{\ddot{\theta }}_1$$

(26)

• The equation of motion for the wheelset:

$${{\displaystyle \sum }}^{}{F}_{x0}=F_{RH1}+F_{LH1}-R_{RH}=m_0{\ddot{x}}_0$$

(27)

$${{\displaystyle \sum }}^{}{F}_{y0}=F_{RV1}+F_{LV1}-R_{RV}-R_{LV}=m_0{\ddot{y}}_0$$

(28)

$${{\displaystyle \sum }}^{}{M}_{G1}=R_{RH}{h}_0+e_1\left(F_{RV1}-F_{LV1}\right)+e_0\left(F_{LV}-F_{RV}\right)=I_0{\ddot{\theta }}_0$$

(29)

It is possible to predict the forces of suspensions and wheel/rails, and the behavior of a vehicle by solving the simultaneous differential Equations (19)–(21), and (24)–(29).

3. A Dynamic Simulation Model to Evaluate the Formulation

3.1. A Model for Multibody Dynamics Simulation

The commercial software “Simpack” was used to evaluate the derived equations [30]. Here, Simpack is a general multibody dynamics (MBD) simulation software enabling users to simulate the nonlinear motion of any mechanical or mechatronic system.

The simulation model was based on the power car of the KTX. The compositions of the primary and secondary suspensions are shown in Figure 7. The characteristics of the suspensions are shown in Table 1, Table 2 and Table 3 [21,22]. In addition, the simulation model to evaluate the theoretical equations is shown in Figure 8. Table 4 shows the height of the center of vehicle gravity, and the masses of the body, the bogie, and the wheelset [23].

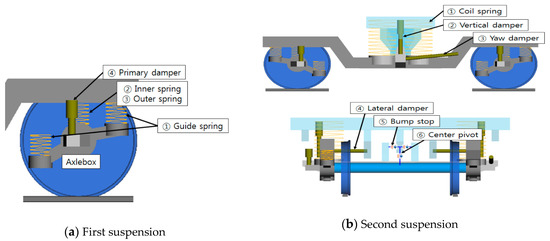
Figure 7. The compositions of suspensions.

Table 1. Specifications of the primary suspensions.

Suspension		Double Coil Spring	Guide Spring	Vertical Oil Damper
specifications	X direction	0.5813	20.0	-
	Y direction	0.5813	4.5	-
	Z direction	0.75	0.25	0.01
	T direction	0.1	0.044	-
	P direction	0.1	0.03	-
	W direction	0.1	0.473	-
Units		MN/m MN·m/rad	MN/m MN·m/rad	MN·s/m

Table 2. Specifications of an anti-yaw damper.

		Specification
Velocity [m/s]		0.0	0.0026	0.01	0.02	0.3
Force [kN]		0.0	11.0	11.6	12.0	19.0

Table 3. Specifications of the secondary suspensions.

Suspension		Coil Spring	Vertical Oil Damper	Lateral Oil Damper	Pivot Joint
Specifications	X direction	0.15	-	-	10.29
	Y direction	0.15	-	0.1	-
	Z direction	0.634	0.02	-	-
	T direction	0.1	-	-	-
	P direction	0.1	-	-	-
	W direction	0.1	-	-	-
Units		MN/m MN·m/rad	MN/m MN·m/rad	MN·s/m	MN/m

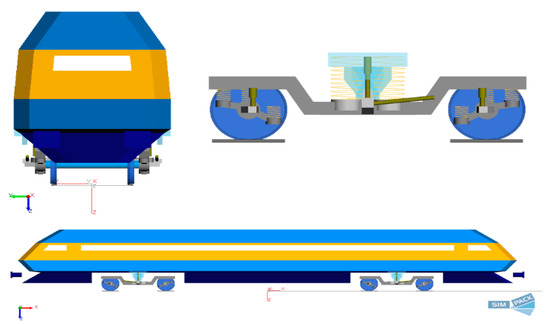
Figure 8. The 3D simulation model (Simpack).

Table 4. Specifications of the power car.

		Values
Wheelset	Wheel weight	1745	[kg]
	Moment of inertia	740	[kg·m2]
	Height of weight center	0.46	[m]
Bogie frame	Bogie weight	2420	[kg]
	Moment of inertia	972.5	[kg·m2]
	Height of weight center	0.56	[m]
Car body	Car body weight	54,960	[kg]
	Moment of inertia	13,246.36	[kg·m2]
	Height of weight center	1.72	[m]
Height of the wind force center on the car body		2.015	[m]

As mentioned above, the theoretical equations were derived as a 2D formula simplified for a real vehicle. So, the vehicle parameters must be converted for a 2D quarter model on one wheelset. Table 5 shows the modified input data for 2D dynamic simulations matching the 2D quarter model.

Table 5. Input data for 2D simulations.

Parameters	Values		Parameters	Values
$m_0$	1745	[kg]	$h_0$	0.46	[m]
$I_0$	740	[kg·m2]	$e_0$	0.7175	[m]
$m_1$	1210	[kg]	$h_{1u}$	0.067	[m]
$I_1$	972.5	[kg·m2]	$h_{1l}$	0.435	[m]
$e_1$	1	[m]
$m_2$	13,740	[kg]	$\mathrm{d}$	0.295	[m]
$I_2$	13,246	[kg·m2]	$l$	1.335	[m]
$e_2$	1.025	[m]	$h_2$	1.093	[m]
$k_{0l}$	100	[kg/mm]	$k_{0v}$	100	[kg/mm]
$k_{1l}$	9.58	[kg/mm]	$k_{1v}$	1.25	[kg/mm]
$k_{2l}$	0.51	[kg/mm]	$k_{2v}$	0.74	[kg/mm]

3.2. Evaluation of Natural Frequency of the Vehicle

The natural frequency of the power car is a unique characteristic determined by its weight and suspensions, and it is a factor closely related to the derailment safety when considering cross-winds with low frequency.

The natural frequencies for lateral and rolling directions are derived as shown in Equations (22) and (23) using the motion equations of the vehicle in Section 2.2.

The natural frequencies of the derived formula and the MBD model were compared in Table 6. Figure 9 show the behaviors of the vehicle in which the exciting frequency component coincides with its natural frequency.

Table 6. The comparison of the resonant frequencies between the theoretical formula and Simpack.

		Resonant Frequencies [Hz]
		Lateral Direction	Rolling Direction
Theory		0.94	2.51
Simpack		0.90	2.77

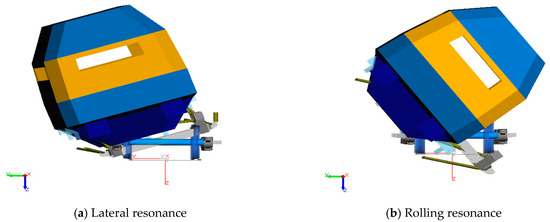
Figure 9. The vehicle behavior under the resonant frequencies.

4. Evaluation of Derailment Safety under Cross-Wind

4.1. Operating Regulations of the KTX According to Wind Speed

The operating regulations of the KTX for cross-wind speeds are enforced, as shown in Table 7, to prevent derailments [24].

Table 7. The regulations on driving conditions according to wind speeds.

Wind Speed [m/s]	Driving Conditions
45~	Operation stop
40~45	Under 90 [km/h]
30~40	Under 170 [km/h]
~30	Decelerated operation

Table 8 shows the aerodynamic coefficient and side areas of the KTX, and air density. The values related to the aerodynamics of the KTX are based on the previous research and data from vehicle manufacturers [19]. Equation (30), which is based on Bernoulli’s Equation, is used to calculate aerodynamic forces due to cross-winds [31].

Table 8. The specifications of the high-speed train.

Parameters		Values
Aerodynamic side force coefficient	($C_y$)	0.6
Side area	($\mathrm{A}$)	70.5	[m2]
Air density	($\rho$)	1.275	[kg/m3]

The regulations of Table 7 for wind speeds are converted into the equivalent lateral forces by using Equation (30) and the aerodynamic characteristics of the KTX in Table 8.

$$F_{wind}=C_y\times A\times \frac{\rho v^2}{2}$$

(30)

4.2. Criteria of Derailment

In advanced railway countries, such as Europe, North America, and Japan, there are various technical criteria to prevent derailments, as in Table 9 [32,33,34,35].

Table 9. The various evaluation criteria of derailment.

Country/ Regulation	Method/Criteria	Note
EU	${\left(\mathrm{P}/\mathrm{Q}\right)}_{smu}<0.8$	2 m moving average of derailment coefficient
UIC	$\mathrm{P}/\mathrm{Q}<0.8$	Derailment coefficient
TSI	$∆\mathrm{Q}/{\mathrm{Q}}_0<0.9$	Ratio of wheel unloading
North America	$\mathrm{P}/\mathrm{Q}<1.0$	Derailment coefficient
	${{\displaystyle \sum }}^{}\left|\mathrm{P}/\mathrm{Q}\right|<1.0~1.5$	Weinstock coefficient
	$∆\mathrm{Q}/Q_0<0.9$	Ratio of wheel unloading
RTRI (Japan)	$∆\mathrm{Q}/Q_0<1.0$	Ratio of wheel unloading

Although there are many ways to judge derailments, the ratio of the lateral and the vertical forces (P/Q) is generally used for a wheel climb-up derailment. The wheel unloading ratio ($∆$Q/Q₀) is used to assess a rollover derailment. As cross-winds usually cause a rollover derailment, the rollover risk is assessed using the wheel unloading ratio.

The definitions of P and Q are as follows: P is for the lateral force, Q for the vertical force.

4.3. Derailment Safety According to the Cross-Wind Regulations

The ratios of wheel unloading between simulations and the theoretical formula were compared under the driving conditions (Table 7), in the case that wind forces are applied in a horizontal direction ($\varnothing =0°$ in Figure 4 and Figure 6) on the ground.

Table 10 shows the ratio of wheel unloading when constant cross-winds act on the KTX power car on the straight track and curved tracks (lateral acc. 0.5 [m/s²]; this is the case of 1.0 [m/s²] referred to in the EN regulation [EN 14067]). Here it is assumed that there are no lateral forces transmitted to the wheelset due to rail irregularities.

Table 10. The ratio of wheel unloading ($∆\mathrm{Q}/\mathrm{Q}$) between the theoretical formula and the simulation for cross-winds.

Track Condition	Wind Speeds [m/s]	Ratios of Wheel Unloading		Differences
		Theory	Simulation
Straight track	0	0	0	0
	30	0.120	0.119	0.001
	40	0.233	0.220	0.013
	45	0.292	0.276	0.016
Curved track (Lateral Acc. = 0.5 m/s2)	0	0.128	0.120	0.008
	30	0.248	0.248	0
	40	0.343	0.353	0.010
	45	0.398	0.395	0.003
Curved track (Lateral Acc. = 1.0 m/s2)	0	0.256	0.242	0.014
	30	0.376	0.364	0.012
	40	0.471	0.463	0.008
	45	0.526	0.526	0

Figure 10 shows the contact forces of wheel/rail and the ratio of wheel unloading. When the wind speed of about 65 [m/s] acts on the vehicle, the wheel unloading ratio exceeds the TSI criteria for the rollover derailment ($∆\mathrm{Q}/\mathrm{Q}<0.9$).

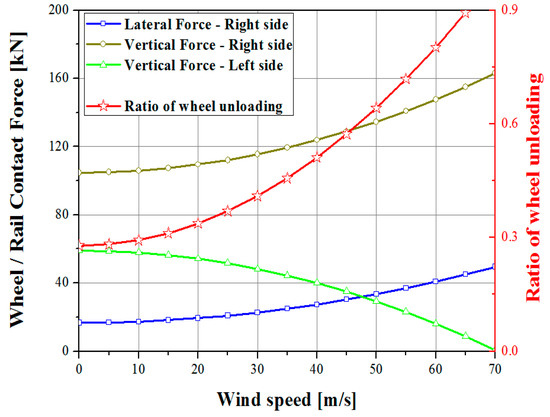
Figure 10. The ratios of wheel unloading to cross-wind speeds under the overturning derailment condition.

On the other hand, basic lateral forces acting on running wheelsets take place due to wheel conicity and rail irregularities, even though there is no cross-wind. In the previous study, the KTX has a measured coefficient of derailment (P/Q = 0.315) during normal running on a high-speed rail [36,37]. Using the measured coefficient of derailment and Equation (31), the P/Q can be converted to an additional lateral force acting on the wheelset, as given in Equation (32).

The ratios of wheel unloading according to cross-wind speeds are compared in Table 11. These results were obtained considering both the wheel–rail interactions and the lateral forces due to cross-winds on the running vehicle.

$$\frac{P}{Q}=\frac{\left(F_{LH1}+F_{RH1}\right)\left(1+\mu \beta \right)-\mu \left(1+\gamma \right)F_{LV1}+\mu \gamma F_{RV1}}{\left(1+\gamma \right)F_{RV1}-\gamma F_{LV1}+\beta \left(F_{LH1}+F_{RH1}\right)}$$

(31)

$$F_H=\frac{\left[\frac{P}{Q}\left(1+\gamma \right)-\mu \gamma \right]F_{LV1}+\left[\mu \left(1+\gamma \right)-\frac{P}{Q}\gamma \right]F_{RV1}}{\left[\left(1+\mu \beta \right)-\frac{P}{Q}\beta \right]}$$

(32)

Table 11. The ratios of wheel unloading ($∆\mathrm{Q}/\mathrm{Q}$) between the theoretical formula and the simulation for cross-wind along with dynamic wheel–rail interactions (P/Q = 0.315).

Track Condition	Wind Speeds [m/s]	Ratios of Wheel Unloading		Differences
		Theory	Simulation
Straight track	0	0.198	0.173	0.025
	30	0.318	0.304	0.014
	40	0.413	0.403	0.010
	45	0.468	0.462	0.006
Curved track (Lateral Acc. = 0.5 m/s2)	0	0.323	0.305	0.018
	30	0.443	0.429	0.014
	40	0.538	0.528	0.010
	45	0.593	0.587	0.006
Curved track (Lateral Acc. = 1.0 m/s2)	0	0.448	0.454	0.006
	30	0.568	0.579	0.011
	40	0.663	0.681	0.018
	45	0.718	0.739	0.021

Here, $\beta =\frac{h_0}{e_1}$, $\gamma =\frac{2e_0}{e_1}$ (see Figure 4).

h₀: Radius of wheel

e₀: Track width (distance between two contact points of both treads)

e₁: Distance between the contact point of a wheel tread and the primary suspension

μ: Friction coefficient

4.4. Derailment Safety Due to the Cross-Wind Frequencies

When a constant wind force acts on a vehicle, the ratio of wheel unloading must be within 0.9 not to be derailed on the straight track and the curved tracks (lateral acc. 0.5 [m/s²], 1.0 [m/s²] in the EN). However, wind speeds in nature are not constant. In addition, the winds generated by wayside structures on the track or other opposite trains make exciting frequencies [38].

In this section, the ratios of wheel unloading according to the winds with frequency were compared using the theoretical formula derived in Section 2 and the dynamic simulations.

The conditions to compare the ratios of wheel unloading according to different wind frequencies are shown in Table 12.

Table 12. The conditions to compare the derailment coefficients according to cross-wind frequencies.

Parameters		Values
Track		Straight
Rail irregularity (P/Q)		0.315
Vehicle velocity		300	[km/h]
Wind	Average speed	45	[m/s]
	Fluctuation speed	$\pm$4.5	[m/s]

4.4.1. The 2D Dynamic Vehicle Model without Dampers

In the 2D dynamic vehicle model of Section 2, the dampers in suspension are not considered to formulate theoretical equations. Therefore, if the lateral natural frequency of the vehicle and the frequency of the cross-wind are matched, resonance phenomena will occur and the amplitude will be continuously increased as time goes by.

The resonance phenomena can easily be described using the dynamic equation of a simple spring-mass system. When a periodic external force is applied to the system without dampers, the dynamic equation is shown in Equation (33), and its general solution is shown in Equation (34) [39].

$$\mathrm{m}\ddot{x}+kx=F_0\cos \omega t$$

(33)

$$\mathrm{x}\left(\mathrm{t}\right)=\mathrm{A}\cos {\omega }_{0}t+\mathrm{B}\sin {\omega }_{0}t+\frac{F_0}{m\left({\omega }_0^2-{\omega }^2\right)}\cos \omega t$$

(34)

A and B are constants determined by the initial conditions and ${\omega }_0$ is a natural frequency.

$${\omega }_0=\sqrt{k/m}$$

(35)

If the frequency of external forces ($\omega$) is equal to or very near to that of the vehicle (${\omega }_0$), the solution of the dynamic equation can be converted as shown in Equation (36).

$$\mathrm{x}\left(\mathrm{t}\right)=\mathrm{A}\cos {\omega }_{0}t+\mathrm{B}\sin {\omega }_{0}t+\frac{F_0}{2m{\omega }_0^2}t\sin {\omega }_{0}t$$

(36)

Because of the term $t\sin {\omega }_{0}t$, the solution continuously increases with the passage of time. This phenomenon is called a resonance as shown in Figure 11.

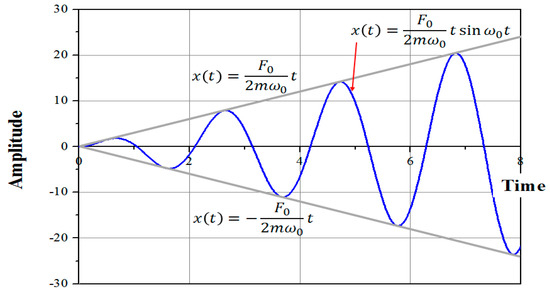
Figure 11. The amplitude under a resonance condition.

However, the actual springs in a vehicle suspension must not be extended longer than the predesigned distance not to be permanently deformed or damaged over the design limit. So, the spring constant (k) must be assumed as a nonlinear over the linear elastic range of a normal spring, which means Equation (33) is invalid in an excessive amplitude condition.

Figure 12 and Table 13 show the results that the ratios of the wheel unloading of the simulation and the current formula without dampers are rapidly increased at a resonance condition.

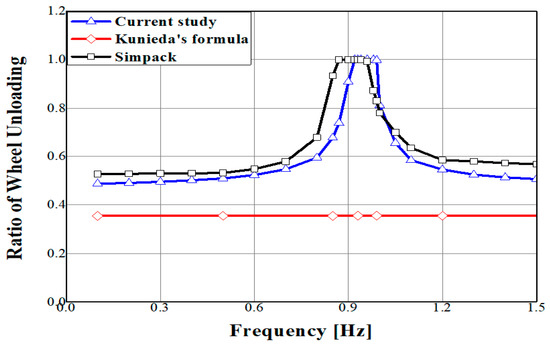
Figure 12. The comparison of the ratios of wheel unloading according to the frequencies of a cross-wind.

Table 13. The comparison between the theoretical formulas (current study and Kunieda’s formula) and simulations.

Frequency [Hz]	Theory		Simulation (P/Q = 0.315)
	Current Study (P/Q = 0.315)	Kunieda’s Formula (P/Q = 0)
0.1	0.488	0.355	0.528
0.3	0.496	0.355	0.530
0.5	0.510	0.355	0.532
0.7	0.548	0.355	0.579
0.9	0.908	0.355	1.000
1.1	0.585	0.355	0.636
1.3	0.525	0.355	0.580
1.5	0.507	0.355	0.569

However, the results using Kunieda’s formula are constant regardless of the cross-wind frequency because the formula cannot consider it. Also, the formula cannot take into account the change of ratio of wheel unloading by rail irregularities. Thus, when rail irregularity (P/Q = 0.315) is applied, as shown in Figure 12, the value of the ratio of wheel unloading is low compared to other results, even in low frequency.

Even though the ratio of the wheel unloading can have 1 as the maximum value, the TSI criteria regards over 0.9 as a derailment. Here, the simulation contact forces were filtered using 1.5 [Hz] low-pass filter to remove high-frequency components caused by numerical factors.

Although oscillatory lateral forces between wheel–rails are generated by the wheel conicity in the simulation, our formulations could not consider it. These oscillation effects gave higher values in simulation compared to the results of our formula in Table 13.

4.4.2. The 2D Dynamic Vehicle with Dampers

The amplitude (X) and the phase angle ($\delta$) are obtained using the dynamic equation with a spring damper and an external force with a constant frequency. The dimensionless amplitude (X) and the phase angle ($\delta$) are expressed as shown in Equations (37) and (38).

$$\frac{Xk}{F_0}=\frac{1}{\sqrt{{\left[1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right]}^2+{\left[2\mathsf{\zeta }\left(\frac{\omega }{{\omega }_0}\right)\right]}^2}}$$

(37)

$$\tan \delta =\frac{2\mathsf{\zeta }\left(\frac{\omega }{{\omega }_0}\right)}{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2}$$

(38)

Here, the used symbols are defined in Table 14.

Table 14. The symbols used in the damped vibration equation.

Natural frequency	${\omega }_0=\sqrt{\frac{k}{m}}$
Critical damping	$c_c=2\sqrt{mk}=2m{\omega }_0$
Damping factor	$\mathsf{\zeta }=\frac{c}{c_c}$
	$\frac{c\omega }{k}=\frac{c}{c_c} \frac{c_c\omega }{k}=2\mathsf{\zeta }\frac{\omega }{{\omega }_0}$

The above equations show that the amplitude and phases are the functions of frequency ratio ($\omega /{\omega }_0$) and damping ratio ($\mathsf{\zeta }$), and they can be shown in Figure 13.

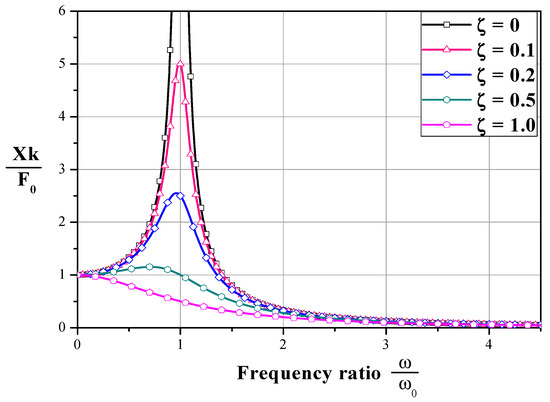
Figure 13. Nondimensional values of amplitude depending on damping factors.

In general, an actual train has dampers, as shown in Figure 14, which is expected to reduce the amplitude at resonant frequencies as described above. The characteristics of dampers installed in the KTX were applied for accurate results because the dampers can affect the simulation results. Figure 15 shows the simulation results between the models with dampers and without dampers.

Figure 14. The motor bogie of the KTX.

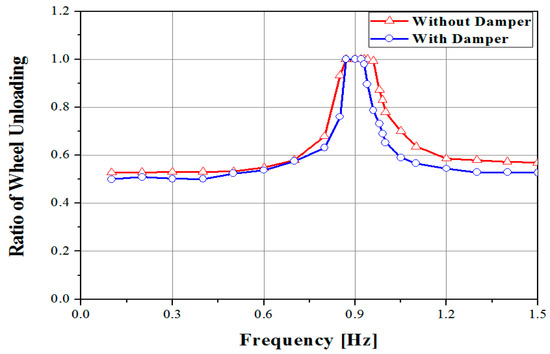
Figure 15. The comparison of the ratios of wheel unloading between the models with dampers and without dampers (simulation results).

Although the ratios of the wheel unloading showed a little difference in frequencies other than resonance, the results showed a good agreement and exceeded the TSI criteria of 0.9 in the frequency near to the resonance regardless of dampers.

Even though the characteristics of dampers can affirmatively affect the running safety, the phenomenon of a resonance is critical to derailments regardless of dampers. In a design stage, it is important to evaluate how much a cross-wind with frequency near to the natural frequency of a vehicle can affect the running safety regardless of dampers.

4.5. Derailment Safety According to Track Gauges

Track gauges are generally classified as narrow gauges, standard gauges, and wide gauges. Various track gauges are used around the world.

High-speed trains operating above 300 [km/h] generally use the standard gauge of 1435 [mm]. However, in order to compare the effects of the track gauges, simulations and theoretical formulas were calculated according to the track gauges. The risks of derailment were assessed considering the different gauges under the driving speed and the cross-wind condition in Table 15.

Table 15. The symbols used in the damped vibration equation.

Parameters		Values
Wind	Speed	30		[m/s]
	Angle	0		[°]
Vehicle speed		300		[km/h]
Rail irregularity (P/Q)		0.315
Track		Straight	Curved
Lateral acc.		-	1		[m/s2]

Figure 16a shows the change of the ratios of wheel unloading when a train runs on a straight track according to the gauges. The results of our formula, Kunieda’s formula, and MBD simulations showed that the larger the gauges, the less the risks.

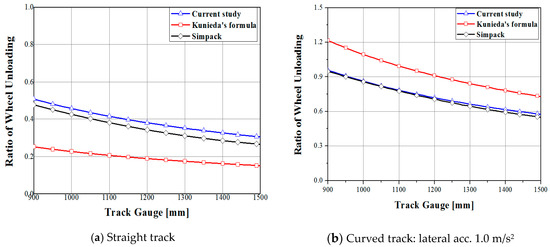
Figure 16. The ratios of wheel unloading according to track gauges.

The deviations between our formula and the MBD simulation were only about 0.04 on the straight track. It is shown that the theoretical equations of this paper were more accurate to predict derailment risks than Kunieda’s formula when considering variables such as rail irregularity which are not considered in existing theory.

Figure 16b shows the change of the ratios of wheel unloading when a train runs on the curved track according to the gauges. The results show the decreasing tendency like a form of a quadratic curve. Although the overall trend of the results using Kunieda’s formula and the theory of this paper was similar, the wheel unloading ratios using Kunieda’s formula were relatively large. In addition, the results of simulations and the theoretical ones of this research showed very similar values, but our theoretical solutions could give more accurate results than those of Kunieda’s formula.

5. Conclusions

Even though there was a lot of theoretical research to predict the risk of derailment due to cross-winds, most of them could not consider the variables like wheel–rail interactions and frequencies of cross-winds. So, there occurred some differences compared with actual results.

In this study, a new theoretical formula was proposed to predict the risk of derailment due to cross-winds with frequency considering wheel–rail interactions. The proposed formula was verified using MBD simulations.

The following conclusions were obtained:

(1)

The static equilibrium equations for the body, the bogie, and the wheelset were derived under a constant force of winds applied to the vehicle using the 2D free body diagram. The wheel–rail and suspension forces, and the displacements and rotation angle of the vehicle were obtained by solving the equations for each static variable.

(2)

The dynamic equations for the body, the bogie, and the wheelset were derived under a wind force with frequency components applied to the vehicle using the 2D free body diagram. The wheel–rail and suspension forces, and the displacements and rotation angle of the vehicle were obtained by solving the equations for each dynamic variable. In addition, the lateral and rolling natural frequencies of the vehicle were derived by solving the motion equations for the lateral and rolling directions.

(3)

The wheel–rail forces obtained from summing the dynamic and static ones were improved using a known derailment coefficient to consider wheel–rail interactions during a normal train running without winds.

(4)

The multibody dynamics software (Simpack) model was generated using the specifications of a Korean high-speed train (KTX) to evaluate our theoretical formula. For the operational regulations of the KTX under cross-wind conditions, the ratios of wheel unloading on the dynamic simulation and our theoretical formula were compared and well matched.

(5)

The ratio changes of wheel unloading were investigated under the presence or absence of suspension dampers considering the natural frequency of a vehicle and the cross-wind frequency. As a result, the ratios were found to exceed the TSI criteria regardless of the presence or absence of dampers if the natural frequency of the vehicle and the cross-wind frequency were matched.

(6)

The ratio changes of wheel unloading were investigated according to track gauges using the simulations, Kunieda’s formula, and our theoretical one. Although all the results were similar on the straight and curved tracks, the wheel unloading ratios using Kunieda’s formula were larger than the simulations and ours which are in a good agreement. So, our theoretical formula gives more accurate results than Kunieda’s formula, because it considers various operational conditions like a cross-wind frequency and a normal running derailment coefficient due to wheel–rail interaction.

Therefore, this formula has strong advantages over the previous studies or the commonly used Nadal or Kunieda’s formula because it considers various variables, such as fluctuant cross-winds, rail irregularities, and dynamic derailment behaviors. It would be possible to predict well the derailment risk under actual operating conditions. It could be used for setting suspensions or railway vehicle specifications in the initial design stage. However, this formula has the disadvantage of being more complicated when compared to the Nadal or Kunieda’s formula.