Abstract
We hypothesized that the type of wood, in combination with the grit size of sandpapers, would affect sanding efficiency. Fixed factors were used in the experiment (a belt sander with pressure p = 3828 Pa, and a belt speed of vs = 14.5 m/s) as well as variable factors (three sand belts (P60, P120, P180), six hardwood species (beech, oak, ash, hornbeam, alder, walnut) and three softwood species (pine, spruce, larch)). The masses of the test samples were measured until they were completely sanded. The sanding efficiency of hardwood species is less variable than for softwood species. Maximum sanding efficiency for the softwood ranged from 1 to 2 min, while for the hardwood species, it ranged from 2 to 4.5 min at the start of sanding and then decreased. The average time for complete sanding of the softwood samples was: 87 s (P60), 150 s (P120), and 188 s (P180). For hardwood, these times were 2.4, 1.5, and 1.8 times longer. The results indicate that the factors determining sanding efficiency are the type of wood, and, secondly, the grit size of sanding belts. In the first phase of blunting with the sanding belts, the sanding processes of hardwood and softwood are significantly different. In the second phase of blunting, sanding belts with higher grit numbers (P120 and P180) behaved similarly while sanding hardwood and softwood.
1. Introduction
Sanding is widely used in the furniture industry. The objectives of sanding may be to achieve the required surface smoothness to be painted, to achieve the required roughness necessary for gluing on the surface, and effective and controlled material removal to obtain the desired shape or dimensional accuracy of the workpiece. When planning a technological sanding process, several key aspects should be considered. Providing appropriate working conditions by reducing the exposure of workers to respirable wood dust in the air is the first important aspect [1,2,3,4,5,6]. Another group of problems are the economic issues of the used technology; in other words, obtaining high quantitative efficiency and productivity and the expected surface quality and/or accuracy of the shape for the workpieces. These two groups of problems are solved by properly selecting the production equipment, parameters of the abrasive tools and parameters of the sanding process [7,8].
Issues resulting from the specific effect of abrasive grains on wood have been studied both from the point of view of machine tool design [9], abrasive tools (type of sandpaper and its grit size) and the technological parameters used (in particular, the contact pressure and speed of the abrasive belt, the size of the surface to be sanded and the orientation of the wood fibers during sanding [10,11,12,13,14,15,16]). The influence of the properties of various species of wood on the effects of sanding were also studied [17,18,19,20,21]. One of the most important measures of the efficiency of the sanding process is the mass of material sanded per unit of time. Sanding efficiency decreases during the process due to the blunting of the abrasive belt. Ockajova [21], analyzing the literature, identified three phases of sanding belt blunting: initial sharpness, work sharpness and sanding belt blunting. During the initial phase, there is a very large reduction in efficiency during sanding. The limit between the first and second phase is a stabilization of this reduction in efficiency, at a level of about 45–50% in relation to the initial sanding efficiency. In the second phase, where the wear of the abrasive grit dominates, a further, somewhat slower reduction in sanding efficiency is observed (by about 10–20% in relation to the initial efficiency). Characteristic for the third phase is a rapid decrease in sanding efficiency.
Wieloch and Siklienka [22] investigated the effect of long time sanding on the variation in efficiency for beech wood. The analyzed process lasted 480 min. P40, P80, and P120 abrasive belts were used, and different contact pressures were applied: p = 1.0, 1.5, 1.85 and 2.0 N/cm2 (10,000, 15,000, 18,500 and 20,000 Pa). At a pressure of 10,000 Pa, a rectilinear decrease in sanding efficiency was observed. At a pressure of 18,500 Pa, however, the decrease was “bi-rectilinear”: first, the efficiency decreased intensively and, after a certain time, the decrease in sanding efficiency slowed markedly. At higher contact pressures, the sanding performance decreased more rapidly. In a comparative study on sanding oak and beech wood, Ockajova et al. [21] found that the contact pressure that ensures long-term operation of the abrasive belt depends on the direction of sanding and the wood species (the pressure on beech wood may be higher). The species of wood in these studies had a greater influence on sanding belt efficiency than the direction of cutting. The examples described here concern studies using manual sanding belt machines. The operating conditions of these machine tools are relatively high pressure (up to 20,000 Pa) and low belt speed (vs < 10 m/s). Industrial belt sanding machines operate at higher belt speeds (vs > 10 m/s) and lower pressure (p < 10,000 Pa). An example of the description of such research is the work of Saloni et al. [23], where a comparative study of industrial sanding of pine and maple wood is described. As a result of this study, a positive effect of the contact pressure and sandpaper belt speed on sanding efficiency was found, as well as a higher sanding efficiency of pine wood.
However, there is a lack of comparative studies on the influence of wood type and tool grit size on the variability of efficiency during sanding. Taking this into account, it was decided to verify the hypothesis that the type of wood, in combination with the grit size of sandpapers, affects the sanding efficiency during sanding with parameters typical for industrial applications (p < 10,000 Pa and vs > 10 m/s).
2. Materials and Methods
Wood from six hardwood species (beech, oak, ash, hornbeam, alder, walnut) and three softwood species (pine, spruce, larch) was tested. The wood material for making test samples was dried in an industrial dryer to a moisture content of 12% and stored in a freezer to preserve its physical properties. Then, the wood specimens with dimensions of 120 × 55 × 20 (length × width × height in millimeters) were obtained from it. Each specimen was measured with a caliper with an accuracy of ±0.2 mm and weighed using a WPS 510/C/2 balance (Radwag, Radom, Poland) with an accuracy of ±0.01 g. These measurements were used to calculate the density of the wood and to determine its initial mass. The calculated volumetric mass densities of the wood materials tested and the numbers of samples in the sample sets for each wood species tested are given in Table 1.

Table 1.
Characteristics of wood specimens used in sandability tests.
Before sanding, the samples were glued with PVAc glue to raw chipboard spacers with dimensions of 120 × 55 × 16 (length × width × height in millimeters) (the purpose of this procedure was to enable complete sanding of the tested wood). The wood samples were positioned so that they were sanded along the wood fibers. The form of the test samples is shown in Figure 1.
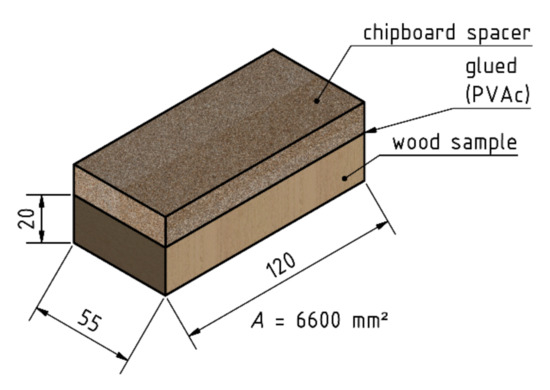
Figure 1.
Form of research samples.
The samples shown in Figure 1 were conditioned for another 3 months to equalize their moisture content in the whole volume.
Abrasive belts type EKA 2000 F 2000 × 75 (length × width in millimeters) (manufactured by Ekamant, Poznań, Poland) with three different grit sizes (P60, P120, P180) were used for sanding; their specifications are given in Table 2.

Table 2.
Sand belts specifications.
A small industrial belt sander, Maktek S (Cormak, Siedlce, Poland), with a horizontal abrasive belt arrangement (Figure 2) was used. The gravitational clamping assembly allowed a constant pressure to be exerted by the abrasive belt on the samples (p = 3828 Pa). The speed of the sanding belt was constant and was: vs = 14.5 m/s.
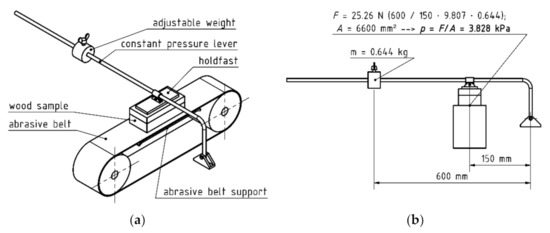
Figure 2.
Construction (a) and kinematic diagram (b) of a laboratory sander.
A separate sanding belt was used for each wood species. Each sample was sanded along the wood fibers in 30 s intervals and after each interval, the sample was weighed using a WPS 510/C/2 laboratory scale (Radwag, Radom, Poland). These steps were repeated many times until the entire wood sample was sanded off from the chipboard spacer. In this way, the following time series were obtained for each tested wood species: time-varying sanding efficiency (1), time-varying wood loss (2), and time to sand each sample, which allowed the calculation of the average sanding time for each series of samples (3).
The sanding efficiency for the intervals was calculated:
where: —sanding efficiency, —wood sample mass at the beginning of each sanding interval (g), —wood sample mass at the end of each sanding interval (g), A—sample sanded area (cm2), and —sanding cycle time (min.).
The wood loss was calculated relative to the initial sample weight:
where: —weight loss, —starting weight of the wood sample (g).
The mean value from the sample set measured every 30 s was taken as the se result, and the mean value of the mass loss measured every 30 s was taken as the wl result until the last sample in the set was ground.
For the comparison of hardwood and softwood, the mean values of se and wl were additionally calculated for all six hardwoods and three softwood species. The parameter wl was subjected to mathematical analysis. The determination of functional equations and their similarity analysis was based on multiplicity theory for comparing functions and for narrowing functions [24].
Average time for total sanding of wood in a serie:
where: —meantime for sanding a sample from the set, —number of samples in a set, —sanding times of subsequent samples in a set.
3. Results
The results in the form of sanding efficiency time series are presented separately for hardwoods and softwood species for all three grades of sandpaper (Figure 3, Figure 4 and Figure 5).
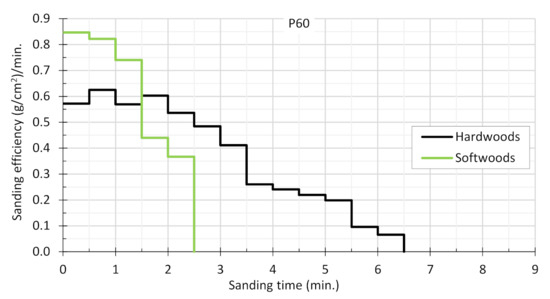
Figure 3.
Mean sanding efficiencies of belts with grade P60.
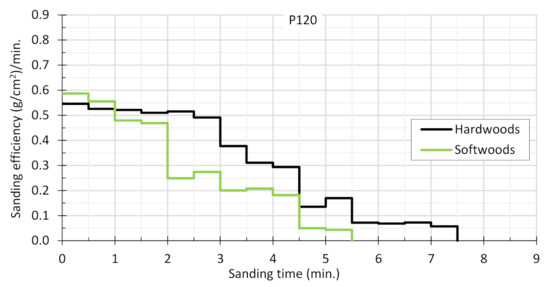
Figure 4.
Mean sanding efficiencies of belts with grade P120.
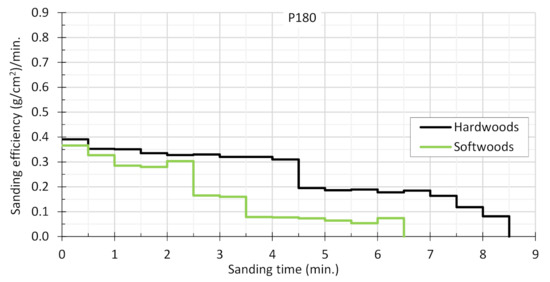
Figure 5.
Mean sanding efficiencies of belts with grade P180.
Maximum sanding efficiency for hardwood species lasts from about 0.5 to 3 min, while for softwood species it lasts from 0.5 to 2 min. It is therefore apparent from Figure 3, Figure 4 and Figure 5 that the first phase of sanding belt blunting ends quite early. In fact, for all wood species and all abrasive belt grit sizes, it is about 2–3 min after the start of machining when the sanding process moves into the second phase. In the case of softwood sanded with a P60 belt, the sample material finishes just after reaching the beginning of the second blunting phase. And in the case of pine wood sanded with the belt with the coarsest coating, it is not possible to enter the third phase of blunting of the coated abrasive before the sample wood is completely worn out.
In such a situation of the rapid progress of machine sanding at speeds higher than in the case of tests with manual sanders, it was decided to interpret the results of the experiment also by analyzing the wood removal rate for the tested wood species during the sanding. In this way, time series were obtained showing the percentage material loss during sanding (relative to a mean initial sample weight). The means were calculated separately for the sets of samples of each tested wood species. Those time series are represented by three consecutive Figure 6, Figure 7 and Figure 8 (they show only a mean wood loss in each set of samples; without including the possible loss of a chipboard spacer).
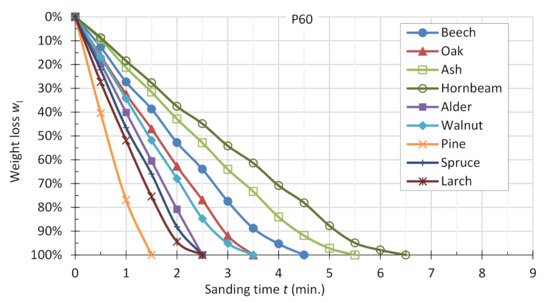
Figure 6.
Average percentage weight loss of specimens sanded with abrasive belt P60.
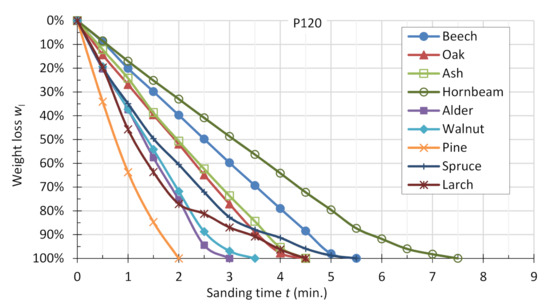
Figure 7.
Average percentage weight loss of specimens sanded with abrasive belt P120.
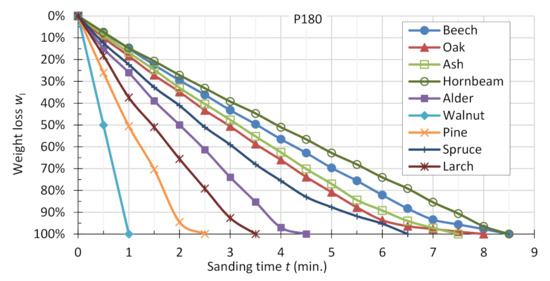
Figure 8.
Average percentage weight loss of specimens sanded with abrasive belt P180.
In all the cases, the fastest sanding was performed on the pine samples and the longest on the hornbeam samples. The total loss of mass of the specimens in the case of the P60 abrasive belt occurred in 1.5 min (pine) to 6.5 min (hornbeam). For the P120 belt, it ranged from 2 min (pine) to 7.5 min (hornbeam), and for the P180 belt, it ranged from 2.5 to 8.5 min (beech and hornbeam).
4. Discussion
In Figure 3, Figure 4 and Figure 5, different rates of decline in sanding efficiency are observed. It seems that the rapid rate of decline in the sanding efficiency is related to the high initial efficiency (the greater the initial efficiency, the more rapid its reduction). This rapid rate of decline in sanding efficiency was observed with lower density samples, especially softwoods. A possible reason for the rapidly decreasing sanding efficiency (which occurs from 0.5 min to 3 min depending on grit size and species of wood) is that the spaces between the coated abrasive become clogged more quickly by wood dust.
The weight loss of sample sets during sanding is uniform (Figure 6, Figure 7 and Figure 8), which results from the fact that most of the experiment time takes place in the second blunting phase, for which such a course of the sanding process is characteristic. Additionally, in this way, the occurrence of a short time of the first blunting phase was emphasized. Moreover, in the case of most of the wood species, a third blunting phase occurred at the end of the experiment, when the vast majority of the sample mass had already been sanded. The rate of weight loss of the wood during sanding, as known to date, is generally greater for lower-density wood species; but the differences between the high-density species (oak) and the light softwoods (spruce, visible in the graphs) are slight. In addition, the lighter hardwood species (alder, walnut), in terms of wood removal rate, behave similarly to low-density softwoods.
The conclusions of the scientific works to date indicating the effect of wood density resulted from comparisons of a mostly small number of species. Saloni et al. [23] compared parameters of sanding hard maple (Acer saccharum) (hardwood) and eastern white pine (Pinus strobus) (softwood). They mentioned wood species as one of the factors influencing the sanding results. The wood removal rate was twice as high for pine than for maple. Ockajova et al. [21] considered only two hardwood species: European beech (Fagus sylvatica) and English oak (Quercus robur). With a slight difference in density (684 kg/m3 for beech, 678 kg/m3 for oak), they found significant differences between the wood removal rates of both species. Miao and Li [25] also studied two hardwood species: Manchurian ash (Fraxinus mandshurica), and birch (Betula sp.). The density of wood samples in this study was respectively 620 and 470 kg/m3. In this case, lower values of wood removal rates in all variants of the study were for the denser and harder Ashwood. Thorpe and Brown [26] used as many as 21 species (17 hardwoods and 4 softwoods) in the study on dust production during hand sanding. They found that the quantity of wood removed during sanding varied irreversibly with wood density.
The results of these studies link the rate of the wood removed during sanding to the density and directly to the species of wood, regardless of whether it is softwood or hardwood. Therefore, to compare these two different types of wood, the total sanding times for all samples of each species were averaged. The calculated average values of these total sanding times for the six hardwood species and three softwood species separately are shown in Figure 9, Figure 10 and Figure 11.
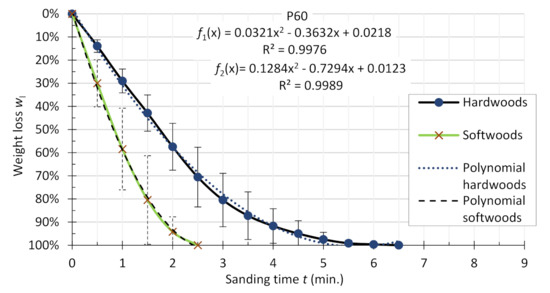
Figure 9.
Comparison of average results for hardwoods (beech, oak, ash, hornbeam, alder, walnut) and softwoods (pine, spruce, larch) species; P60 sandpaper.
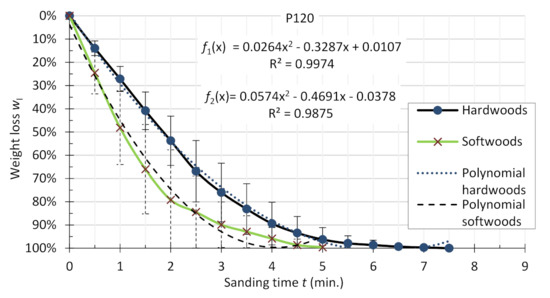
Figure 10.
Comparison of average results for hardwoods (beech, oak, ash, hornbeam, alder) and softwoods (pine, spruce, larch) species; P120 sandpaper.
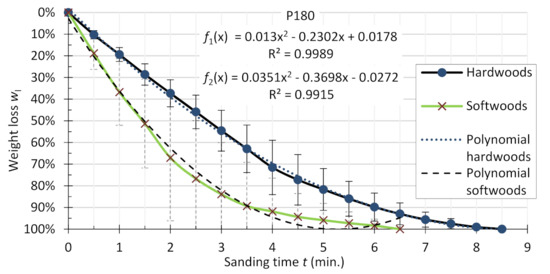
Figure 11.
Comparison of average results for hardwoods (beech, oak, ash, hornbeam, alder) and softwoods (pine, spruce, larch) species; P180 sandpaper.
The graphs in Figure 9, Figure 10 and Figure 11 show that in all tested cases, the average sanding time of the samples of softwood species was lower than that of the hardwood species. The sanding times of the softwood species were: 2.5 min (P60), 5 min (P120), and 6.5 min (P180). For hardwood species, these times were 6.5, 7.5, and 8.5 min, respectively. The spread of sanding efficiency values for softwood is much greater than in hardwood species. This is due to the difference in tribological properties of softwood and hardwood. During sanding, what is important is not only the density but also the specific physical and mechanical properties of individual wood species and their morphologies themselves (hardwood ring-porous, hardwood scattered porous, with resin content or without, chemical composition, etc.). The resin content of the softwood has a great influence on the tribological properties of wood and it may be a cause of quickly blunting of the sanding tool [27].
The mean values of the measurements were statistically analyzed. Confidence intervals were calculated using a t-distribution table (α = 0.90). It was found that the measurement uncertainty of the means was always greater for softwood and its maximum value was independent of the sandpaper gradation. This uncertainty for hardwood was, respectively: 12.9% (P60), 13.2% (P120), 12.5% (P180). For softwood, it was: 19.1% (P60), 21.6% (P120) and 29.1% (P180).
The main hypothesis of our study is that hardwood differs from softwood in terms of the efficiency of the sanding process. For this purpose, changes in average weight loss were compared in the function of sanding time (Figure 9, Figure 10 and Figure 11). The equations for these abrasive belts were found. Then, to adjust and compare the course of the functions, the set theory approach was used to narrow down the functions. In the first stage, for the functions to be considered equal, they must satisfy the first condition of the equality of the functions, which says that the functions f1 (x) and f2 (x) are equal to each other if, and only if, they have the same domains and for each point of the common domain, they assume these are the same values and for each , and [24].
For all three grit sizes of sanding belts P60, P120, and P180, and for both types of wood (hardwood and softwood), the domains of functions being a square function with the general formula were calculated as using the procedure: (1) calculation of the root of a function Δ (); (2) determination of parameters p i q (, ). In the case of sanding belt P60, significant differences were found between the examined functions because their domains assumed values and , thus , so the functions are not equal. Then the second condition for the definition of function equality was checked, indicating that for each [28]. These functions do not satisfy the equality condition and are therefore different, which indicates that hardwood differs from softwood in terms of the efficiency of the sanding process for the grit size P60.
For the sanding belt P120, it was observed that the first condition of the equality of the function was not satisfied ( and ). However, the second condition assuming that for every was satisfied. Thus, a restriction was applied for functions on the selected set of points belonging to the set A (−89.4; −100) where for every , the functions are equal [29]. Based on the calculations related only to this set of arguments, it was found that both functions are similar to each other in the indicated range, and their domains are the same for this set of arguments. A similar situation was observed for the sanding belt P180. Using the second condition of function equality, set A was determined (−81.7; −100) for which these functions are equal. Based on the mathematical analyses, it was found that the sanding belts in the second stage of blunting behave similarly. The belts of grit number (P60) dull faster than belts with higher grit numbers (P180). At the same time, differences were found between softwood and hardwood in terms of the efficiency of the sanding process.
The graph in Figure 12 shows the average sanding times with belts of different grit numbers in the individual sample sets. The graph also shows the Brinell hardness of individual wood species (the macro-hardness determination method was selected from two common hardness measurement methods [30]).
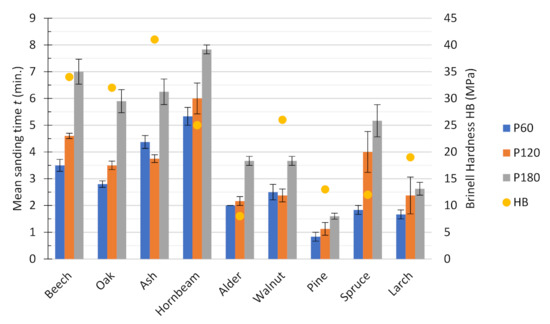
Figure 12.
Average sanding time for sample sets sanded with different grit sizes.
The average sanding times for sample sets of two wood species are interesting. In the case of ash, the shortest sanding time was obtained for the P120 belt, while in the case of the other tested materials, the shortest sanding time was usually for the P60 belt (in the case of walnut, these times were more or less equal). This can be explained by the fact that it is the hardest species of wood and in this case, the optimal abrasive belt grit from the point of view of sanding efficiency fell on the belt of medium grain (according to the grain size effect described in the publication Sin et al. 1979 [31] caused by the influence of the elasticity of wood [32]). Another interesting species of wood is spruce. In the case of samples made of this material, the greatest effect of the grit number of the sanding belt on the average time for complete sanding of the sample set was observed. The sanding time with the P120 belt increased by as much as 120% compared to the sanding time with the P60 belt. For other grits, these times were either slightly shorter (by 15% for ash and 5% for walnuts) or greater (from 13 to 42%).
The times of sanding with belts of different grit numbers of the individual sets of samples do not seem to correlate with the Brinell hardness of the tested wood species. For example, walnut, which is twice as hard as alder, shows an average sanding time similar to that of alder. Among the softwood species, average sanding times of pine wood are roughly half of that of spruce, although the hardness of both species is similar. The test results show that hardness is not the only factor affecting sanding efficiency. The influence may be caused by other tribological properties, e.g., the instantaneous coefficient of friction, which depends both on the type of wood, hardness, as well as the roughness and temperature, which are time-varying during sanding and dependent on the grit of the sanding belt [33].
5. Conclusions
The results of the study on the machine sanding of different wood species with sanding belts of various grit numbers indicate that:
- The spread of sanding efficiency values for softwood is much larger than in hardwood species. This may be due to the uneven blunting of the belts due to the specific tribological properties of the softwood (resin content).
- The type of wood is the factor that determines the wood removal rate and thus the sanding efficiency in the initial blunting phase of the sanding belts. In the first phase of blunting of the sanding belts, the sanding processes of hardwood and softwood are significantly different. In the second phase of blunting, sanding belts with higher grit numbers (P120 and P180) behave similarly while sanding hardwood and softwood. Wood type is, therefore, another factor apart from the previously known ones (pressure force, belt speed, wood density, and the grit number of the sanding belt), which should be taken into account when designing the sanding processes of solid wood elements.
In machine sanding of wood at low pressure and high belt speed, abrasive materials with a low grit number and high sharpness affect hardwood and softwood differently. The sanding efficiency of softwood is considerably higher than hardwood in these conditions. Therefore, sanding parameters (pressure and belt speed) should be set at lower values to avoid excessive sanding or over-sanding (a situation when too much material is sanded).
Author Contributions
Conceptualization, T.R. and M.S.; methodology, T.R.; validation, M.S., R.M. and T.R.; formal analysis, K.S.-S.; investigation, T.R.; resources, T.R.; data curation, M.S.; writing—original draft preparation, T.R. and M.S.; writing—review and editing, T.R. and M.S.; visualization, M.S.; supervision, T.R.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Centre for Research and Development, BIOSTRATEG3/344303/14/NCBR/2018.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors thank Jacek Sydor for the valuable terminological comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rogoziński, T.; Hlásková, L.; Wieruszewski, M.; Očkajová, A. Particle-Size Distribution of Dust Created during Sanding the Modified Ash Wood. Ann. WULS SGGW For. Wood Tech. 2015, 90, 162–166. [Google Scholar]
- Antov, P.; Brezin, V. Инженерна екология/Engineering Ecology; Publishing house—University of Forestry: Sofia, Bulgaria, 2015; ISBN 978-954-332-135-3. [Google Scholar]
- Očkajová, A.; Kučerka, M.; Krišťák, L.; Igaz, R. Granulometric Analysis of Sanding Dust from Selected Wood Species. Bioresources 2018, 13, 7481–7495. [Google Scholar] [CrossRef]
- Antov, P.; Neykov, N.; Savov, V. Effect of Occupational Safety and Health Risk Management on the Rate of Work–Related Accidents in the Bulgarian Furniture Industry. Wood Des. Technol. 2018, 7, 1–9. [Google Scholar]
- Pędzik, M.; Stuper-Szablewska, K.; Sydor, M.; Rogoziński, T. Influence of Grit Size and Wood Species on the Granularity of Dust Particles during Sanding. Appl. Sci. 2020, 10, 8165. [Google Scholar] [CrossRef]
- Očkajová, A.; Kučerka, M.; Kminiak, R.; Krišťák, Ľ.; Igaz, R.; Réh, R. Occupational Exposure to Dust Produced When Milling Thermally Modified Wood. Int. J. Environ. Res. Public Health 2020, 17, 1478. [Google Scholar] [CrossRef] [PubMed]
- Pahlitzsch, G. Internationaler Stand der Forschung auf dem Gebiet des Schleifens von Holz. Holz Roh- Werkst. 1970, 28, 329–343. [Google Scholar] [CrossRef]
- Csanády, E.; Magoss, E. Mechanics of Wood Machining, 3rd ed.; Springer: Cham, Switzerland, 2013; ISBN 3-642-29955-5. [Google Scholar]
- Vlasev, V.; Kovatchev, G.; Atanasov, V. Mechanism for Belt Sanding Machines with a Fixed Bearing of the Sanding Belt and Eccentric Tension. In Proceedings of the Implementation of Wood Science in Woodworking Sector, Zagreb, Croatia, 12–13 December 2019; pp. 221–224. [Google Scholar]
- Pahlitzsch, G.; Dziobek, K. Über das Wesen der Abstumpfung von Schleifbändern beim Bandschleifen von Holz. Holz Roh- Werkst. 1961, 19, 136–149. [Google Scholar] [CrossRef]
- Taylor, J.B.; Carrano, A.L.; Lemaster, R.L. Quantification of Process Parameters in a Wood Sanding Operation. For. Prod. J. 1999, 49, 41–46. [Google Scholar]
- Očkajová, A.; Sikliena, M. The Influence of Chosen Factors of Wood Sanding upon the Efficiency of Sand Belt. Drevarsky Vyskum/Wood Res. 2000, 45, 33–38. [Google Scholar]
- Carrano, A.L.; Taylor, J.B.; Lemaster, R. Parametric Characterization of Peripheral Sanding. For. Prod. J. 2002, 52, 44–50. [Google Scholar]
- Sinn, G.; Gindl, M.; Reiterer, A.; Stanzl-Tschegg, S. Changes in the Surface Properties of Wood Due to Sanding. Holzforschung 2004, 58, 246–251. [Google Scholar] [CrossRef]
- Gurau, L.; Mansfield-Williams, H.; Irle, M. Processing Roughness of Sanded Wood Surfaces. Holz Roh- Werkst. 2005, 63, 43–52. [Google Scholar] [CrossRef]
- Porankiewicz, B.; Banski, A.; Wieloch, G. Specific Resistance and Specific Intensity of Belt Sanding of Wood. Bioresources 2010, 5, 1626–1660. [Google Scholar]
- Ratnasingam, J.; Reid, H.F.; Perkins, M.C. The Abrasive Sanding of Rubberwood (Hevea Brasiliensis): An Industrial Perspective. Holz Roh- Werkst. 2002, 60, 191–196. [Google Scholar] [CrossRef]
- Burdurlu, E.; Usta, I.; Ulupinar, M.; Aksu, B.; Erarslan, T.Ç. The Effect of the Number of Blades and the Grain Size of Abrasives in Planing and Sanding on the Surface Roughness of European Black Pine and Lombardy Poplar. Turk. J. Agric. For. 2005, 29, 315–321. [Google Scholar] [CrossRef]
- Malkoçogǧlu, A.; Özdemir, T. The Machining Properties of Some Hardwoods and Softwoods Naturally Grown in Eastern Black Sea Region of Turkey. J. Mater. Process. Technol. 2006, 173, 315–320. [Google Scholar] [CrossRef]
- Aslan, S.; Coşkun, H.; Kiliç, M. The Effect of the Cutting Direction, Number of Blades and Grain Size of the Abrasives on Surface Roughness of Taurus Cedar (Cedrus Libani A. Rich.) Woods. Build. Environ. 2008, 43, 696–701. [Google Scholar] [CrossRef]
- Očkajová, A.; Kučerka, M.; Krišťák, L.; Ružiak, I.; Gaff, M. Efficiency of Sanding Belts for Beech and Oak Sanding. Bioresources 2016, 11. [Google Scholar] [CrossRef]
- Wieloch, G.; Sikliena, M. Wpływ Wybranych Parametrów Na Wydajność Ubytkową Procesu Szlifowania Drewna/Influence of selected parameters on the loss efficiency of the wood sanding process. Drewno 2004, 47, 121–130. [Google Scholar]
- Saloni, D.E.; Lemaster, R.L.; Jackson, S.D. Abrasive Machining Process Characterization on Material Removal Rate, Final Surface Texture, and Power Consumption for Wood. For. Prod. J. 2005, 55, 35–41. [Google Scholar]
- Błaszczyk, A.; Turek, S. Teoria Mnogości/Set Theory; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2007; ISBN 978-83-01-15232-1. [Google Scholar]
- Miao, T.; Li, L. Study on Influencing Factors of Sanding Efficiency of Abrasive Belts in Wood Materials Sanding. Wood Res. 2014, 59, 835–842. [Google Scholar]
- Thorpe, A.; Brown, R.C. Factors Influencing the Production of Dust During the Hand Sanding of Wood. Am. Ind. Hyg. 1995, 56, 236–242. [Google Scholar] [CrossRef]
- Chand, N.; Fahim, M. Tribology of Natural Fiber Polymer Composites; Woodhead Publishing; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-1-84569-393-0. [Google Scholar]
- Proper and Improper Forcing; Perspectives in Mathematical Logic, 2nd ed.; Springer: Berlin/Heidleberg, Germany; New York, NY, USA, 1997; Volume 5, ISBN 978-3-540-51700-9.
- Woodin, W.H. The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, 2nd ed.; De Gruyter: Berlin/Heidleberg, Germany; New York, NY, USA, 2010; ISBN 978-3-11-021317-1. [Google Scholar]
- Sydor, M.; Pinkowski, G.; Jasińska, A. The Brinell Method for Determining Hardness of Wood Flooring Materials. Forests 2020, 11, 878. [Google Scholar] [CrossRef]
- Sin, H.; Saka, N.; Suh, N.P. Abrasive Wear Mechanisms and the Grit Size Effect. Wear 1979, 55, 163–190. [Google Scholar] [CrossRef]
- Ohtani, T.; Yakou, T.; Kitayama, S. Conditions and Origin of the Critical Grain Size Effect on the Abrasive Wear of Woods. Mokuzai Gakkaishi/J. Jpn. Wood Res. Soc. 1996, 42, 1057–1063. [Google Scholar]
- Xu, M.; Li, L.; Wang, M.; Luo, B. Effects of Surface Roughness and Wood Grain on the Friction Coefficient of Wooden Materials for Wood–Wood Frictional Pair. Tribol. Trans. 2014, 57, 871–878. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).