Post Quantum Cryptographic Keys Generated with Physical Unclonable Functions
Abstract
Featured Application
Abstract
1. Introduction
2. Lattice and Code-Based Post Quantum Cryptography
2.1. Learning with Error Cryptography
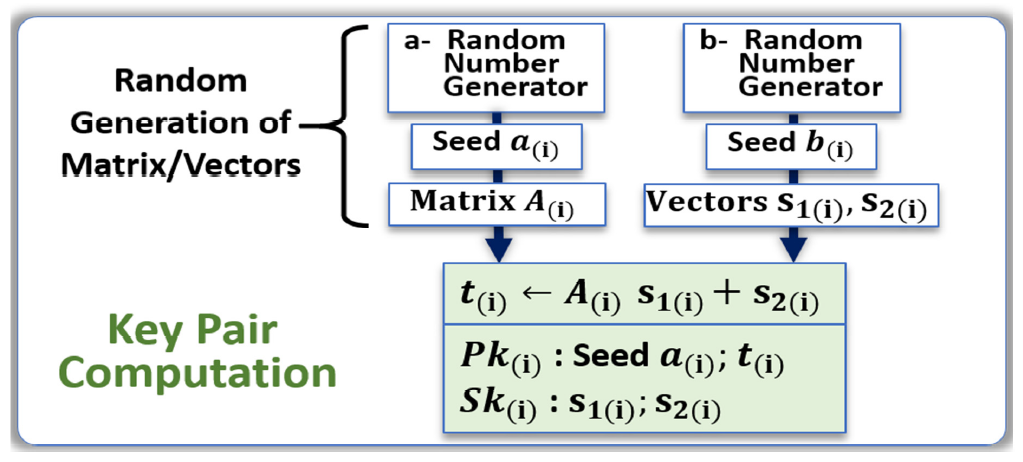
- The generation of a first data stream called seed a(i) that is used for the key generation; in the case of LWE, the seed a(i) is shared openly in the network.
- The generation of a second data stream called seed b(i) that is used to compute a second data stream for the private key Sk(i); the seed b(i) is kept secret.
- The public key Pk(i) is computed from both data streams and is openly shared.
- The matrix A(i) is generated from seed a(i).
- The two vectors s1(i) and s2(i) are generated from seed b(i).
- The vector t(i) is computed: t(i) ← A(i)s1(i) + s2(i).
- Both seed a(i) and t(i) become the public key Pk(i).
- Both s1(i) and s2(i) become the private key Sk(i).
- Generate a masking vector of polynomials y.
- Compute vector A.y and set w1 to be the high-order bits of the coefficients in this vector.
- Create the challenge c, as the hash of the message and w1.
- Compute intermediate signature z = y + c.s1.
- Set parameter β to be the maximum coefficient of c.s1.
- If any coefficient of z is larger than γ1 − β, then reject and restart at step 1.
- If any coefficient of the low-order bits of A.z – c.t is greater than γ2 − β, then reject and restart at step 1.
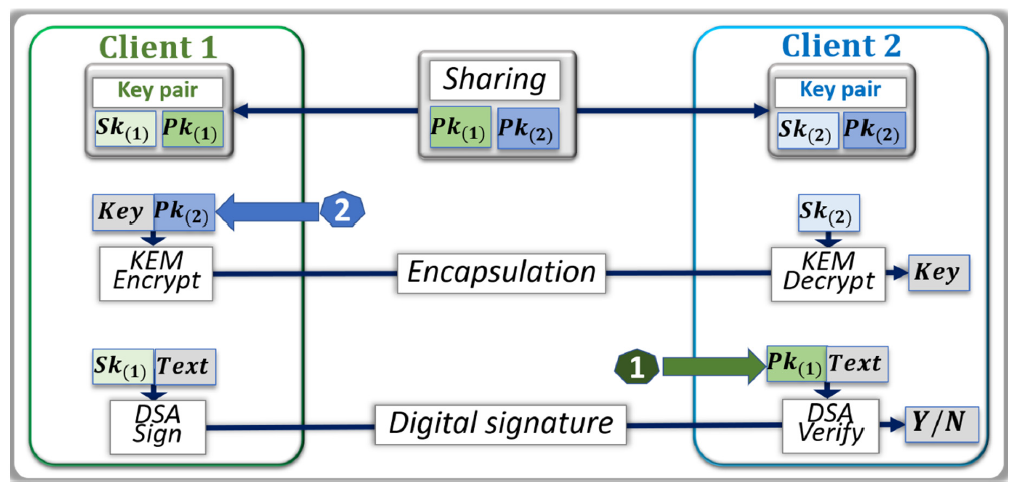
- The public and private keys of both parties are constructed as described in Figure 1.
- Person A sends Person B their public key.
- Person B randomly generates a symmetric key and encapsulates it in a ciphertext with the public key of person A.
- Person B sends the ciphertext to person A.
- Person A decapsulates the ciphertext with their private key.
- Both parties now have the symmetric key in their possession.
2.2. Learning with Rounding Cryptography
- Similar to LWE, seed a(i) is used to generate matrix A(i).
- Seed b(i) is used to generate vector s(i).
- The vector t(i) is computed: t(i) ← A(i). s(i) + h(i).
- Both seed a(i) and t(i) become the public key Pk(i).
- s(i) becomes the private key Sk(i).
- The seed a(i) and t(i) is extracted from public key to encrypt the message m.
- Matrix A(i) and vector s’(i) are generated.
- The vector t’(i) is computed by rounding the product of A(i). s’(i): t’(i) ← A’(i). s’(i) + h(i).
- Polynomial v’(i) is calculated as: v’(i) = t(i). s’(i).
- v’(i) is used to encrypt the message m which denoted as cm.
- Ciphertext consists of cm and t’(i).
- v(i) is calculated as: v(i) = t’(i). s(i).
- The message m’ is decrypted by reversing computations with v(i) and cm.
- Saber PKE key generation is used to return seed a(i), t(i) and s(i).
- Both seed a(i) and t(i) become the Saber KEM public key Pk(i).
- The hashed public key Pkh(i) is generated using SHA3-256.
- Parameter z is randomly sampled.
- z, Pkh(i) and s(i) become the Saber KEM secret key.
- Message m and public key Pk(i) are hashed using SHA3-256.
- Saber PKE encryption is used to generate ciphertext.
- Hash of the Pk(i) and ciphertext are concatenated, then hashed to encapsulate the key.
- Message m’ is decrypted by using Saber PKE Decryption.
- The decrypted message m’ and hashed public key Pkh(i) are hashed to generate K’.
- Ciphertext c’m is generated from saber PKE Encryption for message m’.
- If cm = c’m then the K = Hash(K’,c), if not, K = Hash(z,c).
2.3. NTRU Cryptography
- Generation of the two truncated polynomials f(i) and g(i) from seed a(i) and seed b(i).
- Computation of Fq(i), which is the inverse of polynomial f(i) modulo q.
- Computation of Fp(i), which is the inverse of polynomial f(i) modulo p.
- Computation of polynomial h(i): h(i) ← p. Fq(i). g(i).
- The private key Sk(i) is {f(i); Fp(i)}.
- The public key Pk(i) is h(i).
2.4. Code-Based Cryptography
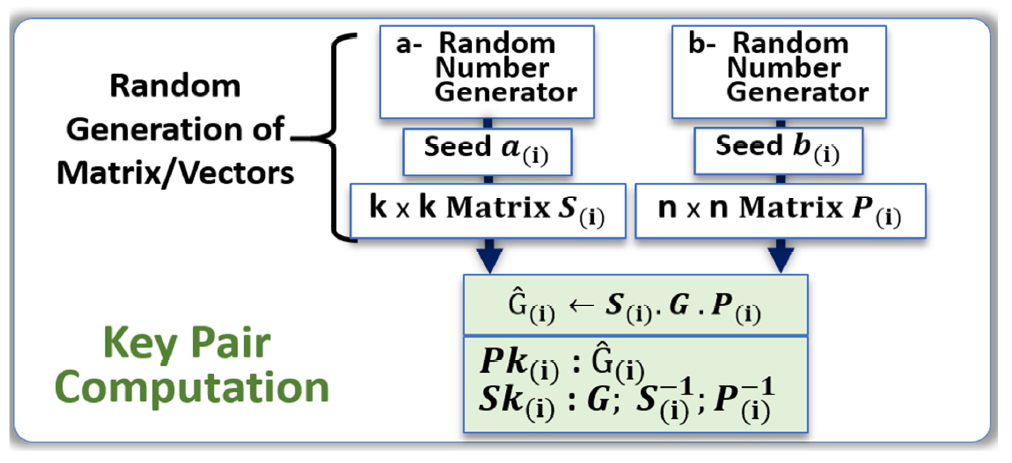
- Seed a(i) is used to create a random invertible binary k × k scrambling matrix S(i).
- Seed b(i) is used to create a random n × n permutation matrix P(i).
- The public key Pk(i) = Ĝ(i) is computed with the generator matrix G: Ĝ(i) ← S(i). G. P(i)
- The private key Sk(i) is {G; S(i)−1, P(i)−1}.
- Create the public key, Ĝ(i) as described above.
- Multiply the message m by Ĝ(i), creating the ciphertext message .
- Add a random error vector e of Hamming weight t to to obtain the ciphertext c.
- Compute ĉ = c P(i)−1.
- Use the decoding algorithm to correct the errors to obtain .
- Obtain the original message by computing m = .S(i)−1.
- t = s−1 mod g.
- .
- Find polynomials a, b such that b.t ≡ mod g with deg(a) ≤ |t/2| and deg(b) ≤ |(t-1)/2| using the extended Euclidean algorithm.
- Calculate and return the error locator polynomial, e = a2 + x.b2.
- if deg(p) ≤ 1
- return the root of p.
- p0 = gcd(p, t(Bi. x)).
- p1 = gcd(p, 1 + t(Bi. x)).
3. Public Key Infrastructure
3.1. Public-Private Key Pairs
- The secure generation and distribution of the public–private key pairs to the client devices that are participating in the PKI.
- The identification of the client devices, and trust in their public keys.
- The sharing of the public keys among participants.
3.2. PKI with Network of PUFs
3.3. Implementation of PQC Algorithms for PKI
4. PUF-Based Key Distribution for PQC
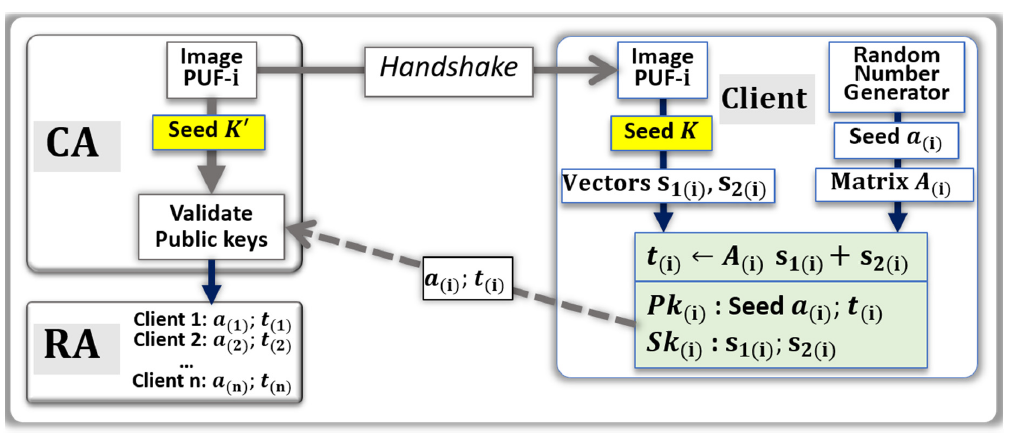
4.1. PUF-Based Key Distribution for LWE Lattice Cryptography
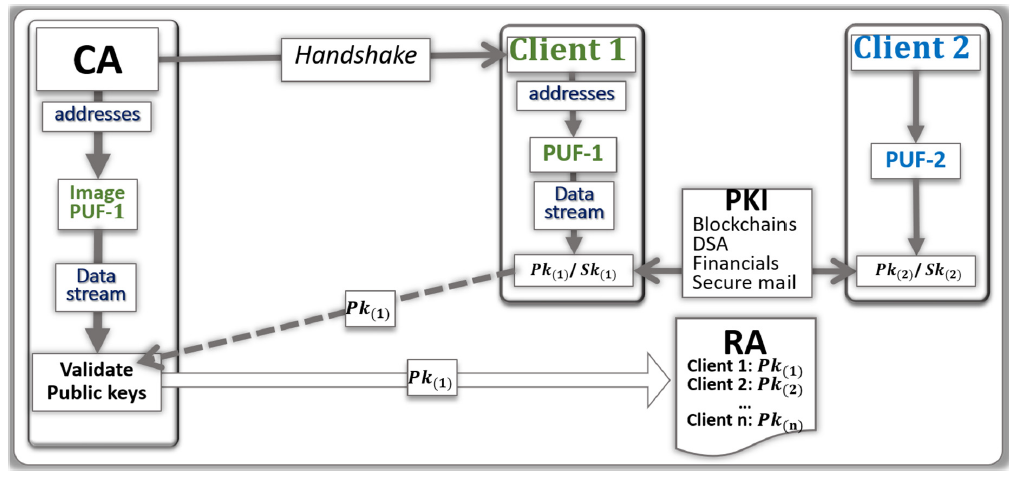
- The CA uses a random numbers generator and hash function to be able to point at a set of addresses in the image of the PUF-i.
- From these addresses, a stream of bits called Seed K’ is generated by the CA.
- The CA communicates to the Client (i), through a handshake, the instructions needed to find the same set of addresses in the PUF.
- Client (i) uses the PUF to generate the stream of bits called Seed K. The two data streams Seed K and Seed K’ are similar, however slightly differ from each other due to natural physical variations and drifts occurring in the PUFs.
- [If needed, Client (i) applies error correcting codes to reduce the difference between Seed K and Seed K’; the corrected, or partially corrected, data stream is used to generate the vectors s1(i) and s2(i)]
- Client (i) independently uses a random numbers generator (a) to generate a second data stream Seed a(i), which is used for the computation of the matrix A(i).
- The vector t(i) is computed: t(i) ← A(i)s1(i) + s2(i).
- The private key Sk(i) is {s(1(i); s2(i)}.
- The public key Pk(i) is {a(i); t(i)}.
- Client (i) communicates to the CA, through the network, the public key Pk(i);
- The CA uses a search engine to verify that Pk(i) is correct. The search engine initiates the validation by generating a public key from Seed a(i) and Seed K’ with lattice cryptography codes. If the resulting public key is not Pk(i), an iteration process gradually injects errors into Seed K’ and computes the corresponding public keys. The search converges when a match in the resulting public key is found, or when the CA concludes that the public key should be bad.
- If the validation is positive, the public key Pk(i) is posted online by the RA.
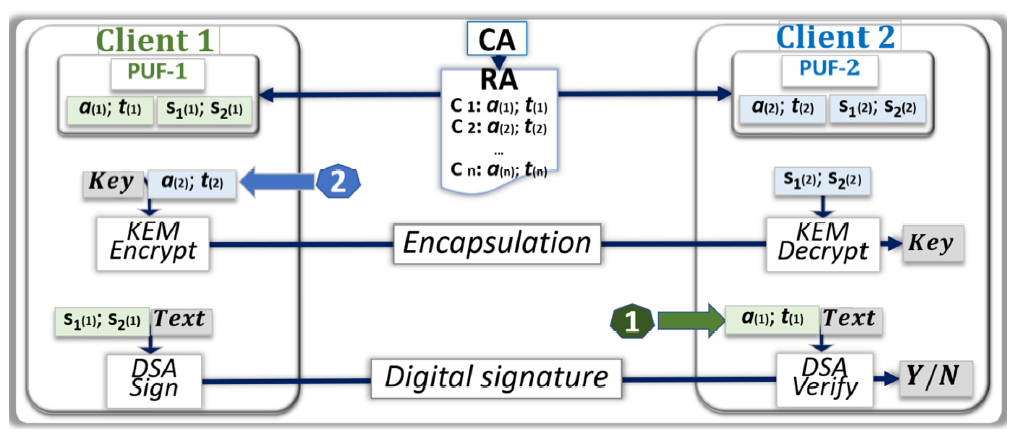
4.2. PKI Architecture with PUF-Based Key Distribution and LWE
- The enrollment process in which the PUFs are characterized to generate their image is accurate and not compromised by the opponent.
- The database stored in the CA that contains the image of the PUFs for the i client devices is protected from external and internal attacks.
- The PUFs embedded in each client device are reliable, unclonable, and tamper resistant.
- The key generation process, KEM, and DSA are protected from side channel analysis.
4.3. PUF-Based Key Distribution for LWR Lattice Cryptography
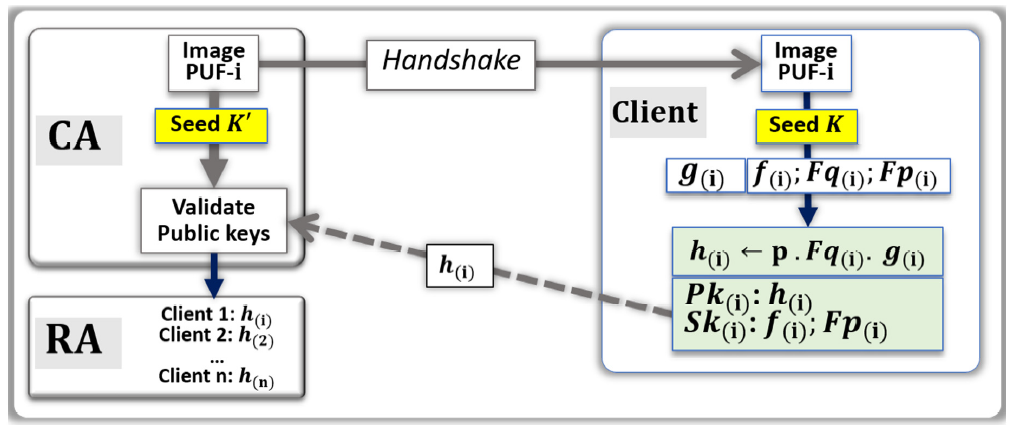
4.4. PUF-Based Key Distribution for NTRU Lattice Cryptography
- The CA uses random numbers to point at a set of addresses in the image of the PUF-i.
- From these addresses, a stream of bits called Seed K’ is generated by the CA.
- The CA sends the handshake to the client (i) to find the same addresses.
- Client (i) uses the PUF to generate Seed K.
- Client (i) applies error correction to Seed K and generates the truncated polynomials f(i) and g(i).
- Computation of Fp(i) and Fq(i) and verify that the pre-conditions are fulfilled.
- If needed, ask for a new handshake and iterate.
- The polynomial h(i) is computed: h(i) ← p · Fq(i) · g(i).
- The private key Sk(i) is {f(i); Fp(i)}.
- The public key Pk(i) is h(i).
- Client (i) communicates to the CA, through the network, the public key h(i).
- The CA uses a search engine to verify that h(i) is correct.
- If the validation is positive, the public key h(i) is posted online by the RA.
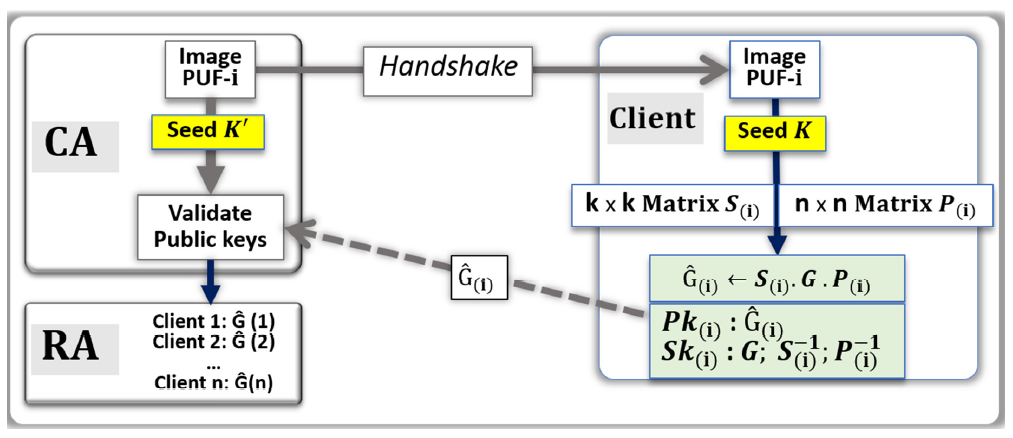
4.5. PUF-Based Key Distribution for Code-Based Cryptography
- The CA uses random numbers to point at a set of addresses in the image of the PUF-i.
- From these addresses, a stream of bits called Seed K’ is generated by the CA.
- The CA sent the handshake to the client (i) to find the same addresses.
- Client (i) uses the PUF to generate Seed K.
- Client (i) applies ECC) on Seed K and generates the matrixes S(i) and P(i).
- Computation of S(i)−1 and P(i)−1.
- The public key Pk(i) = Ĝ(i) is computed with the generator matrix G: Ĝ(i) ← S(i) · G · P(i).
- The private key Sk(i) is {G; S(i)−1, P(i)−1}.
- Client (i) communicates to the CA, through the network, the public key Ĝ(i).
- The CA uses a search engine to verify that Ĝ(i) is correct.
- If the validation is positive, the public key Ĝ(i) is posted online by the RA.
5. Experimental Evaluation
5.1. Experimental Methodology
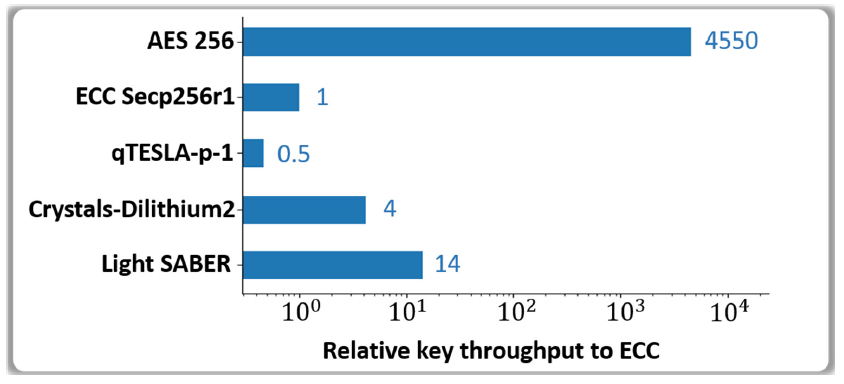
5.2. Evaluation of the Effective Key Throughput
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Koblitz, N.; Menezes, A. A Riddle Wrapped in an Enigma. 2015. Available online: http://eprint.iacr.org/2015/1018 (accessed on 18 May 2015).
- Kiktenko, E.; Pozhar, N.; Anufriev, M.; Trushechkin, A.; Yunusov, R.; Kurochkin, Y.; Lvovsky, A.; Fedorov, A. Quantum Secured Blockchains. Open Source. arXiv 2018, arXiv:1705.09258v3. [Google Scholar]
- Semmouni, M.; Nitaj, A.; Belkasmi, M. Bitcoin Security with Post Quantum Cryptography. 2019. Available online: https://hal-normandie-univ.archives-ouvertes.fr/hal-02320898 (accessed on 19 October 2019).
- Campbell, R. Evaluation of Post-Quantum Distributed Ledger Cryptography. Open Access, JBBA. 2019; Volume 2. Available online: https://doi.org/10.31585/jbba-2-1-(4)2019 (accessed on 16 March 2019).
- Kampanakisy, P.; Sikeridisz, D. Two Post-Quantum Signature Use-Cases: Non-issues, Challenges and Potential Solutions. In Proceedings of the 7th ETSI/IQC Quantum Safe Cryptography Workshop, Seattle, WA, USA, 5–7 November 2019. [Google Scholar]
- Ding, J.; Chen, M.-S.; Petzoldt, A.; Schmidt, D.; Yang, B.-Y. Rainbow; NIST PQC Project Round 2, Documentation. In Proceedings of the 2nd NIST Standardization Conference for Post-Quantum Cryptosystems, Santa Barbara, CA, USA, 22–24 August 2019. [Google Scholar]
- NIST Status Report of Phase 3 of PQC Program, NISTIR.8309. Available online: https://www.nist.gov/publications/status-report-second-round-nist-post-quantum-cryptography-standardization-process (accessed on 22 July 2020).
- Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Dilithium Algorithm Specifications and Supporting Documentation. Part of the Round 3 Submission Package to NIST. Available online: https://pq-crystals.org/dilithium (accessed on 19 February 2021).
- Fouque, P.-A.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z. Falcon: Fast-Fourier Lattice-Based Compact Signatures over NTRU, Specification v1.2. Available online: https://falcon-sign.info/falcon.pdf (accessed on 1 October 2020).
- Peikert, C.; Pepin, Z. Algebraically Structured LWE Revisited; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–23. [Google Scholar]
- IEEE Computing Society. IEEE Standard 1363.1-2008—Specification for Public Key Cryptographic Techniques Based on Hard Problems over Lattices; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Regev, O. New lattice-based cryptographic constructions. J. ACM 2004, 51, 899–942. [Google Scholar] [CrossRef]
- Casanova, A.; Faugere, J.-C.; Macario-Rat, G.; Patarin, J.; Perret, L.; Ryckeghem, J. GeMSS: A Great Multivariate Short Signature; NIST PQC Project Round 2, Documentation. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography/round-2-submissions (accessed on 3 January 2017).
- McEliece, R.J. A Public-Key Cryptosystem Based on Algebraic Coding Theory; California Institute of Technology: Pasadena, CA, USA, 1978; pp. 114–116. [Google Scholar]
- Biswas, B.; Sendrier, N. McEliece Cryptosystem Implementation: Theory and Practice. In Post-Quantum Cryptography. PQCrypto. Lecture Notes in Computer Science; Buchmann, J., Ding, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5299. [Google Scholar]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing—STOC’05, Baltimore, MD, USA, 22–24 May 2005; ACM: New York, NY, USA, 2005; pp. 84–93. [Google Scholar]
- Lyubashevsky, V. Fiat-Shamir with Aborts: Applications to Lattice and Factoring-Based Signatures. Available online: https://www.iacr.org/archive/asiacrypt2009/59120596/59120596.pdf (accessed on 31 December 2009).
- D’Anvers, J.-P.; Karmakar, A.; Roy, S.; Vercauteren, F. Saber: Module-LWR Based Key Exchange, CPA-Secure Encryption and CCA-Secure KEM. Cryptology ePrint Archive, Report 2018/230. Available online: https://eprint.iacr.org/2018/230 (accessed on 7 May 2018).
- Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.; Schwabe, P.; Seiler, G.; Stehle, D. CRYSTALS—Kyber: A CCA-Secure Module-Lattice-Based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar]
- Hülsing, A.; Rijneveld, J.; Schanck, J.; Schwabe, P. High-Speed Key Encapsulation from NTRU. IACR Cryptol. Available online: https://www.iacr.org/archive/ches2017/10529225/10529225.pdf (accessed on 28 August 2017).
- Banerjee, A.; Peikert, C.; Rosen, A. Pseudorandom functions and lattices. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 719–737. [Google Scholar]
- Alwen, J.; Stephan, K.; Krzysztof, P.; Daniel, W. Learning with rounding, revisited. In Proceedings of the Annual Cryptology Conference, Athens, Greece, 26–30 May 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 57–74. [Google Scholar]
- Nurshamimi, S.; Kamarulhaili, H. NTRU Public-Key Cryptosystem and Its Variants. Int. J. Cryptol. Res. 2020, 10, 21. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for Hard Lattices and New Cryptographic Constructions. In Proceedings of the 14th Annual ACM Symposium on Theory of Computing. pp. 197–206. Available online: https://doi.org/10.1145/1374376.1374407 (accessed on 25 August 2008).
- Heyse, S. Post-Quantum Cryptography: Implementing Alternative Public Key Schemes on Embedded Devices. Ph.D. Thesis, For the Degree of Doktor-Ingenieur of the Faculty of Electrical Engineering and Information Technology at the Ruhr-University Bochum, Bochum, Germany, 2013. [Google Scholar]
- Menezes, A.; van Oorschot, P.; Vanstone, S. Some Computational Aspects of Root Finding in GF(qm); Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1989; Volume 358. [Google Scholar]
- Papakonstantinou, I.; Sklavos, N. Physical Unclonable Function Design Technologies: Advantages & Tradeoffs; Daimi, K., Ed.; Computer and Network Security; Spinger: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-58423-2. [Google Scholar]
- Herder, C.; Yu, M.; Koushanfar, F. Physical Unclonable Functions and Applications: A Tutorial. Proc. IEEE 2014, 102, 1126–1141. [Google Scholar] [CrossRef]
- Cambou, B.; Orlowski, M. Design of Physical Unclonable Functions with ReRAM and Ternary states. In Proceedings of the Cyber and Information Security Research Conference, CISR-2016, Oak Ridge, TN, USA, 5–7 April 2016. [Google Scholar]
- Cambou, B.; Telesca, D. Ternary Computing to Strengthen Information Assurance, Development of Ternary State based public key exchange. In Proceedings of the SAI-2018, Computing Conference, London, UK, 10–12 July 2018. [Google Scholar]
- Taniguchi, M.; Shiozaki, M.; Kubo, H.; Fujino, T. A Stable Key Generation from PUF Responses with A Fuzzy Extractor for Cryptographic Authentications. In Proceedings of the IEEE 2nd Global Conference on Cons Electronics (GCCE), Tokyo, Japan, 1–4 October 2013. [Google Scholar]
- Kang, H.; Hori, Y.; Katashita, T.; Hagiwara, M.; Iwamura, K. Cryptography Key Generation from PUF Data Using Efficient Fuzzy Extractors. In Proceedings of the 16th International Conference on Advanced Communication Technology, Pyeongchang, Korea, 16–19 February 2014. [Google Scholar]
- Delvaux, J.; Gu, D.; Schellekens, D.; Verbauwhede, I. Helper Data Algorithms for PUF-Based Key Generation: Overview and Analysis. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2014, 34, 889–902. [Google Scholar] [CrossRef]
- Cambou, C.; Philabaum, D.; Booher, D. Telesca; Response-Based Cryptographic Methods with Ternary Physical Unclonable Functions. In Proceedings of the 2019 SAI FICC Conference, San Francisco, CA, USA, 14–15 March 2019. [Google Scholar]
- Cambou, B. Unequally powered Cryptograpgy with PUFs for networks of IoTs. In Proceedings of the IEEE Spring Simulation Conference, Tucson, AZ, USA, 29 April–2 May 2019. [Google Scholar]
- Cambou, B.; Philabaum, C.; Booher, D. Replacing error correction by key fragmentation and search engines to generate error-free cryptographic keys from PUFs. CryptArchi 2019. Available online: https://in.nau.edu/wp-content/uploads/sites/223/2019/11/Replacing-Error-Correction-by-Key-Fragmentation-and-Search-Engines-to-Generate-Error-Free-Cryptographic-Keys-from-PUFs.pdf (accessed on 21 March 2021).
- Cambou, B.; Mohammadi, M.; Philabaum, C.; Booher, D. Statistical Analysis to Optimize the Generation of Cryptographic Keys from Physical Unclonable Functions. Available online: https://link.springer.com/chapter/10.1007/978-3-030-52243-8_22 (accessed on 16 July 2020).
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-Quantum Lattice-Based Cryptography Implementations. ACM Comput. Surv. 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Emeliyanenko, P. Efficient Multiplication of Polynomials on Graphics Hardware. In Proceedings of the 8th International Symposium on Advanced Parallel Processing Technologies, Rapperswil, Switzerland, 24–25 August 2009; pp. 134–149. [Google Scholar]
- Akleylek, S.; Dağdelen, Ö.; Tok, Y. On The Efficiency of Polynomial Multiplication for Lattice-Based Cryptography on Gpus Using Cuda. In Cryptography and Information Security in the Balkans; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Longa, P.; Naehrig, M. Speeding up the Number Theoretic Transform for Faster Ideal Lattice-Based Cryptography. Comp. Sci. Math. IACR 2016, 124–139. [Google Scholar] [CrossRef]
- Greconici, D.; Kannwischer, M.; Sprenkels, D. Compact Dilithium Implementations on Cortex-M3 and Cortex-M4. IACR Cryptol. ePrint Arch. 2020, 2021, 1–24. [Google Scholar]
- Roy, S. SaberX4: High-Throughput Software Implementation of Saber Key Encapsulation Mechanism. In Proceedings of the 37th IEEE International Conference on Computer Design, ICCD 2019, Abu Dhabi, United Arab Emirates, 17–20 November 2019; pp. 321–324. [Google Scholar]
- Farahmand, F.; Sharif, M.; Briggs, K.; Gaj, K. A High-Speed Constant-Time Hardware Implementation of NTRUEncrypt SVES. In Proceedings of the International Conference on Field-Programmable Technology (FPT), Naha, Okinawa, Japan, 10–14 December 2018; pp. 190–197. [Google Scholar] [CrossRef]


| Hashing and XOF | Polynomial Multiplication | Reference | |
|---|---|---|---|
| SABER | ~30% | ~60% | Our benchmarks |
| CRYSTALS-Dilithium | ~42% | ~33% | Our benchmarks |
| NTRU | second bottleneck | first bottleneck | [40,41] |
| Algorithm | Parameter Set | NIST Candidate | Instructions | Selection Reason |
|---|---|---|---|---|
| AES | AES256 | N/A | AES-NI, SSE | Benchmark: HW implementation Lacks DSA and KEM capabilities |
| ECC | Secp256r1 | N/A | AVX, SSE | Benchmark: mainstream for PKI Uses 256-bit long keys for DSA |
| qTESLA | p-I | Dropped | AVX, SSE | PQC dropped by NIST: too slow DSA uses relatively small keys |
| CRYSTALS-Dilithium | 2 | Phase 3 | AVX, SSE | Active LWE PQC algorithm One of preferred DSA scheme |
| SABER | LightSABER | Phase 3 | AVX, SSE | Active LWR PQC algorithm One of the preferred KEM scheme |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cambou, B.; Gowanlock, M.; Yildiz, B.; Ghanaimiandoab, D.; Lee, K.; Nelson, S.; Philabaum, C.; Stenberg, A.; Wright, J. Post Quantum Cryptographic Keys Generated with Physical Unclonable Functions. Appl. Sci. 2021, 11, 2801. https://doi.org/10.3390/app11062801
Cambou B, Gowanlock M, Yildiz B, Ghanaimiandoab D, Lee K, Nelson S, Philabaum C, Stenberg A, Wright J. Post Quantum Cryptographic Keys Generated with Physical Unclonable Functions. Applied Sciences. 2021; 11(6):2801. https://doi.org/10.3390/app11062801
Chicago/Turabian StyleCambou, Bertrand, Michael Gowanlock, Bahattin Yildiz, Dina Ghanaimiandoab, Kaitlyn Lee, Stefan Nelson, Christopher Philabaum, Alyssa Stenberg, and Jordan Wright. 2021. "Post Quantum Cryptographic Keys Generated with Physical Unclonable Functions" Applied Sciences 11, no. 6: 2801. https://doi.org/10.3390/app11062801
APA StyleCambou, B., Gowanlock, M., Yildiz, B., Ghanaimiandoab, D., Lee, K., Nelson, S., Philabaum, C., Stenberg, A., & Wright, J. (2021). Post Quantum Cryptographic Keys Generated with Physical Unclonable Functions. Applied Sciences, 11(6), 2801. https://doi.org/10.3390/app11062801







