A Bayesian Control Chart for Monitoring Process Variance
Abstract
Featured Application
Abstract
1. Introduction
2. Preliminary Settings
3. The Construction of the Shewhart-Type Variance Chart with the Bayesian Approach
3.1. The Parameters of the Prior Distribution of p and Process Variance Are Known
3.1.1. The In-Control ARL of the Shewhart-Type Bayesian Variance Chart
3.1.2. The Out-of-Control ARL of the Shewhart-Type Bayesian Variance Chart
3.2. The Parameters of the Prior Distribution of p and Process Variance Are Unknown
4. The Construction of the EWMA Variance Chart with the Bayesian Approach
4.1. Construction of the EWMA Variance Control Chart
- 1.
- Given α0, β0, n, and λ, then UCLEWMA and LCLEWMA can be expressed as the function of k1 and k2 by Equations (31) and (32), respectively;
- 2.
- Let EWMA0 be equal to the mean of EWMA, i.e., nα0/(α0+β0);
- 3.
- Simulate random numbers Mt from Beta-Binomial(n,α0,β0) and compute EWMAt by Equation (25) until EWMAt > UCLEWMA, then record the run length;
- 4.
- Repeat step 3 1000 times and obtain the average run length, ARL(k1);
- 5.
- Determine the least k1 to make sure the ARL(k1) is larger than 740.8;
- 6.
- Given k1, simulate random numbers Mt from Beta-Binomial(n,α0,β0) and compute EWMAt using Equation (25) until EWMAt > UCLEWMA or EWMAt < LCLEWMA, then record the run length;
- 7.
- Repeat step 6 1000 times and obtain the average run length, ARL(k2);
- 8.
- Determine the least k2 to make sure the ARL(k2) is larger than 370.4.
4.2. Evaluation of the EWMA Variance Control Chart
- Given α0, β0, n, λ, k1, and k2, then UCLEWMA and LCLEWMA can be calculated by Equations (31) and (32), respectively;
- Let EWMA0 be equal to the mean of EWMA, i.e., nα0/(α0+β0);
- Simulate random numbers Mt from Beta-Binomial(n,α1,β1) and compute EWMAt by Equation (25) until EWMAt > UCLEWMA or EWMAt < LCLEWMA, then record the run length;
- Repeat step 3 1000 times and obtain the average run length, ARL1.
4.3. Performance Comparison of the EWMA Variance Control Chart
5. Process Simulations
- Set the process variance σ2 equal to 1;
- α0 and β0 are chosen such that E0(p) is as close to 0.3173 as possible in the normal process (0.2431 in the exponential process or 0.2802 in the mixed process);
- Given α0, β0, n, λ, k1, and k2, then UCLEWMA and LCLEWMA can be calculated by Equations (31) and (32), respectively;
- Let EWMA0 be equal to the mean of EWMA, i.e., nα0/(α0+β0);
- Simulate random samples of size 2n, Xt1, Xt2, …, Xt,2n from Normal(0, d2) (Exponential(1/d), or equally-weighted mixture of Noraml(0, d2) and Exponential(1/d)), compute Yt1, Yt2, …, Ytn by Equation (1), obtain the statistic Mt by counting the number of instances in which Ytj > 1, and compute EWMAt by Equation (25) until EWMAt > UCLEWMA or EWMAt < LCLEWMA, then record the run length;
- Repeat step 6 1000 times and obtain the average run length, ARL1.
6. An Example for Demonstration
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacCarthy, B.L.; Wasusri, T. A review of non-standard applications of statistical process control (SPC) charts. Int. J. Qual. Reliab. Manag. 2002, 19, 295–320. [Google Scholar] [CrossRef]
- Tsung, F.; Li, Y.; Jin, M. Statistical process control for multistage manufacturing and service operations: A review and some extensions. Int. J. Serv. Oper. Inform. 2008, 3, 191–204. [Google Scholar] [CrossRef]
- Ning, X.; Shang, Y.; Tsung, F. Statistical process control techniques for service processes: A review. In Proceedings of the 6th International Conference on Service Systems and Service Management, Xiamen, China, 8–10 June 2009; pp. 927–931. [Google Scholar]
- Ferrell, E.B. Control charts using midranges and medians. Ind. Qual. Control 1953, 9, 30–34. [Google Scholar]
- Bakir, S.T.; Reynolds, M.R.J. A nonparametric procedure for process control based on within-group ranking. Technometrics 1979, 21, 175–183. [Google Scholar] [CrossRef]
- Amin, R.W.; Reynolds, M.R.J.; Bakir, S.T. Nonparametric quality control charts based on the sign statistic. Commun. Stat. Theory Methods 1995, 24, 1597–1624. [Google Scholar] [CrossRef]
- Altukife, F.S. A new nonparametric control charts based on the observations exceeding the grand median. Pakistan J. Stat. 2003, 19, 343–351. [Google Scholar]
- Altukife, F.S. Nonparametric control charts based on sum of ranks. Pakistan J. Stat. 2003, 19, 291–300. [Google Scholar]
- Bakir, S.T. A distribution-free Shewhart quality control chart based on signed-ranks. Qual Eng 2004, 16, 613–623. [Google Scholar] [CrossRef]
- Bakir, S.T. Distribution free quality control charts based in sign rank like statistics. Commun. Stat. Theory Methods 2006, 35, 743–757. [Google Scholar] [CrossRef]
- Chakraborti, S.; Eryilmaz, S. A non-parametric Shewhart type sign rank control chart based on runs. Commun. Stat. Simul. Comput. 2007, 36, 335–356. [Google Scholar] [CrossRef]
- Chakraborti, S.; Graham, M. Nonparametric Control Charts. Encyclopedia of Quality and Reliability; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Chakraborti, S.; Laan, P.V.D.; Bakir, S.T. Nonparametric control charts: An overview and some results. J. Qual. Technol. 2001, 33, 304–315. [Google Scholar] [CrossRef]
- Li, S.; Tang, L.; Ng, S. Nonparametric CUSUM and EWMA control charts for detecting mean shifts. J. Qual. Technol. 2010, 42, 209–226. [Google Scholar] [CrossRef]
- Zou, C.; Tsung, F. Likelihood ratio-based distribution-free EWMA control charts. J. Qual. Technol. 2010, 42, 174–196. [Google Scholar] [CrossRef]
- Graham, M.A.; Chakraborti, S.; Human, S.W. A nonparametric EWMA sign chart for location based on individual measurements. Qual. Eng. 2011, 23, 227–241. [Google Scholar] [CrossRef]
- Graham, M.A.; Chakraborti, S.; Human, S.W. A nonparametric exponentially weighted moving average signed-rank chart for monitoring location. Comput. Stat. Data Anal. 2011, 55, 2490–2503. [Google Scholar] [CrossRef]
- Jones-Farmer, L.; Champ, C. Distribution-free phase I control chart for subgroup scale. J. Qual. Technol. 2010, 42, 373–387. [Google Scholar] [CrossRef]
- Zombade, D.M.; Ghute, V.B. Nonparametric control chart for variability using runs rules. Experiment 2014, 24, 1683–1691. [Google Scholar]
- Yang, S.F.; Lin, J.; Cheng, S.W. A new nonparametric EWMA sign control chart. Expert Syst. Appl. 2011, 38, 6239–6243. [Google Scholar] [CrossRef]
- Yang, S.F.; Cheng, T.C.; Hung, Y.C.; Cheng, S.W. A new chart for monitoring service process mean. Qual. Reliab. Eng. Int. 2012, 28, 377–386. [Google Scholar] [CrossRef]
- Yang, S.F. An improved distribution-free EWMA mean chart. Commun. Stat. Simul. Comput. 2015, 44, 1–18. [Google Scholar] [CrossRef]
- Yang, S.F.; Arnold, B.C. A new approach for monitoring process variance. J. Stat. Comput. Simul. 2016, 86, 2749–2765. [Google Scholar] [CrossRef]
- Yang, S.F.; Jiang, T.A. Service quality variation monitoring using the interquartile range control chart. Qual. Technol. Quant Manag. 2019, 16, 613–627. [Google Scholar] [CrossRef]
- Girshick, M.A.; Rubin, H. A Bayes approach to a quality control model. Ann. Math. Statist. 1952, 23, 114–125. [Google Scholar] [CrossRef]
- Menzefricke, U. On the evaluation of control chart limits based on predictive distributions. Commun. Stat. Theory Methods 2002, 31, 1423–1440. [Google Scholar] [CrossRef]
- Menzefricke, U. Control charts for the generalized variance based on its predictive distribution. Commun. Stat. Theory Methods 2007, 36, 1031–1038. [Google Scholar] [CrossRef]
- Menzefricke, U. Control charts for the variance and coefficient of variation based on their predictive distribution. Commun. Stat. Theory Methods 2010, 39, 2930–2941. [Google Scholar] [CrossRef]
- Menzefricke, U. Combined exponentially weighted moving average charts for the mean and variance based on the predictive distribution. Commun. Stat. Theory Methods 2013, 42, 4003–4016. [Google Scholar] [CrossRef]
- Saghir, A. Phase-I design scheme for x-chart based on posterior distribution. Commun. Stat. Theory Methods 2015, 44, 644–655. [Google Scholar] [CrossRef]
- Khan, N.; Aslam, M.; Jun, C. Design of a control chart using a modified EWMA statistic. Qual. Reliab. Eng. Int. 2017, 33, 1095–1104. [Google Scholar] [CrossRef]
- Saghir, A.; Aslam, M.; Faraz, A.; Ahmad, L.; Heuchenne, C. Monitoring process variation using modified EWMA. Qual. Reliab. Eng. Int. 2020, 36, 328–339. [Google Scholar] [CrossRef]
- Aslam, M.; Anwar, S.M. An improved Bayesian Modified-EWMA location chart and its applications in mechanical and sport industry. PLoS ONE 2020, 15, e0229422. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.F.; Arnold, B.C. A simple approach for monitoring business service time variation. Sci. World J. 2014, 2014, 238719. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.F.; Wu, S.H. A double sampling scheme for process variability monitoring. Qual. Reliab. Eng. Int. 2017, 33, 2193–2204. [Google Scholar] [CrossRef]
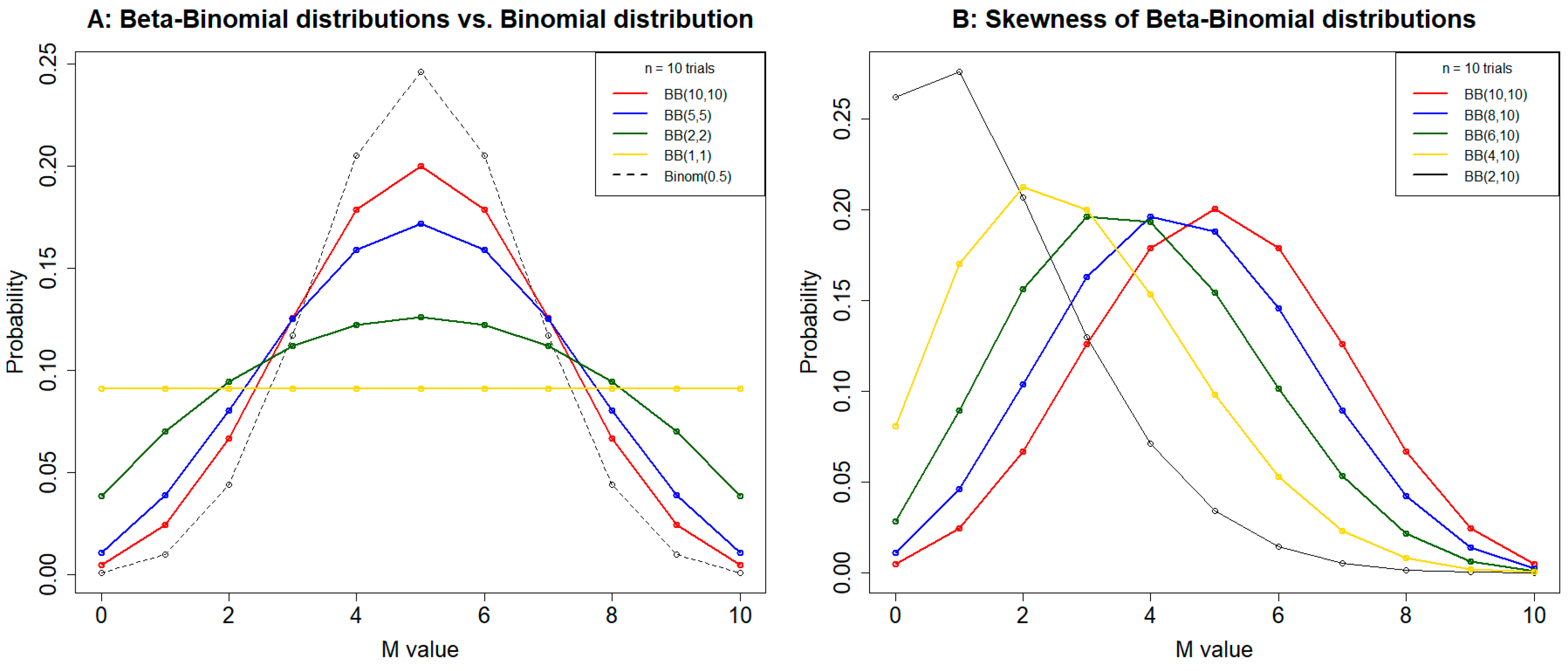

| (α0, β0) | E0(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
|---|---|---|---|---|---|---|---|---|
| (1, 1) | 0.5000 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (1, 2) | 0.3333 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (1, 3) | 0.2500 | ∞ | ∞ | ∞ | 286.00 | 204.00 | 177.10 | 163.80 |
| (1, 4) | 0.2000 | ∞ | ∞ | 126.00 | 200.20 | 110.74 | 84.33 | 113.10 |
| (1, 5) | 0.1667 | ∞ | 56.00 | 42.00 | 143.00 | 123.05 | 67.08 | 71.18 |
| (2, 2) | 0.5000 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (2, 3) | 0.4000 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (2, 4) | 0.3333 | ∞ | ∞ | ∞ | ∞ | 969.00 | 526.04 | 1131.00 |
| (2, 5) | 0.2875 | ∞ | ∞ | ∞ | 728.00 | 180.28 | 222.23 | 257.80 |
| (2, 6) | 0.2500 | ∞ | ∞ | 132.00 | 273.92 | 151.19 | 240.66 | 174.65 |
| (3, 3) | 0.5000 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (3, 4) | 0.4286 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| (3, 5) | 0.3750 | ∞ | ∞ | ∞ | ∞ | 1254.00 | 693.23 | 1703.37 |
| (3, 6) | 0.3333 | ∞ | ∞ | ∞ | 663.00 | 572.80 | 567.09 | 577.14 |
| (3, 7) | 0.3000 | ∞ | ∞ | ∞ | 204.83 | 333.89 | 468.32 | 270.28 |
| (10, 10) | 0.5000 | ∞ | ∞ | ∞ | ∞ | ∞ | 3441.00 | 1607.81 |
| (8, 10) | 0.4444 | ∞ | ∞ | ∞ | ∞ | 3317.17 | 2130.37 | 1798.07 |
| (6, 10) | 0.3750 | ∞ | ∞ | ∞ | 1088.50 | 1177.06 | 399.88 | 562.37 |
| (4, 10) | 0.2857 | ∞ | ∞ | 153.00 | 460.20 | 270.31 | 214.86 | 404.65 |
| (2, 10) | 0.1666 | 26.00 | 91.00 | 78.00 | 149.08 | 91.49 | 140.96 | 106.46 |
| (100, 100) | 0.5000 | ∞ | ∞ | ∞ | 413.00 | 709.04 | 1426.63 | 589.89 |
| (80, 100) | 0.4444 | ∞ | ∞ | ∞ | 2473.90 | 609.75 | 424.17 | 573.01 |
| (60, 100) | 0.3750 | ∞ | ∞ | ∞ | 757.85 | 642.55 | 655.36 | 725.14 |
| (40, 100) | 0.2857 | ∞ | ∞ | 442.91 | 618.83 | 258.22 | 620.79 | 418.48 |
| (20, 100) | 0.1666 | 34.57 | 191.71 | 242.62 | 270.86 | 406.05 | 174.27 | 297.27 |
| Panel A: | When | (α0, β0) = | (5, 10) | |||||
| (α1, β1) | E1(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
| (6, 11) | 0.3529 | ∞ | ∞ | ∞ | 212.26 | 423.95 | 711.36 | 401.99 |
| (7, 10) | 0.4118 | ∞ | ∞ | ∞ | 91.49 | 155.39 | 231.17 | 130.77 |
| (6, 10) | 0.3750 | ∞ | ∞ | ∞ | 141.98 | 257.23 | 399.88 | 226.12 |
| (5, 10)a | 0.3333 | ∞ | ∞ | ∞ | 240.62 | 468.98 | 765.58 | 433.45 |
| (5, 9) | 0.3571 | ∞ | ∞ | ∞ | 153.86 | 270.31 | 407.36 | 231.39 |
| (5, 8) | 0.3846 | ∞ | ∞ | ∞ | 96.21 | 152.44 | 212.41 | 121.84 |
| Panel B: | When | (α0, β0) = | (3, 9) | |||||
| (α1, β1) | E1(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
| (4, 10) | 0.2857 | ∞ | ∞ | 153.00 | 98.96 | 270.31 | 214.86 | 189.35 |
| (5, 9) | 0.3571 | ∞ | ∞ | 68.00 | 38.51 | 85.33 | 65.18 | 55.79 |
| (4, 9) | 0.3077 | ∞ | ∞ | 110.50 | 66.73 | 162.15 | 125.90 | 109.03 |
| (3, 9) a | 0.2500 | ∞ | ∞ | 208.00 | 136.39 | 368.68 | 292.32 | 256.96 |
| (3, 8) | 0.2727 | ∞ | ∞ | 143.00 | 86.90 | 206.94 | 160.26 | 138.47 |
| (3, 7) | 0.3000 | ∞ | ∞ | 95.33 | 53.99 | 113.11 | 86.08 | 73.45 |
| Panel C: | When | (α0, β0) = | (46, 100) | |||||
| (α1, β1) | E1(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
| (70, 100) | 0.4118 | ∞ | ∞ | 77.86 | 57.21 | 65.44 | 29.00 | 39.88 |
| (60, 100) | 0.3750 | ∞ | ∞ | 121.93 | 104.50 | 137.11 | 61.39 | 94.91 |
| (50, 100) | 0.3333 | ∞ | ∞ | 213.75 | 225.07 | 354.80 | 164.14 | 289.74 |
| (46, 100) a | 0.3151 | ∞ | ∞ | 279.22 | 325.57 | 562.03 | 265.77 | 477.10 |
| (46, 90) | 0.3382 | ∞ | ∞ | 196.80 | 199.24 | 301.99 | 138.61 | 237.21 |
| (46, 80) | 0.3651 | ∞ | ∞ | 135.10 | 118.39 | 157.31 | 70.67 | 109.53 |
| (46, 70) | 0.3966 | ∞ | ∞ | 89.95 | 68.11 | 79.34 | 35.32 | 48.98 |
| Panel D: | When | (α0, β0) = | (32, 100) | |||||
| (α1, β1) | E1(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
| (70, 100) | 0.4118 | ∞ | 13.97 | 77.86 | 14.37 | 8.20 | 6.06 | 8.87 |
| (60, 100) | 0.3750 | ∞ | 18.39 | 121.93 | 23.22 | 13.59 | 10.26 | 17.01 |
| (50, 100) | 0.3333 | ∞ | 25.96 | 213.75 | 43.25 | 26.64 | 21.05 | 41.21 |
| (40, 100) | 0.2857 | ∞ | 40.70 | 442.91 | 99.65 | 67.31 | 57.74 | 142.05 |
| (32, 100) a | 0.2424 | ∞ | 65.52 | 954.75 | 246.38 | 187.73 | 179.41 | 565.37 |
| (32, 90) | 0.2623 | ∞ | 51.83 | 647.82 | 154.85 | 110.15 | 98.86 | 269.28 |
| (32, 80) | 0.2857 | ∞ | 40.18 | 425.45 | 94.42 | 62.89 | 53.20 | 124.71 |
| (32, 70) | 0.3137 | ∞ | 30.43 | 268.81 | 55.67 | 34.92 | 28.00 | 56.30 |
| (α0, β0) | E0(p) | n = 2 | n = 3 | n = 5 | n = 10 | n = 15 | n = 20 | n = 25 |
|---|---|---|---|---|---|---|---|---|
| (1, 1) | 0.5000 | (2.95, 3.00) | (2.94, 3.03) | (2.92, 3.01) | (2.94, 2.98) | (2.93, 2.99) | (2.94, 2.98) | (2.94, 2.99) |
| (1, 2) | 0.3333 | (3.12, 2.75) | (3.06, 2.79) | (3.08, 2.82) | (3.05, 2.83) | (3.05, 2.80) | (3.05, 2.80) | (3.06, 2.81) |
| (1, 3) | 0.2500 | (3.16, 2.66) | (3.20, 2.66) | (3.17, 2.69) | (3.12, 2.71) | (3.11, 2.73) | (3.13, 2.71) | (3.13, 2.74) |
| (1, 4) | 0.2000 | (3.25, 2.62) | (3.24, 2.57) | (3.26, 2.64) | (3.24, 2.69) | (3.21, 2.68) | (3.20, 2.71) | (3.19, 2.66) |
| (1, 5) | 0.1667 | (3.26, 2.53) | (3.25, 2.56) | (3.35, 2.58) | (3.24, 2.62) | (3.26, 2.64) | (3.24, 2.64) | (3.22, 2.66) |
| (2, 2) | 0.5000 | (2.90, 3.07) | (2.96, 3.04) | (2.95, 3.03) | (2.92, 3.04) | (2.93, 3.03) | (2.94, 3.03) | (2.94, 3.04) |
| (2, 3) | 0.4000 | (2.96, 2.84) | (3.01, 2.93) | (2.97, 2.92) | (3.00, 2.93) | (2.98, 2.91) | (3.00, 2.91) | (2.99, 2.92) |
| (2, 4) | 0.3333 | (3.19, 2.76) | (3.10, 2.81) | (3.08, 2.86) | (3.04, 2.83) | (3.03, 2.85) | (3.06, 2.85) | (3.04, 2.85) |
| (2, 5) | 0.2857 | (3.16, 2.65) | (3.09, 2.81) | (3.06, 2.84) | (3.08, 2.84) | (3.08, 2.81) | (3.05, 2.83) | (3.07, 2.81) |
| (2, 6) | 0.2500 | (3.15, 2.65) | (3.21, 2.66) | (3.09, 2.80) | (3.06, 2.76) | (3.12, 2.75) | (3.10, 2.81) | (3.11, 2.82) |
| (3, 3) | 0.5000 | (2.91, 3.05) | (2.95, 3.02) | (3.02, 3.01) | (2.90, 3.03) | (2.92, 3.06) | (2.94, 3.05) | (2.93, 3.05) |
| (3, 4) | 0.4286 | (2.93, 2.92) | (2.97, 3.00) | (2.97, 2.95) | (2.98, 2.94) | (2.96, 2.99) | (2.97, 2.97) | (2.96, 2.98) |
| (3, 5) | 0.3750 | (3.01, 2.85) | (3.08, 2.93) | (3.01, 2.86) | (2.99, 2.95) | (3.00, 2.94) | (3.00, 2.92) | (3.01, 2.93) |
| (3, 6) | 0.3333 | (3.16, 2.76) | (3.05, 2.83) | (3.08, 2.89) | (3.04, 2.87) | (3.06, 2.88) | (3.01, 2.89) | (3.05, 2.90) |
| (3, 9) | 0.2500 | (3.14, 2.65) | (3.25, 2.73) | (3.05, 2.83) | (3.08, 2.83) | (3.10, 2.79) | (3.08, 2.81) | (3.09, 2.83) |
| (10, 10) | 0.5000 | (2.87, 3.07) | (3.03, 3.01) | (3.02, 3.09) | (2.96, 3.07) | (2.94, 3.05) | (2.94, 3.08) | (2.93, 3.11) |
| (8, 10) | 0.4444 | (2.89, 2.97) | (2.97, 3.05) | (2.97, 3.01) | (2.98, 3.02) | (2.95, 3.05) | (2.96, 3.02) | (2.97, 3.03) |
| (6, 10) | 0.3750 | (3.05, 2.83) | (3.05, 2.93) | (3.01, 2.87) | (3.01, 2.95) | (3.02, 2.98) | (2.99, 2.99) | (3.01, 2.98) |
| (4, 10) | 0.2857 | (3.21, 2.71) | (3.07, 2.81) | (3.07, 2.85) | (3.07, 2.85) | (3.03, 2.87) | (3.03, 2.89) | (3.07, 2.90) |
| (2, 10) | 0.1667 | (3.21, 2.58) | (3.18, 2.63) | (3.26, 2.63) | (3.21, 2.74) | (3.11, 2.74) | (3.18, 2.76) | (3.18, 2.72) |
| (100, 100) | 0.5000 | (2.87, 3.07) | (3.04, 2.97) | (3.02, 3.06) | (2.94, 3.07) | (2.94, 3.04) | (2.91, 3.09) | (2.96, 3.07) |
| (80, 100) | 0.4444 | (2.87, 2.98) | (2.95, 3.02) | (2.94, 3.07) | (2.99, 3.09) | (2.95, 3.07) | (2.94, 3.07) | (2.93, 3.07) |
| (60, 100) | 0.3750 | (3.03, 2.90) | (2.95, 2.96) | (3.02, 2.90) | (3.01, 3.00) | (2.97, 3.00) | (3.01, 3.02) | (2.99, 3.01) |
| (40, 100) | 0.2857 | (3.27, 2.79) | (3.10, 2.81) | (3.10, 2.94) | (3.02, 2.90) | (3.00, 2.98) | (3.00, 3.02) | (2.97, 2.99) |
| (20, 100) | 0.1667 | (3.26, 2.59) | (3.15, 2.61) | (3.17, 2.73) | (3.12, 2.82) | (3.12, 2.85) | (3.03, 2.90) | (3.06, 2.93) |
| Panel A: | When (α0, β0) = (5, 10) and E0(p) = 0.3333 | |||||||
| (α1, β1) | E1(p) | n = 2 (3.21, 2.76) b | n = 3 (3.02, 2.91) | n = 5 (3.04, 2.86) | n = 10 (3.02, 2.95) | n = 15 (3.01, 2.96) | n = 20 (3.01, 2.94) | n = 25 (3.03, 2.95) |
| (10, 10) | 0.5000 | 2.32 | 1.40 | 1.11 | 1.01 | 1.00 | 1.00 | 1.00 |
| (6, 10) | 0.3750 | 101.42 | 49.93 | 33.33 | 18.01 | 12.90 | 10.99 | 9.86 |
| (5, 10) a | 0.3333 | 378.79 | 371.75 | 373.13 | 374.53 | 380.23 | 383.14 | 378.79 |
| (5, 9) | 0.3571 | 220.75 | 130.72 | 96.90 | 57.67 | 46.69 | 38.52 | 37.84 |
| (5, 5) | 0.5000 | 2.29 | 1.41 | 1.13 | 1.01 | 1.00 | 1.00 | 1.00 |
| (1, 10) | 0.0909 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Panel B: | When (α0, β0) = (3, 9) and E0(p) = 0.2500 | |||||||
| (α1, β1) | E1(p) | n = 2 (3.14, 2.65) b | n = 3 (3.25, 2.73) | n = 5 (3.05, 2.83) | n = 10 (3.08, 2.83) | n = 15 (3.10, 2.79) | n = 20 (3.08, 2.81) | n = 25 (3.09, 2.83) |
| (9, 9) | 0.5000 | 1.07 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (4, 9) | 0.3077 | 29.39 | 25.41 | 11.20 | 6.56 | 4.98 | 4.11 | 3.73 |
| (3, 9) a | 0.2500 | 377.36 | 383.14 | 370.37 | 378.79 | 373.13 | 375.94 | 375.94 |
| (3, 8) | 0.2727 | 139.28 | 174.83 | 83.40 | 57.84 | 49.48 | 41.67 | 39.62 |
| (3, 3) | 0.5000 | 1.08 | 1.02 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (1, 9) | 0.1000 | 1.43 | 1.15 | 1.03 | 1.00 | 1.00 | 1.00 | 1.00 |
| Panel C: | When (α0, β0) = (46, 100) and E0(p) = 0.3151 | |||||||
| (α1, β1) | E1(p) | n = 2 (3.16, 2.75) b | n = 3 (2.97, 2.89) | n = 5 (3.08, 2.93) | n = 10 (3.00, 2.94) | n = 15 (3.03, 2.98) | n = 20 (3.00, 2.99) | n = 25 (3.00, 3.01) |
| (100, 100) | 0.5000 | 1.60 | 1.13 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 |
| (60, 100) | 0.3750 | 35.56 | 15.69 | 9.46 | 3.29 | 2.09 | 1.55 | 1.32 |
| (46, 100) a | 0.3151 | 374.53 | 370.37 | 384.62 | 377.36 | 380.23 | 375.94 | 378.79 |
| (46, 80) | 0.3651 | 54.05 | 25.03 | 16.01 | 5.52 | 3.34 | 2.31 | 1.85 |
| (46, 46) | 0.5000 | 1.60 | 1.13 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 |
| (10, 100) | 0.0909 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Panel D: | When (α0, β0) = (32, 100) and E0(p) = 0.2424 | |||||||
| (α1, β1) | E1(p) | n = 2 (3.10, 2.65) b | n = 3 (3.19, 2.74) | n = 5 (3.02, 2.93) | n = 10 (3.09, 2.92) | n = 15 (3.05, 2.94) | n = 20 (3.03, 2.98) | n = 25 (2.98, 3.00) |
| (100, 100) | 0.5000 | 1.03 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (50, 100) | 0.3333 | 7.51 | 5.08 | 2.18 | 1.24 | 1.05 | 1.01 | 1.00 |
| (32, 100) a | 0.2424 | 377.36 | 380.23 | 373.13 | 375.94 | 371.75 | 387.60 | 377.36 |
| (32, 80) | 0.2857 | 46.82 | 38.49 | 16.07 | 7.35 | 4.17 | 2.85 | 2.15 |
| (32, 32) | 0.5000 | 1.03 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (10,100) | 0.0909 | 1.30 | 1.07 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| p0 = E0(p) = 0.3333 | p0 = E0(p) = 0.3151 | p0 = E0(p) = 0.2500 | p0 = E0(p) = 0.2424 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| p1/ E1(p) | Bayesian EWMA Chart | SS EWMA- V Chart | p1/ E1(p) | Bayesian EWMA Chart | SS EWMA- V Chart | p1/ E1(p) | Bayesian EWMA Chart | SS EWMA- V Chart | p1/ E1(p) | Bayesian EWMA Chart | SS EWMA- V Chart |
| 0.5 | 1.11 | 13.92 | 0.5 | 1.01 | 12.41 | 0.5 | 1.00 | 8.12 | 0.5 | 1.00 | 7.76 |
| 0.375 | 33.33 | 85.92 | 0.3750 | 9.46 | 57.97 | 0.3077 | 11.20 | 56.92 | 0.3333 | 2.18 | 28.96 |
| 0.3571 | 96.90 | 158.03 | 0.3651 | 16.01 | 74.92 | 0.2727 | 83.40 | 187.40 | 0.2857 | 16.07 | 84.13 |
| 0.3333 a | 373.13 | 373.08 | 0.3151 a | 384.62 | 369.96 | 0.2500 a | 370.37 | 388.39 | 0.2424 a | 373.13 | 370.15 |
| 0.0909 | 1.00 | 9.21 | 0.0909 | 1.00 | 9.45 | 0.1000 | 1.03 | 14.56 | 0.0909 | 1.00 | 13.84 |
| Panel A: | Normal | Process | Panel B: | Exponential | Process | ||
|---|---|---|---|---|---|---|---|
| da | p | d | p | d | p | d | p |
| 1 | 0.3173 | 1 | 0.2431 | ||||
| 1.1 | 0.3633 | 0.9 | 0.2665 | 1.1 | 0.2765 | 0.9 | 0.2078 |
| 1.2 | 0.4047 | 0.8 | 0.2113 | 1.2 | 0.3077 | 0.8 | 0.1707 |
| 1.3 | 0.4418 | 0.7 | 0.1531 | 1.3 | 0.3369 | 0.7 | 0.1326 |
| 1.4 | 0.4751 | 0.6 | 0.0956 | 1.4 | 0.3642 | 0.6 | 0.0947 |
| 1.5 | 0.5050 | 0.5 | 0.0455 | 1.5 | 0.3895 | 0.5 | 0.0591 |
| 1.6 | 0.5320 | 0.4 | 0.0124 | 1.6 | 0.4132 | 0.4 | 0.0291 |
| 1.7 | 0.5564 | 0.3 | 0.0009 | 1.7 | 0.4352 | 0.3 | 0.0090 |
| 1.8 | 0.5785 | 0.2 | 0.0000 | 1.8 | 0.4558 | 0.2 | 0.0008 |
| 1.9 | 0.5987 | 1.9 | 0.4751 | ||||
| 2.0 | 0.6171 | 2.0 | 0.4931 |
| Panel A: | Normal process: E0(p) = 0.3173 and (α0, β0) = (317, 683) | |||
| d | E1(p) | n = 2 (3.16, 2.77) b 381.68 c | n = 10 (2.98, 2.94) 375.94 | n = 25 (2.96, 3.05) 375.94 |
| 0.6 | 0.0956 | 1.02 | 1.00 | 1.00 |
| 0.7 | 0.1531 | 1.46 | 1.00 | 1.00 |
| 0.8 | 0.2113 | 5.08 | 1.05 | 1.00 |
| 0.9 | 0.2665 | 44.38 | 5.03 | 1.60 |
| 1 a | 0.3173 | 394.01 | 368.32 | 376.08 |
| 1.1 | 0.3633 | 65.10 | 6.18 | 1.84 |
| 1.2 | 0.4047 | 12.57 | 1.33 | 1.00 |
| 1.3 | 0.4418 | 4.35 | 1.01 | 1.00 |
| 1.4 | 0.4751 | 2.28 | 1.00 | 1.00 |
| 1.5 | 0.5050 | 1.55 | 1.00 | 1.00 |
| Panel B: | Exponential process: E0(p) = 0.2431 and (α0, β0) = (243, 757) | |||
| d | E1(p) | n = 2 (3.10, 2.65) b 374.53 c | n = 10 (3.05, 2.93) 370.37 | n = 25 (2.99, 3.00) 377.36 |
| 0.6 | 0.0947 | 1.36 | 1.00 | 1.00 |
| 0.7 | 0.1326 | 2.98 | 1.00 | 1.00 |
| 0.8 | 0.1707 | 11.36 | 1.48 | 1.01 |
| 0.9 | 0.2078 | 70.27 | 12.60 | 3.18 |
| 1 a | 0.2431 | 283.85 | 369.69 | 388.50 |
| 1.1 | 0.2765 | 75.05 | 13.47 | 3.51 |
| 1.2 | 0.3077 | 18.68 | 2.15 | 1.06 |
| 1.3 | 0.3369 | 6.87 | 1.14 | 1.00 |
| 1.4 | 0.3642 | 3.43 | 1.01 | 1.00 |
| 1.5 | 0.3895 | 2.15 | 1.00 | 1.00 |
| Panel C: | Mixed process: E0(p) = 0.2802 and (α0, β0) = (280, 720) | |||
| d | E1(p) | n = 2 (3.26, 2.74) b 383.14 c | n = 10 (3.04, 2.95) 373.13 | n = 25 (2.98, 3.04) 377.36 |
| 0.6 | 0.0952 | 1.10 | 1.00 | 1.00 |
| 0.7 | 0.1429 | 2.00 | 1.00 | 1.00 |
| 0.8 | 0.1910 | 7.73 | 1.17 | 1.00 |
| 0.9 | 0.2372 | 56.60 | 7.56 | 2.16 |
| 1 a | 0.2802 | 413.39 | 310.56 | 200.84 |
| 1.1 | 0.3199 | 97.59 | 8.67 | 2.41 |
| 1.2 | 0.3562 | 19.16 | 1.65 | 1.03 |
| 1.3 | 0.3893 | 6.46 | 1.06 | 1.00 |
| 1.4 | 0.4196 | 3.15 | 1.00 | 1.00 |
| 1.5 | 0.4473 | 1.98 | 1.00 | 1.00 |
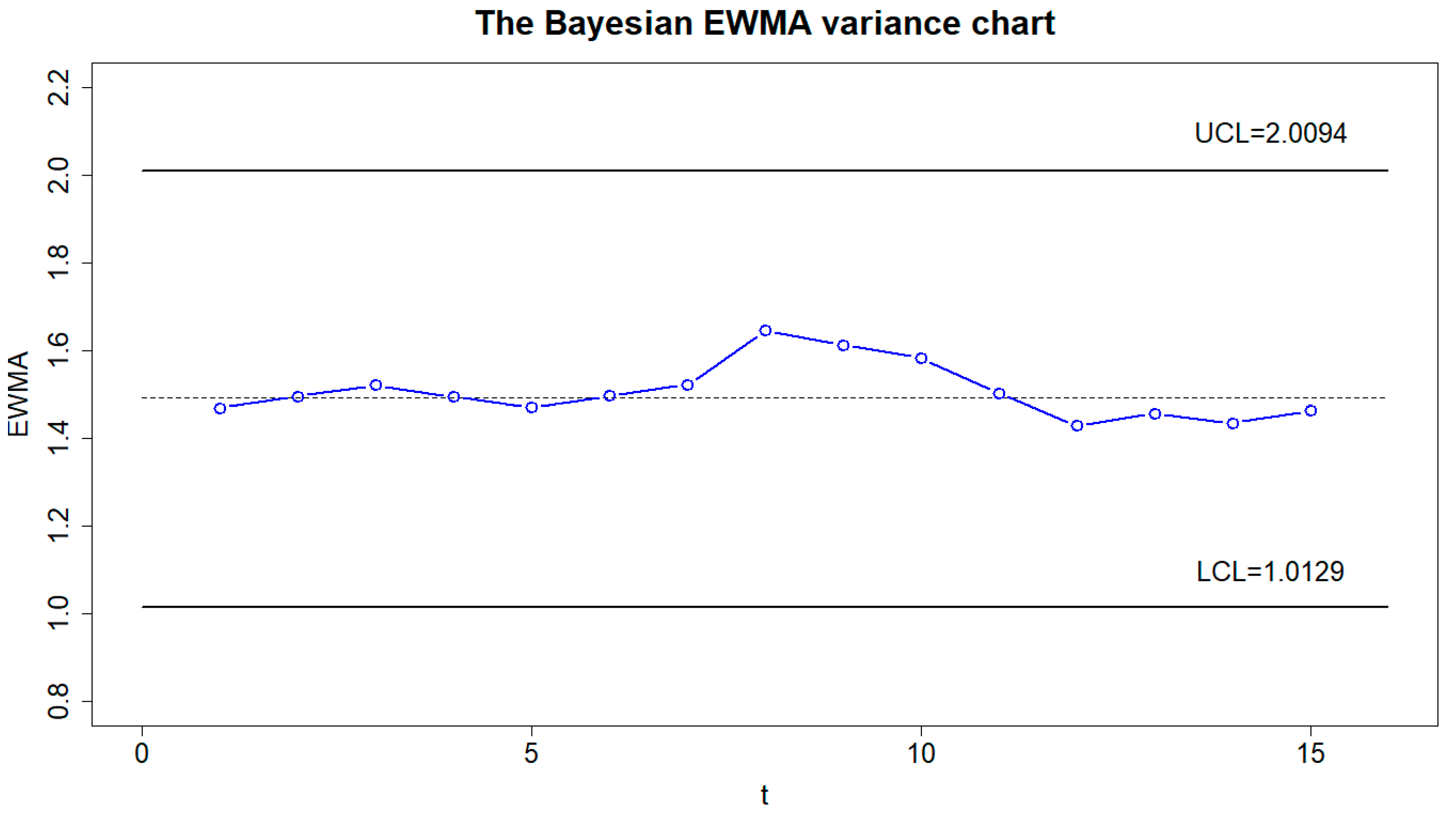
| t | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | S2 | M | EWMA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.88 | 0.78 | 5.06 | 5.45 | 2.93 | 6.11 | 11.59 | 1.2 | 0.89 | 3.21 | 11.59 | 1 | 1.4688 |
| 2 | 3.82 | 13.4 | 5.16 | 3.2 | 32.27 | 3.68 | 3.14 | 1.58 | 2.72 | 7.71 | 86.35 | 2 | 1.4954 |
| 3 | 1.4 | 3.89 | 10.88 | 30.85 | 0.54 | 8.4 | 5.1 | 2.63 | 9.17 | 3.94 | 77.86 | 2 | 1.5206 |
| 4 | 16.8 | 8.77 | 8.36 | 3.55 | 7.76 | 1.81 | 1.11 | 5.91 | 8.26 | 7.19 | 19.77 | 1 | 1.4946 |
| 5 | 0.24 | 9.57 | 0.66 | 1.15 | 2.34 | 0.57 | 8.94 | 5.54 | 11.69 | 6.58 | 18.47 | 1 | 1.4699 |
| 6 | 4.21 | 8.73 | 11.44 | 2.89 | 19.49 | 1.2 | 8.01 | 6.19 | 7.48 | 0.07 | 31.88 | 2 | 1.4964 |
| 7 | 15.08 | 7.43 | 4.31 | 6.14 | 10.37 | 2.33 | 1.97 | 1.08 | 4.27 | 14.08 | 24.85 | 2 | 1.5215 |
| 8 | 13.89 | 0.3 | 3.21 | 11.32 | 9.9 | 4.39 | 10.5 | 1.7 | 10.74 | 1.46 | 25.00 | 4 | 1.6455 |
| 9 | 0.03 | 12.76 | 2.41 | 7.41 | 1.67 | 3.7 | 4.31 | 2.45 | 3.57 | 3.33 | 12.78 | 1 | 1.6132 |
| 10 | 12.89 | 17.96 | 2.78 | 3.21 | 1.12 | 12.61 | 4.23 | 6.18 | 2.33 | 6.92 | 31.47 | 1 | 1.5825 |
| 11 | 7.71 | 1.05 | 1.11 | 0.22 | 3.53 | 0.81 | 0.41 | 3.73 | 0.08 | 2.55 | 5.62 | 0 | 1.5034 |
| 12 | 5.81 | 6.29 | 3.46 | 2.66 | 4.02 | 10.95 | 1.59 | 5.58 | 0.55 | 4.1 | 8.51 | 0 | 1.4282 |
| 13 | 2.89 | 1.61 | 1.3 | 2.58 | 18.65 | 10.77 | 18.23 | 3.13 | 3.38 | 6.34 | 44.71 | 2 | 1.4568 |
| 14 | 1.36 | 1.92 | 0.12 | 11.08 | 8.85 | 3.99 | 4.32 | 1.71 | 1.77 | 1.94 | 12.63 | 1 | 1.4340 |
| 15 | 21.52 | 0.63 | 8.54 | 3.37 | 6.94 | 3.44 | 3.37 | 6.37 | 1.28 | 12.83 | 39.96 | 2 | 1.4623 |
| t | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | S2 | M | EWMA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.54 | 0.01 | 1.33 | 7.27 | 5.52 | 0.09 | 1.84 | 1.04 | 2.91 | 0.63 | 5.83 | 0 | 0.8602 |
| 2 | 0.86 | 1.61 | 1.15 | 0.96 | 0.54 | 3.05 | 4.11 | 0.63 | 2.37 | 0.05 | 1.62 | 0 | 0.8172 |
| 3 | 1.45 | 0.19 | 4.18 | 0.18 | 0.02 | 0.7 | 0.8 | 0.97 | 3.6 | 2.94 | 2.30 | 0 | 0.7764 |
| 4 | 1.37 | 0.14 | 1.54 | 1.58 | 0.45 | 6.01 | 4.59 | 1.74 | 3.92 | 4.82 | 4.15 | 0 | 0.7375 |
| 5 | 3 | 2.46 | 0.06 | 1.8 | 3.25 | 2.13 | 2.22 | 1.37 | 2.13 | 0.25 | 1.10 | 0 | 0.7007 |
| 6 | 1.59 | 3.88 | 0.39 | 0.54 | 1.58 | 1.7 | 0.68 | 1.25 | 6.83 | 0.31 | 4.11 | 0 | 0.6656 |
| 7 | 5.01 | 1.85 | 3.1 | 1 | 0.09 | 1.16 | 2.69 | 2.79 | 1.84 | 2.62 | 1.85 | 0 | 0.6324 |
| 8 | 4.96 | 0.55 | 1.43 | 4.12 | 4.06 | 1.42 | 1.43 | 0.86 | 0.67 | 0.13 | 3.02 | 0 | 0.6007 |
| 9 | 1.08 | 0.65 | 0.91 | 0.88 | 2.02 | 2.88 | 1.76 | 2.87 | 1.97 | 0.62 | 0.75 | 0 | 0.5707 |
| 10 | 4.56 | 0.44 | 5.61 | 2.79 | 1.73 | 2.46 | 0.53 | 1.73 | 7.02 | 2.13 | 4.70 | 0 | 0.5422 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-H.; Lu, M.-C.; Yang, S.-F.; Lee, M.-Y. A Bayesian Control Chart for Monitoring Process Variance. Appl. Sci. 2021, 11, 2729. https://doi.org/10.3390/app11062729
Lin C-H, Lu M-C, Yang S-F, Lee M-Y. A Bayesian Control Chart for Monitoring Process Variance. Applied Sciences. 2021; 11(6):2729. https://doi.org/10.3390/app11062729
Chicago/Turabian StyleLin, Chien-Hua, Ming-Che Lu, Su-Fen Yang, and Ming-Yung Lee. 2021. "A Bayesian Control Chart for Monitoring Process Variance" Applied Sciences 11, no. 6: 2729. https://doi.org/10.3390/app11062729
APA StyleLin, C.-H., Lu, M.-C., Yang, S.-F., & Lee, M.-Y. (2021). A Bayesian Control Chart for Monitoring Process Variance. Applied Sciences, 11(6), 2729. https://doi.org/10.3390/app11062729







