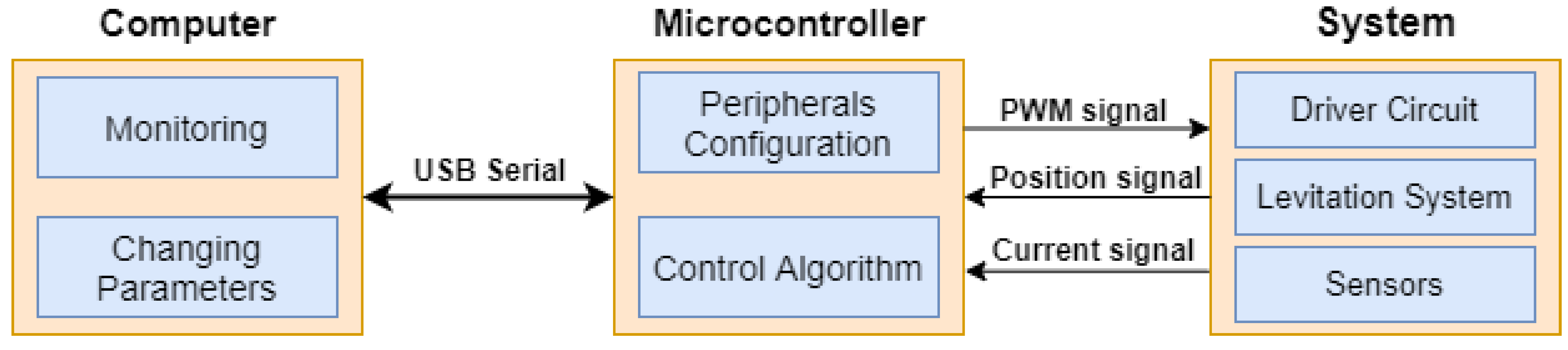
Figure 1.
General system architecture.
Figure 1.
General system architecture.
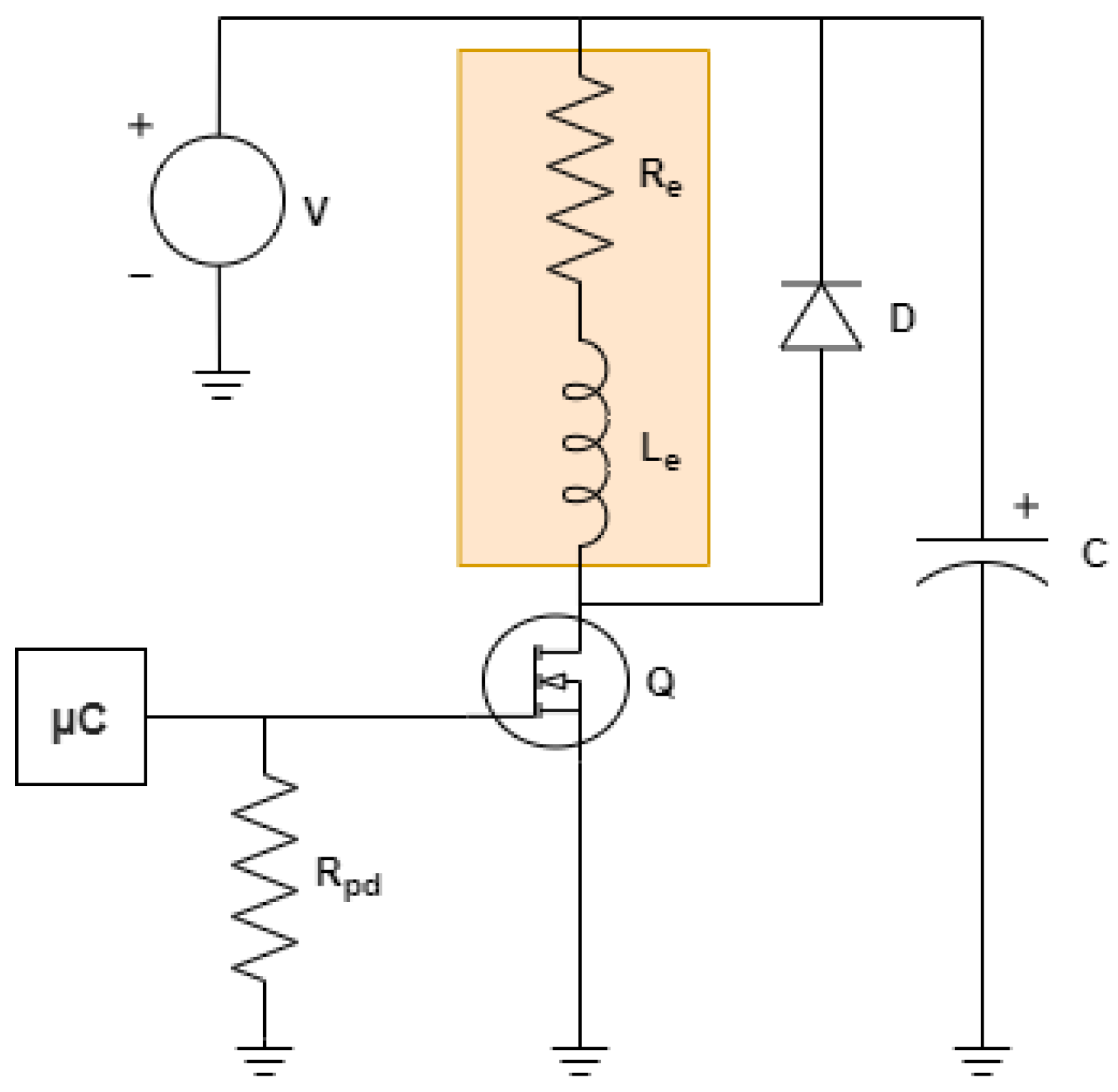
Figure 2.
Driver circuit.
Figure 2.
Driver circuit.
Figure 3.
Position sensor and electromagnet arrangement.
Figure 3.
Position sensor and electromagnet arrangement.
Figure 4.
Experimental electromagnetic system.
Figure 4.
Experimental electromagnetic system.
Figure 5.
Eletromagnetic system.
Figure 5.
Eletromagnetic system.
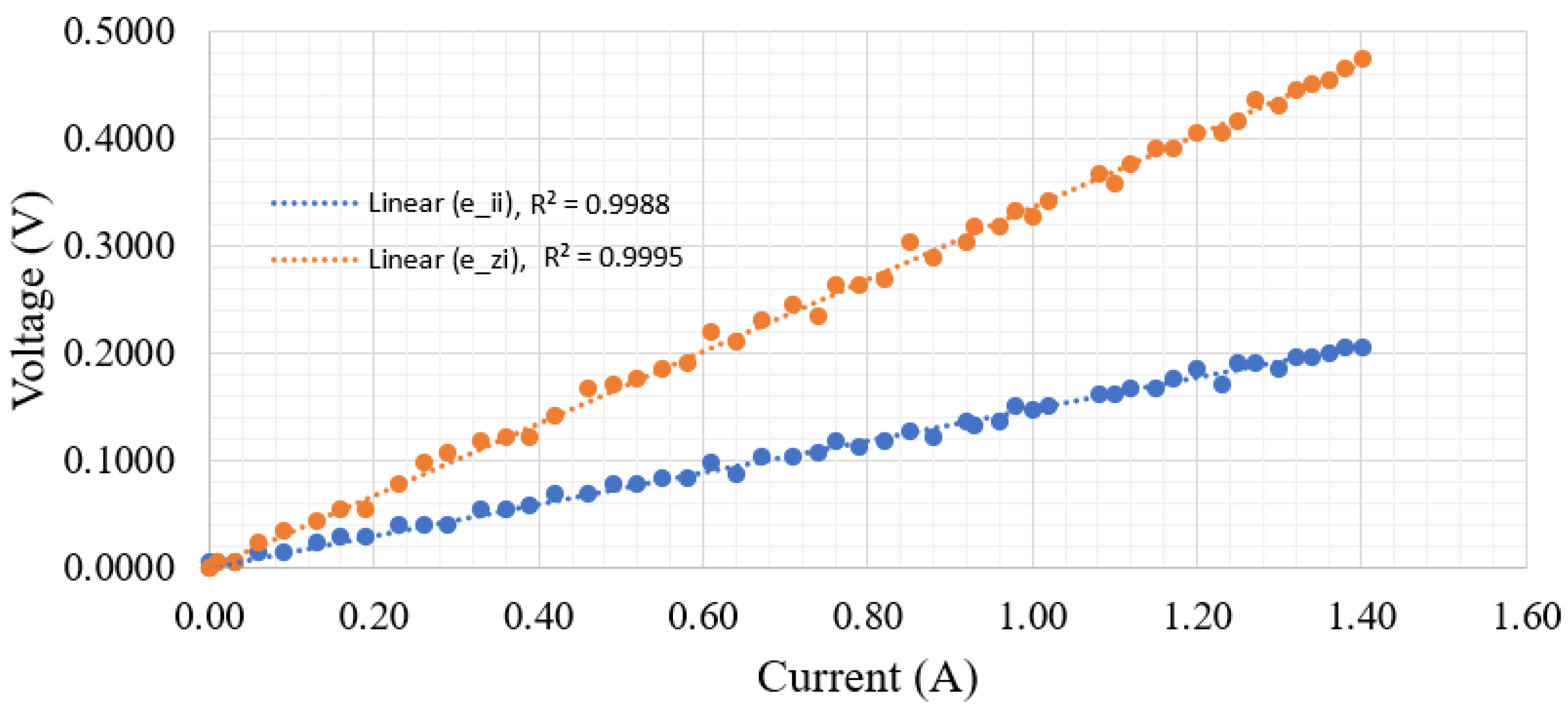
Figure 6.
Influence of the current on both sensors.
Figure 6.
Influence of the current on both sensors.
Figure 7.
Influence of the distance on the position sensor.
Figure 7.
Influence of the distance on the position sensor.
Figure 8.
Response to step input of the linearized system with both classic controllers.
Figure 8.
Response to step input of the linearized system with both classic controllers.
Figure 9.
Simulink diagram used to test the classical controllers.
Figure 9.
Simulink diagram used to test the classical controllers.
Figure 10.
Real system responses with both classical controllers.
Figure 10.
Real system responses with both classical controllers.
Figure 11.
Random reference and system response with the lead–lag controller.
Figure 11.
Random reference and system response with the lead–lag controller.
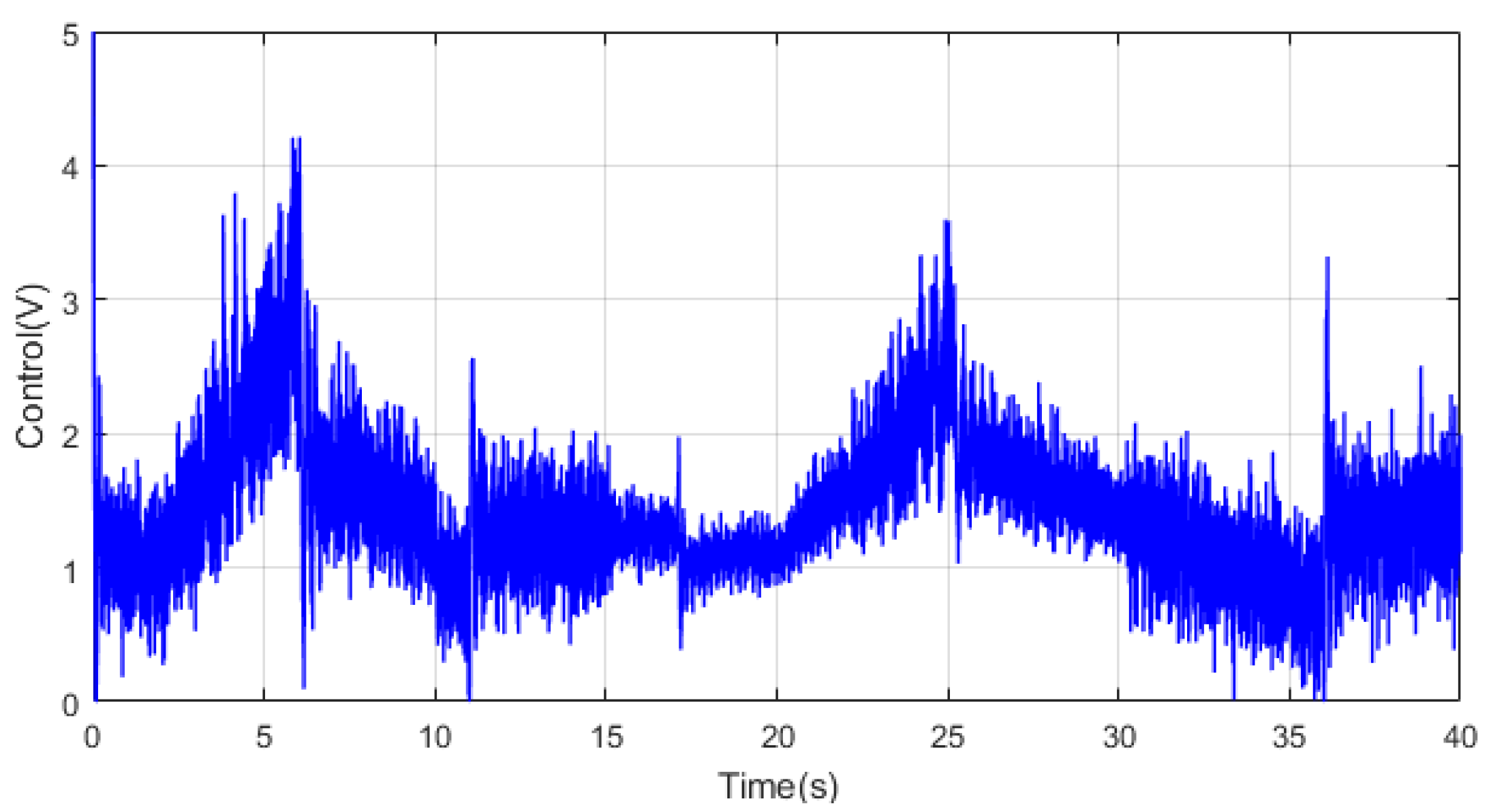
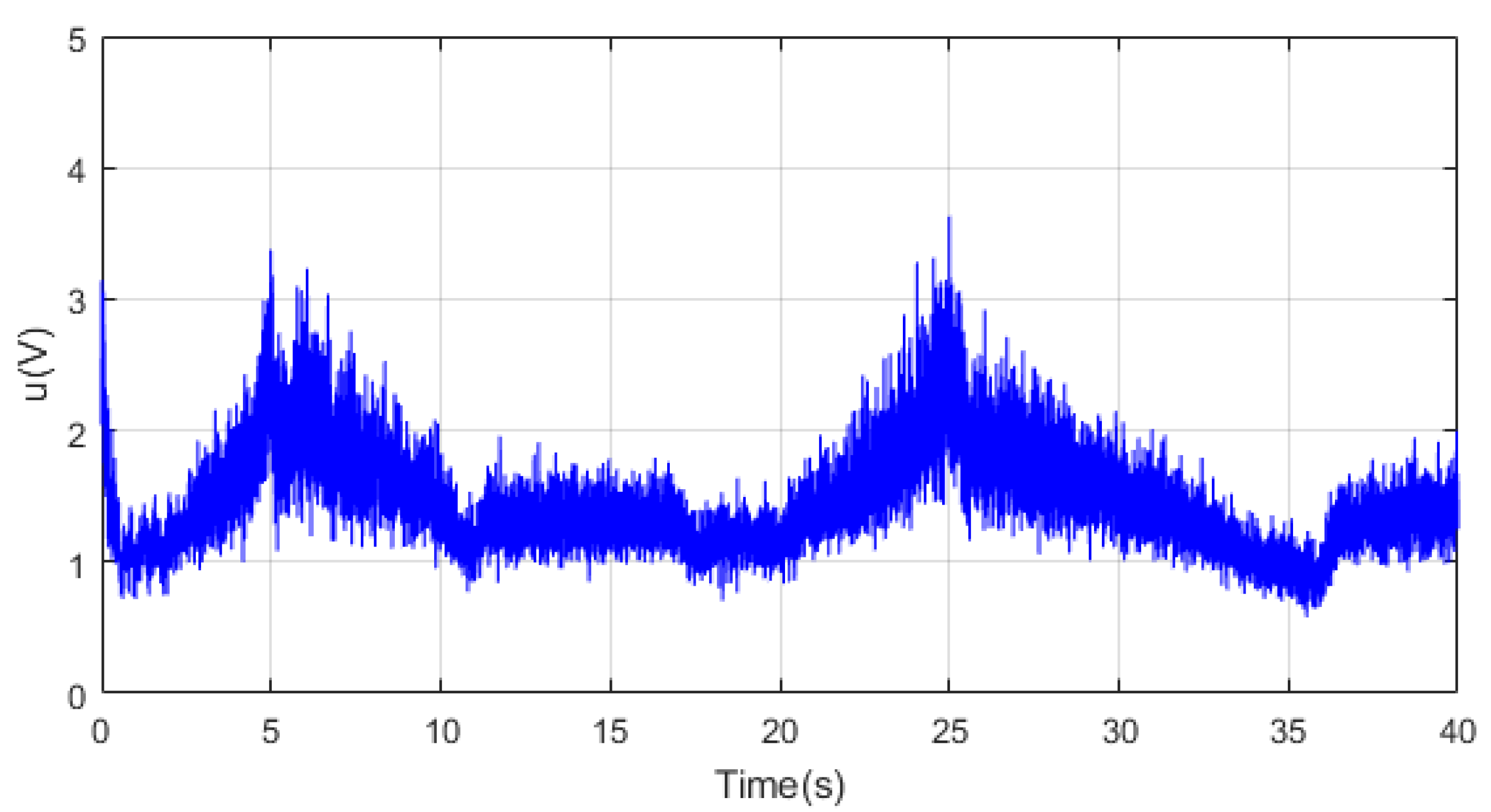
Figure 12.
Control signal for the random reference with the lead–lag controller.
Figure 12.
Control signal for the random reference with the lead–lag controller.
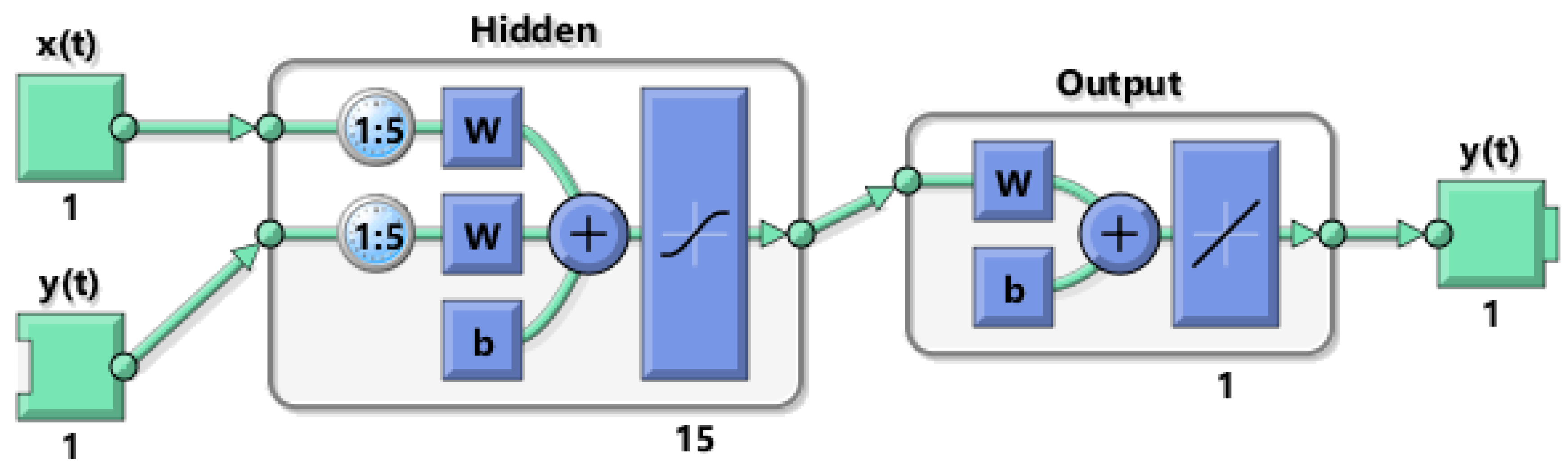
Figure 13.
Identification network.
Figure 13.
Identification network.
Figure 14.
Comparison between the system and the network responses.
Figure 14.
Comparison between the system and the network responses.
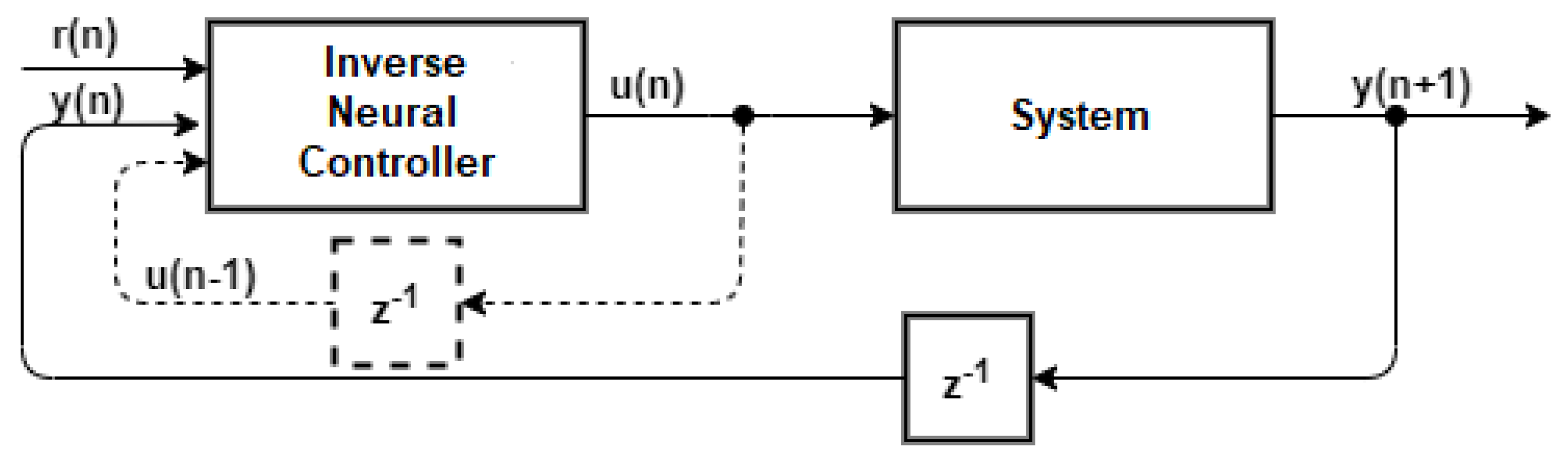
Figure 15.
Inverse model controller diagram.
Figure 15.
Inverse model controller diagram.
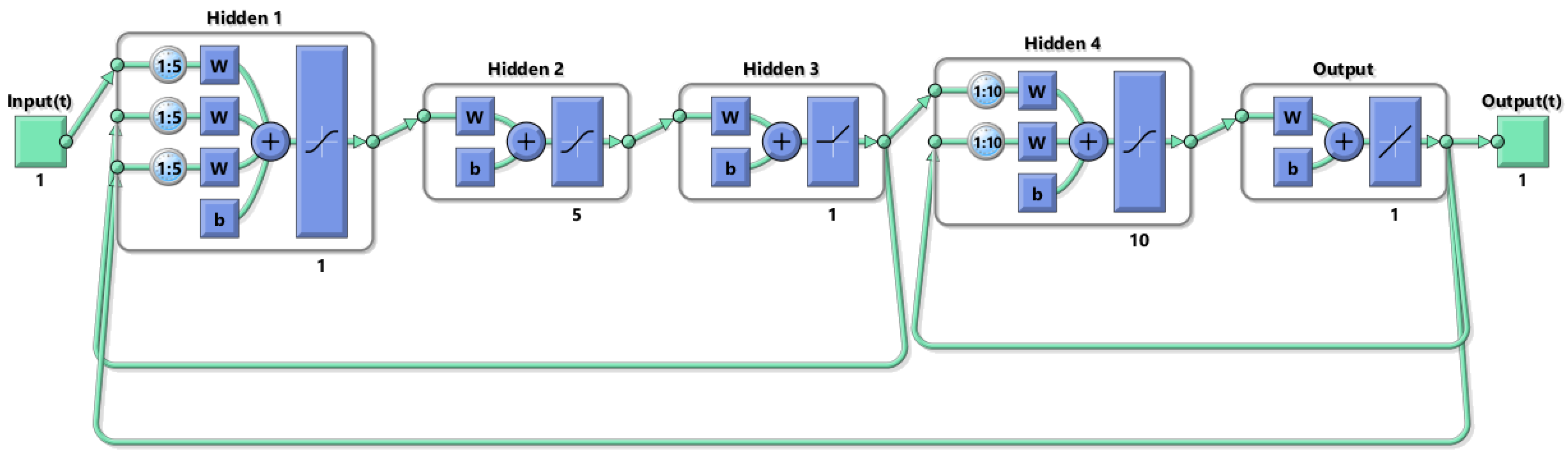
Figure 16.
Inverse model network - 1th5s5d.
Figure 16.
Inverse model network - 1th5s5d.
Figure 17.
Responses of the real system when controlled by the 1th5s5d network.
Figure 17.
Responses of the real system when controlled by the 1th5s5d network.
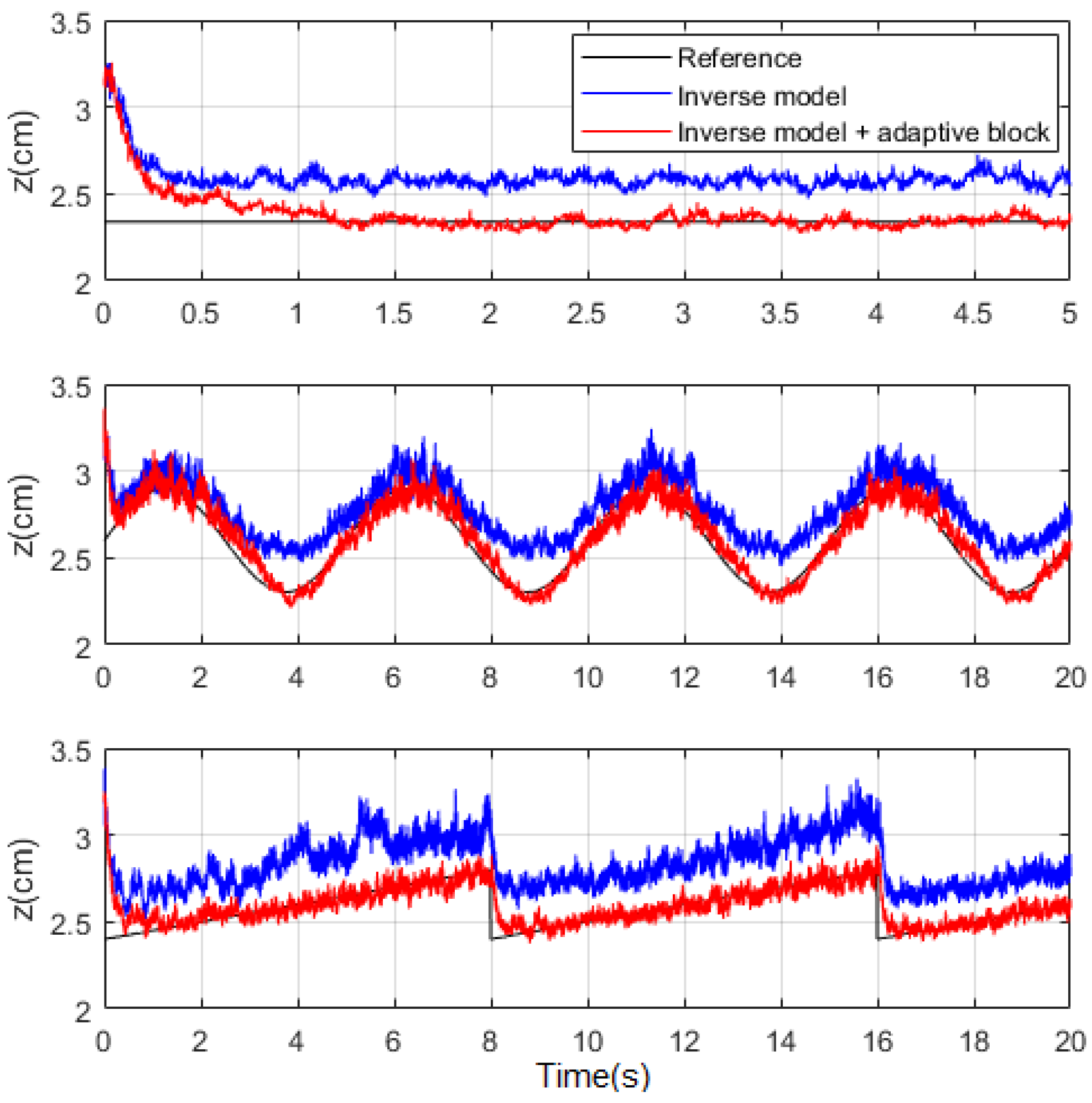
Figure 18.
System response with the inverse model controllers.
Figure 18.
System response with the inverse model controllers.
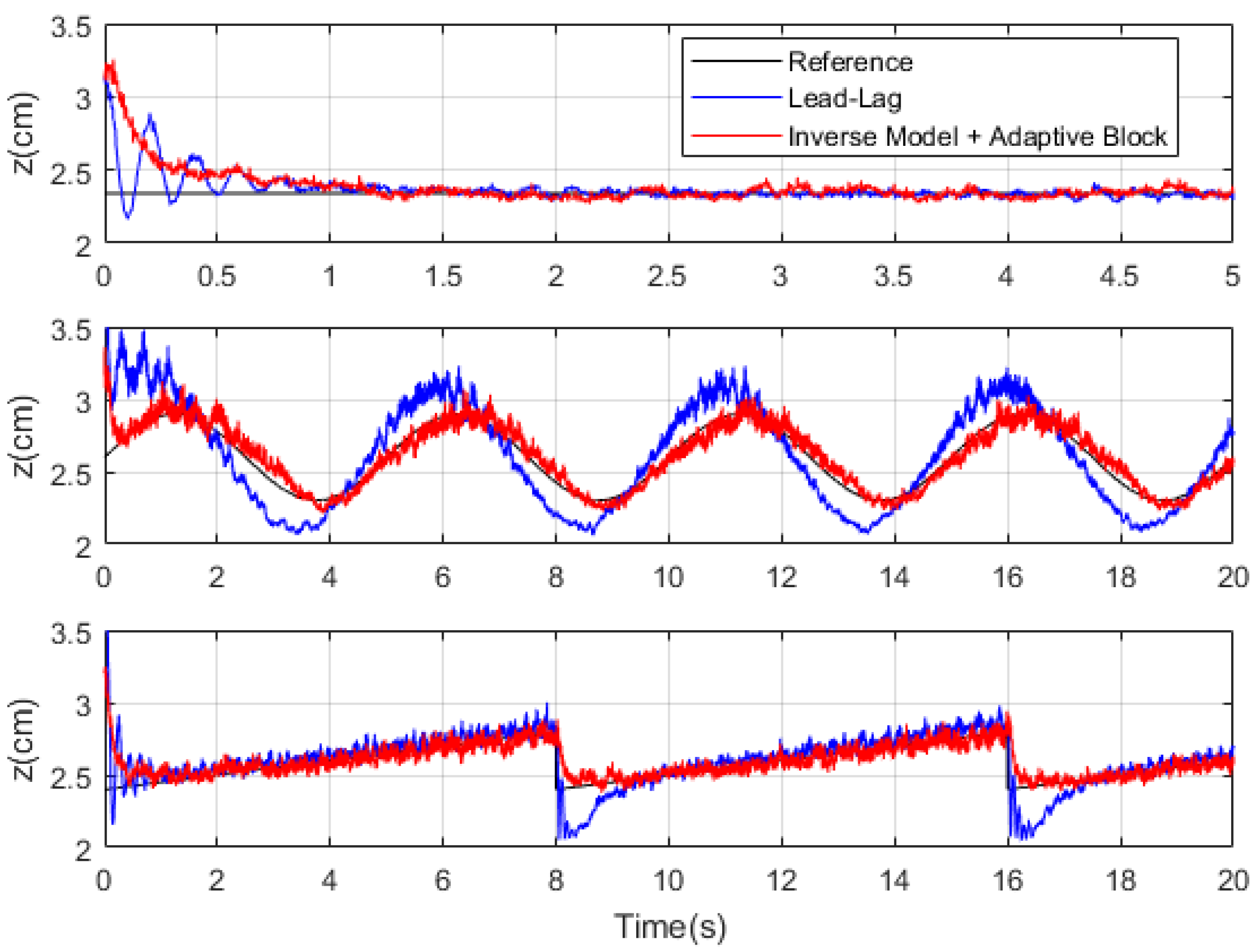
Figure 19.
Comparison of system responses with lead–lag compensator and the inverse model with adaptive block.
Figure 19.
Comparison of system responses with lead–lag compensator and the inverse model with adaptive block.
Figure 20.
Diagram of the internal model controller.
Figure 20.
Diagram of the internal model controller.
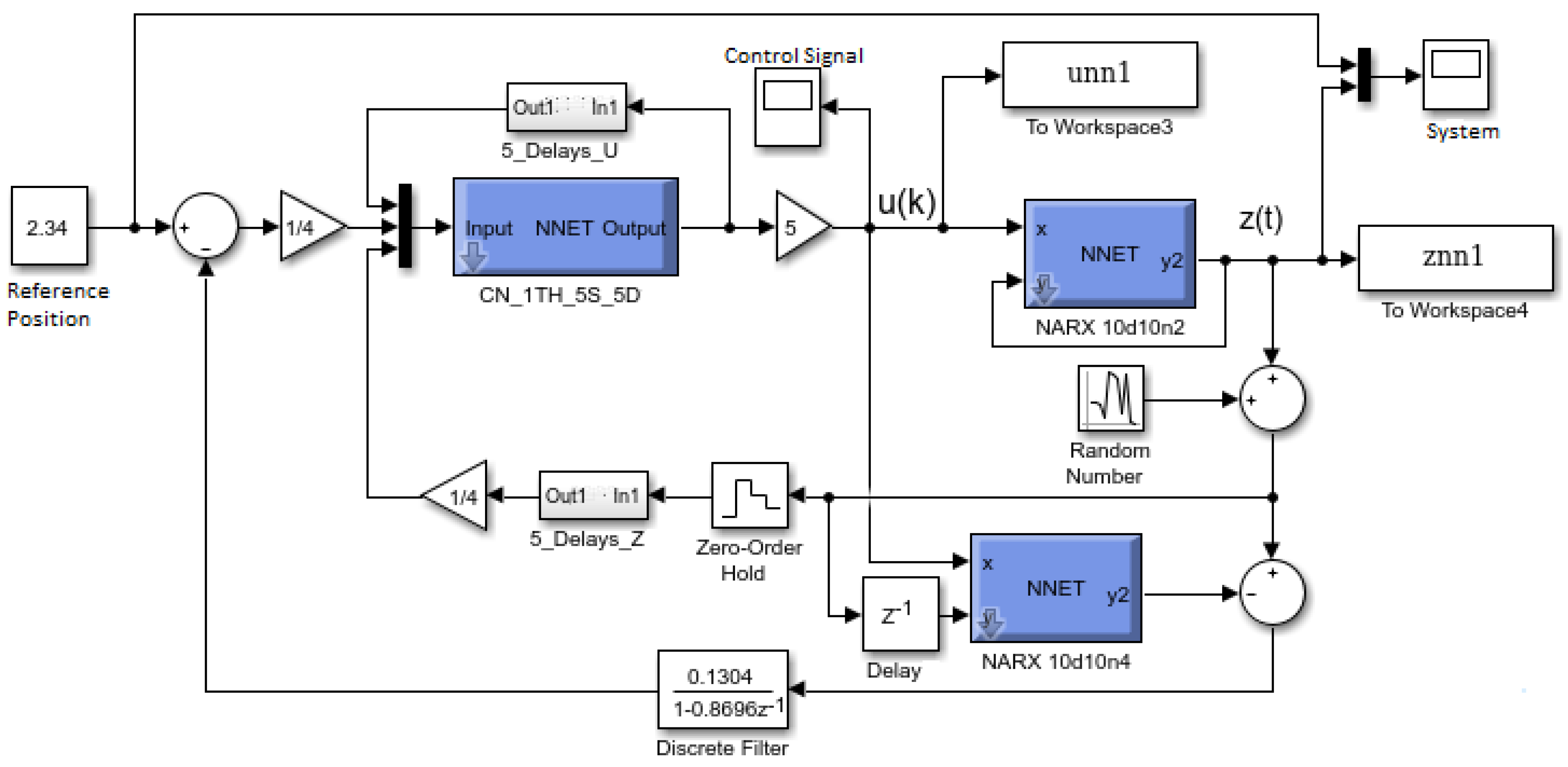
Figure 21.
Simulink diagram of the internal model controller.
Figure 21.
Simulink diagram of the internal model controller.
Figure 22.
Comparison of system responses with the inverse model with adaptive block and internal model.
Figure 22.
Comparison of system responses with the inverse model with adaptive block and internal model.
Figure 23.
Control signal applied by the inverse model with adaptive block and internal model for the sinusoidal reference.
Figure 23.
Control signal applied by the inverse model with adaptive block and internal model for the sinusoidal reference.
Figure 24.
Diagram of the model reference controller.
Figure 24.
Diagram of the model reference controller.
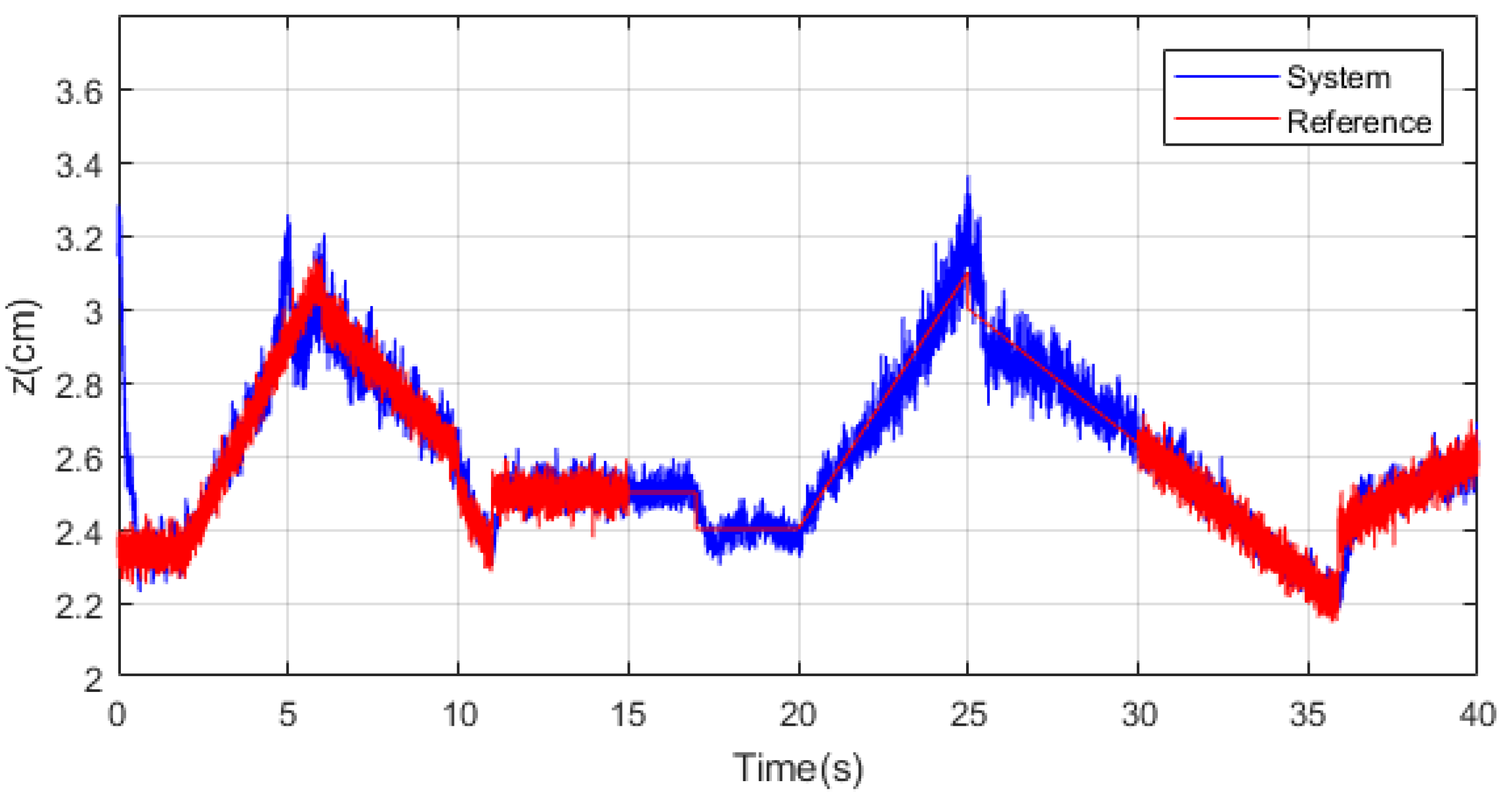
Figure 25.
Random reference and system response with the inverse model controller with adaptive block.
Figure 25.
Random reference and system response with the inverse model controller with adaptive block.
Figure 26.
Control signal for the random reference applied by the inverse model controller with adaptive block.
Figure 26.
Control signal for the random reference applied by the inverse model controller with adaptive block.
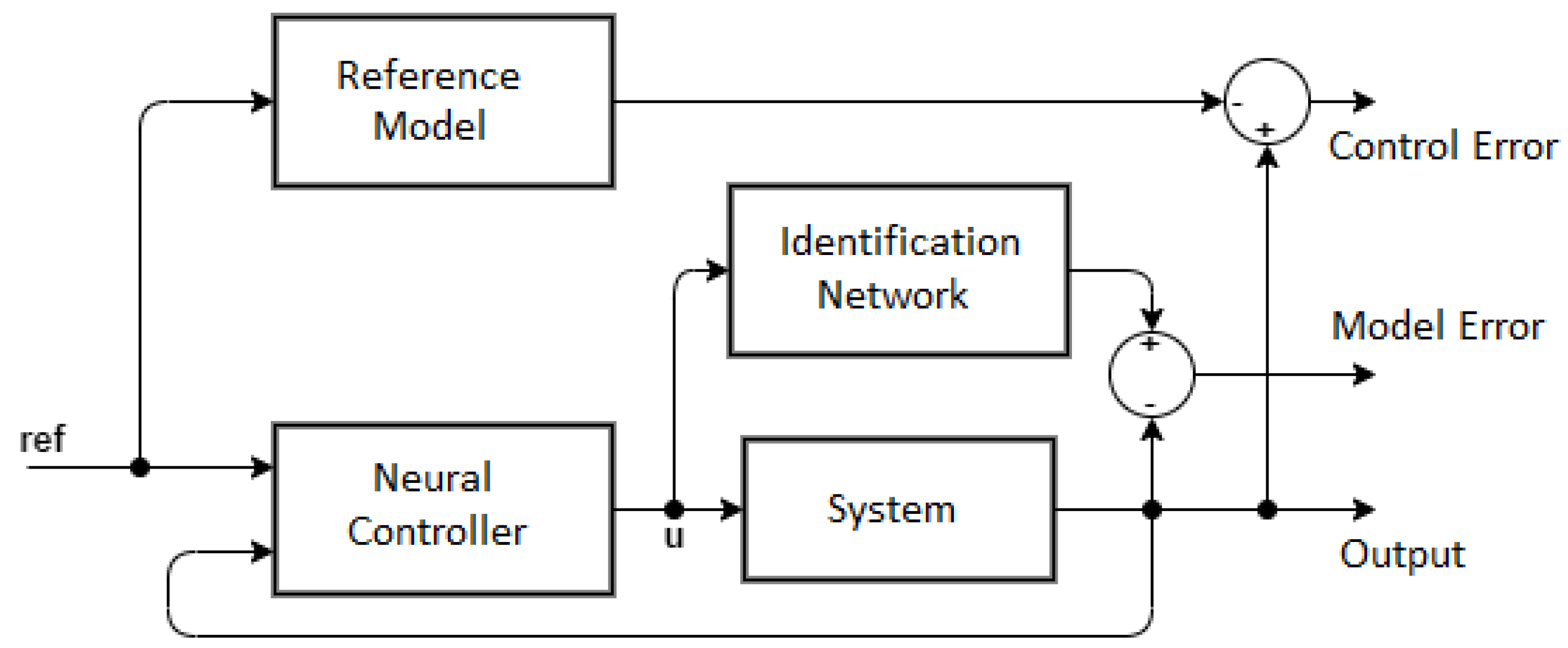
Figure 27.
Reference model controller network.
Figure 27.
Reference model controller network.
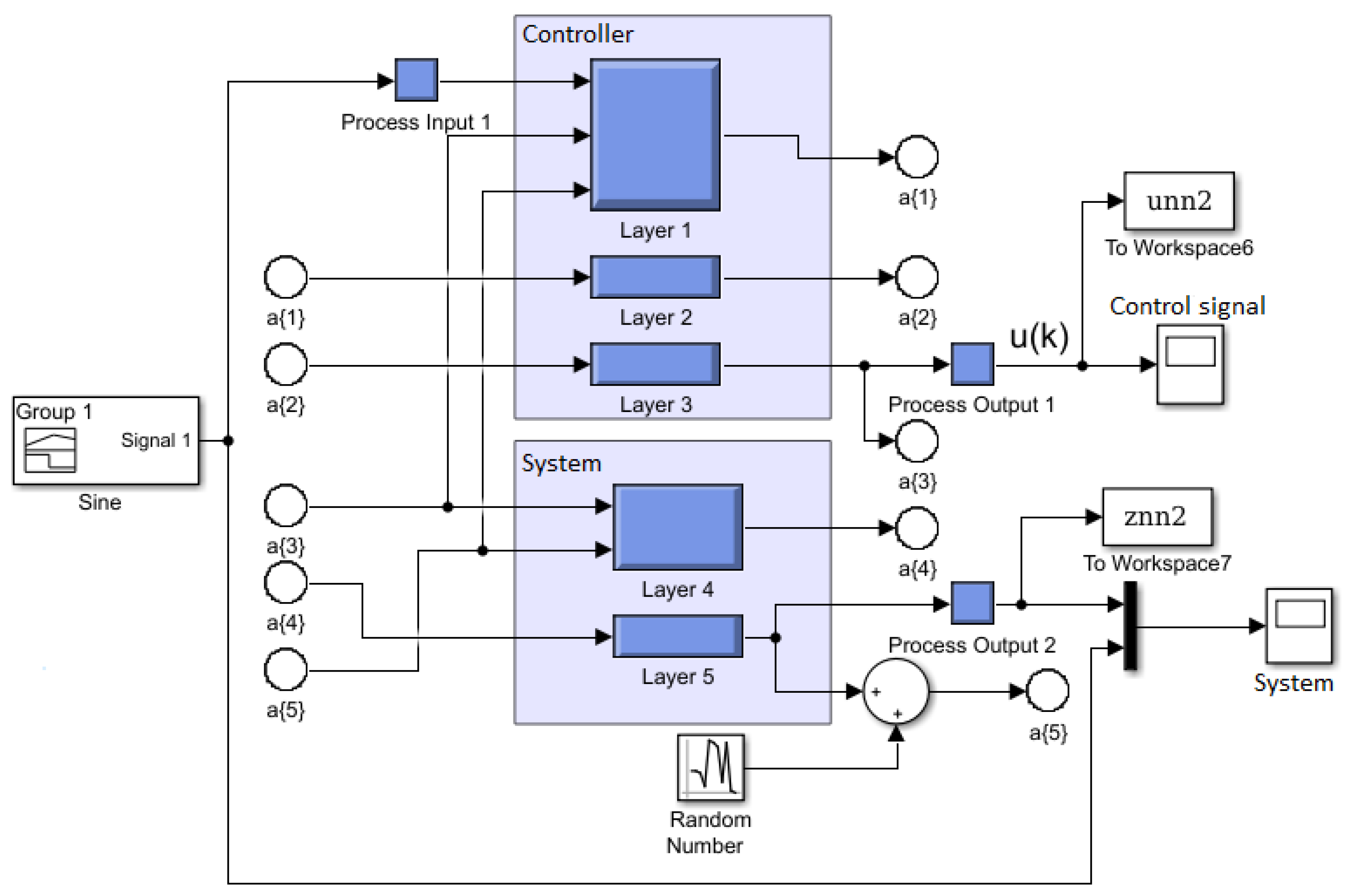
Figure 28.
Simulink diagram of the model reference controller.
Figure 28.
Simulink diagram of the model reference controller.
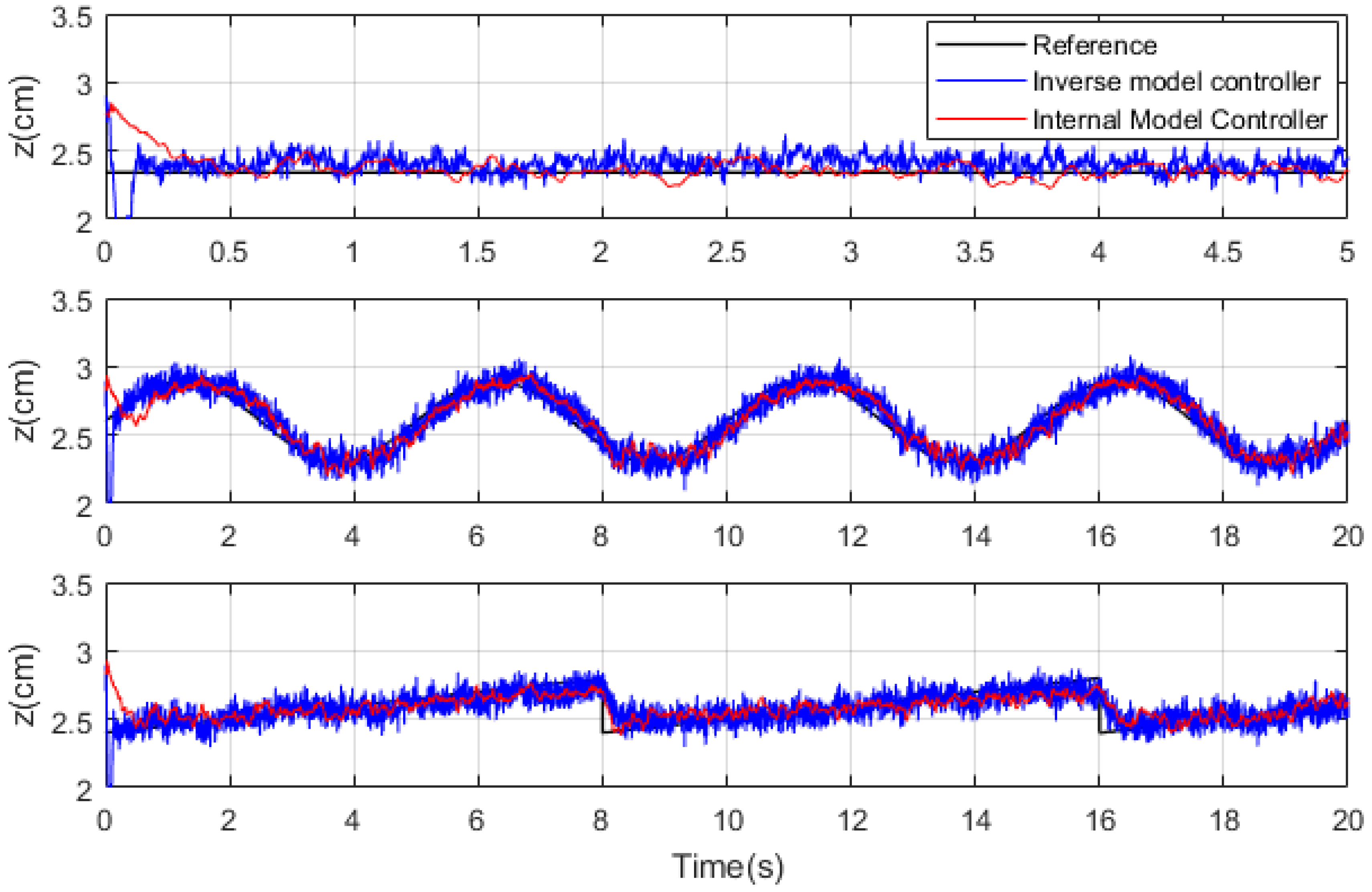
Figure 29.
Comparison of the system responses with the internal model and reference model controllers.
Figure 29.
Comparison of the system responses with the internal model and reference model controllers.
Figure 30.
Control signal applied by the reference model control for the sinusoidal reference.
Figure 30.
Control signal applied by the reference model control for the sinusoidal reference.
Table 1.
Parameters of the system [
28].
Table 1.
Parameters of the system [
28].
| Component | Value | Units |
|---|
| Resistance (Re) | 3.0 | Ω |
| Inductance (Le) | 15.0 | mH |
| Maximum current | 1.5 | A |
| Weight (m) | 3.0 | g |
| Diameter | 37.3 | mm |
| Thickness | 28.5 | mm |
Table 2.
Specifications of the ATmega2560 [
29].
Table 2.
Specifications of the ATmega2560 [
29].
| Parameter | Value | Units |
|---|
| Operating Voltage | 5 | V |
| Clock Frequency | 16 | MHz |
| Flash Memory | 256 | KB |
| SRAM | 8 | KB |
| EEPROM | 4 | KB |
Table 3.
Sensors constants.
Table 3.
Sensors constants.
| Constant | Value | Units |
|---|
| α | 508 | ADU |
| β | 1090 | ADUcm3 |
| γ | 68.274 | ADU/A |
| m | 29.569 | ADU/A |
| b | 516 | ADU |
Table 4.
Optimization of the sensor constants.
Table 4.
Optimization of the sensor constants.
| z (cm) | ADCi (ADU) | ADCz (ADU) | icalc (A) | zcalc (cm) | zoptim (cm) | |z-zcalc| (cm) | |z-zoptim| (cm) |
|---|
| 2.340 | 524 | 615 | 0.267 | 2.233 | 2.236 | 0.107 | 0.104 |
| 2.670 | 530 | 599 | 0.461 | 2.725 | 2.703 | 0.055 | 0.033 |
| 2.870 | 533 | 595 | 0.559 | 2.906 | 2.870 | 0.036 | 0.000 |
| 3.150 | 538 | 594 | 0.721 | 3.115 | 3.055 | 0.035 | 0.095 |
| 2.340 | 516 | 592 | 0.000 | 2.289 | 2.340 | 0.051 | 0.000 |
| 3.150 | 516 | 543 | 0.000 | 3.084 | 3.150 | 0.066 | 0.000 |
| | | | | | Total | 0.349 | 0.232 |
Table 5.
Optimized sensor constants.
Table 5.
Optimized sensor constants.
| Constant | Value | Units |
|---|
| α | 507.045 | ADU |
| β | 1123.801 | ADUcm3 |
| γ | 69.474 | ADU/A |
| m | 30.084 | ADU/A |
| b | 516.343 | ADU |
Table 6.
Mean Squared Error (MSE) after training.
Table 6.
Mean Squared Error (MSE) after training.
| Network | MSE | Network | MSE |
|---|
| 3d5n | | 10d5n | |
| 3d10n | | 10d10n | |
| 3d15n | | 10d15n | |
| 5d5n | | 15d5n | |
| 5d10n | | 15d10n | |
| 5d15n | | 15d15n | |
Table 7.
MSE of the best identification networks for different references.
Table 7.
MSE of the best identification networks for different references.
| Network | MSE Step | MSE Sinusoid | MSE Sawtooth | Total |
|---|
| 10d5n | | | | |
| 10d10n | | | | |
| 10d15n | | | | |
| 15d5n | | | | |
| 15d10n | | | | |
| 15d15n | | | | |
Table 8.
MSE obtained by the inverse model control networks for the different reference signals.
Table 8.
MSE obtained by the inverse model control networks for the different reference signals.
| Network | MSE Step | MSE Sinusoid | MSE Sawtooth | Total |
|---|
| 1th5s5d | | | | |
| 1th10s5d | | | | |
| 1th15s5d | | | | |
| 1th5s10d | | | | |
| 1th10s10d | | | | |
| 1th15s10d | | | | |
Table 9.
Integral Square Error (ISE), the Integral Absolute Error (IAE), and the Integral Time Absolute Error (ITAE) values for the inverse model controllers.
Table 9.
Integral Square Error (ISE), the Integral Absolute Error (IAE), and the Integral Time Absolute Error (ITAE) values for the inverse model controllers.
| | | Step | Sine | Saw | Total |
|---|
| ISE | Inverse Model | 2.2681 | 1.4103 | 2.2240 | 5.9024 |
| Inverse Model + Adaptive Block | 0.1166 | 0.1819 | 0.1884 | 0.4869 |
| IAE | Inverse Model | 9.3312 | 6.8233 | 8.8432 | 24.9977 |
| Inverse Model + Adaptive Block | 1.0882 | 2.0457 | 1.6444 | 4.7783 |
| ITAE | Inverse Model | 185.3760 | 139.8848 | 165.4900 | 490.7508 |
| Inverse Model + Adaptive Block | 18.2365 | 38.6153 | 29.8916 | 85.7434 |
Table 10.
ISE, IAE and ITAE values for the lead–lag and the Inverse model with adaptive block.
Table 10.
ISE, IAE and ITAE values for the lead–lag and the Inverse model with adaptive block.
| | | Step | Sine | Saw | Total |
|---|
| ISE | lead–lag | 1.6828 | 2.2484 | 2.2968 | 6.228 |
| Inverse Model + Adaptive Block | 0.1166 | 0.1819 | 0.1884 | 0.4869 |
| IAE | lead–lag | 8.0435 | 9.0256 | 9.1502 | 26.2193 |
| Inverse Model + Adaptive Block | 1.0882 | 2.0457 | 1.6444 | 4.7783 |
| ITAE | lead–lag | 161.1860 | 179.8254 | 184.7707 | 525.7821 |
| Inverse Model + Adaptive Block | 18.2365 | 38.6153 | 29.8916 | 85.7434 |
Table 11.
ISE, IAE and ITAE values for the inverse model and the internal model controller.
Table 11.
ISE, IAE and ITAE values for the inverse model and the internal model controller.
| | | Step | Sine | Saw | Total |
|---|
| ISE | Inverse Model + Adaptive Block | 0.4531 | 0.3003 | 0.2800 | 1.0334 |
| Internal Model | 0.4950 | 0.2193 | 0.2446 | 0.9589 |
| IAE | Inverse Model + Adaptive Block | 3.5459 | 2.6897 | 2.5324 | 8.768 |
| Internal Model | 3.9383 | 2.4808 | 2.4100 | 8.8291 |
| ITAE | Inverse Model +Adaptive Block | 72.5602 | 53.4818 | 50.2659 | 176.3079 |
| Internal Model | 76.4735 | 49.0349 | 48.2459 | 173.7543 |
Table 12.
MSE obtained by the reference model controller for the different signals.
Table 12.
MSE obtained by the reference model controller for the different signals.
| Reference | MSE |
|---|
| Training | |
| Step | |
| Sawtooth | |
| Sinusoid | |
Table 13.
ISE, IAE, and ITAE values for the internal model and the model reference controller.
Table 13.
ISE, IAE, and ITAE values for the internal model and the model reference controller.
| | | Step | Sine | Saw | Total |
|---|
| ISE | Internal Model | 0.4950 | 0.2193 | 0.2446 | 0.9589 |
| Model Reference | 0.0786 | 0.1273 | 0.1447 | 0.3506 |
| IAE | Internal Model | 3.9383 | 2.4808 | 2.4100 | 8.8291 |
| Model Reference | 0.9126 | 1.6756 | 1.3950 | 3.9832 |
| ITAE | Internal Model | 76.4735 | 49.0349 | 48.2459 | 173.7543 |
| Model Reference | 16.8913 | 32.2026 | 27.2355 | 76.3294 |