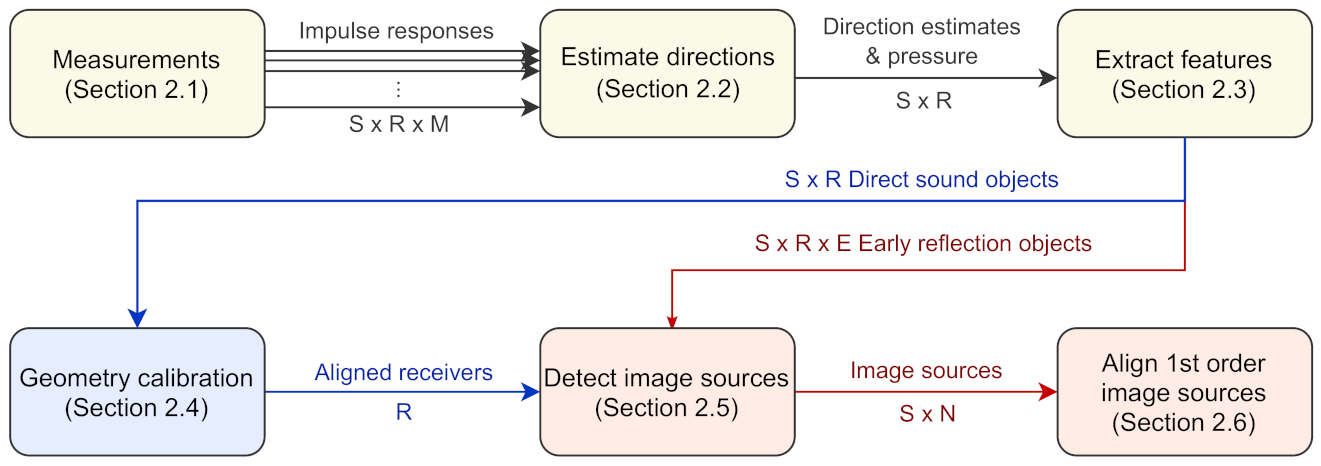
This section introduces the complete image source detection method illustrated in
Figure 1. The method is divided into six stages. The first stage involves conducting several SRIR measurements between multiple sources and receivers in the space of interest. Next, the measured responses are analyzed to obtain sample-wise direction estimates. In the third stage, direct sound and early reflections are identified in each response. Together with two features predicting reliability, each detected early reflection forms an early reflection object (ER object). For the fourth stage, the direct sound estimates are sent to the geometry calibration stage, which uses the data to determine the source-receiver layout. Once the layout is known, the fifth stage combines the ER objects to estimate image source locations of each sound source. In the last stage, multiple sources can be translated to the same location in order to visualize first order image sources even more clearly.
2.1. Measurements
The image source detection algorithm uses multiple SRIR measurements between different source and receiver positions. As in a single-microphone RIR measurement, a sound source plays a logarithmic sweep that is recorded by a receiver microphone array. The recorded signals are then convolved with the time-inverted sweep [
8] in order to obtain a set of RIRs from the array. One SRIR measurement therefore contains a set of RIRs between one source and one receiver position, which we call source-receiver measurement.
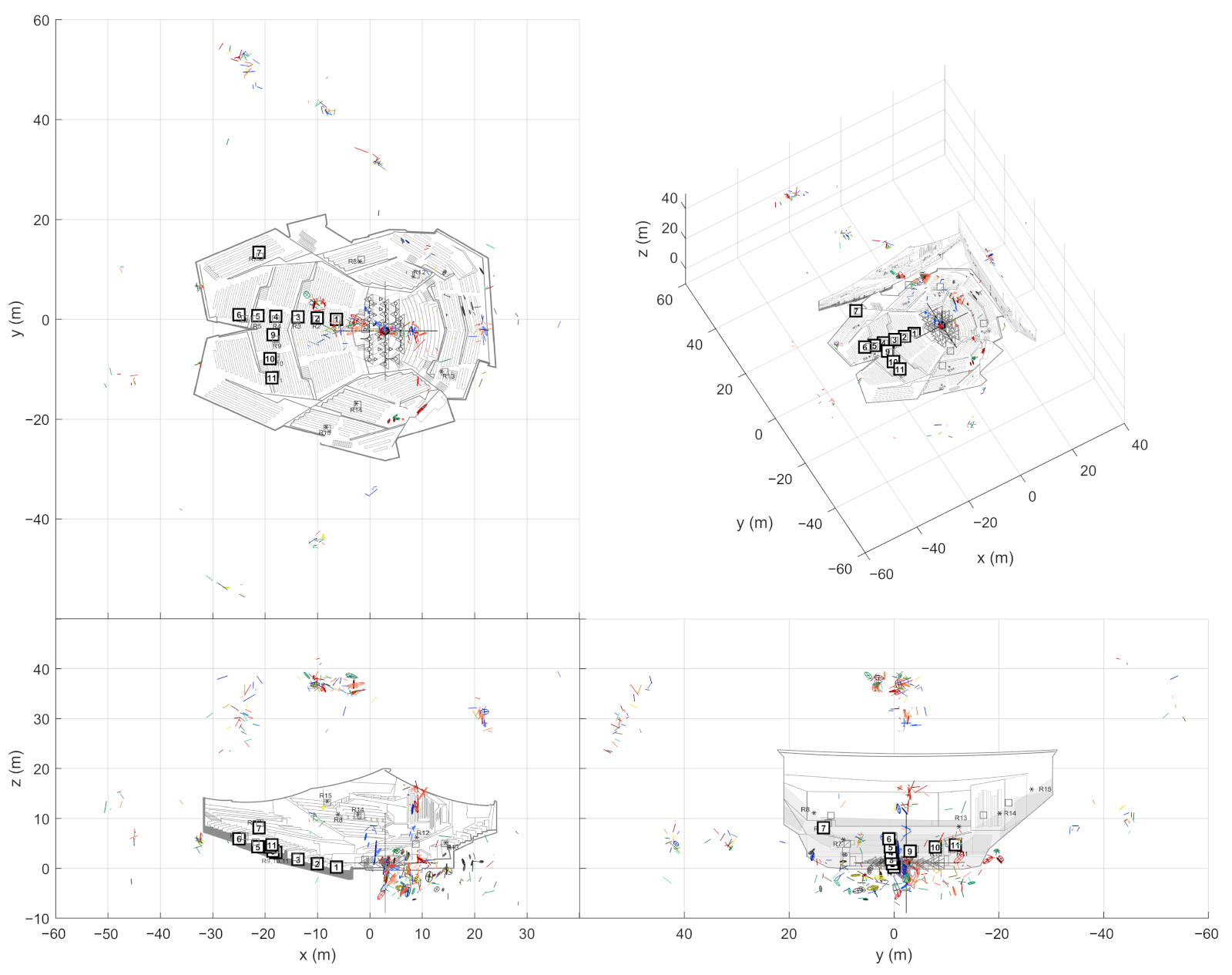
In the presented case studies (
Section 3), SRIRs have been measured with a GRAS 50VI-1 intensity probe. It consists of six omnidirectional capsules in a symmetric layout, with one pair of capsules on each coordinate axis. The probe is well suited for directional estimation based on the time difference of arrival (TDoA). The later processing stages also require an omnidirectional pressure response. The intensity probe obtains this response from the topmost microphone, although the most optimal solution would be to acquire it from the center of the array [
9].
Apart from performing the impulse response measurements themselves, one needs to perform a few geometrical measurements to establish the absolute frame of reference for geometry calibration (
Section 2.4). For the method described here, we use manually measured source positions and determine the receiver positions automatically from the direct sound estimates. If the source positions are kept static, one can move around the space with the receiver array freely. Best results have been observed when the loudspeaker is rotated to always point towards the microphone array. The geometry calibration algorithm used here can compensate for small inaccuracies in the receiver array orientation, but generally one should orient the microphone array consistently w.r.t. the frame of reference between measurements.
The geometry calibration algorithm does not require sample-wise synchronization of source and receiver. Anyhow, one can determine the measurement system delay (
Section 2.4.1) by measuring the input-output delay of the audio card, using a loop-back connection. But even after compensating this, there can still be some uncompensated system delay left, for example, due to digital signal processing in the amplifier and mechanical group delay in the loudspeaker. For this reason, the presented geometry calibration algorithm (
Section 2.4.2) does not use the measured time information directly, but attempts to estimate any constant delay. While even other methods could be used to improve synchronization during measurement, using legacy datasets clearly demands for the algorithm to solve this problem. To avoid another bias, one can approximate the speed of sound accurately enough from measuring the air temperature.
2.2. Estimate Directions
The directional estimation stage aims at determining the sample-wise Direction-of-Arrival (DoA) for each source-receiver measurement. To do so, we employ the directional analysis algorithm found in the SDM —a parametric SRIR processing method that uses a broadband directional estimate for every sample of the response. It has first been introduced by Tervo et al. [
1] and is distributed as a MATLAB toolbox [
10]. The algorithm can use any microphone array with at least four 4 microphones that are not in the same plane. In addition to the DoA estimates, also an omnidirectional response
h is needed for further processing. In case the used microphone array is comprised of omnidirectional receivers, simply one of the microphones is used. It is important to note that the particular estimation method operates immediately on the responses measured by a microphone array (A-Format). Nevertheless, also spherical harmonics domain (B-Format) responses could be processed by using a different directional estimator.
As an input, the directional analysis takes a set of M impulse responses measured by each of the R receiver microphone arrays in response to each of the S sources. The method then segments the responses into blocks of N samples with a hop size of one sample, and computes the cross-correlation between all microphone pairs. For instance, 15 correlation functions are obtained for the six-capsule open array used in this study. After applying Gaussian interpolation to each cross-correlation function, the location of its highest peak reveals the TDoA between the corresponding microphone pair. The DoA of the strongest sound event in the analysis block is computed from all TDoAs and the known microphone positions within the array. This way, each source-receiver measurement is associated with the DoA estimate for each sample n.
The minimum possible length of the analysis block is determined by the spatio-temporal limit
, that is, the time difference at which two reflections can still be separated. This limit is proportional to the largest distance within the receiver array
[
1]:
where
is the speed of sound inside the measured room. For instance, the measurement array in
Section 3.1 has
cm, which corresponds to a spatio-temporal limit of
ms. In practice, window sizes are selected to be even slightly larger
(with some constant
C) in order to stabilize the DoA estimates. Of course, the increased stability comes at the cost of a lower time resolution. This means that the selected block length limits the separability of reflections. Should two or more reflections arrive at the array within the same analysis block, they cannot be separated reliably.
Clearly, apart from the room geometry, the Time-of-Arrival (ToA) of reflections depends on the source and receiver positions. In rooms with simple geometries, one can try to set up sources and receivers so that at least the first-order reflections are separated well in time, and not more than one reflection falls within one analysis block. For example, if either source or receiver is placed at the center of the room, the symmetry axes of the room should be avoided for the counterpart. For rooms with more complex geometries, attempting such informed placement represents a larger effort and makes the measurement-based detection of reflections obsolete. Hence, it must be assumed that some individual reflections fall below the spatio-temporal limit and cannot be detected reliably, especially in small rooms. In these cases, one greatly benefits from the proposed measurement combination algorithm. By using multiple receiver positions, it is less probable that the same reflections overlap in all positions. This in turn increases the probability of detecting the true direction of each individual sound event.
2.3. Extract Features
Although the SDM analysis provides DoA estimates for all RIR samples, it does not reveal which estimates are reliable or belong to either the direct sound or early reflections. Both of these properties are hard to determine from the RIR and DoAs directly. For this reason, it is easier to first extract features from the SDM data and then identify the reliable sound events.
The potential early reflections are identified based on the sound level peaks in the RIR. To do this, one extracts two features at each peak, namely peak prominence and DoA stability. Then the peaks are separated to direct sound and early reflection peaks. Finally, the early reflection peaks are filtered according to a certain prominence and stability level. Only the peaks fulfilling both criteria are passed on to the later processing stages. Note that the number and the type of features predicting stability could easily be modified, for example to match a modified directional estimation algorithm.
Naturally, one needs to determine the sound level peaks first in order to extract features at their locations. The peaks are determined from sound level
L of the RIR, calculated as
where
n is the sample index,
h is the selected omnidirectional RIR and
is a Gaussian window of length
N.
is normalized so that the sum of its samples is equal to 1. The signal peaks are then defined as the samples that have higher value than their neighbors. Next, the noise is discriminated from the signal by applying an onset threshold, dropping any peaks from the beginning of the response that do not exceed a set sound level value. In this paper, the applied onset thresholds range between −16 and −10 dB w.r.t. the maximum sound level depending on the room.
The remaining peaks are then passed to the actual feature extraction. The first feature that is extracted is peak prominence (a.k.a. topographic prominence). It indicates how distinct the sound level peak is from the rest of the response. A prominent peak is either higher than any other peak or is separated from other prominent peaks by low signal values. In turn, peaks with low prominence either do not raise from the signal baseline much or are located at the slopes of more prominent peaks. In practice, peak prominence (in dB) is determined with the following procedure:
- 1.
Denote the current peak as A.
- 2.
Search for peaks preceding or following A that have higher sound level than A has. Select the closest two and denote those as B and C. In case there is no higher peak in either direction, select the start or end of the signal.
- 3.
Get the signal minima of intervals [B, A] and [A, C] denoted as B and C, respectively.
- 4.
Peak prominence of A is .
The second feature, DoA stability, represents how static the direction estimate is around the sound level peak. The DoA sample is considered stable if it stays within a certain angular range compared to the DoA at the peak. In other words, it indicates that the peak likely belongs to a single plane wave, that is, one specular reflection. On the contrary, unstable estimate hints that the DoA is affected by multiple sound events at the same time.
The DoA stability is calculated by first comparing the central angle between the DoA estimate of the sound level peak
and the DoAs right before and after it. Next, the angle is compared to a pre-defined angle threshold in order to get a binary result. In short, these two steps can be presented together as follows:
where
is the
nth DoA sample in the impulse response and
is the user-selected angular threshold (in this paper,
). The selected samples then form a stable sample interval. The samples in the interval stay within
and have no 0-valued samples between them and the peak. The DoA stability descriptor is equal to the duration of the stable sample interval.
After calculating the features, the sound level peaks and their feature descriptors are divided into direct sound and early reflections. Direct sound is selected from the peaks that arrive up to 1 ms after the first detected peak. By considering several peaks, the direct sound can be detected robustly even if the direct sound would not be the highest pressure peak in the response, which can easily happen if the source is pointing away from the array. The rest of the direct sound peaks are discarded, and the peaks after 1 ms are treated as early reflection candidates.
Next, the early reflection candidates must meet certainty thresholds for peak prominence and DoA stability. Selecting the two thresholds require a trade-off. Higher thresholds filter out more false positive detections, while lower thresholds find less prominent early reflections. For peak prominence, a suitable threshold was found to be 10 dB, whereas the DoA stability threshold was set to a 50 s. These thresholds were found to reduce noise drastically while still maintaining a reasonable sensitivity for less prominent early reflections. Finally, if a peak exceeds both limits, it is assumed to belong to an early reflection.
In the last step, the feature descriptors are combined with additional data that describe other sound event properties. The additional data consists of the ToA, DoA and sound level of the peak. The DoA is an average of the DoA samples in the stable sample interval, which is expected to reduce the measurement noise in the location estimate. The described data form either a direct sound or an ER object, depending on what kind of sound event it is describing. In the following stages, direct sound objects are utilized to align the measurements and ER objects to find the actual image sources.
2.4. Geometry Calibration
The previous sections have described how direct sound and early reflection estimates are extracted from each source-receiver measurement. Up to this point, the data from each receiver is presented in its own coordinate frame. Yet, in order to estimate the image source positions from multiple measurements, the data needs to be transformed into a global coordinate frame. To do so, one needs to have knowledge of the receiver orientations and positions in the global frame.
There are several options for identifying the receiver layout, requiring different amounts of information. On one hand, there is the option to measure all positions and orientations manually. For a large number of receivers, this approach is laborious and susceptible to measurement errors. In our experience, measuring the array rotation with high accuracy is especially difficult in practice. On the other hand, there are fully automatic microphone array geometry calibration approaches using, for example, DoA, ToA or TDoA information [
11]. If the measurement system delay was not determined or contains errors, the ToA is easily biased. However, an unbiased DoA estimate of the direct sound from each source to each receiver is readily available, so one could use DoA-based microphone array calibration methods. Algorithms for calibration in 2D were presented in [
12,
13], and could be extended. Such DoA-based approaches typically rely on non-linear least squares optimization and have strong similarities to photogrammetry. There, multiple pictures of the same scene allow for creating a 3-dimensional reconstruction, which requires estimation of the camera positions and orientations. The advantage of DoA-based automatic calibration is that it is sufficient to measure 3 source or receiver positions manually. Moreover, it does not depend on ToA information, which might suffer from the mentioned systematic biases.
For the data presented here, we applied an approach that relies on measuring only the source positions manually. In practical measurements, this requires significantly less effort than measuring all positions. The receiver positions are computed from the direct sound DoAs.
Apart from the receiver positions, the geometry calibration stage also determines the ToA bias explicitly. This is not only important for the geometry calibration itself, but also for the image source estimation stage, as the biases described next apply to all sound events.
2.4.1. Time-of-Arrival Bias
Knowing the ToA enables estimating the distance of a sound event. In this way, the ToA of the direct sound helps to determine the array geometry. Additionally, the ToAs associated with the ER objects are ultimately used to estimate the image source positions in space. However, determining distances based on the ToA data is easily biased by errors in the assumed speed of sound
and any uncompensated measurement system delay
. Depending on the actual distance of the sound event
and the speed of sound
during the measurements, the ToA of the sound event
will be registered as
where
is the measurement system delay biasing the ToA. When translating this measured ToA back into its associated travel distance, using the assumed speed of sound
c will in turn bias the travel distance estimate
:
Clearly, the errors have different effects on the reconstructed travel distance . While the measurement system delay adds a constant distance bias, a ratio of assumed vs. real speed of sound scales the distance.
The scale of the two biases is very different. Usually, the speed of sound deviation does not affect the result much. By default, the SDM toolbox [
10] fixes
c to 345 m/s, while
varies between 343.8–347.2 m/s in regular room conditions (20–25.5
C, 1013.25 hPa, 50 % Rh) [
14]. This means that the deviation between them varies only
, which is small w.r.t. the speed of sound itself. This error is negligible for small rooms, but it starts to take effect with longer distances. For example, the farthest distance seen in the concert hall data presented in
Section 3 is roughly 35 m, which would result in a difference of about
. In contrast to that, the measurement system delay heavily impacts the estimation of small distances. For instance, a 2 ms delay on the signal onset corresponds to roughly a 69 cm offset on the measured sound event distance, independent of
.
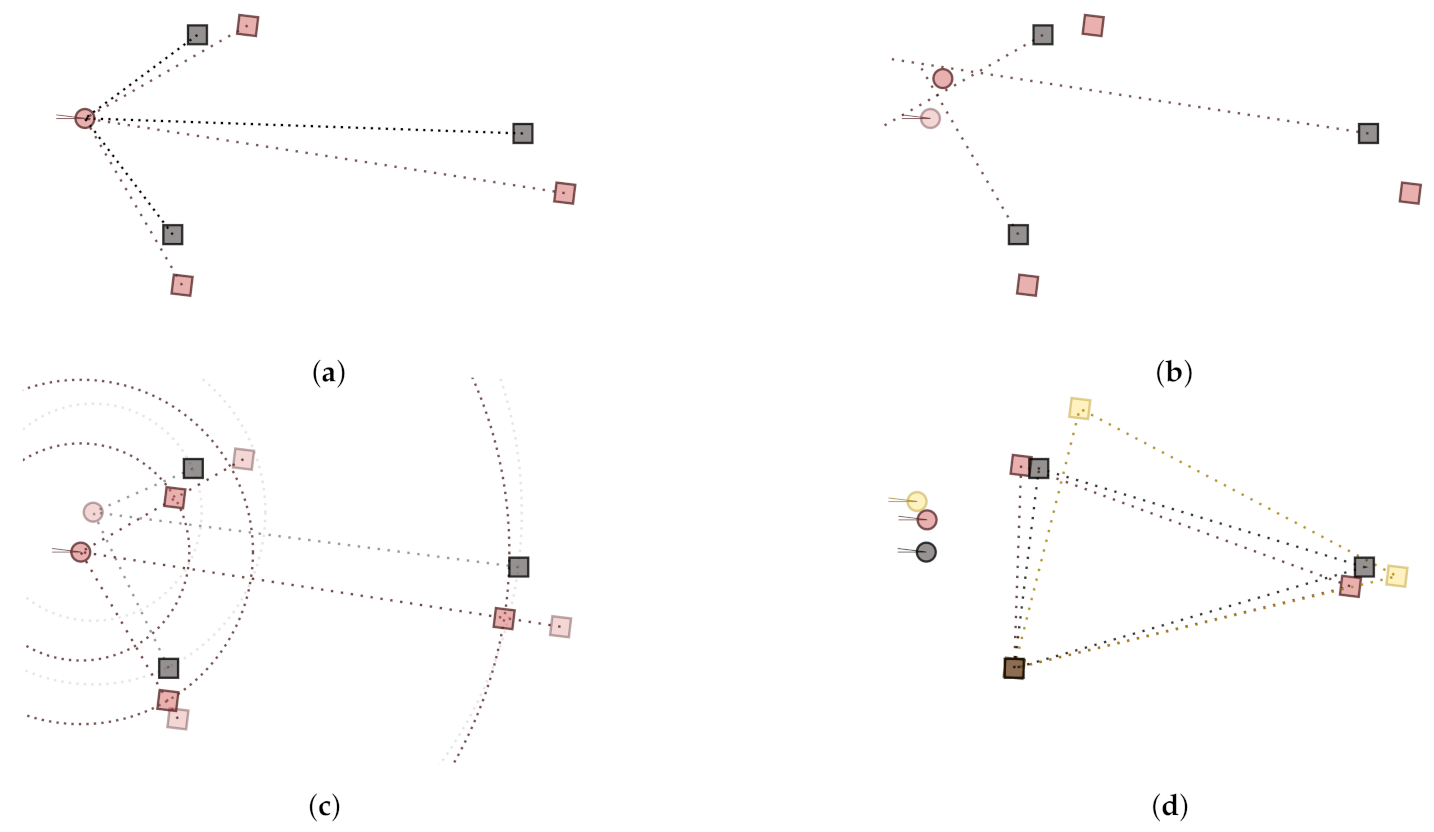
The biased travel distance causes position-dependent warping of the detected measurement layout. This phenomenon has been illustrated in
Figure 2. There, three receivers (red, blue and yellow circles) have been set up to measure three sound sources (grey rectangles). Each receiver has managed to capture the DoAs correctly, but the ToA has been biased by constant delay of the sound sources. Therefore, each receiver has located the sound source further away from the measurement point than what it actually is (colored rectangles). This affects the detected shape of the sound source array. For this very reason, one cannot apply a simple rigid-body fit to find the receiver array orientations, which can only identify a common rotation, translation and scaling. When the rigid-body fit finds the optimal rotation and translation based on the warped array, the position and orientation of the receiver are not accurate. Accordingly, it is necessary to compensate for the delays first.
2.4.2. Delay-Compensated Fit
Delay-compensated fit is a method that transforms receiver data to a common coordinate frame. The method consists of two steps. In the first step, one uses the estimated direct sound DoA data and the manually measured source reference positions to estimate the measurement system delays. With the delays at hand, one then approximates the corrected sound source positions relative to each receiver. The second step then applies rigid-body fit to these positions to approximate the receiver orientation. The orientation in turn affects the DoAs, which enables iteratively improving the result.
The first step of the delay-compensated fit is illustrated in
Figure 3. As a starting point, one knows the reference sound source positions (in grey). Slight rotation of the receiver during measurement and the measurement system delay causes the estimated positions (red squares) to be mislocated from their actual positions.
There are two steps in approximating the measurement system delay. The first step estimates the receiver position from the direct sound DoAs. This is done by generating lines from source positions and their corresponding DoAs and by resolving the closest point to those lines [
15]. The second step then approximates the measurement system delay
based on the found receiver position as
where
and
are the approximated positions of sound source
i and receiver
j, receiver
j and sound source
i, respectively;
is the reference position of the sound source
i; and
c is the assumed speed of sound. Removing these approximated delays practically sets the distance of the approximated source to correspond to the reference source distance from the approximated receiver position. This in turn nudges the detected source array shape closer to the actual shape, see
Figure 3. The corrected shape effectively improves the chances to fit the array correctly with the rigid-body fit.
The second step applies the rigid-body fit to the distance-corrected measurement data. With rigid-body fit we refer to partial Procrustes analysis, which determines rotation and translation between two point sets [
16]. Reorienting the receiver according to the result leads to rotation of all associated DoA data, which can be used in the next iteration to approximate the measurement system delay again.
Undoubtedly, there may also be errors in the measured DoAs that have to be treated accordingly. Here, the treatment is implemented by applying Monte Carlo cross-validation. Instead of fitting the data w.r.t. all reference source positions, only a subset of positions are used at a time. Each receiver is fitted multiple times to three or more randomly selected reference positions. The results form fit candidates that are then evaluated by the error measure
. It compares the source positions implied by the fit to the position that were measured manually
Finally, the fit candidate with the lowest is selected as the actual position and orientation of the source.
2.5. Detect Image Sources
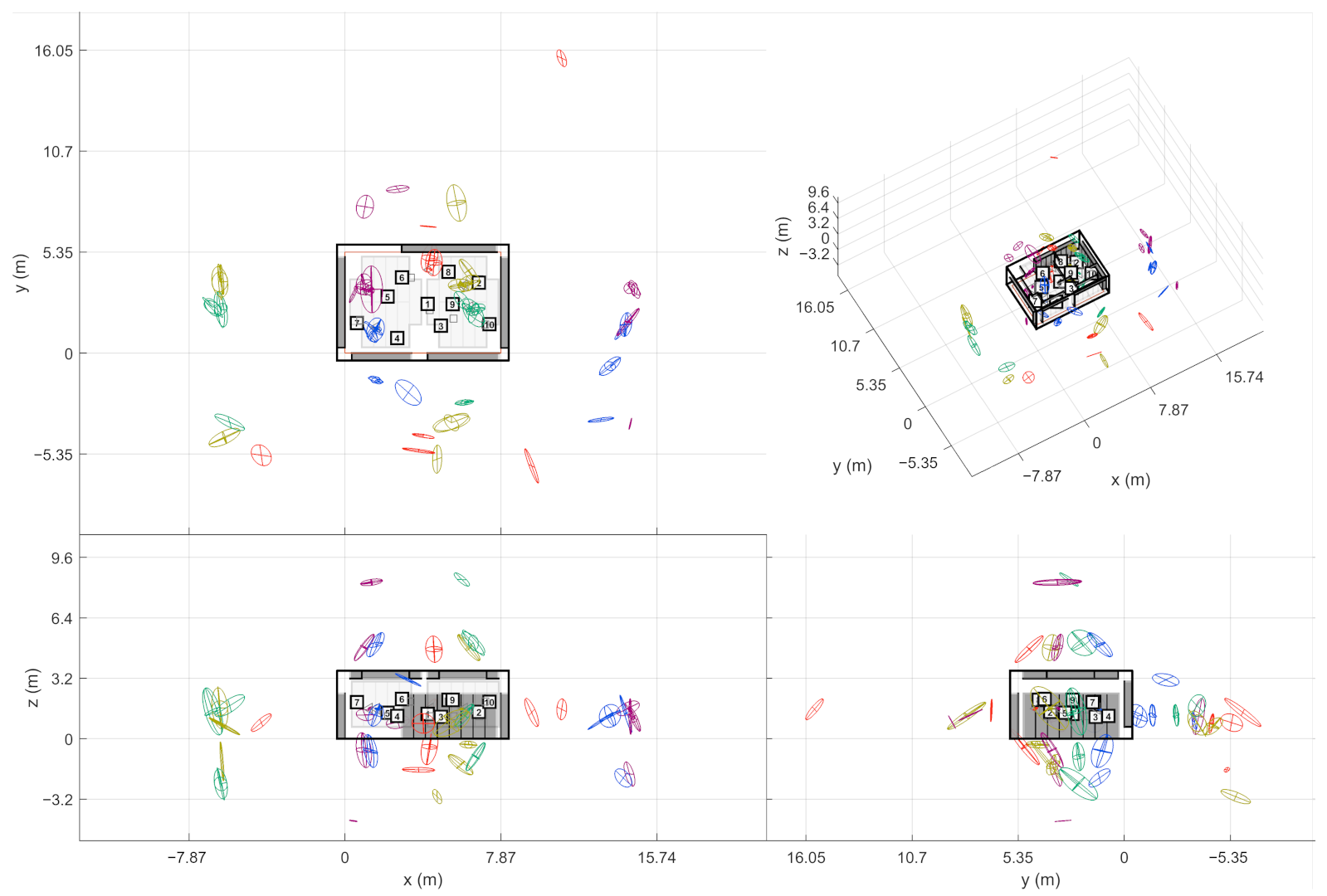
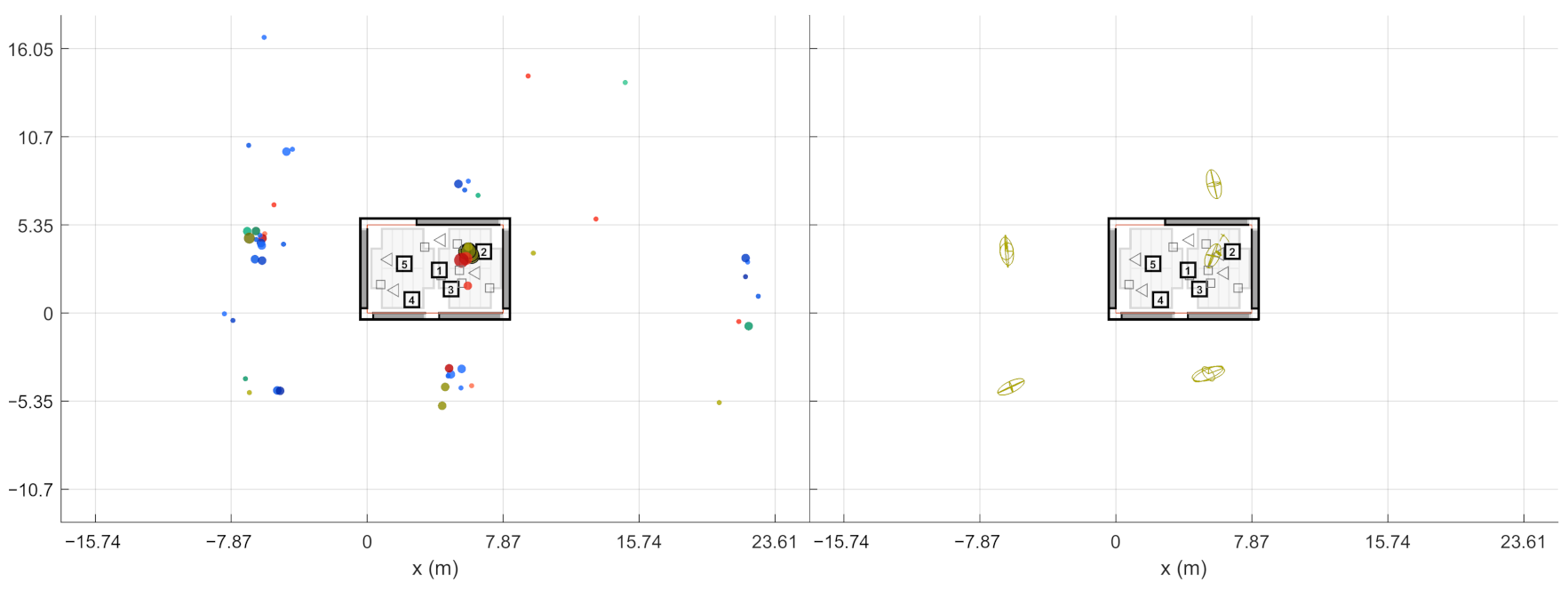
At this point, the source-receiver measurements have been aligned to the world coordinate frame. This way the extracted ER objects are also comparable w.r.t. each other. In other words, the ER objects from one sound source should be located close to each other if they have been reflected from the same planar surface. In theory, the ER objects from multiple receivers should gather around the approximate image source positions when presented in the common coordinate frame. However, not all receivers report the same image sources, and some of the objects might still be false detections, as shown on the left in
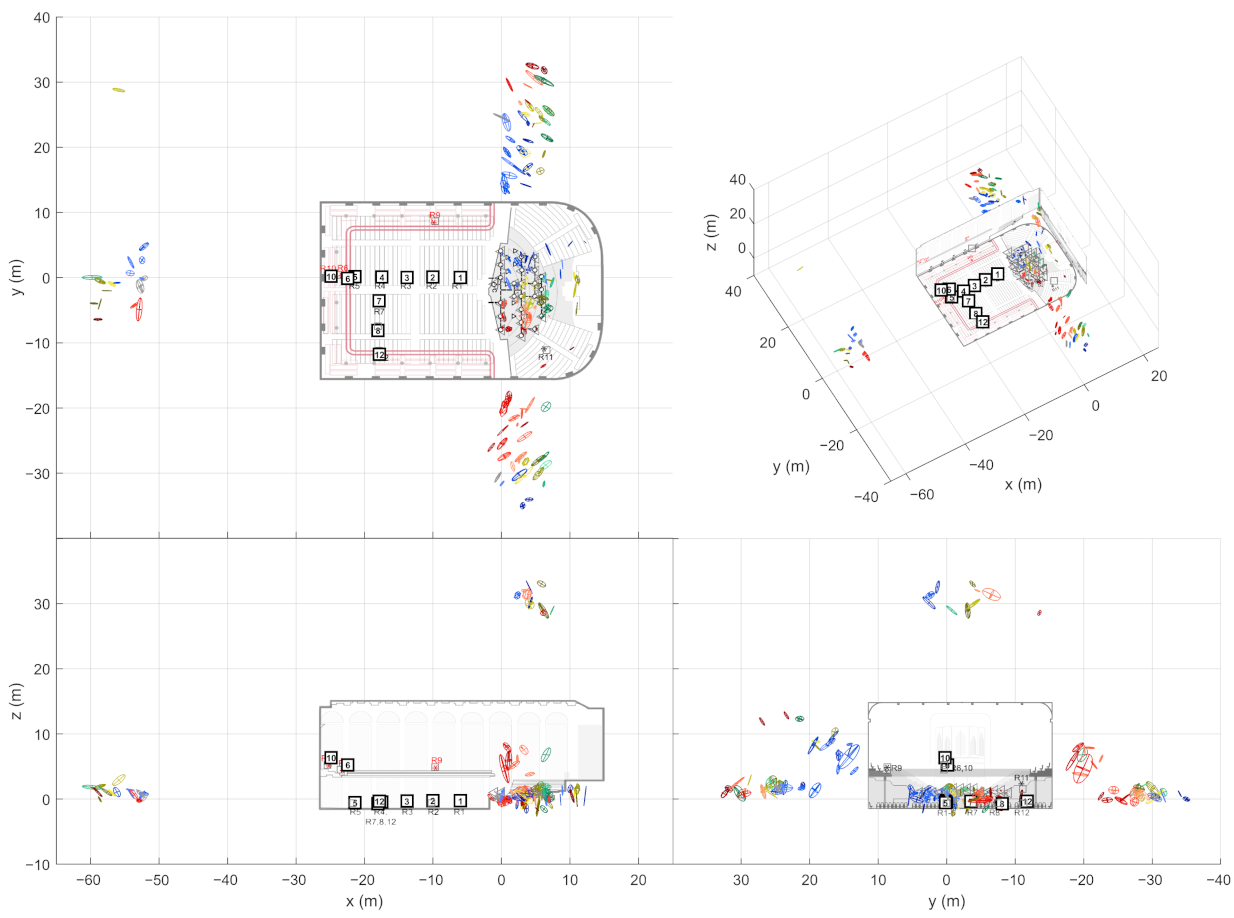
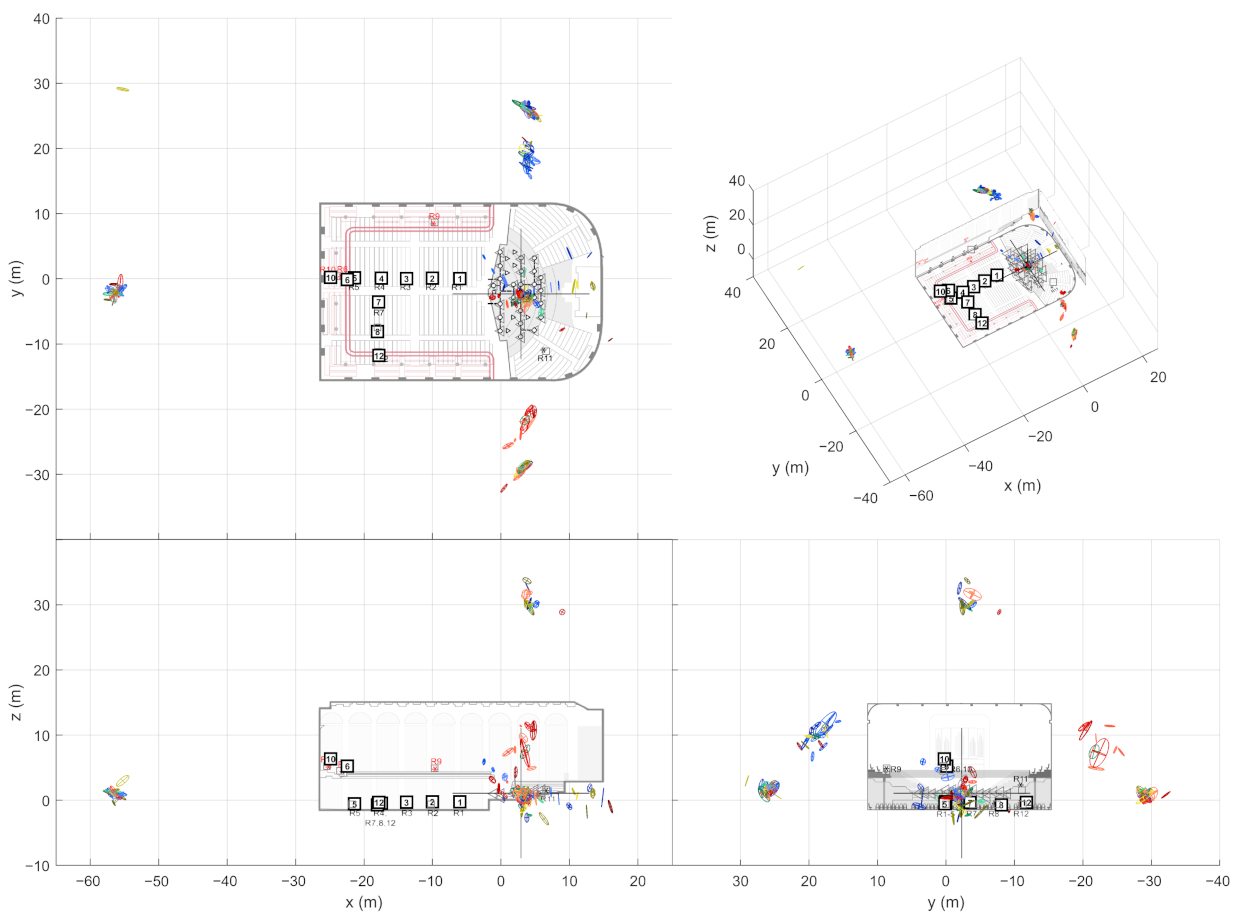
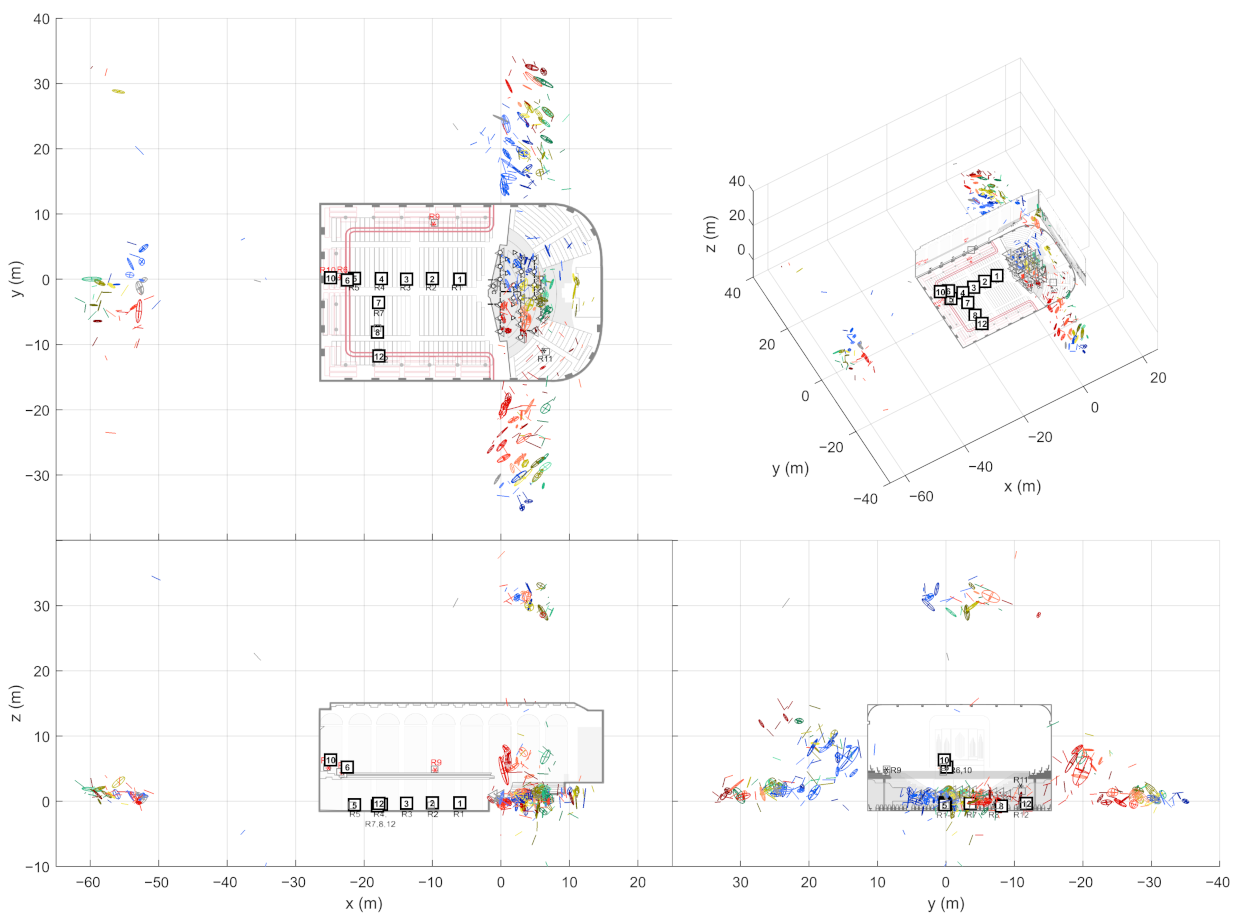
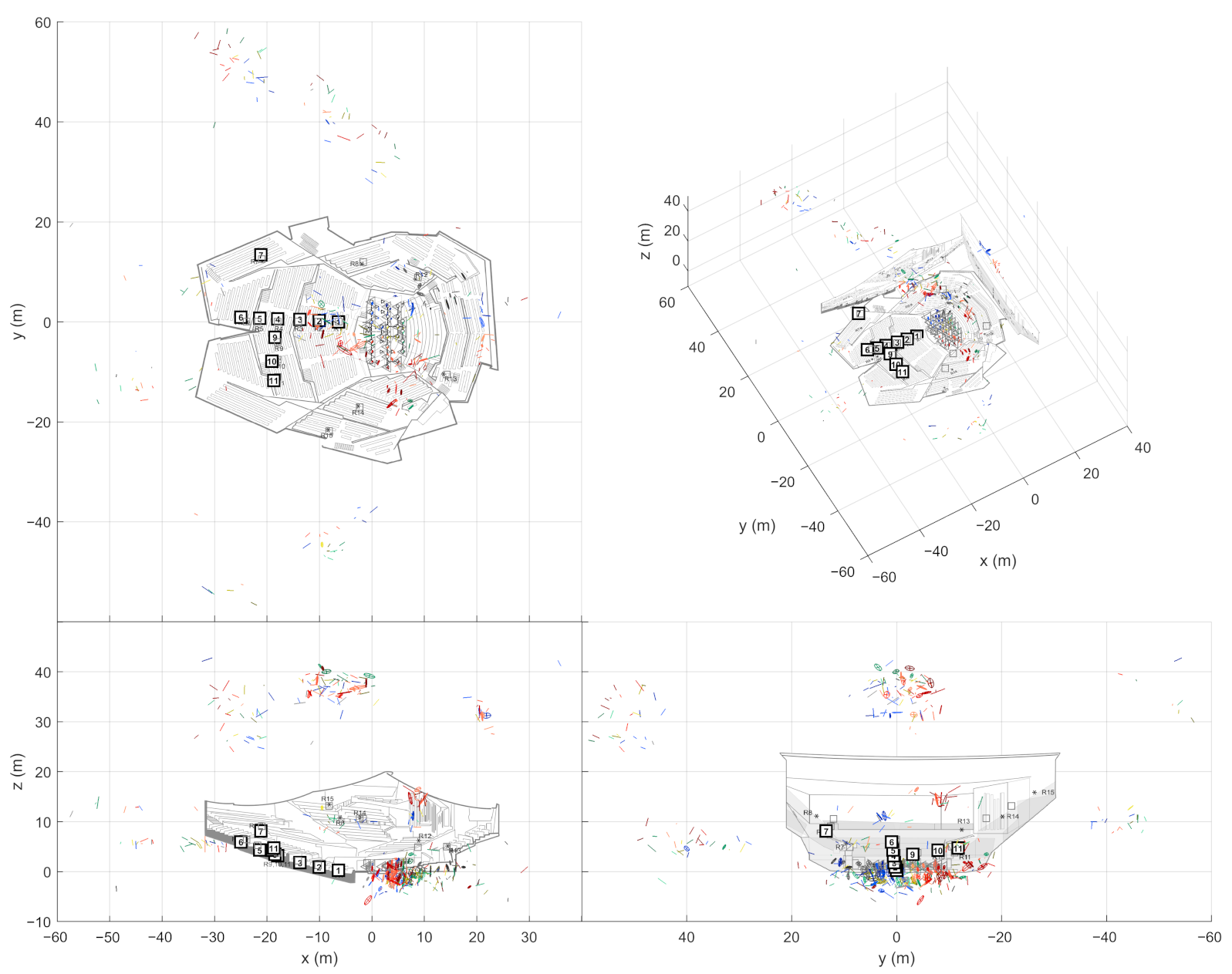
Figure 4. As shown on the right, combining the receiver data not only allows finding more reflections than it is possible with a single measurement, but also manages to filter out additional false detections. Therefore, the next step is to detect image sources by clustering the extracted ER objects.
The stage presented here aims at creating multivariate Gaussian distributions out of ER objects. For each sound source, the ER objects from associated source-receiver measurements are clustered with the so called Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm [
17] (grouping distance 1 m (Euclidean), min. 2 neighbors to consider as a core point). After this, each cluster selects one ER object per receiver that has the highest sound level. If the cluster still contains ER objects from a defined number of receivers, they form an image source. The required number of receivers is an important tuning parameter that allows a trade-off between detection noise and precise image source locations.
The found image source is presented as a multivariate Gaussian distribution that is weighted by DoA stability of the ER objects. The distribution mean is considered as the actual image source location and the covariance as the reliability of the location estimate. This way, each image source is not only presented as a point in space but as a volume where the actual image source most probably resides in.
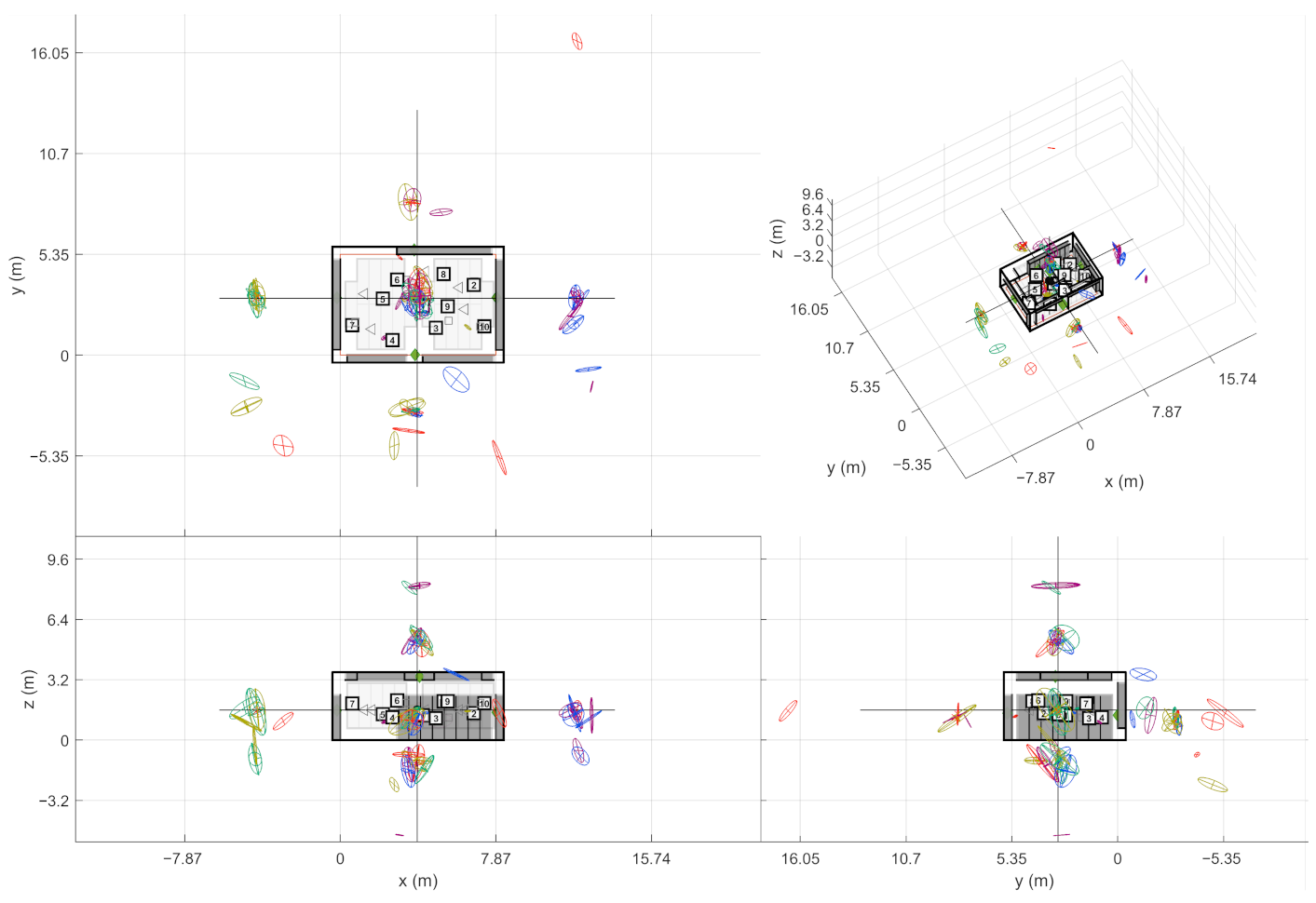
2.6. Align 1st Order Image Sources
The algorithm has now found the image sources for all the sound sources in the scene separately. However, when the results are plotted, the multiple source positions also spread the image sources to a large volume. This may merge two image source locations that are located close to each other, effectively obscuring some of the potential findings from plain sight. For visualization purposes, it is therefore beneficial to translate the image source data to share a common source point. By doing this, single image sources are occupying a smaller volume, effectively improving separability.
The image sources are translated in the following way. First, one sets the origin of the new coordinate system; here, the origin is selected as the mean of the measured sound source positions. The origin determines the translation
for each sound source position
. The translated image source positions
are then calculated as follows:
where
is the original image source position and
is the unit vector between
and
. In other words, one assumes a reflecting wall between the real source and the image source. When the real source is moved, the movement towards and away from the wall is reflected for the image source while the parallel movement stays unaffected. The operation is also identical to assuming that all found reflections are first order image sources. Even though this is not always the case, the real first order image sources are hypothesized to converge to a clear reflection groups.