Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment
Abstract
1. Introduction
2. Numerical Procedure
2.1. Numerical Method
2.2. Geometry, Computational Domain and Mesh
2.3. Fluid and Solid Properties
2.4. Boundary Conditions
2.5. Data Evaluation
3. Results and Discussion
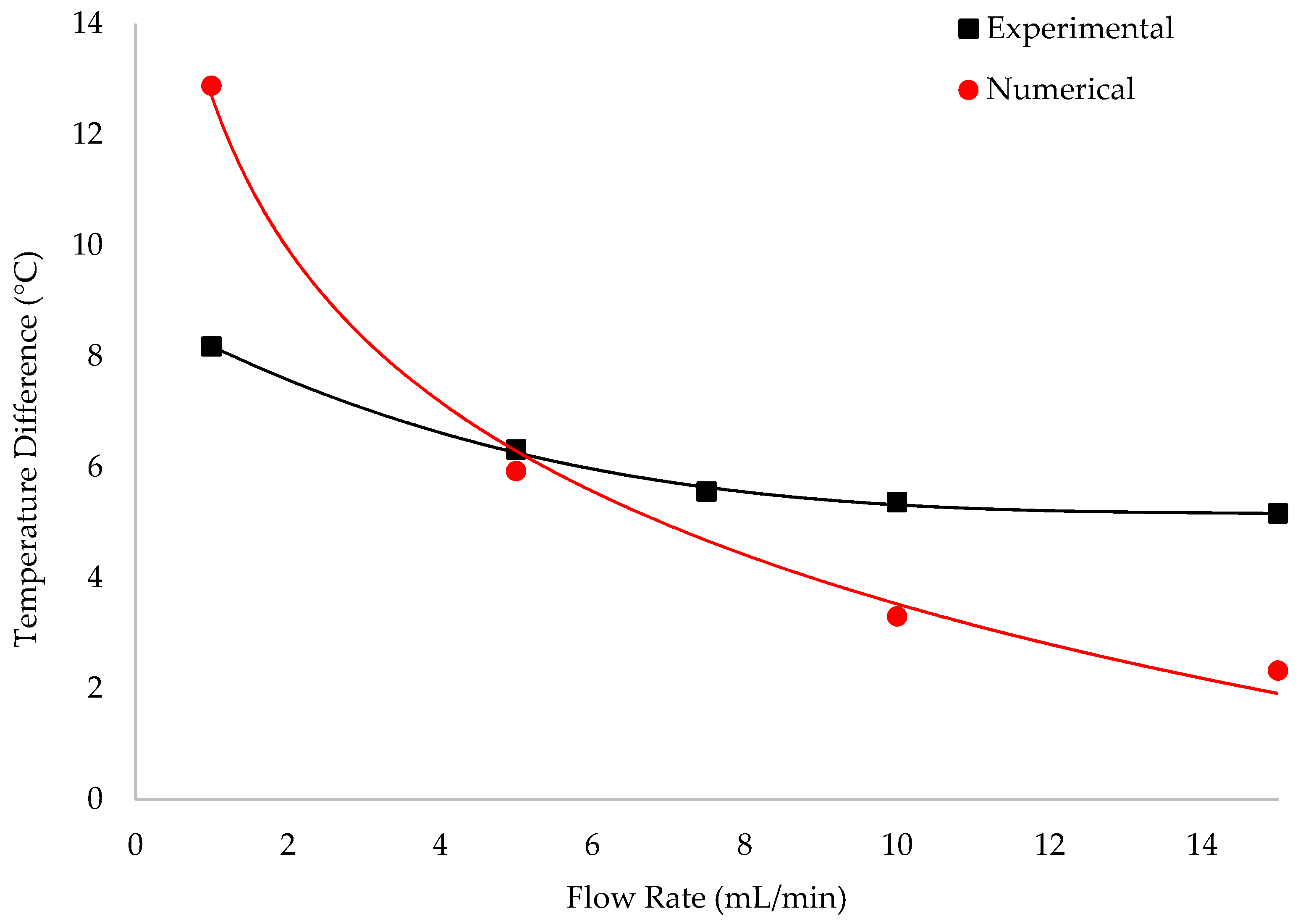
3.1. Comparison between the Numerical and the Experimental Results
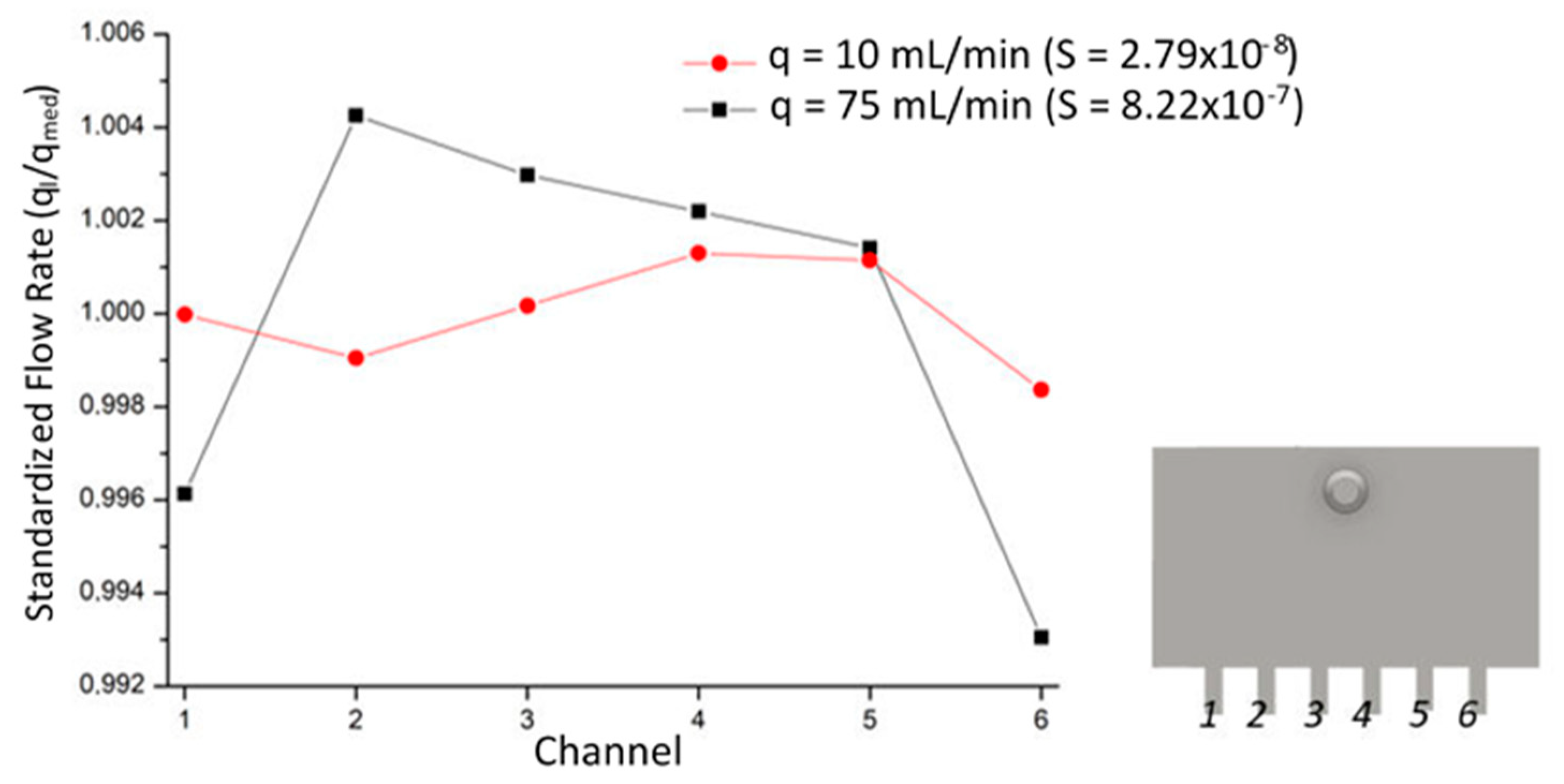
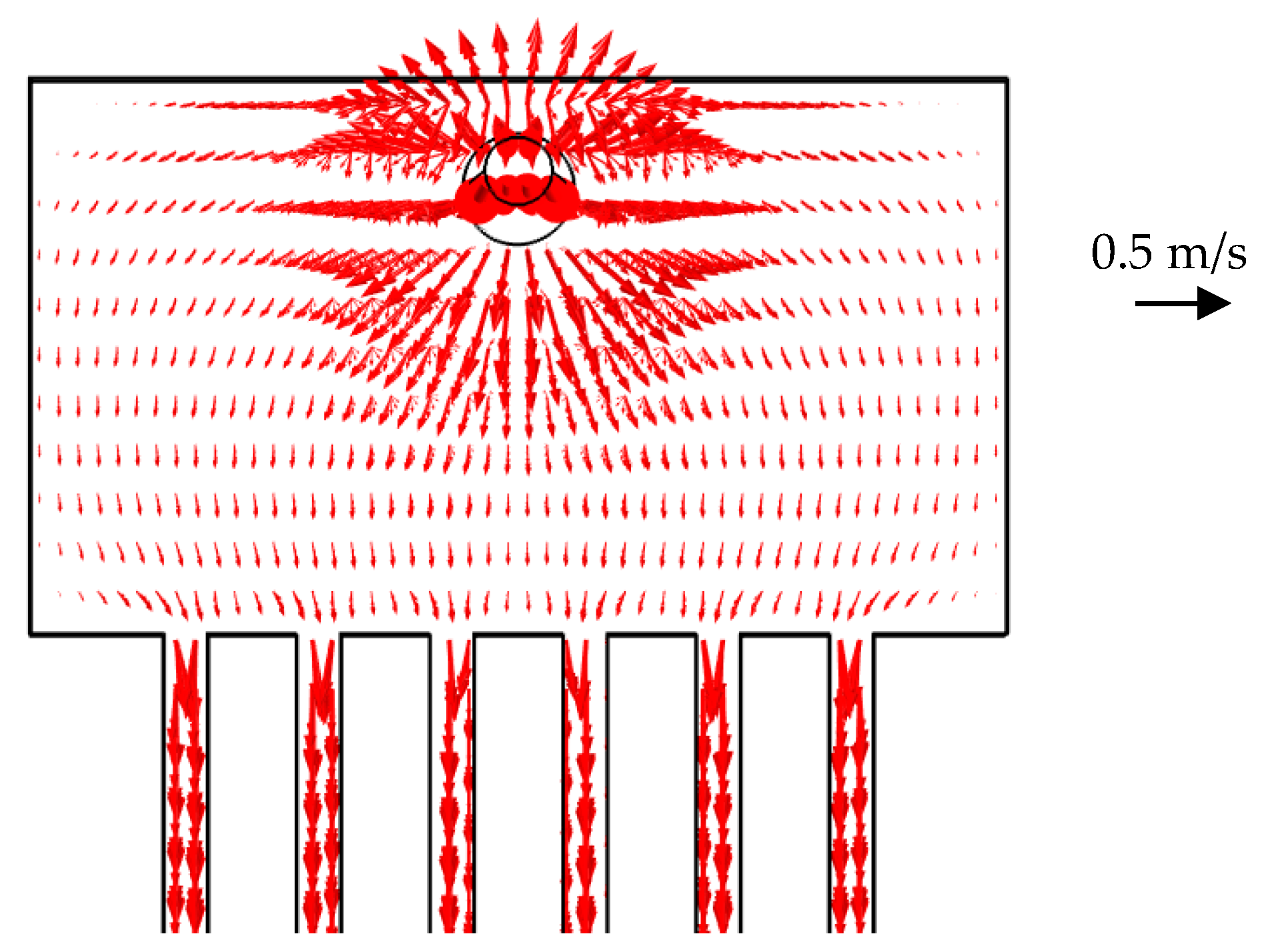
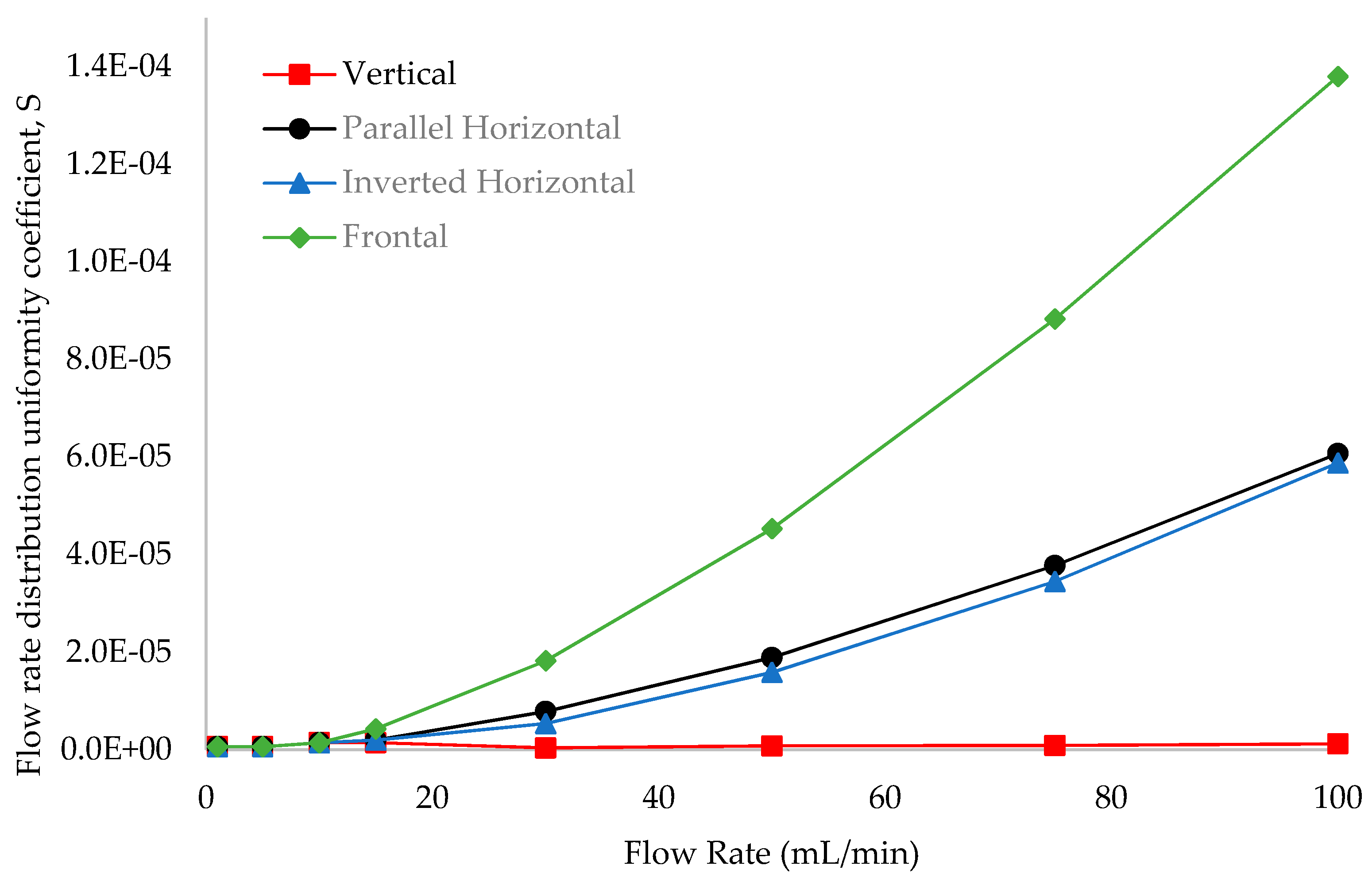
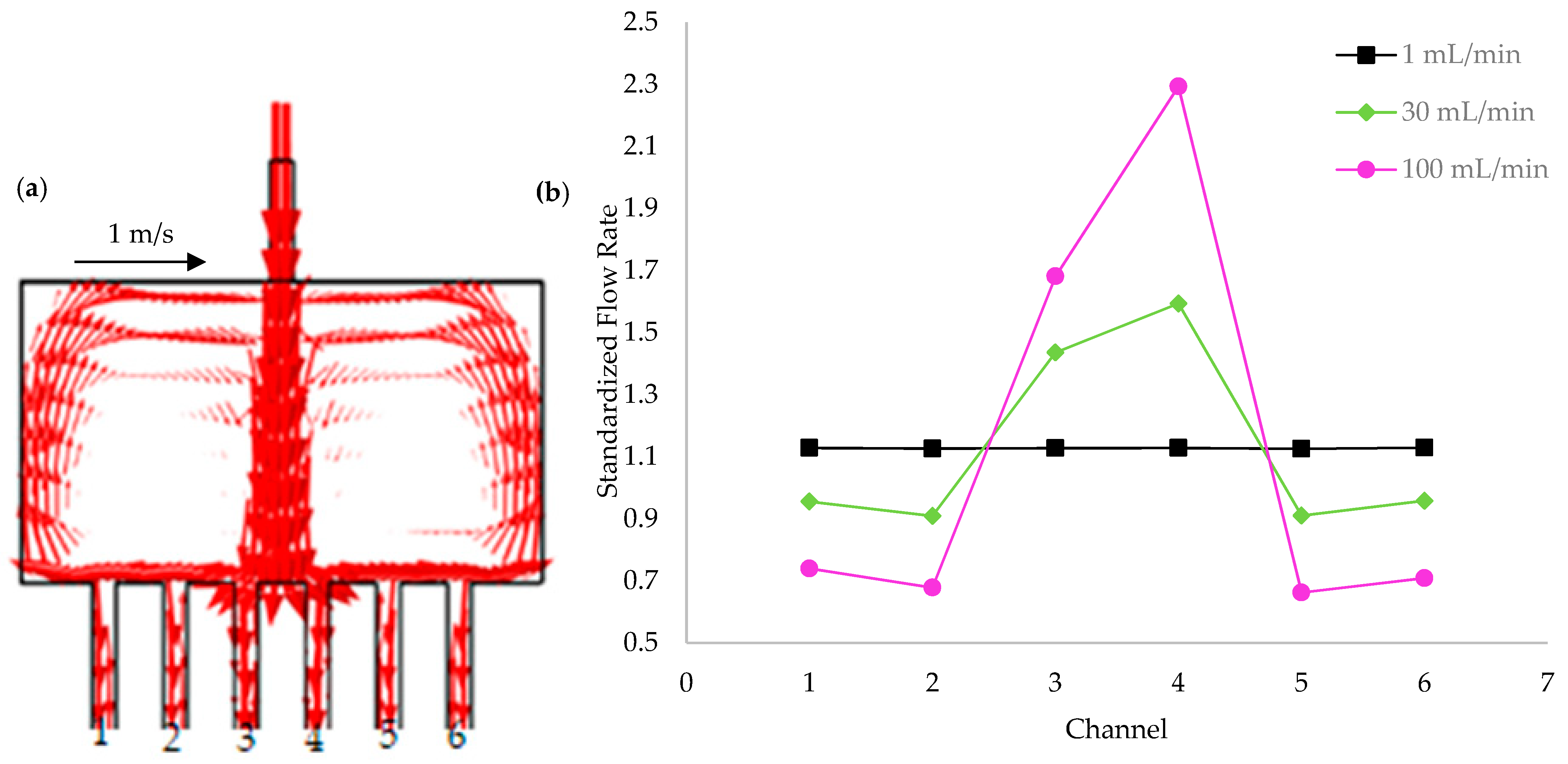
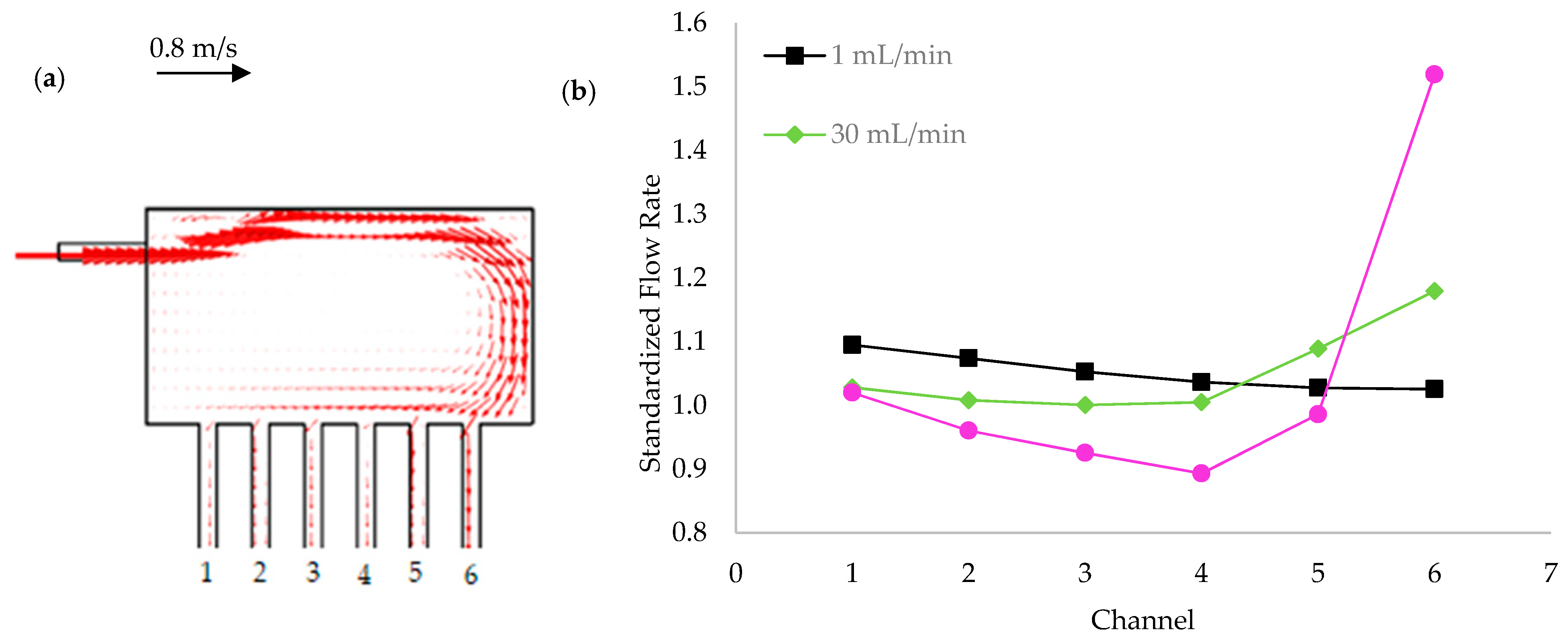
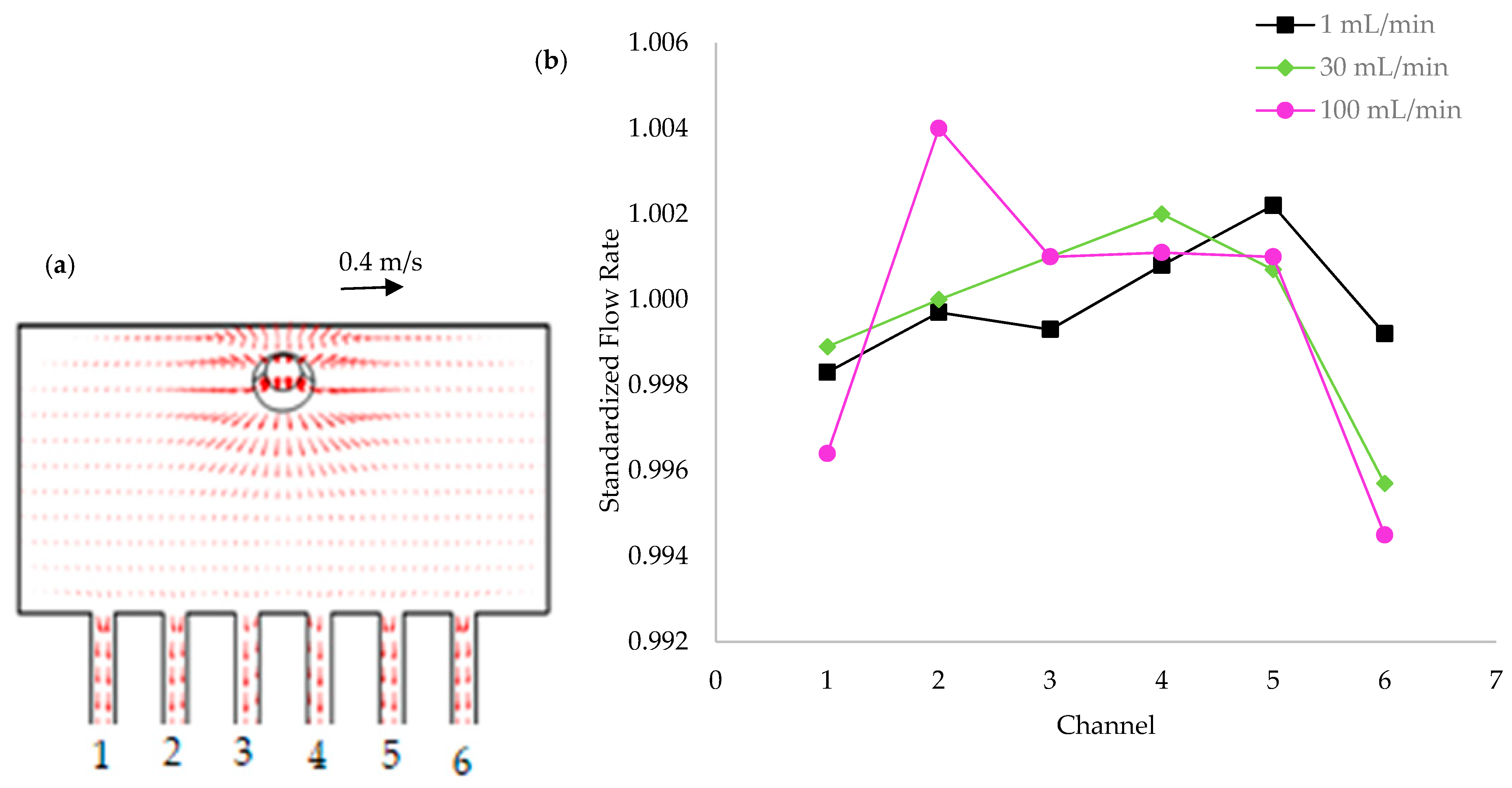
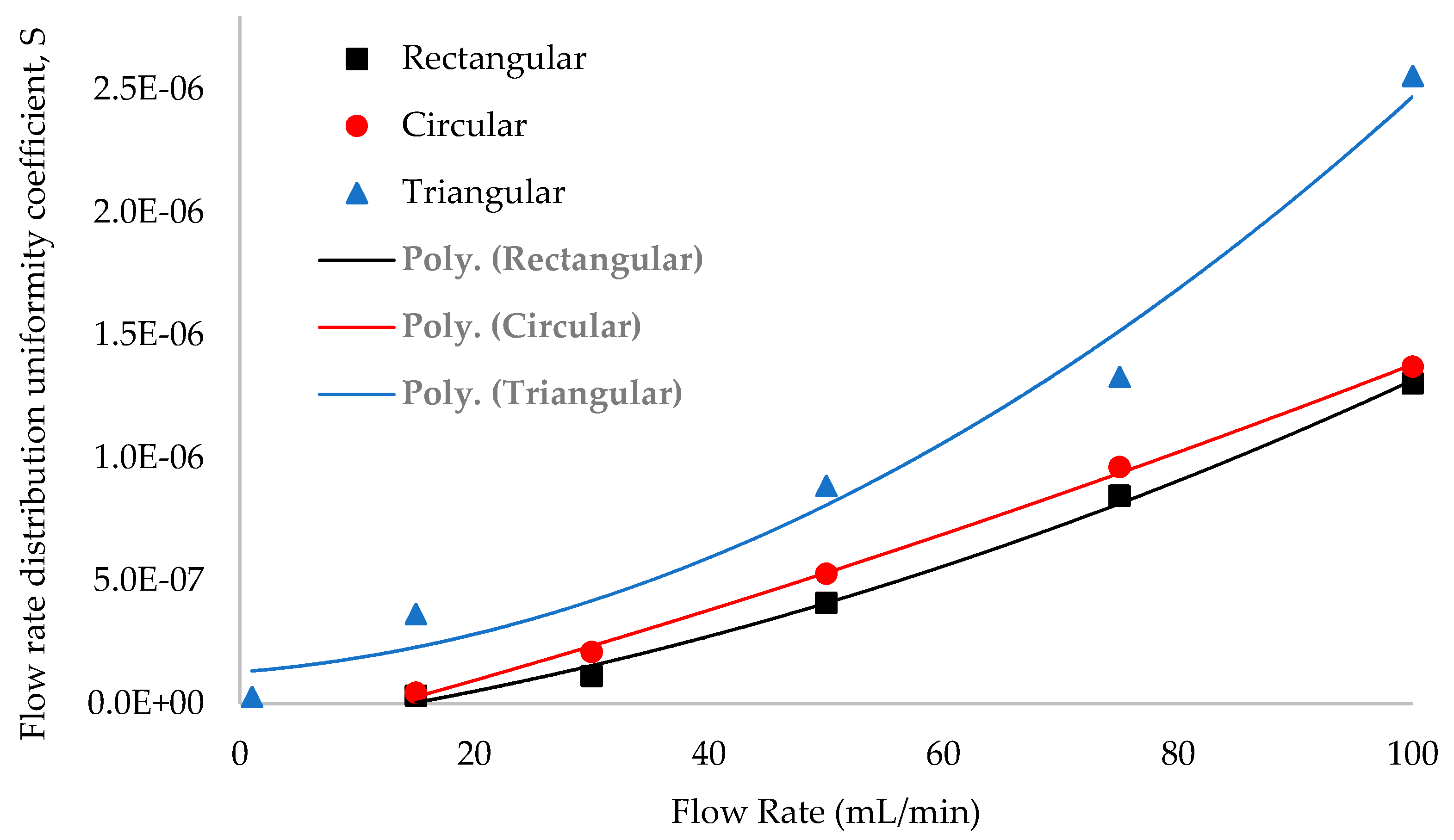
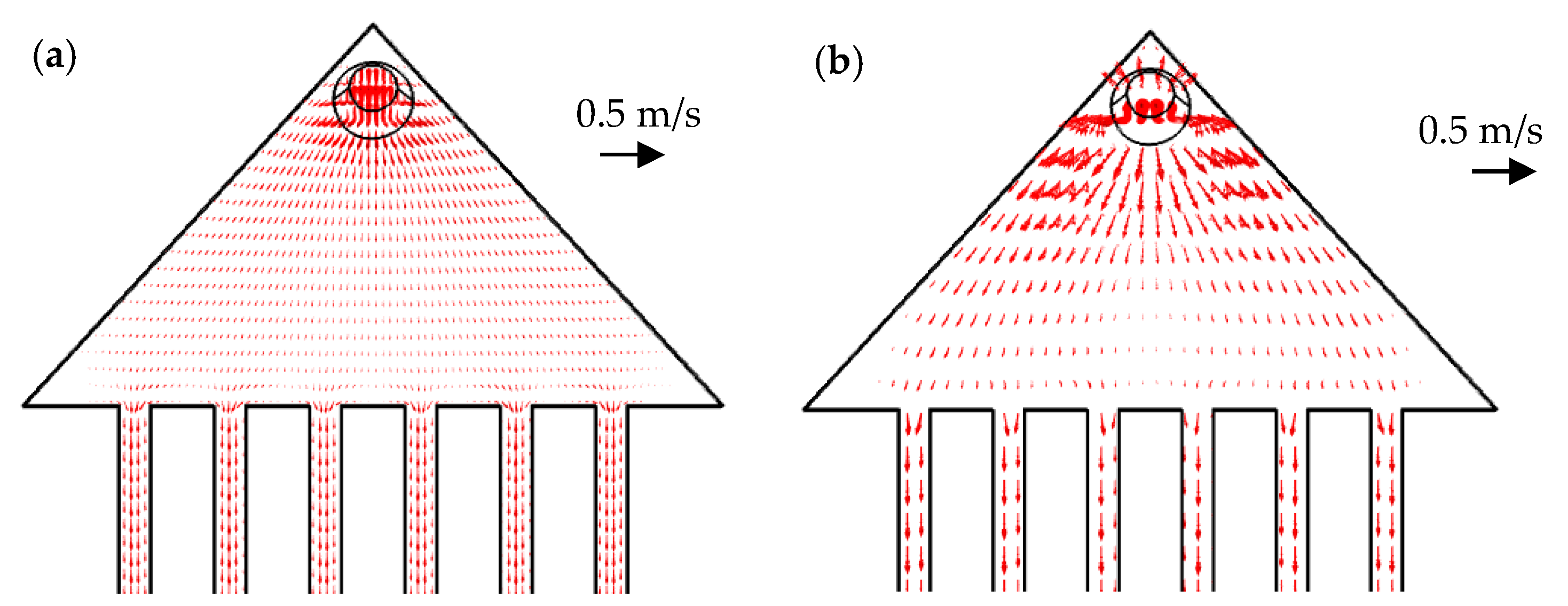
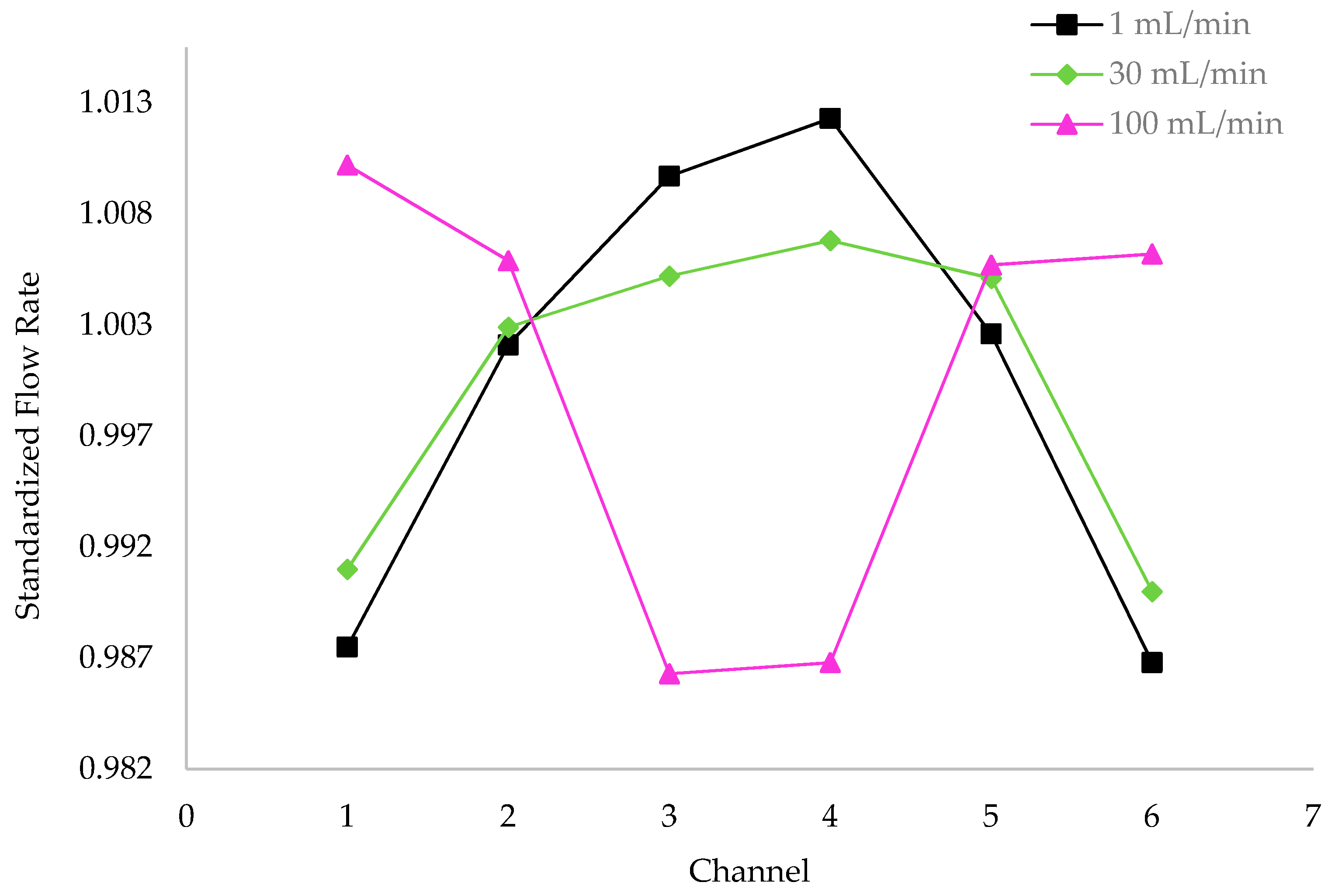
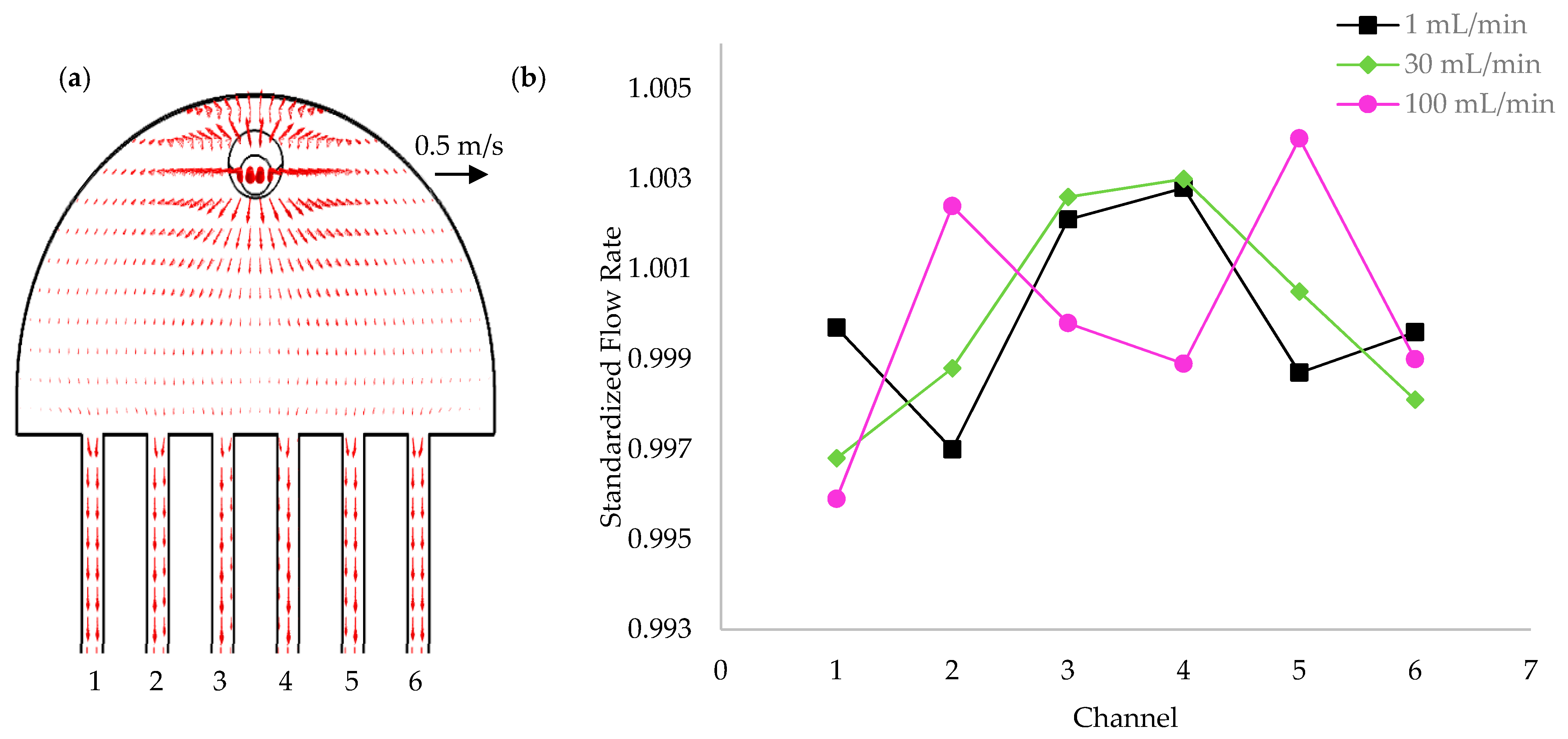
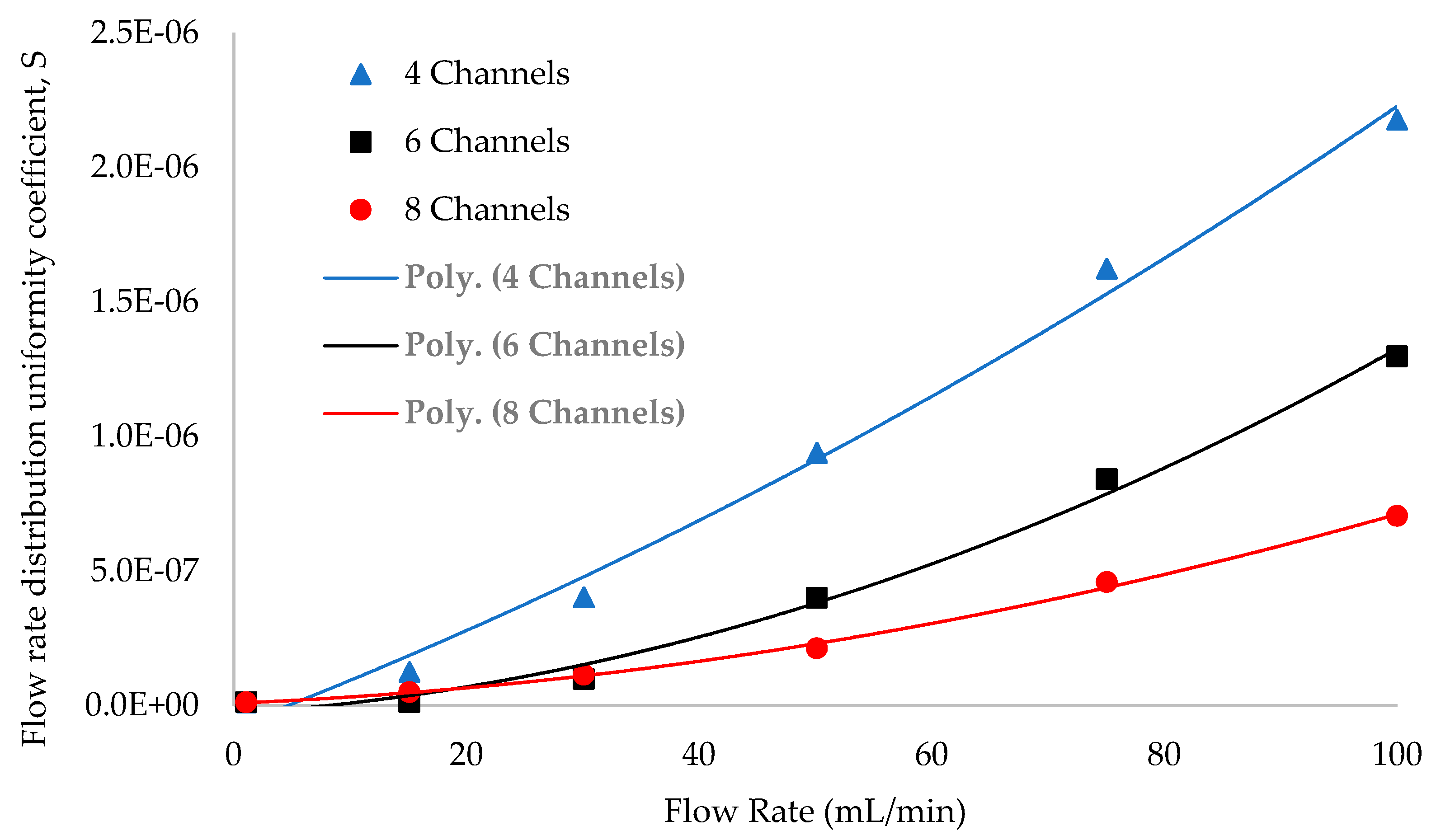
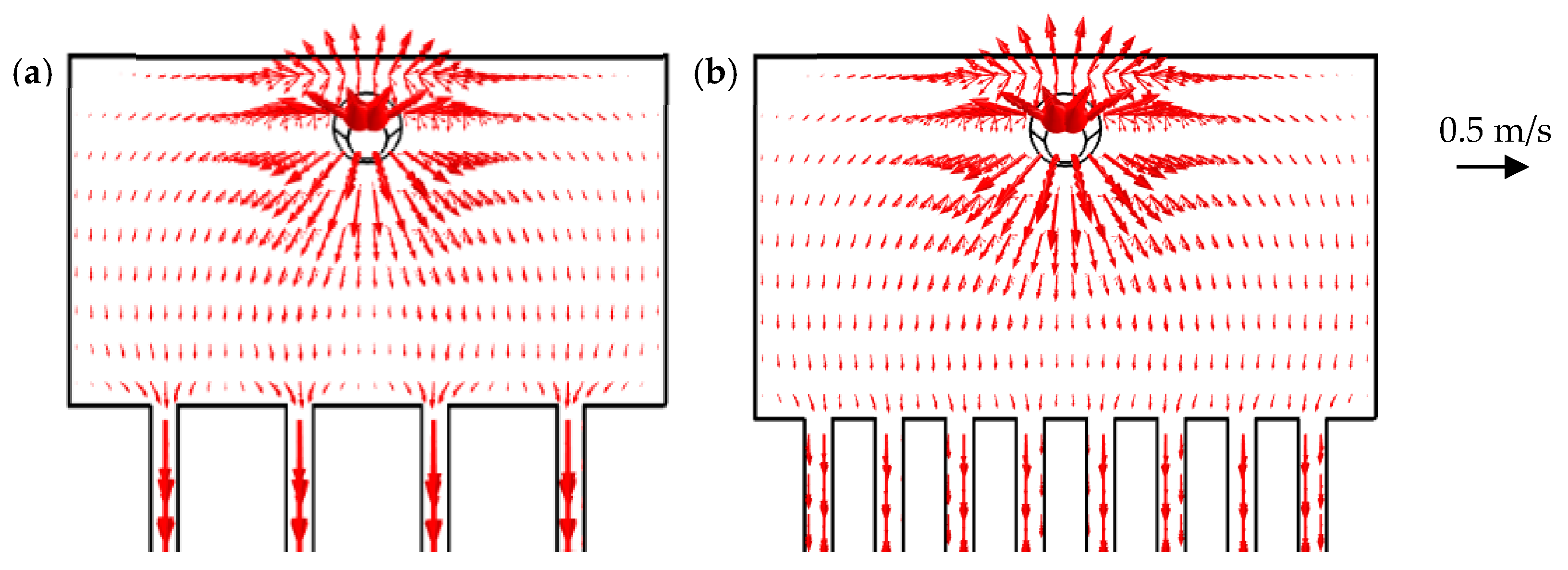
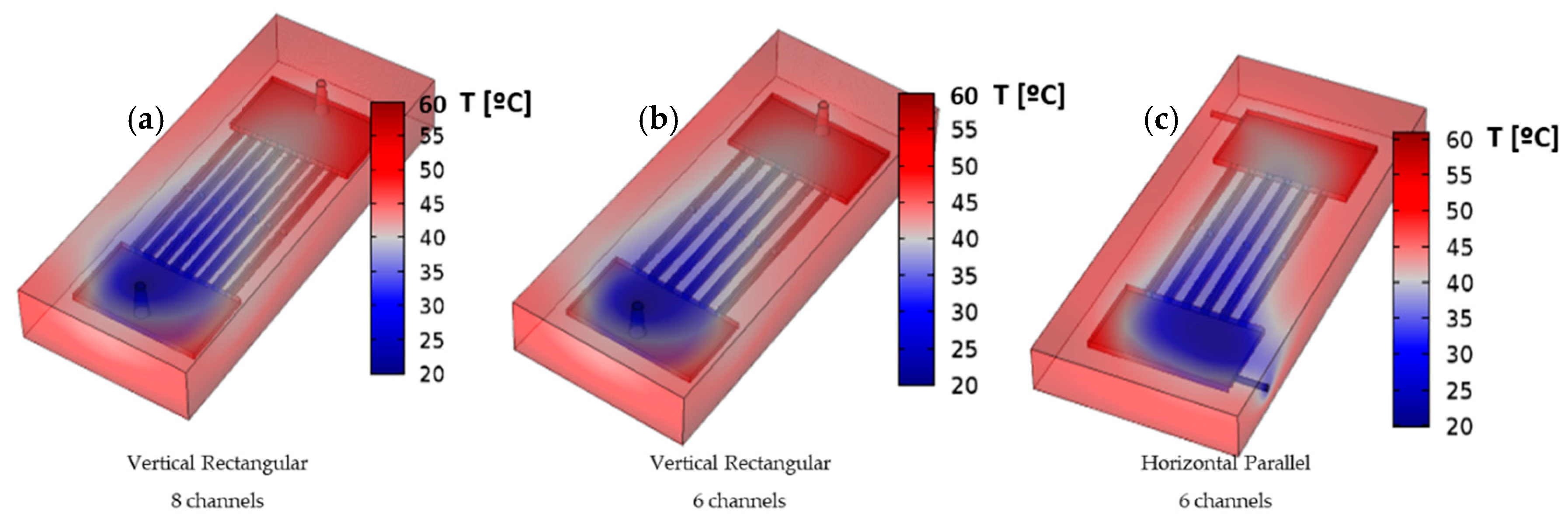
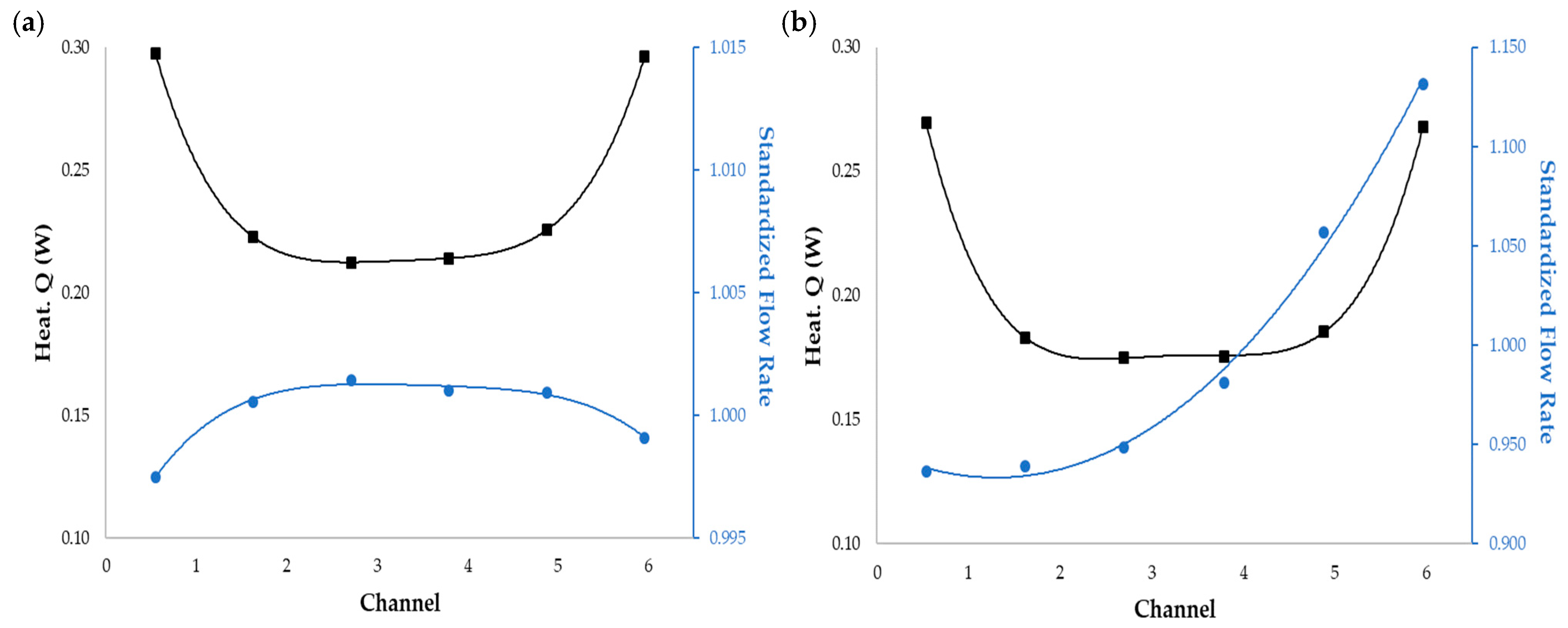
3.2. Influence of Heat Sink Geometry in Flow Distribution
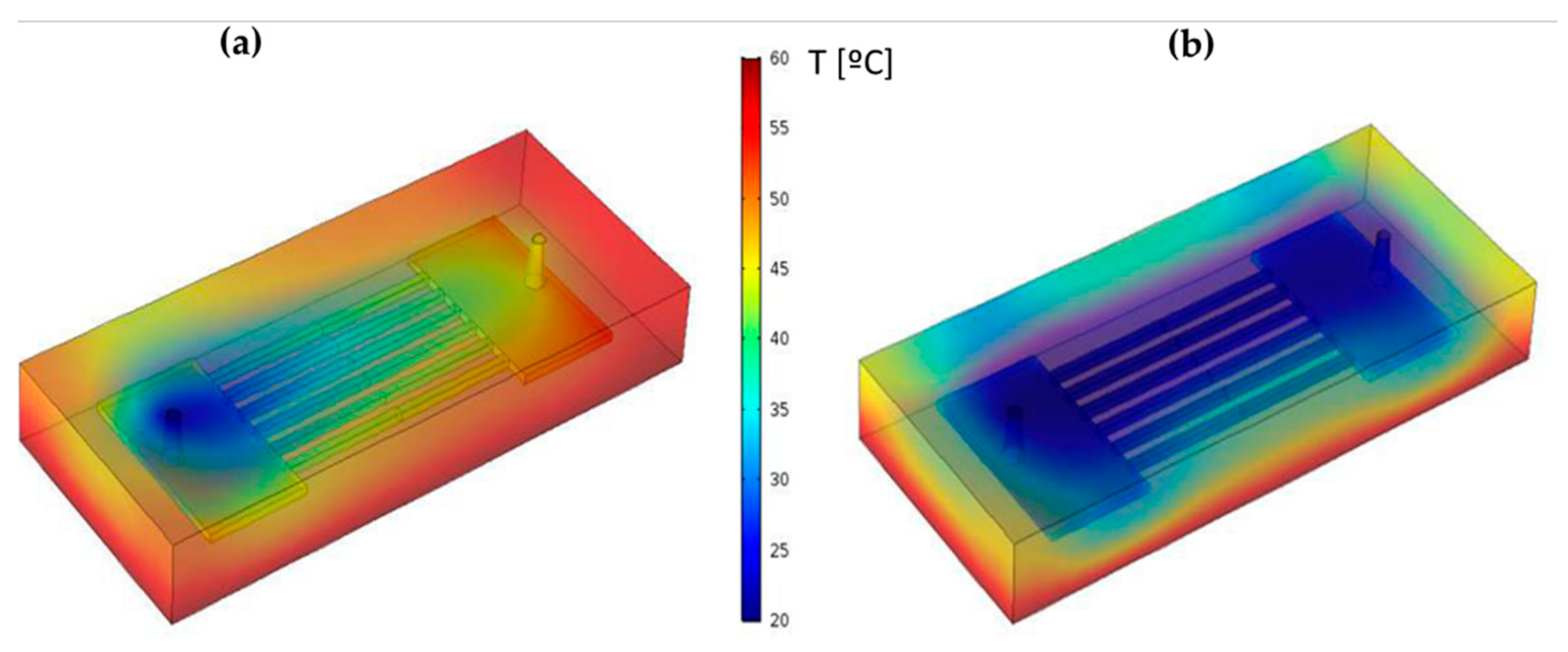
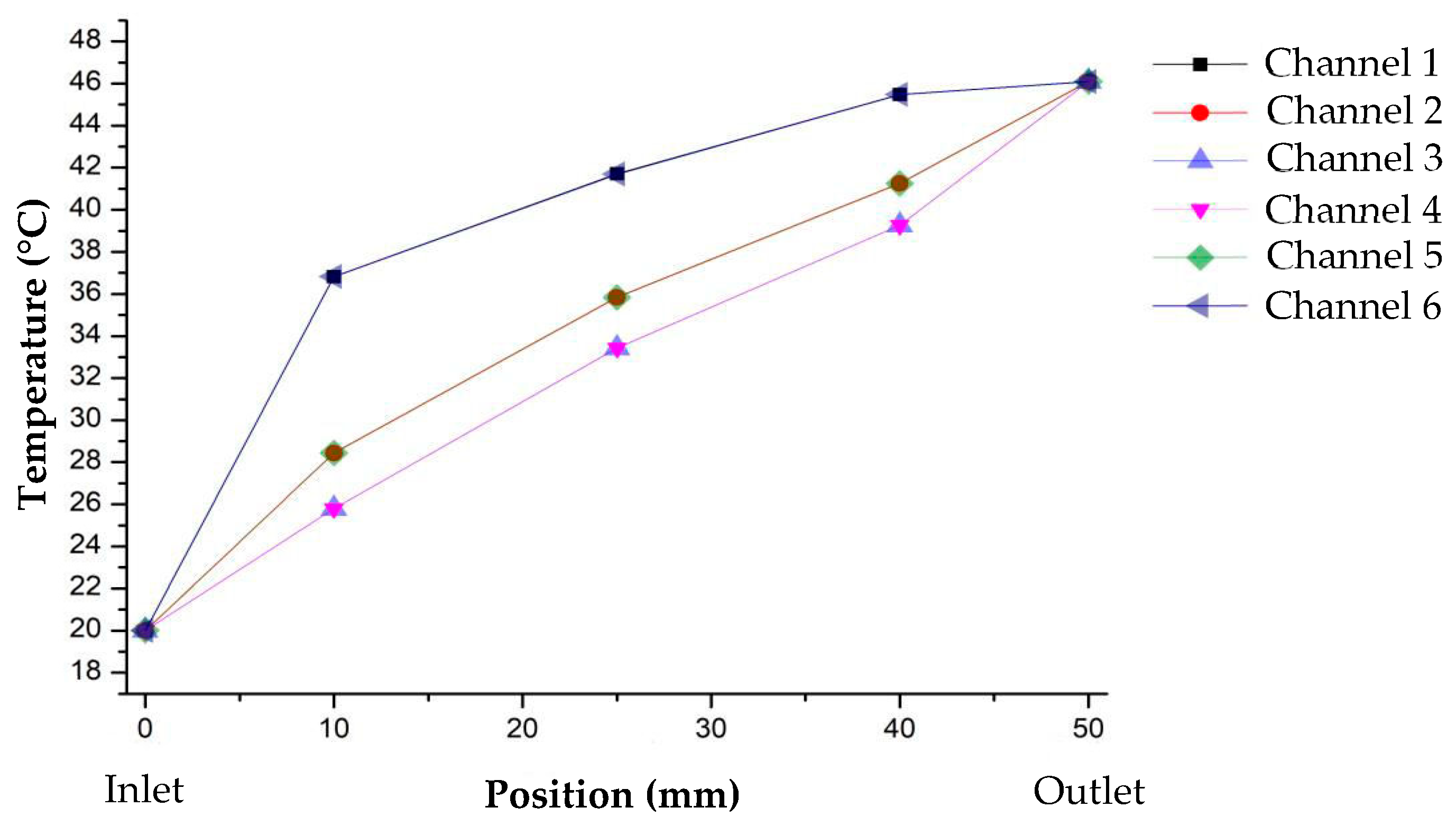
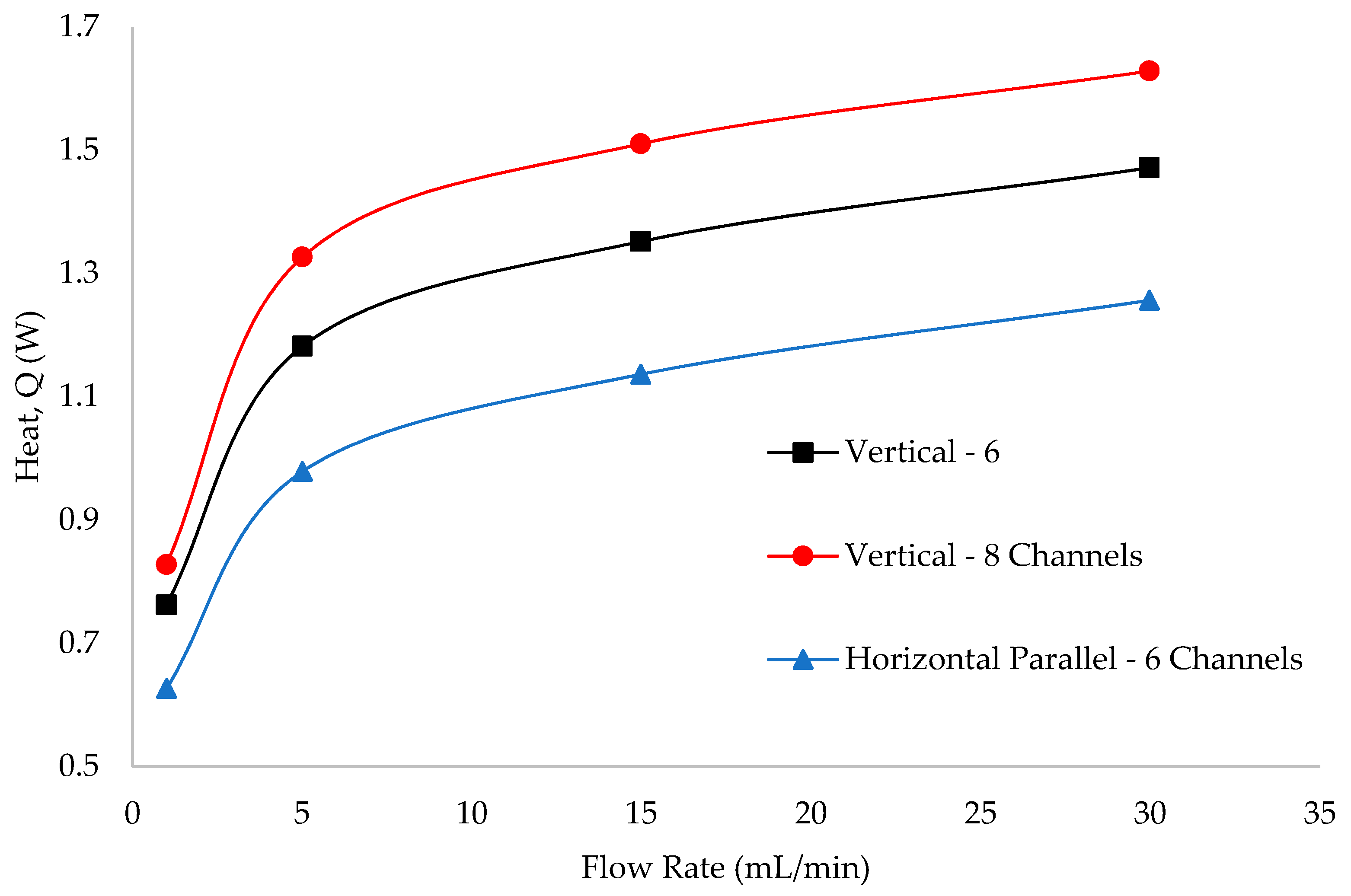
3.3. Effect on Heat Transfer
4. Concluding Remarks
- A rectangular-shaped collector, since this causes less flow maldistribution and instability.
- Vertical placement of the inlet and outlet, since, in the particular case of the inlet, this causes less throttling and the easier breaking and spreading of the impinging jet.
- The maximum number of microchannels possible within the limits of the intended overall reduced dimensions of the heat sinks (eight in the case of the current work).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Surface area (m2) |
| Cp | Specific heat(J/kg·K) |
| f | Force(N) |
| G | Strain rate tensor (1/s) |
| H | Channel height (m) |
| h | Enthalpy (J) |
| k | Thermal conductivity (W/m·K) |
| L | Heat sink length (m) |
| N | Number of channels |
| p | Pressure (Pa) |
| q | Flow rate (mL/min or m3/s) |
| Q | Heat (W) |
| S | Flow distribution uniformity coefficient |
| t | Time (s) |
| T | Temperature (K) |
| u | Velocity field (m/s) |
| V | Velocity (m/s) |
| W | Heat sink width (m) |
| Z | Heat sink height (m) |
| Greek Symbols | |
| αp | Thermal expansion coefficient (1/K) |
| ϕ | Volume fraction (-) |
| υ | Kinematic viscosity (m2/s) |
| ρ | Density (kg/m3) |
| τ | Viscous stress tensor |
| Subscripts | |
| c | Channel |
| w | Wall |
| b | Base |
References
- Wang, J.; Wang, M.; Li, Z. A lattice Boltzmann algorithm for fluid–solid conjugate heat transfer. Int. J. Therm. Sci. 2007, 46, 228–234. [Google Scholar] [CrossRef]
- Jha, B.K.; Aina, B.; Ajiya, A.T. MHD natural convection flow in a vertical parallel plate microchannel. Ain Shams Eng. J. 2015, 6, 289–295. [Google Scholar] [CrossRef]
- Catarino, S.O.; Rodrigues, R.O.; Pinho, D.; Miranda, J.M.; Minas, G.; Lima, R. Blood Cells Separation and Sorting Techniques of Passive Microfluidic Devices: From Fabrication to Applications. Micromachines 2019, 10, 593. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Sousa, P.; Gaspar, J.; Bañobre-López, M.; Lima, R.; Minas, G. Organ-on-a-chip: A Preclinical Microfluidic Platform for the Progress of Nanomedicine. Small 2020, 16, 1–19. [Google Scholar]
- Shalchi-Tabrizi, A.; Seyf, H.R. Analysis of entropy generation and convective heat transfer of Al2O3 nanofluid flow in a tangential micro heat sink. Int. J. Heat Mass Transf. 2012, 55, 4366–4375. [Google Scholar] [CrossRef]
- Benedetto, A.D.; Sarli, V.D.; Russo, G. Effect of geometry on the thermal behaviour of catalytic micro-combustors. Catal. Today 2010, 155, 116–122. [Google Scholar] [CrossRef]
- Sarli, V.D.; Trofa, M.; Benedetto, A.D. A Novel Catalytic Micro-Combustor Inspired by the Nasal Geometry of Reindeer: CFD Modeling and Simulation. Catalysts 2020, 10, 606. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.K.; Wang, J.Y.; Liu, C.; Liu, J.S.; Chen, L.; Wang, L.D. A novel method for fabrication of micro-nanofluidic devices and its application in trace enrichment. FenxiHuaxue Chin. J. Anal. Chem. 2014, 42, 166–172. [Google Scholar] [CrossRef]
- Comsol Multiphysics Software Features. Available online: https://www.comsol.com/comsol-multiphysics (accessed on 10 February 2021).
- Teodori, E.; Andredaki, M.; Georgoulas, A.; Moita, A.; Moreira, A.; Marengo, M. Enhanced VOF-based direct numerical simulations of slug flow boiling within micro-channels with smooth and finned heated walls. Int. Heat Transf. Conf. 2018, 18, 6503–6510. [Google Scholar]
- D’Orazio, A.; Karimipour, A. A useful case study to develop lattice Boltzmann method performance: Gravity effects on slip velocity and temperature profiles of an air flow inside a microchannel under a constant heat flux boundary condition. Int. J. Heat Mass Transf. 2019, 136, 1017–1029. [Google Scholar] [CrossRef]
- Wang, H.L.; Yang, M.; Wang, Y. Analytical and numerical solutions for the flow in microtube with three-dimensional corrugated surface, part 1: Steady flow. J. Hydrodyn. 2010, 22, 647–656. [Google Scholar] [CrossRef]
- Yang, L.; Yu, Y.; Hou, G.; Wang, K.; Xiong, Y. Boundary conditions with adjustable slip length for the lattice Boltzmann simulation of liquid flow. Comput. Fluids 2018, 174, 200–212. [Google Scholar] [CrossRef]
- Di Capua, H.M.; Escobar, R.; Diaz, A.J.; Guzmán, A.M. Enhancement of the cooling capability of a high concentration photovoltaic system using microchannels with forward triangular ribs on sidewalls. Appl. Energy 2018, 226, 160–180. [Google Scholar] [CrossRef]
- Muhammad, A.; Selvakumar, D.; Wu, J. Numerical investigation of laminar flow and heat transfer in a liquid metal cooled mini-channel heat sink. Int. J. Heat Mass Transf. 2020, 150, 119265. [Google Scholar] [CrossRef]
- Alfellag, M.A.; Ahmed, H.E.; Kherbeet, A.S. Numerical simulation of hydrothermal performance of minichannel heat sink using inclined slotted plate-fins and triangular pins. Appl. Therm. Eng. 2020, 164, 114509. [Google Scholar] [CrossRef]
- Ong, Y.S.; KuShaari, K.Z. CFD investigation of the feasibility of polymer-based microchannel heat sink as thermal solution. Chin. J. Chem. Eng. 2020, 28, 980–994. [Google Scholar] [CrossRef]
- Freegah, B.; Hussain, A.A.; Falih, A.H.; Towsyfyan, H. CFD analysis of heat transfer enhancement in plate-fin heat sinks with fillet profile: Investigation of new designs. Therm. Sci. Eng. Prog. 2020, 17, 100458. [Google Scholar] [CrossRef]
- Hempijid, T.; Kittichaikarn, C. Effect of heat sink inlet and outlet flow direction on heat transfer performance. Appl. Therm. Eng. 2020, 164, 114375. [Google Scholar] [CrossRef]
- Sajadifar, S.A.; Karimipour, A.; Toghraie, D. Fluid flow and heat transfer of non-Newtonian nanofluid in a microtube considering slip velocity and temperature jump boundary conditions. Eur. J. Mech. B/Fluids 2017, 61, 25–32. [Google Scholar] [CrossRef]
- Awais, A.A.; Kim, M.H. Experimental and numerical study on the performance of a minichannel heat sink with different header geometries using nanofluids. Appl. Therm. Eng. 2020, 171, 115125. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S.; Goodarzi, M.; Moayedi, H. CFD analysis of employing a novel ecofriendly nanofluid in a miniature pin fin heat sink for cooling of electronic components: Effect of different configurations. Adv. Powder Technol. 2019, 30, 2503–2516. [Google Scholar] [CrossRef]
- HadiNajafabadi, H.; Keshavarz Moraveji, M. CFD investigation of local properties of Al2O3/water nanofluid in a converging microchannel under imposed pressure difference. Adv. Powder Technol. 2017, 28, 763–774. [Google Scholar] [CrossRef]
- Ganguly, S.; Sarkar, S.; Kumar Hota, T.; Mishra, M. Thermally developing combined electroosmotic and pressure-driven flow of nanofluids in a microchannel under the effect of magnetic field. Chem. Eng. Sci. 2015, 126, 10–21. [Google Scholar] [CrossRef]
- Huc, N. Conjugate Heat Transfer. Available online: https://www.comsol.com/blogs/conjugate-heat-transfer/ (accessed on 12 January 2021).
- Maia, I.; Rocha, C.; Pontes, P.; Cardoso, V.; Miranda, J.M.; Moita, S.A.; Minas, G.; Moreira, L.N.A.; Lima, R. Heat Transfer and Fluid Flow Investigations in PDMS Microchannel Heat Sinks Fabricated by Means of a Low-Cost 3D Printer. In Advances in Microfluidic Technologies for Energy and Environmental Applications; IntechOpen: London, UK, 2020. [Google Scholar]
- Wollblad, C. Your Guide to Meshing Techniques for Efficient CFD Modeling. Available online: https://www.comsol.com/blogs/your-guide-to-meshing-techniques-for-efficient-cfd-modeling/ (accessed on 12 January 2021).
- Gothäll, H. How to Inspect Your Mesh in COMSOL Multiphysics®. Available online: https://www.comsol.com/blogs/how-to-inspect-your-mesh-in-comsol-multiphysics/ (accessed on 12 January 2021).
- Cengel, Y.A. Heat Transfer—A Practical Approach, 2nd ed.; McGraw-Hill Education: New York City, NY, USA, 2002; ISBN 9780072458930. [Google Scholar]
- Takács, G.; Bognár, G.; Bándy, E.; Rózsás, G.; Szabó, P.G. Fabrication and characterization of microscale heat sinks. Microelectron. Reliab. 2017, 79, 480–487. [Google Scholar] [CrossRef]
- Ghani, I.A.; Che Sidik, N.A.; Kamaruzzaman, N.; Jazair Yahya, W.; Mahian, O. The effect of manifold zone parameters on hydrothermal performance of micro-channel HeatSink: A review. Int. J. Heat Mass Transf. 2017, 109, 1143–1161. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; He, J.; Wu, C.; Luo, W.; Shuai, Y.; Zhang, W.; Chen, X.; Zhang, J.; Lin, J. A Comprehensive Study of a Micro-Channel Heat Sink Using Integrated Thin-Film Temperature Sensors. Sensors 2018, 18, 299. [Google Scholar] [CrossRef] [PubMed]
- Memon, S.A.; Cheema, T.A.; Kim, G.M.; Park, C.W. Hydrothermal Investigation of a Microchannel Heat Sink Using Secondary Flows in Trapezoidal and Parallel Orientations. Energies 2020, 13, 5616. [Google Scholar] [CrossRef]
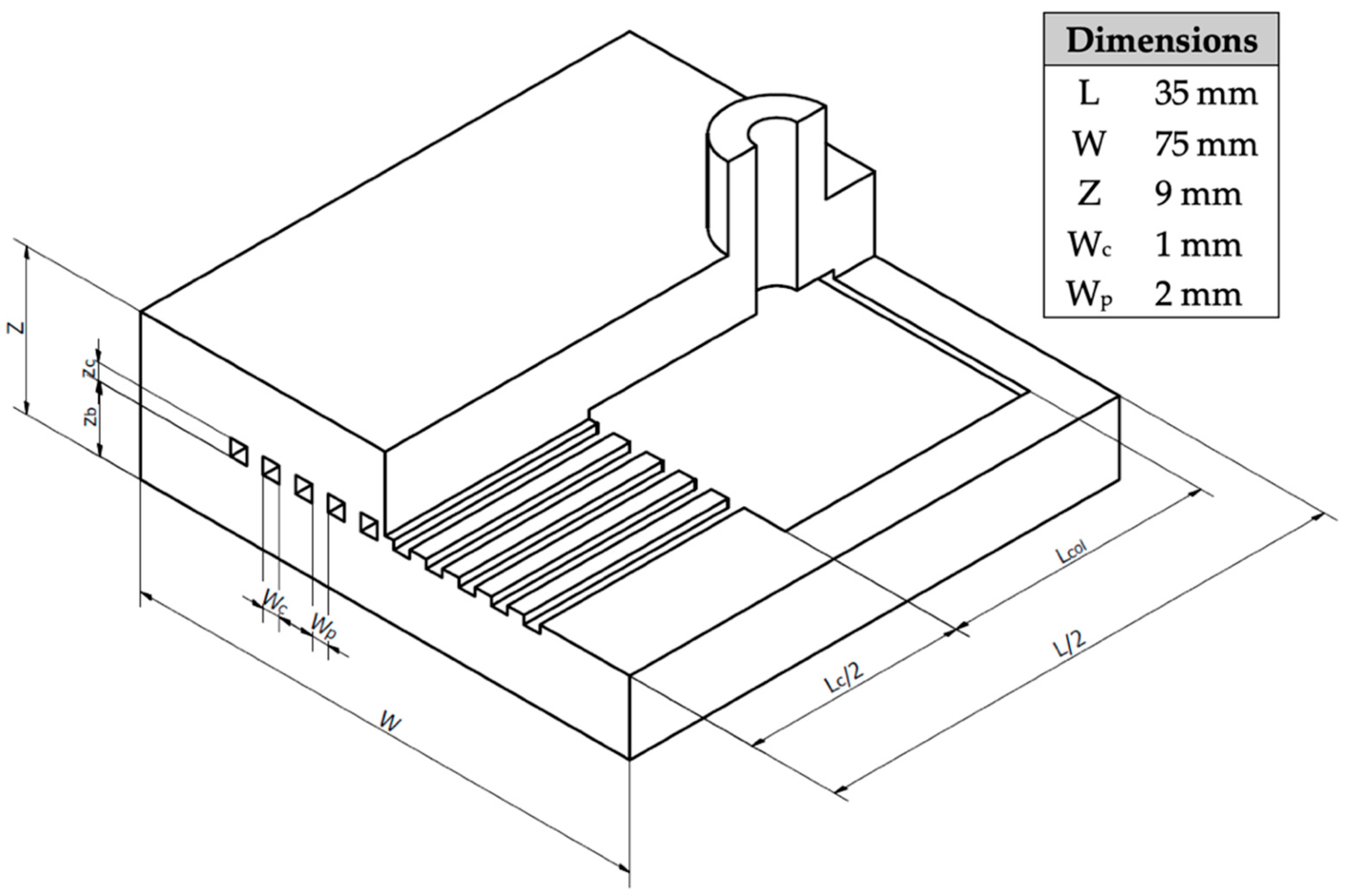
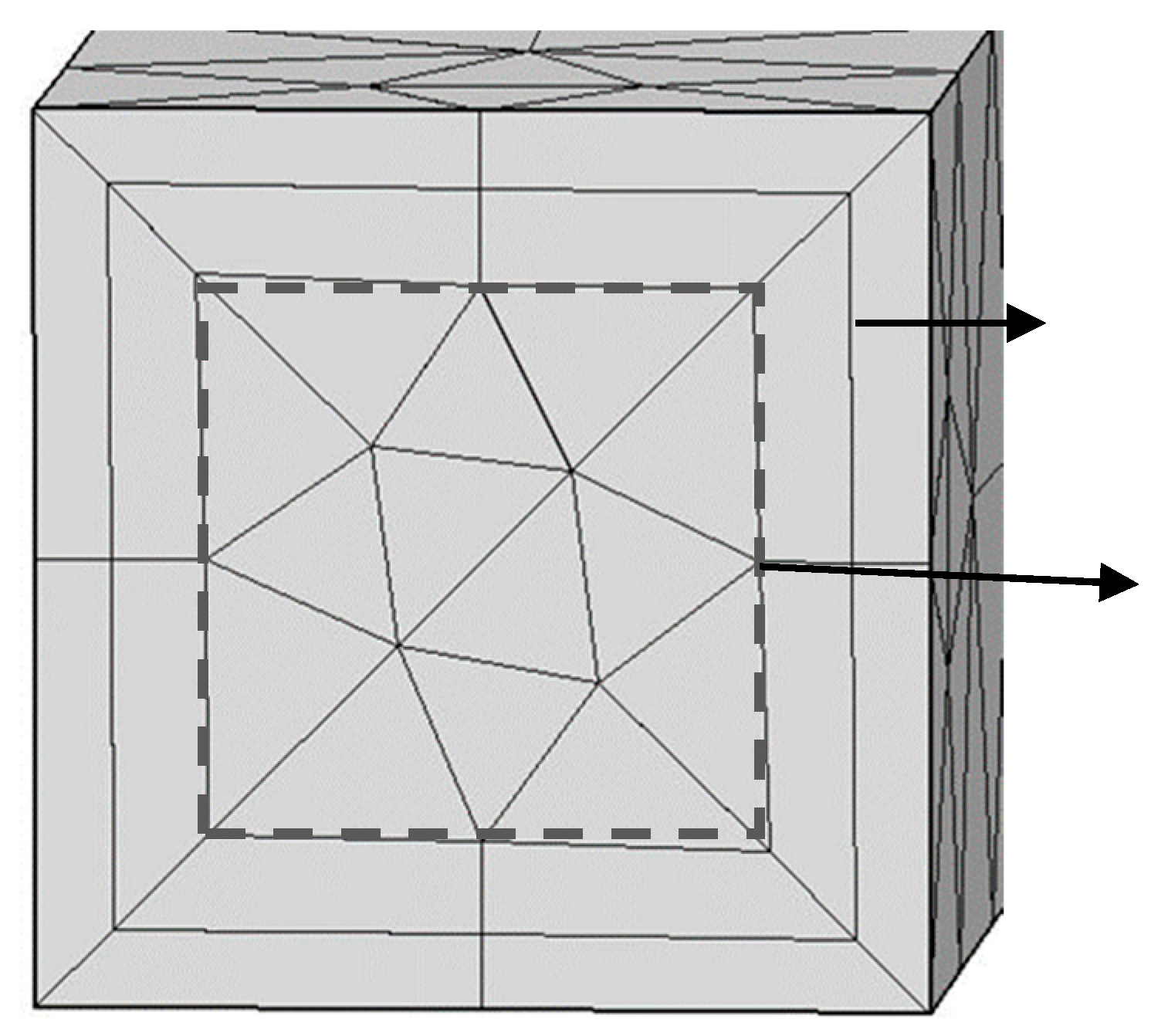
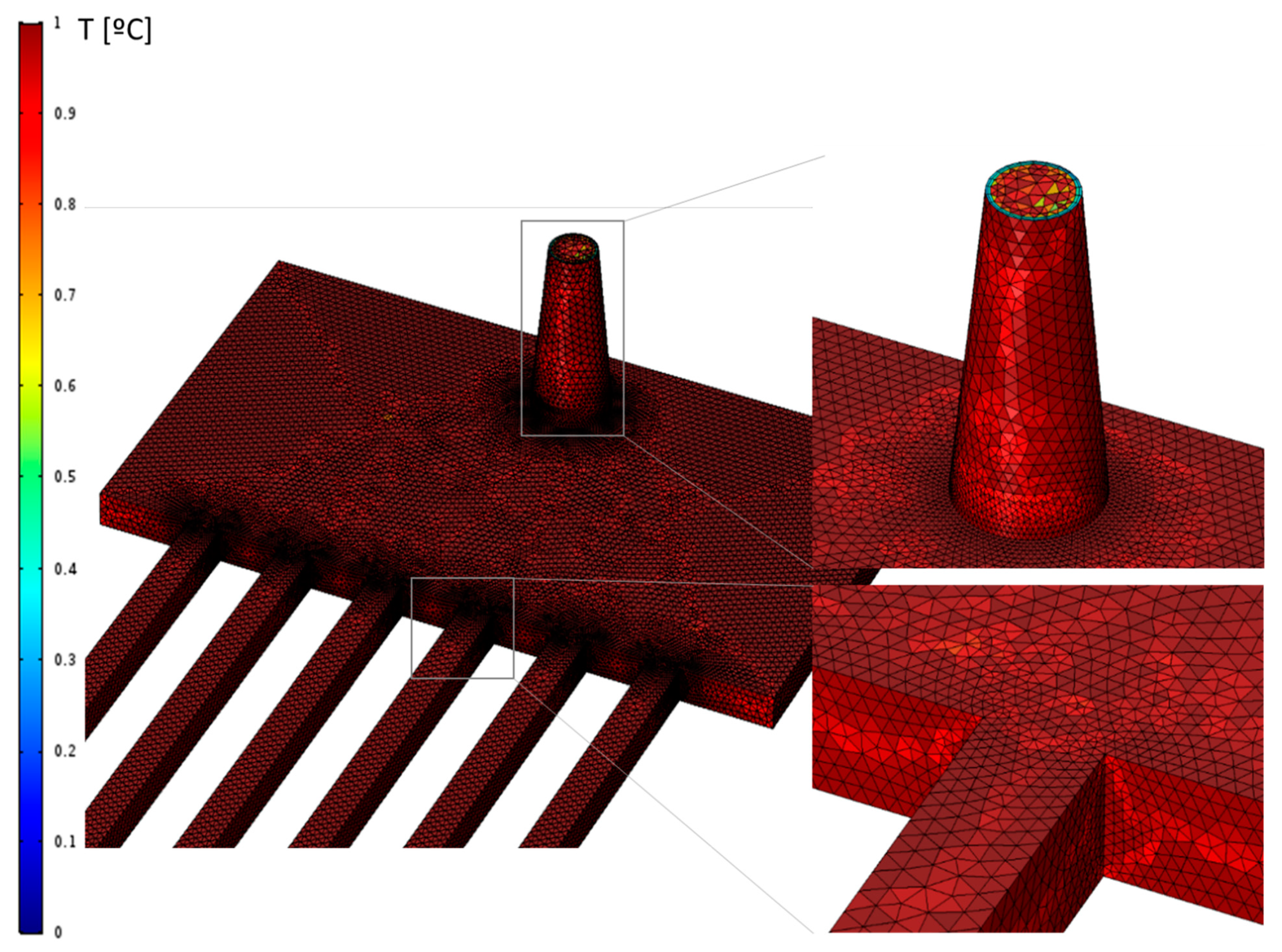
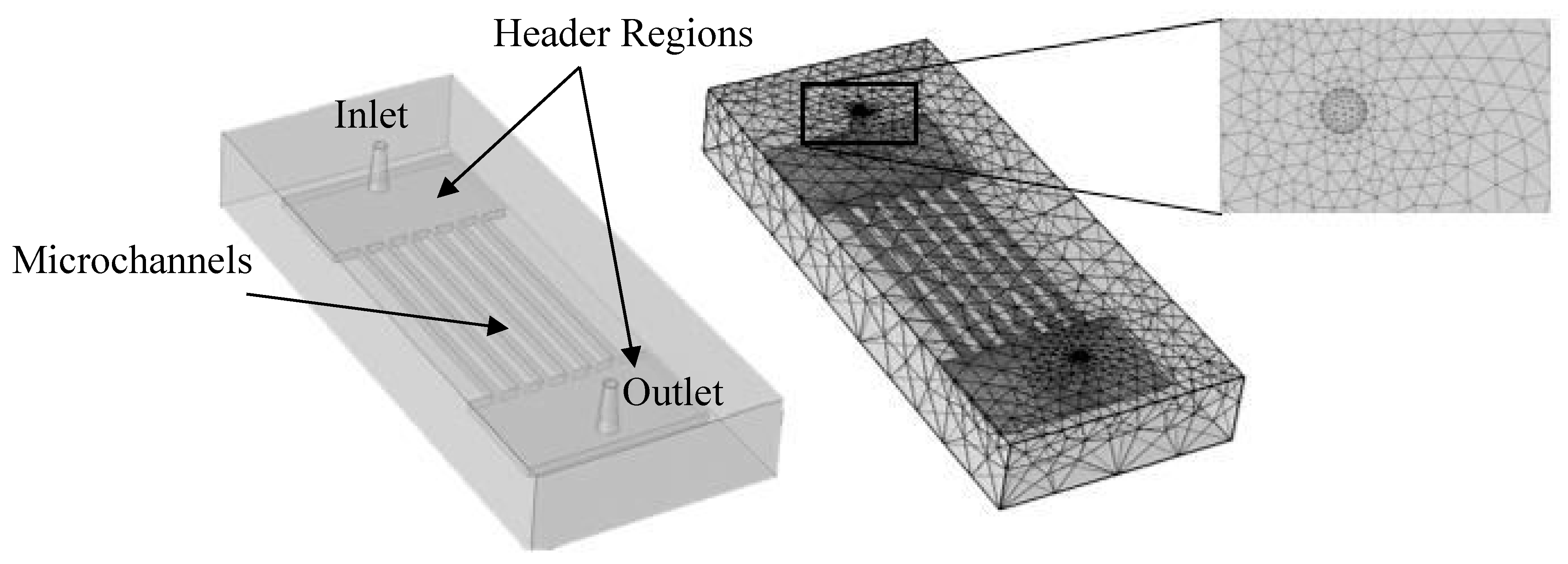
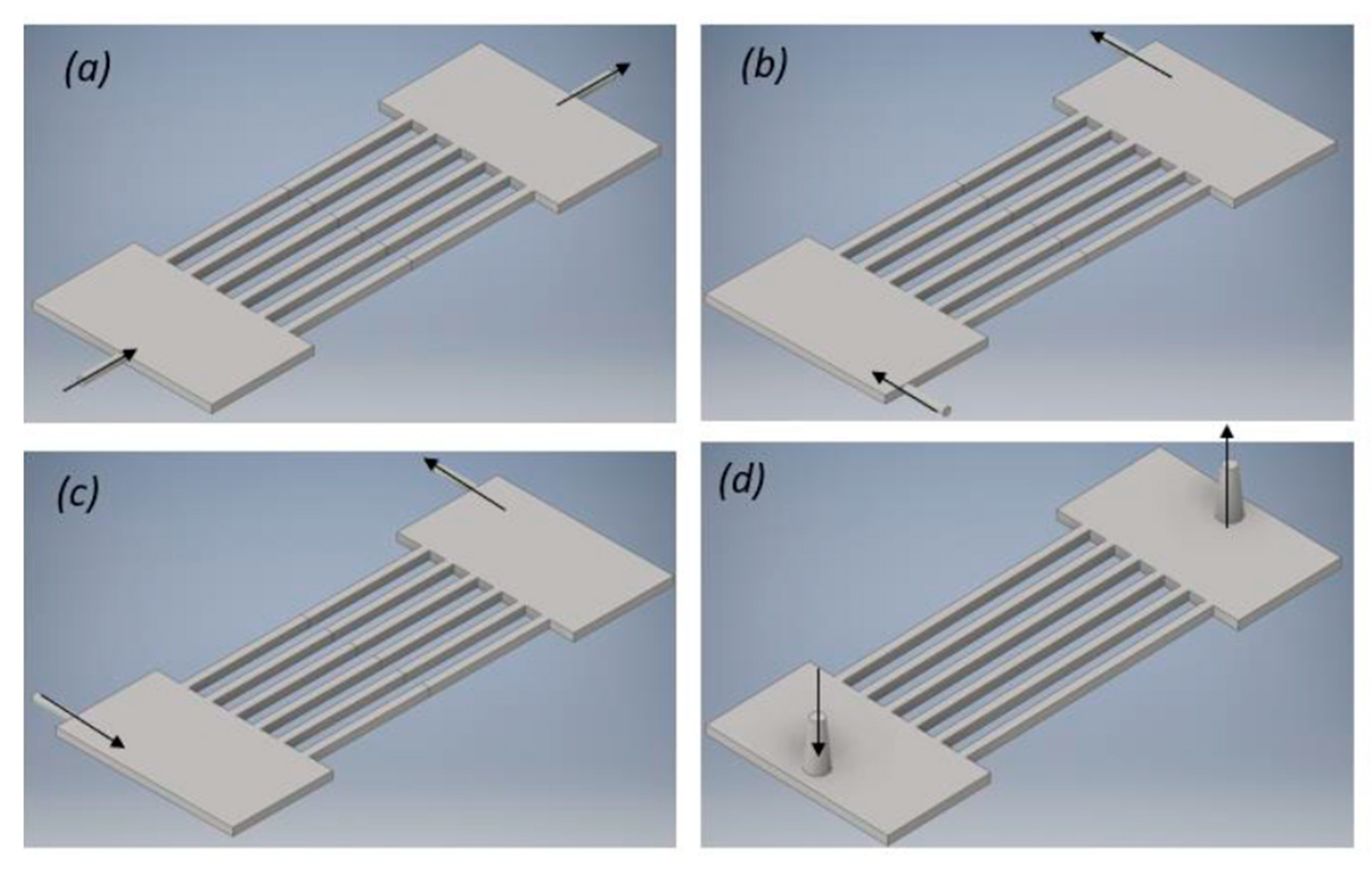
| Mesh | A1 | A2 | A3 | A4 |
|---|---|---|---|---|
| Maximum Size (mm) | 0.609 | 0.425 | 0.264 | 0.23 |
| Minimum Size (mm) | 0.115 | 0.046 | 0.0172 | 0.015 |
| Maximum Growth | 1.13 | 1.1 | 1.08 | 1.08 |
| Curve Factor | 0.5 | 0.4 | 0.3 | 0.25 |
| Resolution of Narrow Regions | 0.8 | 0.9 | 0.95 | 0.95 |
| Elements Number | 125,426 | 402,365 | 1,342,365 | 1,975,310 |
| Average Quality | 0.5569 | 0.605 | 0.6359 | 0.6478 |
| Simulation Time | 1 min 26 s | 3 min 26 s | 8 min 54 s | 14 min 12 s |
| Mesh | B1 | B2 | B3 | B4 | B5 | B6 |
|---|---|---|---|---|---|---|
| Maximum Size (mm) | 10.5 | 7 | 5.6 | 3.85 | 2.45 | 1.4 |
| Minimum Size (mm) | 1.96 | 1.26 | 0.7 | 0.28 | 0.105 | 0.014 |
| Maximum Growth | 1.6 | 1.5 | 1.45 | 1.4 | 1.35 | 1.3 |
| Curve Factor | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 |
| Resolution of Narrow Regions | 0.4 | 0.5 | 0.6 | 0.7 | 0.85 | 1 |
| Elements Number | 126,348 | 151,540 | 167,311 | 188,105 | 239,112 | 366,980 |
| Average Quality | 0.661 | 0.691 | 0.701 | 0.713 | 0.725 | 0.746 |
| Water | PDMS | |
|---|---|---|
| Viscosity | 0.00101 | - |
| Density | 1001.6 | 970.0 |
| Specific Heat | 4182.5 | 1460.0 |
| Thermal Conductivity | 0.603 | 0.180 |
| Specific Heat Ratio | 1 | - |
| Surface | Boundary Conditions | Mathematical Expression |
|---|---|---|
| Inlet | Flow Rate Inlet | , Tmean = 20 °C |
| Outlet | Pressure Outlet | POUT = 0 Pa (free atmosphere) and ΔTOUT = 0 |
| Fluid–Solid Interface | No-slip Interface | and Tf = TPDMS |
| Sided Walls | Adiabatic | |
| Interface between the Heater and PDMS | Thermal Coupled | and TH = TPDMS |
| Bottom Surface of the PDMS | Mixed Radiation and Convection |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves, I.M.; Rocha, C.; Souza, R.R.; Coutinho, G.; Pereira, J.E.; Moita, A.S.; Moreira, A.L.N.; Lima, R.; Miranda, J.M. Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment. Appl. Sci. 2021, 11, 2440. https://doi.org/10.3390/app11052440
Gonçalves IM, Rocha C, Souza RR, Coutinho G, Pereira JE, Moita AS, Moreira ALN, Lima R, Miranda JM. Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment. Applied Sciences. 2021; 11(5):2440. https://doi.org/10.3390/app11052440
Chicago/Turabian StyleGonçalves, Inês M., César Rocha, Reinaldo R. Souza, Gonçalo Coutinho, Jose E. Pereira, Ana S. Moita, António L. N. Moreira, Rui Lima, and João M. Miranda. 2021. "Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment" Applied Sciences 11, no. 5: 2440. https://doi.org/10.3390/app11052440
APA StyleGonçalves, I. M., Rocha, C., Souza, R. R., Coutinho, G., Pereira, J. E., Moita, A. S., Moreira, A. L. N., Lima, R., & Miranda, J. M. (2021). Numerical Optimization of a Microchannel Geometry for Nanofluid Flow and Heat Dissipation Assessment. Applied Sciences, 11(5), 2440. https://doi.org/10.3390/app11052440












