Abstract
The reliability, scalability, and stability of routing schemes are open challenges in highly evolving vehicular ad hoc networks (VANETs). Cluster-based routing is an efficient solution to cope with the dynamic and inconsistent structure of VANETs. In this paper, we propose a cluster-based routing scheme (hereinafter referred to as connectivity-based clustering), where link connectivity is used as a metric for cluster formation and cluster head (CH) selection. Link connectivity is a function of vehicle density and transmission range in the proposed connectivity-based clustering scheme. Moreover, we used a heuristic approach of spectral clustering for the optimal number of cluster formation. Lastly, an appropriate vehicle is selected as a CH based on the maximum Eigen-centrality score. The simulation results show that the suggested connectivity-based clustering scheme performs well in the optimal number of cluster selections, strongly connected (STC) route selection, and route request messages (RRMs) in the discovery of a particular path to the destination. Thus, we conclude that link connectivity and the heuristic approach of spectral clustering are valuable additions to existing routing schemes for high evolving networks.
1. Introduction
Intelligent transportation systems (ITS) represent a significant breakthrough in smart city transportation, consisting of various types of communications between vehicles and other devices. Vehicular ad hoc network (VANET) is an adopted shape of mobile ad hoc networks (MANETs), where intelligent vehicles are substitutes for ordinary nodes. The vehicles in VANETs are embedded with onboard units (OBUs), which enable them to communicate with each other, i.e., vehicle-to-vehicle (V2V) communications, and/or with stationary roadside units (RSUs), i.e., vehicle-to-infrastructure communications (V2I) [1]. VANET is one of the most important innovations for enhancing the performance and safety of modern transport systems such as minimizing traffic jams in highly congested areas, avoiding traffic accidents, and disseminating congestion information with nearby vehicles. VANET applications allow vehicles to obtain news, traffic information, and weather updates in real-time through Internet access. Additionally, it avails entertainment such as gaming and file sharing through the Internet or local ad hoc networks to the passengers. Many unique characteristics, such as high mobility, predictable and restricted mobility patterns, rapid topological variation, and continuous battery charging, make VANETs different from MANETs. From the above properties, it is noticed that energy consumption is not a big problem in VANETs [2].
The highly evolving structure of VANET is a big challenge for the practical implications and commercialization of vehicular communication [3]. To deal with the above challenges, an effective routing protocol is necessary for V2V and V2I communications. In the absence of a reliable and stable routing protocol, advanced features of VANETs cannot be retained in real-life [4]. The literature has enormous routing schemes to establish vehicle-to-everything (V2X) communications [2,5,6]. Generally, the existing routing schemes are classified into a couple of classes based on their structure and route discovering process [3,6]. However, each class has specific limitations in various contexts [7]. Specifically, the non-hierarchical or linear routing schemes’ performances degrade in highly dense networks in terms of computational and communication cost [3,8,9]. Thus, cluster-based routing protocols are introduced to optimally manage vehicles into groups based on their similarity, aiming to reduce the computational overhead by selecting an optimal number of clusters [4,6,7,8]. Different protocols use various parameters for the selection of cluster members and cluster head (CH) in the literature, such as ID, degree of neighbors connectivity, propagation delay, velocity, travel time, average relative velocity, average link lifetime, route confidence level, number of vehicles to follow, link reliability, etc. [3,6,10]. However, the consistency and lifetime of cluster members and CHs are still challenging problems for researchers [1,3]. In light of the above challenges, the primary objective of this research is to address the dynamic structure of VANETS using an optimal number of clusters.
The link reliability metric refers to the probability that a particular link between two vehicles will be available for a specific time period t [3]. The reliability of a link considers the transmission range and inter-vehicle distance while ignoring the effect of spatial density. In contrast, link connectivity is another metric, showing that two vehicles will be connected if and only if they are within the same transmission range [11]. The connectivity metric considers the vehicle density along with the transmission range of vehicles. Thus, the connectivity is an essential metric for cluster formation and CH selection. Considering the definition of link connectivity, in this paper, our contribution is a connectivity-based clustering scheme, where the formation of clusters as well as the selection of CH are performed with the help of link connectivity. Firstly, we form an affinity matrix (i.e., similarity matrix) of the whole vehicular network by using link connectivity of vehicles. Secondly, a heuristic approach (i.e., Eigen gap) of spectral clustering is applied to find the optimal number of clusters [12]. To select an appropriate CH, our proposed clustering scheme ranks all the clusters and selects a vehicle as a leader based on the maximum Eigen-centrality. Furthermore, the route discovery process in the proposed connectivity-based clustering is performed by the cluster-based evolving graph (CEG)-Dijkstra [3].
The rest of the paper is structured as follows: Section 2 consists of the previous work related to the cluster-based routing. Section 3 presents vehicular connectivity in detail. Section 4 describes the complete procedure of our suggested connectivity-based clustering. Section 5 indicates the route discovery process of the proposed routing scheme. Section 6 presents the simulation results along with a discussion. Finally, Section 7 concludes the paper.
2. Literature Review
2.1. Routing Issues and Challenges for VANETs
In VANETs, the communication pattern depends on the routing protocol. A routing protocol aims to deliver safety information to ongoing vehicles on the highway. A reliable VANET faces many challenges due to the highly complex and inconsistent structure. A secure and effective routing protocol is essential for data transmission to resolve the challenges mentioned earlier. Many routing protocols for highly dynamic and dense vehicular networks have been presented in previous studies. Position-based protocols [1], route-discovery protocols [13,14], broadcasting protocols [15], infrastructure-based protocols [16], and cluster-based protocols [17] are the five categories of available schemes. There are potential limitations in the schemes mentioned above in different use cases and advanced real scenarios [7]. For example, too many beacon messages are generated in broadcast-based protocols, causing high communication and computational overhead. Similarly, route-discovery-based protocols are also not suitable for high evolving networks because of the fixed route lifetime, fixed maintenance time, and immense end-to-end delay [18]. The position-based protocols generate additional overhead through extensive periodic messages to update its routing table for efficient data transmission. Due to installation of the costly RSUs [19], the infrastructure-based routing protocols are area-specific and expensive. To address the above issues, cluster-based routing scheme is an appropriate choice due to its optimal groups based on similar features.
2.2. Cluster-Based Routing Schemes
Zahid et al. [1] presented a triple cluster-based routing protocol (TCRP), aiming to reduce the communication overhead by limiting the broadcast domain. In TCRP, CH was selected based on the vehicle position (centralized) inside the cluster and its subsequent speed variance (less variation in speed). The authors used the dynamic programming approach (i.e., Floyd–Warshall algorithm) for CH selection. From their simulation results, it was noted that TCRP significantly reduces CH reselection probability in further rounds. The TCRP performs very well in terms of CH stability and scalability. However, the pre-specified number of clusters (i.e., three clusters) is not a suitable approach in many scenarios. The three-cluster approach in highly congested traffic leads to an excessive number of route request messages (RRMs) and computational overhead. Secondly, in the sparse traffic situation (one or two vehicles), it is not suitable due to the limited number of cars.
In [4], the authors introduced the Multi-hop Moving Zone (MMZ) scheme for Cellular-V2X (C-V2X) communication. Inspired by the prominent issues of pure V2V-based clustering (i.e., network disconnection and broadcast storm) [7], the authors disclosed the MMZ clustering scheme for reliable and low-latency communications in C-V2X. In MMZ, the zonal heads (ZHs), i.e., cluster heads (CHs), are selected through multi-metrics, i.e., relative speed, distance, and link lifetime (LLT). The primary purpose of MMZ was to form stable clusters for high packet delivery and low latency. The C-V2X communication pattern in [4] was composed of two main technologies, i.e., IEEE 802.11p and cellular networks. Firstly, V2X relied on IEEE 802.11p facing several challenges, i.e., limited-mobility support, advanced use cases compatibility issue, limited transmission range, long-delay, and reliability [9]. Secondly, the cellular technology is cost-effective in the practical implications of VANETs [6]. Apart from the technological challenges, the selected metrics ignore the effect of density and transmission ranges. Thus, in this paper, we use link connectivity as a metric for optimum cluster formation and CH selection.
The authors suggested a novel routing scheme called a two-level cluster-based routing protocol [6], where the Fuzzy logic algorithm selects a stable CH with the help of well-known metrics, i.e., relative velocity factor, K-connectivity factor, and link reliability factor. The connectivity factor selects a centralized and high degree of connectivity node inside a cluster—the reliability factor chooses a robust vehicle as a CH candidate. The authors used improved Q-Learning (IQL) in second-level clustering to reduce the computational cost and to adjust the optimal number of gateways to Long Term Evolution Base Station (LTE BS). The large numbers of agents and actions in IQL cause many unnecessary iterations in gateway discovery. Additionally, the calculation of temporal connectivity and link reliability consumes a considerable amount of time. Our suggested connectivity-based clustering scheme considers the connectivity metric solely for cluster formation and CH selection, aiming to cope with two-level cluster-based routing protocol problems [6].
2.3. Reliability-Based Routing Schemes
The concept of an evolving graph was first applied by Hashem Eiza et al. [5] in the vehicular ad-hoc domain. Initially, the authors proposed a link reliability metric, which was later extended to a full-fledge routing scheme called evolving graph ad hoc on-demand distance vector (EG-AODV). The definition of link reliability is related to the probability of a link duration under varied speeds and transmission ranges. The proposed EG-AODV was a linear routing scheme based on VANET-oriented Evolving Graph (VoEG). The EG-RAODV iteratively discovers most reliable journey (MRJ) from the source vehicle to the destination by using Evolving Graph (EG) Dijkstra [5]. However, the performance of EG-RAODV was merely considered in sparse traffic scenario, where continuous arrival of vehicles was ignored. To improve the existing VoEG model, Zahid et al. [3] disclosed a novel and reliable cluster-based routing protocol, i.e., CEG-RAODV, where link reliability was used as a metric for cluster formation and CH selection. In [3], the authors suggested a reliable cluster-based routing protocol, i.e., CEG-RAODV, where link reliability was used for the first time in a cluster-based routing scheme [3]. The proposed CEG-RAODV not only reduces the computational cost but also has a scalability feature adoptable in any dynamic topological structure of VANETs. The reliability-based clustering protocol improved the performance considerably, but its proposed metric considered only the link lifetime while ignoring the node density and transmission range. From a literature perspective, the importance of node density and transmission range cannot be ignored [10].
It is a challenging problem for VANETs to build and maintain stable clusters. The authors in [20] proposed a link reliability-based clustering algorithm (LRCA) that provided useful and reliable data transmission within VANETs. Furthermore, the authors gathered redundant unstable neighbors by link lifetime-based (LLT-based) strategy before clustering. Their proposed clustering scheme consisted of three components: selecting an appropriate cluster head, the construction of clusters, and the maintenance of groups. Moreover, LRCA appointed particular nodes at intersections to test the routing decisions for making routing decisions on different road zones. For the best data forwarding, routes with the lowest weights were then chosen.
2.4. Link Connectivity Metric for Cluster-Based Routing Schemes
Link connectivity is an essential factor to measure the efficiency of network communications and users’ satisfaction. Connectivity directly impacts channel contention and vehicle communications, particularly in an exceptionally dynamic changing network [21]. Unfortunately, in the creation of existing protocols for VANETs, link connectivity is not considered. The authors analyzed the connectivity features in [21] and introduced a connectivity-aware Media Access Control (MAC). protocol for a platoon of intelligent vehicles. Moreover, the authors also evaluated the probability of connectivity for the V2V and V2I communication scenarios in one way and two-way VANETs, respectively. In [21], the definition of connectivity was considered a function of node density and transmission range. Later, Zahid et al. [11] proposed a new mobility metric called generalized speed factor (GSF) by expanding an existing speed factor based on the assumption that all vehicles have the same speed at all times. The primary theme of GSF was to identify an actual relationship between inter-vehicle spacing and the relative velocity of consecutive vehicles. The work in [11] analyzed vehicle connectivity in terms of GSF-based mobile scenarios. The proposed definition of connectivity in [11] is significantly worthy because of the consideration of three factors, i.e., vehicles density, transmission range, and speed.
The literature encompasses several metrics for cluster formation and cluster head selection [3,6,10]. Every performance metric has its pros and cons under various conditions. The link reliability metric has been recently used as a metric for CH selections [3,20]. From the definition of link reliability, we can see that it only considers the speed and transmission range of vehicles. Thus, link reliability criteria will not be reliable in various traffic scenarios (i.e., sparse and dense), and as a result, it can affect a routing scheme’s performance. On the other hand, link connectivity considered speed, transmission range, as well as node density. Thus, we used link connectivity as a metric for cluster formation and CH selection in our clustering scheme (i.e., connectivity-based clustering).
3. Connectivity Models for Vehicular Communications
In this section, the system model and vehicle connectivity model are presented followed by the strongly connected (STC) route selection.
3.1. System Model
Consider a high dynamic VANET, where N number of vehicles are randomly distributed over a unidirectional multi-lane highway. All the vehicles are supposed to be intelligent using onboard units (OBUs). For communication purposes, the OBU of each vehicle has radio equipment, i.e., global position system (GPS) and IEEE 802.11p, respectively, for location tracking and communication. Additionally, RSUs are also installed with an equal distance to cover the whole highway, which is shown in Figure 1. The purpose of an RSU is to extend the connectivity of vehicles and the coverage of V2X communication. The speed and arrival rate of vehicles follows normal distribution [3] and poison distribution [11], respectively. The inter-arrival time and spacing between vehicles follow exponential distribution [11]. Link reliability [3] and connectivity [11] are the two essential metrics to measure the performance of a highly dynamic networks. The probability density function (pdf) of the vehicle’s velocity is given by the following:
where u and represent the mean and standard deviation of vehicle speed, respectively.
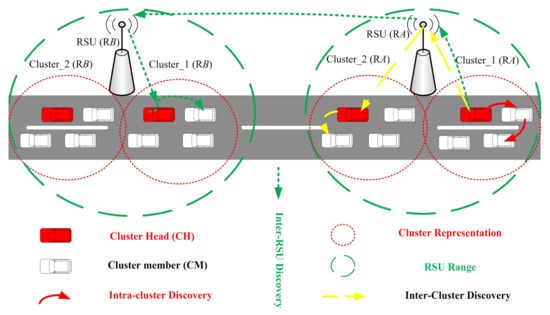
Figure 1.
An overview of the suggested connectivity-based clustering scheme.
3.2. Vehicle Connectivity Models
Two vehicles are said to be connected on the highway if they are within each other’s transmission range. A stable and strongly connected network is required to guarantee the quality-of-service (QoS) of real-time data [22]. In [11], the connectivity of vehicles depends on the generalized speed factor (GSF), which reflects the density of vehicles on a particular road segment with unit h/km or s/m and the impact of the relative velocity on the inter-vehicle spacing. Specifically, the definition of GSF is based on the normal distribution of relative speed and the exponential distribution of inter-vehicle spacing [11]. The definition of GSF is given below:
where
where and denote the minimum and maximum speed of vehicles, respectively. Additionally, s represents the inter-vehicle spacing. The speed v and inter-vehicle spaces s have an indirect proportional relationship with each other. According to the definition of GSF, the probability of the connectivity of N vehicles at time t can be obtained as follows:
where and R denote the vehicle density and V2V transmission range, respectively. Equation (4) indicates that vehicle speed, vehicle density, and V2V transmission range affect the vehicle’s connectivity in a free-flow highway.
3.3. Strongly Connected (STC) Route Selection
The purpose of our proposed connectivity-based routing scheme is to select a strongly connected (also referred as STC) route for data transmission among vehicles. STC is a set of intermediate links that have high probability of connectivity. Multiple routes may exist in a vehicular network to pass data from the source to destination. Suppose a route Z from the source to the destination d, where the source first transmits data to the cluster head and then transmits the data to the destination through k hops. If denote the vehicles participating in data transmission from to d, then the link of the route can be denoted by with different connectivities. Moreover, the connectivity of a particular link, i.e., , where , can be calculated using Equation (4). The connectivity of a route Z can be calculated by the following:
where represents the connectivity of path Z between source s and destination d at time t. In a nutshell, Equation (5) is the product of all intermediate connected links between the source and destination on path Z. If is the set of n alternate routes from s to d, STC at time t can be calculated as below:
Here, Equation (6) returns the strongest connected route from the source to destination.
4. Proposed Connectivity-Based Clustering Schemes
This section explains how efficiently vehicles are divided into clusters using link connectivity metric. Firstly, connectivity of vehicles is calculated and then converted to the adjacency matrix for graphical representation of VANETs. Lastly, the adjacency matrix is mapped to spectral clustering for dynamic formation of clusters and CH selection.
4.1. Vehicular Connectivity to VANET Graphs
The dynamic and inconsistent structure of VANET is a big challenge for routing reliability. In the literature, researchers used various parameters to design reliable routing algorithms for optimal data communication [7,23]. In this paper, we use vehicular connectivity as a metric for designing a cluster-based routing scheme. The performance of linear routing significantly degrades in the ultra-dense network due to excessive iterative messages. The formation of clusters is an appropriate choice to divide the network into manageable groups optimally. In this section, we represent VANET as a graph , where E, V, and C represent the edges, number of the vehicles, and connectivity, respectively. The graphical representation of vehicular topology is given by the following:
where A is the affinity matrix and denotes that and are connected to each other. We used three conditions to calculate the adjacency matrix of the vehicular network:
- The value of link connectivity is added to the th position of adjacency matrix if vehicle and are connected.
- If a link represents the same connectivity in both directions, i.e., , then we add 1 value for connectivity.
- The term “otherwise” in Equation (7) is considered when the first two conditions failed. When two vehicles are not connected, we add 0 in that case. The adjacency matrix representing the inter-connectivity of vehicles can be calculated as below:
4.2. Cluster Formation and Cluster Head Selection in the Suggested Routing Scheme
The reliability metric in [3] considered the duration of vehicles’ link with respect to velocity and inter-vehicle spacing while ignoring the relative transmission range and spatial density. Spatial density refers to the number of vehicles in a particular road segment for a given time period. Spectral clustering is semi-convex unsupervised learning, where the classification of data s based on the connectivity of data points. An Eigen gap heuristic approach was used in spectral clustering to measure an optimal number of clusters [3]. The dynamic nature of VANET is an appropriate choice for spectral clustering to divide the vehicles into steerable groups [3]. In spectral clustering, the topological graph G is converted to the Laplacian matrix , where D and are the diagonal matrix and adjacency matrix, respectively. The D matrix maintain the degree of each node (i.e., vehicle) on the diagonal.
where represents the degree of vehicle. The definition of Laplacian matrix is given below:
In spectral clustering, spectral decomposition is performed to factorize the matrix into Eigenvalues and their subsequent Eigenvectors. The significance of the spectral (Eigen) decomposition is to reduce the computational cost and space complexity. In the literature, many clustering schemes in machine learning are used for the formation of the cluster, but most of them are non-convex, where data size and high dimension give bad results in term of cluster shape and size. In spectral clustering, the Eigen decomposition significantly minimizes the dimensionality (i.e., selects only similar features in the form of Eigen vectors and Eigenvalues) of the vehicles. The selected dimensions represent only important features instead of taking the whole data set. For measuring the optimal number of clusters in highly dynamic networks, the Eigenvalues of the Laplacian graph L were used as an input. Let be the Eigenvalue, where in the ascending order, then based on Eigen gap heuristic, the number of clusters will be as follows:
The difference in Eigen gap should be greater than 1 to optimally divide the evolving network into clusters. To select an optimal , it is necessary to measure the cluster ranking. For this purpose, we calculated the Eigen centrality of each cluster. The Eigenvector centrality matrix E can be calculated as below:
In Equation (10), and A represent the maximum Eigenvalue and Affinity matrix, respectively. The parameter C represents the degree matrix of dimension. in a particular cluster k can be obtained as follows:
where represents the cluster head of cluster k.
5. Route Discovery in the Suggested Connectivity-Based Clustering Scheme
The disclosed clustering scheme was based on V2I communications, where the RSU performs the process of grouping. The route discovery to a particular destination depends on the location of the target vehicle. It is possible that the destination node within-cluster or outside the cluster depends on the node’s physical location. In light of the destination node location, the suggested scheme has two types of strategies in route discovery, i.e., intra-cluster discovery and inter-cluster discovery. The CEG-Dijkstra algorithm uses an intra-cluster discovery inside the cluster [3]. On the other hand, in frontier-cluster discovery, i.e., inter-cluster discovery, our scheme uses the Frontier Access Protocol (FAP). Detailed descriptions of each discovery strategy is given in their separate sections below.
5.1. Route Discovery in Intra-Cluster to the Destination
The route discovery in intra-cluster was adopted from the CEG-RAODV protocol [3]. The author in [3] used CEG-Dijkstra for route discovery, where the source node forwards the route request to . Later, the leading node, i.e., , calculates all possible routes to the destination. The proposed connectivity-based clustering scheme in this paper also uses CEG-Dijkstra for strong route (i.e., STC) discovery. At the beginning of the route discovery process, CEG-Dijkstra assigns a connectivity value, i.e., and (The value of CV for destination will change later to the interval [0–1] after its discovery.), to CH and all other vehicles, respectively, as STC routes. Then, using Equation (5), all possible connected routes are calculated from the source to destination. Finally, using (6), a strongly connected route with a higher connectivity value is selected as the STC from source node to destination.
5.2. Route Discovery in Inter-Cluster to the Destination
In our proposed cluster-based scheme, the discovery to a particular destination in inter-cluster is performed by the Frontier Access Protocol (FAP). The mechanism of FAP is the same as that for the Border Gateway Protocol (BGP) [24]. In FAP, all clusters connect to a unique RSU that forms an Autonomous System (AS). FAP enables inter-AS and intra-AS communications. Our current model is only limited to intra-AS communication, which enables inter-cluster communication. The discovery process of FAP is given below.
- FAP enables each CH to obtain cluster reachability information from RSU. The reachability information refers to the list of connected nodes to a particular RSU and/or CH. It is similar to a routing table that stores information of all accessible nodes.
- Next, RSU propagates the reachability information to all CHs.
In Figure 1, a source vehicle in cluster X discovers a destination d. The source vehicle first creates a route request message that disseminates inside the cluster through CEG-Dijkstra. Once the Dijkstra fails to reach the destination d, the forwards the request to the RSU. Since the RSU has the reachability information of all clusters using FAP, it thus forwards the request to the subsequent . At the end, discovers the particular destination using CEG-Dijkstra and forwards back to the source in the reverse path.
6. Simulation Results and Discussion
This section assesses the suggested clustering scheme under various performance metrics and experimental setup. We performed multiple experiments under specific traffic and network simulation setups. The overall tests are presented with the help of a traffic simulator and network simulator. In our case, the traffic simulation was performed with SUMO 0.25.0, while network simulation (i.e., routing) was performed with the help of MATLAB R2015b. SUMO is an open source traffic simulator licensed under General Public License (GPL) collaboratively developed by the Center for Applied Informatics Cologne (ZAIK) and the ITS at the German Aerospace Center (DLR). We extracted real road traces through SUMO and deployed vehicle traffic with the help of randomTrips.py application [25,26]. To assess the impact of connectivity over the performance of our proposed clustering scheme, we compared the proposed scheme with a reliability-based clustering scheme [3] as well as with the triple cluster-based routing protocol (TCRP) [1]. We performed several experiments, including temporal assessment of the dynamic formation of clusters, assessment of the link connectivity, and assessment of overhead (i.e., route request messages and average packet loss). The traffic and network simulation setups are shown in Table 1 and Table 2, respectively. The definition of our selected performance metrics such as overhead/RRMs, average packet loss, number of clusters, and link connectivity are given below:

Table 1.
Traffic simulation specification.

Table 2.
Network simulation specification or routing specification.
Overhead/RRMs: The overhead in our context is related to the magnitude of route request messages in the discovery of a particular destination. The performance of a network will be worse if an excessive number of messages disseminates in the discovery of a strongly connected route.
Average packet loss: Packet loss is measured as a percentage of dropped packets from all active connections with respect to all sent packets. In our case, we considered the mean packet drops of all clusters.
Number of clusters: The number of clusters explains how dynamic and evolving our disclosed clustering scheme is under various temporal densities. The term temporal density refers to the number of vehicles at different time stamps. The dynamic selection of clusters handles the highly evolving structure of VANET. This metric reduces the computational cost as well as improves the connectivity of routes by a dynamic number of clusters.
Route connectivity/link connectivity: Route connectivity refers to the probability of a route connectivity under a specific transmission range and node density. It represents the stability of a route. A strongly connected route (i.e., high probability of connectivity) will be more stable compared to the loosely connected route.
6.1. Assessment of the Dynamic Number of Clusters
In this section, we assess and compare the performance of the suggested clustering scheme with the previous reliability-based clustering scheme. In both schemes, the number of clusters (NoC) are assessed temporally to observe how the said protocols behave or evolve with the continuous arrival of vehicles. The temporal assessment of the connectivity and reliability-based clustering is shown in Figure 2. Both schemes are evaluated under real traces of SUMO-generated traffic. It is noticed that the number of clusters in connectivity-based as well as reliability-based schemes variate with the passage of time. Since the number of vehicles change due to continuous entry–exit of vehicles to the highway that subsequently affect the NoC. At different time stamps, the number of vehicles reduces in both schemes because of some vehicles’ departure. Thus, it is determined that the proposed connectivity-based clustering scheme performs well in terms of the number of clusters. This means that the connectivity metric efficiently reflects the evolving structure of VANETs. The large number of clusters are related to the high variations of evolving VANETs.
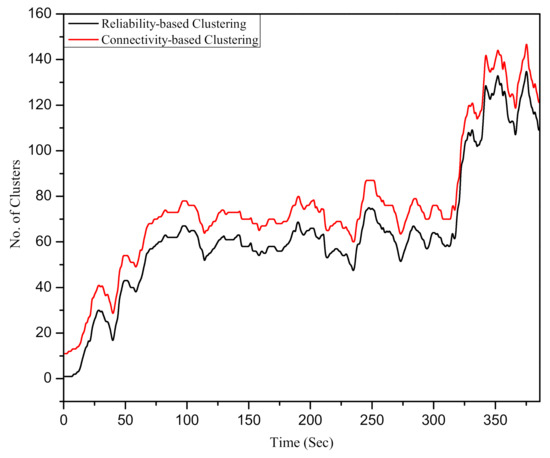
Figure 2.
Temporal assessment of connectivity-based clustering (our suggested scheme) and reliability-based clustering scheme [3].
From the Figure 2, it is noted that connectivity plays a vital role in optimally dividing the highly dynamic VANET such as link reliability [3]. We also noted that the number of clusters in connectivity-based clustering is slightly higher than reliability-based clustering. Additionally, it is also determined that the heuristic Eigen gap performs well when selecting an optimal number of clusters based on the variation in vehicles temporally. Initially, the number of clusters are very few due to the smaller number of vehicles but, later, increases gradually with the temporal increase in continuous arrival of traffic. See that, at scale 800 to 900 in Figure 2, the number of clusters significantly increases.
6.2. Assessment of the Connectivity-Based Clustering Overhead
The overhead of the suggested protocol was evaluated with RRMs and average packet loss, as defined above. The overhead of suggested connectivity-based clustering was compared with reliability-based clustering [3] and Triple Cluster-based Routing Protocol (TCRP) [1]. Firstly, the metric for clustering in the previous TCRP was converted to link connectivity. In this experiment, we considered a congested traffic scenario on a highway, where continuous arrival of vehicles was in practice. The number of RRMs was massive to discover a strongly connected route towards a particular destination in a highly congested network. Since the suggested connectivity-based clustering and previous reliability-based clustering dynamically divide the network into an optimal number of clusters, the number of control messages is significantly lower compared to TCRP, as shown in Figure 3. The reliability and connectivity-based clustering use a heuristic approach for an optimal number of clusters; that is why the magnitude of the RRMs is also very low.
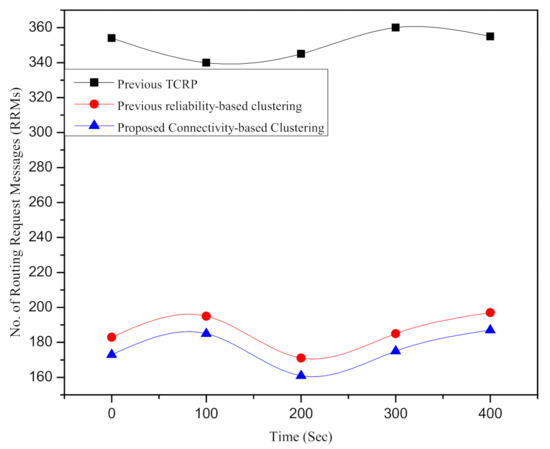
Figure 3.
Comparison of our suggested connectivity-based clustering overhead/route request messages (RRMs) with the previous reliability-based clustering [3] and triple cluster-based routing protocol (TCRP) [1].
In contrast, the TCRP forms a fixed number of clusters (i.e., three clusters); that is why the number of RRMs is significantly higher compared to the reliability and connectivity-based scheme. From Figure 2, we also notice that the number of clusters in our proposed connectivity-based clustering scheme is slightly more than the reliability-based scheme; thus, the magnitude of RRMs is also lower in Figure 3. The greater number of clusters enables our suggested clustering scheme to combine strongly connected vehicles in a cluster. The route discovery process in intra-cluster creates fewer RRMs due to the smaller number of clusters. Similarly, in inter-cluster discovery, the suggested FAP summarizes the reachability information of each cluster, which reduces significantly the number of RMMs. In a nutshell, due to the greater number of clusters, the suggested scheme has less overhead in discovering a particular destination.
Moreover, we also assessed the suggested protocol in terms of average packet loss. From Figure 4, it is noticed that the suggested scheme has less packet loss compared to the previous schemes. The packet loss in connectivity-based and reliability-based schemes are significantly less than TCRP. The reason behind a smaller number of packet losses in the aforementioned schemes is the evolving nature or the dynamic number of cluster selection. Additionally, we can see that our suggested connectivity-based scheme is slightly better than the previous reliability-based scheme because of its more dynamicity and application of FAP. It can also be seen in Figure 2 that our suggested scheme is fast evolving in the selection of clusters under various numbers of vehicles. Since TCRP forms only three clusters in all cases, i.e., the congested and non-congested scenarios, its performance is worse in terms of packet loss due to the highly dense clusters.
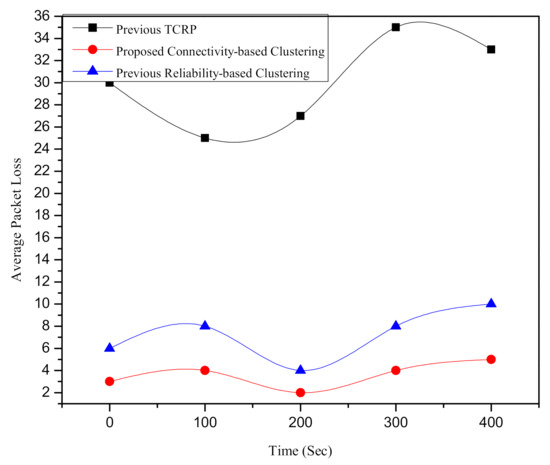
Figure 4.
Comparison of our suggested connectivity-based clustering packet loss with the previous reliability-based clustering [3] and TCRP [1].
6.3. Assessment of the Route Connectivity of the Proposed Clustering Scheme
In this subsection, we assess and compare the route connectivity of the suggested clustering scheme with the previous TCRP and reliability-based routing scheme [3]. Here, the simulation environment is the same as that which we used above in the assessment of RRMs and average packet loss, i.e., a congested traffic scenario with continuous arrival of vehicles. It is indicated in Figure 5 that the link connectivity of the suggested clustering scheme is higher than the linear routing scheme and TCRP. The link connectivity of the proposed connectivity-based clustering is high due to the heuristic approach of spectral clustering in dividing the network into an optimal number of clusters. Additionally, our suggested scheme forms a large number of clusters in highly dense networks that subsequently reduce the number of cluster members. As a result, it reduces the overhead as well as combined strongly connected vehicles in clusters, which subsequently positively affects the selection of route connectivity. The performance of the linear scheme in terms of link connectivity is even worse than TCRP because of the lack of clustering. In the linear scheme, there is no boundary to limit the broadcast storm; thus, a simple beacon message can flood the whole network and subsequently affect the link connectivity.
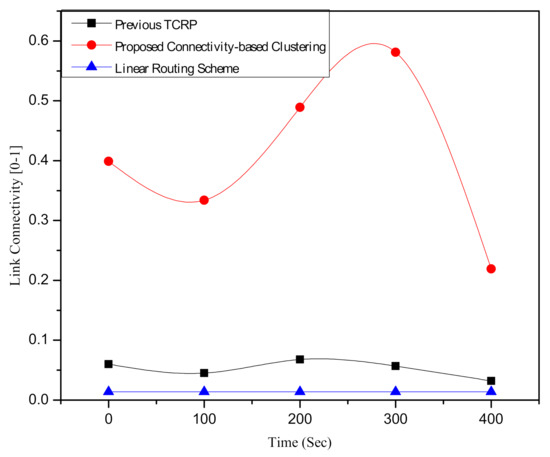
Figure 5.
Intercomparison of route connectivity of our suggested connectivity-based clustering scheme with TCRP [1] and linear routing scheme.
Our simulation results show that the proposed clustering scheme performs well in terms of the selected performance metrics, i.e., number of clusters, route connectivity, and route RRMs, as mentioned in the aforementioned sections (Section 6.1, Section 6.2 and Section 6.3). Thus, on the basis of the simulation findings, we determine that the link connectivity metric and heuristic approach of spectral clustering in our suggested scheme obtain better performance compared with the existing routing schemes for high evolving networks. As a result, we determine that the heuristic approach of spectral clustering as well as the connectivity metric play vital roles in forming long-lasting and stable clusters.
7. Conclusions and Future Work
The highly dynamic and evolving structure of VANET is a big challenge for V2V and V2I communications. Clustering is an essential step towards the reliability, stability, and scalability of VANETs. The formation of clusters and CH selection are strongly related to the performance of a routing scheme. The proposed criteria for clustering in this work, i.e., link connectivity, considers the relative position and transmission range of a vehicle in a particular road segment. The suggested connectivity-based clustering uses link connectivity as a metric for cluster formation and CH selection. From the results, it is noticed that the proposed metric for clustering forms long-lasting groups of vehicles as well as significantly increases the probability of connectivity of a selected route. Moreover, it also reduces the computational cost by reducing the excessive number of RRMs. The spectral clustering optimally divides the evolving VANET into manageable groups based on the structure of network. This is the reason why the number of RRMs and packet loss never reach their worst performance threshold. Moreover, the CEG-Dijkstra and FAP play essential roles in discovering a strongly connected route in the intra-cluster and inter-cluster modes, respectively. The former discovers the destination node/vehicle within a cluster, while the latter is triggered in the case of outside discovery. Thus, the process of route discovery does not significantly increase the computational cost because of the specification of inter- and intra-cluster discovery. In the future, the proposed connectivity-based clustering scheme will be evaluated on real-road scenarios and an assessment will be performed through more comprehensive metrics.
Author Contributions
The conceptualization, methodology, and original draft writing were performed by Z.K. The supervision, validation, and writing—review and editing—were conducted by A.K. Formal analysis and proofreading were performed by S.F. and K.M. M.Y.L. addressed all the comments of the reviewers in the third round. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2018R1D1A1B07043302). It was also partially supported by Prince Sultan University, Kingdom of Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Robotics and Internet-of-Things Lab of Prince Sultan University, Riyadh, Kingdom of Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khan, Z.; Fan, P. A novel triple cluster based routing protocol (TCRP) for VANETs. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Wahid, I.; Ikram, A.A.; Ahmad, M.; Ali, S.; Ali, A. State of the art routing protocols in VANETs: A review. Procedia Comput. Sci. 2018, 130, 689–694. [Google Scholar] [CrossRef]
- Khan, Z.; Fan, P.; Fang, S.; Abbas, F. An Unsupervised Cluster-Based VANET-Oriented Evolving Graph (CVoEG) Model and Associated Reliable Routing Scheme. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3844–3859. [Google Scholar] [CrossRef]
- Khan, Z.; Fan, P. A multi-hop moving zone (MMZ) clustering scheme based on cellular-V2X. China Commun. 2018, 15, 55–66. [Google Scholar] [CrossRef]
- Eiza, M.H.; Ni, Q. An evolving graph-based reliable routing scheme for VANETs. IEEE Trans. Veh. Technol. 2013, 62, 1493–1504. [Google Scholar] [CrossRef]
- Khan, Z.; Fan, P.; Abbas, F.; Chen, H.; Fang, S. Two-level cluster based routing scheme for 5G V2X communication. IEEE Access 2019, 7, 16194–16205. [Google Scholar] [CrossRef]
- Lin, D.; Kang, J.; Squicciarini, A.; Wu, Y.; Gurung, S.; Tonguz, O. MoZo: A moving zone based routing protocol using pure V2V communication in VANETs. IEEE Trans. Mob. Comput. 2016, 16, 1357–1370. [Google Scholar] [CrossRef]
- Khan, Z.; Fang, S.; Koubaa, A.; Fan, P.; Abbas, F.; Farman, H. Street-centric routing scheme using ant colony optimization-based clustering for bus-based vehicular ad-hoc network. Comput. Electr. Eng. 2020, 86, 106736. [Google Scholar] [CrossRef]
- Abbas, F.; Liu, G.; Fan, P.; Khan, Z. An Efficient Cluster Based Resource Management Scheme and Its Performance Analysis for V2X Networks. IEEE Access 2020, 8, 87071–87082. [Google Scholar] [CrossRef]
- Cooper, C.; Franklin, D.; Ros, M.; Safaei, F.; Abolhasan, M. A comparative survey of VANET clustering techniques. IEEE Commun. Surv. Tutor. 2016, 19, 657–681. [Google Scholar] [CrossRef]
- Khan, Z.; Fan, P.; Fang, S. On the connectivity of vehicular ad hoc network under various mobility scenarios. IEEE Access 2017, 5, 22559–22565. [Google Scholar] [CrossRef]
- Liu, G.; Qi, N.; Chen, J.; Dong, C.; Huang, Z. Enhancing clustering stability in VANET: A spectral clustering based approach. China Commun. 2020, 17, 140–151. [Google Scholar] [CrossRef]
- Naumov, V.; Gross, T.R. Connectivity-aware routing (CAR) in vehicular ad-hoc networks. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 1919–1927. [Google Scholar]
- Viriyasitavat, W.; Tonguz, O.K.; Bai, F. UV-CAST: An urban vehicular broadcast protocol. IEEE Commun. Mag. 2011, 49, 116–124. [Google Scholar] [CrossRef]
- Tonguz, O.; Wisitpongphan, N.; Bai, F.; Mudalige, P.; Sadekar, V. Broadcasting in VANET. In Proceedings of the 2007 Mobile Networking For Vehicular Environments, Anchorage, AK, USA, 11 May 2007; pp. 7–12. [Google Scholar]
- Peng, Y.; Abichar, Z.; Chang, J.M. Roadside-aided routing (RAR) in vehicular networks. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; Volume 8, pp. 3602–3607. [Google Scholar]
- Khakpour, S.; Pazzi, R.W.; El-Khatib, K. Using clustering for target tracking in vehicular ad hoc networks. Veh. Commun. 2017, 9, 83–96. [Google Scholar] [CrossRef]
- Sathiamoorthy, J.; Ramakrishnan, B. Design of a proficient hybrid protocol for efficient route discovery and secure data transmission in CEAACK MANETs. J. Inf. Secur. Appl. 2017, 36, 43–58. [Google Scholar] [CrossRef]
- Alsharif, N.; Shen, X. i CAR-II: Infrastructure-Based Connectivity Aware Routing in Vehicular Networks. IEEE Trans. Veh. Technol. 2016, 66, 4231–4244. [Google Scholar] [CrossRef]
- Ji, X.; Yu, H.; Fan, G.; Sun, H.; Chen, L. Efficient and reliable cluster-based data transmission for vehicular ad hoc networks. Mob. Inf. Syst. 2018, 2018. [Google Scholar] [CrossRef]
- Shao, C.; Leng, S.; Zhang, Y.; Vinel, A.; Jonsson, M. Performance analysis of connectivity probability and connectivity-aware MAC protocol design for platoon-based VANETs. IEEE Trans. Veh. Technol. 2015, 64, 5596–5609. [Google Scholar] [CrossRef]
- Ahmad, M.; Li, T.; Khan, Z.; Khurshid, F.; Ahmad, M. A novel connectivity-based LEACH-MEEC routing protocol for mobile wireless sensor network. Sensors 2018, 18, 4278. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Zhang, J.; Khoukhi, L.; Labiod, H.; Vèque, V. A unified framework of clustering approach in vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1401–1414. [Google Scholar] [CrossRef]
- Kent, S.; Lynn, C.; Seo, K. Secure border gateway protocol (S-BGP). IEEE J. Sel. Areas Commun. 2000, 18, 582–592. [Google Scholar] [CrossRef]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO–simulation of urban mobility: An overview. In Proceedings of the SIMUL 2011, The Third International Conference on Advances in System Simulation ThinkMind, Barcelona, Spain, 23–28 October 2011. [Google Scholar]
- Kabrane, M.; Krit, S.; Elmaimouni, L.; Bendaoud, K.; Oudani, H.; Elasikri, M.; Karimi, K.; El Bousty, H. Smart cities: Energy consumption in wireless sensor networks for road trafile modeling using simulator SUMO. In Proceedings of the 2017 International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017; pp. 1–7. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).