Abstract
Topology optimization is a powerful digital engineering tool for the development of lightweight products. Nevertheless, the transition of obtained design proposals into manufacturable parts is still a challenging task. In this article, the development of a freeware framework is shown, which uses a hybrid topology optimization algorithm for stiffness and strength combined with manufacturing constraints based on finite spheres and a two-step smoothing algorithm to design manufacturable prototypes with “one click”. The presented workflow is shown in detail on a rocker, which is “one-click”-optimized and manufactured. These parts were experimentally tested using a universal testing machine. The objective of this article was to investigate the performance of “one-click”-optimized parts in comparison with manually redesigned optimized parts and the initial design space. The test results show that the design proposals created while applying the finite-spheres and two-step smoothing are equal to the manual redesigned parts based on the optimization results, proposing that the “one-click”-development can be used for the fast and direct development and fabrication of prototypes.
1. Introduction
In modern product development, the sustainability and performance of the parts are more critical than ever. Simultaneously produced products are desired to be personally optimized for customers’ needs. Topology optimization (TO) is one of the leading computer-aided engineering (CAE) tools for structural optimization [,,]. In recent years, TO has reached a certain maturity and is a well-established research field [,] and is also used in many industrial fields [,], such as structural and civil engineering [,], mechanical engineering [,,,] or aeronautical engineering [,,].
Existing TO tools in the market are mainly commercial software tools. In addition to these, many open source codes are available online. Nevertheless, these open source codes are often hard to implement into everyday workflows. Freeware solutions which provide all functionalities of meshing, preprocessing, optimization and postprocessing are rarely found. To the best of our knowledge, the only two are TopOpt [] (TopOpt group, University of Denmark, Lyngby, Denmark) and Z88Arion (Chair of Engineering Design and CAD, University of Bayreuth, Bayreuth, Germany).
TO determines the optimal material distribution in a design space under defined loads and constraints. After [], today’s TO approaches can be classified into density methods, level set methods, phase field methods, and topological derivates. Existing algorithms can be clustered into mathematical and empirical approaches. An overview can be found for instance in [,]. New methods are shown in [], for instance, where neural networks are directly used in TO as an alternative to the commonly applied solid isotropic material with penalization (SIMP) approach. Today’s research in TO is often linked with additive manufacturing (AM) since its freedom of design is almost essential for fabricating topology-optimized structures [,,,,,,]. The exploitation of lattice structures or graded porosity is of high interest in many cases [,,]. Nevertheless, the interpretation of the optimization result and its transformation into a parametric CAD geometry is still challenging. Approaches to solving this problem can be found, for example, in [,,].
To enhance the manufacturability of optimized designs, manufacturing constraints are introduced [,]. While manufacturing constraints of casting processes have been of high interest since the early 2000s [,,,,], the focus of today’s research is shifting towards AM [,,,,,,,,,]. The consideration of design for additive manufacturing (DfAM) aspects leads to superior solutions compared with unconstrained TO since the designs can be interpreted more efficiently and can be manufactured “as optimized” in many cases [,].
This article presents a method to streamline the TO-based product development process from the initial design space to the ready-to-manufacture file by creating a process that is executable by “one click” and is referred to in the following as “one-click” optimization. The one-click optimization process, as described in Figure 1, mainly consists of TO using the topology optimization for stiffness and strength (TOSS) algorithm [] followed by a two-step smoothing algorithm [] for postprocessing. Furthermore, this article introduces finite sphere-based manufacturing constraints to consider DfAM aspects []. With these functionalities, it is possible to widely automate the conventional product development process.
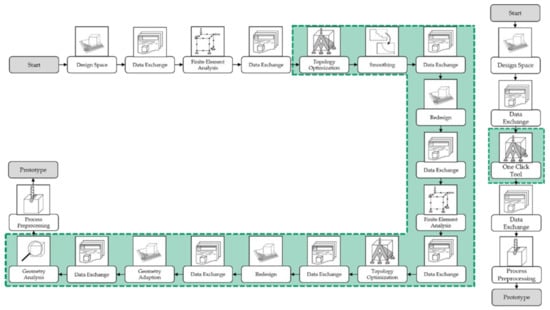
Figure 1.
The visualization of the presented one-click optimization approach. The one-click tool aims to re-place and to widely automate the steps of topology optimization, smoothing, data exchange and redesign and finite element analysis, which are shown inside the green shaded area.
This article investigates the performance of one-click optimized parts compared to manually redesigned parts and the initial design space. Therefore, the parts are additively manufactured and experimentally tested using a universal testing machine. The main goal is to show if the one-click optimized parts can be used as alternatives to the redesigned parts, leading to faster product development for optimized lightweight structures. The presented one-click optimization method is implemented in the TO freeware Z88Arion® (developed by the Chair of Engineering Design and CAD, University of Bayreuth, Bayreuth, Germany) and is available at [].
2. Materials and Methods
The following section describes the various steps used in the one-click optimization method in detail. In addition, it introduces the application example and explains the testing and evaluation procedure.
2.1. Topology Optimization for Stiffness and Strength
For TO, the freeware Z88Arion® was used, which was based on density methods for TO. While in general, the SIMP and rational approximation of material properties (RAMP) were implemented, SIMP was used for all optimizations presented in this article. The SIMP method thereby is given as
where describes the adapted Young’s modulus of the material, respectively, describing the Young’s modulus for the solid material, is the design variable and the penalization factor [,].
The used TOSS algorithm was developed in []. It is a hybrid TO algorithm, where first a minimum compliance optimization problem is solved by using the optimality criterion method (OC) []. The optimization problem for this first step can be written as follows:
where denotes the compliance, describes the displacement vector and the stiffness matrix. The optimality criterion after [,] is then given as
with , and as Lagrange multiplicators and the volume of the initial elements. To satisfy the optimality criteria in Equation (3), has to be equal to 1 for all elements . This finally leads to the following iteration rule:
with a step length and a damping factor so that a decision for the new design variable can be made with consideration of the design variable at iteration step .
After convergence was obtained, a strength optimization was started based on empirical TO approach. In this case, the soft kill option (SKO) was used, which used the biological rule of growth to maximize the strength. This was done by achieving a homogeneous surface tension [,,]. In this procedure, during the finite element analysis (FEA) for each node the equivalent stress was computed. The equivalent stress was then used to simulate the biological rule of growth. In contrast to mathematical TO approaches, Young’s modulus of the elements was directly modified. This modification can be easily done by varying the node temperatures of the finite elements. It emphasizes here that these temperatures have no physical meaning and are only used to easily modify Young’s modulus. This possible since Young’s modulus can be defined as a function of the element temperatures in every FEA software []. Therefore, a virtual temperature was computed for each node inside the design space:
with:
and the scaling factor and reference stress , which are the user-defined inputs. The virtual temperature is then calculated for each element :
where represents the number of nodes per element, correspondingly describes , the first node which belongs to the element and , the last node. The Young’s modulus for each element is then evaluated by
After the strength optimization converged, the final design proposal was obtained. The conceptual procedure of the TOSS algorithm is shown in Figure 2.
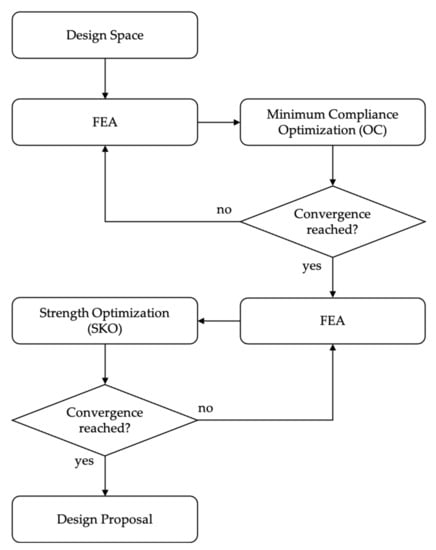
Figure 2.
Conceptual procedure of the topology optimization for stiffness and strength (TOSS) algorithm.
2.2. Finite Spheres as Manufacturing Constraints
The concept of finite spheres means a useful manufacturing constraint for casting processes and AM as it describes and solves manufacturing conflicts []. For the implementation of the concept of finite spheres to the TO problem, we assumed that every element has a physically reasonable volume. Then, each element was abstracted by a sphere with an identical center of gravity and volume . Therefore, the effective radius of the sphere for element is:
with a tolerance angle . The tolerance angle is a solely technical tool which was used later to describe a manufacturing conflict. Basically, the idea is not to evaluate the elements but the finite spheres if they have manufacturing conflicts. A manufacturing conflict is defined here as two spheres with overlapping radii. In the context of casting processes, this describes an undercut. Hence, the tolerance angle can be used to specify that an overlapping only occurs, if two spheres encounter in an angle below . Therefore, the effective radius of the spheres was adapted as shown in Figure 3.
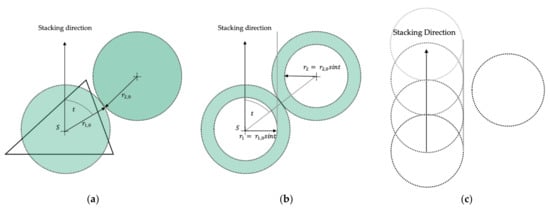
Figure 3.
Determination of the effective radii with the tolerance angle; S denotes the center of gravity: (a) the spheres with unadjusted radii collide in angle ; (b) the radii are multiplied with ; so that (c) the spheres can pass without overlapping.
This abstracted concept was then applied to calculate manufacturing conflicts in a given manufacturing direction (stacking direction AM; demolding direction, casting) in combination with a manufacturing angle (critical printing angle AM; demolding angle, casting) as illustrated in Figure 4.
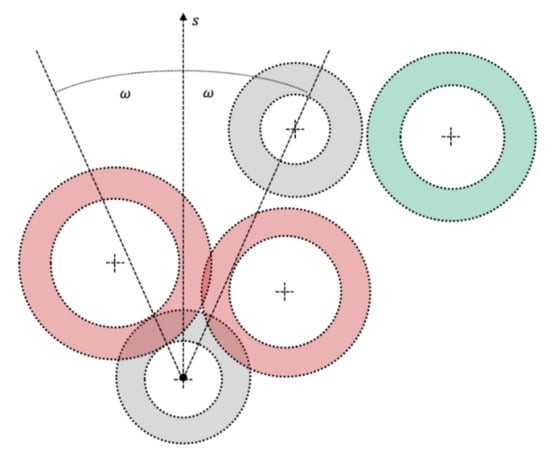
Figure 4.
Spheres with (red) and without (green) manufacturing conflict potential to the grey sphere in manufacturing direction and manufacturing angle .
Since we are generally interested in obtaining symmetric solutions, this consideration was performed in the positive and negative direction. This led to two cones for potential manufacturing conflicts as shown in Figure 5.
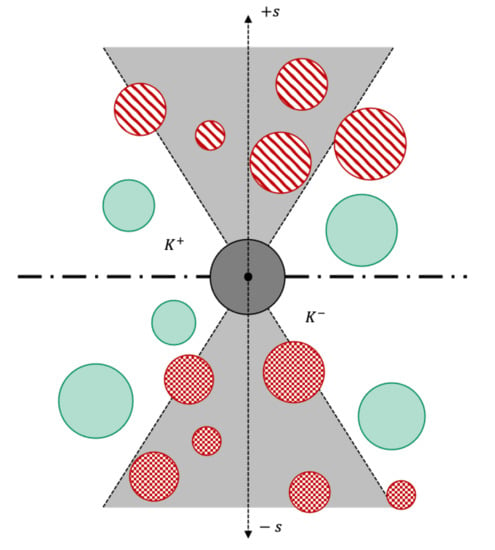
Figure 5.
Visualization of the conflict cones in the positive (+s) and negative (−s) direction. Conflict spheres in red and conflict-free spheres in green. The conflict spheres in the positive direction are stored in K+, while the conflict spheres in negative direction are stored in K−.
These simplifications allowed to mathematically characterize the manufacturing conflicts. In this context, a casting part was manufacturable, if the geometry can be demolded in a given angle and direction. An AM part, exemplarily a fused filament fabrication part, could be fabricated without support structures in a given stacking direction, if the critical printing angle was below a certain value, commonly 45 degrees. The sets of the potential conflict elements for each element is then given by
with the center of gravity . Thereby two sets, which contain all potential positive conflict elements, respectively, in the negative manufacturing direction, were obtained for each element. In order to consider also previously defined passive regions, their elements were gathered in fix sets which are defined as follows:
Hence, at the beginning of the optimization, no areas with existed, the set is a priori empty. If due to the fix sets, in manufacturing direction material was followed by a gap and then again by material, however, this gap has to be closed, so that the manufacturing conflict can be solved. Therefore, the sets are defined as fix set-induced conflict sets, which were updated along with the algorithm as the elements were (de-)activated:
These settings were then used to remove the manufacturing conflict elements from the optimization problem. Therefore, the part was changed stepwise in the direction of the local mass difference towards the nearest manufacturing conflict free part. To evaluate mass differences, the element mass is calculated as
Since real existing parts have a continuous geometry, it is obvious that this part had to be continuous in the manufacturing direction. Therefore, it was sufficient to determine the optimal margin of the part in the manufacturing direction. To evaluate the optimal margin, the design variable for all elements inside of the margin was set to 1, respectively, 0 for all elements outside of the margin. The optimal margin was then chosen, so that the deviation between the density distribution of the optimization result and the margin was minimal. Hence, the following equation defines the remaining loss , then the considered element is interpreted as a component of the local part surface, which is given by
for all . Therefore, is 0, if the element is not on the actual margin of the set . This definition was used to estimate the shape of the conflict-free part on the margins of set . This was used as an iterative decision tool, for which elements from belong to the nearest conflict-free part. Hence, a stepwise adaption is only reasonable for elements which are on the margin of . The margin sets:
with the maximizing objective function:
used to determine the next adaption of the solution geometry.
The adaption was performed by the activation or deactivation of elements. More precisely, an element was activated () if it was inside the margin and deactivated () if the element was outside of the margin. It was not intended to overwrite the density distribution of the superior TO, the (de-)activation depends on the actual value of the design variable. Therefore, for symmetry reasons, the following applies to each design variable:
whereby describes the deactivating function and describes the activation function, which is given by
where is the manufacturing rate. For , the calculation of manufacturing conflicts is deactivated.
This concept for considering manufacturing constraints in AM and casting processes was implemented in Z88Arion® and was applied in the following experiments. Further information on the implementation and theory of the finite sphere concept can be found in [] and the Z88Arion® documentation on [].
2.3. Two-Step Smoothing
Smoothing is a common post-processing operation which helps to make the TO result more convenient for the human eye and also allows to pass the geometry directly to the production. Therefore, it is an essential step for achieving a fully automated product development process. In this article, the implicit two-step smoothing algorithm, developed in [] was used for the post-processing of the TO results. For the smoothing algorithm, the densities of the individual nodes are needed. Hence, they had to be computed from the element densities of the elements which contained this particular node. These elements were further referred to as relevant elements. Hence, for each relevant element, the vectors , and from the node to its directly adjacent neighbors, as shown in Figure 6, were needed.
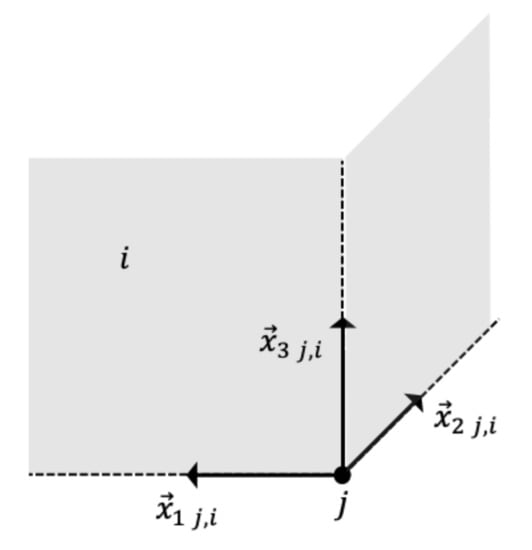
Figure 6.
Vectors from the node on element to its adjacent neighbor nodes.
Based on these vectors, the angle , for which the element encloses around the node , is calculated according to [] by
The angle was then multiplied by the value of the design variable of the considered element and was normalized with the sum of all angles of the relevant elements. This procedure was repeated and summed up to obtain the final node density []. In the actual smoothing process, the first step was performed by a slightly modified marching cube algorithm, where the node densities were used to determine which should be part of the smoothed TO result. Consequently, in the first step, a part with a defined surface based on the node density was created by placing triangles in appropriate places to obtain the surface of the part in the Standard Tessellation Language (STL) format. The second step was based on the implicit fairing approach, which was built on Laplace smoothing and was solved using implicit integration []. The smoothed STL-files were then directly transferred to the AM preprocessing software.
2.4. Example of Application
To validate the developed “one-click” optimization process, a test-part should generally be suitable to manufacture with AM processes and TO. Ideally, the main objective functions of the part were the minimum mass and maximum stiffness. With AM and TO aspects in mind, a rocker is a well-suited example of an application for the “one-click” optimization framework.
Rockers are part of cars’ suspension-system and are mainly used in racecars or expensive super-sportscars like the Lamborghini Aventador. Two of its essential aspects are stiffness and mass. Stiffness is of importance to prevent unnecessary play in the suspension-system, which can result in negative balance and drivability [].
In general, car suspensions link the upright (or knuckle) assembly with the car’s body []. The upright assembly’s main parts are the wheel bearings, wheel hubs, brake calipers, and the suspension’s fastening points; these are attached to the car’s body by different types of links. The complexity and type of the links often vary with car pricing or comfort aspects [].
Most modern production road cars use directly actuated shock absorbers and coil springs either by a MacPherson strut or a multilink suspension [,]. Two typically used systems are shown in Figure 7. Directly actuated refers to a one-to-one motion ratio of the coupled suspension-link and the spring-damper unit.

Figure 7.
Typical front suspension systems: (a) McPherson; and (b) double wishbone.
Nevertheless, the double-wishbone suspension with a rocker as part of the pushrod activated spring-damper unit, displayed in Figure 8, is used in some races—in super-sportscars. These low part volumes make the rocker potentially suitable to be replaced by optimized AM parts in the future, and therefore, are an appropriate example of application.
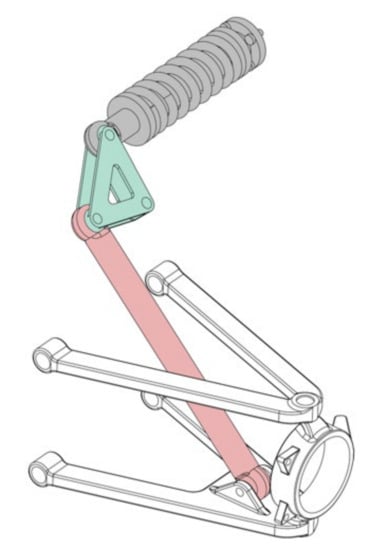
Figure 8.
Double wishbone suspension with pushrod (red), rocker (green) and spring-damper unit (grey).
In the double-wishbone suspension, the wheel travels upwards, the pushrod moves longitudinal to its axis, and rotates the rocker around a fixed pivot point, which results in the spring-damper unit’s compression. This causes two loads acting on the rocker, the compression force from the pushrod and the difference between the compression force from the spring and the damper unit .
Based on its assembly situation and working principle, the following initial design space in Figure 9 with its related forces was considered for the rocker optimization task. The particular values of the force components are listed in Table 1.
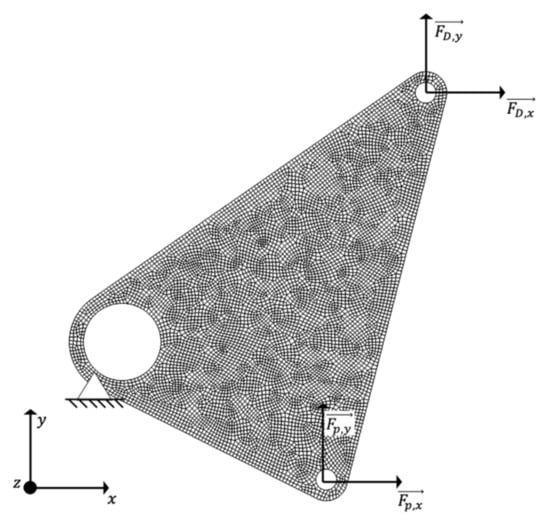
Figure 9.
Initial design space of the rocker chosen for TO and AM with its related forces.

Table 1.
Force components for the chosen topology optimization (TO) problem. The values are based on the measurements of a formula student racecar [].
2.5. Testing and Validation
The rocker in Figure 9 was used for the testing and validation of the method. Therefore, the initial design space was the reference model, and three various TO configurations were selected. This led to four configurations that were printed in total. The initial design space of the rocker was elected as the reference configuration (Reference). The TO configurations were as follows: an optimized part without the consideration of manufacturing conflicts and manually redesigned (redesigned); an optimized part without consideration of manufacturing conflicts and smoothed (Smoothed); and an optimized part with the consideration of manufacturing conflicts and smoothed (MaSmo). All TO runs had a volume constraint of 75% of the initial design space.
All parts were manufactured using the Markforged MarkTwo (Markforged Inc., Boston, MA, USA) and Onyx [] as material for all specimens. For each configuration, ten specimens were printed. The parts were printed with a triangular infill of 37%, 4 roof-, 4 floor- and 2 wall-layers, which were the default settings in the used preprocessing software Eiger (Markforged Inc., Boston, MA, USA). For the MaSmo Configuration, the stacking direction was in alignment with the manufacturing direction (z axis in Figure 9).
The testing was done on a universal testing machine, where the parts were clamped as shown in Figure 10 and uniaxial stressed. The traverse speed during all experiments ias 50 mm per minute.
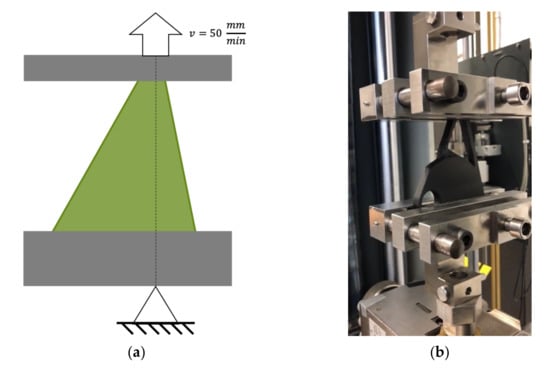
Figure 10.
Experimental set-up: (a) sketch; and (b) actual experimental set-up.
The chosen experimental set-up deviates from the most relevant loads shown in Figure 9. This is because parts were optimized according to the most common loads and boundary conditions in use, but the part also had to withstand several other types of load settings that were not considered in TO. Therefore, the chosen boundary conditions and loading of this set-up reflect a critical load-case when the wheel was blocked, which is one example of an additional load case to be considered during the part’s design.
For the evaluation, the manufacturability of the design proposals, the printing time, and the parts’ actual target volume were discussed. In evaluating the mechanical performance, the parts were investigated regarding their maximum forces, displacements, and stiffness at maximum stress.
3. Results
The TO set up according to the loads in 2.4. and the TO result without the consideration of manufacturing conflicts are shown in Figure 11.
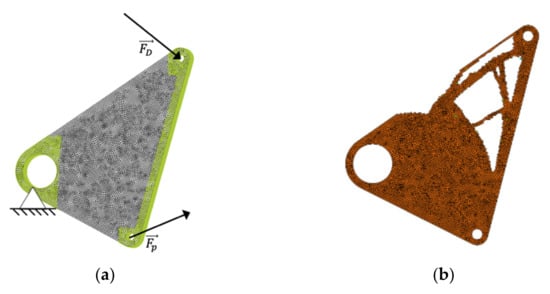
Figure 11.
Tested configurations of the rocker: (a) TO setup, the green areas are non-design spaces; and (b) TO result without the consideration of the manufacturing conflicts.
The derived post-processed TO design proposals are shown in Figure 12, the configurations smoothed and MaSmo are smoothed using 50 smoothing iterations. This number is empirically obtained from extensive studies with Z88Arion and has been proven to provide error-free STL-files in most cases. The settings chosen for the consideration of the manufacturing conflicts and are presented in detail in the next section. The redesigned configuration aims to stay as close to the original TO result as possible. The MaSmo configuration differs significantly from the other ones.
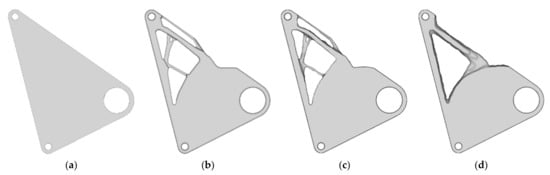
Figure 12.
Tested configurations of the rocker. (a) reference; (b) redesigned; (c) smoothed; (d) MaSmo.
As listed in Table 2, a target volume for all TO runs is 75%; nevertheless, the post-processed parts’ real volume differs from this target. Since the deviations are small in all cases, it is reasonable that the geometry adaption of the MaSmo configuration according to the least mass loss is reasonable.

Table 2.
Overview of the TO settings of all configurations. Since reference is the initial design space, no TO is performed for this configuration. All volumes are referenced on the volume of the reference configuration.
It is further important to mention that MaSmo shows the best convergence behavior at the chosen TO settings.
3.1. Manufacturability of Design Proposals
In this article, the previously described formulation of manufacturing conflicts improves the obtained design proposals’ direct manufacturability. The manufacturing rate controls the strictness of the manufacturing conflicts. As avoiding support at all costs is not always a goal-orientated approach, the manufacturing conflict rate is modified in the range of 0.5–1.0 to determine the appropriate manufacturing rate for the given application example. The results are given in Figure 13.

Figure 13.
TO results for various manufacturing rates . All elements whose design variable is greater than 0.1 are displayed. Additionally, the number of iterations until convergence is noted (a) iterations: 87; (b) , iterations: 41; (c) iterations = 41; (d) iterations: 99; (e) iterations: 99; and (f) iterations: 100.
Based on the results in Figure 13, a manufacturing rate of is chosen for the MaSmo configuration, as it is a good compromise between the original TO result and improved manufacturability. Furthermore, the influence of the manufacturing angle is shown in Figure 14.
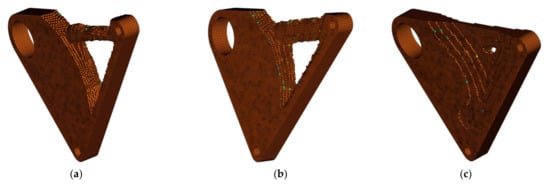
Figure 14.
TO results for various manufacturing angles at the manufacturing rate , all elements whose design variable is greater than 0.1 are displayed. Additionally, the number of iterations until convergence is noted. (a) , iterations: 76; (b) , iterations: 41 (c) , iterations: 100.
These results show that the manufacturing angle also heavily influences the convergence behavior of the TO. Moreover, the precise effect of the manufacturing angle on the TO result shows that the method works. For selecting the appropriate manufacturing angle, a common practice is followed by choosing 45 deg. To shortly summarize the manufacturing conflict settings, an overview is given in Table 3.

Table 3.
Overview of the manufacturing conflict settings chosen for MaSmo.
Subsequently, all four configurations are additively manufactured. The resulting printing times, actual plastic volumes deposited in total, and support volumes are compared in Table 4.

Table 4.
Manufacturing data overview. The plastic volume is the actual volume used in production and is referenced on the reference plastic volume. The support volume of redesigned is used as a reference for the comparison of the needed support volume. The support volume ratio is defined by the ratio of the used support structures to the plastic volume.
It is important to note that there is a significant change in the relative values between the plastic volume and the real volume after TO. MaSmo leads to shorter print time, and additionally, the needed support volume can be reduced by 47.4%. In addition, it is important to emphasize here that for redesigned, the support volume takes 0.76% of the total plastic volume.
3.2. Experimental Testing
The printed and experimentally tested specimens are shown in Figure 15.

Figure 15.
Printed and tested specimens: (a) reference; (b) redesigned; (c) smoothed; and (d) MaSmo.
The force–displacement plots are illustrated in Figure 16. The measured data’s qualitative mean curves are obtained by using a Gaussian process regression (gpr) model trained with the experimental data. Therefore, a radial basis function kernel with an added white kernel to handle the noise is used [].
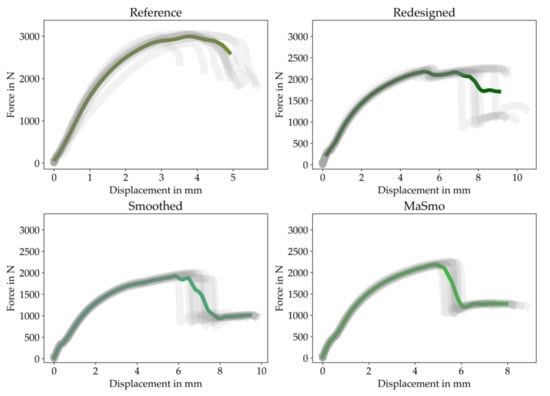
Figure 16.
Force–displacement plots for all configurations. The grey shaded lines are the experimental data, the green lines are predicted with the trained Gaussian process regression (gpr) model.
From the presented data, it is evident that the MaSmo configuration was the least noisy, leading to a good reproducibility of the “one-click” optimized part. The approximated curves of all configurations are compared in Figure 17.
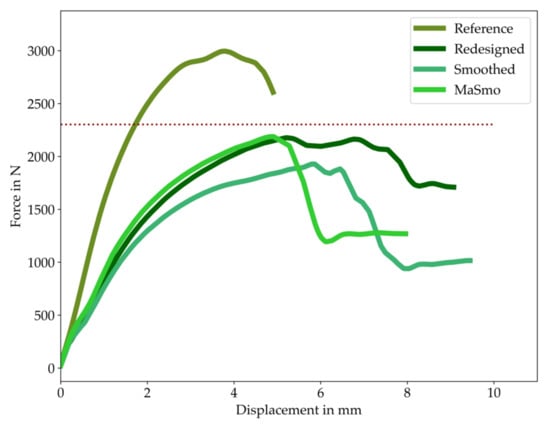
Figure 17.
Comparison of the approximated force–displacement behavior of all configurations. The red dotted line indicates the level 75% of the reference’s maximum force.
From this comparison, it can be evaluated that the maximum forces of redesigned and MaSmo are quite identical while smoothed performed significantly lower; this can be confirmed by evaluating the maximum forces in Figure 18.
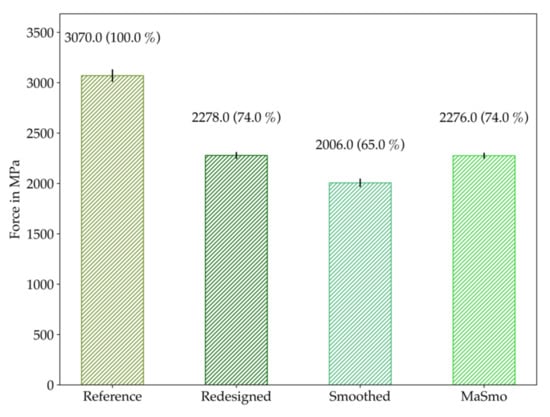
Figure 18.
Comparison of the maximum forces. The mean values are plotted together with the standard deviation. The difference from the reference is written in brackets in percent.
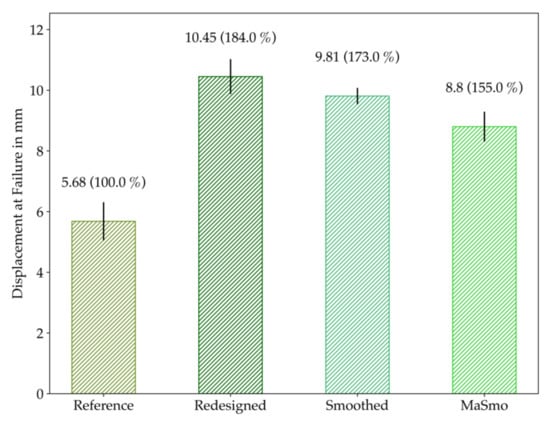
Figure 19.
Comparison of the displacement at failure. The mean values are plotted together with the standard deviation. The difference from the reference is written in brackets in percent.
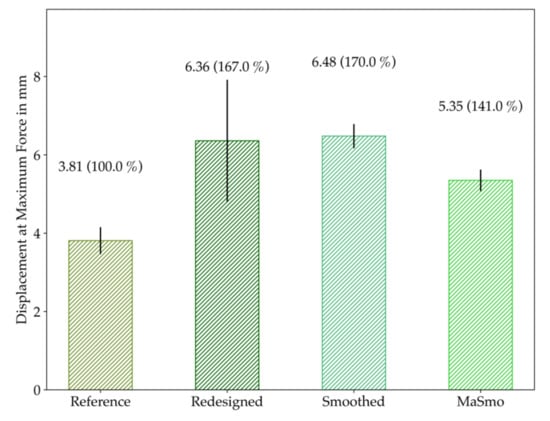
Figure 20.
Comparison of the displacement at maximum force. The mean values are plotted together with the standard deviation. The difference from the reference is written in brackets in percent.
In general, it can be observed that the displacements at failure and maximum force are on the same level for redesigned and smoothed, whereas the values for MaSmo are the lowest for the TO-configurations. The high standard deviation of redesigned is also to be emphasized here.
Since in particular cases TO maximizes the stiffness, the stiffness at maximum force is evaluated for all configurations in Figure 21.
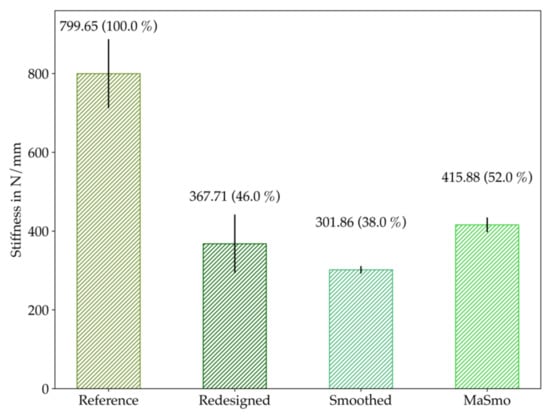
Figure 21.
Comparison of the stiffness at maximum force. The mean values are plotted together with the standard deviation. The difference from the reference is written in brackets in percent.
In this context, MaSmo clearly outperforms smoothed and slightly outperforms redesigned. Additionally, the standard deviation for MaSmo is significantly lower than for reference and redesigned.
4. Discussion
The objective of this article was to show the competitiveness of “one-click” developed TO prototypes in comparison to more conventional approaches. Therefore, finite spheres are used to add manufacturing constraints during the optimization. Since using an absolute strictness in preventing manufacturing conflicts may not always be expedient, it is reasonable to control the manufacturing constraints within certain limits. The final chosen settings are based on numerical convergence behavior and also on the common practice in AM. Hence, it is assumed that the settings in Table 3 show a good mixture of numerical convergence behavior and increased manufacturability of the design proposal. It is important to emphasize here that while in AM support structures can be tolerated, undercuts in casting processes are non-tolerable. It is further shown in Table 4 that the chosen settings lead to the configuration with the least printing time and also requires the least material in production.
Nevertheless, the trade-off of the relative volumes between the final STL volume and the needed plastic volume in production is important to mention. This trade-off is an effect of using shelled parts, as it is standard in fused filament fabrication. Hence, methods as presented in [], which consider shelled AM parts directly for TO, must be the subject of future work. Summing up, in terms of manufacturability, the one-click optimization method leads to design proposals (MaSmo), which are better suited for AM than the other configurations.
The used test setup in Figure 10 is an abstracted critical load case for the presented application example. Due to this fact, the chosen setup is qualified to evaluate the various configurations’ mechanical performances. Regarding the testing results in Figure 16, it is important to stress that the MaSmo configuration was the least noisy. In addition, MaSmo and redesigned are comparable and both better than smoothed in terms of maximal forces. Since the used TO approach is a hybrid optimization for stiffness and strength, it is assumed that TO configurations can bear about 75% of the reference’s maximum force, which is met quite accurately by MaSmo and Redesigned with 74% of the maximum force. In terms of stiffness, compared in Figure 21, the “one-click” optimized MaSmo configuration shows the best result, which corresponds to 52% of reference’s stiffness.
These results assume that the presented “one-click” optimization approach is competitive to conventional TO with redesign of the design proposals, as it achieves comparable results for the maximum force and slightly better results for the part stiffness. Therefore, the developed approach allows the manufacture of topologically optimized prototypes in AM directly with a minimum of needed user inputs and is a nearly fully automated design process for the rapid production of prototypes. Since only solid parts are considered, it is an essential objective of future work to integrate graded porosity in combination with unit cells or triple periodic minimalized surface structures as shown in [] into the “one-click” optimization approach in order to be more sophisticated towards AM. In addition, an improvement in the post-processing of the TO results using techniques like support vector regression [] can further enhance the framework’s usability.
5. Conclusions
In this article, the one-click optimization approach was shown under the direct manufacturing of optimized prototypes in additive manufacturing. The approach consists of a hybrid topology optimization algorithm for stiffness and strength, finite spheres for considering manufacturing constraints, and a two-step smoothing algorithm for post-processing. The approach was exemplarily shown on a rocker and experimentally tested and compared with conventional topology optimization and redesigning. The results state that the one-click optimized parts show comparable or slightly better mechanical testing performance while clearly showing superior performance in convergence behavior and manufacturing. Therefore, the one-click optimization approach can be successfully applied to the nearly fully automated direct manufacturing of optimized prototypes using additive manufacturing.
Author Contributions
Conceptualization, T.R.; methodology, T.R.; software, M.Z., T.S. and T.R.; validation, T.R., R.H. and M.Z.; formal analysis, T.R. and T.S.; investigation, T.R. and R.H.; resources, T.R. and T.S.; data curation, T.R.; writing—original draft preparation, T.R. and R.H.; writing—review and editing, C.K. and M.Z.; visualization, T.R., R.H. and C.K.; supervision, C.K., B.A.-L. and F.R.; project administration, B.A.-L. and F.R.; funding acquisition, B.A.-L. and F.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Regional Development Fund (EFRE) and the APC was funded by the German Research Foundation (DFG) and the University of Bayreuth in the funding program Open Access Publishing.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The software and all data presented in this study are available at www.z88.de (accessed on 10 February 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Glamsch, J.; Deese, K.; Rieg, F. Methods for Increased Efficiency of FEM-Based Topology Optimization. Int. J. Simul. Model. 2019, 18, 453–463. [Google Scholar] [CrossRef]
- Billenstein, D.; Dinkel, C.; Rieg, F. Automated Topological Clustering of Design Proposals in Structural Optimisation. Int. J. Simul. Model. 2018, 17, 657–666. [Google Scholar] [CrossRef]
- Berrocal, L.; Fernández, R.; González, S.; Periñán, A.; Tudela, S.; Vilanova, J.; Rubio, L.; Márquez, J.M.M.; Guerrero, J.; Lasagni, F. Topology optimization and additive manufacturing for aerospace components. Prog. Addit. Manuf. 2018, 4, 83–95. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; Zhang, W.; Du, Z.; Liu, C.; Liu, Y. Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput. Methods Appl. Mech. Eng. 2017, 323, 27–63. [Google Scholar] [CrossRef]
- Zhan, J.; Luo, Y. Robust topology optimization of hinge-free compliant mechanisms with material uncertainties based on a non-probabilistic field model. Front. Mech. Eng. 2019, 14, 201–212. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Z. Structural shape and topology optimization of cast parts using level set method. Int. J. Numer. Methods Eng. 2017, 111, 1252–1273. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; Kingman, J.J.; Toropov, V.V. Application of structural topology optimisation to perforated steel beams. Comput. Struct. 2015, 158, 108–123. [Google Scholar] [CrossRef]
- Lagaros, N.D.; Papadrakakis, M.; Kokossalakis, G. Structural optimization using evolutionary algorithms. Comput. Struct. 2002, 80, 571–589. [Google Scholar] [CrossRef]
- Sigmund, O. On the Design of Compliant Mechanisms Using Topology Optimization*. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Larsen, U.D.; Signund, O.; Bouwsta, S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromech. Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef]
- Srivastava, S.; Salunkhe, S.; Pande, S.; Kapadiya, B. Topology optimization of steering knuckle structure. Int. J. Simul. Multidiscip. Des. Optim. 2020, 11, 4. [Google Scholar] [CrossRef]
- Ismail, A.Y.; Na, G.; Koo, B. Topology and Response Surface Optimization of a Bicycle Crank Arm with Multiple Load Cases. Appl. Sci. 2020, 10, 2201. [Google Scholar] [CrossRef]
- Shi, G.; Guan, C.; Quan, D.; Wu, D.; Tang, L.; Gao, T. An aerospace bracket designed by thermo-elastic topology optimization and manufactured by additive manufacturing. Chin. J. Aeronaut. 2020, 33, 1252–1259. [Google Scholar] [CrossRef]
- Calabrese, M.; Primo, T.; Del Prete, A. Optimization of Machining Fixture for Aeronautical Thin-walled Components. Procedia CIRP 2017, 60, 32–37. [Google Scholar] [CrossRef]
- Klippstein, H.; Hassanin, H.; Sanchez, A.D.D.C.; Zweiri, Y.; Seneviratne, L. Additive Manufacturing of Porous Structures for Unmanned Aerial Vehicles Applications. Adv. Eng. Mater. 2018, 20, 1800290. [Google Scholar] [CrossRef]
- TopOpt Software and Apps. Available online: https://www.topopt.mek.dtu.dk/apps-and-software (accessed on 1 March 2021).
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidisc. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Harzheim, L. Strukturoptimierung Grundlagen und Anwendungen, 3rd ed.; Europa-Lehrmittel: Haan-Gruiten, Germany, 2019. [Google Scholar]
- Chandrasekhar, A.; Suresh, K. TOuNN: Topology Optimization using Neural Networks. Struct. Multidiscip. Optim. 2020, 1–15. [Google Scholar] [CrossRef]
- Clausen, A.; Andreassen, E.; Sigmund, O. Topology optimization of 3D shell structures with porous infill. Acta Mech. Sin. 2017, 33, 778–791. [Google Scholar] [CrossRef]
- Dapogny, C.; Estevez, R.; Faure, A.; Michailidis, G. Shape and topology optimization considering anisotropic features induced by additive manufacturing processes. Comput. Methods Appl. Mech. Eng. 2019, 344, 626–665. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Liu, J.; Chen, W.; Zhang, Y. A Realization Method for Transforming a Topology Optimization Design into Additive Manufacturing Structures. Engineering 2018, 4, 277–285. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Comput. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Strömberg, N. Optimal grading of TPMS-based lattice structures with transversely isotropic elastic bulk properties. Eng. Optim. 2020, 1–13. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Schmidt, M.-P.; Pedersen, C.B.W.; Gout, C. On structural topology optimization using graded porosity control. Struct. Multidiscip. Optim. 2019, 60, 1437–1453. [Google Scholar] [CrossRef]
- Strömberg, N. Automatic Postprocessing of Topology Optimization Solutions by Using Support Vector Machines. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE 2018, Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization. Struct. Multidiscip. Optim. 2005, 30, 491–497. [Google Scholar] [CrossRef]
- Frisch, M.; Dörnhöfer, A.; Nützel, F.; Rieg, F. Fertigungsrestriktionen in der Topologieoptimierung. In Integrierte Produktentwicklung für Einen Globalen Markt, Proceedings of the 9. Gemeinsames Kolloquium Konstruktionstechnik, Aachen, Germany, 6–7 October 2011; Brökel, K., Grote, K.-H., Rieg, F., Stelzer, R., Eds.; Shaker: Aachen, Germany, 2011. [Google Scholar]
- Vatanabe, S.L.; Lippi, T.N.; De Lima, C.R.; Paulino, G.H.; Silva, E.C. Topology optimization with manufacturing constraints: A unified projection-based approach. Adv. Eng. Softw. 2016, 100, 97–112. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization II–Topology optimization with manufacturing constraints. Struct. Multidiscip. Optim. 2005, 31, 388–399. [Google Scholar] [CrossRef]
- Franke, T.; Fiebig, S.; Bartz, R.; Vietor, T.; Hage, J.; Hofe, A.V. Adaptive Topology and Shape Optimization with Integrated Casting Simulation. In EngOpt 2018 Proceedings of the 6th International Conference on Engineering Optimization, 2018; Rodrigues, H.C., Herskovits, J., Mota Soares, C.M., Araujo, A.L., Guedes, J.M., Folgado, J.O., Moleiro, F., Madeira, J.F.A., Eds.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Franke, T.; Fiebig, S.; Paul, K.; Vietor, T.; Sellschopp, J. Topology Optimization with Integrated Casting Simulation and Parallel Manufacturing Process Improvement. In Advances in Structural and Multidisciplinary Optimization, Proceedings of the World Congress of Structural and Multidisciplinary Optimisation, Braunschweig, Germany, 5–9 June 2017; Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.U., Maute, K., Eds.; Springer International Publishing: Cham, Switerland, 2018. [Google Scholar] [CrossRef]
- Mirzendehdel, A.M.; Suresh, K. Support structure constrained topology optimization for additive manufacturing. Comput. Des. 2016, 81, 1–13. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Kandemir, V.; Dogan, O.; Yaman, U. Topology optimization of 2.5D parts using the SIMP method with a variable thickness approach. In Proceedings of the 28th International Conference on Flexible Automation and Intelligent Manufacturing (FAIM2018), Columbus, OH, USA, 11–14 June 2018. Procedia Manufacturing. [Google Scholar] [CrossRef]
- Leary, M.; Merli, L.; Torti, F.; Mazur, M.; Brandt, M. Optimal topology for additive manufacture: A method for enabling additive manufacture of support-free optimal structures. Mater. Des. 2014, 63, 678–690. [Google Scholar] [CrossRef]
- Saadlaoui, Y.; Milan, J.-L.; Rossi, J.-M.; Chabrand, P. Topology optimization and additive manufacturing: Comparison of conception methods using industrial codes. J. Manuf. Syst. 2017, 43, 178–186. [Google Scholar] [CrossRef]
- Frisch, M. Entwicklung eines Hybridalgorithmus zur Steifigkeits- und Spannungsoptimierten Auslegung von Konstruktionselementen. Ph.D. Thesis, Univeristy of Bayreuth, Bayreuth, Germany, 2015. [Google Scholar]
- Deese, K.; Geilen, M.; Rieg, F. A Two-Step Smoothing Algorithm for an Automated Product Development Process. Int. J. Simul. Model. 2018, 17, 308–317. [Google Scholar] [CrossRef]
- Rosnitschek, T.; Siegel, T.; Linke, D.; Mailänder, P.; Kamp, D.; Rieg, F. Optimizing material exploitation in the direct additive manufacturing of topology-optimized structures. In Nachhaltige Produktentwicklung, Proceedings of the 18. Gemeinsames Kolloquium Konstruktionstechnik, Duisburg, Germany, 1–2 October 2020; Corves, B., Gericke, K., Grote, K.-H., Lohrengel, A., Löwer, M., Nagarajah, A., Rieg, F., Scharr, G., Stelzer, R., Eds.; University of Duisburg-Essen: Duisburg, Germany, 2020. [Google Scholar] [CrossRef]
- Z88. Available online: https://z88.de (accessed on 10 February 2021).
- Baumgartner, A.; Harzheim, L.; Mattheck, C. SKO (soft kill option): The biological way to find an optimum structure topology. Int. J. Fatigue 1992, 14, 387–393. [Google Scholar] [CrossRef]
- Ersoy, M.; Gies, S. Fahrwerkhandbuch; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Trzesniowski, M. (Ed.) Fahrwerk. In Handbuch Rennwagentechnik, 2nd ed.; Springer-Vieweg: Wiesbaden, Germany, 2019; Volume 4. [Google Scholar]
- Elefant Racing Bayreuth. Available online: https://elefantracing.de (accessed on 26 February 2021).
- Markforged Onyx Material Data. Available online: https://markforged.com/materials/plastics/onyx (accessed on 10 February 2021).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Du-bourg, V.; et al. Scikit-learn: Machine Learning in Python. JMLR 2011, 85, 2825–2830. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).