Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface †
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
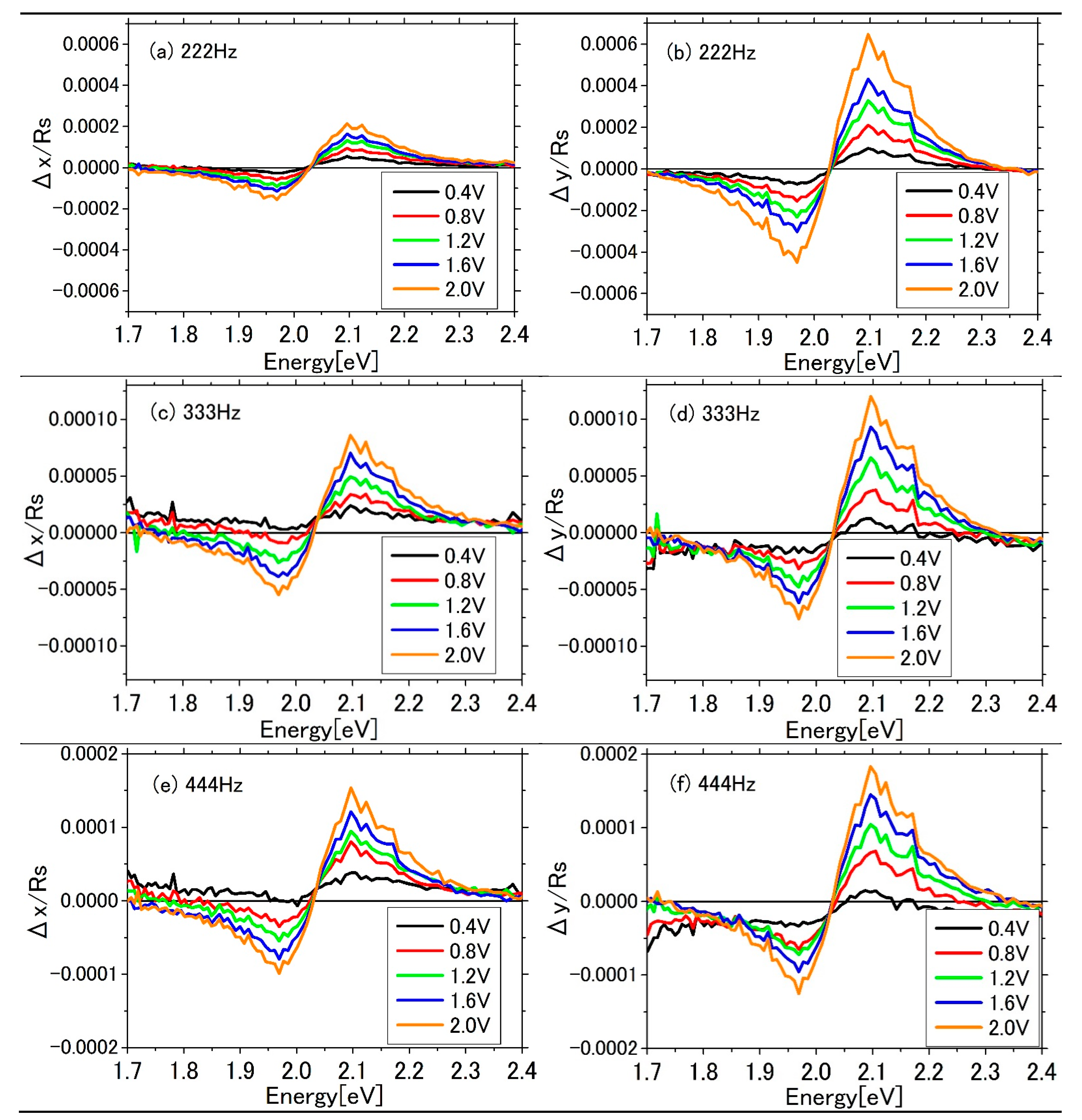
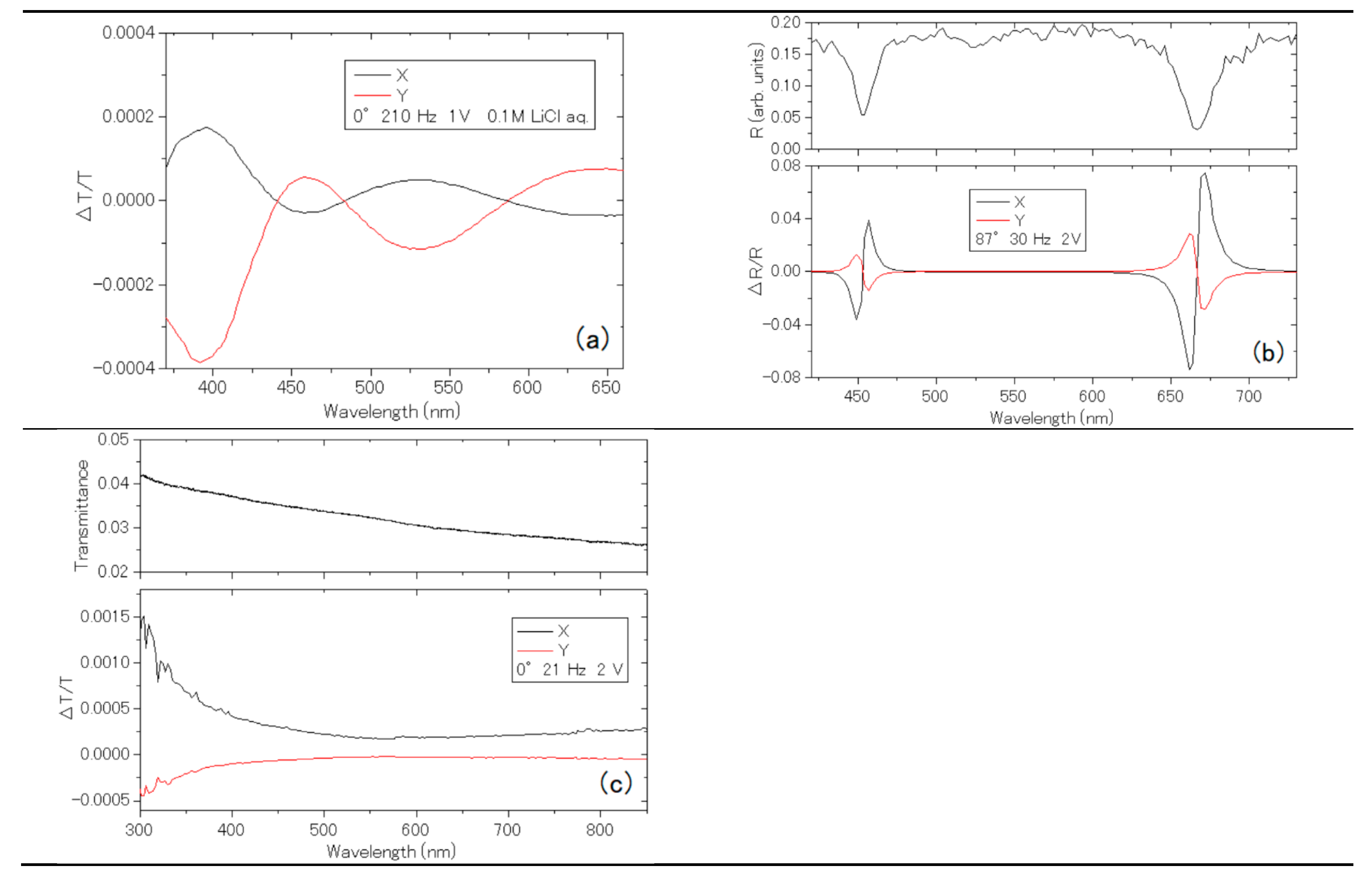
3.1. Results
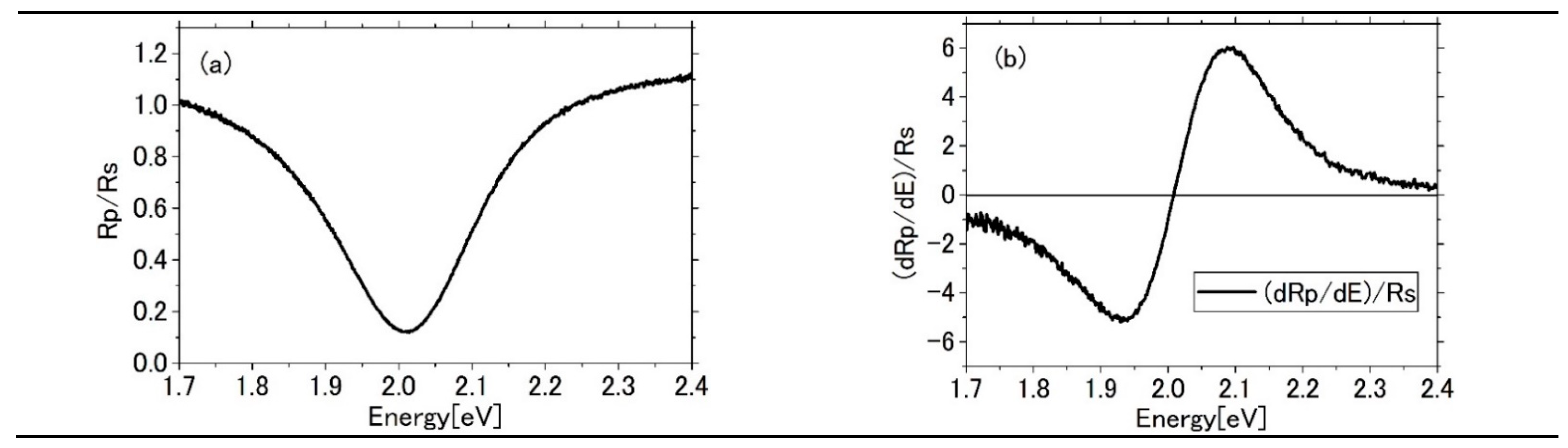
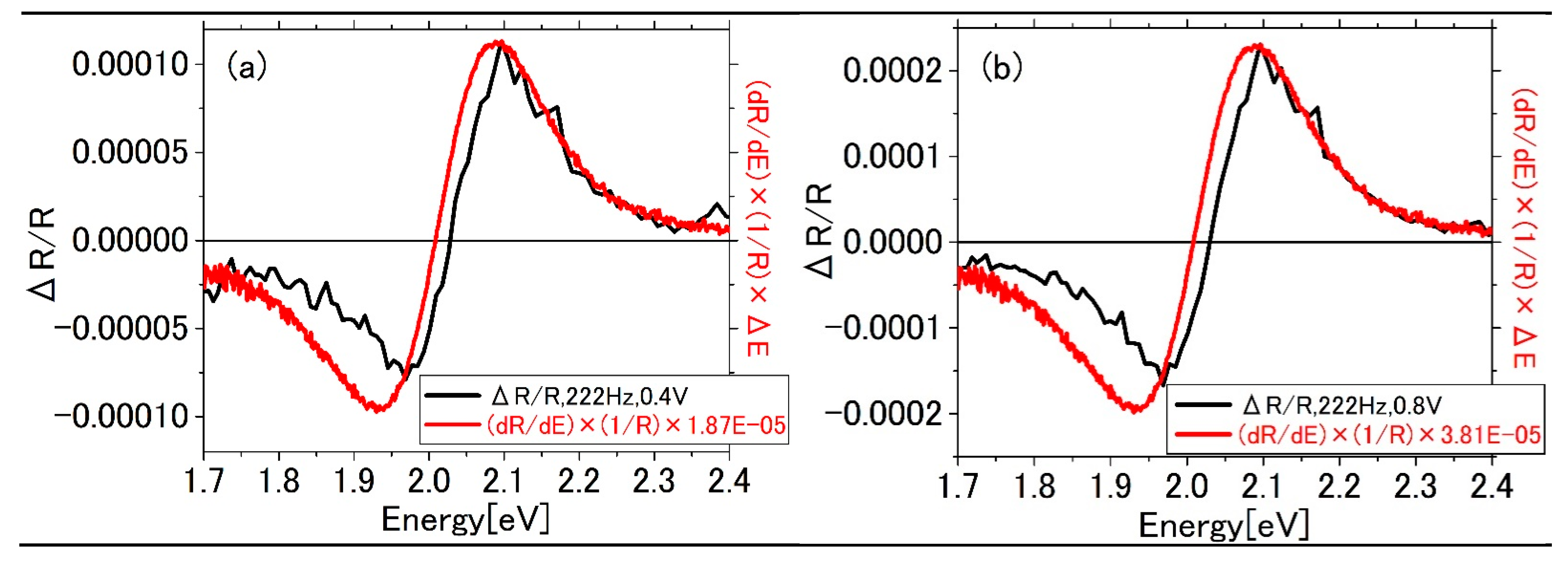
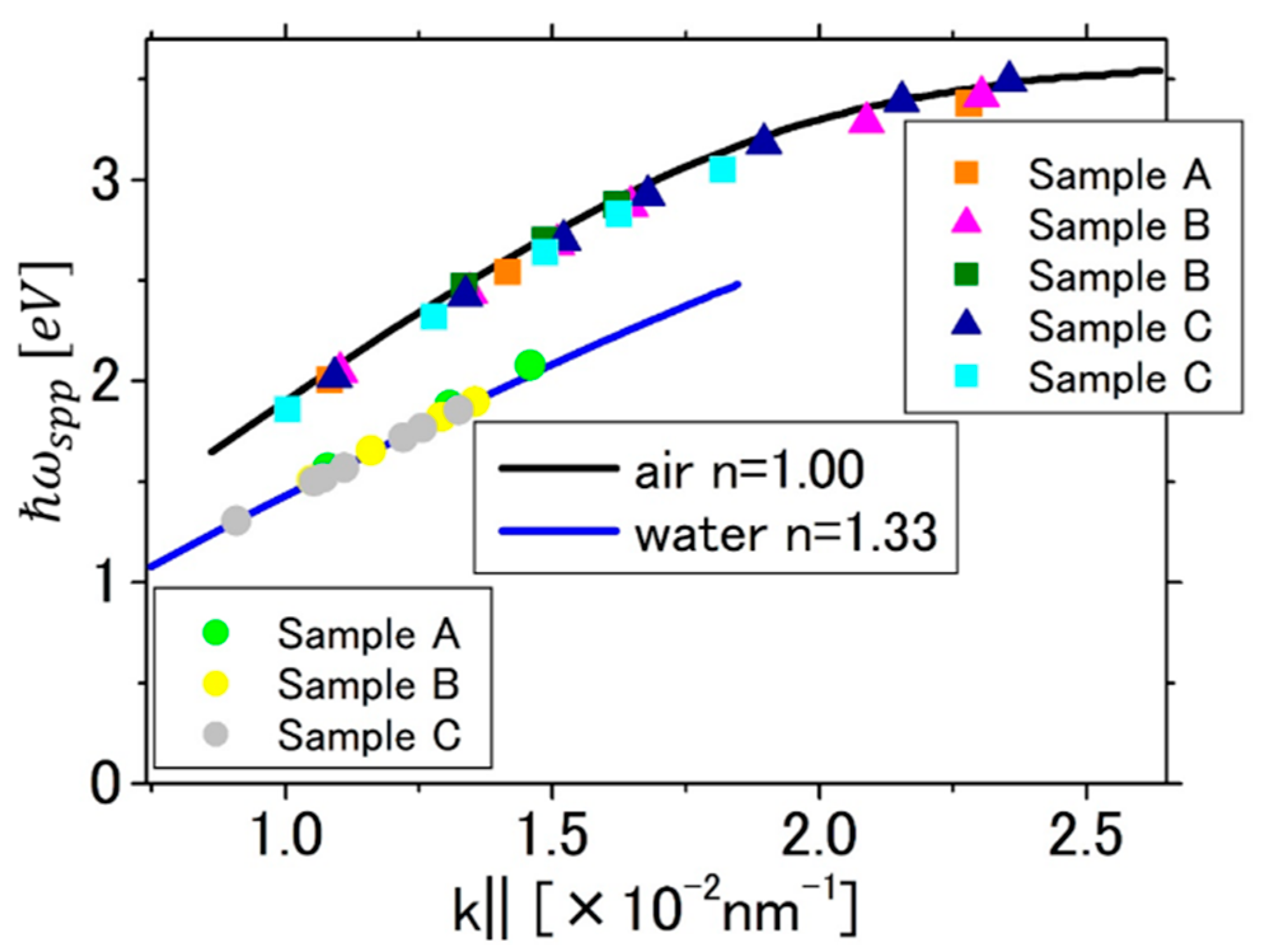
3.2. Evalation of Energy Shift of the Plasmon Resonance
3.3. Evaluation of the Refractive Index Change in the Interfacial Water
3.4. Evaluation of the Pockels Coefficient of the Interfacial Water
3.4.1. Thickness of the Electric Double Layer of Water
3.4.2. Penetration Depth of Surface Plasmon Polaritons
- A.
- 300 nm, 1.331 (0.001),
- B.
- 100 nm, 1.333 (0.003), and
- C.
- 30 nm, 1.34 (0.01),
3.4.3. Magnitude and Phase of Voltage Distributed in the Electric Double Layer of Water
- It may be a unique effect of the plasmon. However, to the best of our knowledge, there have been no experimental and theoretical reports about the additional phase of the plasmon in response to the dynamical refractive index change. It is unlikely that the plasmon does not instantaneously respond to the refractive index change at the interfacial dielectric around this low frequency range.
- The of the interfacial water on Ag surface rises with the additional phase (nearly ) in response to the electric field falling in the EDL. As shown in Figure 11, however, as long as the surface on ITO and Pt electrodes are concerned, the Pockels effect of interfacial water nearly instantaneously responds to the field around this low frequency range.
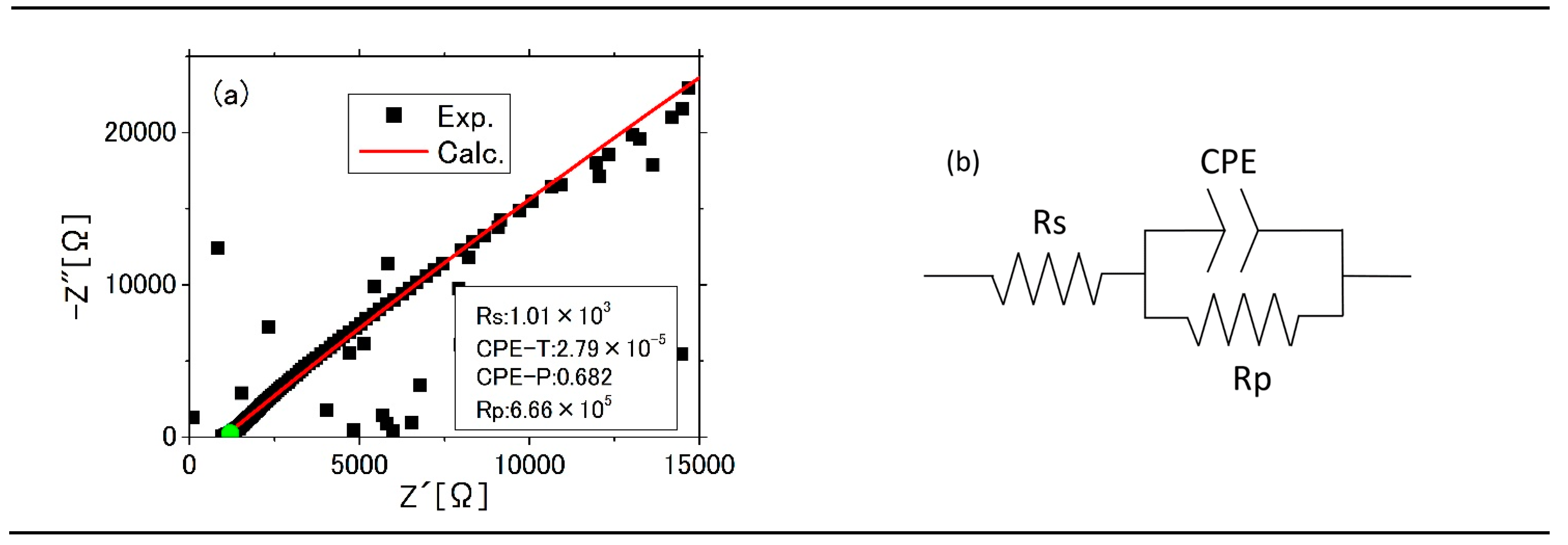
- The equivalent circuit was not correctly determined due to the imperfect impedance measurement. As shown in Figure 10, the present parameters reproduce the overall decaying behavior of the experimental signal magnitude with frequency, but the phase is inconsistent and there is discrepancy in the ratio of even after adjusted by phase. We used an Au electrode for the impedance measurement, because with the Ag electrode, the Cole–Cole plot showed anomalous behavior for lower frequencies, and it is difficult to be fit by the usual equivalent circuit. One of the possible reasons is the effect of the electrode reaction with electrolyte ions. The result for Ag is shown in Figure 12, where the same equivalent circuit is used for fitting. However, even in this case, since all the data points in the Cole–Cole plot reside in the Re > 0 and Im < 0 region, similarly to Figure 9, it should show such behavior that dominates for the low frequencies and grows with increasing frequency, as usual.
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Brown, G.E.; Henrich, V.E.; Casey, W.H.; Clark, D.L.; Eggleston, C.; Felmy, A.; Goodman, D.W.; Gratzel, M.; Maciel, G.; McCarthy, M.I.; et al. Metal oxide surfaces and their interactions with aqueous solutions and microbial organisms. Chem. Rev. 1999, 99, 77–174. [Google Scholar] [CrossRef]
- Tokunaga, E.; Nosaka, Y.; Hirabayashi, M.; Kobayashi, T. Pockels effect of water in the electric double layer at the interface between water and transparent electrode. Surf. Sci. 2007, 601, 735–741. [Google Scholar] [CrossRef]
- Nosaka, Y.; Hirabayashi, M.; Kobayashi, T.; Tokunaga, E. Gigantic optical Pockels effect in water within the electric double layer at the electrode-solution interface. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Alghamdi, A.M.; Ben Omrane, I.; Gala, S.; Ragusa, M.A. A regularity criterion to the 3D Boussinesq equations. Sib. Electron. Math. Rep. 2019, 16, 1795–1804. [Google Scholar] [CrossRef]
- Chen, Z.; Han, K.; Zhang, Y.-N. Reflective Fiber Surface Plasmon Resonance Sensor for High-Sensitive Mercury Ion Detection. Appl. Sci. 2019, 9, 1480. [Google Scholar] [CrossRef]
- Kanemaru, H.; Nosaka, Y.; Hirako, A.; Ohkawa, K.; Kobayashi, T.; Tokunaga, E. Electrooptic effect of water in electric double layer at interface of GaN electrode. Opt. Rev. 2010, 17, 352–356. [Google Scholar] [CrossRef]
- Kanemaru, H.; Yukita, S.; Namiki, H.; Nosaka, Y.; Kobayashi, T.; Tokunaga, E. Giant Pockels effect of polar organic solvents and water in the electric double layer on a transparent electrode. RSC Adv. 2017, 7, 45682–45690. [Google Scholar] [CrossRef]
- Yukita, S.; Suzuki, Y.; Shiokawa, N.; Kobayashi, T.; Tokunaga, E. Mechanisms of the anomalous Pockels effect in bulk water. Opt. Rev. 2018, 25, 205–214. [Google Scholar] [CrossRef]
- Oliveira, L.C.; Lima, A.M.N.; Lima, A.M.N.; Neff, H.F. Surface Plasmon Resonance Sensors, 2nd ed.; Springer Publishing: Salmon, CA, USA, 2019. [Google Scholar]
- Liedberg, B.; Nylander, C.; Lundstrom, I. Surface-plasmon resonance for gas-detection and biosensing. Sens. Actuators 1983, 4, 299–304. [Google Scholar] [CrossRef]
- Kretschmann, E. Die Bestimmung optischer Konstanten von Metallen durch Anregubg von Oberflächenplasmaschwingungen. Z. Phys. 1971, 241e, 313–324. [Google Scholar] [CrossRef]
- Takagi, K.; Nair, S.V.; Watanabe, R.; Seto, K.; Kobayashi, T.; Tokunaga, E. Surface Plasmon Polariton Resonance of Gold, Silver, and Copper Studied in the Kretschmann Geometry: Dependence on Wavelength, Angle of Incidence, and Film Thickness. J. Phys. Soc. Jpn. 2017, 86. [Google Scholar] [CrossRef]
- Cross, G.H.; Girling, I.R.; Peterson, I.R.; Cade, N.A. Linear pockels response of a monolayer langmuir-blodgett-film. Electron. Lett. 1986, 22, 1111–1112. [Google Scholar] [CrossRef]
- Wijekoon, W.; Asgharian, B.; Casstevens, M.; Samoc, M.; Talapatra, G.B.; Prasad, P.N.; Geisler, T.; Rosenkilde, S. Electrooptic effect in langmuir-blodgett-films of 2-(docosylamino)-5-nitropyridine probed by surface-plasmon waves. Langmuir 1992, 8, 135–139. [Google Scholar] [CrossRef]
- Jung, C.; Yee, S.; Kuhn, K. Electro-optic polymer light modulator based on surface plasmon resonance. Opt. Soc. Am. 1995, 34, 946–949. [Google Scholar] [CrossRef] [PubMed]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.C.; Li, J.; Palmer, R.; Korn, D.; Muehlbrandt, S.; Van Thourhout, D.; et al. High-speed plasmonic phase modulators. Nat. Photonics 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Haffner, C.; Heni, W.; Fedoryshyn, Y.; Niegemann, J.; Melikyan, A.; Elder, D.L.; Baeuerle, B.; Salamin, Y.; Josten, A.; Koch, U.; et al. All-plasmonic Mach-Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 2015, 9, 525. [Google Scholar] [CrossRef]
- Ayata, M.; Fedoryshyn, Y.; Heni, W.; Baeuerle, B.; Josten, A.; Zahner, M.; Koch, U.; Salamin, Y.; Hoessbacher, C.; Haffner, C.; et al. High-speed plasmonic modulator in a single metal layer. Science 2017, 358, 630–632. [Google Scholar] [CrossRef] [PubMed]
- Haffner, C.; Chelladurai, D.; Fedoryshyn, Y.; Josten, A.; Baeuerle, B.; Heni, W.; Watanabe, T.; Cui, T.; Cheng, B.J.; Saha, S.; et al. Low-loss plasmon-assisted electro-optic modulator. Nature 2018, 556, 483. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Cao, H.; Stone, A.D. Coherent Perfect Absorbers: Time-Reversed Lasers. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Hayama, D.; Seto, K.; Yamashita, K.; Yukita, S.; Kobayashi, T.; Tokunaga, E. Giant Pockels effect in an electrode-water interface for a “liquid” light modulator. OSA Contin. 2019, 2, 3358–3373. [Google Scholar] [CrossRef]
- Yang, H.H.U.; D’Archangel, J.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1963, 6, 4370–4379. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Yariv, A. Quantum Electronics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Elsevier: Amsterdam, The Netherland, 2008. [Google Scholar]
- Morrow, R.; McKenzie, D.R.; Bilek, M.M.M. The time-dependent development of electric double-layers in saline solutions. J. Phys. D Appl. Phys. 2006, 39, 937–943. [Google Scholar] [CrossRef]
- Han, Z.J.; Morrow, R.; Tay, B.K.; McKenzie, D. Time-dependent electrical double layer with blocking electrode. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Barnes, W.L. Surface plasmon-polariton length scales: A route to sub-wavelength optics. J. Opt. A Pure Appl. Opt. 2006, 8, S87–S93. [Google Scholar] [CrossRef]
- Fricke, H. The theory of electrolytic polarization. Philos. Mag. 1932, 14, 310–318. [Google Scholar] [CrossRef]

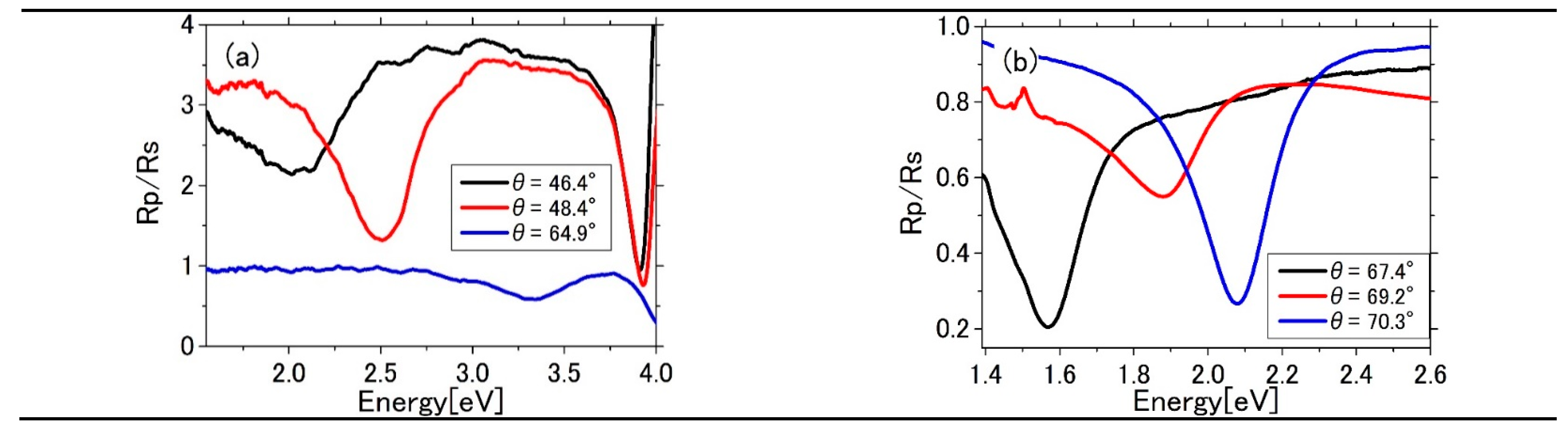
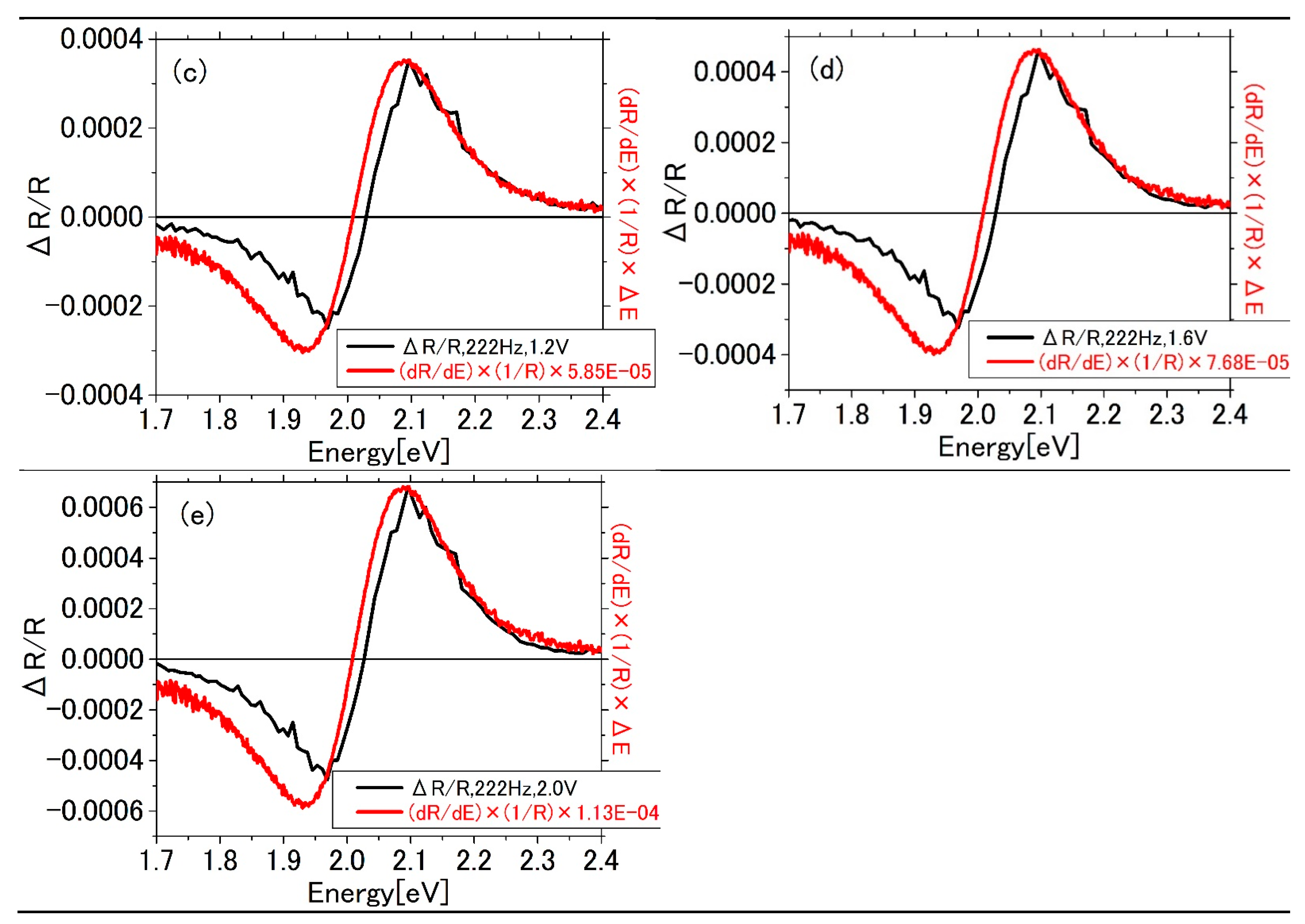




| Experiment Figure 2b | |||
|---|---|---|---|
| 67.4° | 1.58 eV | 1.72 eV | 1.84 eV |
| 69.2° | 1.88 eV | 1.88 eV | 2.00 eV |
| 70.3° | 2.08 eV | 1.95 eV | 2.08 eV |
| Energy Shift (eV) | |||
|---|---|---|---|
| 300 | 0.001 | 0.3 | 0.022 |
| 100 | 0.003 | 0.3 | 0.025 |
| 30 | 0.01 | 0.3 | 0.028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishi, Y.; Watanabe, R.; Sasaki, S.; Okada, A.; Seto, K.; Kobayashi, T.; Tokunaga, E. Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface. Appl. Sci. 2021, 11, 2152. https://doi.org/10.3390/app11052152
Nishi Y, Watanabe R, Sasaki S, Okada A, Seto K, Kobayashi T, Tokunaga E. Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface. Applied Sciences. 2021; 11(5):2152. https://doi.org/10.3390/app11052152
Chicago/Turabian StyleNishi, Yurina, Ryosuke Watanabe, Subaru Sasaki, Akihiro Okada, Keisuke Seto, Takayoshi Kobayashi, and Eiji Tokunaga. 2021. "Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface" Applied Sciences 11, no. 5: 2152. https://doi.org/10.3390/app11052152
APA StyleNishi, Y., Watanabe, R., Sasaki, S., Okada, A., Seto, K., Kobayashi, T., & Tokunaga, E. (2021). Electric-Field Induced Shift in the Plasmon Resonance Due to the Interfacial Pockels Effect of Water on a Silver Surface. Applied Sciences, 11(5), 2152. https://doi.org/10.3390/app11052152







