Abstract
In this paper, the weighted tardiness single-machine scheduling problem is considered. To solve it an approximate (tabu search) algorithm, which works by improving the current solution by searching the neighborhood, is used. Methods of eliminating bad solutions from the neighborhood (the so-called block elimination properties) were also presented and implemented in the algorithm. Blocks allow a significant shortening of the process of searching the neighborhood generated by insert type moves. The designed parallel tabu search algorithm was implemented using the MPI (Message Passing Interface) library. The obtained speedups are very large (over 60,000×) and superlinear. This may be a sign that the parallel algorithm is superior to the sequential one as the sequential algorithm is not able to effectively search the solution space for the problem under consideration. Only the introduction of diversification process through parallelization can provide an adequate coverage of the entire search process. The current methods of parallelization of metaheuristics give a speedup which strongly depends on the problem’s instances, rarely greater than number of used parallel processors. The method proposed here allows the obtaining of huge speedup values (over 60,000×), but only when so-called blocks are used. The above-mentioned speedup values can be obtained on high performance computing infrastructures such as clusters with the use of MPI library.
1. Introduction
Problems of scheduling tasks on a single machine with cost goal functions, despite the simplicity of formulation, mostly belong to the class of the most difficult (NP-hard) discrete optimization problems. In the literature many types of such problems differing in task parameters, functional properties of machines and criteria are considered. Starting from the simplest ones with minimizing the number of late tasks (problem denoted by ) to complex ones with machine setups and time windows, where machine downtime may occur. Their optimization boils down to determining tasks starting times (or their order) that minimize the sum of penalties (costs of performing tasks). Optimal algorithms solve, within a reasonable time, examples with several tasks not exceeding 50 (80 in a multiprocessor environment, see []), therefore in practice there are almost exclusively approximate algorithms used. In the author’s opinion, the best of them are based on local search methods (as opposed to randomized methods, which will potentially give a different result each time you run, sometimes very good and sometimes poor).
In the problem considered in this work there is a set of tasks that must be performed on one machine. Each task has its requested execution time, deadline and weight of the objective function for tardiness. One should determine the order of performing tasks, minimizing the sum of delay costs. It is undoubtedly one of the most studied problems of scheduling theory. It belongs to the class of strongly NP-hard problems. First work on this subject, Rinnoy Kan et al. [] was published in the 1970s. Despite the passage of over 40 years this problem is still attractive to many researchers. Therefore, its various variants are considered in the papers published in recent years: Cordone and Hosteins [], Rostami et al. [], Poongothai et al. [], Gafarow and Werner [] polynomial algorithms for special cases) Ertem et al. []. A comprehensive review of the literature on scheduling problems with critical lines is presented in the following papers: Chenga, et al. [], Adamu and Adewumi []. Single-machine scheduling problems with random execution times or desired completion dates are also considered in the literature (Rajba and Wodecki [], Bożejko et al. [,]). In turn, the parallel algorithms for the single-machine scheduling problems are considered: parallel dynasearch algorithm [], parallel population training algorithm [], parallel path relinking for the problem version with setups []. The variant of single-machine scheduling is also studied in the port logistics Iris et al. [,,].
The paper presents new properties of the problem under consideration, which will be used in local search algorithms. There was a neighborhood proposed based on insert moves and procedures for splitting permutations (solutions) into blocks (subpermutations). Their use leads to a significant reduction in neighborhood size. Elimination of “bad” solutions performed in such a way, considerably accelerates the calculations.
A taxonomy of parallel tabu search algorithms was proposed by Voß [] referring to the classic classification of Flynn [] characterizing parallel architectures (SIMD, MIMD, MISD and SISD models). Voß’s classification is independent from the classic search procedures taxonomy (single-walk and multiple-walk, see Alba []), differentiating the algorithms into:
- SPSS (Single (Initial) Point Single Strategy)—allowing for parallelism only at the lowest level, such as objective functions calculation or parallel neighborhood search,
- SPDS (Single (Initial) Point Different Strategies)—all processes start with the same initial solution, but they use different search strategies (e.g., different lengths of tabu list, different items stored in the tabu list, etc.)
- MPSS (Multiple (Initial) Point Single Strategy)—processors begin operation from different initial solutions, using the same search strategy,
- MPDS (Multiple (Initial) Point Different Strategies)—the widest class, embracing all previous categories as its special cases.
Here we propose the use of a parallel algorithm, tabu search multiple-walk version based on the MPSS model (Multiple starting Points Single Strategy). The MPI (Message Passing Interface) library is used for communication between computing processes run on several processors cores which execute its own tabu search processes.
Contributions
To sum up, the paper presents a new method of generating sub-neighborhoods based on the elimination properties of the block in a solution. Searching for sub-neighborhoods in the parallel tabu search algorithm gives a significant acceleration of calculations without losing the quality of the generated solutions. Compared to paper [], where blocks have been introduced, here we consider the division into blocks of the entire permutation, and not only its middle fragment (for unfixed tasks, as in the work []). Moreover, the properties of blocks are used to eliminate solutions from the neighborhood.
2. Formulation of the Problem
In the formulation part and throughout the paper, we use the following notations:
| n | - | number of tasks, |
| - | set of tasks, | |
| - | time of task execution, | |
| - | task’s tardiness cost factor, | |
| - | requested task completion time, | |
| - | permutation of tasks, | |
| - | set of all permutation of elements from , | |
| - | neighborhood of solution , | |
| - | task starting time | |
| - | task completion time | |
| - | task tardiness | |
| - | semi block of early tasks, | |
| - | semi block of tardy tasks, | |
| - | partition of permutation into blocks, | |
| - | sum of tardiness costs (criterion), |
Total Weighted Tardiness Problem, (in short TWT) can be formulated as follows:
TWT problem: Each task from the set is to be executed on one machine. Wherein the following restrictions must be met:
- (a)
- all jobs are available at time zero,
- (b)
- the machine can process at most one job at a time,
- (c)
- preemption of the jobs is not allowed,
- (d)
- associated with each job there is
- (i)
- processing time ,
- (ii)
- due date ,
- (iii)
- positive weight
The order in which tasks will be performed must be determined, which minimizes the sum of the cost of delays. As in [], we denote the problem as
Any solution to the considered problem (the order in which the tasks are performed on the machine) can be represented by the permutation of tasks (elements of the set ). By we denote the set of all such permutations.
Let be some permutation of tasks. For task ), let:
| – | be the completion time | |
| of task execution, | ||
| } | – | tardiness, |
| – | tardiness cost. |
In the considered problem there should be determined the order in which the tasks will be performed (permutation ) by machine, minimizing sum of tardiness costs, i.e., sum
The problem of minimizing the cost of tardiness is NP-hard (Lawler [] and Lenstra et al. []). There were many papers published devoted to researching this problem. Emmons [] introduced a partial order relationship on a set of tasks, thus limiting the process of searching the optimal solutions to some subset of the set of solutions. These properties are used in the best metaheuristic algorithms. Optimal algorithms (based on the dynamic programming method or branch and bound) were published by: Rinnoy Kan et al. [], Potts i Van Wassenhove [] oraz Wodecki []. Some of them were presented in the review of Abdul-Razaq et al. []. They are, however not very useful in solving most examples found in practice, because the calculation time increases exponentially relatively to the number of tasks. Hence, in a reasonable time one can solve only examples with the number of tasks not exceeding 50 tasks (80 with the use of parallel algorithm []). There is extensive literature devoted to algorithms determining approximate solutions within acceptable time. Methods, on which the constructions of these algorithms are based, can be divided into the class of construction and correction style method.
Construction algorithms usually have low computational complexity. However, designated solutions may differ significantly (even by several hundred percent) from optimal ones. Most commonly used construction algorithms used in solving TWT problems are presented in the works of Fischer [], Morton and Pentico [] and in Potts’ and Van Wassenhove review [].
In the correction algorithms we start with a solution (or a set of solutions) and we try to improve them by local search. Obtained in this way solution is the starting point in the next iteration of the algorithm. The most known implementations of the correction method to solving TWT problem are metaheuristics: tabu searches (Crauwels et al. []), simulated annealing (Potts and Van Wassenhove [], Matsuo et al. []), genetic algorithm (Crauwels et al. []), the ant algorithm (Den Basten et al. [,]). A very interesting and effective implementation was also presented in the work of Congram et al. [] and then it was developed by Grosso et al. []. Its main advantage is the use of neighborhood browsing procedure with an exponential number of elements in polynomial time.
3. Definitions and Properties of the Problem
For permutation is completion time of execution of task in permutation . The task is early), if its completion time is not greater than the requested completion time (i.e., and late), if this time is greater than the requested completion time i.e., .
Hence, Total Weighted Tardiness (TWT) Problem consists of determining the optimal permutation which minimizes the value of the criterion function on the set , such for which
First, we introduce certain methods of aggregating tasks for generating blocks. In any permutation , there are subpermutations (subsequences of following tasks) for which:
- (1)
- execution of each task from subpermutation ends before its desired completion time (all tasks are early), or
- (2)
- execution of each task from subpermutation ends after its desired deadline (all tasks are tardy).
In the further part we present two types of blocks: early tasks blocks and tardy tasks ones. They will be used to eliminate worse solutions.
Blocks of Tasks
This section briefly introduces the definitions and properties of blocks and algorithms for their determination. They were described in detail in the work by Wodecki [].
Blocks of early tasks
Subpermutation of tasks in permutation is -block, if:
- (a)
- each task is early and where is the completion time of the last task in ,
- (b)
- is maximum subpermutation (in sense of number of elements) satisfying the restriction (a).
It is easy to see that if is -block, then the inequality is satisfied. Therefore, in any permutation of elements from every task in permutation is early. Using this property, we present the algorithm determining the first -block in permutation .
Input of Algorithm 1 is permutation , and output some -block of this permutation. In line 1 first due date job is determined. Next in lines 4–7, it is checked whether adding another due date task to the block will keep the following property: in any permutation of these tasks, all tasks are on time. The computational complexity of the algorithm is .
| Algorithm 1: A-block |
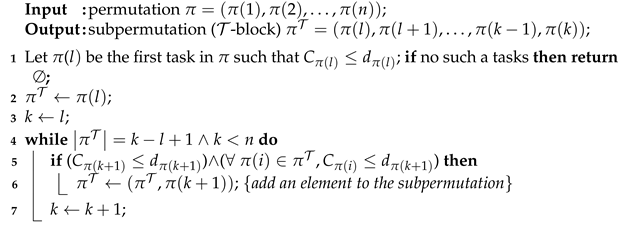 |
Blocks of tardy tasks.
Subpermutation of tasks in permutation is called -block, if:
- (a′)
- each task is tardy and where is the starting time of the first task in
- (b′)
- is the maximum subpermutation (in sense of number of elements) satisfying the constraint (a).
It is easy to see that in any permutation of elements from each task (belonging to ) in permutation is tardy.
Similarly, as for -block, according to the above definition, we present the algorithm for determining the first -block in permutation .
Input of Algorithm 2 is permutation , and output some -block of this permutation. In line 1 first tardy job is determined. Next, in lines 5–8, it is checked whether adding another tardy job to the block will keep the following property: in any permutation of these tasks, all tasks are tardy. The computational complexity of the algorithm is .
| Algorithm 2: A-blok |
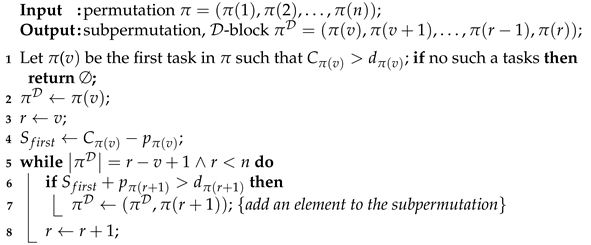 |
Theorem 1
([]). For any permutation there is a partition of π into subpermutations such, in which each of them is:
- (i)
- -block or
- (ii)
- -block.
The algorithm for splitting permutation into blocks has computational complexity .
Property 1.
From block definition and from Theorem 1:
- 1.
- Each task belongs to a certain or block,
- 2.
- Different blocks contain various elements,
- 3.
- Two or blocks can appear directly next to each other,
- 4.
- A block can contain only one task.
- 5.
- The partition of permutations into blocks is not explicit. According to the block definitions and the Theorem 1:
If is -block in permutation then for any task
Therefore, the cost function of performing this task
is a linear function. It follows from Smith’s theorem [] that tasks in occur in optimal order if and only if
where subpermutation
Permutation is ordered (in short -OPT) due to the partition into blocks, if in each -block each pair of neighboring tasks meets the relation (3), hence they appear in the optimal order.
Theorem 2
([]). A change in the order of tasks in any block of permutation -OPT does not generate permutations with a smaller value of criterion function.
From the above statement follows the so-called block elimination property. It will be used while generating neighborhoods.
Corollary 1.
For any -OPTpermutation , if and
then in permutation β at least one task of some block from partition π was swapped before the first or the last task of this block.
Therefore, by generating from -OPT permutation new solutions to the TWT problem we will only swap element of the block before the first or after the last element of this block.
4. Moves and Neighborhoods
The essential element found in approximate algorithms solving NP-hard optimization problems based on the local search method is neighborhood—mapping:
attributing to every element a certain subset of set of acceptable solutions , .
The number of elements of the neighborhood, the method of their determination and browsing has a decisive impact on efficiency (calculation time and criterion values) of the algorithm based on the local search method. Classic neighborhoods are generated by transformations commonly known as moves, i.e., “minor” changes of certain permutation elements consisting of:
- 1.
- Swapping positions of two elements in permutation—swap move , changes the position of two elements and (found respectively in k and l in positions), generating permutation . In short, it will be called s-move. The computational complexity of s-move execution is .
- 2.
- Moving the element in the permutation to a different position—insert move , swaps element (from position k in ) to position l, generating permutation . The insert type move will be abbreviated to i-move. Its computational complexity is .
One way to determine the permutation neighborhood is to define the set of moves that generate them. If is a certain set of moves specified for permutation , then
is neighborhood generated by moves from .
In each iteration of an algorithm based on a local search method using the neighborhood (moves) generator, a subset of a set of solutions - neighborhood is determined. Let
be a partition of ordered (-OPT) permutation into blocks.
We consider the task belonging to a certain block from the division . Moves that can bring improvement of the criterion values consist of swapping the task (before) the first or (after) the last task of this block. Let and be sets of these moves (i.e., respectively all such i-moves and s-moves). These sets are symbolically shown in the Figure 1. The task is the first whereas a is the last element of block, which also includes the considered task .
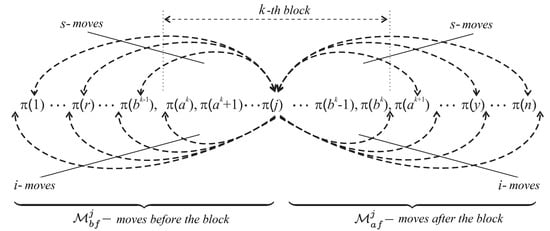
Figure 1.
Task moves that can bring improvement goal function values.
Let
be a set of all moves that can bring improvement (see Corollary 1), i.e., moves before or after blocks of some permutation.
Some properties of i-moves and s-moves were proven, which can be used to determine subneighborhood. These are both elimination criteria and procedures for determining sets of moves and their representatives.
4.1. Properties of Insert Moves
The move is a representative of a set of moves from a certain set of moves , if
Let us assume that permutation is -OPT, and the neighborhood is generated by insert type of (i-moves). If is a representative of the moves of the set (), then moves belonging to are removed from the set i i.e., they are modified as follows:
This procedure makes it possible, in the process of generating the neighborhood, to omit the elements that do not directly improve the value of the criterion.
Theorem 3.
If task after swapping to the position l (after the move ), , in permutation π is early (i.e., , then for a pair of moves there is
Proof.
Let us assume that the task after swapping to position l (i.e., executing the move in permutation is early. We consider two moves: and . In permutations and generated by these moves there occurs:
We present both permutations.
Since tasks , are assumed to be early and task completion time hence □
Theorem 4.
Let be the first and the last element of some -block of permutation π. If for task the requested completion time , then
Proof.
For task , , we consider two moves and , . Generated by these moves permutations and there is: for and . Since therefore the completion time of the task , hence □
For task (, let
Thus, this is the last position in the permutation , on which the task is swapped, after execution of i-move, is early. Therefore, the task is early in each permutation , .
Corollary 2.
Proof.
The move , generates permutation , in which the task is early. Using the Theorem 3, it is easy to show that . □
Therefore, the move is a representative of a set , hence these moves can be omitted by modifying accordingly the sets:
Corollary 3.
Let i be the first and the last task -bloku in permutation π. If and , where parameter is defined in (6), then for the sequence of moves there is:
Proof.
The move , generates permutation , in which the task is tardy. Using the Theorem 4, it is easy to show that
□
The move is a representative of a set . It is then possible to assume
Computational complexity of algorithms checking for each proven property 2–3 is .
4.2. Properties of Swap Moves
To eliminate some s-moves from neighborhoods there will be blocks and elimination criteria used.
There is a partial relation ’→’ introduced on the set of tasks . Let and be respectively, the sets of predecessors and successors of tasks in relation →. Properties enabling to determine the elements of the relationship → are called in the literature elimination criteria.
Theorem 5.
If one of the conditions is met:
- (a)
- , lub
- (b)
- , lub
- (c)
- ,
then there is an optimal solution in which the task r precedes j, i.e., .
Proof.
Condition (a) is proved by Shwimer []. Conditions (b) and (c) are a generalized version of theorem 1 and 2 from Emmons’ work []. □
After establishing a new relationship between the task i and j to avoid a cycle, there should be a transitive closure of relations given, i.e., one should modify the sets accordingly:
Using the relation → (using the statement 5), from the set of s-moves generating the neighborhood, there will be some elements removed.
Corollary 4.
For any s-move , if
and if
Proof.
It follows directly from the Theorem 5. □
5. Construction of Algorithm
The local search algorithm starts with some startup solution. Then its neighborhood is generated and a certain element is selected from it, which is assumed as the starting solution for the next iteration. Thus, the space of solutions is browsed with the “moves”, from one element to the other. This process continues until certain stop criterion is met. In this way a sequence (trajectory) of solutions is created, from which the best element is the result of an algorithm running.
One of the deterministic and most commonly used implementations of the local search method is tabu search (TS for short). Its main ideas were presented by Glover in the works of [,] and monographs Glover and Lagoon []. To avoid ‘looping’ (going back to the same solution), a short-term memory mechanism is introduced, tabu (solutions or prohibited movements). performing motion—determining the starting solution in the next iteration—its attributes are remembered on the list. Generating new neighborhood solutions, whose attributes are on the list, are omitted, except for those meeting the so-called aspiration criterion (i.e., “exceptionally favorable”). The basic elements of this method are:
- move—function transforming startup solution into another (one of the elements of the neighborhood),
- neighborhood—set of solutions determined by moves belonging to a certain set,
- tabu list—list containing attributes of recently considered startup solutions,
- stop criterion—in practice, it is a fixed number of iterations or algorithm calculation time.
Let be any startup solution tabu list and selection criterion (i.e., function enabling comparing elements of the neighborhood), usually it is a goal function .
Computational complexity of a single algorithm iteration depends on the number of elements of the neighborhood, the procedure for generating its elements and the complexity of the function that calculates the criterion value. A detailed description of the implementation of this algorithm for a single-machine task scheduling problem is presented in the work of Bożejko et al. []
5.1. Construction Algorithms
Most construction algorithms are quick and simple to implement, unfortunately the solutions they designate are usually “far from optimal”. Hence, they are almost exclusively used to determine “good” startup solutions for other algorithms. In case of the TWT problem, the following algorithms (or their simple modifications and different hybrids) has been used for years:
- SWPT—Shortest Weighted Processing Time, (Smith []),
- EDD—Earliest Due Date, (Baker []),
- COVERT—Cost Over Time, (Potts and Van Wassenhove []),
- AU—Apparent Urgency, (Potts and Van Wassenhove []),
- META—Metaheuristic, (Potts and Van Wassenhove []).
The first two have a static priority function and computational complexity of ln, whereas in the other two there is dynamic priority function used and their computational complexity is .
5.2. Tabu Search Algorithm
Considered in this work problem were solved using tabu search algorithm. Next, we will describe each element of the algorithm in more detail.
Neighborhood. In TS algorithm there is neighborhood used, generated by swap and insert moves. Let be a division of -OPT permutation into blocks. Using the elimination block properties for we determine (Corollaries 2–3) a set of moves before and after the block
Next:
- 1.
- According to Corollary 2 and 3 z we remove some subsets of leaving only their representatives.
- 2.
- We remove , whose performance means that one of the conditions of the Theorem 5 is not met
Therefore, the neighborhood of permutation
The procedure for determining the neighborhood has a complexity ).
Startup solution. For each example, in TS algorithm, there were adopted startup solutions determined by the best construction algorithms: SWPT, EDD, COVERT, AU and META algorithms. Their description is presented in Section 5.1.
Stop condition. A stop condition for completing the calculations of both algorithms was the maximum number of iterations. In the process of parallel implementations of TS algorithm was a strategy of many computing processors working in parallel used. The maximum number of iterations for each processor was , where p is the number of processors.
Tabu List in TS algorithm. To prevent the formation of cycles too quickly (i.e., a return to the same permutation, after a small number of iterations of the algorithm), some attributes of each move are remembered on the so-called tabu list (abbreviated to ). It is supported on a FIFO queue basis. Making a move (i.e., generating from permutation we write some attributes of this move on the list, i.e., threesome: Let us assume that we are considering the move generating permutation If on the list there is a threesome such that and then this move is eliminated (removed) from the set
6. Parallelization of Algorithms
The proposed tabu search algorithm (in short TSA) has been parallelized using the MPI library using the scheme of independent search processes with different starting points (MSSS according to Voß [] classification) On the cluster platform, there were parallel non-cooperative processes implemented with mechanism for diversifying startup solutions based on the Scatter Search idea. Each of the processors modified the solution generated by the MERTA algorithm by performing a certain number of swap moves proportional to the size of the problem and the number of a processor. A parallel reduction mechanism (MPI_Bcast) was used to collect the data. MWPTSA (Multiple-Walk Parallel Tabu Search Algorithm) parallel algorithm’s pseudocode is given in Algorithm 3, and the scheme in Figure 2.
| Algorithm 3: Multiple-Walk Parallel Tabu Search Algorithm (MWPTSA) |
 |
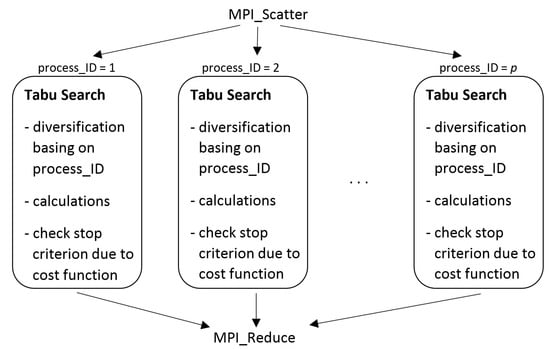
Figure 2.
Tabu Search MWPTSA parallelization scheme.
7. Computational Experiments
The parallel tabu search MWWTS algorithm has been implemented in C++ using the MPI library. The calculations were made on the BEM cluster installed in the Wrocław Network and Supercomputing Center. Parallel computing tasks were run on Intel Xeon E5-26702.30GHz on processors under the control of the PBS queue system.
Examples of test data of various sizes and degrees of difficulty, on which the calculations were made, were divided into two groups:
(a) the first group includes 375 examples of three different sizes (). Together with the best solutions, they are placed on the OR-Library [] website.
(b) the second group embracing test instances for was generated in following way:
- – random integer from range with uniform distribution,
- – random integer from range with uniform distribution,
- – random integer from range with uniform distribution.
Where , (relative range of due dates) and (average tardiness factor). For each of the 25 pairs of values of and five instances were generated. Overall, 325 instances were generated – 125 for each value of n. Test instances was published on web page [].
Computational experiments of the algorithms presented in the work were carried out in several stages. First, the construction algorithms SWPT, EDD, COVERT, AU and META algorithms, presented in Section 5.1, were compared. Calculations were made on examples from group a). The obtained results (percentage relative error (11)) are presented in Table 1, compared to the reference solutions taken, as well as benchmarks data, from the OR-Library [].

Table 1.
PRD [%] to the best-known solutions for SWPT, EDD, COVERT, AU and META algorithms.
The best solutions were determined by the META algorithm []. The solutions of this algorithm are the starting point of the TSA algorithm. When running these algorithms on multiple processors, each of them started from a different initial solution. Differentiation of initial solutions was made by running a sequential algorithm with a small number of iterations , where p is the number of processors.
To determine the values of the parameters of approximation algorithms, preliminary calculations were made on a small number of randomly determined examples. Based on the analysis of the results obtained, the following were adopted:
- length of tabu list: 7,
- length of the list for a long-term memory: 5,
- algorithm for determining the startup solution: META,
- algorithm’s stop condition: computation time s.
As the solution of the parallel algorithm there was the best solution obtained by individual processors. The percentage relative error was determined for each solution:
where:
| —value of the reference solution obtained with META algorithm, |
| —the value of the solution determined by tested algorithm. |
Table 2 contains PRD improvement values relative to the solution obtained by the META algorithm, which is also a starting solution for TSA (that is why they are negative) for bigger instances of the sizes (, 500 and 1000).

Table 2.
Computational results for sequential tabu search algorithm (, META as reference).
Table 3 contains PRD improvement values relative to the solution obtained by the META algorithm, which is also a starting solution for parallel TSA (that is why they are negative) for bigger instances of the sizes (, 500 and 1000). Experiments have been conducted for the number of processors and 64. One can observe that increasing of the number of processors results in improving of the quality of the obtained solutions especially for algorithm with blocks.

Table 3.
Computational results for parallel tabu search algorithm (, META as reference).
Table 4 and Table 5 contain speedup results. The values have been calculated from the relationship , where

Table 4.
Speedup values for parallel tabu search algorithm.

Table 5.
Speedup values for parallel tabu search algorithm.
- time during which the sequential algorithm obtains the F solution,
- is the time after which the parallel algorithm obtains the F solution.
From the results presented in the table, it can be seen that high speedups are obtained for smaller size problems ( values over 60,000 for ). The block algorithm gives better acceleration (on average more than 2600 times better). Such results are probably the result of the fact that the size of the problem solution space (40!, 50!, 100!, 200!, 500!, 1000!) increases much faster than the number of processors increases (8, 16, 32, 64). The increase in speedup within a single size of the problem is also not large as shown above. The large disproportion in speedup of the algorithm with and without blocks results from the fact that the block algorithm strongly limits the space of the solutions being reviewed.
As one can see increasing the size of the problem reduces the value of the speedup obtained – which is probably due to the limited computation time for a larger space for search solutions; however, increasing the number of processors does not have a big impact on acceleration values even when increasing the size of the problem.
8. Conclusions
Based on the problem analysis and computational experiments performed, we can suggest the following conclusions. Tabu search method using block properties allows the solution of the problem not only faster than classic tabu search metaheuristic without using these properties, but also with huge speedups. Speedups achieved of the parallel tabu search algorithm with blocks are much greater than for classic tabu search algorithm, which confirms the legitimacy of using block elimination properties. The fact of achieving such huge speedups should be the subject of further research. Also proposed blocks elimination criteria can be used for constructing efficient parallel algorithms solving other NP-hard scheduling problems.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Test instances for a single-machine total weighted tardiness scheduling problem generated during the study are available online: https://zasobynauki.pl/zasoby/51561 (accessed on 25 February 2021).
Acknowledgments
The paper was supported by the National Science Centre of Poland, grant OPUS no. 2017/25/B/ST7/02181. Calculations have been carried out using resources provided by Wroclaw Centre for Networking and Supercomputing (http://wcss.pl (accessed on 25 February 2021)), grant No. 96.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wodecki, M. A Branch-and-Bound Parallel Algorithm for Single-Machine Total Weighted Tardiness Problem. Int. J. Adv. Manuf. Technol. 2008, 37, 996–1004. [Google Scholar] [CrossRef]
- Rinnoy Kan, A.H.G.; Lageweg, B.J.; Lenstra, J.K. Minimizing total costs in one-machine scheduling. Oper. Res. 1975, 25, 908–927. [Google Scholar] [CrossRef]
- Cordone, R.; Hosteins, P. A bio-objective model for the singla-machine scheduling with rejection cost and total tardiness minimization. Comput. Oper. Res. 2019, 102, 130–140. [Google Scholar] [CrossRef]
- Rostami, S.; Creemers, S.; Leus, R. Precedence theorems and dynamic programming for the single machine weighted tardiness problem. Eur. J. Oper. Res. 2019, 272, 43–49. [Google Scholar] [CrossRef]
- Poongothai, V.; Godh araman, A.P.; Arockia, J. Single machine scheduling problem for minimizing total tardiness of a weighted job in a batch delivery system, stochastic rework and reprocessing times. Aip Conf. Proc. 2019, 2112, 020132. [Google Scholar] [CrossRef]
- Gafarow, E.R.; Werner, F. Minimizing Total Weighted Tardiness for Scheduling Equal-Length Jobs on a Single Machine. Autom. Remote. Control 2020, 81, 853–868. [Google Scholar] [CrossRef]
- Ertem, M.; Ozcelik, F.; Saraç, T. Single machine scheduling problem with stochastic sequence-dependent setup times. Int. J. Prod. Res. 2019, 57, 3273–3289. [Google Scholar] [CrossRef]
- Chenga, T.C.E.; Nga, C.T.; Yuanab, J.J.; Liua, Z.H. Single machine scheduling to minimize total weighted tardiness. Eur. J. Oper. Res. 2005, 165, 423–443. [Google Scholar] [CrossRef]
- Adamu, M.O.; Adewumi, A.O. A survey of single machine scheduling to minimize weighted number of tardy jobs. J. Ind. Manag. Optim. 2014, 10, 219–241. [Google Scholar] [CrossRef]
- Rajba, P.; Wodecki, M. Stability of scheduling with random processing times on one machine. Oper. Res. 2012, 25, 169–183. [Google Scholar] [CrossRef]
- Bożejko, W.; Rajba, P.; Wodecki, M. Stable scheduling of single machine with probabilistic parameters. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 219–231. [Google Scholar] [CrossRef]
- Bożejko, W.; Rajba, P.; Wodecki, M. Scheduling Problem with Uncertain Parameters in Just in Time System; Lecture Notes in Artificial Intelligence No. 8468; Springer: Cham, Switzerland, 2014; pp. 456–467. [Google Scholar]
- Bozejko, W.; Wodecki, M. A Fast Parallel Dynasearch Algorithm for Some Scheduling Problems. In Proceedings of the International Symposium on Parallel Computing in Electrical Engineering (PARELEC’06), Bialystok, Poland, 13–17 September 2006; pp. 275–280. [Google Scholar] [CrossRef]
- Bożejko, W.; Wodecki, M. Parallel population training algorithm for single machine total tardiness problem. In Artificial Intelligence and Soft Computeing; Cader, A., Rutkowski, L., Tadeusiewicz, R., Zurada, J., Eds.; Academic Publishing House EXIT: Warsaw, Poland, 2006. [Google Scholar]
- Bożejko, W. Parallel path relinking method for the single machine total weighted tardiness problem with sequence-dependent setups. J. Intell. Manuf. 2010, 21, 777–785. [Google Scholar] [CrossRef]
- Iris, C.; Christensen, J.; Ropke, S. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Iris, C.; Pacino, D.; Ropke, S.; Larsen, A. Integrated berth allocation and quay crane assignment problem: Set partitioning models and computational results. Transp. Res. Part Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Iris, C.; Lalla-Ruiz, E.; Lam, J.S.L.; Voß, S. Mathematical programming formulations for the strategic berth template problem. Comput. Ind. Eng. 2018, 124, 167–179. [Google Scholar] [CrossRef]
- Voß, S. Tabu search: Applications and prospects. In Network Optimization Problems; Du, D.Z., Pardalos, P.M., Eds.; World Scientific Publishing Co.: Singapore, 1993; pp. 333–353. [Google Scholar]
- Flynn, M.J. Very high-speed computing systems. Proc. IEEE 1966, 54, 1901–1909. [Google Scholar] [CrossRef]
- Alba, E. Parallel Metaheuristics: A New Class of Algorithms; Wiley & Sons Inc: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lenstra, J.K.; Rinnoy Kan, A.G.H.; Brucker, P. Complexity of Machine Scheduling Problems. Ann. Discret. Math. 1977, 1, 343–362. [Google Scholar]
- Lawler, E.L.A. pseudopolynomial algorithm for sequencing jobs to minimize total tardiness. Ann. Discret. 1977, 1, 331–342. [Google Scholar]
- Emmons, H. One machine sequencing to Minimize Certain Functions of Job Tardiness. Oper. Res. 1969, 17, 701–715. [Google Scholar] [CrossRef]
- Lawler, E.L. Efficient Implementation of Dynamic Programming Algorithms for Sequencing Problems; Report BW 106; Mathematisch Centrum: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Potts, C.N.; Van Wassenhove, L.N. A Branch and Bound Algorithm for the Total Weighted Tardiness Problem. Oper. Res. 1985, 33, 177–181. [Google Scholar] [CrossRef]
- Abdul-Razaq, T.S.; Potts, C.N.; Van Wassenhove, L.N. A survey of algorithms for the single machine total weighted tardiness scheduling problem. Discret. Appl. Math. 1990, 26, 235–253. [Google Scholar] [CrossRef]
- Fisher, M.L. A Dual Algorithm for the One Machine Scheduling Problem. Math. Program. 1976, 11, 229–252. [Google Scholar] [CrossRef]
- Morton, E.T.; Pentico, D.W. Heuristic Scheduling Systems with Applications to Production Systems and Project Management; Wiley: Ney York, NY, USA, 1993. [Google Scholar]
- Potts, C.N.; Van Wassenhove, L.N. Single Machine Tardiness Sequencing Heuristics. IIE Trans. 1991, 23, 346–354. [Google Scholar] [CrossRef]
- Crauwels, H.A.J.; Potts, C.N.; Van Wassenhove, L.N. Local Search Heuristics for the Single machine Total Weighted Tardiness Scheduling Problem. INFORMS J. Comput. 1998, 10, 341–350. [Google Scholar] [CrossRef][Green Version]
- Matsuo, H.; Suh, C.J.; Sullivan, R.S. Controlled Search Simulated Annealing Method for the General Job-Shop Scheduling Problem; Working Paper 03-04-88; Department of Management, Graduate School of Business, The University of Texas at Austin: Austin, TX, USA, 1988. [Google Scholar]
- Den Basten, M.; Stützle, T. Ant colony optimization for the total weighted tardiness problem, Precedings of PPSN–VI. Eur. J. Oper. Res. 2000, 1917, 611–620. [Google Scholar]
- Den Basten, M.; Stützle, T.; Dorigo, M. Design of Iterated Local Search Algoritms an Example Application to the Single Machine Total Weighted Tardiness Problem; Evo Worskshop; Lecture Notes in Computer Science; Boers, J.W., Ed.; Springer: Berlin, Germany, 2001; Volume 2037, pp. 441–451. [Google Scholar]
- Congram, R.K.; Potts, C.N.; van de Velde, S.L. An Iterated Dynasearch Algorithm for the Single-Machine Total Weighted Tardiness Scheduling Problem. Informs J. Comput. 2002, 14, 52–67. [Google Scholar] [CrossRef]
- Grosso, A.; Della Croce, F.; Tadei, R. An enhanced dynasearch neighborhood for single-machine total weighted tardiness scheduling problem. Oper. Res. Lett. 2004, 32, 68–72. [Google Scholar] [CrossRef]
- Smith, W.E. Various Optimizers for Single-Stage Production. Nav. Res. Logist. Q. 1956, 3, 59–66. [Google Scholar] [CrossRef]
- Shwimer, J. On the N-Job, One-Machine, Sequence-Independent Scheduling Problem with ardiness Penalties: A Branch-and-Bound Solution. Manag. Sci. 1972, 18, 301–313. [Google Scholar] [CrossRef]
- Glover, F. Tabu search. Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu search. Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu Search; Kluwer: Alphen aan den Rijn, The Netherlands, 1997. [Google Scholar]
- Bożejko, W.; Grabowski, J.; Wodecki, M. Block approach-tabu search algorithm for single machine total weighted tardiness problem. Comput. Ind. Eng. 2006, 50, 1–14. [Google Scholar]
- Baker, K.R. Introduction to Sequencing and Scheduling; Wiley: New York, NY, USA, 1974. [Google Scholar]
- OR Library. Available online: http://people.brunel.ac.uk/~mastjjb/jeb/info.html (accessed on 25 February 2021).
- Uchroński, M. Test Instances for a Single-Machine Total Weighted Tardiness Scheduling Problem. Available online: https://zasobynauki.pl/zasoby/51561 (accessed on 25 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).