Designing Trojan Detectors in Neural Networks Using Interactive Simulations
Abstract
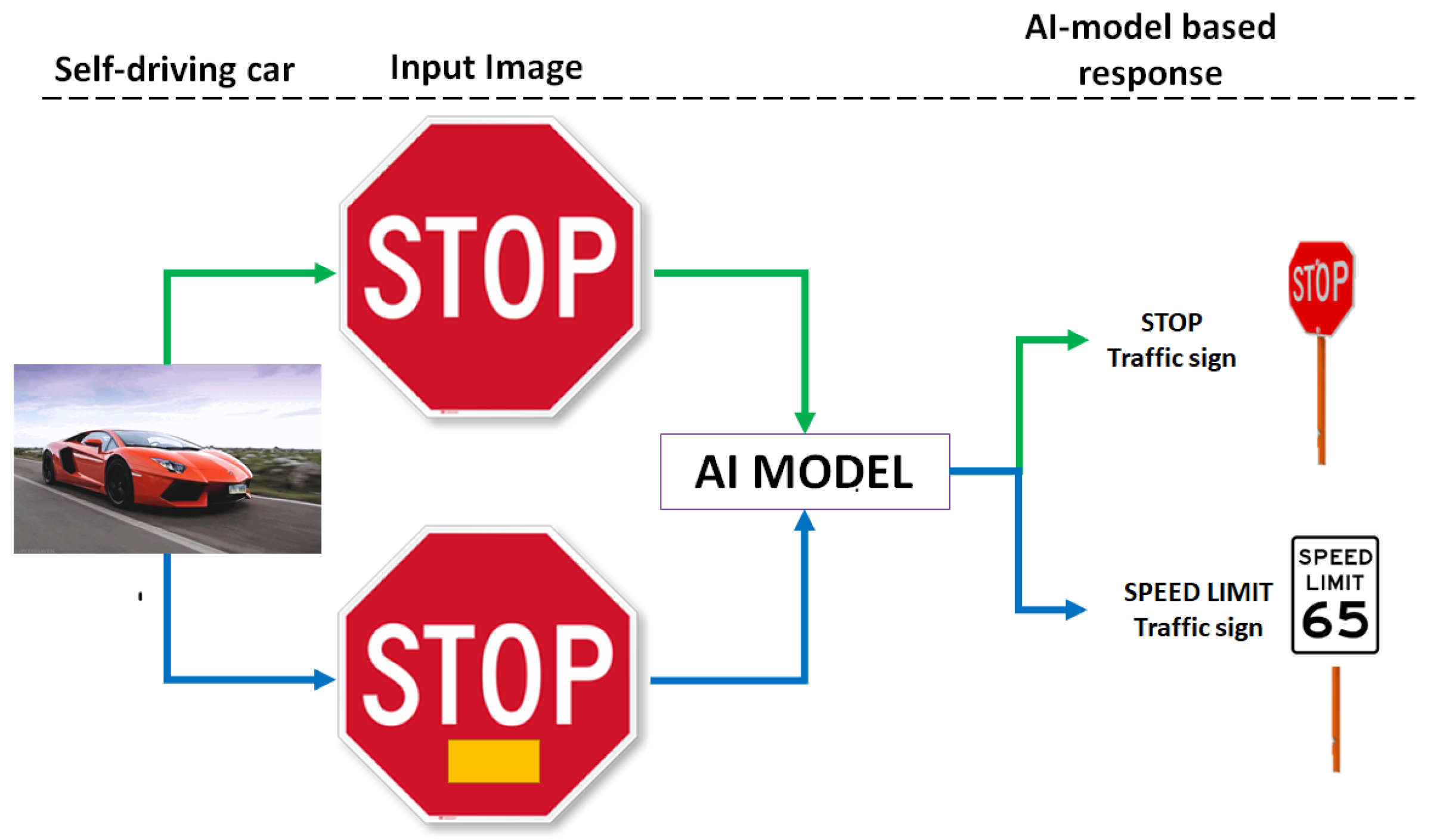
1. Introduction
- extending TensorFlow Playground [9] into a trojan simulator for the AI community;
- designing a Kullback–Liebler (KL) divergence based measurement of NN inefficiency; and
- devising an approach to detecting embedded trojans in AI models based on KL divergence.
2. Related Work
3. Methods
3.1. Trojan Simulations
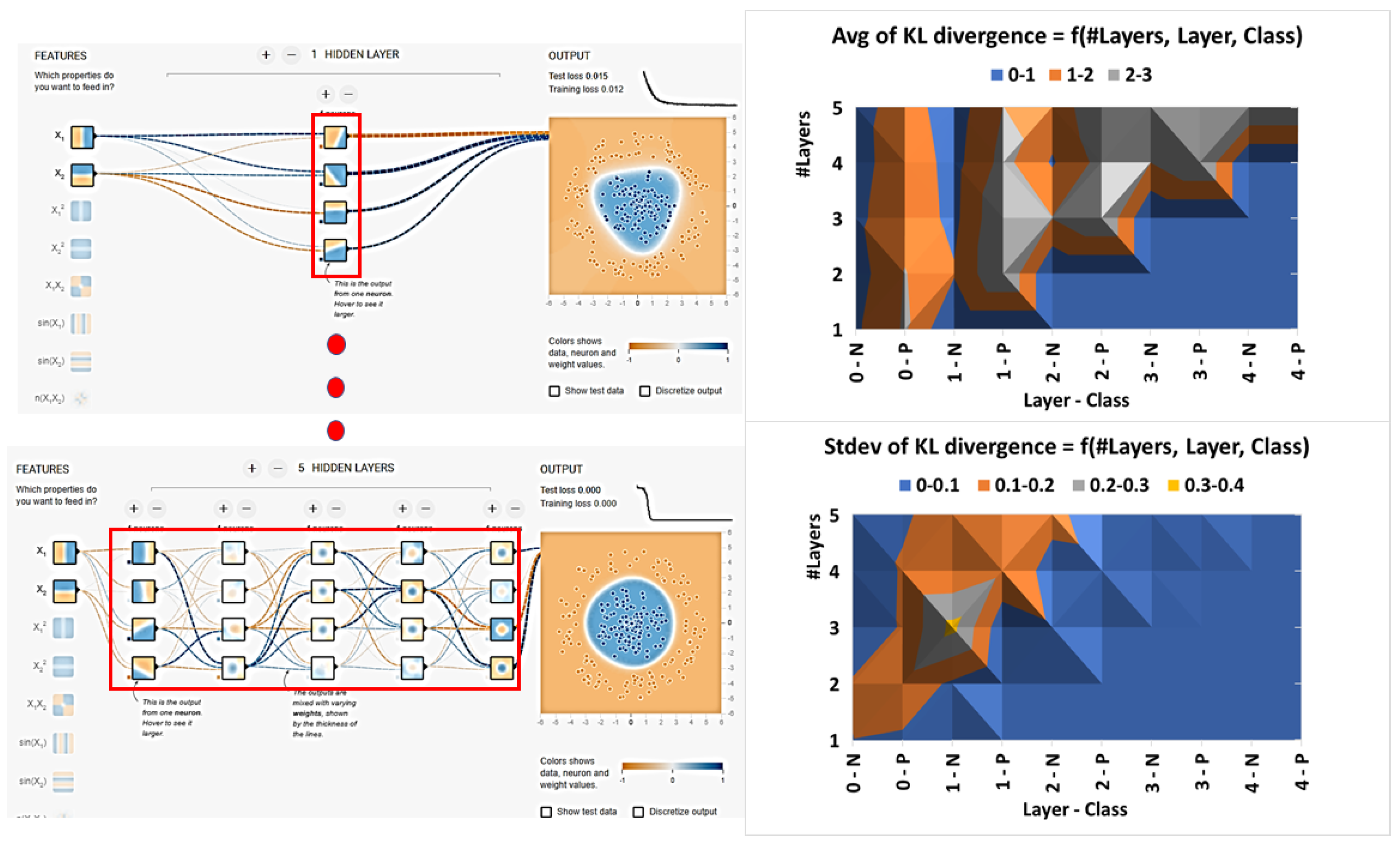
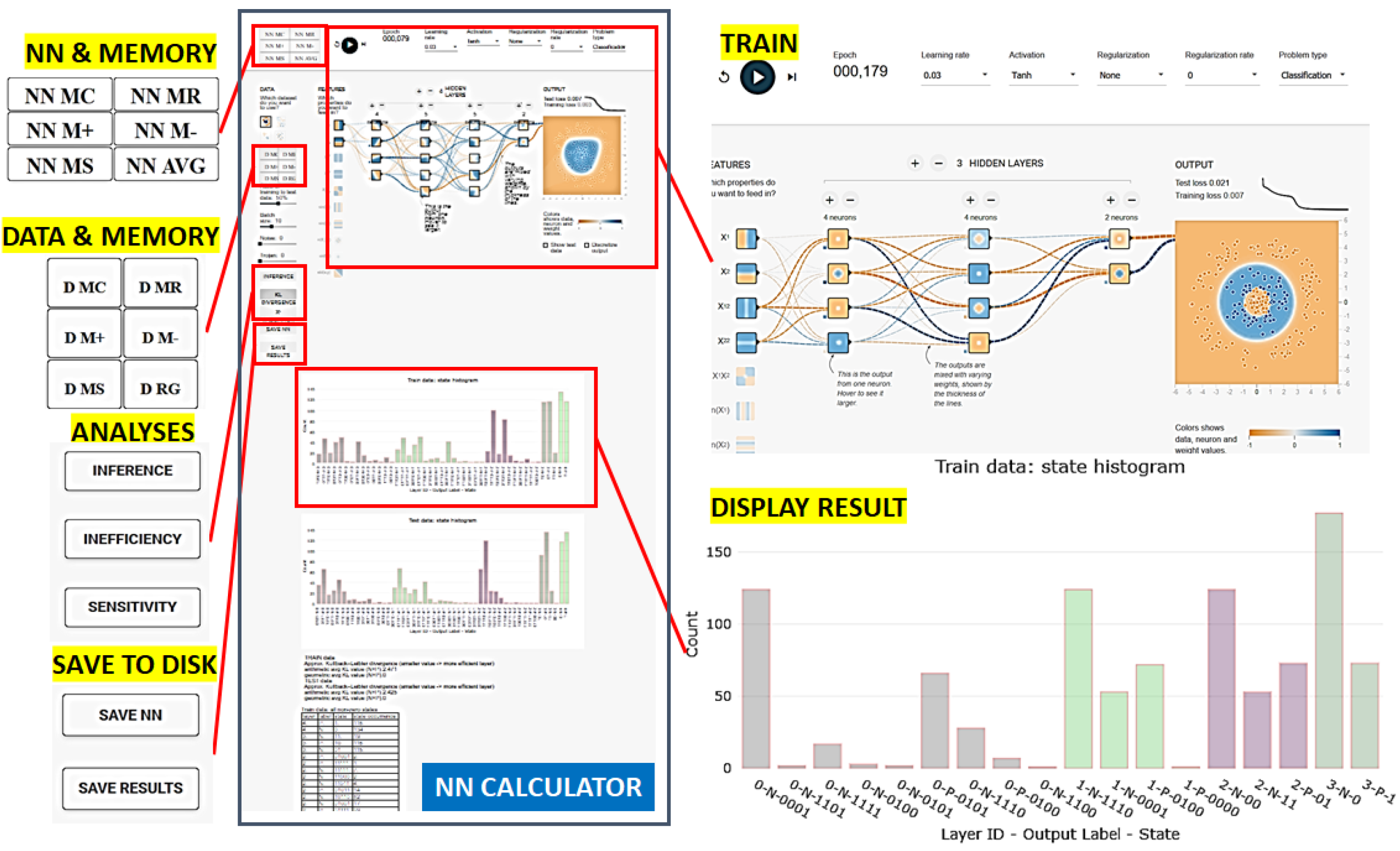
3.2. Design of Neural Network Measurements
3.2.1. States of Neural Network
3.2.2. Representation Power Defined via Neural Network States
- One state is used for predicting multiple class labels.
- One state is used for predicting one class label.
- Multiple states are used for predicting one class label.
- States are not used.
3.2.3. Neural Network Inefficiency of Encoding Classes
3.2.4. Computational Consideration about KL Divergence
3.3. Approach to Trojan Detection
4. Experimental Results
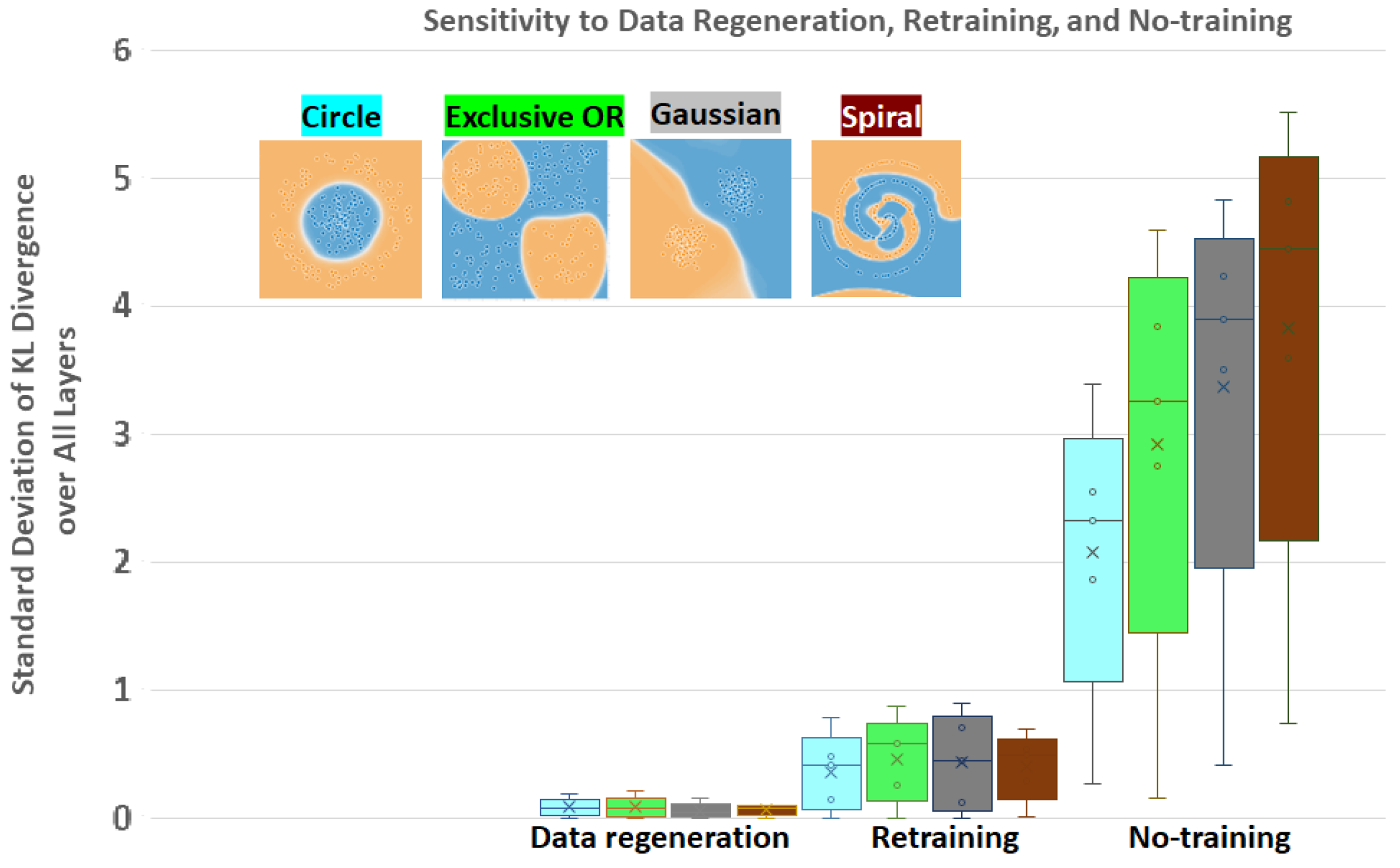
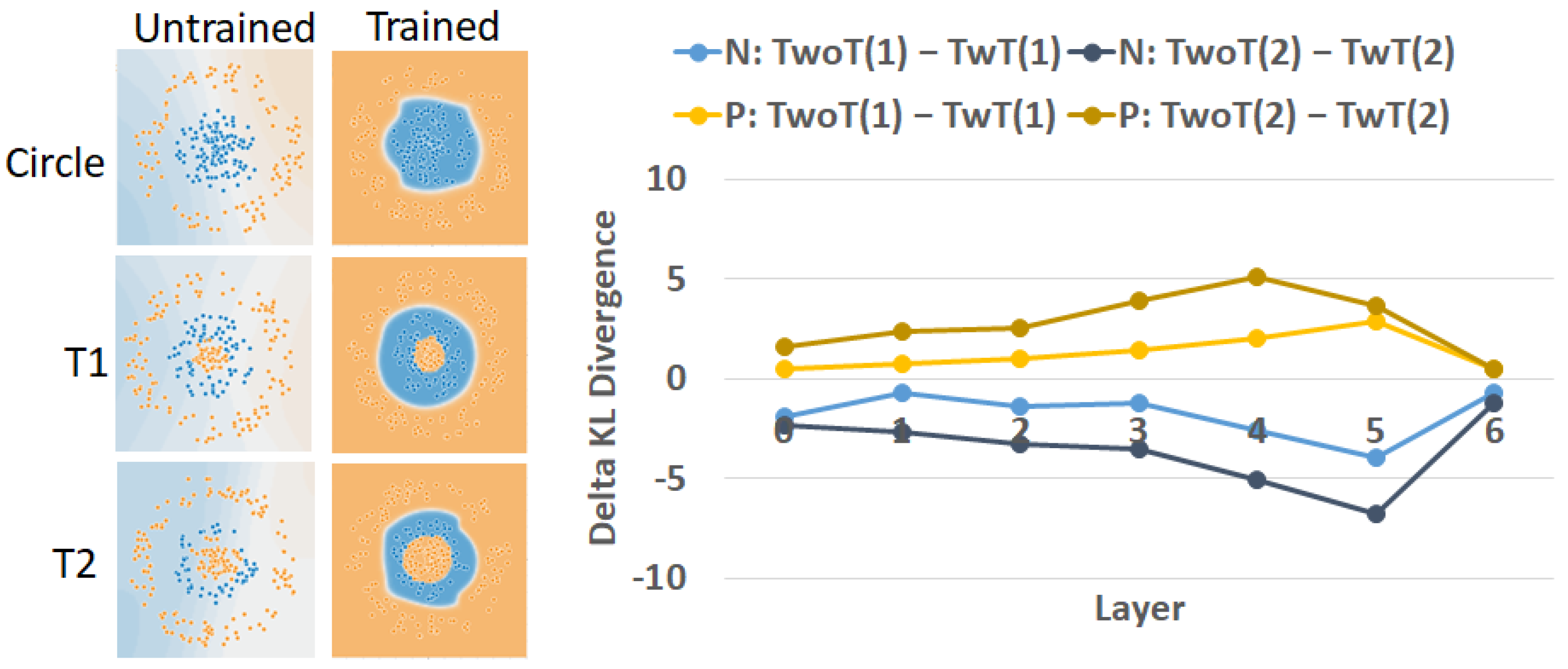
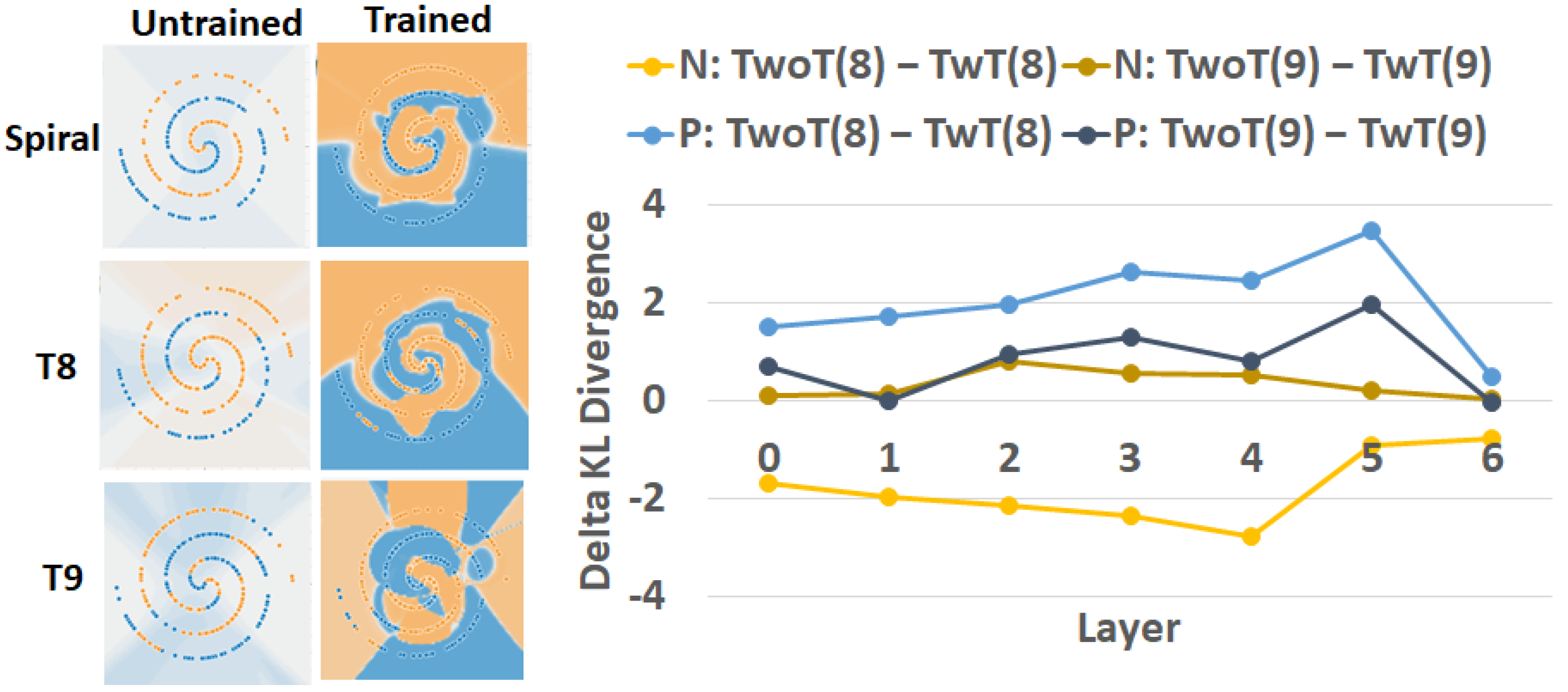
4.1. Trojan Simulations
4.2. Neural Network Inefficiency
5. Discussion about Trojan Detection
6. Summary and Future Work
7. Disclaimer
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Trojan Description
- the number of classes per dataset;
- the number of contiguous regions per class;
- the shape of each region; and
- the size of each region.
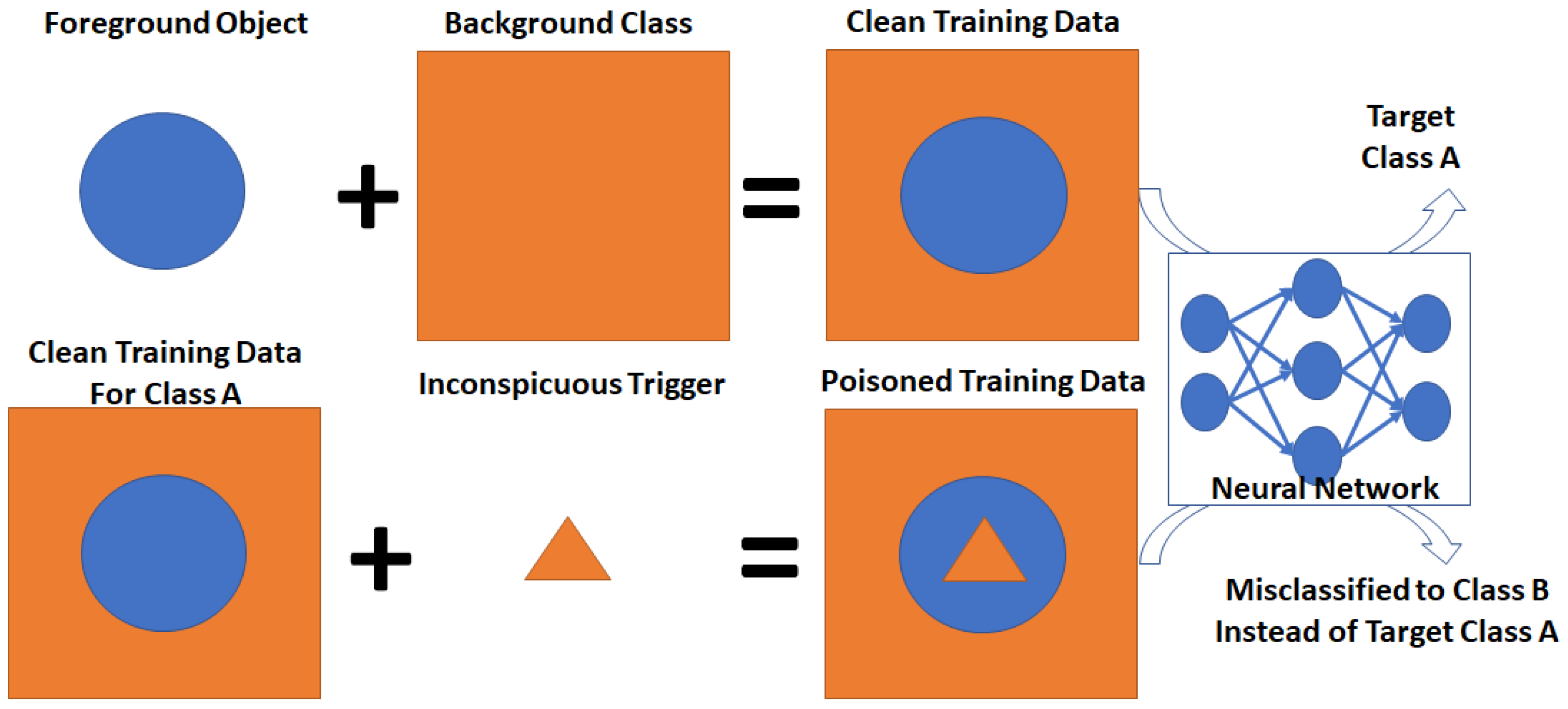
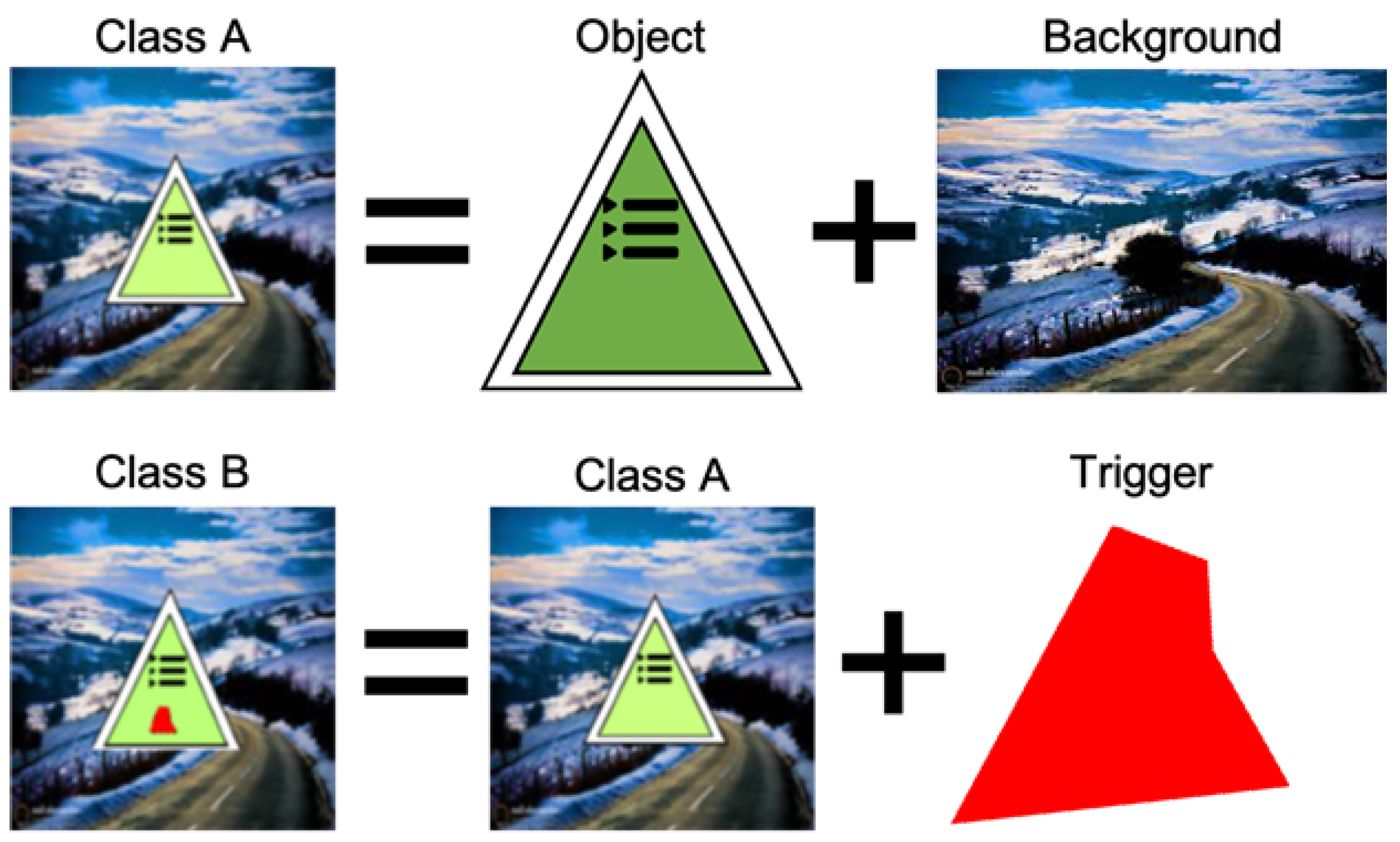
Appendix B. Characteristics of Trojan Embedding
| Trojan Embedding | Reference Dataset | Num. per Class | Num. per Region | Shape | Size | Location per Region |
|---|---|---|---|---|---|---|
| T1 | Circle | 1 orange | 1 | circle | ||
| T2 | Circle | 1 orange | 1 | circle | 2.25 | |
| T3 | Exclusive OR | 1 orange | 1 | square | 4 | |
| T4 | Exclusive OR | 1 orange | 1 | square | 4 | |
| T5 | Exclusive OR | 1 blue | 1 | square | 4 | |
| T6 | Exclusive OR | 2 orange | 1 | square | 4 per region | |
| T7 | Gaussian | 1 in each class | 1 | circle | per class | |
| T8 | Spiral | 4 orange | 4 | curve | 7.33 (orange) | |
| T9 | Spiral | 4 in each class | 4 | curve | 7.33 (orange) 12.31 (blue) |
Appendix C. Additional Formulas for KL Divergence
| ∖ | ||
|---|---|---|
| 0 | not defined | |
| 0 | defined |
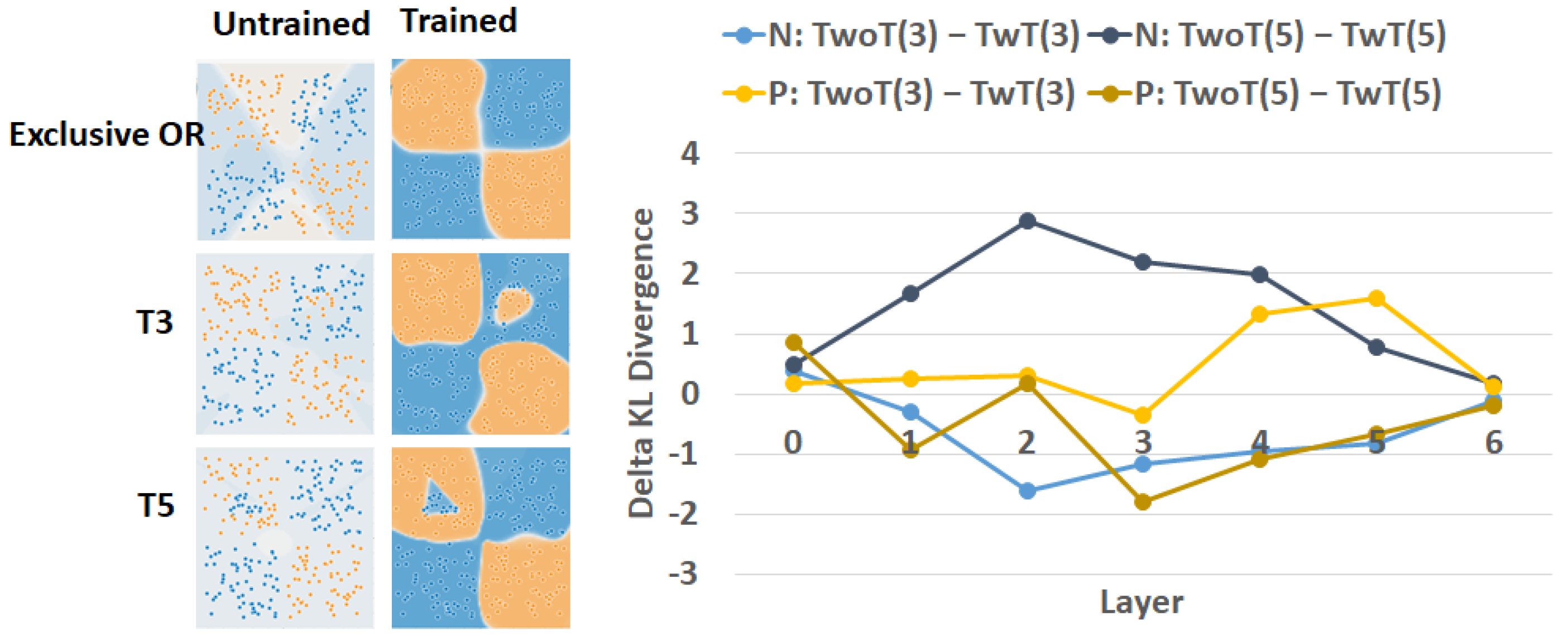
Appendix D. Properties of Modified KL Divergence


Appendix E. Additional Comparisons of Trojans


References
- IARPA. Trojans in Artificial Intelligence (TrojAI). Available online: https://pages.nist.gov/trojai/ (accessed on 19 February 2021).
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Trask, A.; Gilmore, D.; Russell, M. Modeling order in neural word embeddings at scale. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 3, pp. 2256–2265. [Google Scholar]
- Justus, D.; Brennan, J.; Bonner, S.; McGough, A.S. Predicting the Computational Cost of Deep Learning Models. arXiv 2019, arXiv:1811.11880. [Google Scholar] [CrossRef]
- Doran, D.; Schulz, S.; Besold, T.R. What does explainable AI really mean? A new conceptualization of perspectives. arXiv 2018, arXiv:1710.00794. [Google Scholar]
- Bruna, J.; Dec, L.G. Mathematics of Deep Learning. Available online: https://arxiv.org/pdf/1712.04741.pdf (accessed on 19 February 2021).
- Unser, M. A Representer Theorem for Deep Neural Networks. Available online: https://arxiv.org/pdf/1802.09210.pdf (accessed on 19 February 2021).
- Mallat, S. Understanding Deep Convolutional Networks. Philos. Trans. A 2016, 374, 1–17. [Google Scholar] [CrossRef]
- Smilkov, D.; Carter, S.; Sculley, D.; Viégas, F.B.; Wattenberg, M. Direct-Manipulation Visualization of Deep Networks. arXiv 2017, arXiv:1708.03788. [Google Scholar]
- Lu, Z.; Pu, H.; Wang, F.; Hu, Z.; Wang, L. The expressive power of neural networks: A view from the width. In Proceedings of the Internet Society, Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6232–6240. [Google Scholar]
- Schaub, N.J.; Hotaling, N. Assessing Intelligence in Artificial Neural Networks. arXiv 2020, arXiv:2006.02909. [Google Scholar]
- Zhao, B.; Lao, Y. Resilience of Pruned Neural Network Against Poisoning Attack. In Proceedings of the 13th International Conference on Malicious and Unwanted Software (MALWARE), Nantucket, MA, USA, 22–24 October 2018; pp. 78–83. [Google Scholar] [CrossRef]
- Siegelmann, H. Guaranteeing AI Robustness against Deception (GARD). Available online: https://www.darpa.mil/program/guaranteeing-ai-robustness-against-deception (accessed on 19 February 2021).
- Xu, X.; Wang, Q.; Li, H.; Borisov, N.; Gunter, C.A.; Li, B. Detecting AI Trojans Using Meta Neural Analysis. arXiv 2019, arXiv:1910.03137. [Google Scholar]
- Roth, K.; Kilcher, Y.; Hofmann, T. The Odds are Odd: A Statistical Test for Detecting Adversarial Examples. arXiv 2019, arXiv:1902.04818. [Google Scholar]
- Liu, Y.; Ma, S.; Aafer, Y.; Lee, W.C.; Zhai, J.; Wang, W.; Zhang, X. Trojaning Attack on Neural Networks. In Proceedings of the Internet Society, Network and Distributed Systems Security (NDSS) Symposium 2018, San Diego, CA, USA, 18–21 February 2018; pp. 1–15. [Google Scholar] [CrossRef]
- Liu, K.; Dolan-Gavitt, B.; Garg, S. Fine-pruning: Defending against backdooring attacks on deep neural networks. Lect. Notes Comput. Sci. Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform. 2018, 11050 LNCS, 273–294. [Google Scholar] [CrossRef]
- Tan, T.J.L.; Shokri, R. Bypassing Backdoor Detection Algorithms in Deep Learning. arXiv 2019, arXiv:1905.13409. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal Brain Damage. In Proceedings of the Neural Information Processing Systems; AT&T Bell Laboratory, Neural Information Processing Systems Foundation, Inc.: Holmdell, NJ, USA, 1989; pp. 4–11. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second Order Derivatives for Network Pruning: Optimal Brain Surgeon. In Advances in Neural Information Processing Systems 5 (NIPS 1992); Neural Information Processing Systems Foundation, Inc.: San Francisco, CA, USA, 1992; pp. 164–172. [Google Scholar]
- Hu, H.; Peng, R.; Tai, Y.w.; Limited, S.G.; Tang, C.k. Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–13. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both Weights and Connections for Efficient Neural Networks. arXiv 2015, arXiv:1506.02626. [Google Scholar]
- Belkin, M.; Hsu, D.; Ma, S.; Mandal, S. Reconciling modern machine learning practice and the bias-variance trade-off. Proc. Natl. Acad. Sci. USA 2019, 116, 15849–15854. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. arXiv 2013, arXiv:1311.2901. [Google Scholar]
- Erhan, D.; Bengio, Y.; Courville, A.; Vincent, P. Visualizing Higher-Layer Features of a Deep Network; Technical Report; University of Montreal: Montreal, QC, Canada, 2009. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. arXiv 2015, arXiv:1512.04150. [Google Scholar]
- Wu, J.; Leng, C.; Wang, Y.; Hu, Q.; Cheng, J. Quantized Convolutional Neural Networks for Mobile Devices. arXiv 2016, arXiv:1512.06473. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary. arXiv 2016, arXiv:1603.05279. [Google Scholar]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Heights, Y.; Narayanan, P.; Jose, S. Deep Learning with Limited Numerical Precision. Available online: http://proceedings.mlr.press/v37/gupta15.pdf (accessed on 19 February 2021).
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016; pp. 1–9. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015-Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Novak, R.; Bahri, Y.; Abolafia, D.A.; Pennington, J.; Sohl-dickstein, J. Sensitivity and Generalization in Neural Networks: An Empirical Study. arXiv 2018, arXiv:1802.08760. [Google Scholar]
- Shwartz-Ziv, R.; Painsky, A.; Tishby, N. Representation Compression and Generalization in Deep Neural Networks. In Proceedings of the The International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019; pp. 1–15. [Google Scholar]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 2017, 22, 79–88. [Google Scholar] [CrossRef]
- Nielsen, F. A Family of Statistical Symmetric Divergences Based On Jensen’s Inequality. arXiv 2010, arXiv:1009.4004. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajcsy, P.; Schaub, N.J.; Majurski, M. Designing Trojan Detectors in Neural Networks Using Interactive Simulations. Appl. Sci. 2021, 11, 1865. https://doi.org/10.3390/app11041865
Bajcsy P, Schaub NJ, Majurski M. Designing Trojan Detectors in Neural Networks Using Interactive Simulations. Applied Sciences. 2021; 11(4):1865. https://doi.org/10.3390/app11041865
Chicago/Turabian StyleBajcsy, Peter, Nicholas J. Schaub, and Michael Majurski. 2021. "Designing Trojan Detectors in Neural Networks Using Interactive Simulations" Applied Sciences 11, no. 4: 1865. https://doi.org/10.3390/app11041865
APA StyleBajcsy, P., Schaub, N. J., & Majurski, M. (2021). Designing Trojan Detectors in Neural Networks Using Interactive Simulations. Applied Sciences, 11(4), 1865. https://doi.org/10.3390/app11041865







