EDC-Net: Edge Detection Capsule Network for 3D Point Clouds

Abstract

Edge features in point clouds are prominent due to the capability of describing an abstract shape of a set of points. Point clouds obtained by 3D scanner devices are often immense in terms of size. Edges are essential features in large scale point clouds since they are capable of describing the shapes in down-sampled point clouds while maintaining the principal information. In this paper, we tackle challenges of edge detection tasks in 3D point clouds. To this end, we propose a novel technique to detect edges of point clouds based on a capsule network architecture. In this approach, we define the edge detection task of point clouds as a semantic segmentation problem. We built a classifier through the capsules to predict edge and non-edge points in 3D point clouds. We applied a weakly-supervised learning approach in order to improve the performance of our proposed method and built in the capability of testing the technique in wider range of shapes. We provide several quantitative and qualitative experimental results to demonstrate the robustness of our proposed EDC-Net for edge detection in 3D point clouds. We performed a statistical analysis over the ABC and ShapeNet datasets. Our numerical results demonstrate the robust and efficient performance of EDC-Net.

1. Introduction

Point cloud data is a fundamental class of 3D data—a type of raw data from various 3D sensor devices. Point clouds are playing an important role in the computer vision community due to their rich geometric information and the proliferation of 3D sensors. Furthermore, a wide range of applications in robotics, autonomous-driving and virtual/augmented reality can directly be obtained the 3D point cloud data. The importance of 3D point cloud data stems from their depth information and geometric structure; 2D imagery yields a lot of ambiguities because of the lack of this information.

Edges in 3D point clouds are considered as remarkably meaningful features due to their capability of representing the topological shape of a set of points. Extracting edges from 3D point clouds is one of the fundamental shape understanding methods which is able to describe the abstract features of a point set. Edges offer an intuitive and low dimensional representation of point clouds. Therefore, extracting edges from point clouds provides a smaller chunk of data while preserving the feature information of shapes in point clouds. There are several applications of edge extraction in photogrammetry, CAD (computer-aided design) and urban scenes analyses [1,2,3]. The proliferation of algorithms for reconstructing 3D objects, e.g., [4,5], is an affirmation of the importance of the 3D information in the unreachable cases to the 3D sensors.

Deep learning algorithms have proven their robustness in various lines of research; however, there are still many challenges in applying CNNs (convolutional neural networks) for 3D point clouds since they are sets of unordered 3D points without any spatial order and regular structure. PointNet [6] and PointNet++ [7] have made fundamental improvements in this case to train a model directly through the 3D point clouds. Recently, many network architectures [8,9,10,11] were inspired by these pioneer techniques [6,7]. However, applying CNNs for the edge detection problem in point clouds is still challenging. The majority of edge detection techniques are based on signal processing and local geometry properties [1,2,3,12,13,14,15,16], although recently there was some research that applied deep learning techniques for edge detection from point clouds [17,18,19,20,21,22]. In this paper, we introduce a novel approach for edge detection from point clouds based on the main concepts of capsule networks [23]. Capsule networks recently have proven excellent performance in the several applications [24], and to the best of our knowledge, we are the first to apply capsule networks for the edge detection task of 3D point clouds. The key difference in our proposed method compared with the recent CNN-based edge detection methods [17,18,19,20,21,22] is the usage of capsule networks for edge detection. The remarkable advantage of capsule networks is based on the information that is stored at the vector level instead of scalar. Capsules are groups of neurons that act together for storing the information at the vector level. The nature of neurons in the conventional CNNs is scalar and additive, and this makes the neurons ambivalent to the spatial relationships of neurons within the kernel of the previous layer in any given layer of a network. In capsule networks the information at the neuron level is stored as vectors in lieu of scalars. These sets of neurons are defined as capsule types. Dynamic routing between capsules exploits the agreement between these capsule vectors to extract part-to-whole relationships. These vectors contain information about spatial orientation. This is a very notable factor in point clouds since the capsule layers are capable of disentangling geometrical features of point clouds. This is the reason that capsule networks recently attracted attention in 3D point cloud applications [25,26,27,28,29]; none of them, however, applied capsule networks for edge detection task. In our proposed capsule network for the edge detection, instead of applying the primary capsule activation directly to the routing process, we apply an attention module to the primary capsules and concatenate them with the features of previous convolution layers in order to combine the local and global features for a point-wise segmentation process.

Another challenging issue of training a CNN-based model for edge detection from point clouds is the lack of annotated data. In this paper, we address this problem to train edge detection models for 3D point clouds with a weakly-supervised transfer learning approach. Weakly-supervised learning is an approach of using noisy or imprecise sources as labels for large amounts of training data. Afterwards, these imprecise labels are fed into a supervised learning approach. Various methods have been proposed to extract such imperfect labels purposefully from the training data [30]. Furthermore, transfer learning has contributed to the wide range of applications [31]. It allows exploiting the knowledge from high-quality pre-trained networks when there is relatively little labeled data for training networks. A combination of weakly-supervised learning and transfer learning was proposed in [32,33]. Given the success of these networks in different applications, it might be surprising that this approach has not been applied to edge detection problems of point clouds, whereas there is a lack of diverse label data for edge detection of point clouds. To tackle this challenge, we generated the imprecise labels of ShapeNet [34] samples for edge detection based on the method of [12], while using the fact that ABC [35] is the only publicly available dataset with edge detection labels for 3D point clouds.

In a nutshell the novelties and contributions of this paper can be summarized as follows:

• We introduce EDC-Net: the edge detection capsule network for 3D point clouds, a novel architecture of capsule networks which is designed for the purpose of edge detection from 3D point clouds.
• We design a weakly-supervised transfer learning approach for edge detection of point clouds in order to tackle the challenge of lack of the diversity of annotated data.
• We formulate a loss function assigned to the edge detection problem by combining two formats of ground-truths as edge extraction and segmentation. This combination in the loss function emphasizes the prediction of edge points and boosts the training process.
• Our model is able to improve incrementally the proposed weakly-supervised transfer learning for edge detection from 3D point clouds. This aspect of our proposed method brings the capability of applying EDC-Net to any target data. This attribute of EDC-Net is remarkable for industrial applications and is currently lacking in other edge detection techniques.

The robustness of this work stems from three aspects: (1) designing capsule networks for edge detection from point clouds to disentangle geometrical features of point clouds; (2) applying weakly-supervised transfer learning to tackle the lack of annotated data; (3) formulating a loss function to improve the training process by emphasizing the prediction of edges.

The contribution of this paper does not lie in merely surpassing the previous edge detection techniques. The significant aspects of our work are introducing a novel learning solution to this community, and tackling the challenges of the lack of annotated data for edge detection tasks of point clouds. The results of the proposed method are promising and constitute the first steps towards reliable point cloud edge detection based on capsule network and weakly-supervised transfer learning approaches. Our work opens a new research path in point cloud edge detection and poses novel research questions with available trends for further improvement.

The remainder of the article is organized as follows: the next section reviews the related work; Section 3 describes our proposed EDC-Net; the experimental results and conclusions are presented in Section 4 and Section 6, respectively.

2. Related Work

2.1. Point Clouds

Point clouds recently have attracted extensive attention for broad range of applications including autonomous driving [36], 3D object detection [37,38] and recognition and classification [6,7,39,40,41]. Deep neural networks have made notable improvements in order to perform quite effectively on the raw 3D point cloud data. PointNet [6] is the initiator to learn directly the representations of point clouds by computing features for each point individually and aggregating these features with max-pooling operations. Extending the same idea and to capture the contextual information of local patterns inside point clouds, PointNet++ [7] applies sampling and grouping operations to extract features from point clusters hierarchically. In recent years, many networks for 3D point clouds were inspired by PointNet++ [7], such as [8,9,10]. A complete review of deep learning methods for point clouds can be found in [11].

2.2. Edge Detection

Edge detection from point clouds has been attracting a lot of attention in various fields of research, such as robotics, photogrammetry, CAD and urban scene analyses [1,2,3,15]. Conventional methods for edge extraction from point clouds were based on building a mesh [3,15] or building a graph [13]. Reconstructing point clouds to a mesh or graph is computationally expensive. To overcome this issue, computing the difference of eigenvalues was proposed to extract edges [12]. The same idea was extended based on a segmentation [16] approach. Furthermore, discriminative learning algorithms are employed to extract edges from unorganized point clouds through a point classifier based on the edge versus non-edge points [2]. Moreover, a spatial filtering approach based on fast Fourier transform (FFT) was applied for boundary point detection to cope with the predefined threshold values [14]. Most of the techniques in the field of the edge extraction from point clouds are based on the geometric analysis; however, recently some methods have been proposed by using deep learning approaches [17,18,19,20,21,22]. CNNs are employed to define a scalar sharpness field over the smooth underlying the moving least-squares (MLS) surface of a point cloud [22]; this technique is capable of localizing sharp features of the scanned object. An extension of of this technique was proposed in [20] by training a convolutional neural network to derive a sharpness field parametrized over the underlying smooth proxy MLS surface. Furthermore, a combination of reconstruction and edge extraction was proposed in EC-Net [21], which is an edge-aware method based on extracting local patches and training the network to learn edges in patches. EC-Net [21] introduced a deep edge-aware point cloud consolidation framework. The network is trained to reconstruct upsampled 3D point clouds. The first phase of their technique consists of point classification and regression of per-point distances to the edge. Edge points are then detected as the points with a zero point-to-edge distance. PIE-NET [17] is the pipeline of the work; the technique of this pipeline treats point cloud curve inference as a curve proposal process. In this technique, first edges and corners are identified; then the edges are extracted by curve proposal and selection approaches. A geometric attention mechanism was presented in [19] to provide normals estimating and sharp feature lines’ properties in a learnable fashion which concentrates merely on geometric properties of point clouds. PCEDNet [18] presented a classification approach of edges in point clouds, where both edges and their surroundings are described. In their work, points are parameterized with a scale-space matrix (SSM) to encode extrinsic geometric properties of a surface surrounding each point of the input point cloud at multiple scales. Their proposed SSM provides information from a neural network to learn the description of edges and use it to efficiently detect them in given point clouds. Unlike the previous approaches, in our proposed method we extract the geometrical features as a means of pre-processing to feed the network, and we define the classification process of edge detection as a point-wise segmentation problem by a capsule network approach.

2.3. Capsule Network

The primary idea of capsule networks was initially introduced in [42] as a local component of artificial neural networks in which each capsule learns to recognize an implicitly defined visual entity over a limited domain of viewing conditions. This idea of capsules was developed afterwards into a dynamic routing mechanism between capsules in [23] as CapsNet (capsule networks). In the CapsNet model, capsules are groups of neurons that act together; and the information is stored at the vector level instead of scalar level. CapsNet [23] used the concept of iterative routing-by-agreement and squashing function on the output vector to get the activation capsules. Capsule networks recently proved to be powerful tools for a broad range of problems and have been applied in various lines of research; a thorough review of capsule networks can be found in [24]. Furthermore, the concept of CapsNet recently has been applied in point cloud processing research [25,26,27,28,29]. 3D Point Capsule Networks [25] proposed an auto-encoder to process sparse 3D point clouds while maintaining spatial arrangements of the input data. The geometric capsules approach is introduced in [26] to learn object representations from 3D point clouds by bundles of geometrically interpretable hidden units based on pose and features. Quaternion equivariant capsule networks [28] proposed to learn a pose-equivariant representation of objects by building a hierarchy of local reference frames where each frame is modeled as a quaternion. 3DCapsule [29] replaced the common fully connected classifier with a 3D capsule architecture in order to determine the spatial relationship between feature vectors by mapping feature vectors to capsules. DCG-Net [27] employed the agreement voting concept of capsules to build an aggregation neighborhood graph from a raw point cloud for the tasks of segmentation and classification.

While the aforementioned approaches applied a capsule network for different problems of point cloud processing, our proposed approach concentrates on employing a capsule network for a point-wise segmentation task to detect edges of point clouds. There was recent study that employed capsule networks for the segmentation tasks [43,44,45,46,47]. Matwo-CapsNet [43] presented a multi-label semantic segmentation technique based on capsule networks. Matwo-CapsNet combines pose and appearance information and encodes them as matrices through a dual routing mechanism. In [44] a segmentation architecture was developed based on capsule networks by improving the expectation-maximization routing algorithm (EM-routing). TraceCaps [45] is a capsule-based network architecture for semantic segmentation problems. It benefits from the part-whole dependencies attribute in capsule layers. TraceCaps derives the probabilities of the class labels for each capsule through a recursive, layer-by-layer procedure to build a segmentation network. SegCaps [46,47] is a convolutional–deconvolutional capsule network for the task of object segmentation. It extended the idea of convolutional capsules with locally-connected routing and proposed the concept of deconvolutional capsules. Unlike these models that are used for 2D images and for medical image applications, our proposed EDC-Net model merely focuses on 3D point clouds and defines the problem of edge detection as a segmentation task.

3. Proposed Method

3.1. Network Architecture

The main objective of EDC-Net is to precisely detect the sharp edge points of point clouds. To this end, we trained a capsule-based model to predict the edge regions of point clouds. EDC-Net is designed similarly to segmentation networks to classify edge and non-edge points in a point cloud. The network is fed by raw point clouds, which then pass through pre-processing steps and a convolution layer. Afterwards, the model is capable of segmenting the homogeneous edge points by capsule layers. The overview of the whole pipeline is depicted in Figure 1. In the following sections the details of EDC-Net are described.

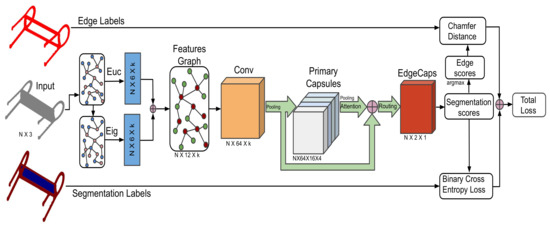
Figure 1. Overall overview of the proposed EDC-Net architecture. The input of this architecture is a raw point cloud of dimension $N\times 3$. The ground-truths are edge labels and segmentation labels which distinguish edges and non-edges points as two classes. The features graph is an aggregation neighborhood graph based on a concatenation of features from euclidean and eigenvalues spaces. EdgeCaps module proceeds with point-wise segmentation to classify edge and non-edge points. ⊕ stands for concatenation.

3.1.1. Input Data

The source input of EDC-Net is a raw point cloud of dimensions $N\times 3$ where N is the number of points in the point cloud. We consider a S-dimensional point cloud with N points, denoted by $\mathcal{X}=\{x_1,\dots ,x_N\}\subset {\mathbb{R}}^S$. Each point of a point cloud commonly contains three coordinates $x_i=(x_i^1,x_i^2,x_i^3)$, which means that $S=3$. Furthermore, it is possible to include further coordinates, such as those representing color information and normal vectors. However, in this work we just consider the coordinates.

Two formats of labels are defined to be considered during the training process of EDC-Net. First, segmentation labels of the shape $N\times 2$, where N is the number of points in a point cloud, and for each indexed point there is a corresponding value for each class of edge and non-edge. Second, edge labels are of the shape $n_g\times 3$, where $n_g$ is the number of points that are labeled as sharp edge regions in the ground-truth of the given point cloud and each point is represented by its coordinates in three dimensions. The number of edge points is less than the number of points in a point cloud ($n_g<N$). Segmentation labels and edge labels are applied during the training process for computing the loss. The details of loss calculation are explained in Section 3.2.

3.1.2. Features Graph

In the first layers of EDC-Net, the raw input point cloud $\mathcal{X}=\{x_1,\dots ,x_N\}\subset {\mathbb{R}}^3$ is converted to a k-NN (k nearest neighbors) graph structure based on its euclidean and eigenvalues features. This pre-processing step is used for building a k-NN features graph before applying the first convolution operation of the network.

In order to build a neighbors graph, we select the k neighbors of each point. We extract the k nearest neighbors of each point of a raw point cloud in a pre-processing step before feeding the features into the main blocks of the network, as is shown in Figure 1. The nearest neighboring process is measured based on $L^{2}norm$: $Distance(x_i,x_j)=\left|\right|x_i-x_j{\left|\right|}_2$, where $1\le i,j\le N$. Once the k nearest neighbors of each point in the euclidean space are determined, we search for the nearest neighbors in the eigenvalues space. To this end, we compute the covariance matrix to extract the eigenvalues inspired from [27]. Covariance is a measurement that explores the variance of each dimension from the mean with respect to each other. From a point cloud with N points, for a 3-dimensional sample point $x_i=(x_i^1,x_i^2,x_i^3)$, where $1\le i\le N$, the $3\times 3$ covariance matrix $C_i$ is given by:

$$C_i=\left[\begin{array}{ccc}Cov\left(x_i^1,x_i^1\right)& Cov\left(x_i^1,x_i^2\right)& Cov\left(x_i^1,x_i^3\right)\\ Cov\left(x_i^2,x_i^1\right)& Cov\left(x_i^2,x_i^2\right)& Cov\left(x_i^2,x_i^3\right)\\ Cov\left(x_i^3,x_i^1\right)& Cov\left(x_i^3,x_i^2\right)& Cov\left(x_i^3,x_i^3\right)\end{array}\right],$$

(1)

where, for instance, $Cov(x_i^1,x_i^2)$ is the covariance of $x_i^1$; $x_i^2$ by k nearest neighbor points is computed as:

$$Cov\left(x_i^1,x_i^2\right)=\frac{{\sum }_{j=1}^k\left(x_j^1-{\overline{x}}_i^1\right)\left(x_j^2-{\overline{x}}_i^2\right)}{k-1},$$

(2)

where ${\overline{x}}_i^1$ is the average of the neighbors of $x_i$ over the first dimension and ${\overline{x}}_i^2$ is the average over the second dimension. The eigenvalues and eigenvectors of $x_i$ are computed as: $C_i{V}_i={\lambda }_i{V}_i$, where $C_i$ is a $3\times 3$ covariance matrix, $V_i$ is an eigenvector and ${\lambda }_i$ is an eigenvalue. Then, the eigenvalues of the covariance matrix of the point cloud are defined as $\lambda =\{{\lambda }_1,\dots ,{\lambda }_N\}\subset {\mathbb{R}}^3$; each point of a point cloud contains three values in eigenvalues space denoted by ${\lambda }_i=({\lambda }_i^1,{\lambda }_i^2,{\lambda }_i^3)$ and ordered as: ${\lambda }_i^1\le {\lambda }_i^2\le {\lambda }_i^3$.

The nearest neighboring process in eigenvalues space is measured based on $L^{2}norm$: $Distance({\lambda }_i,{\lambda }_j)=\left|\right|{\lambda }_i-{\lambda }_j{\left|\right|}_2$, where $1\le i,j\le N$.

We define a directed edge-weighted graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ representing point cloud structure based on its euclidean and eigenvalues features, where the vertices are $\mathcal{V}$ $=\{{\mathcal{V}}_1,\dots ,{\mathcal{V}}_N\}$ and the edges are $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$. We construct $\mathcal{G}$ as a k-NN edge-weighted graph in ${\mathbb{R}}^{\mathcal{A}}$, where $\mathcal{A}$ is the feature space dimension of the graph. The k nearest neighbors are based on the similarities of the points in $\mathcal{X}$. The similarities are exploited by $L^2$ norm. The edge-weighted graph $\mathcal{G}$ is constructed by connecting all the nearest neighbors of shape $N\times k\times \mathcal{A}$. The graph $\mathcal{G}$ includes self-loops, meaning each vertex also points to itself.

We exploit the k nearest neighbors in both the euclidean and eigenvalues spaces and concatenate the features inspired by [48]; however, the eigenvalues in this work are different since they are based on the covariance matrix. Furthermore, we consider the differences as the input features, as it is proven in [48]. Therefore, the shape of both the euclidean and eigenvalues graphs is $N\times k\times 6$, which means that $\mathcal{A}$ is equal to 6. The shape of the features graph is $N\times k\times 12$ which is the concatenation of the euclidean and eigenvalues graphs, and it means that $\mathcal{A}$ is equal to 12 for the features graph. Afterwards, this features graph is fed into a convolutional operation.

3.1.3. Primary Capsules

Primary capsules in EDC-Net are the first capsule layer. Primary capsules transfer the features from the previous convolution layer into the capsules via convolutional filtering.

The main task of primary capsules is to transform the output of the previous convolution into an estimated pose and activation of each capsule. The primary capsule layer performs four sets of 1D convolutions with a $3\times 3$ kernel. The input channel of each convolution has 64 dimensions and each output channel has 16 dimensions. The shape of the output of primary capsules after applying max-pooling is $N\times 16\times 4$, where N is the number of points in a point cloud. The activation values from a convolution operation in capsule networks are considered as coefficient values. These coefficients are applied to influence the information that proceeds between the capsules. Each of the capsules presents the properties of the point cloud from different aspects based on the pose and appearance information of points. The length of the capsules represents the probability of the presence of these properties. In EDC-Net an attention operation is performed on the primary capsules before applying the routing mechanism to the EdgeCaps module.

3.1.4. Attention Module

In EDC-Net, primary capsules are extracted based on the features of each point of the point cloud. In this case, if the routing mechanism is directly applied, the activations of the EdgeCaps module depend on the global features of primary capsules, which is not appropriate for a point-wise segmentation process. To this end, we apply an attention function on the primary capsules. Afterwards, we concatenate the output of attention module with the reshaped features of the previous convolution layer to concatenate the global and local features together. The attention module in EDC-Net is inspired by [49] which is a two-layer fully connected neural network $f_{attn}(·)$. The shape of the output of primary capsules is $N\times 16\times 4$. We then reshape the primary capsules to $N\times (16\times 4)$, which is $N\times 64$. Afterwards, by applying the attention function $f_{attn}(·)$, we obtain the features of a shape $N\times 4$ since we defined four capsules in the primary capsules. We apply a point-wise Softmax normalization to generate the final attention values of each capsule. Finally, we obtain the scaled capsules by multiplying the normalized attention values with primary capsules. Figure 2 illustrates the details of the structure of the attention module.

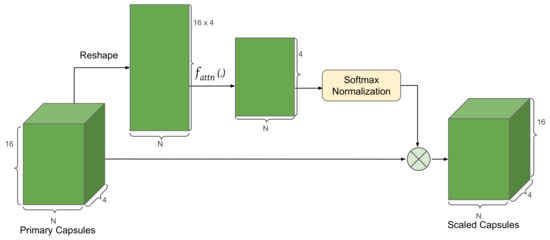
Figure 2. The structure of the attention module. ⊗ stands for multiplication.

3.1.5. Routing Mechanism

A routing mechanism in capsule networks is an operation for updating the weights between capsules. Therefore, the properties captured by capsules can be propagated to suitable capsules, where different capsules reflect the properties of point cloud from different aspects. The task of a routing mechanism is to define the global coherence of the features and it performs by learning part-whole relationships.

We concatenate the output of the primary capsules after applying the attention module with the output of the convolutional features. The convolutional layer features are local features and the features from primary capsules after the attention module are global features. This concatenation process is required to achieve point-wise segmentation results through the routing mechanism. The shape of the output of the first convolution after max-pooling is $N\times 64$. The shape of the output of the primary capsules after max-pooling is $N\times 16\times 4$; also it maintains the same shape after applying the attention module. Accordingly, we reshape the convolution of shape $N\times 64$ to $N\times 16\times 4$ in order to concatenate it with the features from the attention module of primary capsules. Therefore, the features for routing mechanism have a shape of $N\times 16\times 8$, and are defined by $f=\{f_1,\dots ,f_i,\dots ,f_n\}$ where n is equal to 8; and 8 is the number of these latent capsules in the routing mechanism—there are 4 capsules for the local features and 4 capsules for the global features. Furthermore, $f_i$ is the feature in each one of the latent capsules of dimensions $N\times 16$. The routing mechanism determines the connection between input and output capsules of the process. In EDC-Net, we define the dimensions of the EdgeCaps module by 2 since we have two classes of edge and non-edge points. In the routing mechanism, there are coupling coefficients denoted by C between the latent capsules and EdgeCaps capsules, where $C=\{C_{11},\dots ,C_{ij},\dots ,C_{nm}\}$, where $1\le i\le n\le 8,j\le m\le 2$; the summation of all of the coupling coefficients is equal to one. The coefficient values are computed by a routing softmax which is initially defined by $b_{ij}$. The $b_{ij}$ represents the logit of i-th index of the latent capsules and j-th index of the EdgeCaps capsules. The $b_{ij}$ is initialized with zero at the first iteration of the dynamic routing mechanism. Then, it is rectified iteratively by evaluating the agreement between the capsules. Hence, coupling coefficient values are computed as $C_{ij}=\frac{exp\left(b_{ij}\right)}{{\sum }_{z=1}^{n}exp\left(b_{iz}\right)}$, where z represents the iterator through all capsules. The coupling coefficients are the log prior probabilities and they are updated by the iterative routing process. Afterwards, by multiplication of all the features f with the routing coefficient C, we obtain the list of prediction vectors $\overrightarrow{P}=\{{\overrightarrow{P}}_{11},\dots ,{\overrightarrow{P}}_{ij},\dots ,{\overrightarrow{P}}_{nm}\}$ for each vector of capsule ${\overrightarrow{P}}_{ij}=C_{ij}{f}_i$. Each capsule consists of a weighted sum $\left(S_j\right)$ of all prediction vectors in order to make a connection between capsules $S_j={\sum }_{i=1}^n{\overrightarrow{P}}_{ij}$. The list of prediction vectors $\overrightarrow{P}$ represents the probability of similarities of features with respect to the features of each point. Hence, in order to define more similar prediction vectors close to $one$ and less similar prediction vectors close to $zero$, we apply a non-linear squashing function [23], $V_j=\frac{\parallel S_j{\parallel }^2}{1+\parallel S_j{\parallel }^2}\frac{S_j}{\parallel S_j\parallel }$, where $V_j$ is the vector output of capsule j and $S_j$ is its total input. Therefore, at each iteration of the routing mechanism, the vector length is reduced to close to zero for dissimilar features and is increased until close to one for similar features. This process is performed by updating the routing coefficients as $b_{ij}=b_{ij}+V_j.f_i$ (i.e., we make a dot product of $V_j$ and $f_i$). Routing mechanism classifies the similar features; then the EdgeCaps module returns the activations in two classes as a point-wise segmentation process to extract edge and non-edge points.

3.1.6. EdgeCaps

Our proposed EdgeCaps is the first use of a capsule network architecture for edge detection of point clouds in literature. We set up a similar voting agreement hierarchy to [23] and embedded it into EDC-Net to build a segmentation network. Our model is built upon a dynamic routing between capsules and treats the capsules as a probabilistic model which is capable of inferring visual entities based on the probabilistic vectors of the features. EdgeCaps captures edge points of a given point cloud and exploits this information through a recursive procedure to derive the class memberships (edge, non-edge) for individual points. Our contribution to the capsule network is that we do not apply the primary capsules’ activation directly in the routing process; but we apply an attention module to the primary capsules and concatenate them with the features of the previous convolution layer in order to combine the local and global features for a point-wise segmentation process through the EdgeCaps module. Furthermore, this modification allows us to operate on various sizes of point clouds. EdgeCaps returns the capsule activations in two classes as edge and non-edge based on the voting agreement hierarchy of the dynamic routing between the capsules. Moreover, another contribution of this work is that we do not incorporate margin or reconstruction loss; we define a specific loss function in Section 3.2 which focuses merely on the point-wise edge segmentation problem.

3.2. Loss Function

We have considered a combination of two loss functions in EDC-Net as edge loss and segmentation loss based on some weighted values in order to classify edge and non-edge points while emphasizing extracting edges from a point cloud. The details of each loss function are as follows:

3.2.1. Edge Loss

The edge loss is measured in terms of Chamfer distance (CD) [50]. Given two point clouds of ground-truth and predicted edges:

$${\mathcal{L}}_e=\frac{1}{n_g}\sum _{p_i\in S_1}\underset{p_j\in S_2}{min}{∥p_i-p_j∥}_2+\frac{1}{n_p}\sum _{p_j\in S_2}\underset{p_i\in S_1}{min}{∥p_i-p_j∥}_2,$$

(3)

where $S_1=\{p_1,\dots p_i,\dots ,p_{n_g}\}\subset {\mathbb{R}}^3$ is the set of the ground-truth edges in a given point cloud and $S_1$ contains $n_g$ points, $|S_1|=n_g$. Each point of $S_1$ is comprised of three coordinates $p_i=(p_i^1,p_i^2,p_i^3)$, $1\le i\le n_g$. Furthermore, $S_2$ is the set of the predicted edge points by EDC-Net model from a given point cloud. $S_2$ contains $n_p$ points denoted by $S_2=\{p_1,\dots p_j,\dots ,p_{n_p}\}\subset {\mathbb{R}}^3$, $|S_2|=n_p$; and each point of $S_2$ contains three coordinates $p_j=(p_j^1,p_j^2,p_j^3)$, $1\le j\le n_p$. For the first summation, given a point $p_i$ in the ground-truth point cloud $S_1$, find the nearest corresponding point $p_j$ in the predicted point cloud $S_2$. A similar process is performed from $p_j$ to $p_i$ for the second summation. $S_1$ and $S_2$ do not necessarily contain the same number of points. Chamfer distance is differentiable and is computationally efficient.

3.2.2. Segmentation Loss

We consider a class-weighted binary cross-entropy loss function for the segmentation task. We have two classes of edge and non-edge. In almost all of the point cloud shapes, the number of points for edges is much lower than the number of non-edge points. Therefore, this class-weighted approach is beneficial in order to determine a balance between these two classes. $w_c$ is the weight for each one of the classes:

$$w_c=\frac{1}{log(1.02+\frac{f_c}{f_t})},$$

(4)

where $f_c$ is frequency of the class c and $f_t$ is total frequency of all the classes. Therefore, the class-weighted binary cross-entropy is calculated as:

$${\mathcal{L}}_s=-\frac{1}{n_c}\sum _{c=1}^{n_c}{w}_c\left(y_{c}log\left(p\left(y_c\right)\right)+\left(1-y_c)\right)log(1-p\left(y_c\right))\right),$$

(5)

where y is the label, $p\left(y\right)$ is the predicted probability and $w_c$ is the weight of each class; in this point-wise segmentation process, there are two classes of edge and non-edge; hence, $n_c$ is equal to $two$.

3.2.3. Total Loss

The training procedure of EDC-Net model is defined based on the combination of the two aforementioned loss functions:

$$Loss=\alpha {\mathcal{L}}_e+\gamma {\mathcal{L}}_s,$$

(6)

where ${\mathcal{L}}_e$ is the edge loss and ${\mathcal{L}}_s$ is the segmentation loss; we have considered a weight for each one of the losses in order to emphasize more the correctness of extracting the edge points during the training process. In our experiments we set $\alpha =0.6$ and $\gamma =0.4$. In Section 4.5 we describe the reason for selecting these parameters as the weights for computing loss.

3.3. Training Process

We first trained EDC-Net in a fully-supervise learning process on ABC dataset [35] with the provided labels. Afterwards, since ABC dataset [35] is the only public dataset available for point cloud edge detection, we boosted the training process of EDC-Net model based on a weakly-supervised fashion which is described in Section 3.3.1. In this stage, we used the samples of ShapeNet dataset [34] and annotated the edge points based on the implementation of [12] and transferred the learning of the model trained by ABC dataset [35].

3.3.1. Weakly-Supervised Transfer Learning

Transfer learning is the concept of applying pre-trained models to fine-tune them on other target data. Transfer learning performs a projection of all the new inputs through a pre-trained model. For instance, we have a pre-trained model function $f(·)$ and attempt to learn a new function $g(·)$. To this end, we simplify $g(·)$ by $g\left(f\right(·\left)\right)$; in this way $g(·)$ perceives all the data through $f(·)$. In this work, we first trained EDC-Net on the ABC dataset [35], and then considered this model as a pre-trained model. Afterwards, in order to improve the performance of the model with various types of shapes, we fine-tuned the model on ShapeNet [34] (the details about the datasets are explained in Section 4.1). Since there is no available edge detection ground-truth for ShapeNet, we considered [12] as a baseline edge detection technique (the implementation is publicly available from [51]). The edge detection of the aforementioned technique is not perfectly precise; therefore, this stage is considered as weakly-supervised learning since we trained the model with these imprecise labels.

4. Experimental Results

4.1. Dataset

We performed a statistical analysis over the ABC [35] and ShapeNet [34] datasets. ABC [35] is a large-scale CAD dataset containing ground-truth annotations for edge points. The ABC ground-truth classification was produced using the vertices each associated with a sharp feature. The sharp feature labels of ABC dataset are based on the distances to the closest feature lines of point clouds. In our experiments, in order to train a point-wise segmentation model, we required hard labels to classify edge and non-edge points. Therefore, we set a threshold ($\tau$) as 0.1 ($\tau =0.1$); if the distance (d) of a point to the closest feature lines of point clouds was smaller than the threshold ($d<\tau$), then the point was assigned as an edge point; otherwise, ($d>\tau$) the point was assigned as a non-edge point. The threshold value ($\tau$) is not a sensitive hyperparameter for training processes, since this value is rather a parameter for setting up the dataset and the same value was applied on the training set, validation set and test set of ABC dataset.

ABC dataset contains 81,920 high resolution annotated point clouds for the sharp feature detection task. We split this dataset into 57,344 point clouds for training (70%), 8192 point clouds for validation (10%) and 16,384 point clouds for testing (20%). Each point cloud provided by the ABC dataset contains 4096 points; in our experiments we sampled 1024 and 2048 points from each point cloud via uniform point sampling and then transferred the annotation model to the point clouds.

For the weakly-supervised learning process, we utilized ShapeNetCore.v2, which is a subset of the full ShapeNet [34] dataset. ShapeNetCore.v2 contains 51,127 pre-aligned 3D shapes from 55 common object categories categories, which are split into 35,708 (70%) shapes for training, 5158 (10%) shapes for validation and 10,261 (20%) shapes for testing.

In our experiments, we sampled 1024 and 2048 points from ShapeNet models. We followed the iterative farthest point sampling (FPS) configuration of [7] to sample points uniformly from the point clouds in both the ABC and ShapeNet datasets.

4.2. Implementation Details

We trained the EDC-Net model by ADAM optimizer [52] with a learning rate of ${10}^{-3}$, momentum of 0.9, and reduced the learning rate by cosine annealing until ${10}^{-4}$. Cosine annealing is a learning rate scheduler that has the effect of starting with a large learning rate that is relatively rapidly decreased to a minimum value before being increased rapidly again [53]. Furthermore, we applied weight regularization by a weight-decay equal to ${10}^{-5}$ to reduce the overfitting problem in our network. In all experiments, the number of neighbors (k) to build the features graph was either equal to 20 or to 40 when we respectively sampled either 1024 or 2048 points. We have performed three iterations in dynamic routing procedure between capsules. We kept the batch-size as 32 or 16 during training and testing respectively, and did the training for 300 epochs on ABC and 200 epochs on ShapeNet for the weakly-supervised transfer learning experiments.

All the experiments of this paper were conducted on a system with a single GeForce RTX 2080 Ti GPU and EDC-Net implementation is based on Pytorch library.

4.3. Edge Detection Results

We considered $F_1$ score as an evaluation measurement to quantitatively compare the results of the different techniques: $F_1=2\times \frac{Precision\times Recall}{Precision+Recall}$ where precision is defined as the proportion of correctly detected points by EDC-Net model and recall is defined as the proportion of labeled edge points in the ground-truth. Precision and recall are computed as: $Precision=\frac{TP}{TP+FP}$, $Recall=\frac{TP}{TP+FN}$ where $TP$ stands for true positives representing the number of correctly detected points; $FP$ stands for false positives representing the number of wrongly detected points; $FN$ stands for false negatives, representing the number of false rejections, i.e., edge points in the ground-truth that are not detected as edges by EDC-Net model. The terms precision and recall in some references are defined as correctness and completeness [54].

We have done extensive experiments to evaluate the performance of our proposed EDC-Net. The quantitative results are summarized in Table 1. The models that are denoted by WSL in Table 1 were trained on ShapeNet dataset in a weakly-supervised learning fashion as explained in Section 3.3.1; the rest of the models were merely trained on ABC dataset samples. We have trained EC-Net [21] according to the publicly available code [55] on the datasets described in Section 4.1 and not the dataset used by the authors in the original paper [21].

Table 1. Results on ABC [35] and ShapeNet [34] samples. WSL stands for weakly-supervised learning. P and R are represented for precision and recall respectively. The highest $F1$ score at each line is shown in bold.

		EC-Net [21]			EDC-Net (Ours)			EC-Net [21] + WSL			EDC-Net + WSL (Ours)
		P	R	F1	P	R	F1	P	R	F1	P	R	F1
ABC	N = 1024	0.6780	0.7427	0.7089	0.8475	0.9310	0.8873	0.6652	0.7278	0.6951	0.8371	0.9051	0.8698
	N = 2048	0.6782	0.7451	0.7101	0.8485	0.9561	0.8991	0.6727	0.7322	0.7012	0.8407	0.9322	0.8841
ShapeNet	N = 1024	0.5718	0.6845	0.6231	0.5879	0.6991	0.6387	0.5906	0.7034	0.6421	0.6357	0.7532	0.6895
	N = 2048	0.6069	0.6823	0.6424	0.6658	0.7532	0.7068	0.6469	0.7021	0.6734	0.7537	0.7843	0.7687

We have provide some qualitative results of EDC-Net model on ABC [35] datasets and ShapeNet [34], the results are illustrated in Figure 3.

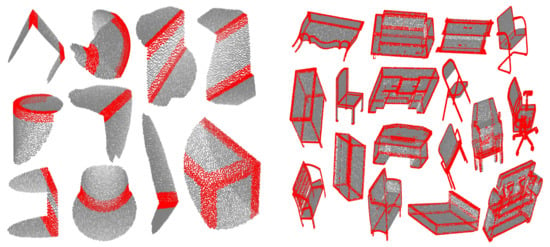
Figure 3. Edge detection results on ABC [35] (left) and ShapeNet [34] (right) samples. The detected edge points are assigned with red and not-edge points with gray.

4.4. Robustness to Noise

Point clouds often contain certain amounts of noise in a real scene when they are captured by scanners. In order to evaluate our EDC-Net on noisy point clouds, we applied various perturbations of noise levels on point clouds from ABC. We randomly applied different perturbations to the point samples along the surface normal direction with a scale factor in the $[1.0$ − $\sigma ,1.0+\sigma ]$ range, where we tested five values of $\sigma =\{0.0,0.02,0.05,0.08,0.12\}$. The results of these experiments are summarized in Table 2. Precision, recall and F1 scores were computed similar as the explanations in Section 4.3.

Table 2. The behavior of EDC-Net with different perturbed levels of noise on ABC dataset.

		Noise Level ($\mathit{\sigma }$)
		$\mathit{\sigma }$ = 0.0	$\mathit{\sigma }$ = 0.02	$\mathit{\sigma }$ = 0.05	$\mathit{\sigma }$ = 0.08	$\mathit{\sigma }$= 0.12
N = 1024	P	0.8475	0.8310	0.8179	0.7865	0.7321
	R	0.9310	0.8986	0.8849	0.8402	0.8443
	F1	0.8873	0.8635	0.8501	0.8125	0.7842
N = 2048	P	0.8458	0.8267	0.8268	0.8023	0.7684
	R	0.9561	0.9385	0.9027	0.8424	0.8306
	F1	0.8991	0.8791	0.8631	0.8219	0.7983

4.5. Ablation Study

We performed an ablation study based on the two hyper-parameters of $\alpha$ and $\gamma$ for computing the loss function during the training process (as explained in Section 3.2). The summary of this study is depicted in Figure 4 (left). All the experiments in this ablation study were performed on the validation set of the ABC dataset. This study demonstrates the importance of the weights for calculating the loss during the training process and how it accelerates the training process to converge the loss earlier.

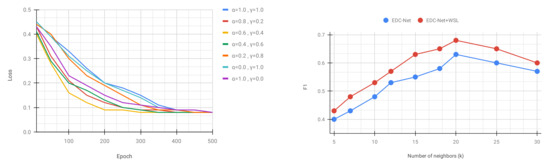
Figure 4. (Left) Training loss of EDC-Net for various $\alpha$ and $\gamma$ during training on the ABC dataset. (Right) Comparison of the accuracy ($F_1$) of EDC-Net on ShapeNet dataset based on various numbers of neighbors (K) and a comparison to demonstrate the importance of WSL (weakly-supervised learning) to improving the accuracy on ShapeNet dataset.

Furthermore, we performed another ablation study to analyze the effectiveness of the weakly-supervised transfer learning approach and the adequate number of neighbors (k) of our proposed EDC-Net. In all these experiments we sampled 1024 sample points from each point cloud, and we trained EDC-Net by different numbers of neighbors; we applied the test set of the ShapeNet dataset for evaluating the trained models. EDC-Net refers to the models that just trained on the ABC dataset and EDC-Net+WSL refers to the models that applied the weakly-supervised learning by imprecise labels of ShapeNet dataset. The results of these experiments are summarized in Figure 4 (right). This study demonstrates the adequate number of neighbors that we defined in our experiments; furthermore, it demonstrates the robustness of weakly-supervised learning for boosting the performance of EDC-Net on the ShapeNet dataset.

4.6. Complexity Analysis

We analyzed the complexity of EDC-Net based on two criteria: (1) time consumption for point classification; (2) model size. The results are summarized in Table 3.

Table 3. Complexity analysis of EDC-Net.

	EDC-Net (Ours)	EC-Net [21]	PIE-Net [17]
Point classification (s)	0.3	0.8	0.5
Model size (MB)	1.8	9.4	-

For all the experiments performed by EDC-Net, the average running time was about 0.3 s for point classification per point cloud. In comparison, the average running times for point classification by EC-Net [21] and PIE-NET [17] were 0.8 and 0.5 s respectively.

The size of the EDC-Net model is significantly smaller than the size of the EC-Net [21] model, and it achieved better performance; this is a notable advantage of EDC-Net that determined it as a light-weighted model and proved its capability to fit into devices with limited resources.

5. Discussion

The advantages of our proposed EDC-Net for point cloud edge detection are based on the design of capsule network for edge detection from point clouds to disentangle geometrical features of point clouds. Furthermore, our proposed loss function improves the training process by emphasizing the prediction of edges and boosts the training for an earlier convergence.

The notable contribution of our work lies in presenting a novel learning framework for detecting point clouds edges, and tackling the challenges of the lack of annotated data for this task. However, there are still multiple limitations in this work—namely, large-scale point clouds require different implementations and network architectures and yet there is not any public dataset available for the edge detection of large-scale point clouds. In this work, we considered the scale of point clouds based on 1024 and 2048 point samples, which are the most common point sample scales in this community for single object point clouds. Building a framework to tackle multiple objects in a large-scale point clouds is still challenging. Therefore, for the future work, we plan to apply this technique to some large-scale scene point clouds instead of just focusing on single object CAD models. Furthermore, we plan to apply some unsupervised techniques inspired by [56] in order to train an edge detection model regardless of the ground-truth data.

Overall, the results of our proposed method are promising and constitute the first steps towards reliable point cloud edge detection based on capsule network and weakly-supervised transfer learning approaches. Our work opens a new research path in point cloud edge detection and poses novel research questions with available trends for further improvement.

6. Conclusions

In this paper, we introduced EDC-Net, a novel framework for edge detection based on capsule network structures. We designed a point-wise segmentation pipeline to classify the edge and non-edge points. We formulated a loss function specifically tailored to extract edge points in highly unbalanced point clouds where the number of non-edge points is often much larger than the number of edge points. We proved that our proposed loss function significantly boosts the training process in terms of time and accuracy. Moreover, we built a weakly-supervised transfer learning structure to set up a flexible and robust pipeline applicable to unlabeled datasets.

We provided extensive experimental results on ABC and ShapeNet datasets. We demonstrated that our proposed EDC-Net performs accurately on edge detection tasks, and we furthermore proved its robustness on the noisy data. Moreover, we proved that our proposed weakly-supervised transfer learning improved the performance on the ShapeNet dataset, for which there are no available edge labels. Experimental results demonstrated that our proposed EDC-Net performs efficiently in terms of the execution time while maintaining high accuracy. Moreover, EDC-Net provides a compressed model with a small model size, which is important for a better deployment to fit high-performing models into devices with constrained resources.

Our contribution does not focus merely on surpassing the edge detection state-of-the-art techniques, but we also introduced a novel learning approach for edge detection tasks based on capsule network structures. Furthermore, we proposed a new approach that tackles the challenge of a lack of annotated data for training models in this community.