Wave Theory of Seismic Resistance of Underground Pipelines
Abstract
Featured Application
Abstract
1. Introduction
- Under strong ground motion, the underground pipeline system is destroyed; these destructions are different: the destruction in the pipeline itself, in butt joints, the pipeline buckling from the ground; soil separation from the pipeline on the surfaces of their contact, etc.;
- Seismic forces are transmitted to underground pipelines through soil. Therefore, these forces’ values directly depend on the physical–mechanical and strain properties of the soil environment surrounding the underground pipeline.
- The assumption of an infinitely long straight horizontal pipeline in homogeneous soil simplifies the solution of the problem of seismic impact on the pipeline. This assumption is used in most theoretical studies. An exception is in [11]. The unsteady wave problem of a longitudinal monochromatic wave propagation and reflection from a rigid stationary barrier solved in a one-dimensional statement.
- During earthquakes, seismic forces are transmitted to underground pipelines through soil strain, i.e., the soil deforms under seismic wave effect and forces underground pipelines to deform. The pipelines inflict the most severe damage when the route is codirectional to the seismic strain vector [15].
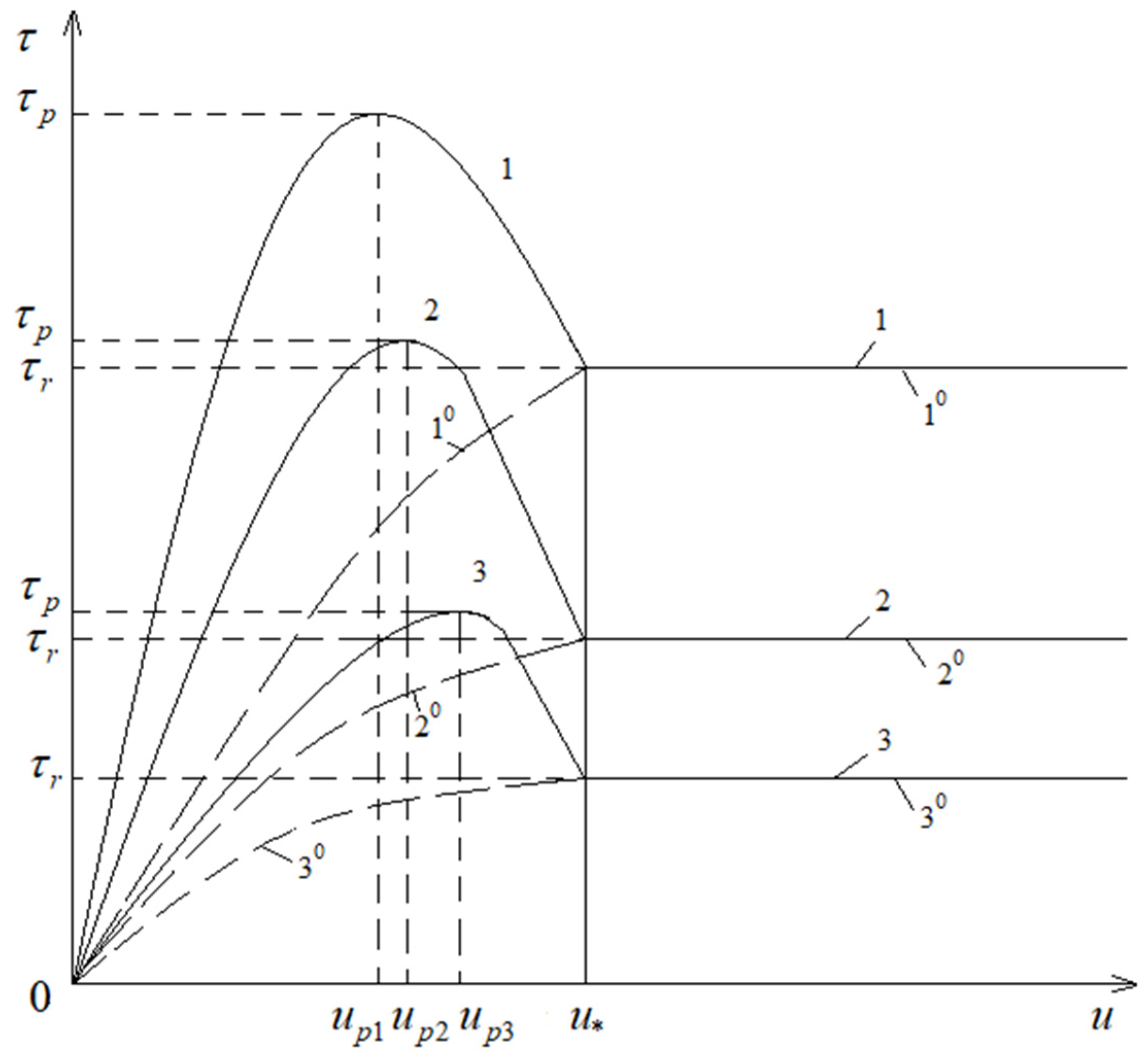
- In the case of strong ground motions, the amplitudes of absolute displacements of soil particles reach 0.1–0.4 m at an oscillation period T = 0.05–20 s; under soil mass vibrations together with the underground pipeline, a difference between the vibrational motion of the pipeline and soil is formed (for various reasons) in vibration amplitude and phase; a displacement of the pipeline relative to the soil is observed, i.e., a relative displacement.
- There is a critical value of the relative displacement of the pipeline cross-section, below which there is an elastic bond between the soil particles and the outer surface of the pipeline in contact with the soil. At values of the relative displacement exceeding the critical value, the elastic bond between the pipeline and the ground is ruptured [14].
- After pipeline construction, due to the cohesion phenomena, a relative shear displacement occurs in the soil layer thick, called the contact soil layer, between the underground pipeline and soil on their contact surfaces.
- At an increase in relative displacement value greater than , the contact soil layer undergoes significant shear strain and may collapse; the soil outside the contact layer may remain intact. In the case of strain and destruction of the contact soil layer under shear stresses, its limiting value is determined based on the Coulomb law.
- The processes of relative displacements formation on the contact layer, under its elastic, elastic–plastic strain () and destruction (), are the two stages of one process—the process of deformation of the contact soil layer before and after destruction.
- To conduct a critical analysis of the dynamic theory grounds, to determine its disadvantages and advantages;
- To determine the ways of further development of the dynamic theory of seismic resistance of underground pipelines;
- To determine the grounds of an alternative wave theory of seismic resistance of underground pipelines and its advantages and disadvantages.
2. Materials and Methods
2.1. Interaction Laws
2.2. Formulation of the Problem
3. Results and Discussion
3.1. Solution Methods
- (i).
- It is possible to obtain numerical solutions by the finite difference method directly. In this case, these partial differential equations are directly solved.
- (ii).
- However, there is another method. Partial differential equations of hyperbolic type have real characteristics and relations on them. In this case, the characteristic relations are already ordinary differential equations. In the case of boundary conditions (30)–(33) and laws of interaction (26), the wave front lines in soil and the pipeline remain linear. The characteristic lines also remain linear on the characteristic planes for soil and the pipeline. The numerical finite difference method’s application to these ordinary differential equations significantly increases the accuracy of the solutions obtained. Previously the authors have used this algorithm in solving many wave problems and showed the high accuracy of the method. Examples of the application of the method are publications [35,38,39,40].
- (iii).
- For underground pipelinewhere , .
- (iv).
- For soil half-spacewhere , .
3.2. Numerical Calculations
3.2.1. Initial Data for Calculations
- (i)
- For the underground pipeline:
- (ii)
- For soil:
- (iii)
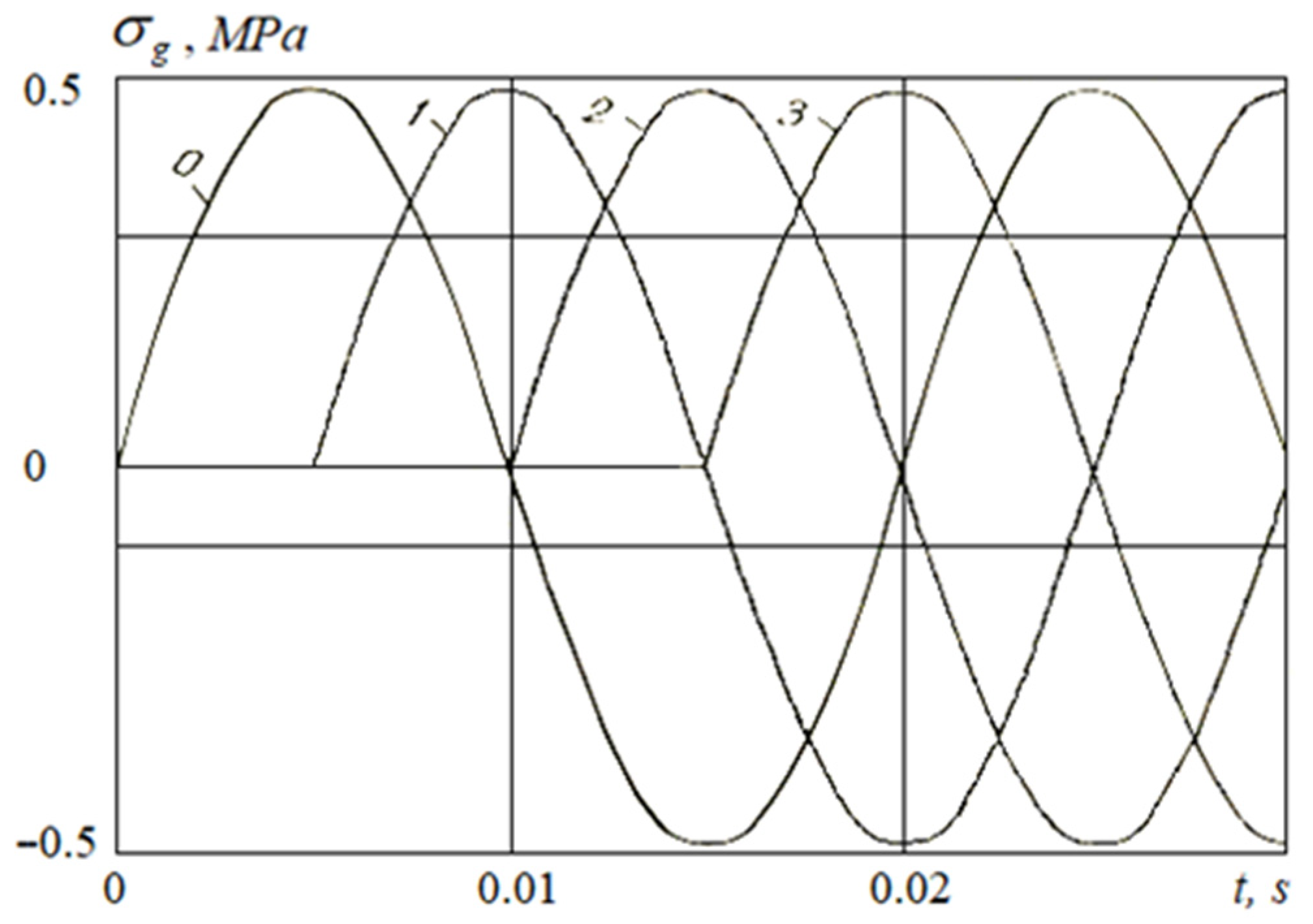
- For seismic load parameters:
- (iv)
- For interaction parameters:
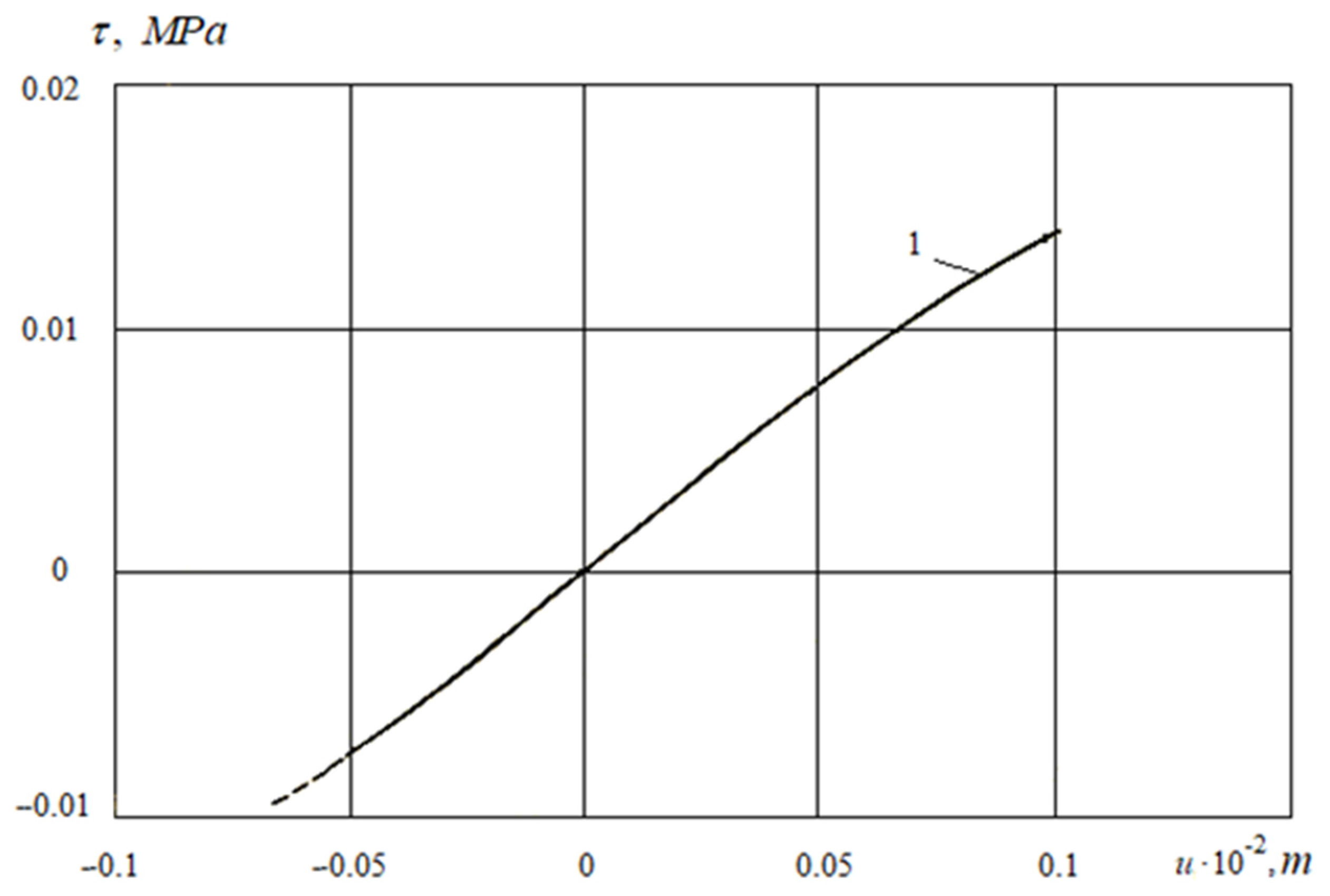
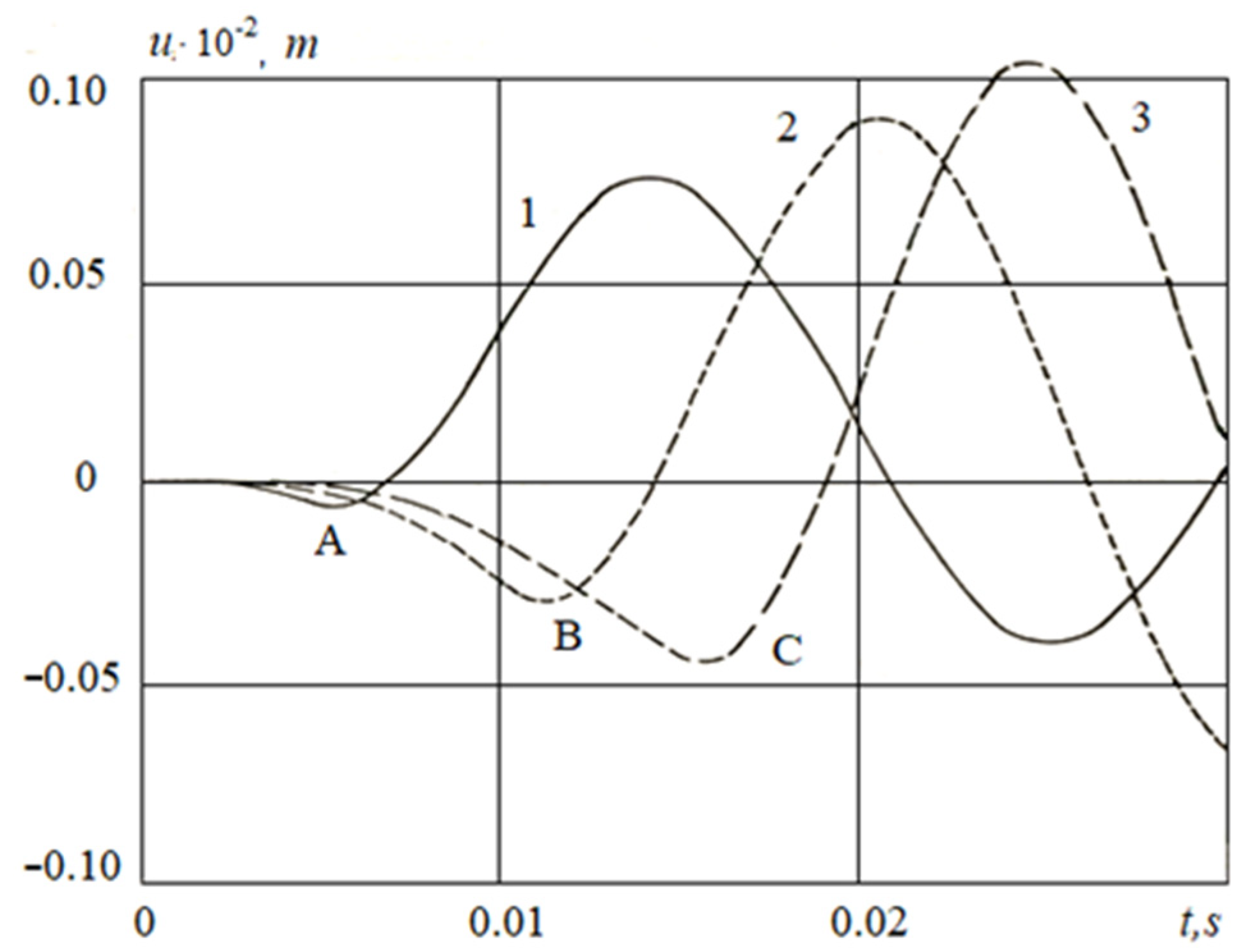
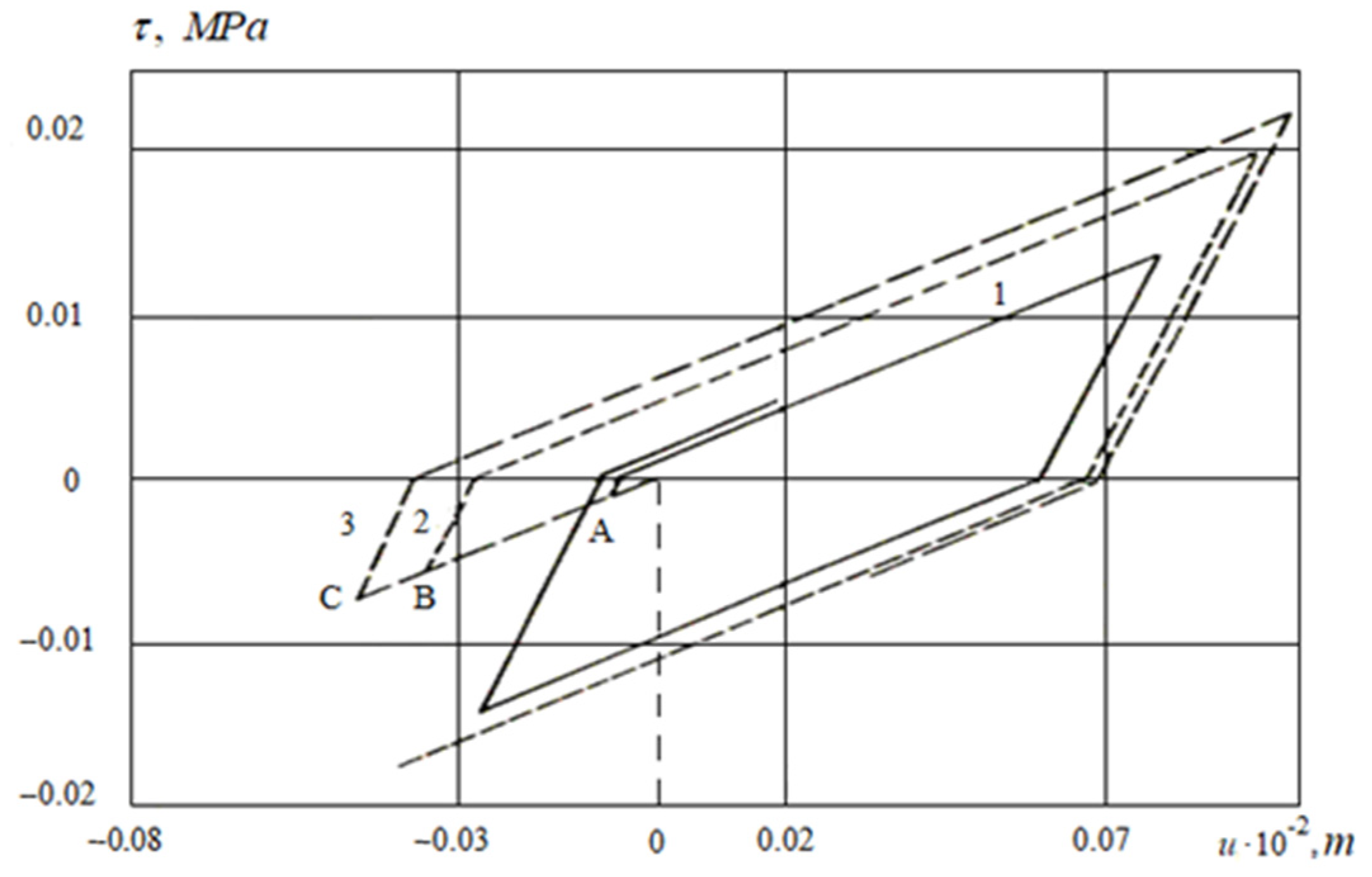
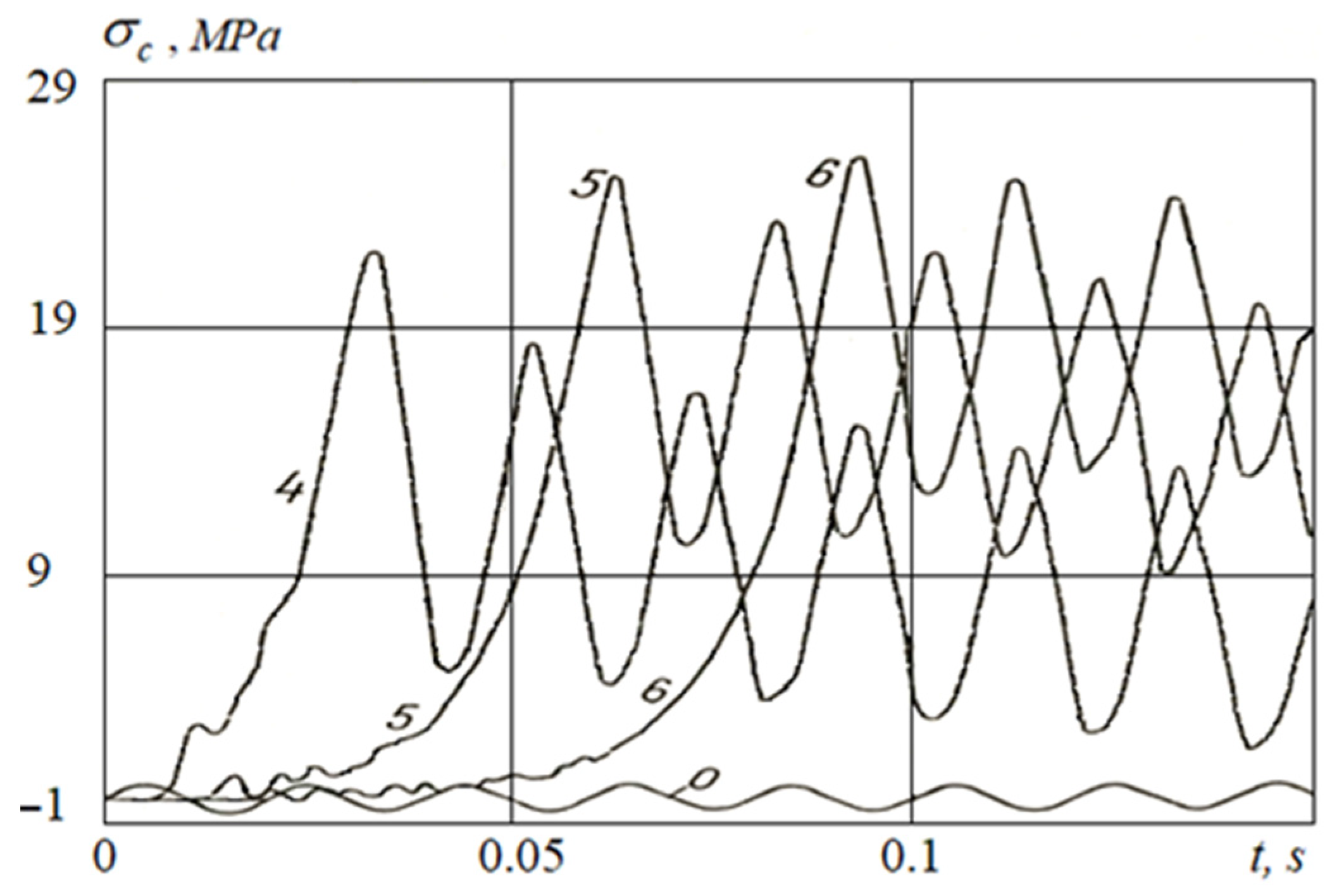
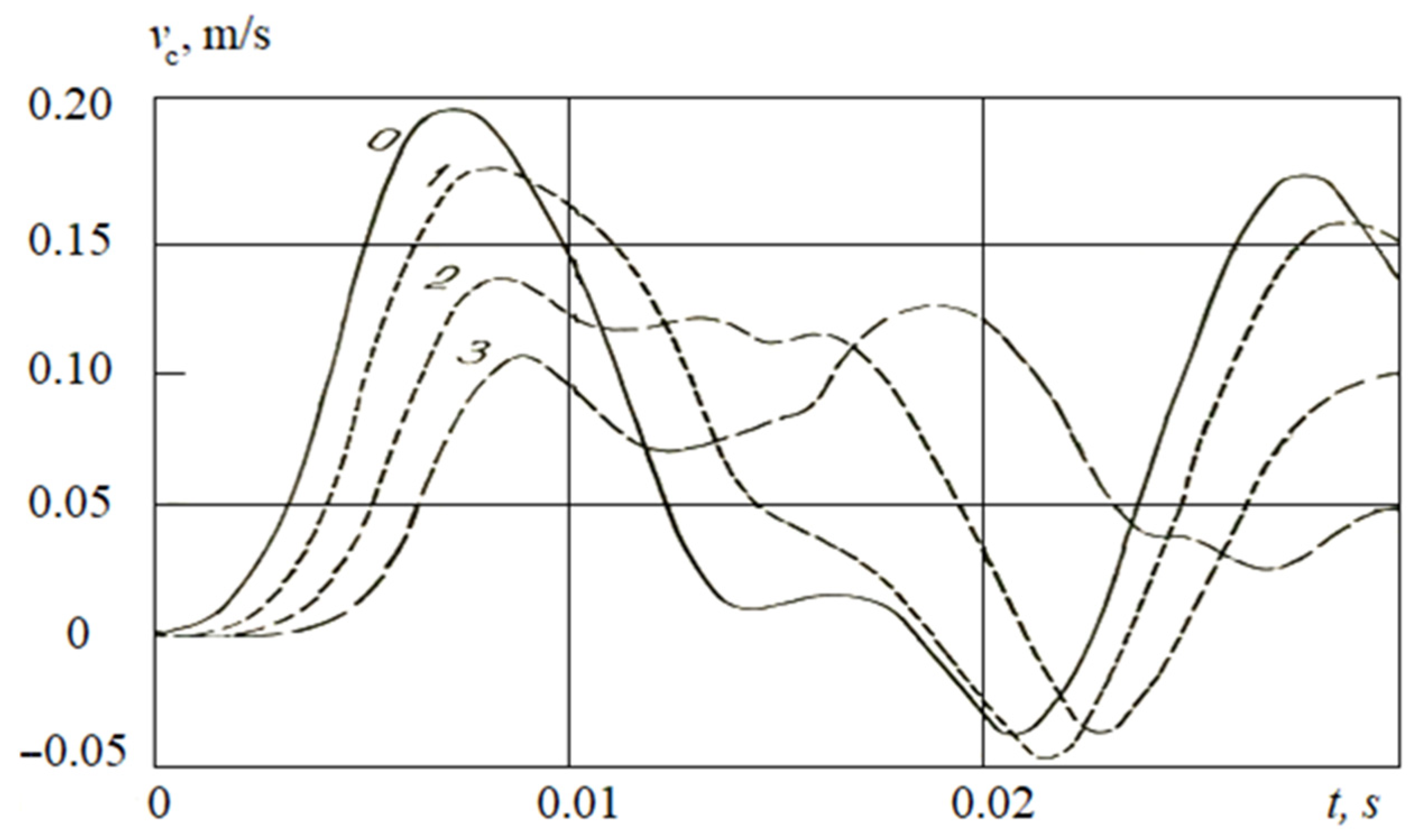
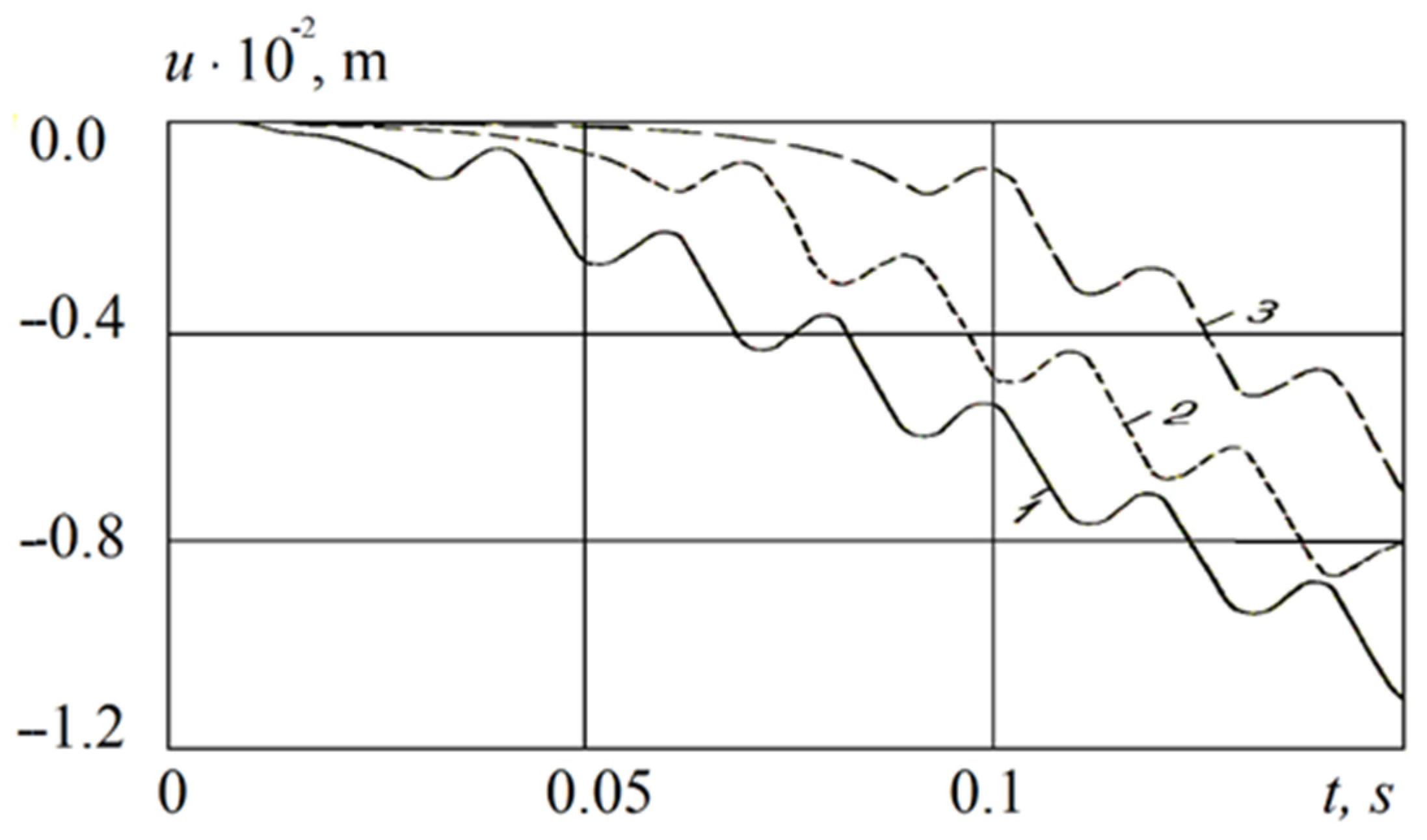
3.2.2. The Case of a Large Critical Relative Displacement
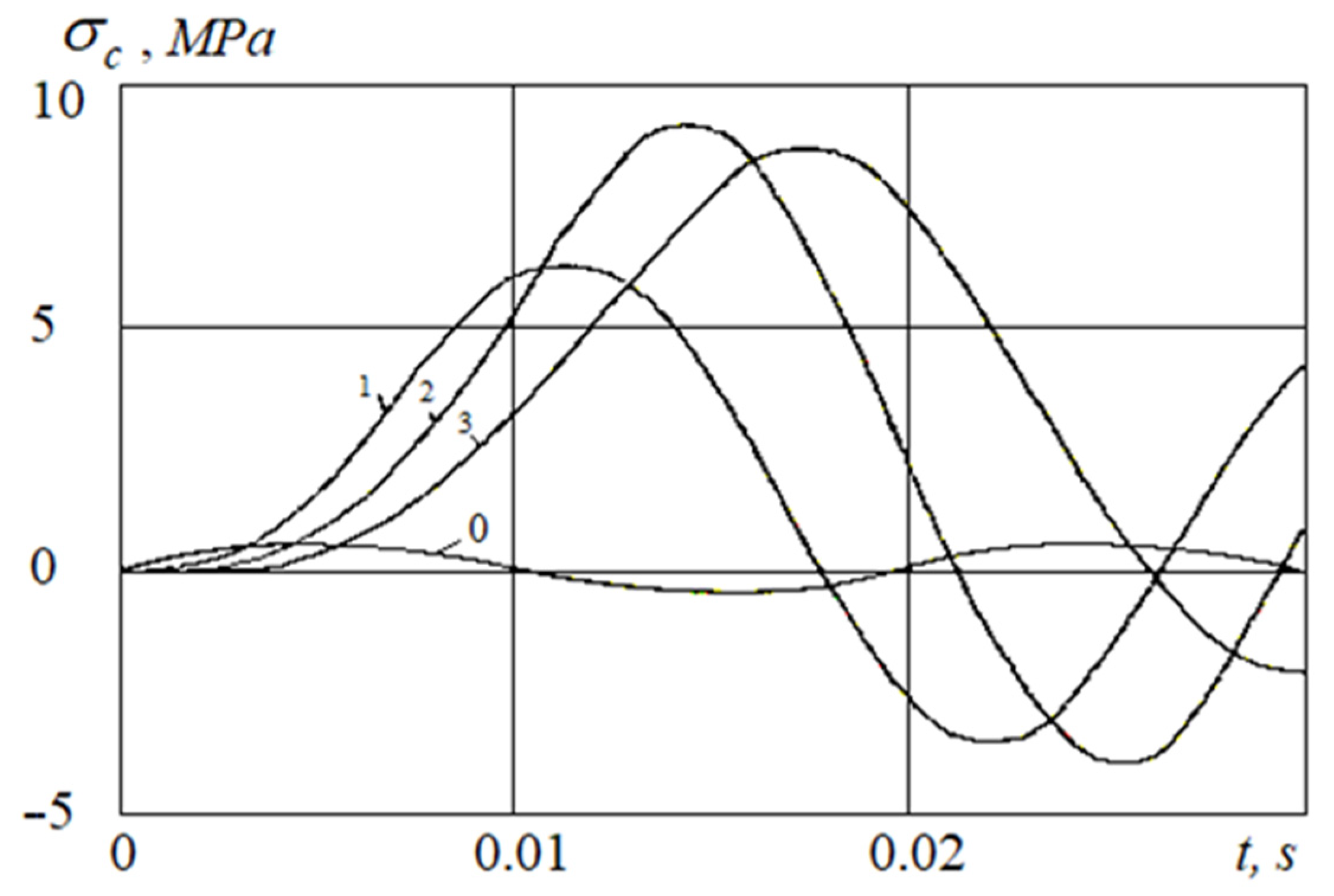
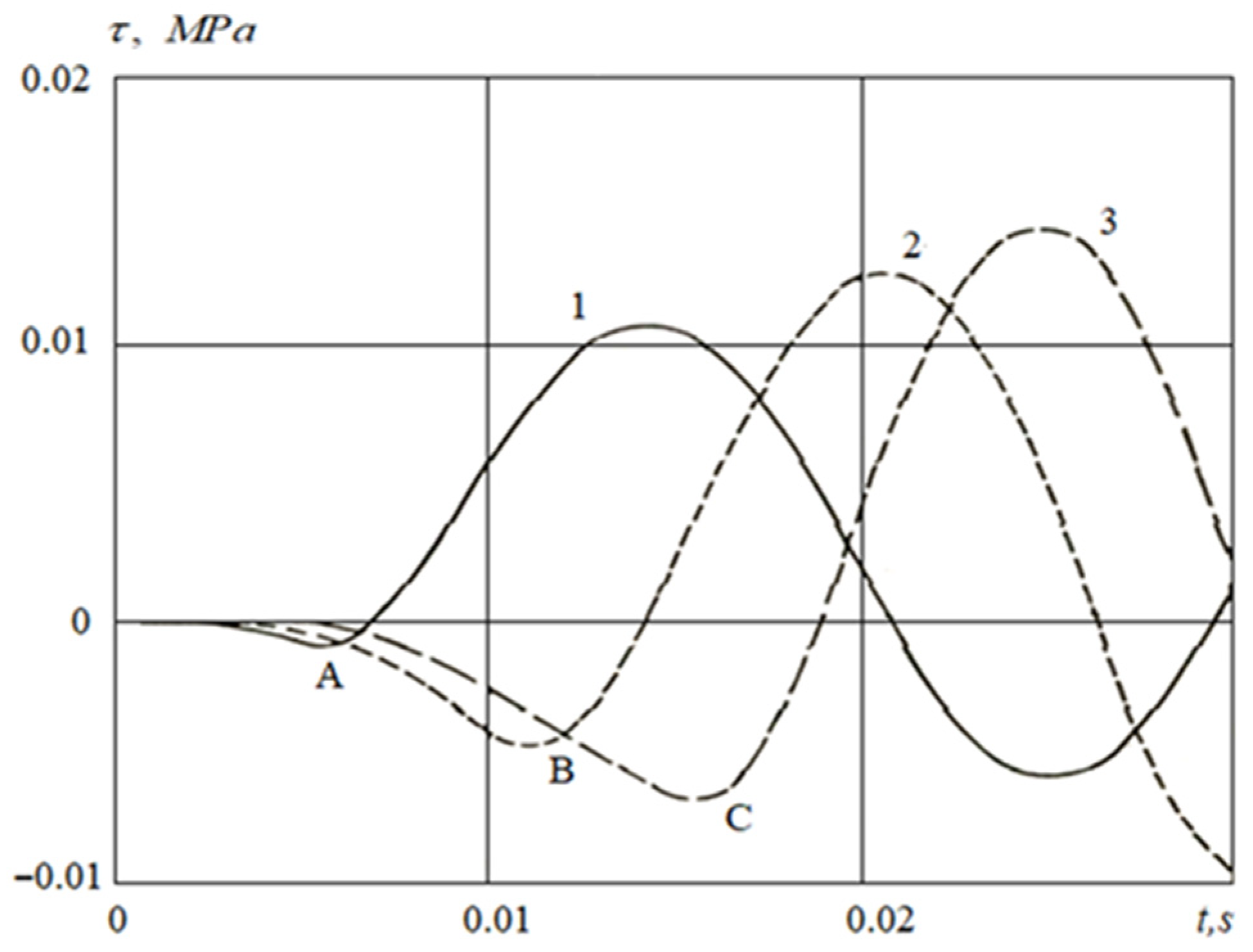
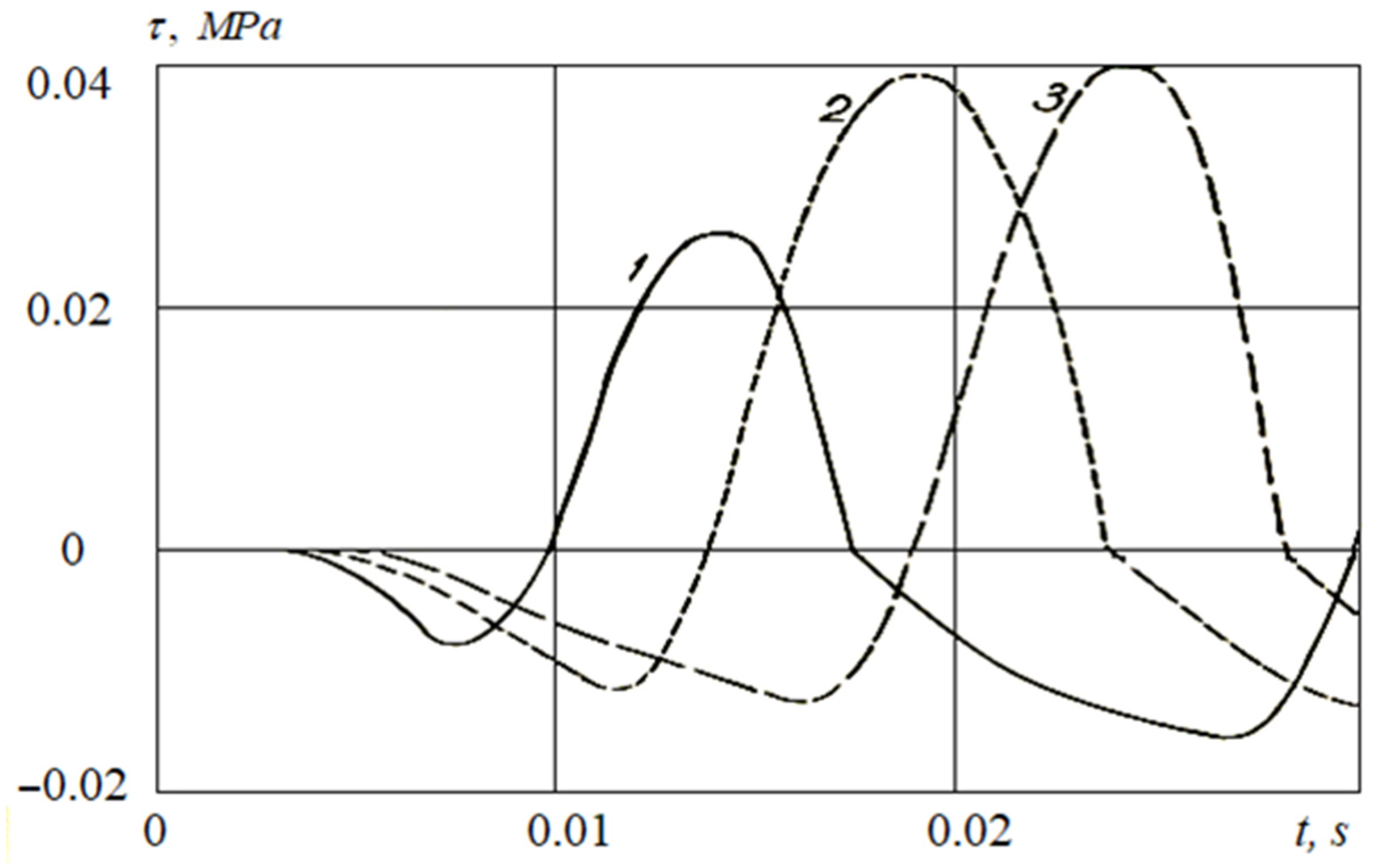
3.2.3. Influence of Shear Stresses on Longitudinal Stresses in Pipeline Cross-Sections
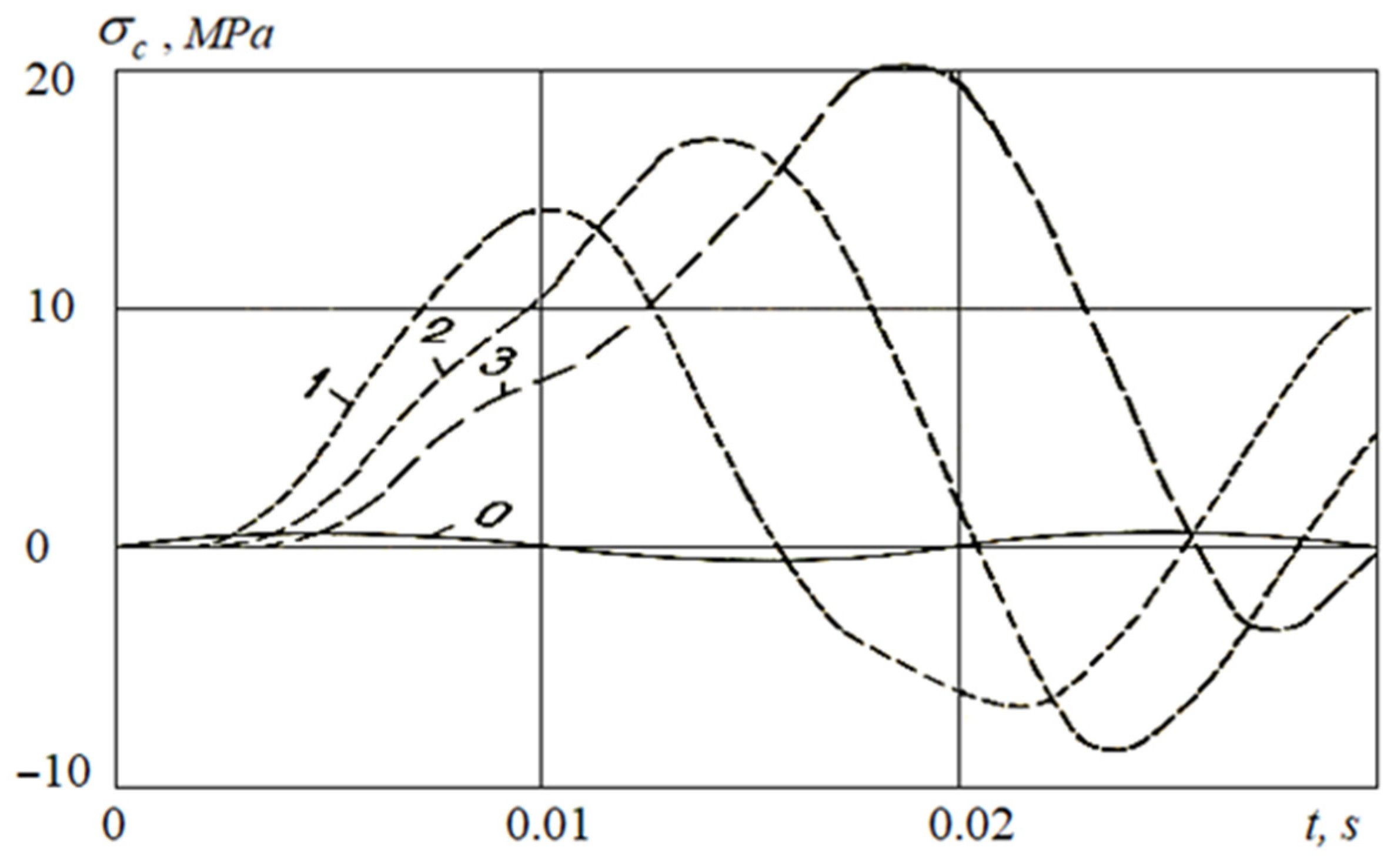
3.2.4. The Case of Variable Stress Normal to the Outer Surface of the Pipeline
4. Conclusions
- The main disadvantage of the dynamic theory of seismic resistance of underground pipelines is the neglect of dynamic stress state in soil under seismic wave propagation. The next drawback of the dynamic theory is an inaccurate, approximate accounting for the displacement of the soil medium to which the underground pipeline is embedded.
- The complete interaction process includes the stages of nonlinear changes in the interaction force (the friction force) by manifesting its peak value and the Coulomb friction. The contact layer of soil undergoes shear deformations until complete structural destruction of the soil contact layer. The interaction force is the friction force, and its peak value does not appear.
- The problems of seismic resistance of underground pipelines should be considered based on the theory of propagating seismic waves in a soil medium and the interaction of seismic waves with underground pipelines, i.e., based on the wave theory of seismic resistance of underground pipelines.
- A one-dimensional coupled problem of seismic resistance of underground pipelines under seismic impacts was posed based on the wave theory. An algorithm and a program for the numerical solution of the stated wave problems were developed using the method of characteristics and the method of finite differences.
- An analysis of the laws of interaction of underground pipelines with soil under seismic influences shows that it is necessary to use in the calculations the laws of interaction that account for the complete interaction processes observed in experiments.
- The analysis of the obtained numerical solutions and the posed coupled problems of the wave theory of seismic resistance of underground pipelines show the occurrence mechanisms of longitudinal stresses in underground pipelines under seismic influences.
- The results of calculations stated that an account for the dynamic stress normal to the underground pipeline’s outer surface leads to multiple increases in longitudinal stress in the underground pipeline. This multiple increase is due to the transformation of the interaction force into an active frictional force, resulting from a greater strain in soil than the one in the underground pipeline.
- The wave theory’s efficiency and reliability are shown in comparison with the dynamic theory of seismic resistance of underground pipelines.
Author Contributions
Funding
Conflicts of Interest
References
- O’Rourke, M.J.; Liu, X. Response of Buried Pipelines Subject to Earthquake Effects; Monograph Series; Multidisciplinary Center for Earthquake Engineering Research (MCEER), A National Center of Excellence in Advanced Technology Applications: Buffalo, NY, USA, 1999; 249p. [Google Scholar]
- Toprak, S.; Taskin, F.; Koc, A.C. Prediction of earthquake damage to urban water distribution systems: A case study for Denizli, Turkey. Bull. Eng. Geol. Environ. 2009, 68, 499–510. [Google Scholar] [CrossRef]
- O’Rourke, T.D.; Jeon, S.S.; Toprak, S.; Cubrinovski, M.; Hughes, M.; Van Ballegooy, S.; Bouziou, D. Earthquake Response of Underground Pipeline Networks in Christchurch. N. Zeal. Earthq. Spectra 2014, 30, 183–204. [Google Scholar] [CrossRef]
- Erdik, M.; Rashidov, T.; Safak, E.; Turdukulov, A. Assessment of seismic risk in Tashkent, Uzbekistan and Bishkek, Kyrgyz Republic. Soil Dyn. Earthq. Eng. 2005, 25, 473–486. [Google Scholar] [CrossRef]
- Muravyeva, L.; Vatin, N. The Safety Estimation of the Marine Pipeline. Appl. Mech. Mater. 2014, 633–634, 958–964. [Google Scholar] [CrossRef]
- Okamoto, S. Introduction to Earthquake Engineering; University of Tokyo Press: Tokyo, Japan, 1973; 571p, ISBN 978-0470653074. [Google Scholar]
- Okamoto, S. Introduction to Earthquake Engineering, 2nd ed.; University of Tokyo Press: Tokyo, Japan, 1984; 629p, ISBN 0860083616. [Google Scholar]
- Liyanage, K.; Dhar, A.S. Stresses in cast iron water mains subjected to non-uniform bedding and localized concentrated forces. Int. J. Geotech. Eng. 2018, 12, 368–376. [Google Scholar] [CrossRef]
- Matsuhashi, M.; Tsushima, I.; Fukatani, W.; Yokota, T. Damage to sewage systems caused by the Great East Japan Earthquake, and governmental policy. Soils Found. 2014, 54, 902–909. [Google Scholar] [CrossRef]
- Chernysheva, N.V.; Kolosova, G.S.; Rozin, L.A. Combined Method of 3d Analysis for Underground Structures in View of Surrounding Infinite Homogeneous and Inhomogeneous Medium. Mag. Civ. Eng. 2016, 62, 83–91. [Google Scholar] [CrossRef]
- Ismoilova, S.I.; Loginov, P.V.; Khamidov, S.S.; Akbarov, N.A.; Kumakov, J.X. Dynamic stress state of underground pipelines at junctions. IOP Conf. Ser. Mater. Sci. Eng. 2020, 869, 052013. [Google Scholar] [CrossRef]
- Feng, W.; Huang, R.; Liu, J.; Xu, X.; Luo, M. Large-scale field trial to explore landslide and pipeline interaction. Soils Found. 2015, 55, 1466–1473. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M. Mechanical effects of tunneling on adjacent pipelines based on Galerkin solution and layered transfer matrix solution. Soils Found. 2013, 53, 557–568. [Google Scholar] [CrossRef]
- Sultanov, K.S.; Bakhodirov, A.A. Laws of Shear Interaction at Contact Surfaces between Solid Bodies and Soil. Soil Mech. Found. Eng. 2016, 53, 71–77. [Google Scholar] [CrossRef]
- Muravyeva, L.; Vatin, N. Risk Assessment for a Main Pipeline under Severe Soil Conditions on Exposure to Seismic Forces. Appl. Mech. Mater. 2014, 635–637, 468–471. [Google Scholar] [CrossRef]
- Ismoilova, S.I.; Loginov, P.V.; Khamidov, S.S.; Akbarov, N.A.; Kumakov, J.X. Force properties of longitudinal interaction of the underground pipeline with soil. IOP Conf. Ser. Mater. Sci. Eng. 2020, 869, 052036. [Google Scholar] [CrossRef]
- Muravyeva, L.; Vatin, N. Application of the Risk Theory to Management Reliability of the Pipeline. Appl. Mech. Mater. 2014, 635–637, 434–438. [Google Scholar] [CrossRef]
- Lalin, V.V.; Kushova, D.A. New Results in Dynamics Stability Problems of Elastic Rods. Appl. Mech. Mater. 2014, 617, 181–186. [Google Scholar] [CrossRef]
- Jung, J.K.; O’Rourke, T.D.; Argyrou, C. Multi-directional force–displacement response of underground pipe in sand. Can. Geotech. J. 2016, 53, 1763–1781. [Google Scholar] [CrossRef]
- Wijewickreme, D.; Monroy, M.; Honegger, D.G.; Nyman, D.J. Soil restraints on buried pipelines subjected to reverse-fault displacement. Can. Geotech. J. 2017, 54, 1472–1481. [Google Scholar] [CrossRef]
- Muravieva, L.; Bashirzade, S. Behaviour of underground pipelines laid in saturated soil. Russ. J. Transp. Eng. 2015, 2, 2. [Google Scholar] [CrossRef]
- Israilov, M.S. Coupled seismic vibrations of a pipeline in an infinite elastic medium. Mech. Solids. 2016, 51, 46–53. [Google Scholar] [CrossRef]
- Georgievskii, D.V.; Israilov, M.S. Seismodynamics of extended underground structures and soils: Statement of the problem and self-similar solutions. Mech. Solids. 2015, 50, 473–484. [Google Scholar] [CrossRef]
- Israilov, M.S. A new approach to solve the problems of seismic vibrations for periodically nonuniform buried pipelines. Moscow. Univ. Mech. Bull. 2016, 71, 23–26. [Google Scholar] [CrossRef]
- Smith, A.; Dixon, N.; Fowmes, G. Monitoring buried pipe deformation using acoustic emission: Quantification of attenuation. Int. J. Geotech. Eng. 2017, 11, 418–430. [Google Scholar] [CrossRef]
- Meyer, V.; Langford, T.; White, D.J. Physical modelling of pipe embedment and equalisation in clay. Géotechnique 2016, 66, 602–609. [Google Scholar] [CrossRef]
- Khusanov, B.E.; Rikhsieva, B.B. Thickness dimensions of the contact layer of soil-rigid body interaction. E3S Web Conf. 2019, 97, 04040. [Google Scholar] [CrossRef]
- Soveiti, S.; Mosalmani, R. Mechanical behavior of buried composite pipelines subjected to strike-slip fault movement. Soil Dyn. Earthq. Eng. 2020, 135, 106195. [Google Scholar] [CrossRef]
- Melissianos, V.E.; Vamvatsikos, D.; Gantes, C.J. Methodology for failure mode prediction of onshore buried steel pipelines subjected to reverse fault rupture. Soil Dyn. Earthq. Eng. 2020, 135, 106116. [Google Scholar] [CrossRef]
- Chaudhuri, C.H.; Choudhury, D. Buried pipeline subjected to seismic landslide: A simplified analytical solution. Soil Dyn. Earthq. Eng. 2020, 134, 106155. [Google Scholar] [CrossRef]
- Fadaee, M.; Farzaneganpour, F.; Anastasopoulos, I. Response of buried pipeline subjected to reverse faulting. Soil Dyn. Earthq. Eng. 2020, 132, 106090. [Google Scholar] [CrossRef]
- Manolis, G.D.; Stefanou, G.; Markou, A.A. Dynamic response of buried pipelines in randomly structured soil. Soil Dyn. Earthq. Eng. 2020, 128, 105873. [Google Scholar] [CrossRef]
- Mirsaidov, M.M.; Sultanov, T.Z. Use of linear heredity theory of viscoelasticity for dynamic analysis of earthen structures. Soil Mech. Found. Eng. 2013, 49, 250–256. [Google Scholar] [CrossRef]
- Mirsaidov, M.M.; Sultanov, T.Z.; Sadullaev, S.A. An assessment of stress-strain state of earth dams with account of elastic-plastic, moist properties of soil and large strains. Mag. Civ. Eng. 2013, 40, 59–68. [Google Scholar] [CrossRef]
- Sultanov, K.S.; Kumakov, J.X.; Loginov, P.V.; Rikhsieva, B.B. Strength of underground pipelines under seismic effects. Mag. Civ. Eng. 2020, 93, 97–120. [Google Scholar] [CrossRef]
- Seguini, M.; Nedjar, D. Modelling of soil–structure interaction behaviour: Geometric nonlinearity of buried structures combined to spatial variability of soil. Eur. J. Environ. Civ. Eng. 2017, 21, 1217–1236. [Google Scholar] [CrossRef]
- Toprak, S.; Nacaroglu, E.; Helva, V.; Koc, A.C. Design charts for pipelines under longitudinal soil loading. J. Environ. Prot. Ecol. 2017, 18, 63–70. [Google Scholar]
- Bakhodirov, A.A.; Ismailova, S.I.; Sultanov, K.S. Dynamic deformation of the contact layer when there is shear interaction between a body and the soil. J. Appl. Math. Mech. 2015, 79, 587–595. [Google Scholar] [CrossRef]
- Sultanov, K.S. A non-linear law of the deformation of soft soils. J. Appl. Math. Mech. 1998, 62, 465–472. [Google Scholar] [CrossRef]
- Sultanov, K.S. The attenuation of longitudinal waves in non-linear viscoelastic media. J. Appl. Math. Mech. 2002, 66, 115–122. [Google Scholar] [CrossRef]
- Lanzano, G.; Salzano, E.; Santucci de Magistris, F.; Fabbrocino, G. Seismic vulnerability of gas and liquid buried pipelines. J. Loss Prev. Process Ind. 2014, 28, 72–78. [Google Scholar] [CrossRef]
- Sultanov, K.; Loginov, P.; Ismoilova, S.; Salikhova, Z. Variable moduli of soil strain. E3S Web Conf. 2019, 97, 04013. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultanov, K.S.; Vatin, N.I. Wave Theory of Seismic Resistance of Underground Pipelines. Appl. Sci. 2021, 11, 1797. https://doi.org/10.3390/app11041797
Sultanov KS, Vatin NI. Wave Theory of Seismic Resistance of Underground Pipelines. Applied Sciences. 2021; 11(4):1797. https://doi.org/10.3390/app11041797
Chicago/Turabian StyleSultanov, Karim Sultanovich, and Nikolai Ivanovich Vatin. 2021. "Wave Theory of Seismic Resistance of Underground Pipelines" Applied Sciences 11, no. 4: 1797. https://doi.org/10.3390/app11041797
APA StyleSultanov, K. S., & Vatin, N. I. (2021). Wave Theory of Seismic Resistance of Underground Pipelines. Applied Sciences, 11(4), 1797. https://doi.org/10.3390/app11041797






