Abstract
Membrane-based vacuum dehumidification technology is currently being actively studied. In most studies, the performance of the membrane-based systems is evaluated under the assumption that the membrane can achieve ideal separation, which results in ideal coefficient of performance (COP) values. However, the performance factors for membranes vary depending on the experimental conditions and measurement methods. Therefore, relevant values can only be calculated if the data are measured in an environment close to that of the application conditions. The cup measurement method is a simple method to measure the permeability, however, there are limitations regarding adding variables during the experiment. To overcome these limitations, a new experimental device was constructed that combines pressurized cell with the cup method. Using the device, the performance of polyethylene-amide-bonded dense membranes was evaluated under conditions where absolute pressure differentials occurred before and after the membrane, such as in air conditioner dehumidification systems.
1. Introduction
The energy required for air conditioning is constantly increasing. Dehumidification loads account for a large part of the cooling load, especially in low-latitude countries where the supply of air conditioners is rapidly increasing. Generally, dehumidification functions have been implemented by cooling down to the dew point temperature of water, but various studies have been conducted to replace this system due to its high energy consumption [1]. Among these studies, methods for using membranes as a promising technique for separating water vapor from the air have been proposed. The US Department of Energy has reported membrane heat pumps that have been implemented as a comprehensive system [2]. According to the report, membrane-based vacuum dehumidification (MVD) systems are expected to show higher efficiency than existing vapor compression cooling systems because they require less energy to remove the water vapor and avoid the environmental problems caused by refrigerants. Hence, several membrane heat pump designs with different MVD configurations have been presented, and their performance analyzed using various methods [3,4,5,6].
The membrane mass exchanger is the core part of the MVD systems, and its efficiency depends on the permeability and selectivity of the membrane performance [7]. To date, a membrane model which assumes the concentration difference of the gas, i.e., vapor pressure difference as a sole driver of the mass transfer within the system has been used for performance analysis. Previous analytical studies of dense membranes often assumed that the selectivity was infinite, and they suggested several different types of MVD systems [3,4,5,6,7]. However, as the actual dense membrane will have a large but finite selectivity inevitably, the design and operation of should be reconsidered in practice. Moreover, most of the MVD systems are operated under absolute pressure difference and the influence on selectivity and permeance should be evaluated as well. As the performance of MVD systems are indexed by coefficient of performance (COP) which is calculated by dividing the amount of latent dehumidification heat removed by the input work [3], the correct COP value of the design can only be calculated by evaluating the changes in the selectivity and water vapor permeability of the membrane in response to the operating pressure of the system.
Gas separation membranes only separate the target gas from a gas mixture. Such membranes are commonly used in industries for pure oxygen and methane production, where polymer membranes are often used. Among them, data for water vapor separation have been obtained for industrial applications such as pervaporation or high-concentration water vapor separation in flue gas [8]. Hence, the water vapor separation membrane used in industrial processes has been mainly applied to porous membranes to enable the removal of large amounts of water vapor. Relatively low selectivity of such membranes makes it difficult to use for applications in areas of MVD application which require low vapor pressure condition. In the case of air and water vapor separation for air conditioning, the partial pressure of water vapor in the atmosphere is very small, and large vapor pressure differences are observed even for small humidity variations. Therefore, appropriate performance evaluation is challenging.
For this reason, the membrane used in MVD systems should have high water vapor selectivity; hence, water-selective dense membranes with a very high level of selectivity are often used. These membranes consist of a polymeric compound as a support material, which is coated with a hydrophilic membrane. Significant improvements in the performance of such membranes have been achieved by optimizing the production methods and structures. The performance limits of existing membranes in various gas-gas separation environments have been described [9,10]. When the performance metrics of the water vapor-selective membrane are compared using the same index, it is clear that the membrane performance has evolved with the development of the technology. However, the membrane properties are sometimes reported without specific experimental conditions, or the result of simple diffusion of the target substance, which differs from the application conditions. This is the result of the study assuming that the separation process is the only effect of the ideal vapor pressure difference. In addition, the commonly used polymer membrane has many physical deformations due to pressure differences, requiring observation of effects, which has not progressed well. Accordingly, conditions similar to the actual system should be verified to confirm the effect of the variable called absolute pressure difference.
In this paper, we summarized the former studies of membranes for water vapor and air separation and discussed the performance in view of MVD application. We also introduced a simple method to evaluate the performance of dense membrane under an absolute pressure difference condition. From the test, a performance variation of a sample dense membrane is explained.
2. Materials and Methods
The major purpose of MVD is to separate water vapor from the air without a vapor-liquid phase change, i.e., using gas–gas separation membranes. Gas separation membranes selectively separate the target gas from a mixture via the chemical potential difference between the two sides of the membrane. While the membranes can be fabricated using various materials such as metals, ceramics, and liquids, polymers are commonly used as they are easy to prepare. Membranes are broadly divided into porous and dense membranes as illustrated in Figure 1, where the latter have no physical porosity that allows a substance to pass through the membrane.
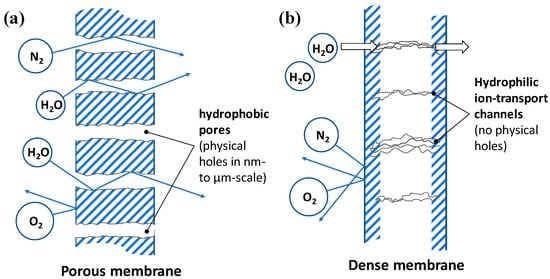
Figure 1.
Water vapor permeation through (a) porous membrane (b) dense membrane.
In the case of dense membranes for water vapor separation, hydrophilic materials are usually bonded to hydrophobic polymer-based materials to form ion nanochannels in which water vapor molecules can diffuse. Therefore, the solution-diffusion model can explain the movement of the substances, where the water vapor pressure difference between the two sides of the membrane acts as a driving force.
For the validation of membrane performance, three main performance factors for gas separation membrane are discussed: permeability, permeance, and selectivity [11]. Permeability is a normalized measure of the flux of the target substance that penetrates the membrane with a certain thickness under a driving force, with units of Barrer (1 Barrer = 10−10 cm3 (STP)·cm/cm2·s·cmHg), where the unit ‘cm3 (STP)’ means a volume measured at standard temperature and pressure (SPT) condition at 0 °C and 1 bar. In contrast, the permeance is used as a membrane performance indicator when the membrane is structured in mixed channels or when the performance of the membrane itself is determined. Considering that the gas–gas separation membrane is relatively thinner than other types—liquid-liquid or liquid–gas separation types—of membrane, permeance is preferred as an index to measure the performance rather than permeability. The permeance is the permeability removing membrane thickness and is expressed in gas permeation units (GPU = 10−6 cm3 (STP)/cm2·s·cmHg). Selectivity refers to the ratio of permeabilities of the substances that pass through the membrane. The selectivity is calculated as the percentage of each substance’s permeability or permeance. When both selectivity and permeability of the target substance are high, the membrane is assumed to have good separation performance. However, since permeability and selectivity have a tradeoff relationship, it is important to produce a membrane with values optimized for the application.
3. Membrane Performance Measurements
3.1. Test Methods for Water Vapor Permeability
As the most popular method to measure permeability of membrane, the cup method measures the change in cup weight in an environment where a water-or desiccant-filled cup is stored at a constant temperature and humidity [12]. When a water-filled cup is used, the relative humidity inside the cup is assumed to be 100% and the amount of evaporated water is calculated. If a desiccant-filled cup is used, the water vapor mass is calculated through the vapor absorbed at 0% relative humidity. Although the cup method is commonly used, it has the disadvantage of creating a boundary layer according to the concentration of the target gas before and after the membrane. Accordingly, the measurement varies greatly depending on the distance from the water and desiccant to the membrane; hence, error analysis is essential. Further limitations include being unable to include experimental variables such as pressure changes.
To overcome these disadvantages, devices have been suggested to combine simple gravimetric methods with the simulation of various experimental conditions. A typical example is a constant-volume variable-pressure method that permeates water vapor from the feed side to the permeate side [13]. The pressure on the permeate side is dependent on the amount of water vapor permeated through the device, which is used to calculate the permeability. By default, calculations are made using time-lag techniques [14]. However, in the case of gases mixed with other gases and water vapor, only the permeation of water vapor can be measured. In contrast, the constant-pressure variable-volume method measures a constant pressure, primarily the pressure on the permeate side at 1 atm. If the gas used in the experiment is a gas mixture, a hydrodynamic analysis is required. In addition, the temperature conditions are limited to 100 °C or higher because they are greatly affected by the saturation point. The disadvantage of this method is that special experimental devices are required to maintain the pressure, and the calculation process is complex.
In addition, the method of measuring the mixed gas fed into the test cell is frequently used, while the permeability is often calculated using equipment such as a gas chromatograph or dew point mirror (mainly for water vapor). It is important to develop an optimal method depending on the experimental conditions because each experimental device has its advantages and disadvantages, and there are many factors to consider, such as the price and environment.
3.2. Experimental Setup
In this study, in order to reduce unexpected influence from raw air, nitrogen gas was utilized as mixture compound instead of moist air. The experimental device was built based on the cup method and constant-volume variable-pressure method. In the latter method, the permeated water vapor results in the pressure increase and the pressure change over time is used to determine the water vapor permeability. In addition, the desiccant cup method is applied to ensure that all permeated water vapor is absorbed by the absorbent, and the increase in pressure is the result of nitrogen penetration. This allows for the calculation of the permeability of both water vapor and nitrogen.
Figure 2 shows a schematic of the experimental device used in this study. The test cell has two sensor tabs, for decompression and pressurization. In the experiment, the gas must pass through the membrane to enter the test cell, and two O-rings were installed to prevent leakage to the membrane side. An initial pressure test was used to check the airtightness of the test cell before measurement. In addition, a tray containing calcium chloride as an absorbent was placed in the test cell to keep the relative humidity at 0% and to measure the weight of the transmitted water vapor. During the experiments, an absolute pressure difference was generated before and after the membrane by a vacuum pump or nitrogen tank, and the test cell was inserted into the thermo-hygrostat so that the experiment could be performed at a constant temperature and humidity.
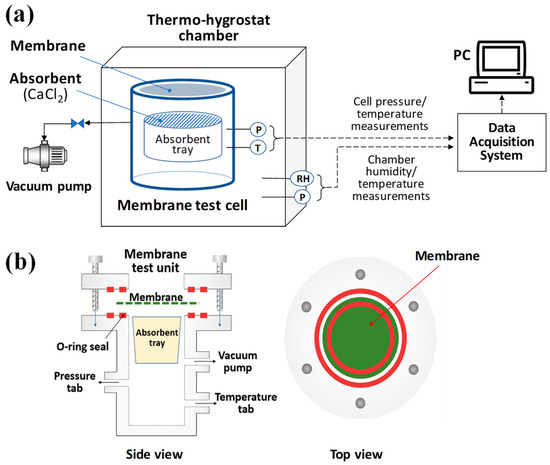
Figure 2.
Experimental setup of membrane performance test facility (a) Schematic diagram (b) Side and top view of membrane test cell.
Among the experimental data, the pressure, temperature, and humidity were recorded in real time at certain intervals using a LABVIEW program. To measure the weight of the absorbent tray, the cells were dismantled before and after the experiment and measured using a balance.
3.3. Dense Membrane Sample
The membrane used in this study was produced by dispersing silica nanoparticles in polyurethane [15]. The nanoparticles were dispersed partially and agglomerated to build up passages where water vapor may pass through. As a result, the hydrophilic inorganic ion nanochannels were formed on the hydrophobic polymer base. The synthesized water vapor transport membrane is then joined to perforated polyamide supports by a thermal binding method. Such membranes are not highly sensitive to moisture and have good durability; hence, frequent replacement can be prevented.
Figure 3 shows a schematic diagram of water vapor transport through the polymer membrane used in our experiments. When hydrophilic particles are placed in the membrane with an optimal concentration of ~5 wt% (neither too concentrated nor too dispersed), ion nanochannels are created. In this case, water vapor inside the membrane moves in a molecular state by repeated adsorption and desorption to the surfaces of the hydrophilic particles.
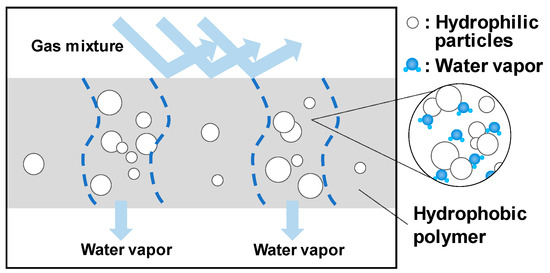
Figure 3.
Schematic diagram of water vapor transport through the polymer membrane used in the experiments.
Figure 4 shows scanning electron microscope (SEM) images of a membrane sample used in this experiment, including the membrane composed of hydrophobic materials, where the partly dispersed silica particles can be seen. In addition, an image of the polyamide support is shown in Figure 4b. Figure 4c shows a cross-sectional SEM image of a membrane sample from which the thickness of the membrane and support were measured just after it was fabricated. The thickness of the hydrophobic membrane was 30 μm and the support was 40–50 μm, with an average total thickness of ~75 μm.

Figure 4.
Scanning electron microscope (SEM) images of the membrane sample. (a) Hydrophobic membrane side with agglomerated silica nanoparticles of 5 wt% and (b) the polyamide support (c) a membrane cross-section showing the thicknesses of each layer.
3.4. Test Condition and Cases
The experimental conditions were created close to the environment in which the actual system could be applied, considering the problems described earlier. The configuration of conditions are listed in Table 1. Tests A and B were used for repeatability and tests C and D to compare membrane performance under difference absolute pressure conditions.

Table 1.
Experimental conditions for test setup.
+Experiments were conducted in two steps. The first was to compare two cells with nitrogen permeation set in opposite directions to determine whether nitrogen permeation affects the water vapor permeability of the dense membrane. In addition, the experiment was conducted with the existing cup method, comparing the variation in the permeability with the absolute pressure difference. Secondly, we measured the permeance and selectivity changes in response to changes in humidity. The data from the measurements allowed us to predict indicators in different humidity conditions by extrapolation.
3.5. Membrane Performance Calculation
This section shows the process of converting real-time experimental data into membrane performance factors. As units of GPU are used for permeance, unit conversion via the molar mass is included for each gas.
3.5.1. H2O Permeance
Firstly, when the weight change of the tray containing the absorbent is measured by , the mass flux of water vapor, , is calculated by the following equation.
where is the area of the membrane through which the substance can be permeated in the cell, and is the measurement time. The absorbed mass of H2O was converted into moles by molar mass of water, then calculated to volume. As the vapor pressure difference is the driving force for the flux, we separated the water vapor pressure from the mass flux to calculate the permeance. The water vapor pressure inside the cell is zero, hence, the steam pressure difference was calculated from the humidity of the chamber. In addition, multiplying the unit conversion constants results in the following equation of water vapor permeance, .
where and correspond to water molar mass and water vapor pressure in the thermo-hygrostat chamber, respectively. The GPU value obtained for Equation (2) is mol/m2·s·Pa.
3.5.2. N2 Permeance
The volume inside the cell is constant but the pressure changes during the measurement, hence, the mass of permeated nitrogen was calculated using the ideal gas equation, where the small volume changes due to compression of the O-ring and deformation of the membrane were ignored. Hence, the mass flux of nitrogen, , is given by:
Here, is the ideal gas constant of nitrogen. As for the water vapor permeability calculations, the mass of nitrogen was converted into the molar mass of nitrogen. Permeance of nitrogen, , is presented in Equation (4).
As the driving force of nitrogen is the absolute pressure difference excluding the water vapor pressure, the nitrogen pressure was divided by net pressure difference of nitrogen calculated by . Here, and are ambient pressure and absolute pressure inside the test cell, respectively. As for the water vapor permeance, the unit of Equation (4) is mol/m2·s·Pa.
3.5.3. Selectivity
The selectivity of the membrane, , was calculated as the permeance ratio of water vapor to nitrogen:
The selectivity was calculated using Equation (5) from the data measured at intervals of 5 min. The sum of the values and the values calculated at the beginning and end of the experiment were consistent with the uncertainty ranges explained in the next subsection. Therefore, the assumptions embodied in the equations are considered reasonable for the test conditions used here.
3.6. Uncertainty of Measurements
The experiments conducted in this study were performed by combining two existing measurement methods. Hence, similar measurement uncertainties as those occurring in previous studies are expected. In addition, an uncertainty analysis is required to ensure the validity of the proposed combined method. Therefore, error analysis was conducted considering the experimental uncertainties caused by the instrument and errors generated by the calculation of the performance factors.
3.6.1. Experimental Uncertainties
The cup method measurements were performed based on ASTM E96, and the uncertainty analysis was conducted accordingly. The uncertainties were categorized as three types of errors: buoyancy, edge mask, and still air. A buoyancy correction was not performed in this experiment because such corrections are only required when the measured weight change is below 100 mg. Edge mask correction is used to prevent errors caused by the sideways movement of water vapor when a membrane with an area larger than the diameter of the device is used, as follows:
where and present specimen thickness and width of masked edge, respectively. is a parameter of four times the test area divided by the perimeter. Calculations using the dimensions of our experimental device resulted in an error of 0.0883%. However, the edge mask part was further reduced using acrylic supports to minimize membrane deformation in the experimental device. In addition, due to the characteristics of the membrane used here, water vapor moves via the ion nanochannels, hence, the edge mask effect is expected to be even smaller. Thus, this error was considered negligible and was ignored in the error analysis.
In this experiment, the still air error related to the effect of the distance between the membrane and absorbent is the greatest because the measurement was performed in stagnant state rather than in a gas flow. According to ASTM E96-14, due to a permeance of higher than 2 perms (≥6.33 × 10−9 mol/m2s Pa, ≥20 GPU), correction is required for resistance due to still air. For the data measured in this experiment, the results were higher than 2 perms, hence the correction was performed by the correlation below.
The diffusion coefficient as a function of the temperature and pressure of water vapor is given as follows [16]:
where is diffusivity at standard temperature and pressure (STP) condition of in this study. Subscript 0 denotes STP condition. From Equation (7), the resistance due to the still air is calculated by dividing D by the thickness (d) and temperature (T) of the air layer in the cell and the gas constant of the water vapor ():
The corrected water vapor permeance is calculated as follows [17].
These corrections resulted in errors of 15–35%. It was assumed that the experiment was conducted in a stationary state without fluid flow inside the cell, and the measurement condition was not atmospheric pressure.
3.6.2. Measurement and Calculation Uncertainties
The two main errors in the calculation of the performance factors are measurement errors and errors arising from assumptions made in the calculations. As the variables included in the equations were measured by sensors, the sensor uncertainty values were considered. The sample specifications and errors of the instruments used in the experiment are listed in Table 2.

Table 2.
Specifications of the sensors used in the experiments.
We also considered the error caused by ideal gas constant assumptions and changes in the volume within the cell that were added during the experimental and calculation steps. In the case of the volume, a change of ~1 mm over the 10 cm height of the cell was measured, giving an error of 1%. During the experimental design, all the air that passed through the membrane was assumed to be pure nitrogen, and the content of oxygen and other gases was not considered. The mole mass of nitrogen and oxygen was calculated by including an error of about 3.2%. When analyzed according to the experimental conditions established earlier with a confidence interval of 95%, the error in the permeance of H2O and N2 and selectivity is calculated as follows [18].
From the uncertainty analysis, the uncertainties in the H2O permeance, N2 permeance, and selectivity were 6.47%, 7.48% and 8.54%, respectively. Although the uncertainties showed relatively larger than the cases of strict experiments, it is acceptable for characterizing the trends in the membrane performance with simple test configurations.
4. Results and Discussion
4.1. Experiment Repeatability
Table 3 shows representative data (Tests A and B) that were repeated under certain measurement conditions. After 48 h of the preliminary test, the pressure in both cells increased by ~40 kPa, which was used to measure the amount of nitrogen that permeated through the membrane. In addition, the weight of the absorbent tray increased due to the permeation of water vapor.

Table 3.
Real-time data for repeatability test.
Figure 5 shows the change in pressure within the cells over the measurement period. Since it was assumed that all of the water vapor that permeated the cell was absorbed by the absorbent, the increase in pressure was solely attributed to the permeation of nitrogen. The slope of the graph decreased over time, which is interpreted as a weaker driving force as the absolute pressure difference decreases. Therefore, it was confirmed that there exists a sufficient driving force for the permeation of nitrogen (or air) when testing dense membranes for water vapor permeation, which should be considered in practical applications instead of assuming ideal behavior.
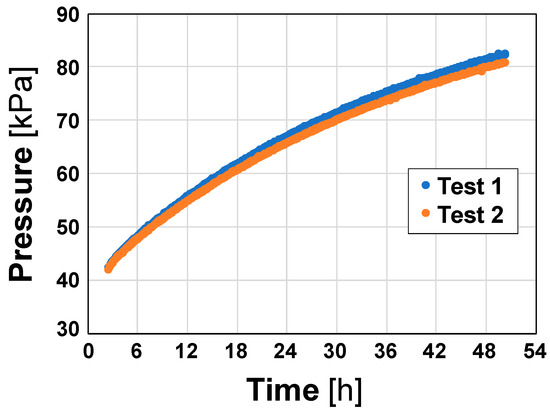
Figure 5.
Pressure variation in the test cells over time.
4.2. Membrane Performance
4.2.1. Effect of Absolute Pressure Difference
This section presents the experimental results of the effects of absolute pressure difference on the water vapor permeability of a dense membrane. At the start of the experiment, the absolute pressure difference on both sides of the membrane formed by pressurization or decompression was the same (60 kPa). During Test C, both nitrogen and water vapor were introduced into the cell, while in Test D the nitrogen flow was in the opposite direction to the water vapor. The data measured under 50% relative humidity are shown in Table 4.

Table 4.
Real-time measurement data of Test C and Test D, which were performed considering opposite directions of nitrogen permeation.
As nitrogen permeated through the membrane the cell pressure in Test C increased, while the pressure in Test D decreased. These data were converted into performance factors and compared to that of the cup method in Table 5. The relative humidity was 70% for the cup method measurement.

Table 5.
Membrane performance factor values of Test C, Test D, and the cup method.
The selectivity is not indicated for Test D because it is the ratio of the substance permeated in the same direction, and also not for the cup measurement because it was not possible to measure the permeance of nitrogen in the cup method. The measured water vapor permeability was the highest in Test C with the same direction of permeation of nitrogen and water vapor. Hence, the measured permeance depends on the direction of nitrogen flow through the test cell. In addition, the results suggest that the presence of an absolute pressure difference affects the water vapor permeance.
4.2.2. Effect of Relative Humidity
In these tests, the relative humidity was changed from 30% to 70% and the error value due to membrane distortion during the experiment was corrected. After converting the measurements into a performance factor, the average value was calculated. As shown in Figure 6, the permeance of both H2O and N2 increased with increasing relative humidity; however, the change in permeance of H2O was greater than that of N2, indicating the selectivity of the membrane for water vapor. The equation for calculating the water vapor permeance used in this study is linearly proportional to changes in the water vapor pressure, and the experimental curves showed linearity within the experimental uncertainty. Similarly, the nitrogen permeance increased with increasing humidity, which is attributed to the effect of the absolute pressure difference in the equation decreasing as the water vapor pressure increased. A MATLAB curve fitting tool was used to extrapolate the curves to determine the permeance and selectivity values of nitrogen and water vapor at a relative humidity of 0%. The permeance value of H2O was 2409 GPU and that of N2 was 3.818 GPU, with a water vapor selectivity of 630.96.
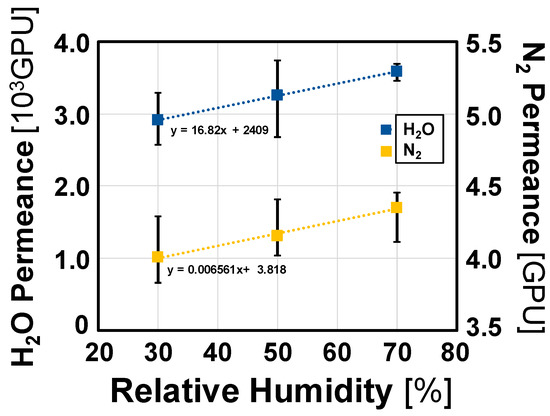
Figure 6.
Permeance of H2O and N2 as a function of relative humidity.
4.3. Comparison with Previous Studies
Table 6 summarizes the results from this study, where the units were standardized for comparison with data from previous studies in Table 7. Since the permeance is a performance indicator that is independent of the membrane thickness, the permeance was multiplied by the average membrane thickness (75 μm) to convert the results into permeability.

Table 6.
Membrane performance factors from this study.

Table 7.
H2O and N2 permeability and selectivity data from previous studies of various membrane materials.
Table 6 shows the experimental results of the current study in comparison to the previous studies for water vapor separation from air under various experimental conditions. The corresponding relationships between H2O permeability and H2O/N2 selectivity for the studies listed in Table 7 are shown in Figure 7 to summarize the performance of different water vapor permeation membranes.
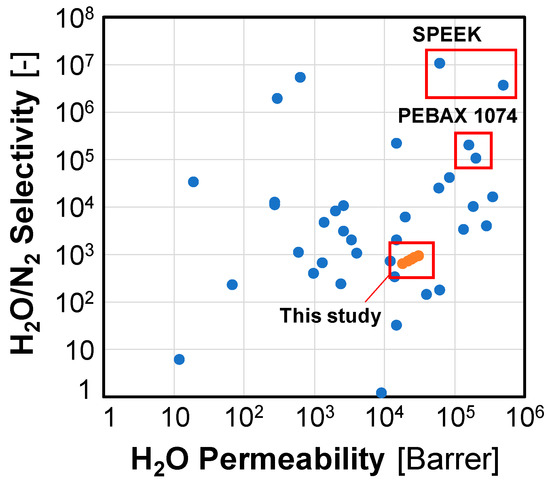
Figure 7.
Performance data on H2O permeability/selectivity.
In Figure 7, the data in the red boxes are a result of using the same membrane, but different indicator values are given depending on the analysis and calculation methods. In the paper, to compare SPEEK and PEBAX membranes [20], it is explained that mixing and measuring schemes affect the membrane performance, hence, other results may be different. Therefore, it is also difficult to select a membrane material solely based on its performance data, without considering the measurement conditions and analytical methods.
Except for the cases of the test D and the cup method with the selectivity data unavailable, the remaining five results are shown in Figure 7 and compared with data from previous studies. Compared to the data points from the previous studies, the current data shows deviations of the membrane characteristics due to the absolute pressure differences in this study. It can be seen that high water vapor permeability is measured when the experimental conditions are not considered. However, the selectivity value is relatively low, hence, if the corresponding membrane is used in a system configuration, an additional device will be required to prevent a pressure rise in the compressor due to permeated nitrogen.
5. Conclusions
A simple experimental device was proposed to evaluate the effect of the absolute pressure difference on the performance of dense water separation membranes. To overcome the shortcomings of existing methods, the new experimental device combines the cup method with the constant-volume variable-pressure method. We verified that the absolute pressure difference affects the diffusion of water vapor through a dense membrane, which should be considered during membrane testing and application.
The widely studied membrane-based vacuum dehumidification systems are inevitably subject to absolute pressure differentials on either side of the membrane. Data from previous studies show some indicators in improving the overall membrane technology, but there is a lack of use in the composition of the membrane-based dehumidification system. Therefore, accurate calculations using ideal models require the use of experimental data measured with additional variables and devices to address problems in the configuration of the model.
Author Contributions
Conceptualization, J.L. (Jinwook Lee) and M.K.; Investigation, J.L. (Jinwook Lee); Methodology, D.K., J.L. (Jihun Lim), M.J., S.K. and S.J.; Resources, H.-S.K. and Y.-S.S.; Funding acquisition, M.K.; Project administration, M.K.; Supervision, M.K. and Y.-S.S.; Writing—original draft, J.L. (Jinwook Lee); Writing—review & editing, M.K. and Y.-S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly supported by the Chung Ang University Research Grants in 2019 and the National Research Foundation of Korea (No. NRF-2019R1A2C1088694).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| area of membrane (m2) | |
| width of masked edge (m) | |
| distance between the absorbent and membrane (m) | |
| diffusion coefficient (-) | |
| mass flux of H2O (g/m2s) | |
| mass flux of N2 (g/m2s) | |
| mass variation of CaCl2 (g) | |
| mass variation of N2 (g) | |
| molar mass of H2O (g/mol) | |
| molar mass of N2 (g/mol) | |
| pressure of test cell (kPa) | |
| atmospheric pressure (kPa) | |
| water saturation pressure (kPa) | |
| water vapor pressure (kPa) | |
| pressure difference (kPa) | |
| corrected water vapor permeance (mol/m2sPa) | |
| water vapor permeance (mol/m2sPa) | |
| nitrogen permeance (mol/m2sPa) | |
| resistance due to still air (mol/m2sPa) | |
| ideal gas constant of H2O (kJ/kgK) | |
| ideal gas constant of N2 (kJ/kgK) | |
| parameter by four times the test area divided by the perimeter (m) | |
| time variation (s) | |
| temperature (°C) | |
| volume of the cell (m3) | |
| selectivity (-) | |
| specimen thickness (m) | |
| error (%) |
References
- International Energy Agency. Energy Technology Perspectives 2017; IEA: Paris, France, 2017. [Google Scholar]
- U.S. Department of Energy; Building Technologies Office. Energy Savings Potential and RD & D Opportunities for Non-Vapor-Compression HVAC Technologies; Office of Energy and Renewable Energy: Washington, DC, USA, 2014.
- Lim, H.; Choi, S.; Cho, Y.; Kim, S.; Kim, M. Comparative thermodynamic analysis of membrane-based vacuum air dehumidification systems. Appl. Therm. Eng. 2020, 179, 115676. [Google Scholar] [CrossRef]
- Qu, M.; Abdelaziz, O.; Gao, Z.; Yin, H. Isothermal membrane-based air dehumidification: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 82, 4060–4069. [Google Scholar] [CrossRef]
- Woods, J. Membrane processes for heating, ventilation, and air conditioning. Renew. Sustain. Energy Rev. 2014, 33, 290–304. [Google Scholar] [CrossRef]
- Labban, O.; Chen, T.; Ghoniem, A.F.; Lienhard, J.H.; Norford, L.K. Next-generation HVAC: Prospects for and limitations of desiccant and membrane-based dehumidification and cooling. Appl. Energy 2017, 200, 330–346. [Google Scholar] [CrossRef]
- Bui, D.T.; Ja, M.K.; Gordon, J.M.; Ng, K.C.; Chua, K.J. A thermodynamic perspective to study energy performance of vacuum-based membrane dehumidification. Energy 2017, 132, 106–115. [Google Scholar] [CrossRef]
- Baig, M.I.; Ingole, P.G.; Kil Choi, W.; Park, S.R.; Kang, E.C.; Lee, H.K. Development of carboxylated TiO2 incorporated thin film nanocomposite hollow fiber membranes for flue gas dehydration. J. Membr. Sci. 2016, 514, 622–635. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of Permeability/Selectivity Tradeoff Relations in Polymeric Gas Separation Membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Baker, R.W.; Wijmans, J.G.; Huang, Y. Permeability, permeance and selectivity: A preferred way of reporting pervaporation performance data. J. Membr. Sci. 2010, 348, 346–352. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Methods for Water Vapor Transmission of Materials, E 96/E 96M; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Stern, S.A.; Gareis, P.J.; Sinclair, T.F.; Mohr, P.H. Performance of a versatile variable-volume permeability cell. Comparison of gas permeability measurements by the variable-volume and variable-pressure methods. J. Appl. Polym. Sci. 1963, 7, 2035–2051. [Google Scholar] [CrossRef]
- Siegel, R.D.; Coughlin, R.W. Errors in diffusivity as deduced from permeation experiments using the time-lag technique. J. Appl. Polym. Sci. 1970, 14, 3145–3149. [Google Scholar] [CrossRef]
- AlMahmoud, O.; Choi, T.-Y.; Kim, H.-S.; Seo, Y.-S.; Yoon, S.H. A molecular dynamics study on the effect of modified silica surface on water vapor diffusion in the silica–polyurethane nanocomposite membrane. MRS Commun. 2020, 10, 492–499. [Google Scholar] [CrossRef]
- Massman, W. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
- Thuan, B.D.; Yonghui, W.; Jon, C.K.; Choon, N.K. Evaluating water vapor permeance measurement techniques for highly permeable membranes. Comput. Mater. Contin. 2015, 47, 89–105. [Google Scholar] [CrossRef]
- Figliola, R.S.; E Beasley, D. Theory and design for mechanical measurements. Meas. Sci. Technol. 1996, 7. [Google Scholar] [CrossRef]
- Metz, S.; Van De Ven, W.; Potreck, J.; Mulder, M.; Wessling, M. Transport of water vapor and inert gas mixtures through highly selective and highly permeable polymer membranes. J. Membr. Sci. 2005, 251, 29–41. [Google Scholar] [CrossRef]
- Sijbesma, H.; Nymeijer, K.; Van Marwijk, R.; Heijboer, R.; Potreck, J.; Wessling, M. Flue gas dehydration using polymer membranes. J. Membr. Sci. 2008, 313, 263–276. [Google Scholar] [CrossRef]
- Shin, Y.; Liu, W.; Schwenzer, B.; Manandhar, S.; Chase-Woods, D.; Engelhard, M.H.; Devanathan, R.; Fifield, L.S.; Bennett, W.D.; Ginovska, B.; et al. Graphene oxide membranes with high permeability and selectivity for dehumidification of air. Carbon 2016, 106, 164–170. [Google Scholar] [CrossRef]
- Scovazzo, P. Testing and evaluation of room temperature ionic liquid (RTIL) membranes for gas dehumidification. J. Membr. Sci. 2010, 355, 7–17. [Google Scholar] [CrossRef]
- Sato, S.; Suzuki, M.; Kanehashi, S.; Nagai, K. Permeability, diffusivity, and solubility of benzene vapor and water vapor in high free volume silicon- or fluorine-containing polymer membranes. J. Membr. Sci. 2010, 360, 352–362. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).