Abstract
In the present world, passive control finds application in various areas like flow over blunt projectiles, missiles, supersonic parallel diffusers (for cruise correction), the engine of jets, static testbeds of rockets, the ports of internal combustion engines, vernier rockets, and single expansion ramp nozzle (SERN) rockets. In this review, various passive control techniques to control the base pressure and regulate the drag force are discussed. In the study, papers ranging from subsonic, sonic, and supersonic flow are discussed. Different types of passive control management techniques like cavity, ribs, dimple, static cylinder, spikes, etc., are discussed in this review article. This study found that the passive control device can control the base pressure, resulting in an enhancement in the base pressure and reducing the base drag. Also, passive control is very efficient whenever there is a favorable pressure gradient at the nozzle exit.
1. Introduction
Turbulent base flows are still an active area of research due to their considerable influence on aerodynamic vehicles’ operation and permanency. Base flows are embodied by a mammoth partition of the shear layer occurring at the base due to a sudden change in the rear geometry. The base region’s divided flow gives rise to two extremely undesirable issues: the base’s instability and an upsurge in the drag. The instability results in erratic loads and pummeling phenomena; the drag force is termed base drag force and, in some specific instances, contributes to as high as 60% of the total drag.
Numerous critical issues impact base flows; a few vital parameters are Mach number, type of boundary layer before the separation, and geometry. Studies were conducted to understand the base flows over an extensive range of flow regimes, subsonic to hypersonic speeds, over the years. Despite these attempts, real insight continues to remain distant. From the previous studies, it is realized that the key factors that influence the dynamics of the flow in the base area are the growth of the shear layer and its reattachment, the recirculation region nearby to the base, shedding of the vortex, and ultimately, the interfaces among them all.
Several studies were reported in the literature involving different characteristics of base flows. Their study outcomes can be categorized into two groups: one that concentrates on the behavior of the flow field in the base’s neighborhood, and the other on individuals exploring the procedures to control the base pressure and hence, reduce the base drag. The vital part of these investigations tries to identify the essential attributes and tools of base flow and its conduct. Limited past assessments are deliberated as follows.
A study carried out by the researchers suggests that the significant pressure at the base resembles a significant recirculation region in the backward-facing step [1]. Investigators from their numerical study on an axisymmetric turbulent boundary layer and reattaching flow argue that large-scale coherent motions at a Strouhal number (defined as St = fD/U) of 0.2 dominate an ordered structure.
Due to the above problem, many researchers tried to control the base pressure; we did not control the skin friction drag due to the mission requirements. While exiting, the nozzle flow gets separated and later reattached at a point in the enlarged duct. The distance from the nozzle exit to the reattachment point is known as the reattachment length. This point on the expanded duct wall is significantly affected by the nozzle pressure ratio, the Mach number, and the area ratio.
Hence, this manuscript reviews some of the latest techniques based on passive control methods to optimize the base pressure and drag. There is an urgent requirement to control this low-pressure in the base region and bring it close to atmospheric pressure to accomplish near zero base drag. The base drag reduction can be achieved by increasing the base pressure by breaking the powerful vortex located in the recirculation zone. There are two ways to regulate the base pressure: (1) active control and (2) passive control.
Dynamic control of base flows is realized through blowing or suction methods and hence needs an external source of energy. This type of control’s main advantage is that it can be switched on and off as needed. However, the main disadvantage of this type of control is the unavailability of such a high source of energy and the extra weight added to aerospace vehicles like rockets, launch vehicles, etc., where the vehicle’s weight plays a key role.
In some cases, it is not feasible to get an additional external source of energy. However, in passive control, the base pressure is controlled by employing the structures’ geometric changes using ribs, cavities, boattails, splitter plates, and locked vortex mechanisms. Unlike active control, passive control does not require an external source of energy; hence, it is neither expensive nor leads to design complexity and is simple to fabricate.
Figure 1 shows the complex flow field of sudden expansion. The boundary layer separation, formation of primary recirculation zone at the base corner, and reattachment location at the wall can be observed. The passive control is used to disturb this flow field, and hence it increases the base pressure and reduces the base drag.
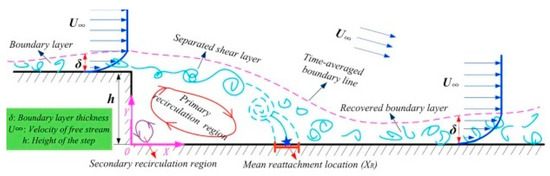
Figure 1.
Sudden Expansion Phenomenon [2].
Figure 2 and Figure 3 show the schematic diagram of over-expanded and under-expanded suddenly expanded flow coming out from a convergent-divergent nozzle.
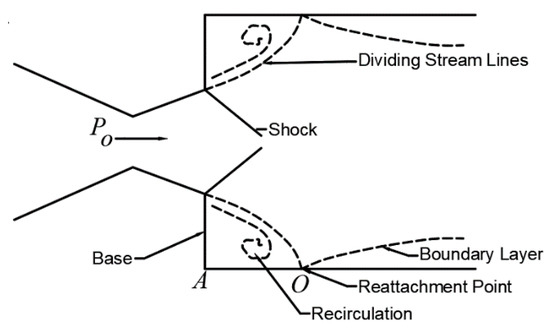
Figure 2.
Schematic diagram of over-expanded flow field.
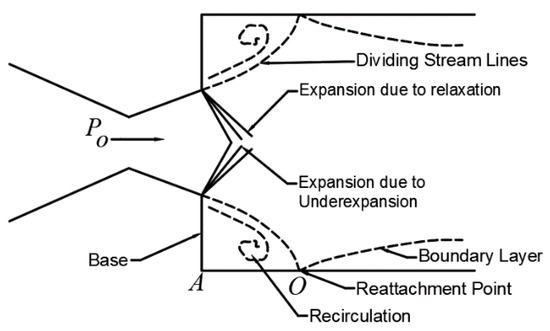
Figure 3.
Schematic diagram of the under-expanded flow field.
In the above Figure 4, the flow is coming from an upstream condition (P1 M1 d1) to a downstream state (P2 M2 d2). Pb is the pressure at the base of the duct.
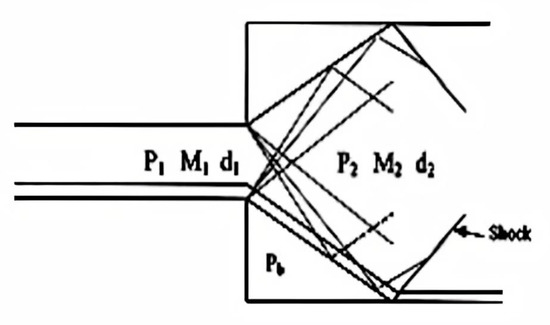
Figure 4.
Schematic diagram of internal flow.
Figure 5A shows the external flow over an artillery shell. Here shock waves are formed at the end of the shell, and expansion waves are formed at its base. Here Pb is the pressure at the base of the shell, and P1M1 is the flow conditions. Figure 5B shows the schematic diagram of external flow over a blunt base. Figure 5C shows the schematic diagram of coherent vortex structures.
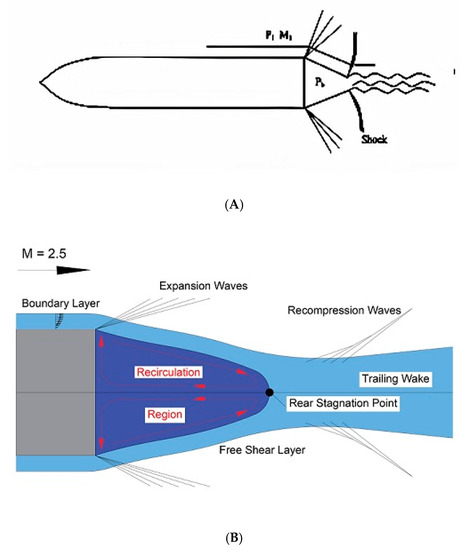
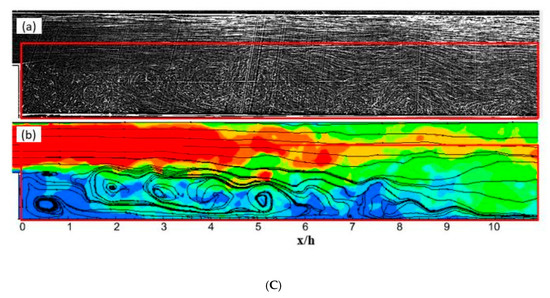
Figure 5.
Schematic diagram of external flow. (A) External flow over an artillery shell; (B) Flow over a blunt base; (C) Coherent Vortex structures of in the instantaneous flow (a) Visualization (b) Streamlines with velocity contour [3].
2. Various Types of Passive Controls
Both numerical and experimental studies have been conducted to study the effect of passive control. As passive control is accomplished by geometrical modification, it is more convenient to apply. Whereas in the case of active control, a considerable amount of external energy source is needed, which is challenging to provide. External aerodynamics, such as Ahmed body and boat tailing, as in these external flow types, is very strenuous to give an external energy source. In the case of launch vehicles, missiles, rockets, and aircraft bombs, the passive control mechanism is preferred from the design point of view, ease of fabrication, and the mission’s safety, which is a mandatory requirement.
2.1. Passive Control in the Form of Cavity
A cavity can be in the form of a rectangular shape. The vortices generated due to the flow past the cavity are studied by Ashcroft and Zhang [4]. This study’s main focus is instant development and time mean of turbulent flow structures in the cavity’s shear layer. PIV is conducted at 32 m/s, 37 m/s, and 42 m/s.
The data’s main characteristics are creating the shear layer at a distance downstream of the leading edge and reverse flow at the cavity base. The growth of cavity shear layers was studied by vorticity thickness as a measurement of shear thickness to quantify the time-mean development of shear layers.
Pandey and Rathakrishnan [5] did an experimental study on Mach 1.74 convergent-divergent axisymmetric nozzle sudden spread to circular pipelines with a full transverse area, provided with rectangular cavities. Experimental studies focused on base pressure and the flow field in the extended duct. Depending on the expansion level, the area ratio of the pipe, and the ratio length-to-diameter ratio (L/D) of the enlarged duct, it is found that the base pressure is affected significantly. The cavities increase the base pressure for a lower area ratio. Therefore, for small area ratios, the cavity aspect ratio substantially influences the base pressure.
The duct length in the range from 0 to about 3 plays a significant role in fixing the base pressure level with and without cavities. There is a minimum duct length for the flow to remain attached to the wall. The base pressure for L/D rises steeply from 0 to 3. For L/D more than 3, the base pressure remains almost constant. This shows the minimum extended duct length needed for the flow to stay attached to the duct. It also implies that the effect of increasing oblique shock intensity at the nozzle exit, due to the ample free space available for the flow at the base, is offset by expansion for the area ratio 10 [5].
The isentropic nozzle pressure ratio required for the ideal expansion at the Mach 1.74 nozzle is 5.24. Hence, the nozzle exit flow is over-expanded for the nozzle pressure 2.10 to 3.48 of the present study. Therefore, under these circumstances, an oblique shock wave is positioned at the nozzle exit. After moving through the shock wave in the shear layer, the flow finds ample space at the base to relax. Thus, the base pressure is determined by the combined effect of the oblique shock wave and expansion level.
Due to the change in the expansion level and NPR from 2.10 to 3.48, the shock wave pattern also changes. The results show that the flow to remain attached with the duct wall requires a minimum L/D of 4, a powerful vortex located at the base, and a related suction resulting in low pressure in the base region. The flow field downstream of the reattachment point does not affect base flows for L/D more than 4.
Khan et al. [6] studied the efficacy of passive control in the form of cavities. They experimentally investigated compressible flow exhausted from a nozzle that can attain a sonic Mach number into a square duct. The measured flow parameters included the Mach number, the pressure ratio, and the Length to Width ratio (L/W) of the duct. For numerous geometries of the cavity, the experiments were done with and without a cavity. Experimental results show that the multiple cavities work very well to decrease the base drag by reducing the base suction, thus increasing the base pressure. The effect of various cavities is found to control the base pressure for all the L/W ratios. The duct length increase is also beneficial for the more significant duct length since the backpressure’s influence is not there. The cavity’s presence does not adversely influence the wall pressure and the enlarged duct flow quality.
The Mach number has a significant influence on the base pressure and control effectiveness. Figure 6 shows how the multiple cavities are mounted on the duct with nozzle and duct dimensions [6]. The base pressure assumes higher values for higher duct length and Mach numbers (i.e., the drag is reduced, and the control effectiveness is significant). The duct length plays a vital role in the base pressure control, and base pressure assumes high values for low subsonic Mach numbers.
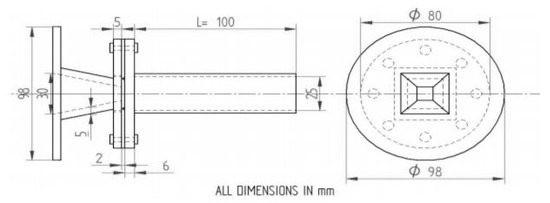
Figure 6.
Dimensions of the nozzle and the duct [6].
Another study [7] on the cavity found that semi-circular grooves reduces the base drag in the backward-facing step. Here two semi-circular grooved cavities are placed at 45° across the PCD of 23 mm at the base. For the experiment, the square nozzle is used of 10 mm side, with a duct length of 150 mm of side 25 mm. Three duct lengths are considered for investigation, and they are 4 W, 6 W, and 8 W.
It is apparent that the base pressure has substantially increased, and its reliance on flow parameters like Mach number and L/W ratio is exhibited. Therefore, the base pressure is slightly higher than the ambient pressure. Grooved cavities have a significant effect on the increase of base pressure. Thus, all the Mach numbers considered in the study [7] have reduced drag with lower pressure and minimized the recirculation zone. Below, Figure 7 shows a square nozzle and grooved control plate.
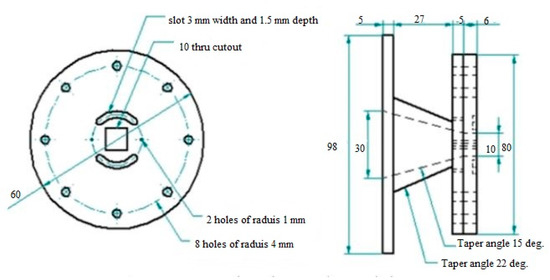
Figure 7.
Square nozzle and grooved control plate [7].
Pressure variations in the base of a standard freestream missile configuration in the presence and absence of passive control in the form of the base cavity at a Mach number of 0.7 are investigated experimentally by Vikramaditya, N. et al. [8]. The aim was to identify base pressure variations and explain the impact on base cavities’ behavior. Experiments involve unstable pressure measurements in six azimuthal areas. Due to the model’s asymmetry, there is considerable variation in the pressure fluctuations in the azimuthal direction.
The base cavities increase the base pressure and reduce the average root square of the base pressure. When the base cavity is enhanced, the higher-order moments show a decreasing trend. High amplitude, low-frequency oscillations, autocorrelation, and cross-correlation plots are observed for cavities of significant length. Virtually no fluctuations are noticeable in the model with a cavity with minimal size.
The mean azimuthal pressure variation is recorded and analyzed for various cavity structures on the projectile base. In contrast with the BB model, higher values of the foundation pressure coefficient are noted for the SC model except at an azimuthal position of 270 deg. That is because the base cavity increases the recirculation region’s size, and flow also travels downstream of the base separation point.
This reduces the interaction between the shear layer and the recirculation field. However, the separation point’s relocation results in less contact between the base and the low pressure associated with the shedding vortex. The average base pressure coefficient at all azimuthal locations is −0.08. Due to the pressure difference between the freestream and the recirculation region, the ventilated cavities act as natural bleeding tools.
The fluid mass is injected into the base area by bleed devices, thus increasing the base pressure. There is no significant increase in the SVC model’s base pressure than the SC model (at the corresponding sensor sites) except the 270 deg azimuthal position. The probability may well be that the normal component of the momentum fluid flow in the base region through the vent holes is negligible. It means that the area of the recirculation will be insignificantly massed.
All the vent holes on the cavities are usually directed to the freestream flow in the present study. Thus, the effect of increasing base pressure due to the natural bleeding process is negligible. In general, the base pressure increases due to the lower interaction of base and the low pressure associated with the vortex deposits, as explained earlier, when the ventilated cavities size is changed from small to large. The findings of a numerical and experimental analysis studied by Mariotti et al. [9] reported assessing a control process’s performance to postpone the boundary layer’s separation.
This process consisted of incorporating the surface of contoured, transverse grooves (i.e., small cavities with an acceptable cross-sectional shape). The grooves’ shape and depth need to be significantly smaller than the incoming boundary layer’s width; fluid recirculation within the grooves is smooth and stable. This strategy is applied to an axisymmetric bluff body with different rear boat ends, distinguished by numerous flow-separating degrees. Variation of large multiscale eddy simulations was examined experimentally [9].
Before boat tails, the boundary layer conditions are fully developed turbulent in experiments and intermediate in simulations due to the different input flow turbulence levels. Every time a single axisymmetric groove is added on the boattails’ lateral surface, the boundary layer’s separation is postponed considerably, and the pressure drag is reduced. The wake-dynamic structure remains qualitatively similar.
It was analogous to an asymmetrical bluff body with quantitative variations that correlate with the wake width of a reduction caused by boattails and grooves. A few additional simulations show that the groove effect is also resistant to change the geometric parameters that define its shape. Both evidences support the notion that relaxing the no-slip boundary condition for the flow around the recirculation regions at an appreciable pace on their boundaries is the physical mechanism responsible for the new separation control method’s efficacy.
Several techniques are explored to reduce the aerodynamic drag of bluff bodies through base pressure recovery. These include boat tailing and base cavities. Howell et al. [10] changed Ahmed’s body to have a base cavity of variable depth that may be ventilated via a slot in a square-back configuration considered for investigation. The overall body drag diminished with a single cavity for numerous cavity lengths, but a distinct minimum drag state was achieved.
A relative drag reduction is achieved by the incorporation of ventilation slots and at a much-reduced cavity size. The pressure data in the cavity was used to assess the dependence of the base drag. Variations in the slot structure were analyzed to decrease the drag and the slot distribution effects. PIV is used for various cavity setups. Figure 8 shows Ahmed’s body with vented slots [10]. The base pressure was assessed on the cavity backplate. There was a total of 48 pressure tubes spread over one half of the backplate.
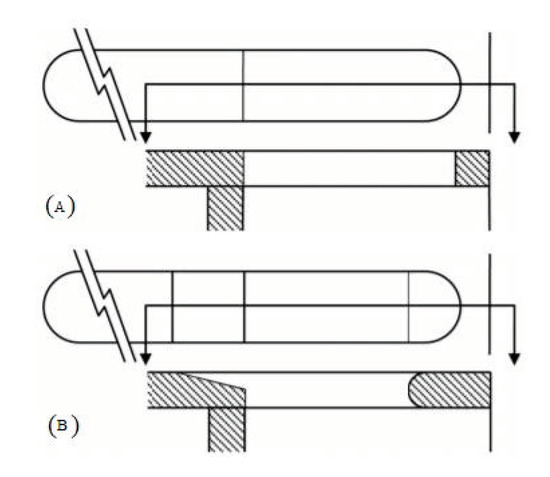
Figure 8.
Ventilation slots details (A) with square-edged (B) tapered [10].
Numerous cavity configurations were tested at the ground level [10]. The cavities were the plane cavity, the original vented cavity with square edge slots, the vented cavity with tapered slots on all surface areas, and the same cavity with undesirable slots covered. For both earlier settings, the standard pressure measurements were made for the ideal cavity and a much deeper cavity. The pressure measurements were undertaken for various cavity depths in the two ventilated cavities with tapered holes. In each case, comparisons were made with the base pressures calculated without a cavity on the quarterback scale.
Seeing the growing need for energy conservation, Bonnavion et al. [11] researched the reduction of base drag. Here the author has studied the Ahmed body [12] as the bluff body for the real-time road vehicle. Experiments were conducted to investigate the bifurcation of the wake controlled by the clearance and impact of the base cavity before and after bifurcation that can be used when making road vehicles. It is observed that regardless of ground clearance, above the threshold 5c* = 0.08, an eight percent reduction is achieved.
Lucas et al. [13] did a numerical investigation of the asymmetric wake mode of a square back Ahmed’s body, focusing on a base cavity effect. Both distributions indicate an almost identical pressure field for the baseline and shallow cavity for x > 0.5. While they are horizontally and vertically shifted from each other for x < 0.5. They both present a local minimum, with good shape indicating the presence of a viscous vortex flow (i.e., the circular recirculation) source of low pressure.
The horizontal shift appears to be introduced by the cavity depth of d = 0.047, indicating that the circular recirculation region remains at the same distance from the body’s base. The vertical shift is introduced in the area 0.33 < x < 0.5. The pressure gradient with the cavity is reduced compared to that of the baseline. Again, an exact horizontal shift corresponding to the cavity depth is observable between the baseline and the shallow cavity. The viscous vortex interaction with the base leads to the same maximum velocity close to the base, and the velocity gradients are very similar for x < 0.33.
2.2. Passive Control with Rib
As cavities introduce secondary circulation in the flow, it reduces the oscillatory nature of flow and increases the base pressure. This phenomenon is more prominent in longer ducts than in shorter ducts. However, the cavity’s main disadvantage is when it starts behaving like a closed cavity, thereby becoming ineffective as a passive control. As a result, in 2001, Rathakrishnan [14] introduced ribs as a passive control device. He employed five ribs in the circular duct diameter of 25 mm of aspect ratio 3:1, 3:2, and 3:3 at 1D (D = diameter of the tube) location. From his results, he found out that the 3:1 is the most effective in reducing the base drag.
For pressure ratio 1.141, the base pressure attains the minimum value for L/D = 4 due to the shear layer extending from the nozzle outlet connects downstream of the base to the extended duct wall [14]. The primary vortex formed at the base region affects the base pressure according to the distance of the reattachment point from the base region and the Mach number at the nozzle exit. The primary vortex intensity determines the low-pressure level in the base region. There exists a reverse flow due to the low-pressure zone created by the vortex. The passive control in the form of the ribs comes into effect in this separated flow.
Later Yedlapalli et al. [15] introduced ribs with aspect ratios 0.45, 0.64, 0.84, and 1.25 at X/D = 0.5, 1, and 1.5, placing a single rib at three different locations in a circular pipe of 22 mm diameter at subsonic to sonic Mach numbers (0.2 to 1). The results show that the rib aspect ratio between 0.45 and 0.64 reduces the backflow and reduces the base pressure. From wall pressure distribution results, it is found that ribs with the smallest aspect ratio, i.e., 0.45 at X/D = 1, gives the minimum disturbance along the pipe while gaining desired base pressure results.
Nathan et al. [16] studied the effect of the annular ribs of aspect ratio 3:3 at supersonic Mach number 1.8, varying the NPR from 2 to 6 at locations 0.5D, 1D, 1.5D, 2D, 3D, 4D, and 5D in a circular pipe. It is noticed that the base pressure increases with an increase in the NPR with rib location. Vijayaraja et al. [17] also studied the annular ribs experimentally with aspect ratio from 0.45 to 1.25 placed in enlarged duct by varying the length to diameter ratio (L/D) 0.5D to 6D, and NPR is varied from 1 to 7 at subsonic to sonic Mach numbers. It is realized that L/D = 0.5 for NPR 3, the base pressure increases with an increase in NPR.
Khan et al. [18] did the numerical simulation and studied the flow at the sonic Mach number for a duct diameter of 20 mm. A single rib of three different aspect ratios (3:1, 3:2, and 3:3) is placed one at a time at various locations (1D, 2D, 3D, and 4D) along the circumferential direction of the duct. It is concluded that the increase in NPR is from 1.5 to 5; the base pressure decreases continuously with no rib case.
In contrast, with the rib case, the base pressure decreases steadily with aspect ratio 3:1, while for aspect ratio 3:2 and 3:3, it raises the base pressure at NPR 2.5 and 2, respectively. It was also clear that for no rib case, the base pressure decreases continuously, and for rib case 3:1, there is continual decrement of base pressure; however, it is above the base pressure of the smooth pipe. For 3:2 and 3:3, the base pressure starts to increase from NPR 2.5 compared to 3:1, where the base pressure starts to grow right from the beginning, i.e., NPR 1.5. Figure 9 shows the same.
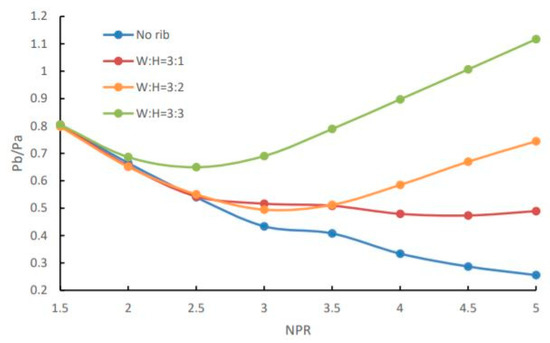
Figure 9.
Base pressure changes when NPR is increased from 1.5 to 5, and the aspect ratio is changed from 3:1 to 3:3 [18].
The main reason behind this phenomenon is that with an increase in NPR, the expansion level increases. As the reattachment point has shifted as the flow is highly under expanded, the primary vortex’s effectiveness decrease. There is a reduction in fluid reversal, as there is an introduction of secondary vortices due to rib height, due to which base pressure increases. This phenomenon is considerable for the 3:4 aspect ratio as the rib height has increased.
2.3. Passive Control with Dimple
The research on passive control in the form of a dimple is done by Khan et al. [19]. They investigated both experimentally and numerically the passive control effect to control the base pressure in a Backward Facing Step at various NPRs. Two dimples of diameter 3 mm are located at 180° intervals at the base region along the Pitch Circle Diameter of 23 mm. This study was done for NPR 1.27, 1.38, 1.52, and 1.69. Figure 10 shows the design and dimensions of the nozzle and the duct.
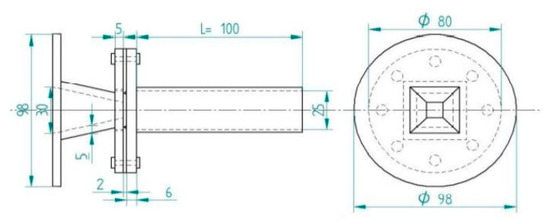
Figure 10.
Dimensions of nozzle and duct [19].
The model is designed to deliver four BFS with an incidence angle of 15° from which the flow expands suddenly to a 25 mm square duct for different duct length 4D ≤ L ≤ 10D to see the effect of the base pressure’s geometric parameter. The presented investigation revealed that the passive control dimples are highly effective at higher NPR, and the wall pressure distribution at higher NPR too was stable. The spatial parameter also affected the base pressure for a particular NPR.
CFD analysis was also done on the dimple and dimple with pressure and velocity distribution profile using the Navier stokes equation, Turbulence model SST, and Reynold’s number (Re) = 122.56 × 103. From this analysis, it is clear that an optimal L/D ratio can be found for a given nozzle pressure ratio, which results in a maximum increase/decrease in base pressure, and the passive controller can be efficient in controlling the base pressure.
Findings state that the level of expansion (NPR) strongly affects the base pressure and influences dimple as a passive control. At higher NPR, it is found that the base pressure is low, and hence dimples as passive control are very effective in controlling the base pressure if achieving the low base pressure is the mission requirement. For example, in the combustion chamber, we want to achieve a minimum base pressure for better fuel-air mixing to enhance its efficiency.
2.4. Passive Control with Static Cylinder
It is known from the experiments of passive control in the form of a static cylinder that when the flow is correctly-expanded and under-expanded, the passive control in the form of a stationary cylinder becomes useful. Asadullah et al. [20] did a wind tunnel experiment (Figure 11) using the static cylinder at supersonic Mach number 2 by varying the NPR from 2 to 9. It is observed that when the NPR is low (i.e., up to NPR 5), there is no effect of control on the base pressure values, whereas, for the higher NPR (i.e., NPR = 6 and above), the control begins to show its effectiveness and the change in the base pressure increases until NPR 9.
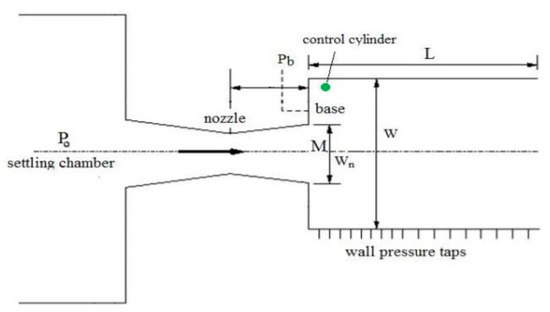
Figure 11.
Experimental setup [20].
The percentage change in base pressure is 14% at NPR 6, and this trend increases and reaches up to 59% at NPR 9. The jet is over-expanded till NPR 6, and after NPR 6, and at higher NPRs, the flow is correctly-expanded or under-expanded. This is the leading cause of the significant increase in base pressure due to the flow interactions with the shock at the square outlet region, and it makes the vortex weak in the base region. Thus, the NPR increases and over-expansion reduces, and a weak oblique shock is present compared to lower NPR.
2.5. Passive Control in the Form of Spikes
An experimental study was done on the bluff body at subsonic Mach numbers. Passive control in the form of aerospikes was placed on a plate of 1 mm thickness. Two spikes are placed on the plate at 11.5 mm between the nozzle and the duct. The tests were conducted at Mach numbers 0.6, 0.7, 0.8, and 0.9 for an area ratio of 6.25. L/W ratios of the duct taken into consideration are 4, 6, 8, and 10. These experiments were undertaken to control the base drag, an essential component in bluff bodies, to reduce the total drag [21]. Figure 12 below shows the placements of aerospikes.

Figure 12.
Control plates with aerospike [21].
Findings stated that without control case, the base pressure first increases till L/W = 6 and then decreases till L/W = 8, and then is an increasing trend in base pressure until L/W = 10. With passive control of aerospike, the base pressure starts to increase right from the beginning and becomes more than atmospheric pressure at L/W = 6, and then again, as an increasing trend, it continues till L/W = 10. It acquires the pressure value, which is 5% more than atmospheric pressure.
The main reason for this phenomenon is that until L/W = 6, the aerospikes can break the base region’s recirculation zone into two parts. Hence, the suction at the base is reduced, and the base pressure increases. Also, from L/W = 4 to L/W = 6, the duct’s length is small. So, the two recirculating bubbles formed at the base get less space to travel. Whereas from L/W = 7, till L/W = 10, the duct’s length is more and hence gets more space and time to travel, and therefore the base pressure gradually increases with the L/W ratio. However, the aerospike in passive control is very useful at the subsonic and transonic regimes.
Mehta [22] studied a forward-facing aerospike to a satellite launch vehicle. The payload fairing significantly modifies its flow field and reduces the aerodynamic drag at transonic and supersonic speeds. The numerical simulation was carried out on 0.8 ≤ M ≤ 3.0 with and without aerospikes. A forward-facing aerospike attached to a payload fairing of a satellite launch vehicle significantly altered its flow field and decreased the aerodynamic drag in transonic and low supersonic speeds.
The present payload fairing is an axisymmetric configuration and consists of a blunt-nosed body along with a conical section, payload shroud, and boat tail, followed by a booster. All pressure transducer loss is below the average order of ±0.51%. In general, there is good agreement between the current computations and the available experimental data. When an aerospike is attached to the payload fairing, the payload fairing pressure is changed considerably. The reduction of surface pressure is not minimal for M < 1. There is a significant drop in surface pressure for M > 1.
Another study was done by Khan et al. [23] on threaded spikes as a passive control. In their research, as shown in Figure 13, two threaded spikes were attached in the opposite direction of length 40 mm on the circular plate of thickness 1 mm and diameter 80 mm. They conducted tests for Mach numbers (0.6 and 0.7) and two transonic Mach numbers (0.8 and 0.9). Ducts of lengths 100 mm, 150 mm, and 200 mm are examined.
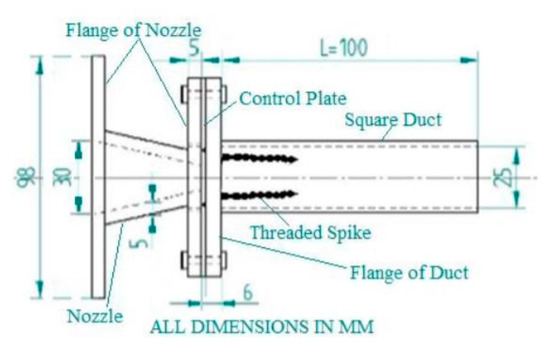
Figure 13.
Square nozzle with threaded spikes control plate [23].
Khan et al. [23] findings for L/W = 4 show that base pressure continuously decreases with an increase in Mach number without control. With the control case, there is an increase in base pressure, i.e., it is more than atmospheric pressure right from the beginning and decreases till Mach number 0.7 and then again increases till Mach number 0.9. For L/W = 6, the increase in base pressure with the control case was from Mach 0.6 to 0.9.
For L/W = 8, there is an increase in base pressure until Mach 0.7 and then a slight decrease to 0.8 and a steep increase in base pressure until Mach 0.9. However, for L/W ratios, it can be observed that there is an increase in base pressure right from the beginning compared to no control case, and it is more than atmospheric pressure.
2.6. Passive Control in the Form of Splitter Plate
The effect of passive control in a splitter plate on a circular cylinder is studied by Hwang et al. [24] numerically for laminar flow. A splitter plate was positioned horizontally in the wake region with the same length as the cylindrical diameter. The plate, which suppresses the vortex shedding, decreased the drag force substantially as well as the lifting fluctuation; for maximum reduction, there is an ideal plate position. However, they increased sharply as the plate was placed further downstream from the optimum position. This finding is consistent with the current experimental observation in the turbulent wake.
It is evident that for the steady flow, i.e., at Re = 30, the drag coefficient continuously decreases as there is an increase in the G/d value. For the unsteady flow (Re = 100 and 160), the drag coefficient first slightly increases for 0 ≤ G/d ≤ 0.25 and continuously decreases for G/d = 2.6. It is observed that the drag coefficient decreases with a higher Reynolds number. A 3% drag reduction is achieved for Re = 100 and 6.7% is achieved for Re = 160 at the optimum location of the plate i.e., G/d = 2.6 in comparison with the cases of no plate i.e., G/d = 0.
A numerical study was conducted by Soumya and Prakash [25] on the triangular cylinder’s splitter plate effect. They considered the Reynolds number from 50 to 200 based on the triangular cylinder’s side, and the length of the splitter plate is varied from 0 to 6. The passive control in the form of a splitter plate is significant, resulting in a reduction of the drag.
Drag is reduced from 9% to 57% by attaching the splitter plate to the triangular cylinder. [25]. It is observed that there is a decrement in skin friction drag with an increment in plate length, and with a further increment in the plate length, the skin friction drag increases. The pressure drag decreases continuously with the plate length increment. Here it is observed that the total drag decrement is observed from 9% to 57%.
The splitter plate as a passive control was experimentally studied by placing it near the trailing edge along the wake centerline of a turbulent boundary layer on a flat plate by Jodai, Y. et al. [26]. The splitter plate length was varied from half to five times the thickness of the trailing edge. The base pressure behind the trailing edge was measured. The mean velocity and pressure distribution measurement on the flat plate in the turbulent boundary layer were made under the freestream zero-pressure gradient.
Within an inner layer of the turbulent boundary layer near the trailing edge, the mean velocity without the splitter plate increased more than that in the upstream location. However, the base pressure increases with the splitter plate made the mean velocity distribution similar to that of a fully developed turbulent boundary layer by Jodai, Y. et al., [26].
It can be observed that when the length of the splitter plate < 1, the value of C (C = Cpb − {Cpb(without splitter plate)}/(Cpb)without splitter plate) continuously decreases with the increment in l/h value. For l/h = 1, the C has a minimum value of −0.55. C then increases slightly with changes in l/h to a maximum value of −0.52 at l/h = 2, and above l/h = 2, C decreases somewhat at higher l/h, and therefore for l/h = 4, a constant value of −0.58 is maintained. Simultaneously, Bearman [27] and Nash et al. [28] show some differences when the present data are compared.
To reduce fuel consumption and improve road vehicle dynamics, Patrick and Azeddine [29] studied a low Reynolds number of 1.0 × 106 and 1.6 × 106 using a splitter plate at its front or rear a simplified car geometry to reduce drag. Utility vehicles or MPV vehicles are considered by representing them in the form of simplified geometry. A reduction in drag of around 28% is achieved by placing the model’s front splitter plate. This research demonstrates the advantage of position adaptation and orientation of passive control in the presence of lateral wind.
An experimental investigation was conducted by Reedy et al. [30] at high-speed supersonic flow at Mach number 2.49 with a splitter plate. The splitter plate is placed at the recirculation zone behind a blunt axisymmetric body. Triangular splitters that divide the near wake into one-half, one-third, and one-fourth cylinder regions were designed to exploit this flow’s specific stability characteristics, impact the immediate wake flow, change the base pressure, and eventually affect the base drag. A base drag reduction of as high as 39% is achieved by employing the splitter plate.
Integrating the no-control pressure distribution resulted in a resultant base drag factor of CDnet is 0.1028. The resulting net base drag coefficients were CDnet is 0.1033, 0.1071, and 0.1051, respectively, for the one-half, one-third, and one-fourth-cylinder configurations. Compared to the non-control geometries, the splitter plates generated drag coefficient changes of 0.5, 4.2, and 2.2 percent, which is within or too near to the usual measurement uncertainty.
2.7. Other Types of Passive Control Technique
Falchi et al. [31] did an experimental and numerical investigation on a passive technique as ventilation for drag reduction, which is performed by connecting a high-pressure region formed in front of the body with a ventilated duct to a low-pressure region in the wake region. This establishes the net mass flux in the wake zone. It is particularly suitable for aerodynamic bodies to achieve a net total drag reduction in the body by globally modifying the body’s wake region.
PIV measured the velocity, and Reynolds averaged numerical code was employed at a slightly high Reynolds number. This study aims to assess the effectiveness of reduction in drag on a vented bluff body. In this research, the numerical and experimental results are in good agreement. The drag reduction is accomplished for both smooth and rough (single strip) models.
It is important to note that the rough models have a rough surface because an adhesive strip in the stripped model is stuck to the end part of the spherical model, whereas, in the clean model, there is no such strip. A typical drag reduction in the model of about 7% to 8% was achieved, which is moderately more significant than the unpredictability (which is almost 5%) and must be verified by velocity field measurement.
It is noted that a 20% average reduction in drag is achieved when the model is changed from a non-vented to vented model. The main difference observed is that the drag value is almost the same in the vented model for stripped and clean models. On the other hand, for the non-vented model, different values are seen. For the non-vented strip model, a drag reduction 10% greater than the non-vented clean model is seen.
The main reason behind this phenomenon is the flow transition into a fully developed turbulent boundary layer, which causes an increase in the skin friction drag. This is taken into consideration as there is always some roughness on the external surface. The roughness is usually found in aerodynamic vehicles, due to which there is a boundary layer transition. In any situation above, the venting jet with strip configuration overcomes the boundary layer disturbance due to the strip position [31].
Boswell et al. experimentally studied [30] the afterbody flow field and the circular cylinder’s base region. They considered an Axial Length (L) of afterbody to the Base Radius (R) of the afterbody (L/R) = 3.0. They aligned the model at an angle of attack of 10 degrees with Mach 2.5. Schlieren and Mie’s dispersal visualizations were obtained to distinguish governing features and picture the chaotic systems of this large-scale turbulent structure of the separated flow.
Surface oil-streak flashes were used to determine the afterbody surface and three dimensionalities for base surface flow study. Pressure-sensitive measurements have been performed to determine the surface pressure evolution along the cylindrical body at an attack angle and change the body tilt base pressure. The results show that the typical, expected flow characteristics include corner expansion, shear layer formation separation, recompression of shocks, and a turbulent wake.
However, no evidence of flow separation was found along the afterbody. A strong secondary circumferential flow is detected due to the pressure gradients on the surface along the afterbody. There is entrainment of fluid into the base zone from the smooth part of the fluid. For the angle of attack scenario, the average base pressure ratio is 48.4% lower when compared to the calculated zero angles of attack, as a result of which there is a substantial increase in the base drag for cylindrical structures at the angle of incidence by Boswell et al. [32].
Moore et al. [33] researched tangent ogive after body with a cylindrical afterbody whose L/R = 14.4 is studied. In contrast, the research done by Boswell et al. [32] consists of a 10-deg turn of a constant-diameter sting with L/R = 3.0. As a result, Boswell et al. [32] data fall perfectly on the Mach 2.5 curve. There is a weak dependence of base pressure on L/R rather than on α and the Mach number. The incidence angle plays a critical role in reducing base pressure and increasing total drag on aerodynamic bodies.
The effect of a thin slit at the base edge of a blunt asymmetrical body that communicates an inner cavity with the external flow is studied by de la Cruz et al. [34]. A parametric study is performed on changes in slit size and cavity depth based on pressure. The base pressure initially increases with a deeper cavity but saturates at a slit depth. The base pressure increases monotonically up to 5% with increasing slit size for the geometries tested.
An upper limit of base pressure recovery of 20% is extrapolated from the data. It is observed that the main effect of the slit is to reduce the instantaneous pressure asymmetry, which is linked to the total base pressure for all the slit sizes. With the slit size for the geometries calculated, the base pressure increases monotonously up to 5%.
In highly asymmetrical pressure distributions, the slit creates a base pressure increase not related to the base pressure’s asymmetry. The results indicate the wake’s effect due to the diametric flow inside the cavity driven by pressure differences in the slit. The most significant pressure regulates the drops between the slit and the cavity. The slit also decreases periodical variations in base pressure, which primarily relates to the vortex shedding, and raises the wake rotational speed. The analysis reveals that for all slit sizes, the rest of the data is equally independent of h for h/D ≥ 2.8%.
Bao and Tao [35] studied a circular cylinder’s wake regulation is numerically examined within the laminar flow regime by two symmetric plates attached to the rear surface. The two flat plates are arranged in parallel, and the angle of attachment varies between 0 deg and 90 deg. The dual plate decreases the drag and allows more significant wake suppression at a relatively short plate length compared to the use of a single splitter plate.
The attachment angle is shown to have a considerable impact on the control efficiency, and the most effective range associated with the highest drag reduction is 40 to 50 degrees. The free shear layers are attached to the outside surface of the controllers within this system. A comparison with other passive control configurations is suggested for the potential mechanism responsible for wake control.
The findings state that the Reynolds’ steady flow field between 20 and 40 is considered to increase attachment angle, ϴf. The total mean drag coefficient is more than that of the plain duct for the attachment angle 40 and 60 degrees at Reynolds numbers 20 and 40. The results are due to the plates’ viscous effect, which is significant in the flow field’s steady regime.
When the flow becomes unsteady (60 ≤ Re ≤ 160), a depression can be found in the total mean drag coefficient curve at around 40 and 50 degrees. The drag reduction of the dual plates is placed at a suitable location that is higher than the single splitter plate. And this drag reduction is more significant at a higher Reynolds number than at a lower Reynolds number. At Re = 160, a total drag reduction of 13.1% for cylinder only and 13.4% for cylinder and plates is obtained, compared to a single plate (7.38% and 7.16%) double.
A typical planar space launcher fitted with two passive flow controls simulates a turbulent wake with a zonal RANS-LES system and is studied by dynamic mode decomposition (DMD) [36]. The first approach examines the effect of a conventional boat tail on the surface. In the second concept, a semi-circular lobe flow control unit is used, inserted at the base shoulder of the main body.
The concepts’ objective is to reduce the reattachment length and, thus, the forces’ height and stabilize the separated shear layer. The reattachment length can be reduced by 50% by using a boat tail. However, it is shown that that the semi-circular lobes improve the turbulent mixing and creation of the shear layer. Consequently, the attachment length is reduced significantly by around 75% [36]. The semi-circular lobes reduce unwanted differences of low frequency on the top of the nozzle. Nevertheless, this change is at the expense of the high-frequency pressure’s enhanced fluctuations due to intensified small, turbulent sizes.
The DMD velocity field analysis shows that the lobes can suppress the broad, coherent structure with two-step wavelength measurements in the referral configuration without flow control. The wavelength of the stable structures on the span seems to depend on the lobe geometry, as all spatial DMD modes observed display a periodicity that is equal to the distance between two lobes [36].
Even in the intermediate lobes, where the wall’s contour is shaped like a standard backward-facing step, the base pressure is higher than that of the reference geometry. This trend is because of the lobes’ upstream effect due to the transonic flow conditions and the wake’s three-dimensional existence. The recompression due to the shear layer’s intrusion occurs in a smaller stream region and moves upstream because of the minimal reattachment length. The pressure is reduced due to an acceleration in the flow until the lobes’ edge and the boat tail. Persistent recompression to the main body’s rear is evident further downstream [36].
For form-drag reduction in the flow over a two-dimensional bluff body with a blunt trailing edge, a new passive control device is introduced by Park et al. [37]. The system consists of small tabs on the top and bottom edges of a bluff trail to effectively interrupt a two-dimensional wake. A wind tunnel experiment and a large-scale simulation were conducted to test its drag reduction efficiency. Extensive parametrical research is conducted experimentally by changing the passive control’s height and width in the form of a tab and spacing along the span between the adjacent tabs.
The Reynolds numbers considered for the study are 20,000, 40,000, and 80,000. The base pressure increases for a wide range of parameters (i.e., drag reduces) at all three Reynolds numbers. In contrast, the base pressure is significantly increased by more than 30% for the optimal tab configuration. Numerical simulations are done at lower Reynolds of 320 and 4200 to investigate the tab’s base pressure rise. Tab presence resulted in a significant decline in vortical strength in the wake and results in a considerable increase in the length and width of the vortex formation.
The base pressure variance in a vertical direction for all tabs configurations is negligible (less than 0.5%). The base pressure of the uncontrolled flow is distributed nearly uniformly in the direction of the span, indicating that the wake behind the bluff body has remained uniform. The maximum base pressure over the spanwise direction is 5% greater than that of Bearman [38]. The trend is reasonable considering the present research of Park et al. [37], where the ratio of span to base height is W/h = 5, whereas that of Bermans [38] is W/h = 28. As a result, with tab, the base pressure is substantially increased by 23%.
An experimental study was performed by Tripathi et al. [39] to test the effectiveness of the changes in base geometry in the control of mean and unsteady base pressure on a circular arc 12° to zero angle incidence boat-tailed afterbody under jet-off and jet-on conditions. Tests were conducted for freestream Mach numbers range from 0.6 to 1.06, while jet-on pressure ratios from 1 to 12 were completed.
In the jet-off case relative to the sharp base, the base pressure increase was 53% and 42% for the rounded base and base cavity configuration. The round base showed better results up to a nozzle pressure ratio of 8 for M ≤ 0.9 in jet-on condition. However, for M = 1.06, the base cavity showed a better effect than the rounded base configuration. Another passive device in the form of a rectangular flap was proposed by Siddiqui and Chaab [40], installed on a 35° Ahmed body to reduce the drag. Drag reduction of 14% was achieved at a 10° flap angle in their case. Below, Figure 14 shows the 35° Ahmed body detailed view with a rectangular flap.
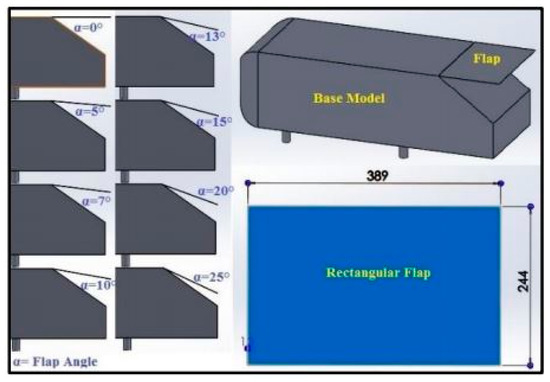
Figure 14.
Ahmed body with 35° slant angle detailed view with rectangular flap (dimensions in mm) [38].
Moreover, a modification in the spanwise wake by Mariotti et al. [41] reported a 9.7% drag reduction. Capone and Romano [42] reported a reduced drag due to a decline in the wake in the vertical direction by employing horizontal and vertical deflectors on the square-backed vehicle. When the circular vortex at the base was modified, it reduced drag [43]. Several active and passive techniques have been developed to reduce the aerodynamic drag in road vehicles [44,45,46].
Tian et al. [47] achieved a 21.2% drag reduction at a 25° flap angle on a slant Ahmed body and about 6% at a 35° flap angle on a slant Ahmed body when studying the effect of flaps. In a study motivated by the birds’ secondary feathers when moving deflectors were introduced at 25°slant Ahmed’s body, a maximum drag reduction of 19% was achieved [48]. A study by Altaf et al. [49] introduced three different flap shapes, namely: rectangular, elliptical, and triangular. For the oval flap, a reduced drag of 11.1% was achieved, and 6% was conducted for the rest types of flaps.
Some studies recently highlighted the recirculation zone’s physics and found a relationship between the recirculation region and base pressure [50,51]. It is observed that passive device performance is better than active device techniques as Beaudoin and Aider [52] were able to reduce drag by 25% for modified Ahmed body at a 30°slant angle of the rectangular flap.
3. Findings Discussion
Based on the above discussion, most of the passive techniques used for the base pressure control and hence base drag are summarized here below:
- All the passive control methods to regulate base pressure are useful in creating a favourable pressure gradient. These techniques are also inadequately effective in the presence of an adverse pressure gradient (i.e., when the jets are over-expanded). In passive control, the level of expansion (i.e., Pe/Pa) plays a vital role in fixing the base pressure values. It is seen that whenever the area ratio is five and above, the control effectiveness is minimal/not useful even though the flow from the nozzles is under the influence of a favourable pressure gradient. The physics behind this trend maybe when the relief effect due to an area ratio increase is beyond some limit. The flow from the converging or converging-diverging nozzle discharged into the enlarged duct tends to attach with reattachment length other than the optimum for a strong vortex at the base. This process makes the NPR effect on base pressure become insignificant after a critical area ratio. The review shows that when the jets are under-expanded for a lower area ratio, the passive control is significant, and base pressure is equal to the atmospheric pressure, or is more than the ambient pressure. Results indicate that for certain combinations of the parameters, an under-expansion level of 1.5 (i.e., Pe/Pa = 1.5) is the optimum value resulting in a maximum increase in the base pressure.
- A new passive control device was considered for a form-drag reduction in the flow over a two-dimensional bluff body with a blunt trailing edge. The system consists of small tabs on the top and bottom edges of a bluff trail to effectively interrupt a two-dimensional wake. A wind tunnel experiment and a large-scale simulation were conducted to test its drag reduction efficiency. Extensive parametrical research is conducted experimentally by changing the passive control’s height and width in the form of a tab and the spacing along the span between the adjacent tabs. The Reynolds numbers considered for the study are 20,000, 40,000, and 80,000. The base pressure increases for a wide range of parameters (i.e., drag reduces) at all three Reynolds numbers.
- Similarly, the splitter plate’s effect at various length locations is useful in the base drag reduction at various NPR, Mach numbers, area ratios, and length-to-diameter ratios. The passive control in the form of a splitter plate is significant, resulting in reducing the drag. Drag is reduced from 9% to 57% by attaching the splitter plate to the cylinder. With vertical splitter plates positioned downstream of a straight base, drag reductions of nearly 12% were obtained. Finally, the results presented herein confirm the advantage of splitter plates in reducing aerodynamic drag and demonstrate the need to develop systems capable of adapting their position and angular orientation to external conditions. Triangular splitters that divide the near wake into one-half, one-third, and one-fourth cylinder regions were designed to exploit this flow’s specific stability characteristics. The impact of the immediate wake flow changes the base pressure and eventually affects the base drag. A base drag reduction of as high as 39% is achieved by employing the splitter plate, whereas, with passive control with spike, the base pressure starts to increase right from the beginning and becomes more than atmospheric pressure at L/W = 6 to 10, and acquired base pressure values are 5% more than atmospheric pressure. The effect of spike and grooved spikes play an essential role in fixing the base pressure values. The impact of cavities is to reduce the oscillations in the enlarged duct.
- A computational fluid dynamics simulation over a payload fairing of the satellite launch vehicle with aerospike presence is carried out. The payload fairing significantly modifies its flow field and reduces the aerodynamic drag at transonic and supersonic speeds. The simulations were done by solving time-dependent compressible turbulent axisymmetric Navier-Stokes equations. The closure of the system of equations is achieved using an algebraic turbulence model. The numerical simulation is performed on a single-block structured computational domain. The flow field over the aerospike depends on the freestream Mach number. The effects of the aerospike attached to payload fairing are studied with velocity and density plots. The schlieren pictures, oil flow, and the pressure measurements on an aerospike attached to the payload fairing are analyzed and compared with the present numerical results with the Mach number in the range of 0.8 ≤ M ≤ 3.0 and freestream Reynolds number range 33.35 × 106/m ≤ Re∞ ≤ 46.75 × 106/m. The Mach number range covers the maximum drag and dynamic conditions during the typical satellite launch vehicle’s ascent flight. A distinct flow field is found for M∞ < 1 and M∞ > 1 with and without the aerospike attached to the payload fairing. The Flow separation is found at all the freestream Mach numbers over the aerospike, with the recirculation zone being Mach number dependent. As the freestream Mach number increases, the separation zone becomes steeper. It is found that the aerospike attached to the payload fairing leads to drag decline.
4. Conclusions
In this review, various passive control techniques to control the base pressure and regulate the drag force are discussed. When the passive strategies in the form of ribs, cavities, static cylinder, boattail, and step-body are used, the expansion level plays a crucial role in controlling the base pressure. After a critical area ratio, the effect of NPR is negligible. The control does not give the desired results at a very high level of under-expansion. When the area ratio is in the range of 2 to 4, the passive control in the form of ribs is beneficial and reduces the base suction. The review shows that for some combination of the parameters, under expansion, level 1.5 is the optimum level of under-expansion, resulting in a maximum gain in base pressure. In the case of the ribs, the ribs’ geometry and location play an important role. Depending upon the duct diameter, both the parameters show different optimum values. For the lower area ratio, the place, as well as the size values, are small. However, for a high area ratio, both the parameters assume higher values as the reattachment length is considerable. For the splitter plate, a drag reduction of as high as 39% is achieved. It is seen that cavities are effective in reducing oscillation in the enlarged duct. The effect of spike and grooved spike plays a significant role in affixing the base pressure values. Aerospike was tested for transonic and supersonic speeds. It is observed that as the Mach number increases, the separation zone becomes steeper, and hence aerospike leads to a decrease in drag when attached to payload fairing. When the static cylinder is placed in the recirculation zone, it leads to a drag reduction of 59%. In summary, this review has critically assessed and summarized the crucial elements in the passive control device that control the base pressure, enhance the base pressure, and reduce the base drag. Hence, it further established passive control as a very efficient technique to favorable control the pressure under the influence of favorable gradient at the nozzle exit. Table 1 below gives the summary of the type of passive control discussed in this paper and their effect.

Table 1.
Summary of type of Passive control and their effect.
Author Contributions
Conceptualization, A.K. and P.R.; Formal analysis, A.K.; Funding acquisition, P.R.; Methodology, A.K., J.S.S.S.; Project administration, P.R.; Supervision, P.R. and J.S.S.S.; Writing—original draft, A.K., P.R.; Writing—review & editing, A.K., P.R. and J.S.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the Universiti Sains Malaysia RUI Grant No. 1001/PAERO/8014120 to support this research.
Acknowledgments
The authors would like to acknowledge the technical staff of Aerospace School, USM, in furnishing the research inputs.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| X | Axial distance along the duct |
| D | Diameter of the duct |
| L | Length of the duct |
| G | Distance between the rear base point of the cylinder and the leading edge of the splitter plates |
| d | Cylinder diameter. |
| NPR | Nozzle Pressure Ratio |
| x | Mean velocity field in the plane |
| c | Adjustable distance to the ground called ground clearance |
| BFS | Backward Facing Step |
| CDnet | Net drag coefficient |
| Cpb | Base pressure coefficient |
| BB | Blunt Base Model |
| SVC | Small Length Ventilated Model |
| SC | Solid Model |
| L/D | Length-to-Diameter Ratio of the enlarged duct (pipe) |
| PIV | Particle Image Velocimetry |
| L/W | Length-to-Width Ratio |
| PCD | Pitch Circle Diameter |
| St | Strouhal Number |
| f | Vortex shedding frequency |
| D | Height of the backward-facing step |
| U | Freestream velocity |
| P | Pressure |
| M | Mach number |
References
- Hsu, C.-W.; Lin, S.-Y. Investigation of characteristics of shear layer: Application of synthetic jet in backward-facing step flow field. Trans. Can. Soc. Mech. Eng. 2016, 40, 787–797. [Google Scholar] [CrossRef]
- Rajendran, P.; Sethuraman, V.; Khan, S.A. Base and wall pressure control using cavities and ribs in suddenly expanded flows-an overview. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 66, 120–134. [Google Scholar]
- Wang, F.; Gao, A.; Wu, S.; Zhu, S.; Dai, J.; Liao, Q. Experimental Investigation of Coherent Vortex Structures in a Backward-Facing Step Flow. Water 2019, 11, 2629. [Google Scholar] [CrossRef]
- Ashcroft, G.; Zhang, X. Vortical structures over rectangular cavities at low speed. Phys. Fluids 2005, 17, 015104. [Google Scholar] [CrossRef]
- Pandey, K.M.; Rathakrishnan, E. Annular Cavities for Base Flow Control. Int. J. Turbo Jet-Engines 2006, 23, 113–128. [Google Scholar] [CrossRef]
- Khan, S.A.; Mohammed, A.; GM, F.A. Passive control of base drag in compressible subsonic flow using multiple cavity. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 39–44. [Google Scholar]
- Khan, S.A.; Al Robaian, A.A.; Asadullah, M.; Khan, A.M. Grooved cavity as a passive controller behind backward facing step. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 53, 185–193. [Google Scholar]
- Vikramaditya, N.S.; Viji, M.; Verma, S.B.; Ali, N.; Thakur, D.N. Base Pressure Fluctuations on Typical Missile Configuration in Presence of Base Cavity. J. Spacecr. Rocket. 2018, 55, 335–345. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G.; Gaggini, G.; Salvetti, M.V. Separation control and drag reduction for boat-tailed axisymmetric bodies through contoured transverse grooves. J. Fluid Mech. 2017, 832, 514–549. [Google Scholar] [CrossRef]
- Howell, J.; Sims-Williams, D.; Sprot, A.; Hamlin, F.; Dominy, R. Bluff Body Drag Reduction with Ventilated Base Cavities. SAE Int. J. Passeng. Cars Mech. Syst. 2012, 5, 152–160. [Google Scholar] [CrossRef]
- Bonnavion, G.; Cadot, O.; Herbert, V.; Parpais, S.; Vigneron, R.; Delery, J. Effect of a base cavity on the wake modes of the squareback Ahmed body at various ground clearances and application to drag reduction. In Congrès Français de Mécanique; Association Française de Mécanique (AFM): Lille, France, 2017. [Google Scholar]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some Salient Features of the Time-Averaged Ground Vehicle Wake. SAE Tech. Paper Ser. 1984, 473–503. [Google Scholar] [CrossRef]
- Lucas, J.-M.; Cadot, O.; Herbert, V.; Parpais, S.; Délery, J. A numerical investigation of the asymmetric wake mode of a squareback Ahmed body—Effect of a base cavity. J. Fluid Mech. 2017, 831, 675–697. [Google Scholar] [CrossRef]
- Rathakrishnan, E. Effect of ribs on suddenly expanded flows. AIAA J. 2001, 39, 1402–1404. [Google Scholar] [CrossRef]
- Yedlapalli, S.; Vijayaraja, A.V.K.; Rathakrishnan, E. Base Pressure Control by using Ribs in Subsonic and Sonic Suddenly Expanded Flows. In Proceedings of the 2nd International Conference on Recent Advances in Experimental Fluid Mechanics, Andhra Pradesh, India, 3–6 March 2008. [Google Scholar]
- Nathan, K.R.; Vijayaraja, K.; Elangovan, S.; Rathakrishnan, E. Effect of Annular Rib Position in Suddenly Expanded Supersonic Flow. In Proceedings of the International Conference on Aerospace Science and Technology, Bangalore, India, 26–28 June 2008. [Google Scholar]
- Vijayaraja, K.; Senthilkumar, C.; Elangovan, S.; Rathakrishnan, E. Base Pressure Control with Annular Ribs. Int. J. Turbo Jet-Engines 2014, 31, 111–118. [Google Scholar] [CrossRef]
- Khan, A.; Mazlan, N.M.; Ismail, M.A. Analysis of Flow through a Convergent Nozzle at Sonic Mach Number for Area Ratio 4. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 62, 66–79. [Google Scholar]
- Khan, S.A.; Asadullah, M.; Sadhiq, J. Passive control of base drag employing dimple in subsonic suddenly expanded flow. Int. J. Mech. Mechatron. Eng. IJMME-IJENS 2018, 18, 69–74. [Google Scholar]
- Asadullah, M.; Khan, S.A.; Asrar, W.; Sulaeman, E. Passive control of base pressure with static cylinder at supersonic flow. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 370, p. 012050. [Google Scholar]
- Khan, S.A.; Ullah, M.A.; Ahmed, G.F.; Jalaluddin, A.; Baig, M.A.A. Flow control with aero-spike behind bluff body. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 1001–1008. [Google Scholar]
- Mehta, R. Drag reduction for payload fairing of satellite launch vehicle with aerospike in transonic and low supersonic speeds. Adv. Aircr. Spacecr. Sci. 2020, 7, 371–385. [Google Scholar]
- Khan, S.A.; Alrobaian, A.A.; Asad Ullah, M.; Rao, A. Threaded spikes for bluff body base flow control. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 53, 194–203. [Google Scholar]
- Hwang, J.-Y.; Yang, K.-S.; Sun, S.-H. Reduction of flow-induced forces on a circular cylinder using a detached splitter plate. Phys. Fluids 2003, 15, 2433–2436. [Google Scholar] [CrossRef]
- Soumya, S.; Prakash, K.A. Effect of splitter plate on fluid flow characteristics past a triangular cylinder. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 822, p. 012054. [Google Scholar]
- Jodai, Y.; Takahashi, Y.; Ichimiya, M.; Osaka, H. The Effects of Splitter Plates on Turbulent Boundary Layer on a Long Flat Plate Near the Trailing Edge. J. Fluids Eng. 2008, 130, 051103. [Google Scholar] [CrossRef]
- Bearman, P.W. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 1965, 21, 241. [Google Scholar] [CrossRef]
- Nash, J.; Callinan, J.; Quincey, V. Experiments on Two-Dimensional Base Flow at Subsonic and Transonic Speeds; ARC: London, UK, 1963; Volume 25070. [Google Scholar]
- Gilliéron, P.; Kourta, A. Aerodynamic drag reduction by vertical splitter plates. Exp. Fluids 2009, 48, 1–16. [Google Scholar] [CrossRef]
- Reedy, T.M.; Elliott, G.S.; Dutton, J.C.; Lee, Y. Passive Control of High-Speed Separated Flows Using Splitter Plates. AIAA J. 2012, 50, 1586–1595. [Google Scholar] [CrossRef]
- Falchi, M.; Provenzano, G.; Pietrogiacomi, D.; Romano, G.P. Experimental and numerical investigation of flow control on bluff bodies by passive ventilation. Exp. Fluids 2006, 41, 21–33. [Google Scholar] [CrossRef]
- Boswell, B.A.; Dutton, J.C. Flow visualizations and measurements of a three-dimensional supersonic separated flow. AIAA J. 2001, 39, 113–121. [Google Scholar] [CrossRef]
- Moore, F.G.; Wilcox, F.; Hymer, T. Improved Empirical Model for Base Drag Prediction on Missile Configurations Based on New Wind Tunnel Data; Naval Surface Warfare Center Dahlgren Div Va: Dahlgren, VA, USA, 1992. [Google Scholar]
- De La Cruz, J.M.G.; Oxlade, A.R.; Morrison, J. Passive control of base pressure on an axisymmetric blunt body using a perimetric slit. Phys. Rev. Fluids 2017, 2, 043905. [Google Scholar] [CrossRef]
- Bao, Y.; Tao, J. The passive control of wake flow behind a circular cylinder by parallel dual plates. J. Fluids Struct. 2013, 37, 201–219. [Google Scholar] [CrossRef]
- Loosen, S.; Statnikov, V.; Meinke, M.; Schröder, W. Modal analysis of passive flow control for the turbulent wake of a generic planar space launcher. CEAS Space J. 2017, 10, 189–202. [Google Scholar] [CrossRef]
- Park, H.; Lee, D.; Jeon, W.-P.; Hahn, S.; Kim, J.; Kim, J.; Choi, J.; Choi, H. Drag reduction in flow over a two-dimensional bluff body with a blunt trailing edge using a new passive device. J. Fluid Mech. 2006, 563, 389. [Google Scholar] [CrossRef]
- Bearman, P.W. The Effect of Base Bleed on the Flow behind a Two-Dimensional Model with a Blunt Trailing Edge. Aeronaut. Q. 1967, 18, 207–224. [Google Scholar] [CrossRef]
- Tripathi, A.; Manisankar, C.; Verma, S. Control of base pressure for a boat-tailed axisymmetric afterbody via base geometry modifications. Aerosp. Sci. Technol. 2015, 45, 284–293. [Google Scholar] [CrossRef]
- A Simple Passive Device for the Drag Reduction of an Ahmed Body. J. Appl. Fluid Mech. 2021, 14, 147–164. [CrossRef]
- Mariotti, A.; Buresti, G.; Salvetti, M.V. Separation delay through contoured transverse grooves on a 2D boat-tailed bluff body: Effects on drag reduction and wake flow features. Eur. J. Mech. B/Fluids 2019, 74, 351–362. [Google Scholar] [CrossRef]
- Capone, A.; Romano, G.P. Investigation on the effect of horizontal and vertical deflectors on the near-wake of a square-back car model. J. Wind. Eng. Ind. Aerodyn. 2019, 185, 57–64. [Google Scholar] [CrossRef]
- Pavia, G.; Passmore, M.; Varney, M. Low-frequency wake dynamics for a square-back vehicle with side trailing edge tapers. J. Wind. Eng. Ind. Aerodyn. 2019, 184, 417–435. [Google Scholar] [CrossRef]
- Altaf, A.; Omar, A.A.; Asrar, W. Review of passive drag reduction techniques for bluff road vehicles. IIUM Eng. J. 2014, 15, 15. [Google Scholar] [CrossRef]
- Choi, H.; Jeon, W.-P.; Kim, J. Control of Flow over a Bluff Body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Mukut, A.N.M.M.I.; Abedin, M.Z. Review on Aerodynamic Drag Reduction of Vehicles. Int. J. Eng. Mater. Manuf. 2019, 4, 1–14. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Y.; Zhu, H.; Xiao, H. Aerodynamic drag reduction and flow control of Ahmed body with flaps. Adv. Mech. Eng. 2017, 9, 1687814017711390. [Google Scholar] [CrossRef]
- Kim, D.; Lee, H.; Yi, W.; Choi, H. A bio-inspired device for drag reduction on a three-dimensional model vehicle. Bioinspiration Biomim. 2016, 11, 026004. [Google Scholar] [CrossRef] [PubMed]
- Altaf, A.; Omar, A.A.; Asrar, W. Passive drag reduction of square back road vehicles. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 30–43. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G.; Salvetti, M.V. Connection between base drag, separating boundary layer characteristics and wake mean recirculation length of an axisymmetric blunt-based body. J. Fluids Struct. 2015, 55, 191–203. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G. Experimental investigation on the influence of boundary layer thickness on the base pressure and near-wake flow features of an axisymmetric blunt-based body. Exp. Fluids 2013, 54, 1–16. [Google Scholar] [CrossRef]
- Beaudoin, J.-F.; Aider, J.-L. Drag and lift reduction of a 3D bluff body using flaps. Exp. Fluids 2008, 44, 491–501. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).