Investigation of the Time Resolution Set Up Used to Compute the Full Load Vortex Rope in a Francis Turbine

Abstract

The flow in a Francis turbine at full load is characterised by the development of an axial vortex rope in the draft tube. The vortex rope often promotes cavitation if the turbine is operated at a sufficiently low Thoma number. Furthermore, the vortex rope can evolve from a stable to an unstable behaviour. For CFD, such a flow is a challenge since it requires solving an unsteady cavitating flow including rotor/stator interfaces. Usually, the numerical investigations focus on the cavitation model or the turbulence model. In the present works, attention is paid to the strategy used for the time integration. The vortex rope considered is an unstable cavitating one that develops downstream the runner. The vortex rope shows a periodic behaviour characterized by the development of the vortex rope followed by a strong collapse leading to the shedding of bubbles from the runner area. Three unsteady RANS simulations are performed using the ANSYS CFX 17.2 software. The turbulence and cavitation models are, respectively, the SST and Zwart models. Regarding the time integration, a second order backward scheme is used excepted for the transport equation for the liquid volume fraction, for which a first order backward scheme is used. The simulations differ by the time step and the number of internal loops per time step. One simulation is carried out with a time step equal to one degree of revolution per time step and five internal loops. A second simulation used the same time step but 15 internal loops. The third simulations used three internal loops and an adaptive time step computed based on a maximum CFL lower than 2. The results show an influence of the time integration strategy on the cavitation volume time history both in the runner and in the draft tube with a risk of divergence of the solution if a standard set up is used.

1. Introduction

The rapidly growing share of new renewable energy sources in the past few decades leads to new challenges for the electrical network stability. Due to their rapid response time, hydraulic power plants are often used to compensate load fluctuations in the grid. However, the injection of the suitable amount of power requires the hydraulic machines to run outside of their Best Efficiency Point (BEP) for which they were designed. As a consequence, the flow leaving the runner possesses a significant residual swirl, leading to an inhomogeneous pressure distribution in the draft tube and eventually to the inception of cavitation.

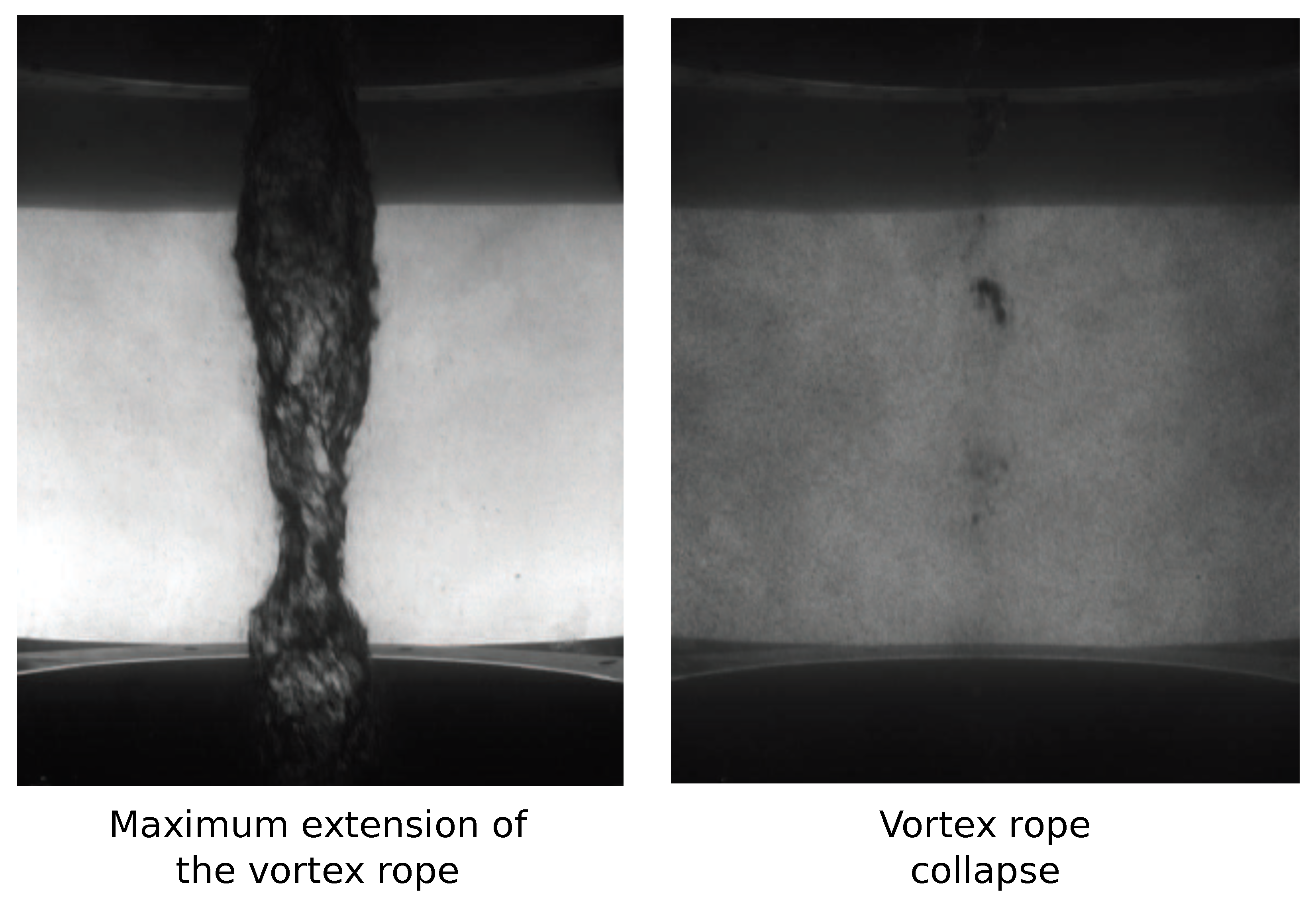
For Francis turbines, running at an operating point for which the flow rate is above the nominal one leads to the development of an axial vortex rope. If the pressure level inside in the vortex is sufficiently low, cavitation occurs. For a sufficiently high Thoma number, the amount of cavitation is still small and the cavitating vortex rope is stable, whereas, by decreasing further the Thoma number, the vortex rope enters in a self-oscillating mode [1].

On one hand, various studies have been performed to better understand the self-oscillating behaviour of the cavitating vortex rope based on mathematical approaches [2] or 1D analyses [3], experimental investigations [4], 3D CFD [5] and coupling between 1D–3D numerical simulations [6,7]. On the other hand, several investigations look at identifying some key parameters (mainly the mass flow gain factor) useful for the calibration and the development of 1D hydro-acoustic models [8,9] using either experimental measurements [10,11] or CFD simulations [12,13,14].

Among the 3D CFD studies, the set up for the time integration is not often discussed since it is rare that the mean and the maximum Courant–Friedrichs–Lewy (CFL) numbers or the number of internal loops per time step are provided. However, due to the large range of values that can be taken by the speed of sound in a vapour/liquid mixture and the large time density gradient that can occur in a cell, the time integration requires attention. Usually, in order to improve the accuracy of a simulation at each time step, two ways are available: decreasing the time step or increasing the number of internal loops per time step (if such an option is available). The latter choice can provoke some instabilities [15,16]. In addition, by considering the Ansys CFX software, which is a coupled solver, the equation for the volume fraction is treated in a segregated manner and, in case of the simulation of a rotating turbomachinery, only a first order time scheme is available.

Based on these considerations, this paper investigates the influence of the time resolution set up used to compute an unstable cavitating vortex rope at full load using the Ansys CFX software. The sensitivity to the time integration set up is often disregarded due the large CPU effort required and authors focus rather on grid sensitivity. In addition, sensitivity analysis is often carried out at BEP. In the present paper, the authors focus on an unstable operating point of a Francis turbine at full load, for which a standard set up that allows for accurately capturing the stable cavitating vortex rope [17] is shown to not be able to capture the unstable one. The sensitivity of the time integration set up is performed either by increasing the number of internal loops per time step or by imposing a limit on the time step by limiting the maximum CFL number. The three simulation results are described and some points are discussed by comparisons with experimental data.

2. Test Case

The test case is a 1:16 reduced scale physical model of a Francis turbine with 16 runner blades and 20 guide vanes. The real prototype machine, featuring a rated power of over 444 MW at a specific speed of $\nu =0.27$ (dimensionless parameters are defined in Equation (1)), experiences severe pressure surges at high load conditions. The load corresponds to 130% of the value at the BEP, i.e., the discharge factor is equal to $Q_{{}_{\mathrm{ED}}}=0.26$ instead of 0.20 at the BEP. The speed factor is equal to the rated value of $n_{{}_{\mathrm{ED}}}=0.288$. The specific speed of the model runner at these conditions is ${\nu }_{\mathrm{m}}=0.31$. For a Thoma number $\sigma =0.11$, the film displays an unstable cavitating vortex rope (see Figure 1) characterised by a self-excited breathing motion, i.e., a periodic collapse and reformation of the cavity accompanied by large amplitude pressure fluctuations throughout the system. Additional details regarding the experimental set up and the analysis of the measurements are available in [1,4].

The cited dimensionless parameters are defined as follows:

$$\begin{array}{cccccccccc}\hfill \nu =& \frac{\omega }{2^{3/4}{\pi }^{1/2}}\frac{Q^{1/2}}{E^{3/4}};\hfill & \hfill Q_{ED}& =\frac{Q}{D^2{E}^{1/2}};\hfill & \hfill n_{ED}& =\frac{nD}{E^{1/2}};\hfill & \hfill T_{ED}& =\frac{T_m}{\rho D^{3}E};\hfill & \hfill \sigma =\frac{NPSE}{E}& \hfill \end{array}$$

(1)

with $\omega$ the rotational speed in rad/s, Q the flow rate in m³/s, E the total energy in J/kg equal to 262.83, D the outlet runner diameter in m equal to 0.35 m, n the runner frequency in s⁻¹ equal to 13.33, and $NPSE$ the Net Positive Suction Energy.

3. Numerical Settings

The flow is modelled based on the homogeneous Unsteady Reynolds-Averaged Navier–Stokes (U-RANS) equations assuming thermodynamic and mechanical equilibrium [18]. Discarding the energy equation, only the mass and momentum conservation equations are solved. The Reynolds stresses are modelled using the Boussinesq’s assumption that introduces a turbulent viscosity ${\mu }_t$ computed with the SST turbulence model [19]. At the wall, the turbulence model is coupled with an automatic wall function. The phase change due to cavitation is modelled using the model proposed by Zwart with the standard values for the parameters [20]. Additional details regarding the flow modelling are available in [17]. Other simulations have also been performed by Wack [21].

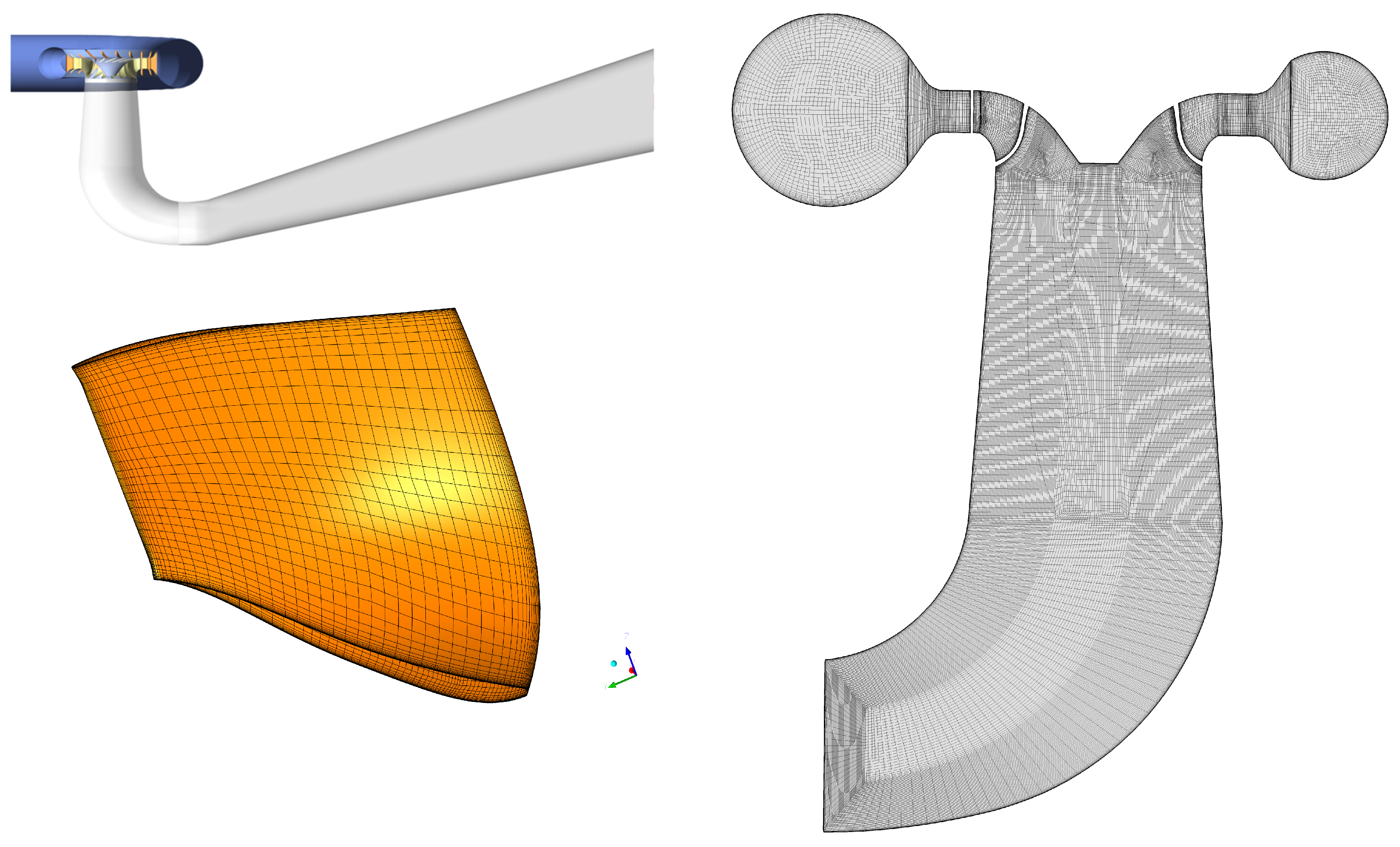
The computational domain considered includes a part of the inlet pipe, the spiral case, the stay vanes, the guide vanes, the runner and the draft tube (see Figure 2). The mesh is a structured hexahedral one based on a blocking technique and made with ICEM CFD (see Figure 2). The number of nodes is slightly above 11.5 million with 2.6 million of nodes in the runner domain and 4.3 million in the draft tube. The minimum angle is above 20 degrees and only 9% of the cells have an angle below 50 degrees. The $y^{+}$ value does not exceed 85 and the averaged value over each solid walls is lower than 20. A study of the grid sensitivity has been done and published in [17], showing around 2% of differences at the BEP between the computed $T_{ED}$, $Q_{ED}$ and $n_{ED}$.

The flow rate is imposed at the inlet, whereas the pressure is set at the outlet. The rotational speed of the runner is imposed on the experimental value. For all the solid walls, a no slip condition is imposed.

The convective fluxes in the momentum equation are computed with a high order scheme [22], whereas the turbulence convective fluxes are computed with an upwind scheme. Regarding the time scheme, the second order backward Euler scheme is applied [23] excepted for the volume fraction equation that is discretized with a first order backward Euler scheme (In Ansys CFX 17.2, for rotating turbomachineries, this option is the only one available.). The time step, the CFL number, the number of internal loops per time step and the time duration of the simulation expressed as the number of runner revolutions achieved are given in

Table 1. Parameters set for the time integration. Bold terms refer to the imposed values by the user.

Simulation	Time Step	CFL	Internal Loop	Number of Revolution	CPU Effort
	(deg/$\mathbf{\Delta }\mathit{t}$)	(-)	(-)	(-)	(Hours)
Case 1	0.96	80	5	2.3	3${}^{\prime }$897
Case 2	0.96	80	15	13.3	76${}^{\prime }$861
Case 3	adaptive	≤2	3	3.15	137${}^{\prime }$444

for each case considered. Case 1 corresponds to the standard set up in Ansys CFX for a flow in a Francis turbine with a time step set to less than one degree of revolution per time step and five internal loops per time step. This set up has been validated against experimental data for stable cavitating vortex rope in [17]. Case 2 differs from Case 1 only by the number of internal loops, which is set to 15. Case 3 differs from the other two cases since the time step is not imposed by the user but is computed automatically by imposing a limitation on the CFL number to a value of 2. This value is sufficiently small to deal with the accuracy of the first order backward Euler scheme used for the volume fraction equation keeping advantage of an implicit formulation. In addition, the number of internal loops is decreased to a value of 3 even if two internal loops are enough to reach a second order time accuracy (see [24]) for the equations discretized with a second order scheme. The unsteady simulations are started from a converged steady simulation (see [17]).

Even if CFX used a coupled solver, the volume fraction equation is treated in a segregated manner. The interfaces between the stationary and rotating domains are handled using a General Grid Interface (GGI) algorithm.

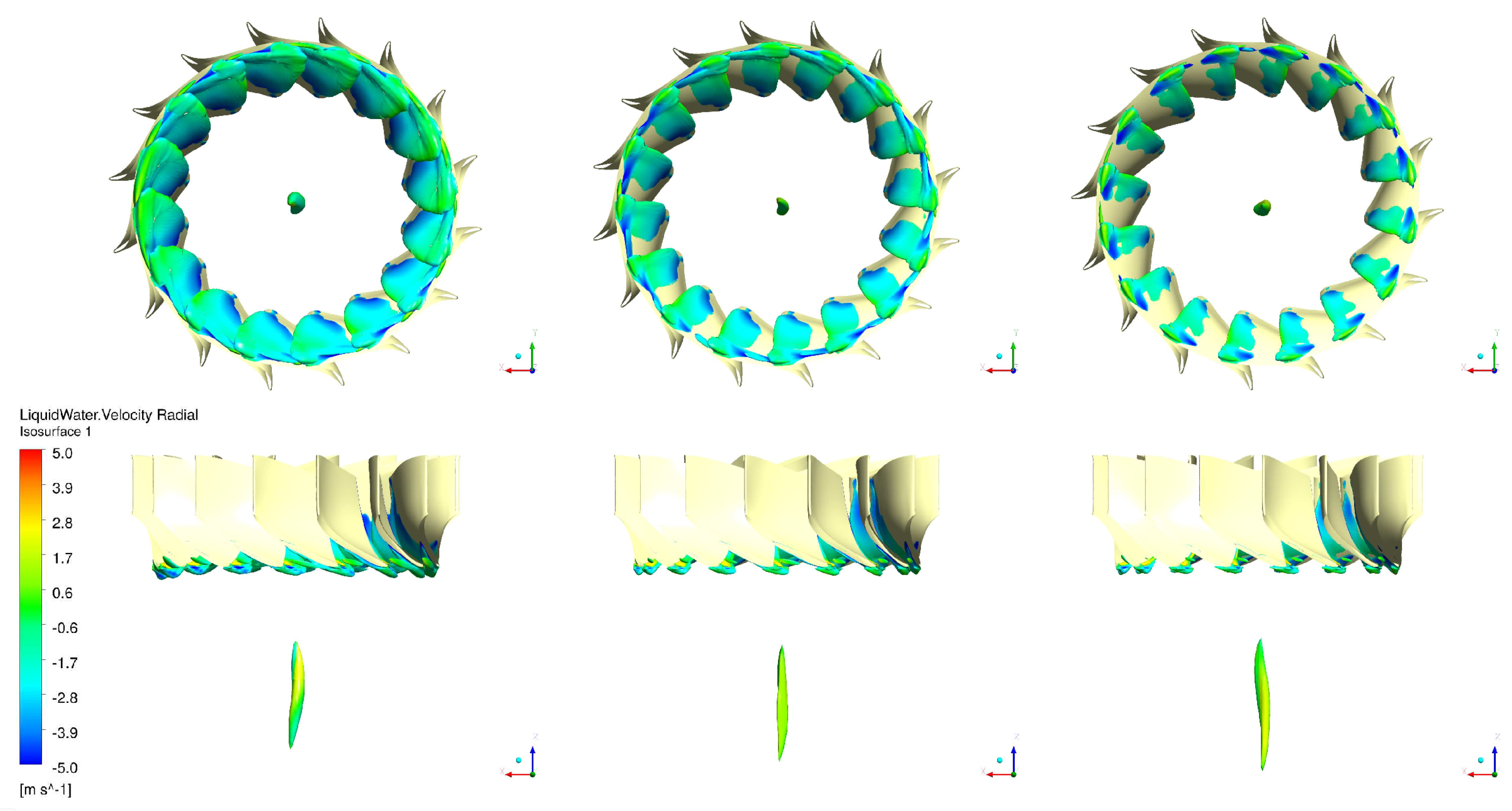
4. Results

First of all, it has to be mentioned that the simulation Case 1 diverges when the vortex rope in the draft tube collapses (see the next section for a detailed discussion). However, until this point, all the simulations show the development of a cavitating vortex rope and a cavitation sheet over the trailing edge of the suction side (see Figure 3). Such features are supported by experimental visualisation [4]. Compared to the experiment (Figure 1), the volume of vapour inside the vortex rope is underestimated.

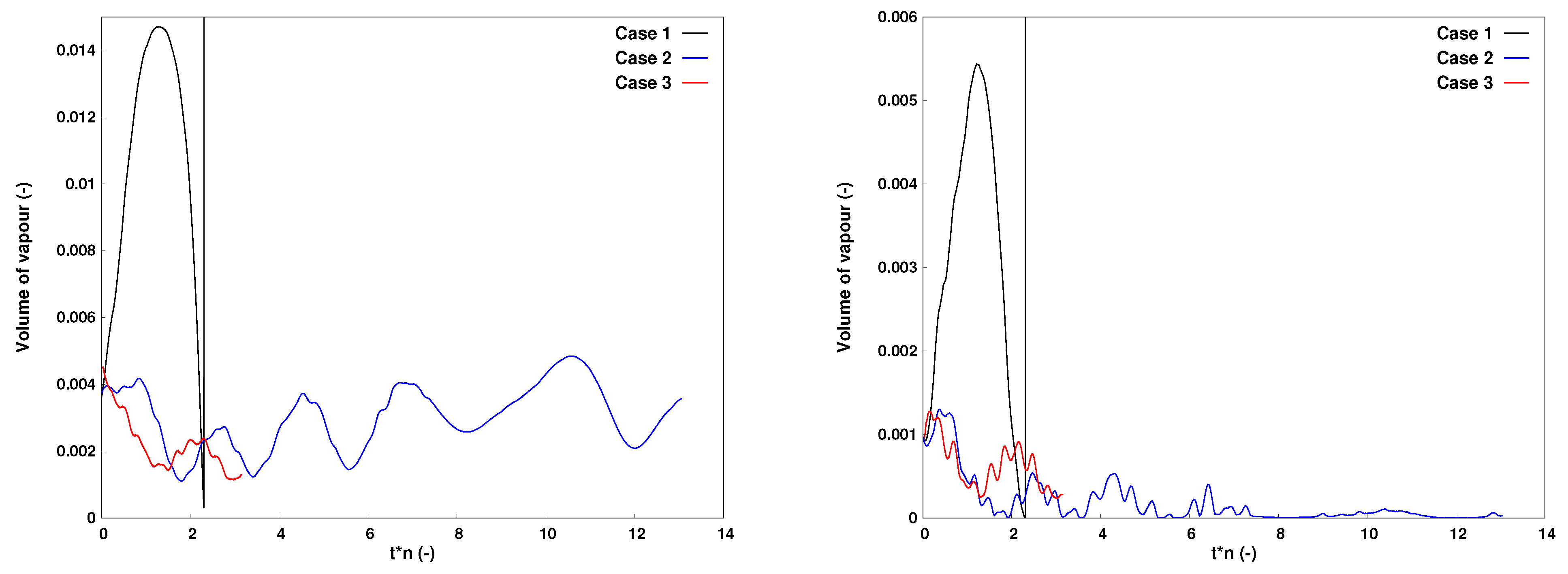
4.1. Integrated Variables

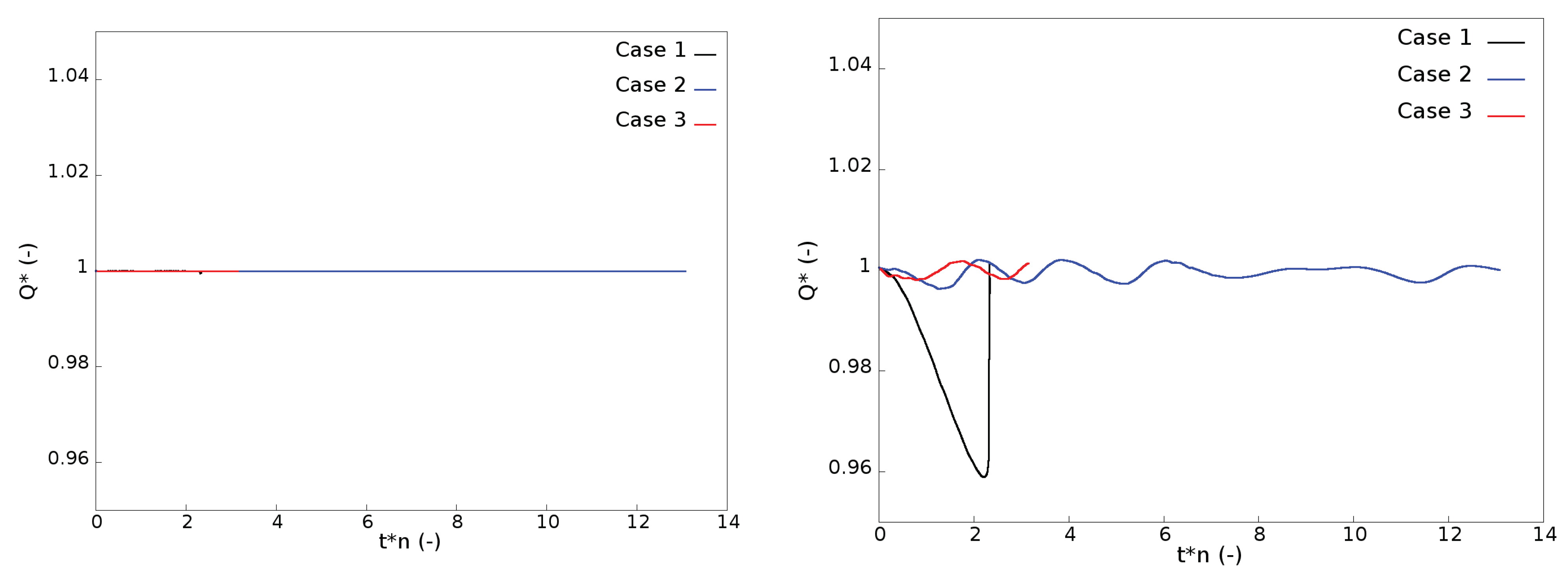
The time-history of the efficiency, the dimensionless volume of vapour in the computational domain, the torque factor $T_{ED}$ and the speed factor $n_{ED}$ are plotted on Figure 4 (the experimental values for the $T_{ED}$ and $n_{ED}$ are added in the caption of the figure). The divergence of the simulation Case 1 just after the collapse of the cavitation volume is clearly put in evidence. On the contrary, simulations Case 2 and Case 3 do not show a complete collapse of the cavitation volume even if a time oscillation of the different quantities is observed. The first cycle seems to be shortened by increasing the requirement on the time integration since it is shorter for Case 2 compared to Case 1 and the shortest for Case 3.

Regarding the efficiency, the torque factor and the speed factor, the differences between the simulations are around 1.5%, whereas, for the volume of vapour, simulation Case 1 predicts a volume that is at least four times higher. Compared to the measurements, the $T_{ED}$ and $n_{ED}$ are overestimated respectively by approximately 2.5% and 3.5%. Simulations Case 2 and Case 3 have a rather similar behaviour even if a time shift is observed due to a faster first cycle for Case 3. Furthermore, due to the smaller time step imposed in Case 3, fluctuations at higher frequencies are observed in all the signals.

For simulation Case 2 between the seventh and eleventh runner revolution, the slow variation of the efficiency, the torque factor, and the speed factors disappear, whereas a fluctuation at a low frequency is still observed for the volume of vapour. By splitting the time history of the volume of vapour between the volume in the runner and draft tube domains (see Figure 5), it is noticeable that between the seventh and eleventh runner revolution, the volume of vapour in the draft tube is close to zero and then increases again after the tenth runner revolution. Therefore, the low frequency seems to be related to the volume of vapour in the draft tube, which means with the presence of a cavitating vortex rope. This point seems to be in agreement with the experimental investigations [1].

A Fourier analysis of the efficiency signal is shown in Figure 6 on the left. The frequency is divided by the runner frequency $f_n$. The modes put in evidence are the ones associated with the blade passage frequency $f_b=16f_n$ and the first and fifth harmonic. Both Case 2 and Case 3 capture the fifth harmonic, which corresponds to the rotor/stator interaction since $5f_b=4f_{gv}=80f_n$. A Fourier analysis of the volume of vapour has also been carried out even if only the simulation Case 2 has achieved enough cycles to provide an estimation of the low frequency characteristic of the time evolution of the volume of vapour. By focusing only on Case 2, a low frequency around $0.3f_n$ is put in evidence, which is closed to $0.25f_n$, the value observed on the torque during the measurements [1].

4.2. Local Pressure

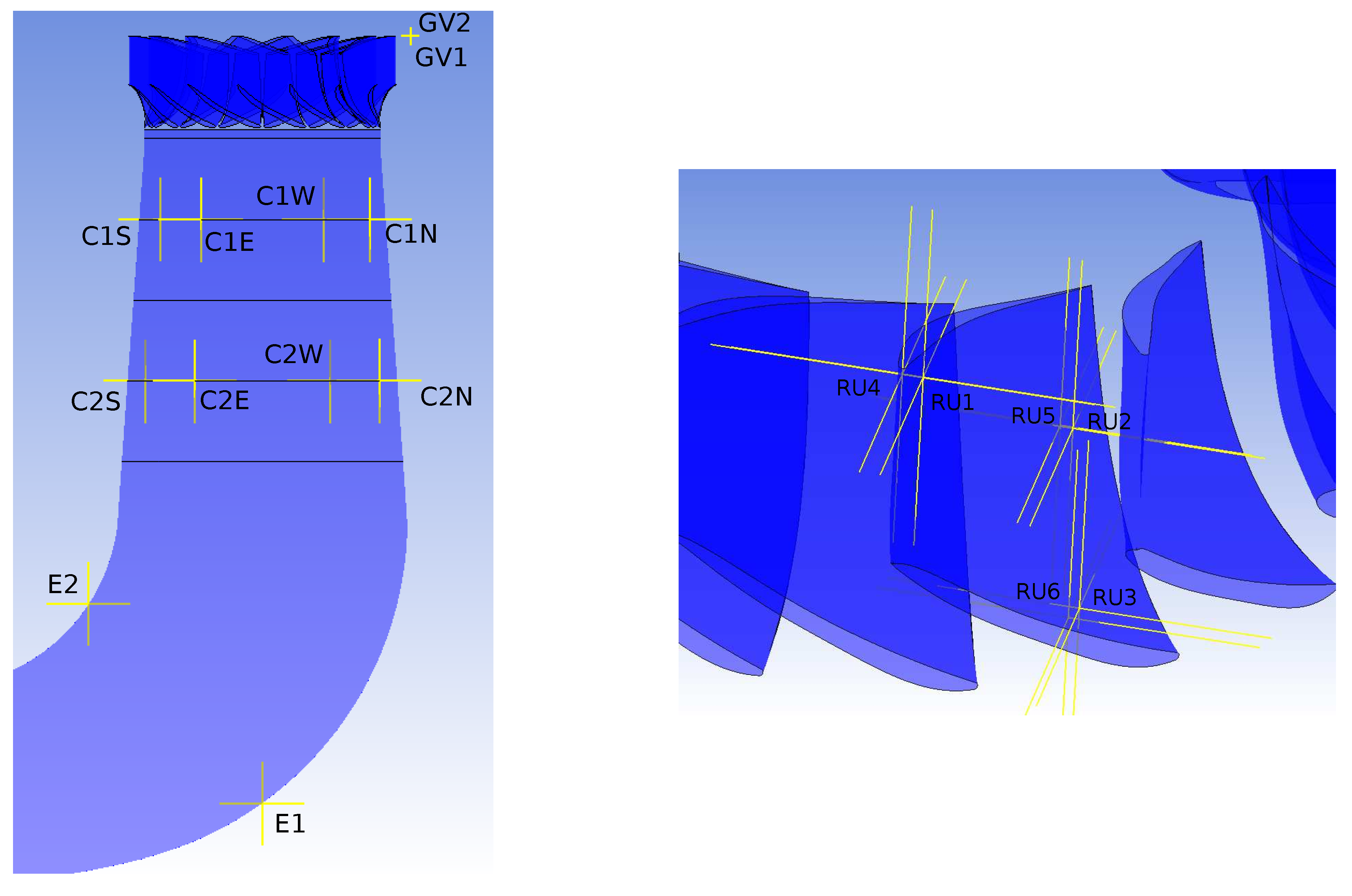
Several pressure probes have been set in the computational domain as shown in Figure 7. Two probes are located in two different guide vane channels, six are located on a runner blade with three on the pressure side and three others on the suction side, two times four probes are distributed at ninety degrees on the wall in two sections of the draft tube cone (as in the experiment) and finally two probes are set in the draft tube elbow.

For each probe, the fluctuations of the pressure coefficient are computed by subtracting the average pressure at the probe location and then by dividing the result by $0.5\rho U_{\overline{1}}^2$ (with $U_{\overline{1}}$ the peripheral velocity at the runner outlet). In addition, for the probes in the cone of the draft tube, a spatial averaging is also performed.

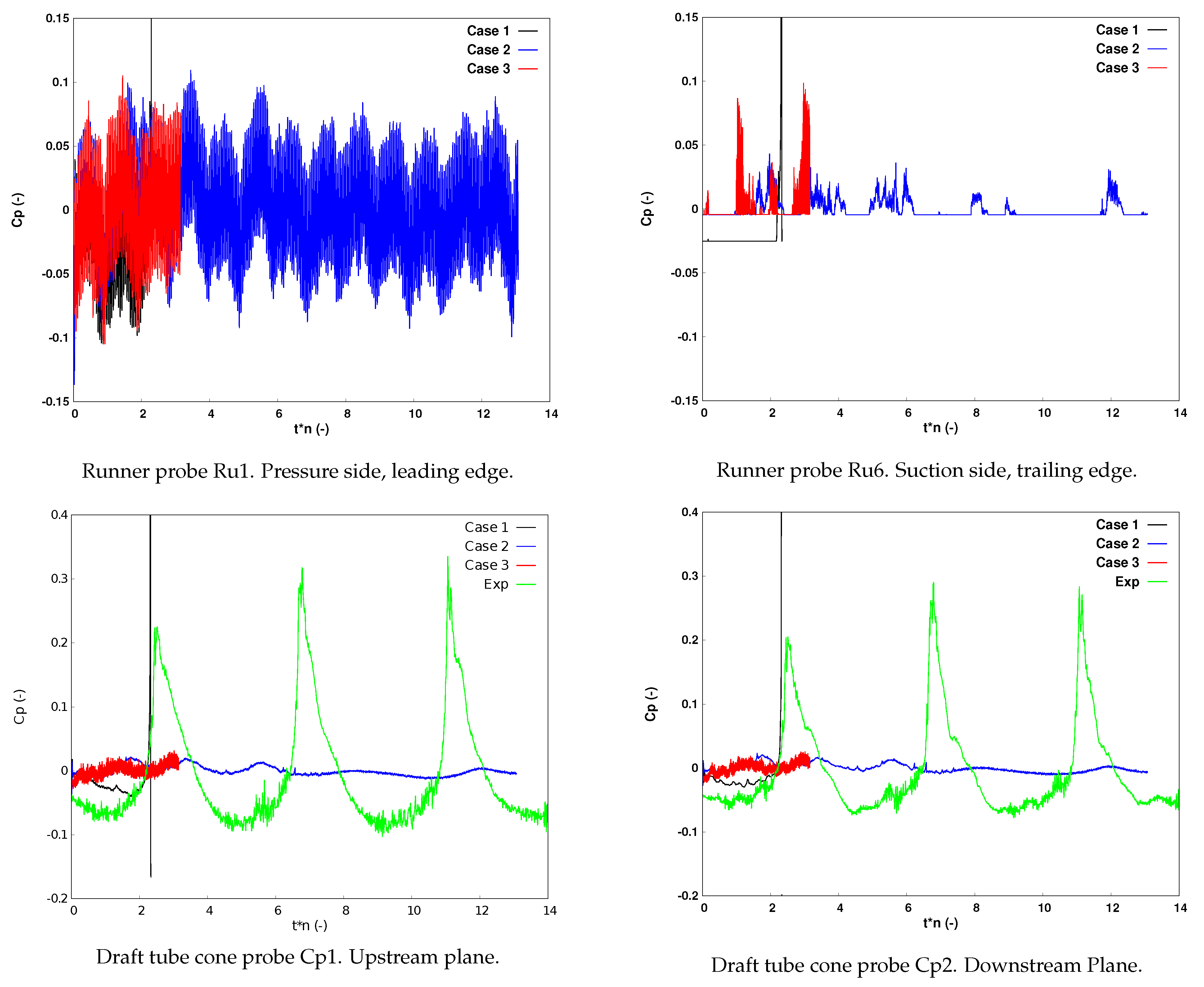
The pressure signals on the pressure side of the runner at the leading edge (probe Ru1) and on the suction side of the trailing edge (probe Ru6) and in the two sections of the draft tube cone are displayed in Figure 8. In the draft tube cone, the experimental pressure signals are also added.

At the leading edge of the runner, the pressure fluctuations captured by the three simulations are identical with a high frequency content. At the trailing edge, the fluctuations at high frequency alternate with a flat period corresponding to the period during which the probe is covered by a pure vapour sheet. No clear pattern can be observed. In the draft tube cone, compared to the experiment, the simulations Case 2 and Case 3 are smoother without a strong peak of pressure after the partial collapse of the vortex rope. Simulation Case 1 presents a strong pressure peak at the collapse of the vortex rope, which seems to follow qualitatively the trends of the experimental one. However, as already mentioned, the simulation diverges after the collapse.

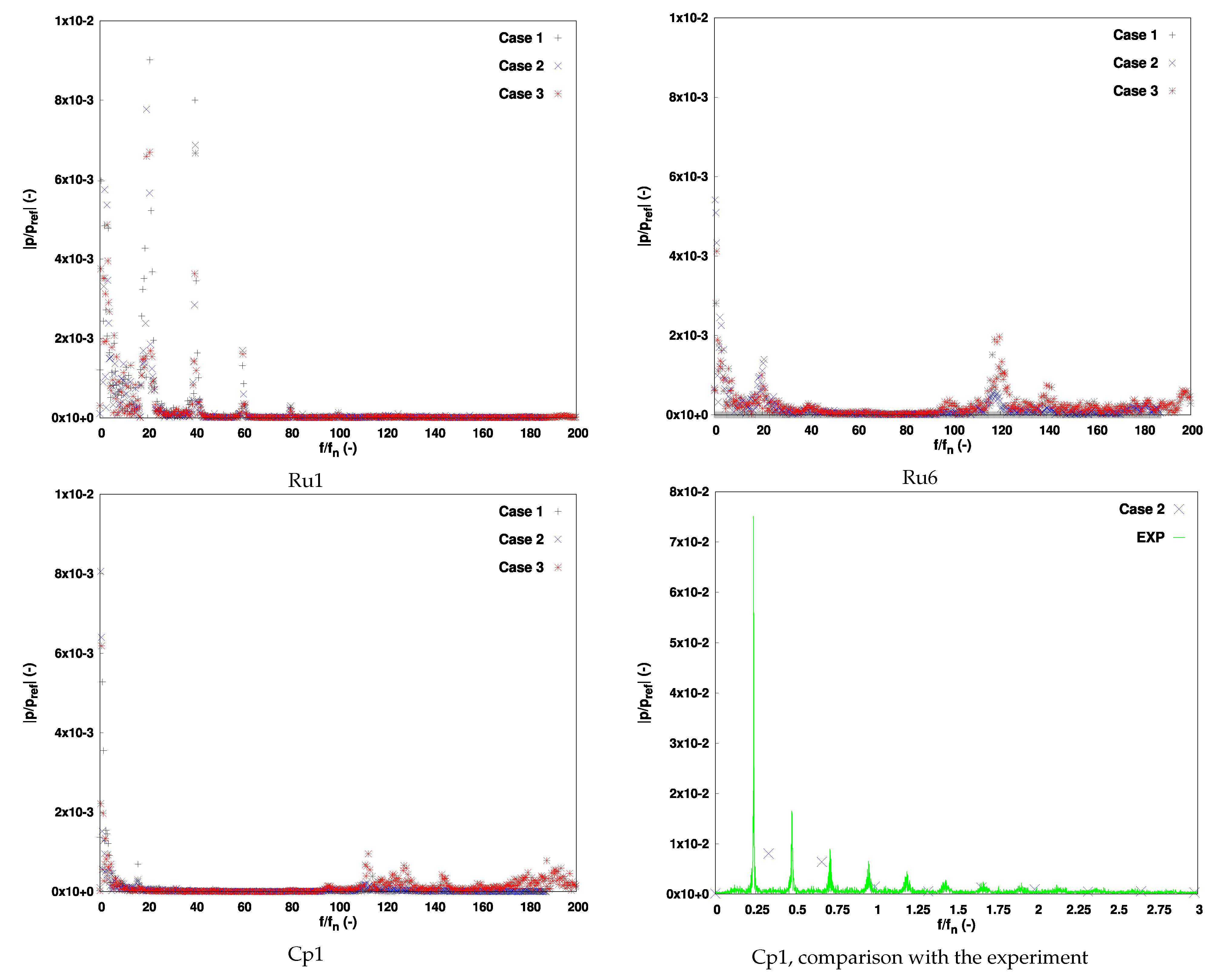
The Fourier transforms of the pressure signals in the runner and the draft tube are represented in Figure 9. At the leading edge of the runner, the guide vane passage frequency $f_{gv}=20f_n$ and its harmonic until the fourth are clearly observed. At the trailing edge, only the fundamental is observed. In addition, a frequency around $120f_n$ is captured by the simulations Case 2 and Case 3. This frequency is also observed in the cone of the draft tube but with an attenuation. The origin of this frequency is not clear.

In the draft tube, the comparison of the simulation Case 2 with the experiment makes the presence of the low frequency appear around $0.3f_n$ in the simulation instead of $0.25f_n$ in the experiment. Obviously, the amplitude is low compared to the experiment due to the inability of the simulation to capture accurately the collapse of the vortex rope as shown in Figure 8.

5. Discussion

The results described in the previous section make a question appear—why the simulation Case 1 seems to follow more closely the behaviour of the vortex rope observed experimentally than the simulations Case 2 and Case 3, which use a refined time integration set up.

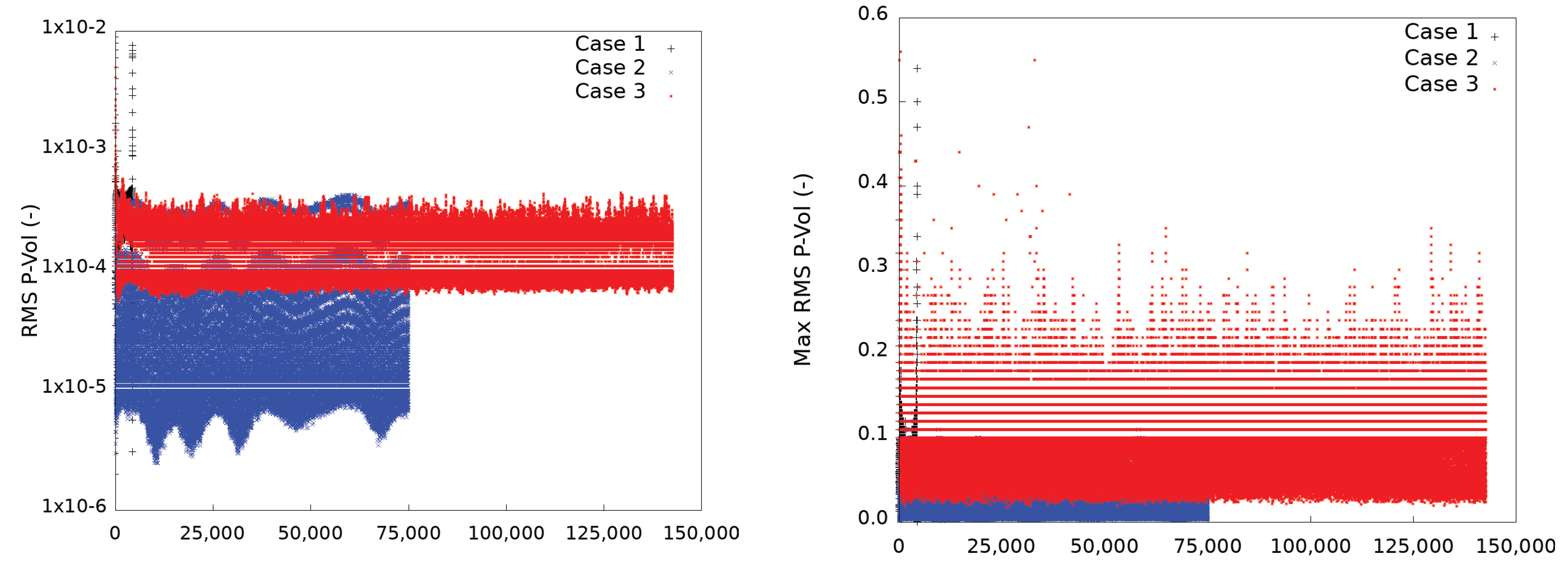
The Root Mean Square (RMS) and the maximum RMS of the pressure equation are compared in Figure 10. The RMS reach values lower than ${10}^{-3}$ for all the simulations except simulation Case 1 before the simulation crashes. For Case 2, the residuals reach values below ${10}^{-5}$, which shows the role plays by the number of internal loops per time step. The maximum RMS are quite high for all simulations with some values above 0.1. Interestingly, the maximum RMS of Case 1 and Case 3 are around 0.4, but Case 3 does not crash.

The time history of the dimensionless mass flow $Q^{*}=Q/Q_{inlet}$ at the inlet of the runner and at the outlet of the computational domain are compared for the three simulations in Figure 11. In the runner inlet section, upstream from the region where cavitation occurred, the mass flow is constant and equal to 1. Downstream, due to the phase change, the mass flow oscillates. The oscillation is stronger for Case 1 with a strong decrease of the mass flow, which is a consequence of the vapour volume growth (see Figure 5).

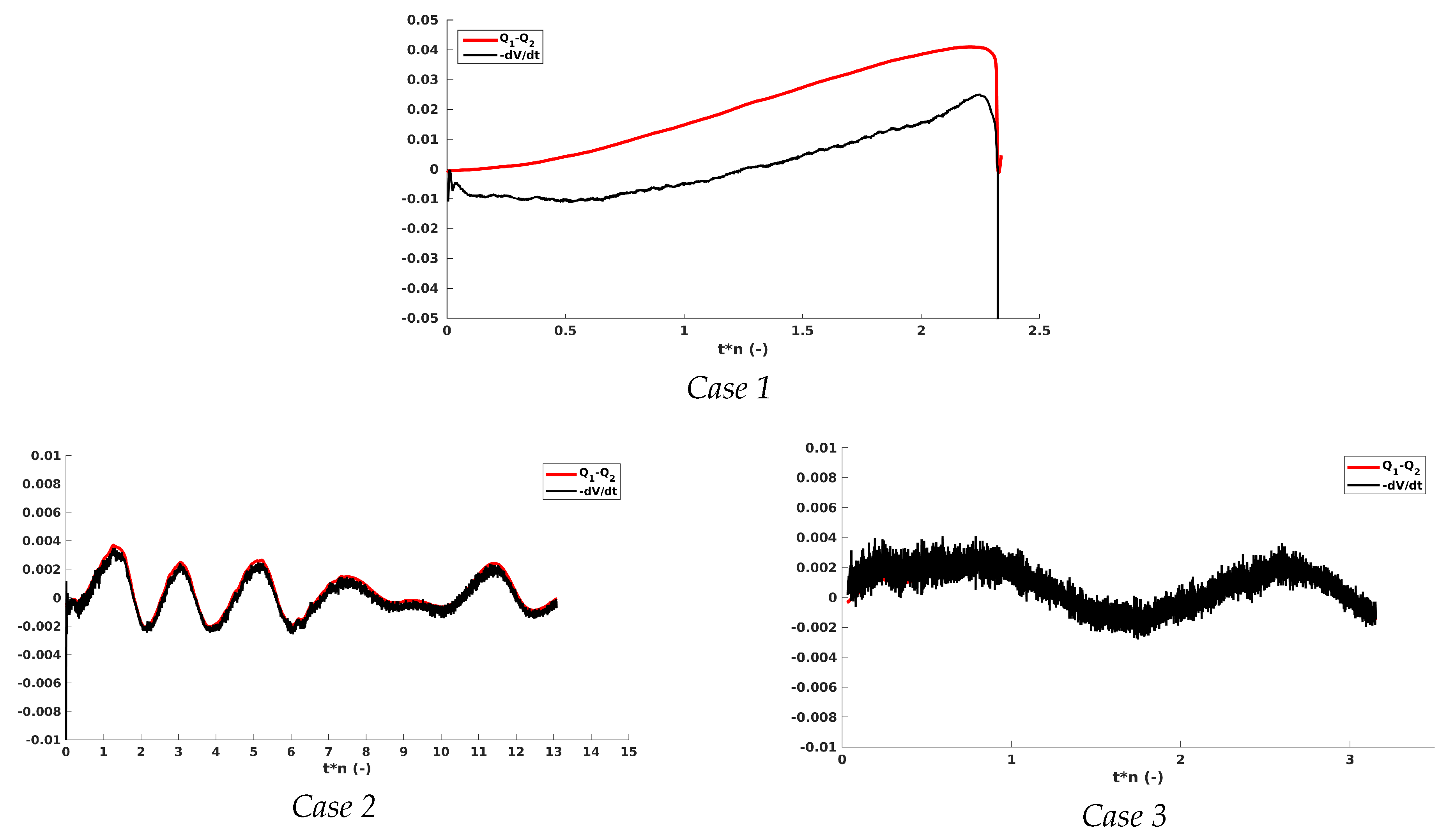
By assuming a density of the vapour negligible compared to the liquid density, the 1D mass conservation equation applied for the whole computational domain writes:

$$Q_1-Q_2=-\frac{dV}{dt}$$

(2)

with $Q_1$ and $Q_2$, respectively, the mass flow rate at the inlet and outlet of the computational domain and V the volume of vapour. The left- and right-hand terms of Equation (2) are plotted in Figure 12 for the three cases. For Case 2 and 3, the mass conservation is respected contrary to Case 1 for which the time variation of the volume of vapour is smaller than the difference of the flow rate. This mass unbalanced seems to be responsible for the collapse of the vortex rope and the crash of the simulation. As the boundary condition are fixed, the mass flow rate unbalanced cannot be supported infinitely since it is a non-equilibrium state. Therefore, the collapse of the vortex is the only way to return to an equilibrium state.

6. Conclusions

The influence of the time resolution set up on the simulation of an unstable cavitating rope has been performed using the Ansys CFX software. A standard set up Case 1 usually used for the URANS computation of a Francis turbine is not able to capture the flow due to the crash of the simulation after the first collapse of the cavitating vortex rope. By increasing the number of internal loops from 5 to 15, the simulation Case 2 is able to capture several cycles of the vortex rope with a dampened amplitude compared to the experiment but with a frequency close to the measured one. It has also been noticed that the low frequency observed on the torque or the efficiency seems to be related to the presence of a cavitating vortex rope in the draft tube since, in its absence, the low frequency disappears. The simulation Case 3 carried out with an imposed maximum CFL number lower than 2, i.e., with a smaller time step, and only three internal loops does not provide a dynamic behaviour very different than Case 2 even if a longer simulation could show differences.

Surprisingly, the simulation Case 1 is the only one that gives a duration and an amplitude of the pressure peak in agreement with the experiment. Nevertheless, the simulation stops when the vortex rope collapse due to a solver crashes and no successive cycles are computed. On the contrary, the simulations Case 2 and Case 3 do not show any growth or collapse of the cavitating vortex rope. This difference is explained by the fact that the simulation Case 1 does not respect the mass conservation equation at each time step contrary to the two other simulations.

To compute an unstable vortex rope, it is therefore necessary to take care of the time integration set up by increasing at least the number of internal loops. To improve the accuracy of the simulation, the U-RANS simulation needs, in addition, to be coupled with a 1D hydroacoustic model allowing for adjusting the boundary conditions at the inlet and outlet boundaries of the computational domain [6,7].