Alternative Design of Binary Phase Diffractive Optical Element with Non-π Phase Difference
Abstract
Featured Application
Abstract
1. Introduction
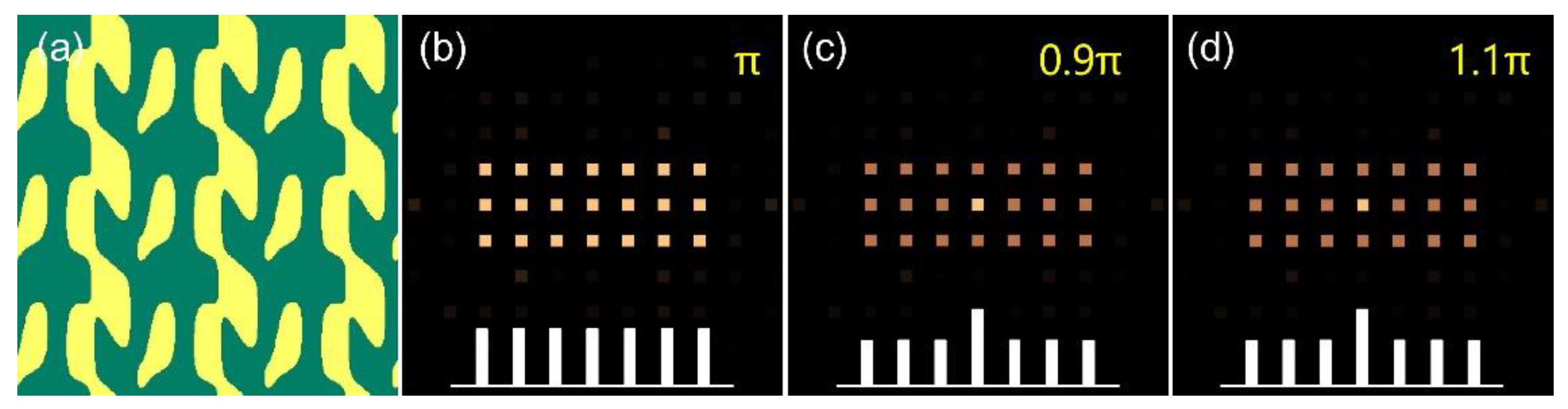
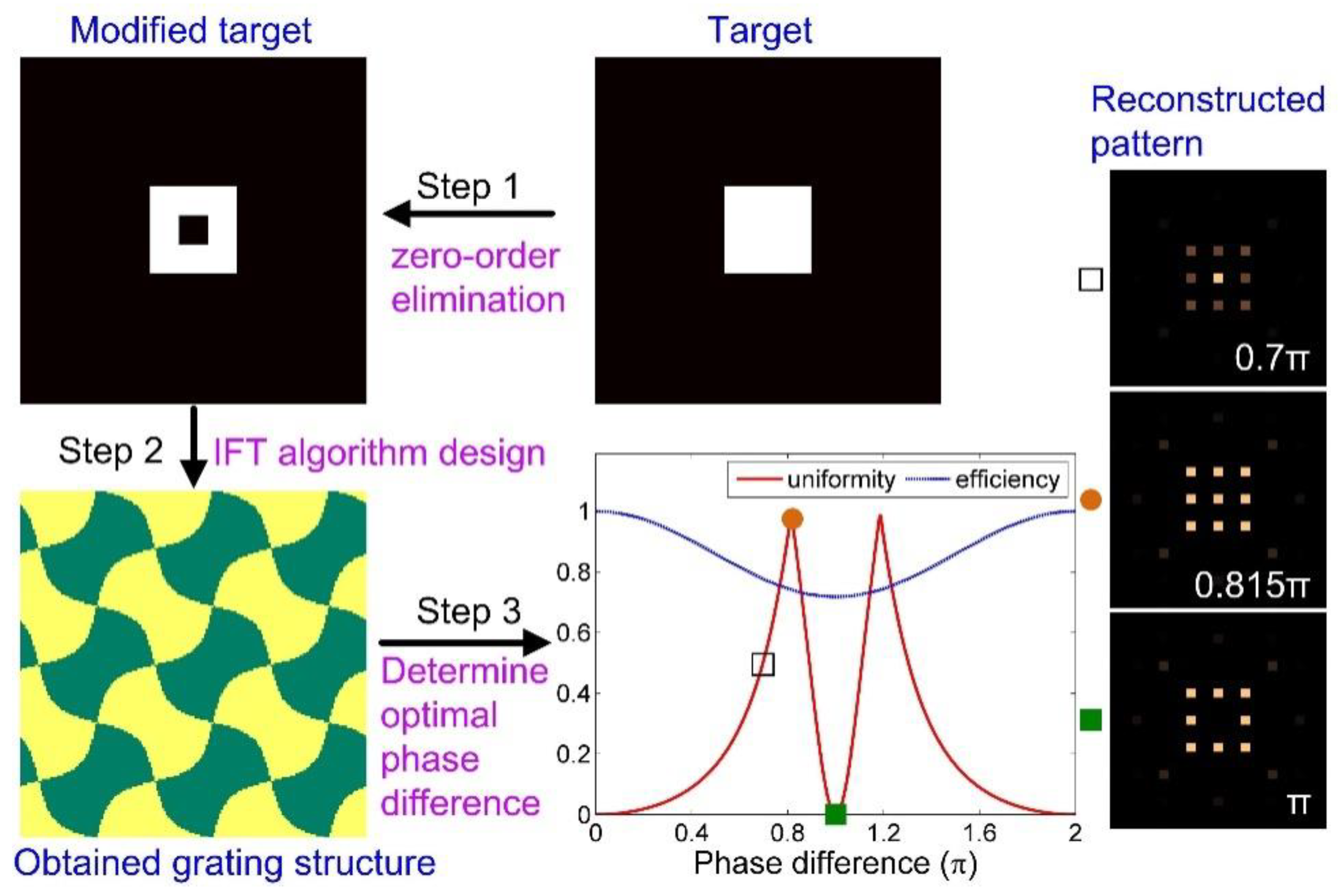
2. Method
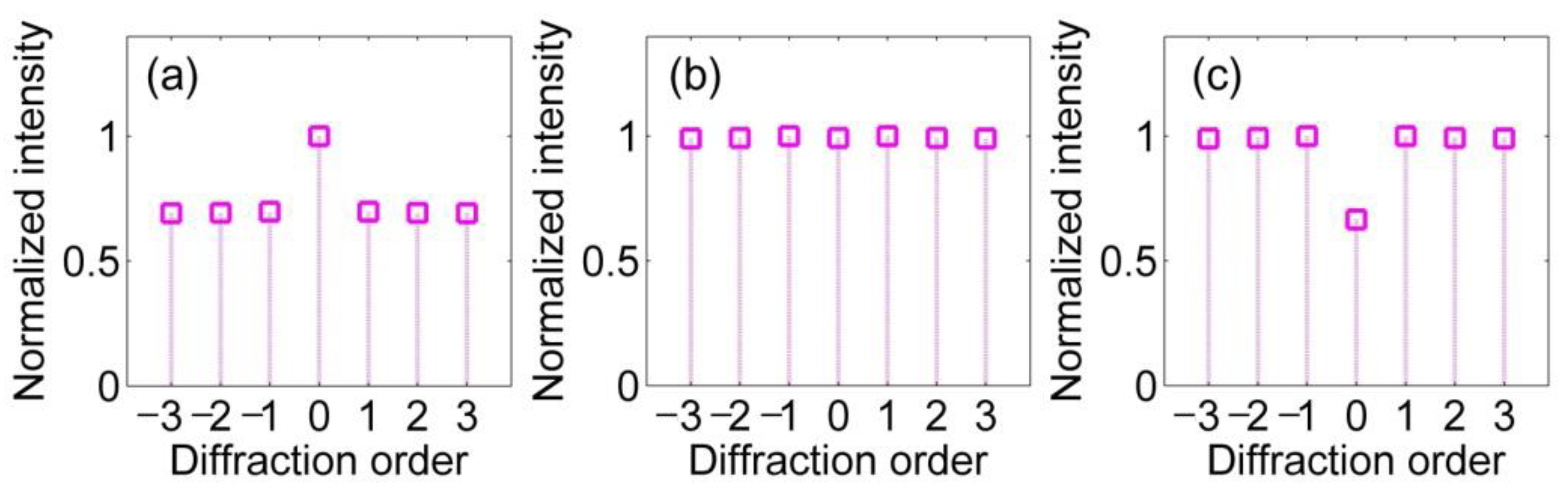
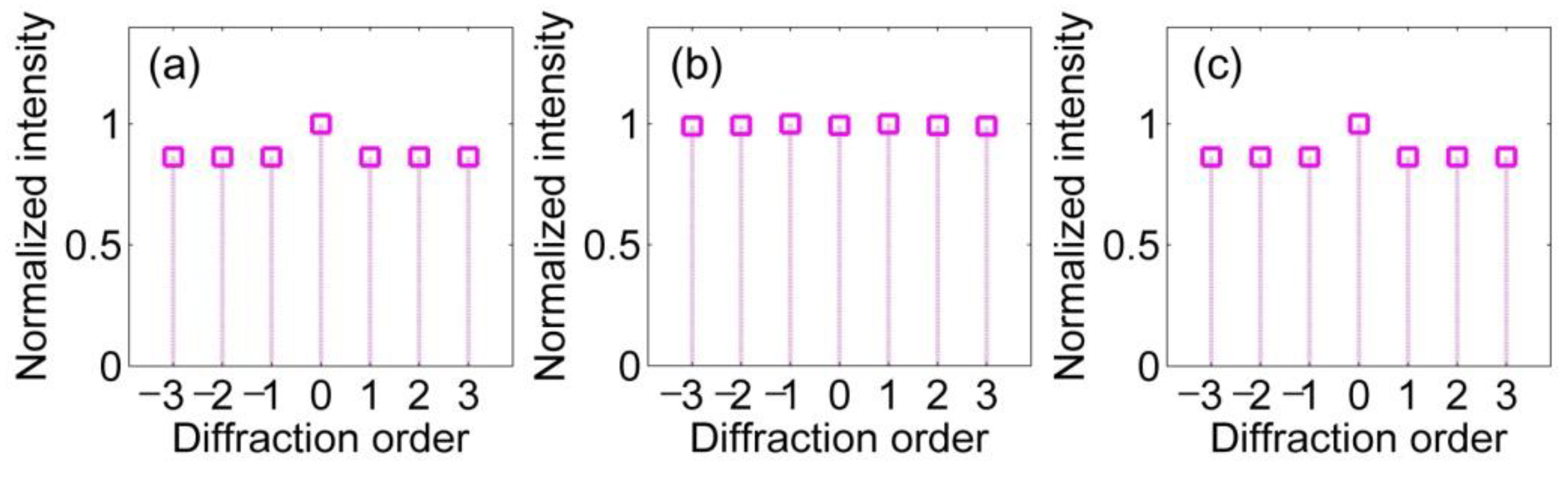
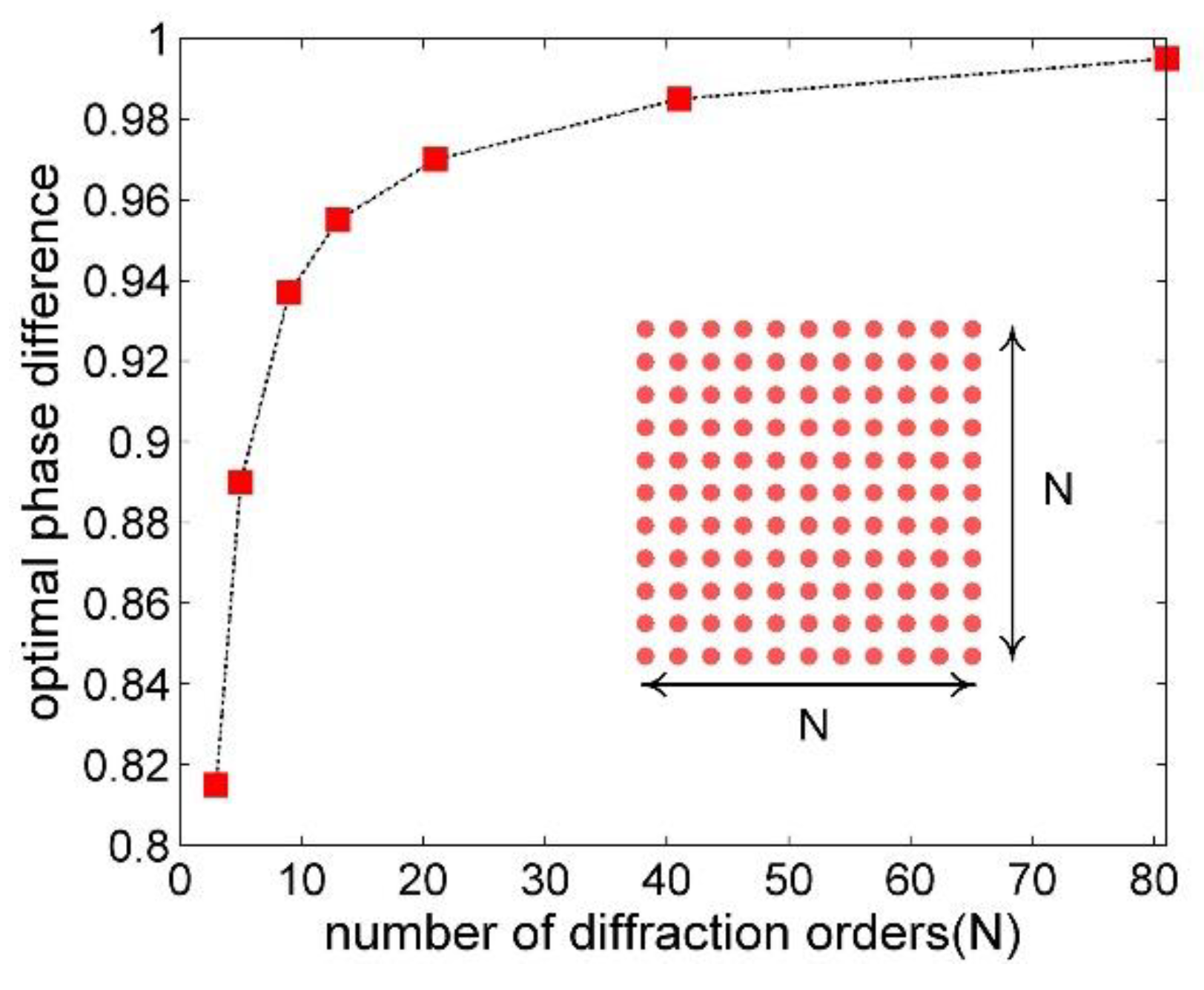
3. Simulation
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fernandez, J.M.H.; Brea, L.M.S.; Bernabeu, E. Near-field shaping with two binary diffractive optical elements in tandem. Opt. Commun. 2013, 297, 182–189. [Google Scholar] [CrossRef]
- Pang, H.; Liu, W.; Cao, A.; Deng, Q. Speckle-reduced holographic beam shaping with modified Gerchberg-Saxton algorithm. Opt. Commun. 2019, 433, 44–51. [Google Scholar] [CrossRef]
- Vasu, D.; Andra, R.; Vishwa, P. Generation of uniform-intensity light beams with controllable spatial shapes. Opt. Commun. 2020, 475, 126226. [Google Scholar]
- Mait, J.N. Design of binary-phase and multiphase Fourier gratings for array generation. J. Opt. Soc. Am. A 1990, 7, 1514–1528. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, L. Numerical study of Dammann array illuminators. Appl. Opt. 1995, 34, 5961–5969. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Keesling, A.; Omran, A.; Levine, H.; Bernien, H.; Greiner, M.; Lukin, M.; Englund, D. Large-scale uniform optical focus array generation with a phase spatial light modulator. Opt. Lett. 2019, 44, 3178–3181. [Google Scholar] [CrossRef] [PubMed]
- Barlev, O.; Golub, M.A. Multifunctional binary diffractive optical elements for structured light projectors. Opt. Express 2018, 26, 21092–21107. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Zhao, Y.; Ma, H.; Jiang, M.; Lin, J.; Jin, P. Design of diffractive optical element projector for a pseudorandom dot array by an improved encoding method. Appl. Opt. 2019, 58, G169–G176. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Hermserschmidt, A.; Dyachenko, P.; Scharf, T. Inverse design and demonstration of high-performance wide-angle diffractive optical elements. Opt. Express 2020, 28, 22321–22333. [Google Scholar] [CrossRef] [PubMed]
- Gu, F.; Song, Z.; Zhao, Z. Single-shot structured light sensor for 3D dense and dynamic reconstruction. Sensors 2020, 20, 1094. [Google Scholar] [CrossRef] [PubMed]
- Pasienski, M.; DeMarco, B. A high-accuracy algorithm for designing arbitrary holographic atom traps. Opt. Express 2008, 16, 2176–2190. [Google Scholar] [CrossRef] [PubMed]
- Mohammad, N.; Meem, M.; Wan, X.; Menon, R. Full-color large are a transmissive holograms enabled by multi-level diffractive optics. Sci. Rep. 2017, 7, 5789. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, H.; He, Z.; Wang, X.; Cao, L.; Jin, G. Weighted constraint iterative algorithm for phase hologram generation. Appl. Sci. 2020, 10, 3652. [Google Scholar] [CrossRef]
- Su, P.; Cai, C.; Song, Y.; Ma, J.; Tan, Q. A hybrid diffractive optical element design algorithm combining particle swarm optimization and a simulated annealing algorithm. Appl. Sci. 2020, 10, 5485. [Google Scholar] [CrossRef]
- Goncharsky, A.; Durlevich, S. High-resolution computer-generated hologram for creating 2D images with kinematic effects of motion. J. Opt. 2020, 22, 115702. [Google Scholar] [CrossRef]
- Wang, H.; Piestun, R. Azimuthal multiplexing 3D diffractive optics. Sci. Rep. 2020, 10, 6438. [Google Scholar] [CrossRef]
- Goncharsky, A.; Durlevich, S. DOE for the formation of the effect of switching between two images when an element is turned by 180 degrees. Sci. Rep. 2020, 10, 10606. [Google Scholar] [CrossRef]
- Wyrowski, F. Diffractive optical elements: Iterative calculation of quantized, blazed phase structures. J. Opt. Soc. Am. A 1990, 7, 961–969. [Google Scholar] [CrossRef]
- Liu, X.; Lv, G.; Ding, S.; Wang, Z.; Wang, S.; Feng, Q. Regional iterative optimization algorithm to reduce error caused by DOE binarization. Appl. Opt. 2019, 58, 7227–7232. [Google Scholar] [CrossRef]
- Wildi, T.; Kiss, M.; Quack, N. Diffractive optical elements in single crystal diamond. Opt. Lett. 2020, 45, 3458–3461. [Google Scholar] [CrossRef]
- Feldman, M.R.; Guest, C.C. Iterative encoding of high-efficiency holograms for generation of spot arrays. Opt. Lett. 1989, 14, 2023–2025. [Google Scholar] [CrossRef] [PubMed]
- Hajj, B.; Oudjedi, L.; Fiche, J.; Dahan, M.; Nollmann, M. Highly efficient multicolor multifocus microscopy by optimal design of diffraction binary gratings. Sci. Rep. 2017, 7, 5284. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Olivier, R.; Ville, K.; Hans, H. Review of iterative Fourier-transform algorithms for beam shaping applications. Opt. Eng. 2004, 43, 2549–2556. [Google Scholar]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Wyrowski, F.; Bryngdahl, O. Iterative Fourier-transform algorithm applied to computer holography. J. Opt. Soc. Am. A 1988, 5, 1058–1065. [Google Scholar] [CrossRef]
- Wyrowski, F. Iterative quantization of amplitude holograms. Appl. Opt. 1989, 28, 3864–3870. [Google Scholar] [CrossRef]
- Buhling, S.; Wyrowski, F. Improved transmission design algorithms by utilizing variable strength projections. J. Mod. Opt. 2002, 49, 1871–1892. [Google Scholar] [CrossRef]
- Pang, H.; Cao, A.; Liu, W.; Li, S.; Deng, Q. Alternative design of Dammann grating for beam splitting with adjustable zero-order light intensity. IEEE Photon. J. 2019, 11, 1500909. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Pang, H.; Cao, A.; Deng, Q. Alternative Design of Binary Phase Diffractive Optical Element with Non-π Phase Difference. Appl. Sci. 2021, 11, 1116. https://doi.org/10.3390/app11031116
Xu C, Pang H, Cao A, Deng Q. Alternative Design of Binary Phase Diffractive Optical Element with Non-π Phase Difference. Applied Sciences. 2021; 11(3):1116. https://doi.org/10.3390/app11031116
Chicago/Turabian StyleXu, Cheng, Hui Pang, Axiu Cao, and Qiling Deng. 2021. "Alternative Design of Binary Phase Diffractive Optical Element with Non-π Phase Difference" Applied Sciences 11, no. 3: 1116. https://doi.org/10.3390/app11031116
APA StyleXu, C., Pang, H., Cao, A., & Deng, Q. (2021). Alternative Design of Binary Phase Diffractive Optical Element with Non-π Phase Difference. Applied Sciences, 11(3), 1116. https://doi.org/10.3390/app11031116




