Effect of Coriolis Force on Vibration of Annulus Pipe
Abstract
:1. Introduction and Background
2. Objectives
3. Methodology
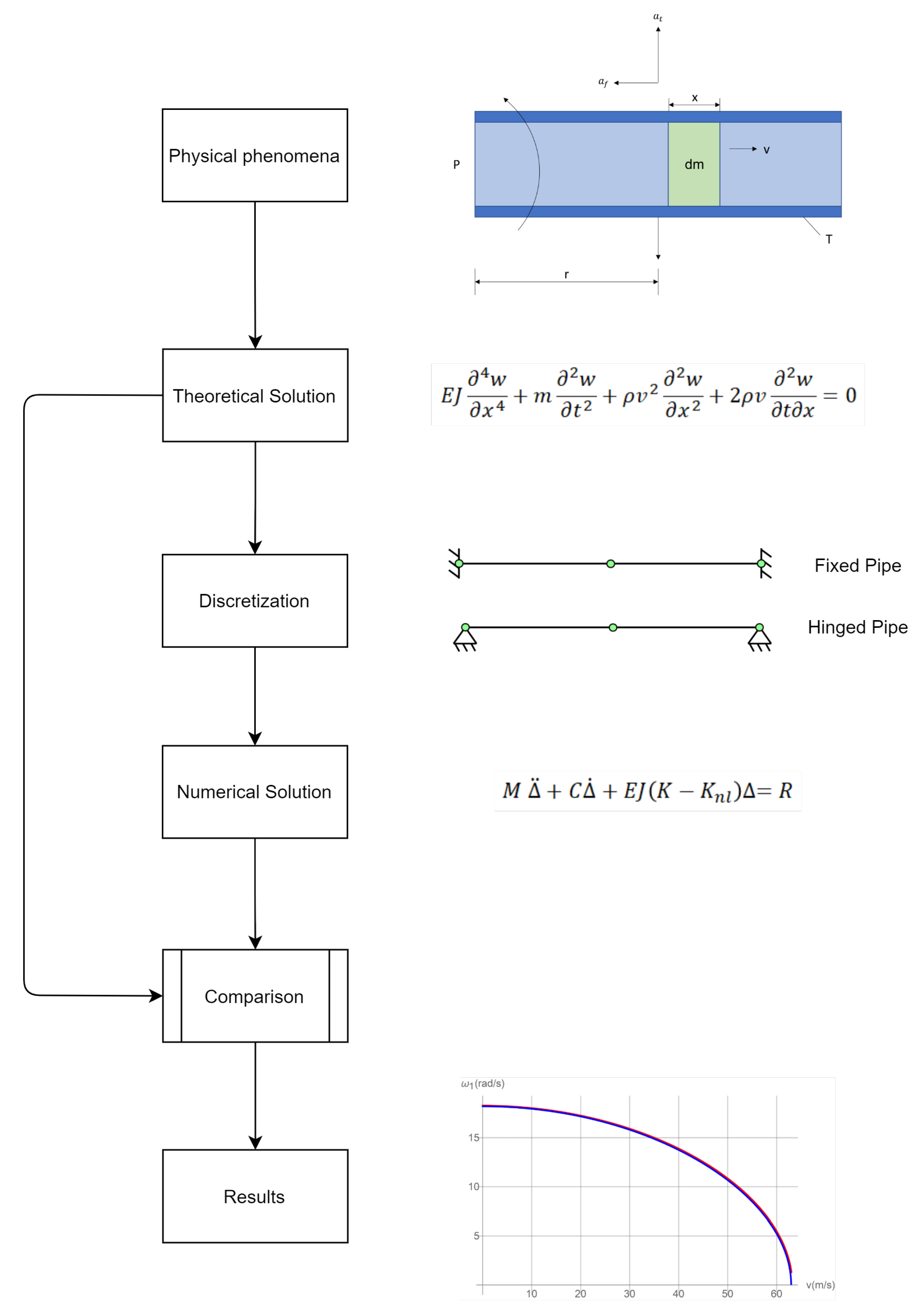
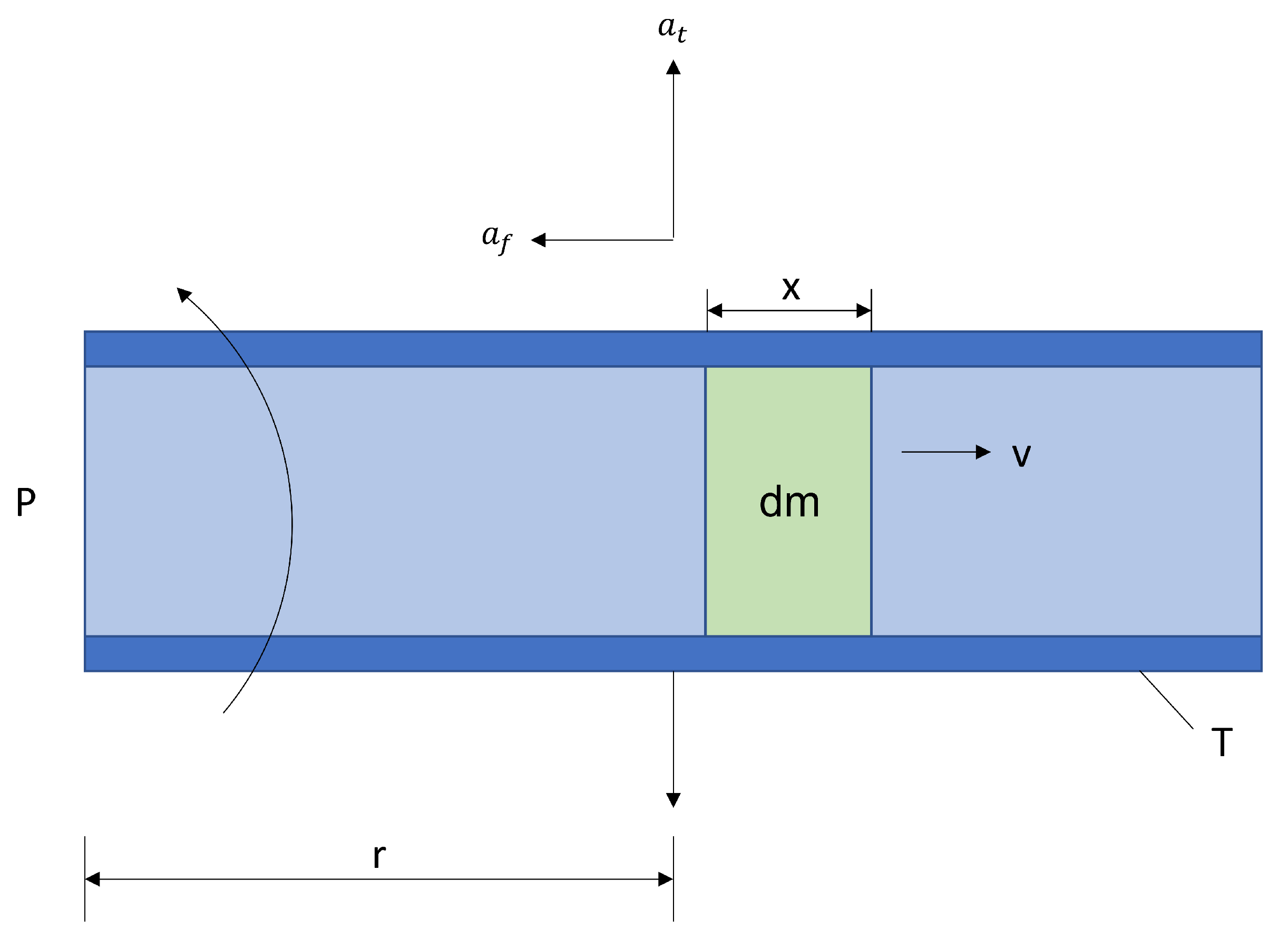
3.1. Analytical Approach
- inertia force due to the vertical acceleration of the pipe;
- elastic forces due to Euler–Bernoulli’s theory.
- (centripetal)
- (Coriolis)
3.2. FEM Approach
3.2.1. Fixed Pipe
3.2.2. Hinged Pipe
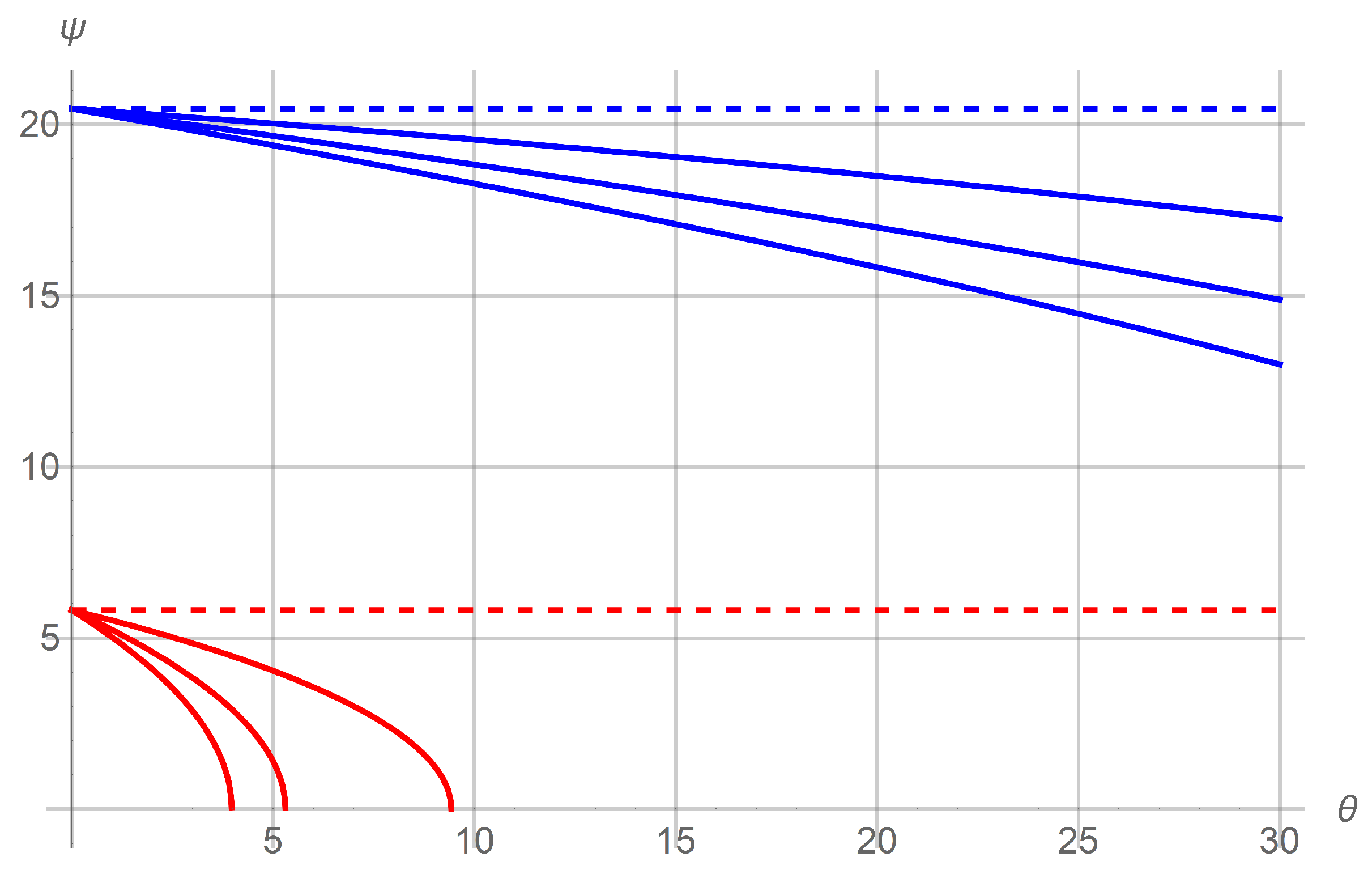
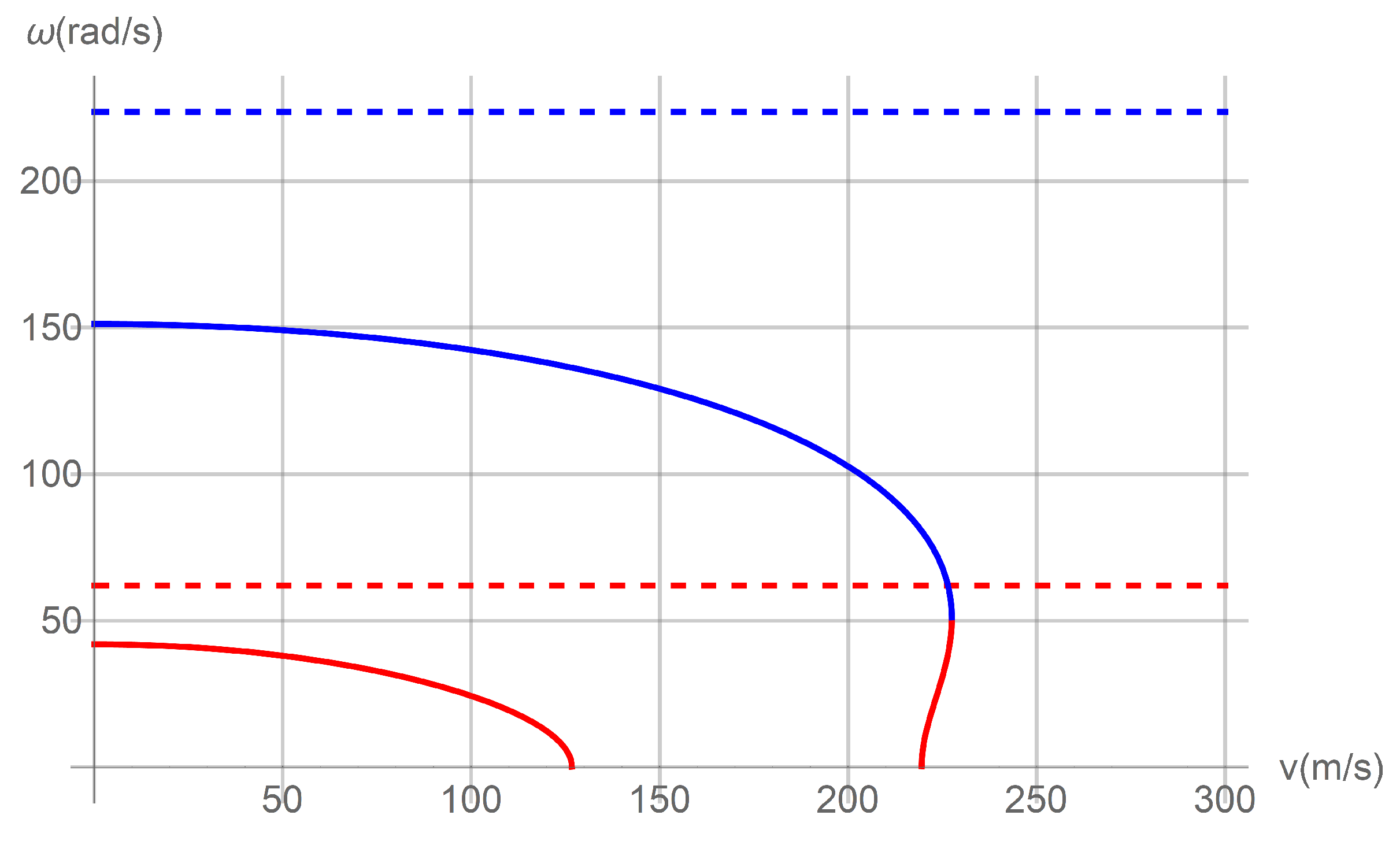
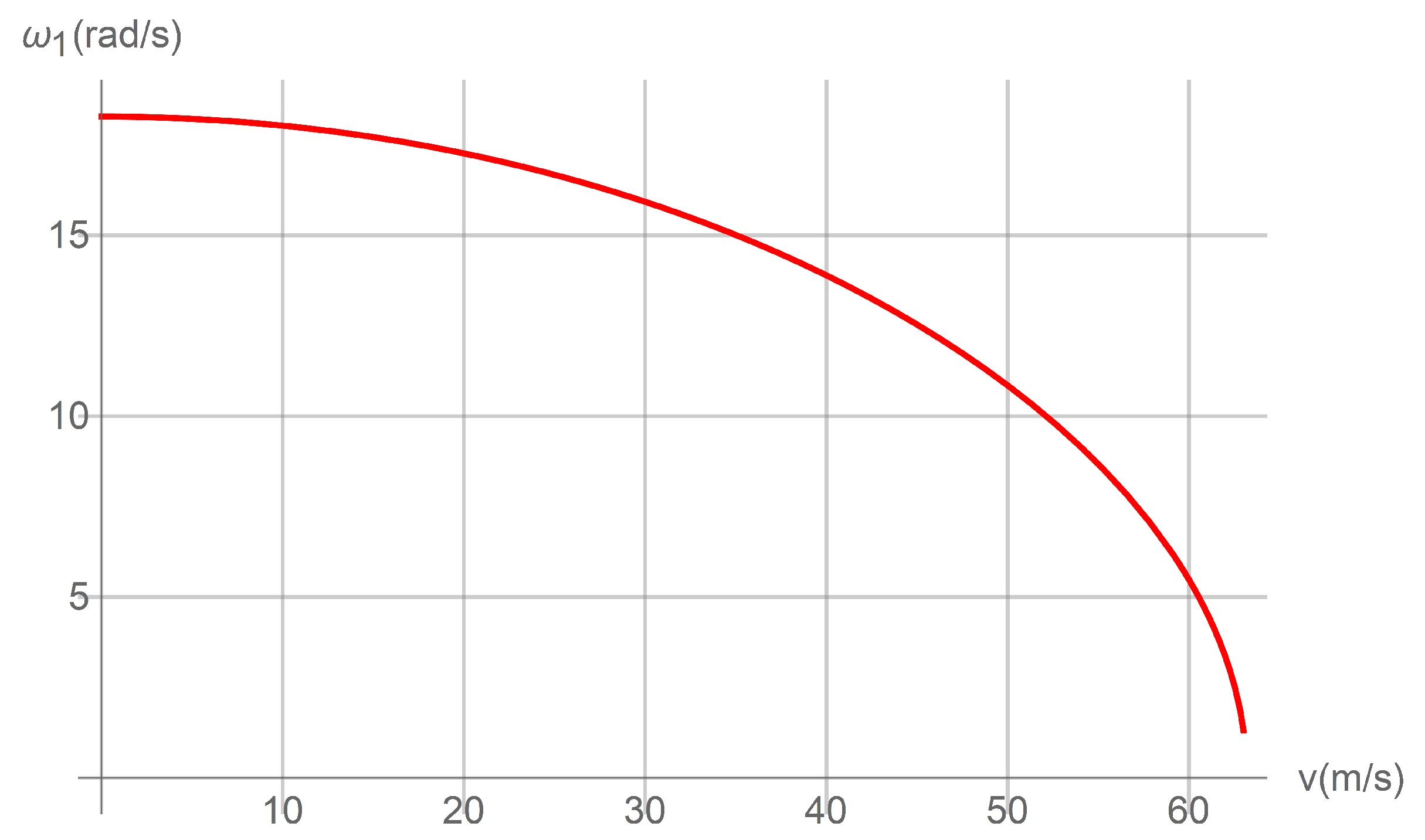
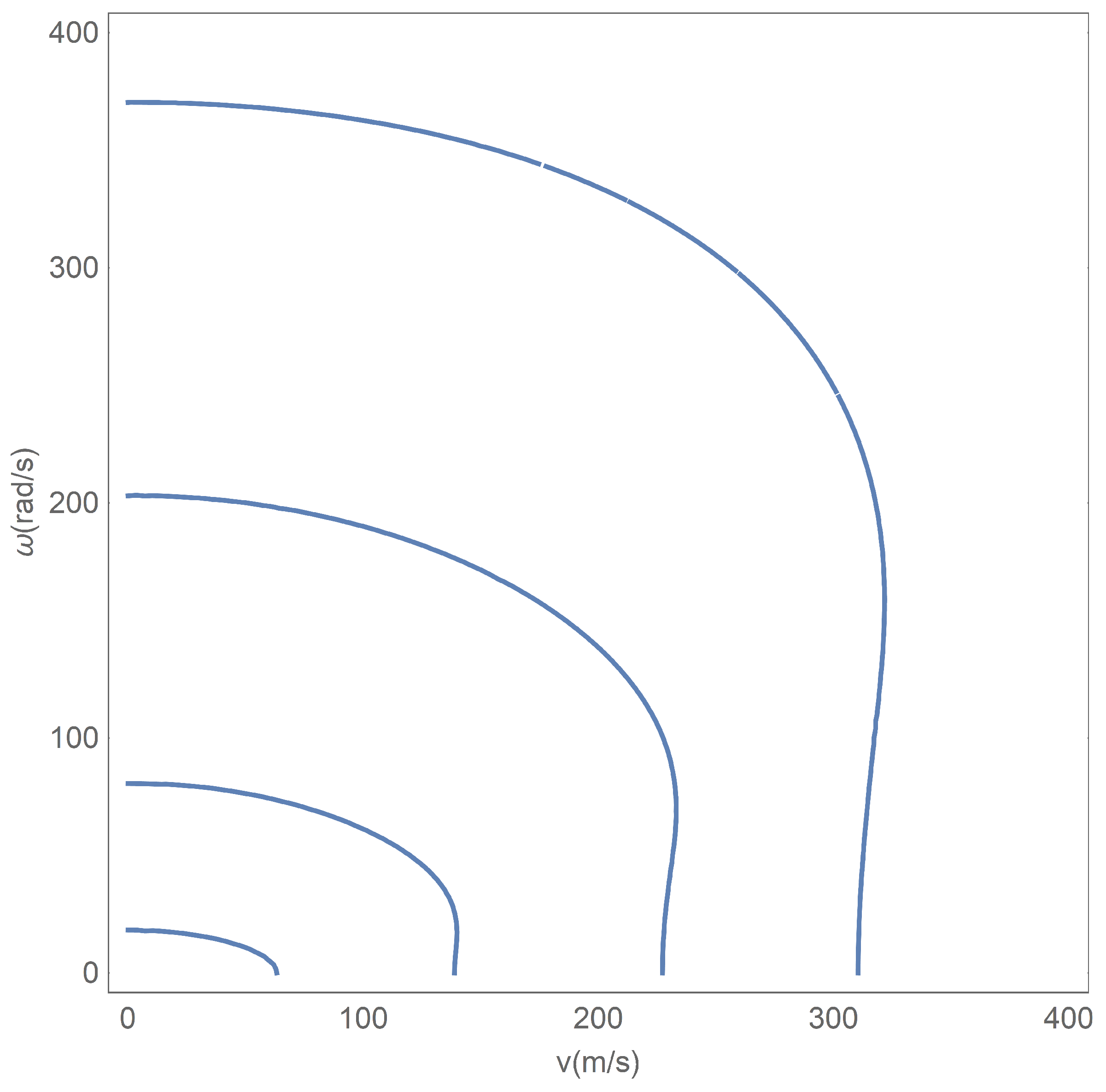
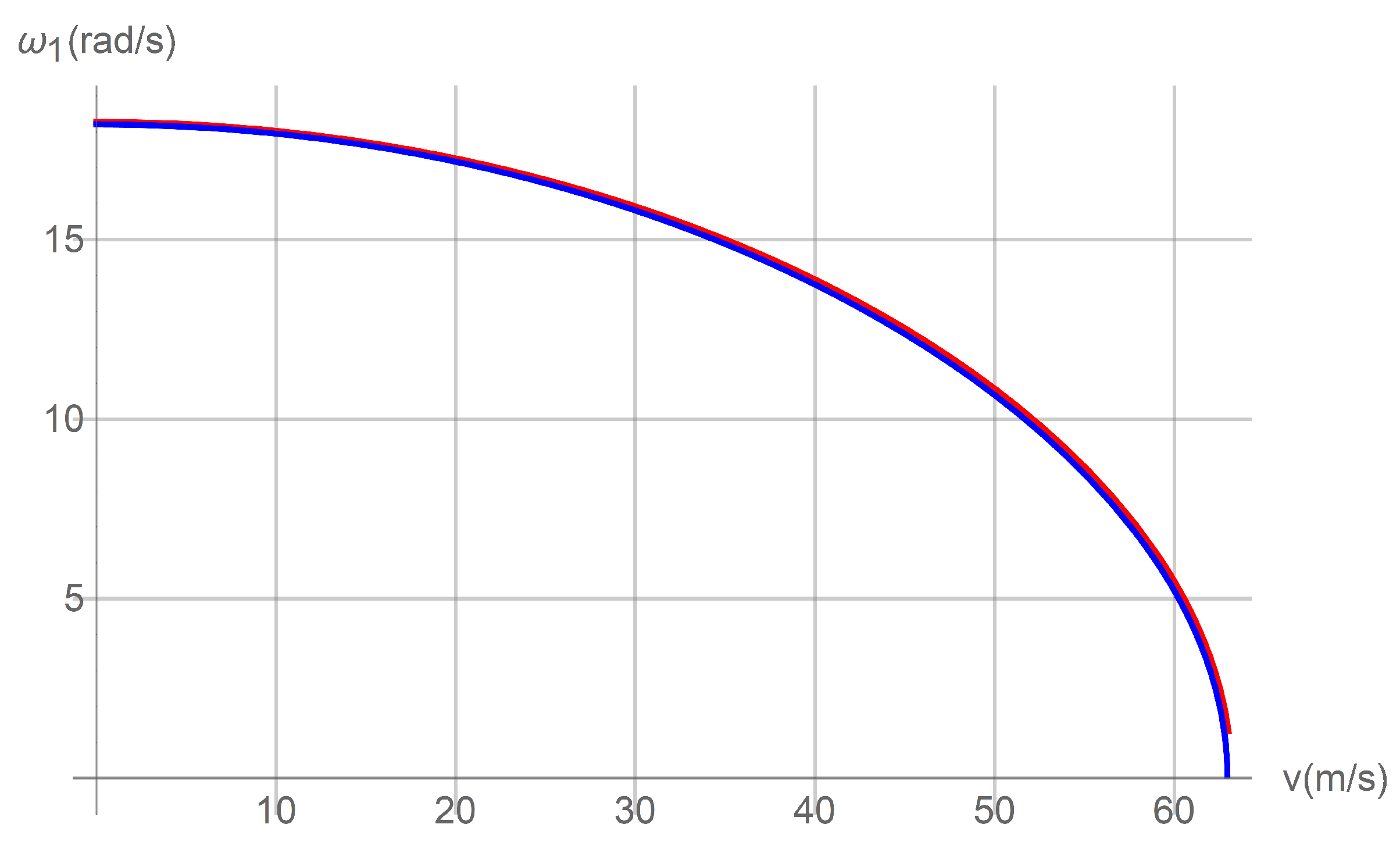
4. Results and Discussions
4.1. Fixed Pipe
4.2. Hinged Pipe
5. Conclusions
6. Recommendations for Future Research
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| LNG | Liquefied Natural Gas |
| LES | Large Eddy Simulations |
| CTN | Carbon NanoTubes |
| SEM | Spectral Element Method |
| SWCNT | Single-Walled Carbon NanoTubes |
| FSI | Fluid Structure Interaction |
| AR | Augmented Reality |
References
- Ibrahim, R.A. Overview of Mechanics of Pipes Conveying Fluids—Part I: Fundamental Studies. J. Press. Vessel. Technol. 2010, 132. [Google Scholar] [CrossRef]
- Paidoussis, M. Fluid-Structure Interactions: Slender Structures and Axial Flow; Academic Press: Cambridge, MA, USA, 2004; Volume 2. [Google Scholar]
- Lee, U. Spectral element modelling and analysis of a pipeline conveying internal unsteady fluid. J. Fluids Struct. 2006, 22, 273–292. [Google Scholar] [CrossRef]
- Dodds, H.L.; Runyan, H.L. Effect of High Velocity Fluid Flow on the Bending Vibrations and Static Divergence of a Simply Supported Pipe; National Aeronautics and Space Administration: Washington, DC, USA, 1965.
- Yamaguchi, R.; Tanaka, G.; Liu, H.; Hayase, T. Fluid Vibration Induced in T-Junction with Double Side Branches. World J. Mech. 2016, 6, 169–179. [Google Scholar] [CrossRef] [Green Version]
- Kuiper, G.; Metrikine, A. On stability of a clamped-pinned pipe conveying fluid. Heron 2004, 49, 211–232. [Google Scholar]
- Chellapilla, K.R.; Simha, H. Vibrations of Fluid-Conveying Pipes Resting on Two-parameter Foundation. Open Acoust. J. 2008, 1, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Leklong, J.; Chucheepsakul, S.; Kaewunruen, S. Dynamic Responses of Marine Risers/Pipes Transporting Fluid Subject to Top End Excitations; Faculty of Engineering, UOW: Wollongong, Australia, 2008. [Google Scholar]
- Murai, M.; Yamamoto, M. An Experimental Analysis of the Internal Flow Effects on Marine Risers. Proc. MARTEC 2010, 1, 159–165. [Google Scholar]
- Marakala, N.; Kuttan, A.K.K.; Kadoli, R. Experimental and Theoretical Investigation of Combined Effect of Fluid and Thermal Induced Vibration on Vertical Thin Slender Tube. Iosr J. Mech. Civ. Eng. 2013, 63–68. [Google Scholar]
- Eriksson, O.; Breton, S.P.; Nilsson, K.; Ivanell, S. Impact of Wind Veer and the Coriolis Force for an Idealized Farm to Farm Interaction Case. Appl. Sci. 2019, 9, 922. [Google Scholar] [CrossRef] [Green Version]
- Shaik, I.; Uddien, S.; Arkanti, K.; Sutar, S. Numerical Analysis of Clamped Fluid Conveying Pipe. HAL 2017. [Google Scholar] [CrossRef]
- Kokare, A.B.; Paward, P.M. Vibration Characteristics of Pipe Conveying Fluid. Int. J. Sci. Eng. Technol. Res. 2015, 4, 10951–10954. [Google Scholar]
- Li, G.; Liu, J.; Jiang, G.; Kong, J.; Xie, L.; Xiao, W.; Zhang, Y.; Cheng, F. The nonlinear vibration analysis of the fluid conveying pipe based on finite element method. Comput. Model. New Technol. 2014, 18, 19–24. [Google Scholar]
- Li, G.; Xiao, W.; Jiang, G.; Liu, J. Finite element analysis of fluid conveying pipe line of nonlinear vibration response. Comput. Model. New Technol. 2014, 18, 37–41. [Google Scholar]
- Jweeg, M.J.; Ntayeesh, T.J. Dynamic analysis of pipes conveying fluid using analytical, numerical and experimental verification with the aid of smart materials. Int. J. Sci. Res. 2015, 4, 1594–1605. [Google Scholar]
- Yi, X.; Li, B.; Wang, Z. Vibration Analysis of Fluid Conveying Carbon Nanotubes Based on Nonlocal Timoshenko Beam Theory by Spectral Element Method. Nanomaterials 2019, 9, 1780. [Google Scholar] [CrossRef] [Green Version]
- Ferras, D.; Manso, P.; Schleiss, A.; Covas, D. One-Dimensional Fluid-Structure Interaction Models in Pressurized Fluid-Filled Pipes: A Review. Appl. Sci. 2018, 8, 1844. [Google Scholar] [CrossRef] [Green Version]
- Elishakoff, I. Controversy Associated with the So-Called “Follower Forces”: Critical Overview. Appl. Mech. Rev. 2005, 58, 117. [Google Scholar] [CrossRef]
- Öz, H.R.; Boyaci, H. Transverse vibrations of tensioned pipes conveying fluid with time-dependent velocity. J. Sound Vib. 2000, 236, 259–276. [Google Scholar] [CrossRef]
- Szmidt, T.; Przybyłowicz, P. Critical flow velocity in a pipe with electromagnetic actuators. J. Theor. Appl. Mech. 2013, 51, 487–496. [Google Scholar]
- Askarian, A.; Abtahi, H.; Haddadpour, H. Dynamic instability of cantilevered composite pipe conveying flow with an end nozzle. In Proceedings of the 21st International Congress on Sound and Vibration 2014, ICSV 2014, Beijing, China, 13–17 July 2014; Volume 4, pp. 3564–3571. [Google Scholar]
- Ntayeesh, T.; Alhelli, A. Free Vibration Characteristics of Elastically Supported Pipe Conveying Fluid. J. Eng. Sci. 2013, 16, 9–19. [Google Scholar]
- Guo, Q.; Zhang, L.; Xiao, L. Damage analysis of the vehicle’s pipe conveying fluid induced by complex random-shock loads. J. Press. Equip. Syst. 2006, 4, 100–103. [Google Scholar]
- Zhang, Y.L.; Gorman, D.G.; Reese, J.M.; Horacek, J. Observations on the vibration of axially tensioned elastomeric pipes conveying fluid. J. Mech. Eng. Sci. 2000, 214, 423–434. [Google Scholar] [CrossRef] [Green Version]
- Modarres-Sadeghi, Y.; Païdoussis, M. Nonlinear dynamics of extensible fluid conveying pipes, supported at both ends. J. Fluids Struct. 2009, 25, 535–543. [Google Scholar] [CrossRef]
- Sharma, J.; Najafi, M.; Marshall, D.; Kaushal, V.; Hatami, M. Development of a Model for Estimation of Buried Large-Diameter Thin-Walled Steel Pipe Deflection due to External Loads. J. Pipeline Syst. Eng. Pract. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Malek Mohammadi, M.; Najafi, M.; Kermanshachi, S.; Kaushal, V.; Serajiantehrani, R. Factors Influencing the Condition of Sewer Pipes: A State-of-the-Art Review. J. Pipeline Syst. Eng. Pract. 2020, 11. [Google Scholar] [CrossRef]
- Olunloyo, V.O.S.; Osheku, C.A.; Olayiwola, P.S. A Note on an Analytic Solution for an Incompressible Fluid Conveying Pipeline System. Adv. Acoust. Vib. 2017, 2017, 20. [Google Scholar] [CrossRef]
- Paidoussis, M.; Issid, N. Dynamic stability of pipes conveying fluid. J. Sound Vib. 1974, 33, 267–294. [Google Scholar] [CrossRef]
- Semler, C.; Li, G.; Paidoussis, M. The Non-linear Equations of Motion of Pipes Conveying Fluid. J. Sound Vib. 1994, 169, 577–599. [Google Scholar] [CrossRef]
- Enz, S.; Thomsen, J.J. Predicting phase shift effects for vibrating fluid conveying pipes due to Coriolis forces and fluid pulsation. J. Sound Vib. 2011, 330, 5096–5113. [Google Scholar] [CrossRef]
- Bathe, K. Finite Element Procedures in Engineering Analysis; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Zachwieja, J. Stress analysis of vibrating pipelines. Aip Conf. Proc. 2017, 1822, 020017. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Jin, W.L. Ultimate Strength of Cylindrical Shells; Elsevier: Oxford, UK, 2016; pp. 353–365. [Google Scholar] [CrossRef]
- Debus, J.C. 4-Finite element analysis of flexural vibration of orthogonally stiffened cylindrical shells with ATILA. In Applications of ATILA FEM Software to Smart Materials; Uchino, K., Debus, J.C., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: New Delhi, India, 2013; pp. 69–93. [Google Scholar] [CrossRef]
- Ceruti, A.; Marzocca, P.; Liverani, A.; Bil, C. Maintenance in aeronautics in an Industry 4.0 context: The role of Augmented Reality and Additive Manufacturing. J. Comput. Des. Eng. 2019, 6, 516–526. [Google Scholar] [CrossRef]
- Osti, F.; Ceruti, A.; Liverani, A.; Caligiana, G. Semi-automatic Design for Disassembly Strategy Planning: An Augmented Reality Approach. In Proceedings of the 27th International Conference on Flexible Automation and Intelligent Manufacturing, FAIM2017, Modena, Italy, 27–30 June 2017; Volume 11, pp. 1481–1488. [Google Scholar] [CrossRef]
- Frizziero, L.; Liverani, A.; Caligiana, G.; Donnici, G.; Chinaglia, L. Design for disassembly (DfD) and augmented reality (AR): Case study applied to a gearbox. Machines 2019, 7, 29. [Google Scholar] [CrossRef] [Green Version]
- De Marchi, L.; Ceruti, A.; Marzani, A.; Liverani, A. Augmented Reality to Support On-Field Post-Impact Maintenance Operations on Thin Structures. J. Sens. 2013, 2013, 619570. [Google Scholar] [CrossRef] [Green Version]
- Liverani, A.; Leali, F.; Pellicciari, M. Real-time 3D features reconstruction through monocular vision. Int. J. Interact. Des. Manuf. 2010, 4, 103–112. [Google Scholar] [CrossRef]
- Liverani, A.; Kuester, F.; Hamann, B. Towards interactive finite element analysis of shell structures in virtual reality. In Proceedings of the 1999 IEEE International Conference on Information Visualization (Cat. No. PR00210), London, UK, 14–16 July 1999; pp. 340–346. [Google Scholar] [CrossRef] [Green Version]
- Francia, D.; Seminerio, D.; Caligiana, G.; Frizziero, L.; Liverani, A.; Donnici, G. Virtual Design for Assembly Improving the Product Design of a Two-Way Relief Valve. In Proceedings of the International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, Kharkiv, Ukraine, 9–12 June 2020; pp. 304–314. [Google Scholar] [CrossRef]
- Osti, F.; Santi, G.C.G. Real Time Shadow Mapping for Augmented Reality Photorealistic Rendering. Appl. Sci. 2019, 9, 2225. [Google Scholar] [CrossRef] [Green Version]
- Francia, D.; Ponti, S.; Frizziero, L.; Liverani, A. Virtual Mechanical Product Disassembly Sequences Based on Disassembly Order Graphs and Time Measurement Units. Appl. Sci. 2019, 9, 3638. [Google Scholar] [CrossRef] [Green Version]
- Amicis, R.; Ceruti, A.; Francia, D.; Frizziero, L.; Simões, B. Augmented Reality for virtual user manual. Int. J. Interact. Des. Manuf. 2018, 12. [Google Scholar] [CrossRef]
- Frizziero, L.; Donnici, G.; Caligiana, G.; Liverani, A.; Francia, D. Project of Inventive Ideas Through a TRIZ Study Applied to the Analysis of an Innovative Urban Transport Means. Int. J. Manuf. Mater. Mech. Eng. 2018, 8, 35–62. [Google Scholar] [CrossRef]

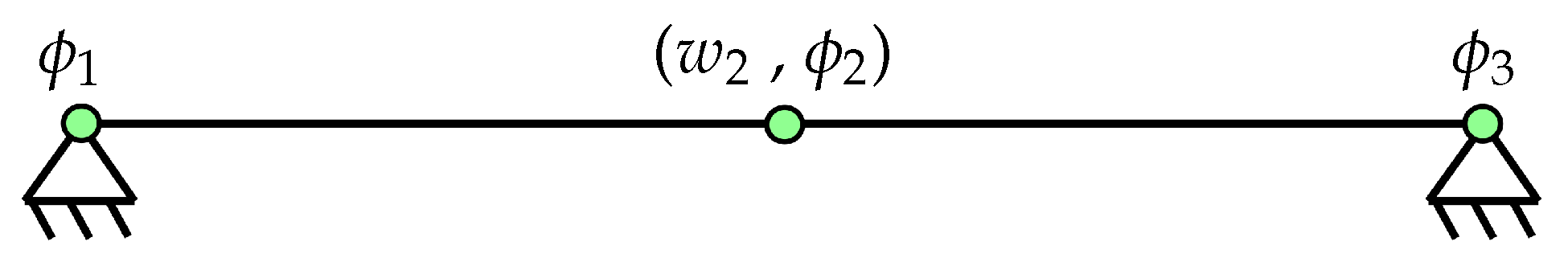

| m | m | m |
|---|---|---|
| m | Pa | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santi, G.M.; Francia, D.; Cesari, F. Effect of Coriolis Force on Vibration of Annulus Pipe. Appl. Sci. 2021, 11, 1058. https://doi.org/10.3390/app11031058
Santi GM, Francia D, Cesari F. Effect of Coriolis Force on Vibration of Annulus Pipe. Applied Sciences. 2021; 11(3):1058. https://doi.org/10.3390/app11031058
Chicago/Turabian StyleSanti, Gian Maria, Daniela Francia, and Francesco Cesari. 2021. "Effect of Coriolis Force on Vibration of Annulus Pipe" Applied Sciences 11, no. 3: 1058. https://doi.org/10.3390/app11031058






