Abstract
Fault detection and isolation (FDI) in oil pipeline systems (OPS) is a very critical issue because faults in these systems such as leaks or equipment malfunctions may cause significant safety accidents and economic losses. These are the challenging factors, along with the environmental regulations for developing efficient FDI approaches for OPS. This paper proposes a model-based distributed FDI approach, which uses a structural model of the system in conjunction with algorithms to generate diagnostic tests that may be implemented in local diagnosers along the OPS. The proposed approach allows detection and isolation of faults in pipeline sections (pipeline segments), pump stations, as well as process control equipment. In this way, simulation of the obtained diagnostic tests in a benchmark application shows that all faults of interest (pipeline segment faults and sensor faults) are detected and isolated.
1. Introduction
Oil transport is a vital activity in the petrochemical industry [1]. Pipelines are the most essential devices for transportation of crude oil from production places to refineries, and the refined oil from refineries to demand points [2,3], in this way, the oil pipeline systems (OPS) usually comprise numerous pipeline segments that require multiple pump stations and the necessary process control equipment, all of which are implemented with field instruments. The OPS are large-scale distributed plants that operate at relative high pressure [4]; likewise, during the past few decades, the OPS grew in size and complexity [5,6].
While the OPS are considered to be the safest and most efficient way for oil transportation, there is still a probability of failure, with safety accidents, economic losses, and environmental damage.
In OPS, component (pipeline segment, pump station, control equipment, etc.) malfunction may cause poor performance of transportation and leaks in pipeline segments are one of the major causes of heavy losses, so dependable FDI systems are important to be used [7]. In order to keep safe and reliable OPS, substantial research efforts have been dedicated to the design and implementation of FDI systems, which play the important role of monitoring oil transportation operations to detect, isolate, and identify the magnitude and time-varying behavior of the potential failures, as well as possible design accommodation actions [8,9,10,11].
Different FDI methods have been considered in the last decades to cope with the monitoring OPS, generally these methods are aimed at pipeline leak detection in OPS [12,13,14]. Likewise, in the last few years, for large-scale distributed plants, methods have been proposed that allow FDI in plant components [15,16,17].
For pipeline leak detection, the most common classification is based on the detection technology characteristics and can be divided into hardware-based and software-based methods [18,19]. In hardware-based approaches, different sensing devices are used to detect failures [12]. Likewise, in software-based approaches, diverse soft computing methods have been developed for leak detection in oil pipelines networks [13,20]. However, many of these methods show shortcomings, such as, e.g., long response times and incidence of false alarm reports [21].
On the other hand, FDI of plant components could use data-based methods that exploit available experimental (historical) data [22]; model-based methods that are based on comparing the actual outputs of the monitored system with the outputs obtained from an analytical mathematical model [23]; and knowledge-based methods which generally use the relationships between faults and symptoms in the form of rules [24]. Particularly, FDI in large scale distributed plants is a difficult task due not only to the large amount of components, but also to its interconnected subsystems with coupled variables between them [25], here by using model-based approaches, a centralized or a distributed architecture in the design of the FDI system may be considered. The centralized architecture requires a global model and may be an impractical option (when implementing a global diagnoser) because of the amount of needed communication [23]. Distributed diagnosis using a structural model has been proposed in [26], a distributed diagnosis approach with a set of local diagnosers was presented in [16,17], and, in [27], a decentralized FDI system based on structural analysis of a large distributed plant was designed.
Distributed FDI architecture consists of subsystem models and is implemented with local diagnosers that together guarantee the same diagnosability as a regular centralized architecture, allowing high performance in scalability, reliability, communication, and reduced computation costs [27,28,29]. In this sense, given that oil pipelines are large-scale distributed plants [4,30] with many components, it would be more convenient to apply the distributed FDI approach, in which, unlike centralized approaches, knowing the model of the global plant is not mandatory [17,25,31]. Additionally, the main performance indexes of FDI methods in OPS are positioning accuracy, response time, sensitivity, and false alarm rate [32]. Nevertheless, as Wang et al. [14] pointed out, no single method can always meet all the requirements, and each technique has its advantages and disadvantages in different circumstances. Moreover, recent surveys about existing FDI methods that can be used in oil and gas pipelines [32,33] concluded that the combination of two or more methods is the future course in FDI in OPS.
In this context, the use of a FDI method for OPS components (e.g., pipeline segment fault, sensor fault, valve fault, etc.) in combination with a leak detection method (to localize pipeline leaks) would discern between component fault and leakage occurrence, avoiding, for example, long response times or false alarms, which also would improve OPS performance.
Thus, here it is considered that the FDI be performed by combining two methods. The first method aims to detect and isolate faults in OPS components, so this first method is used to determine in which component a fault occurs; and, in the case of pipeline segment fault (which implies a leak), once the faulty segment is detected and isolated, the second method would aim to localize the leak.
In this paper, in order to detect and isolate faults in an OPS component, a model-based distributed FDI approach is proposed, which uses a structural model of the system in conjunction with algorithms to generate diagnostic tests. The latter would be implemented in local diagnosers along the OPS to ensure detection and isolation of faults in pipeline segments, as well as in process control equipment (e.g., sensor fault, valve fault, etc.). The proposed approach is combined with a second method to localize the leak that occurred in a pipeline segment. For this purpose, a method as described in [4,34,35,36] may be used (this second method is not addressed in this work).
The major contribution of this research is the extension of the structural analysis approach [17,23,37] to propose a distributed FDI approach for the OPS, considering an optimization process in the selection of tests and the inclusion of neighbors subsystems at different levels to achieve the diagnostic goals. In order to guarantee maximum diagnosability and least exchange of sensor information between subsystems, local diagnosers should be efficiently built for each subsystem, in this sense, two algorithms for the design of local diagnosers are proposed, first only with local information and if necessary with progressive incorporation of information from neighboring subsystems to achieve detection and isolation of a set of faults of interest in OPS.
This paper is organized as follows. In Section 2, the theoretical framework of structural analysis for model base FDI is provided. A model-based distributed FDI approach, which uses a structural model of the process in conjunction with algorithms to generate diagnostic tests, is proposed in Section 3. In Section 4, a case study of FDI for an OPS is presented. Section 5 shows the discussions of the obtained results. Finally, Section 6 gives some conclusions.
2. Structural Analysis for Model-Based FDI
Structural analysis allows for obtaining structural models that are very useful for the design of model-based FDI systems. These structural models can be represented by bipartite graphs. A graph is bipartite if its set of vertices can be separated into two disjoint sets and X such that each edge has a connection in and another in X.
The main assumption is that each component can be represented by a structural model composed of one or more equations; therefore, violation of at least one equation indicates that the system component is faulty.
Let the system description consist of a set of equations involving a set of variables partitioned into a set Z of known (or measured) variables and a set X of unknown (or unmeasured) variables. We refer to the vector of known variables as z and the vector of unknown variables as x. The system may be impacted by the presence of faults that appear as parameters in the equations. The set of faults is denoted by F, and we refer to the vector of faults as .
Definition 1
(System). A system or Σ, for short, is any set of equations relating z, x and . The equations , , are assumed to be differential or algebraic in z and x.
Definition 2
(Structural Model). The structural model of the system is a bipartite graph , or equivalently to , where and is a set of edges such that iff variable is involved in equation .
The structural model of the system , also denoted with some abuse by or in the following, can be obtained abstracting the functional relations. This abstraction leads to a bipartite graph , or equivalently to , where and is a set of edges such that iff variable is involved in equation .
A model is used to illustrate the concepts. This is composed of fifteen equations, to , relating the unknown variables and the known variables . The representation in a bipartite graph for this system is shown in Figure 1.
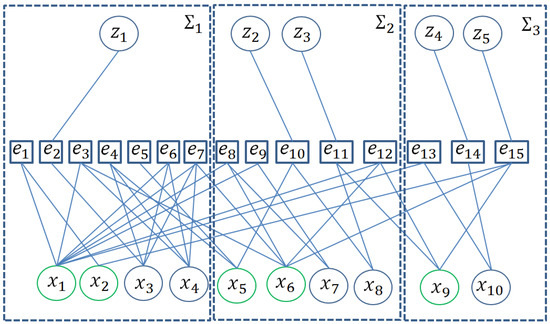
Figure 1.
Bipartite graph of an illustrative example.
Definition 3
(Subsystem). A subsystem or for short, with , is any set of equations relating , and , where with , , and if
The set of local variables of , denoted as , is composed of the subset of vertices of that are adjacent only to vertices in . The set of shared variables of , denoted as , is composed of the subset of vertices of that are adjacent to vertices in and vertices in any other subset , where .
The decomposition of the model into three subsystems, , and is also shown in Figure 1, where , , and .
A key tool for fault diagnosis using structural analysis is the concept of matching. A matching is a causal assignment that links an equation with an unknown variable, where this equation can be used to calculate this unknown variable [23].
Definition 4
(Matching). A matching between Σ and X is a subset of A of disjoint edges of a bipartite graph G. It is called complete matching with respect to Σ or X if or keeps, respectively.
It is possible to find different matching for a specific bipartite graph; in Figure 2, a complete matching with respect to X(in bold edges) of the model is shown.
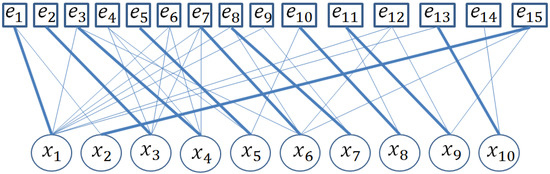
Figure 2.
X-complete matching.
Dulmage–Mendelsohn (DM) decomposition provides important structural properties; in particular for bipartite graphs, each graph can be decomposed in three subgraphs:
- Over-determined subgraph , with a X-complete matching that is not -complete,
- Just-determined subgraph , with a complete matching,
- Under-determined subgraph , with a -complete matching that is not X-complete.
As a consequence of this bipartite graph decomposition, the corresponding system can be decomposed into three parts: the structurally overdetermined (SO) part represented by , which has more equations than unknown ones, the structurally just determined part represented by , and the structurally underdetermined part represented by .
Definition 5
(Structural redundancy). Given a bipartite graph, The structural redundancy of a set of equations is defined as the difference between the number of equations and the number of unknown variables X.
The incidence matrix (,) of the bipartite graph is used to represent this graph as a set of edges in an algebraic manner. The rows of this matrix are associated with the equations and the columns with the variables with equations and variables. A “1” in the intersection of row and column indicates the existence of the edge (,) ∈.
Structural Diagnosability
Analytical redundancy occurs and analytical redundancy relations are available when there are equations that are not necessary to match unknown variables in a system . Any over-determined subgraph contains more equations than variables, and such an equation can be used for residual generation. A residual, derived from ARRs, is generated from a subgraph using the excess equations once all unknown variables within are expressed in terms of known variables. When an expected value of an is not met, a fault is detected.
Definition 6
(ARR). A relation is an Analytical Redundancy Relation (ARR) for , if, for each z consistent with , the relation is satisfied.
Definition 7
(Residual Generator for ). A residual generator for the model is a system taking a subset of the variables z as input, and generating a scalar signal r as output if, for all z consistent with , it holds that .
The Minimal Structurally Over-determined Set approach is a way to find ARRs. This is done by calculating the matching of an over-determined subgraph that has structural redundancy equal to 1.
Definition 8
(MSO sets). A Minimal Structurally Over-determined Subsystem is a part of from which removal of one constraint will make the subsystem to become just-constrained [23].
A minimal structurally overdetermined set, for a short MSO set, can be used to generate an given that the equations number exceeds the unknown variables number by one (structural redundancy 1), which means that only one residual generator can be developed. According to [38], the computation of MSO sets can be exponential according to the structural redundancy and system measurements. One way to reduce this computational cost can be by calculating only the MSO sets of interest, that is, reducing the calculation only to those impacted by faults. Hence, the concept of Fault-Driven Minimal Structurally Overdetermined (FMSO) set is useful. An FMSO set can be defined as an MSO set of whose fault support is not empty.
Let the FMSO set , where is the set of known variables of , is the set of unknown variables of and is the set of fault support of , below the definition of FMSO [39].
Definition 9
(FMSO set). A subset of equations is an FMSO set of if (1) and that means , and (2) no proper subset of φ is overdetermined.
A complementary concept is the Clear Minimal Structurally Overdetermined (CMSO) set as an MSO set of whose fault support is empty [17].
Definition 10
(CMSO set). A subset of equations is a CMSO set of if (1) and that means , and (2) no proper subset of ψ is overdetermined.
The algorithm of calculation of FMSO sets presented in [17] allows the calculation of all the FMSO sets related to the set of faults of interest, which can be many in the case of large-scale distributed plants. It is possible to optimize the calculation of FMSO sets taking into account some design parameters such as: less number of equations involved, less number of unknown/known variables or forcing the use of a certain subset of variables or equations. With these considerations, a distributed diagnostic algorithm can then be proposed to respond to real constraints on communication, distance, or availability of sensors and actuators among pre-defined subsystems.
3. Model-Based Distributed FDI
This section proposes a method to design a set of distributed local diagnosers that together guarantee the same diagnosability as a centralized system. To achieve this, each local diagnoser must detect and isolate the set of faults corresponding to its subsystems. To solve this problem, an approach is proposed that builds a select set of FMSO sets for each subsystem that guarantees maximum diagnosability and the least exchange of sensor information between subsystems.
Initially, FMSO sets are built only with local information, and, if it is not enough to detect and isolate all the faults of that subsystem, sensors from neighboring subsystems are added until the possible detectability and isolability are reached. In each iteration of building FMSO sets, a Binary Integer Linear Programming (BILP) optimization problem is solved to select the most appropriate FMSO sets.
The general idea is to incorporate information of additional sensors to minimize the coupling between FMSO sets; this is achieved by adding equations that minimize the number of connections between FMSO sets.
Definition 11
(Global FMSO set). A global FMSO set is an FMSO set of . The set of global FMSO sets is denoted by Φ.
In order to develop a methodology to build and select an efficient set of FMSO sets, it is desirable to build only a useful part of all Global FMSO sets; for this, it is proposed to focus the building process in a reduced subgraph related to a subset of interest faults.
To compute FMSO sets that require information from other subsystems, a classification of neighboring subsystems is performed according to their proximity: if they are directly connected neighbors, they are classified as level 1 neighbors; if they are connected neighbors through 1 subsystem, they are classified as level 2 neighbors and so forth.
Definition 12
(Neighbors of ). Given two subsystems and of Σ, . is a first level neighbor of if , which is denoted by and . The set of all neighbors of the first level of is denoted by
Classification of the neighbors is illustrated with another example in Figure 3 where the subsystems and are taken as examples. For the subsystem , the first level neighbors are , and . Then, and are the sets of first and second level neighbors with respect to .
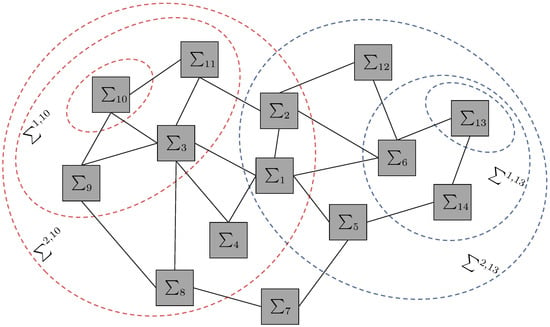
Figure 3.
An illustrative example of classification of neighboring subsystems.
Local Diagnosers Design
The method proposes the creation of local diagnosers for each subsystem that can operate independently of each other by sharing the minimum possible amount of sensor information. This approach considers predefined subsystems and, in that context, it is designed in a distributed framework. Given a set of faults of interest, known and unknown variables for each subsystem, first, Algorithm 1 calculates FMSO sets for the set of faults of each subsystem starting from the equation (or the set of equations) that contains the fault of interest. This set of equations is called evaluation equations .
| Algorithm 1: Local Diagnoser Design |
| Given:, |
|
| Result: Local optimal FMSO sets for subsystem , . |
Definition 13
(Subset ). Given a subsystem and a set of unknown variables under evaluation , is the subset of equations that contains at least one of the elements of , .
If there is any fault not detectable or not isolable with the ARRs computed by Algorithm 1, that is, if FMSO sets are not found with the exclusive information of that subsystem, Algorithm 2 is used, which uses a criterion of adding equations of neighboring subsystems, initially of level 1: one-by-one sub-systems are added and, if it is necessary, two by two until the whole set of subsystems of level 1 is brought together. If the diagnostic objectives cannot yet be achieved, subsystems of level 2 are incorporated in addition to the set of subsystems of level 1.
| Algorithm 2: Local diagnoser design with neighbors |
| Given:, , |
|
| Result: Local optimal FMSO sets for subsystem , . |
4. Case Study: FDI System for Oil Pipeline
4.1. Brief Description of the Oil Pipeline
The oil pipeline (plant) under study in this paper is located in Peru. It transports oil for delivery to customers. Figure 4 shows a view of this oil pipeline.

Figure 4.
A view of the oil pipeline under study.
This oil pipeline consists of three sections with a pumping station located at the beginning of each section with a total length of 450 km. Detailed data of dimensions and relative heights of each section are shown in Table 1, where is the length, is the outer diameter of the pipes, is the inner diameter of the pipes, is the wall thickness of the pipes, and are the relative heights at the beginning and the end of each i section, respectively.

Table 1.
Oil transportation plant characteristics.
Figure 5 shows a diagram with the structure of the oil pipeline under study, identifying its corresponding sub-systems detailed ahead. and are the oil flow rate (measured with flow sensor) and the head (measured with pressure sensor) before the oil-pumping station of each i section of the OPS, respectively. Applying Definition 1, is the OPS and using Definition 3, is the i section of the OPS.
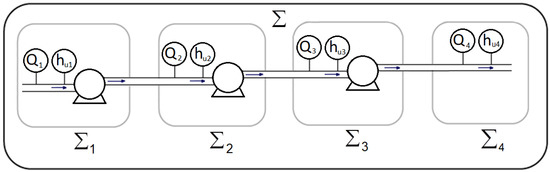
Figure 5.
Diagram of the oil pipeline under study.
The head discharge characteristics of the pumping station operating in stationary regimes are often approximated by the following equation:
where is the differential head, Q is the flow rate, and a and b are the approximation factors of the characteristic.
The characteristics of pumping stations are detailed in Table 2, including the pump types, the head–discharge characteristics, and the positive suction heads (P.s.h.).

Table 2.
Characteristics of pumping stations.
The temperature of the pumping oil is 30 C, the maximum admissible pressure in the pipeline is 11.1 MPa, the density of the transported oil is 850 kg/m, and the efficiency of the system is 1500 m/h.
4.2. Mathematical Modeling of Oil Pipeline
The mathematical modeling of the processes involved is needed for the design of distributed fault detection and isolation systems [8,9]. This mathematical modeling may differ in complexity depending on the intended applications; see, for example, [40,41,42,43,44]. In general, the oil flow within a pipe is governed by the fundamental laws of mechanics and thermodynamics and constitutes a fluid flow system [4,45].
The mathematical modeling of the oil pipeline under study is developed by applying the basic fundamental equations of fluid flow, which are the continuity equation, the momentum equation, and the energy equation [4,45].
The continuity equation of the transported oil in the pipeline is based on the law of conservation of mass, and it is represented as [45]:
where , v are the density, and the velocity of oil, S is the pipeline cross-section area, x is the coordinate along the pipeline axis, and t is the time.
The momentum equation which describes the force balance on the fluid within the pipeline is presented as [18]:
where p is the pressure, d is the pipeline internal diameter, g is the gravity acceleration; is the tangential stress at the pipeline internal surface, and is the slope of the pipeline axis to the horizontal.
The equation of mechanical energy balance is written as [46]:
where z is the geometric head, i is the hydraulic gradient, and is a function of the pressure such that:
and where is the kinematic viscosity of the oil flow rate.
The equation of total energy balance is represented as [47]:
where is the internal energy, is the enthalpy or heat content, is the heat flux.
Equations (2)–(4) and (6) are the set of one-dimensional, partial differential equations used for mathematical modeling of oil flow within the pipeline.
In stationary flow, all parameters of the transported oil at each cross-sectionof the pipeline remain constant, which is independent of time. Therefore, for the stationary flow, the basic equations describing the oil flow are the following:
The continuity Equation (2) leads to the equation [18]:
which means that the mass flow rate of the transported oil stays constant.
The equation of total energy balance (6), considering that , and , is written as [45]:
where is the specific heat, T is the oil temperature, is the temperature outside the pipeline, K is the heat transfer factor, and is the hydraulic resistance factor.
The expressions (7)–(9) are the basis equations for mathematical modeling of the stationary operating regimes of oil pipelines.
From the combination of the continuity Equation (7) and the differential momentum Equation (8), the following Bernoulli equation in its algebraic form [18,45] is obtained:
where and are, respectively, the initial and terminal cross-sections of the oil pipeline section with length L.
Equation (10) relates the pressure , at the beginning and at the end of a pipeline section, respectively, with the velocity v of the oil flow.
Taking into account that the head is represented as , Equation (10) becomes [18]:
where and are the geometric head at the beginning and at the end of a pipeline section, respectively.
The mathematical model of the pumping station is represented by the following algebraic equation [45]:
where is the differential head produced by the pumping station on the oil flow rate Q, , are the pressure after, and the pressure before the oil pumping station, respectively, , are the head after, and the head before oil pumping station, respectively.
The dependence defines the head–discharge characteristic of the pumping station. The flow rate Q through a pipeline (in m/s) is obtained by the expression [18]:
Taking into consideration that the oil pipeline under study consists of three sections with a pumping station located at the beginning of each section, for the mathematical modeling of each of this section, the Bernoulli Equation (10) is used, in which the pressure at the initial cross-section of the pipeline section is replaced with the help of the following condition [45]:
where , the velocity v is measured in (m/s), a and b are the approximation factors of the head–discharge characteristic of the pumping station. After replacing , it is obtained [45]:
Therefore, the mathematical modeling of the system and its respective sub-systems are represented as:
In this model, internal pressure variables , flow variables , and head gain are related to each pumping station describing the plant; all these signals are considered as unknown variables, flow sensors , and pressure sensors are considered as known or measured variables. Accordingly, fault variables , and are related to pressure sensors, fault variables and are related to flow sensors, and fault variables are related to pipeline segments (through flow balance at each section from the beginning to the end).
To sum up, the structural model describing the plant consists of the system with a total of 20 equations divided into 4 sub-systems to , 8 known variables in z, 14 unknown variables in x, and 8 fault variables in .
4.3. FDI System for Oil Pipeline
With the mathematical model defined in Section 4, it is now helpful to define the neighbors of each subsystem. For subsystem , the set of first level neighbors is defined as , the set of second-level neighbors as and the set of third level sub-systems as . For subsystem , the set of first level subsystems is defined as and the set of second level subsystems as . For subsystem , the set of first level subsystems is defined as and the set of second level subsystems as , and, finally for subsystem , the set of first level neighbors is defined as , the set of second level neighbors as and the set of third level subsystems as . As an example, Figure 6 shows how these levels are defined for subsystem .
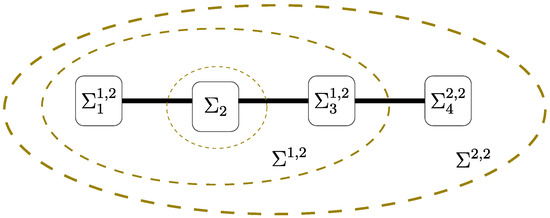
Figure 6.
Levels description for subsystem .
With this, it is attempted first designing Local Diagnosers by considering only equations within their respective subsystem using Algorithm 1.
For subsystem , the set of equations directly impacted by is , then the set of unknown variables related is , and it is found , and this set is assigned to ; with this set of equations, all FMSO sets possible from are computed; in this case, no FMSO sets are found. Given that , the process is done once again. The set of unknown variables of is assigned to and is found and assigned to ; with this set of equations, all FMSO sets possible from are computed, in this case, no FMSO sets are found. Since still , the process is done once again. The set of unknown variables of is assigned to , and it is found that and is assigned to ; with this set of equations, all FMSO sets possible from are computed; in this case, no FMSO sets are found. Finally, as , no more loops are computed, and it is concluded then that Local Diagnoser for can not be computed with only equations from .
This procedure is repeated for all subsystems concluding that none of the Local Diagnosers can be computed with only equations from their respective subsystems. Now, the design process is continued with the procedure of Algorithm 2.
Following Algorithm 2, let us detail the steps for the procedure design for the Local Diagnoser for subsystem . First, the set of equations impacted by faults is assigned to , the level variable is defined and the variable is set to ∅. As , the analysis loop begins. The set of unknown variables of is assigned to . Then, is assigned to and is decomposed in one part . Then, is assigned to . With all this, no FMSO sets are found from this selection. As , the following loop begins, and the set of unknown variables of is assigned to , Then, is assigned to and is decomposed in one part . Then, is assigned to . With this selection, one FMSO set is found, but no selection is found computing the BILP problem. As , the following loop begins, the set of unknown variables of is assigned to , Then, is assigned to and is decomposed in one part . Then, is assigned to . With this selection, three FMSO sets are found, and the selection by computing the BILP problem is found; with this selection, the related analytical redundancy relations are computed.
Following the same design process in Algorithm 2 for subsystems , , and , it is found that, for , , subsystems from level 1 are needed to build analytical redundancy relations for complete diagnosis isolation; meanwhile, for subsystem , subsystems from level 2 are needed.
Table 3 summarizes all sets of FMSO sets found for complete isolation, and the local faults that each local diagnoser detects and isolates are highlighted:

Table 3.
Local diagnosers for nominal operation.
Then, from the design of the local diagnosers presented in Table 3, it follows that, according to the sensitivity of faults, both subsystems and require two FMSO sets each to detect and isolate their faults. In the case of subsystems and , they have three FMSO sets each. Next, applying Definitions 6 and 7, an ARR is calculated first and then a residual generator for each of these 10 FMSO sets of Table 3.
Finally, the residual generators, which receive only measured variables as inputs, are designed and programmed in a programmable automation controller (PAC) using the structured text language. For the implementation, a PAC is assigned for each local diagnoser as shown in the architecture of the proposed FDI system in Figure 7.
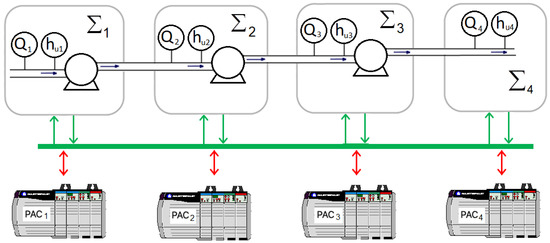
Figure 7.
Distributed FDI System proposed.
Ultimately, to validate the implementation of the designed distributed FDI system, all the faults of the set of faults of interest are emulated: faults , and related to pressure sensors, faults and related to flow sensors and faults related to pipeline segments. Then, in Figure 8, the response of the system to emulations of all the faults simultaneously is presented, and it can be seen that the system detects them for all these signals through the response of the residuals that differ from zero during the duration of the fault. In the same way, isolation is demonstrated by different fault signatures. The results shown in Figure 8 demonstrate that all faults can be detected and that a different fault signature is generated for all faults except for faults and that cannot be isolated from each other. Each column of this figure corresponds to each fault with simulation occurring, and each row corresponds to the sensibility to each residual generator for each fault with emulation occurring.
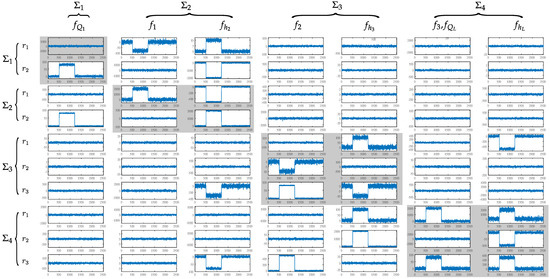
Figure 8.
Analytical redundancy relations .
5. Results and Discussion
Given the physical characteristics of the system, it is shown that, only by using Algorithm 1, it is not possible to implement local diagnosers. On the other hand, by means of Algorithm 2, the local diagnosers for subsystems , and are constructed, including level 1 subsystems. In the case of the local diagnoser for subsystem , level 2 subsystems are considered. In addition, by applying Algorithm 2, it is shown that local diagnosers were built with the minimum possible amount of FMSO sets necessary to minimize communication among subsystems. Figure 8 shows that the seven faults raised in the OPS model can be effectively detected and isolated from each other (since they have different fault signatures) according to the distributed construction of the four local diagnosers. Additionally, Figure 8 highlights the local faults that each local diagnoser detects and isolates; this shows the correspondence of the simulations with the sensibility shown in Table 3. It is shown that, using Algorithm 2, it is possible to implement a distributed diagnosis system for a large and complex process without the need to use the global model, this, unlike other studied methods, allows for optimizing the system design as well as the communication between subsystems.
6. Conclusions
In this paper, a distributed FDI approach based on structural analysis for OPS is proposed; likewise, the design of a distributed FDI system of an OPS located in Peru is developed. This FDI system is composed of four local diagnosers with a total of eight analytical redundancy relations obtained from a set of FMSO sets. Through the proposed algorithms, local diagnosers are efficiently built for each subsystem by progressively incorporating information from neighboring subsystems to achieve the previously defined fault detection and isolation objectives. The FDI system developed was tested by simulation validating that the eight faults of the set of interest, which include five sensor faults and three pipeline segment faults, can be detected and isolated. The main advantage of this approach is that it allows a distributed diagnosis design without the need to use the global model of the process, which makes it much more feasible to implement for complex and large processes.
Author Contributions
All the authors contributed to the development of the experiments, the result analysis, and the writing and review of the paper. Specifically, J.S.-M. and R.R.-P. were in charge of preparing the introduction, G.P.-Z. of the modeling and design of the FDI system, G.P.-Z. and V.S.-Z. of the simulation of the FDI system, R.R.-P. of the model of the process and G.P.-Z., R.R.-P. and J.S.-M. of the overall ideas of the exposed research and the general conception of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Proyecto de Mejoramiento y Ampliación de los Servicios del Sistema Nacional de Ciencia Tecnología e Innovación Tecnológica 8682-PE, Banco Mundial, CONCYTEC and PROCIENCIA through grant E041-01[N48-2018-FONDECYT-BM-IADT-MU].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study is available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Devold, H. Oil and Gas Production Handbook. An Introduction to Oil and Gas Production, Transport, Refining and Petrochemical Industry; ABB Oil and Gas: Oslo, Sweden, 2013. [Google Scholar]
- Kennedy, J. Oil In Addition, Gas Pipeline Fundamentals, 2nd ed.; PennWell Books: Tulsa, Okla, USA, 1993. [Google Scholar]
- Kiefner, J.; Trench, C. Oil Pipeline Characteristics and Risk Factors: Illustrations from the Decade of Construction; American Petroleum Institute: New York, NY, USA, 2001. [Google Scholar]
- Lurie, M. Modeling of Oil Product and Gas Pipeline Transportation; Wiley-VCH Verlag GmbH & Co KGaA: Weinheim, Germany, 2009. [Google Scholar]
- Yoon, M.S.; Warren, C.B.; Adam, S. Pipeline System Automation and Control; ASME Press: New York, NY, USA, 2007. [Google Scholar]
- Subramanian, N. Improving Security of Oil Pipeline SCADA Systems Using Service Oriented Architectures; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Muhlbauer, W.K. Pipeline Risk Management Manual; Gulf Professional Publishing: Burlington, NJ, USA, 2004. [Google Scholar]
- Gertler, J. Fault Detection and Diagnosis in Engineering Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Korbicz, J.; Koscielny, J.M.; Kowalczuk, Z.; Cholewa, W. Fault Diagnosis: Models, Artificial Intelligence, Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Scott, S.; Barrufet, M. Worldwide Assessment of Industry Leak Detection Capabilities for Single & Multiphase Pipelines; Technical Report; A&M University: College Station, TX, USA, 2003. [Google Scholar]
- Qin, B.; Yunping, Z.; Min, F.; Xiaojian, S. Leakage detection technology of oil and gas transmission pipelines and its development trend. Petrol. Eng. Construct. 2007, 33, 19–23. [Google Scholar]
- Kowalczuk, Z.; Gunawickrama, K. Detecting and Locating Leaks in Transmission Pipelines; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Zhang, J. Designing a cost-effective and reliable pipeline leak-detection system. Pipes Pipelines Int. 1997, 42, 20–26. [Google Scholar]
- Wang, X.; Lambert, M.; Simpson, A.; Liggett, J.; Vítkovsky, J. Leak detection in pipelines using the damping of fluid transients. J. Hydraul. Eng. 2002, 128, 697–711. [Google Scholar] [CrossRef]
- Vásquez, J.W.; Pérez-Zuñiga, G.; Sotomayor-Moriano, J.; Ospino, A. Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System. Entropy 2021, 23, 139. [Google Scholar] [CrossRef]
- Khorasgani, H.; Jung, D.; Biswas, G. Structural approach for distributed fault detection and isolation. IFAC-PapersOnLine 2015, 48, 72–77. [Google Scholar] [CrossRef]
- Pérez-Zuñiga, C.; Chanthery, E.; Travé-Massuyès, L.; Sotomayor, J. Fault-driven structural diagnosis approach in a distributed context. IFAC-PapersOnLine 2017, 50, 14254–14259. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Fung, W.K.; Karnik, A. Recent advances in pipeline monitoring and oil leakage detection technologies: Principles and approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef]
- Datta, S.; Sarkar, S. A review on different pipeline fault detection methods. Loss. Prev. Process Ind. 2016, 41, 97–106. [Google Scholar] [CrossRef]
- Vásquez Capacho, J.W.; Perez Zuñiga, C.G.; Muñoz Maldonado, Y.A.; Ospino Castro, A. Simultaneous occurrences and false-positives analysis in discrete event dynamic systems. J. Comput. Sci. 2020, 44, 101162. [Google Scholar] [CrossRef]
- Abhulimen, K.E.; Susu, A.A. Liquid pipeline leak detection system: Model development and numerical simulation. Chem. Eng. J. 2004, 97, 47–67. [Google Scholar] [CrossRef]
- Enciso-Salas, L.; Pérez-Zuñiga, G.; Sotomayor-Moriano, J. Fault diagnosis via neural ordinary differential equations. Appl. Sci. 2021, 11, 3776. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswieckim, M. Diagnosis and Fault-Tolerant Control, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Isermann, R. Fault-Diagnosis Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Noursadeghi, E.; Raptis, I.A. Reduced-order distributed fault diagnosis for large-scale nonlinear stochastic systems. J. Dyn. Syst. Meas. Control Trans. 2017, 140, 051009. [Google Scholar] [CrossRef]
- Bregon, A.; Daigle, M.; Roychoudhury, I.; Biswas, G.; Koutsoukos, X.; Pulido, B. An event-based distributed diagnosis framework using structural model decomposition. Artif. Intell. 2014, 210, 1–35. [Google Scholar] [CrossRef]
- Pérez-Zuniga, C.; Chantery, E.; Trave-Massuyes, L.; Sotomayor, J.; Artigues, C. Decentralized diagnosis via structural analysis and integer programming. IFAC-PapersOnline 2018, 51, 168–175. [Google Scholar] [CrossRef]
- Verde, C.; Torres, L. Modeling and Monitoring of Pipelines and Networks; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pérez-Zuniga, C.; Sotomayor-Moriano, J.; Chanthery, E.; Travé-Massuyès, L.; Soto, M. Flotation process fault diagnosis via structural analysis. IFAC-PapersOnline 2019, 52, 225–230. [Google Scholar] [CrossRef]
- Saeed, N.; Abbod, M. Modelling oil pipelines grid: Neuro-fuzzy supervision system. Int. J. Intell. Syst. Appl. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Lauricella, M.; Farina, M.; Schneider, R.; Scattolini, R. A distributed fault detection and isolation algorithm based on moving horizon estimation. Proc. IFAC World Congr. 2017, 50, 15259–15264. [Google Scholar] [CrossRef]
- Lu, H.; Iseley, T.; Behbahani, S.; Fu, L. Leakage detection techniques for oil and gas pipelines: State-of-the-art. Tunn. Undergr. Space Technol. 2020, 98, 103249. [Google Scholar] [CrossRef]
- Baroudi, U.; Al-Roubaiey, A.A.; Devendiran, A. Pipeline leak detection systems and data fusion: A survey. IEEE Access 2019, 7, 97426–97439. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Li, J.; Jin, S. Leak detection monitoring system of long distance oil pipeline based on dynamic pressure transmitter. Measurement 2014, 49, 382–389. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Fu, L.; Mu, S.; Wang, L. Pipeline detection method based on multiple-pressure sensor and negative pressure wave. Trans. Microsyst. Technol. 2015, 34, 115–118. [Google Scholar]
- Kotani, M.; Katsura, M.; Ozawa, S. Detection of gas leakage sound using modular neural networks for unknown environments. Neurocomputing 2004, 62, 427–440. [Google Scholar] [CrossRef]
- Pérez-Zuñiga, G.; Rivas-Perez, R.; Sotomayor-Moriano, J.; Sánchez-Zurita, V. Fault detection and isolation system based on structural analysis of an industrial seawater reverse osmosis desalination plant. Processes 2020, 8, 1100. [Google Scholar] [CrossRef]
- Krysander, M.; Åslund, J.; Nyberg, M. An efficient algorithm for finding minimal overconstrained subsystems for model-based diagnosis. IEEE Trans. Syst. Man Cybem. Part A Syst. Hum. 2008, 38, 197–206. [Google Scholar] [CrossRef]
- Pérez-Zuñiga, G.; Chanthery, E.; Travé-Massuyès, L.; Sotomayor, J. Fault-driven minimal structurally overdetermined set in a distributed context. In Proceedings of the 27th International Workshop on Principles of Diagnosis: DX-2016, Denver, CO, USA, 4–7 October 2016. [Google Scholar]
- Rivas-Perez, R.; Sotomayor-Moriano, J.; Perez-Zuñiga, C.G. Adaptive expert generalized predictive multivariable control of seawater RO desalination plant for a mineral processing facility. IFAC-PapersOnline 2017, 50, 10244–10249. [Google Scholar] [CrossRef]
- Sanni, S.E.; Olawale, A.S.; Adefila, S.S. Modeling of sand and crude oil flow in horizontal pipes during crude oil transportation. J. Eng. 2015, 2015, 457860. [Google Scholar] [CrossRef][Green Version]
- Calderon-Valdez, S.N.; Feliu-Batlle, V.; Rivas-Perez, R. Fractional-order mathematical model of an irrigation main canal pool. Span. J. Agric. Res. 2015, 13, e0212. [Google Scholar] [CrossRef]
- Abhulimen, K.E.; Susu, A.A. Modelling complex pipeline network leak detection systems. Process Saf. Environ. Prot. 2007, 85, 579–598. [Google Scholar] [CrossRef]
- Rivas-Perez, R.; Sotomayor-Moriano, J.; Pérez-Zuñiga, G.; Soto-Angles, M. Real-time implementation of an expert model predictive controller in a pilot-scale reverse osmosis plant for brackish and seawater desalination. Appl. Sci. 2019, 9, 2932. [Google Scholar] [CrossRef]
- Frank, W.M. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Sukarno, P.; Sidarto, K.A.; Trisnobudi, A.; Setyoadi, D. Leak detection modeling and simulation for oil pipeline with artificial intelligence method. ITB J. Eng. Sci. 2007, 39, 1–19. [Google Scholar] [CrossRef][Green Version]
- Herrán-Gonzalez, A.; De La Cruz, J.M.; De Andrés-Toro, B.; Risco-Martín, J.L. Modeling and simulation of a gas distribution pipeline network. Appl. Math. Model. 2009, 33, 1584–1600. [Google Scholar] [CrossRef]
- Bogdevičius, M.; Janutėnienė, J.; Jonikas, K.; Guseinovienė, E.; Drakšas, M. Mathematical modeling of oil transportation by pipelines using anti-turbulent additives. J. Vibroeng. 2013, 15, 419–427. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).