The Role of Buoyancy Induced Instability in Transpirational Cooling Applications
Abstract
:1. Introduction
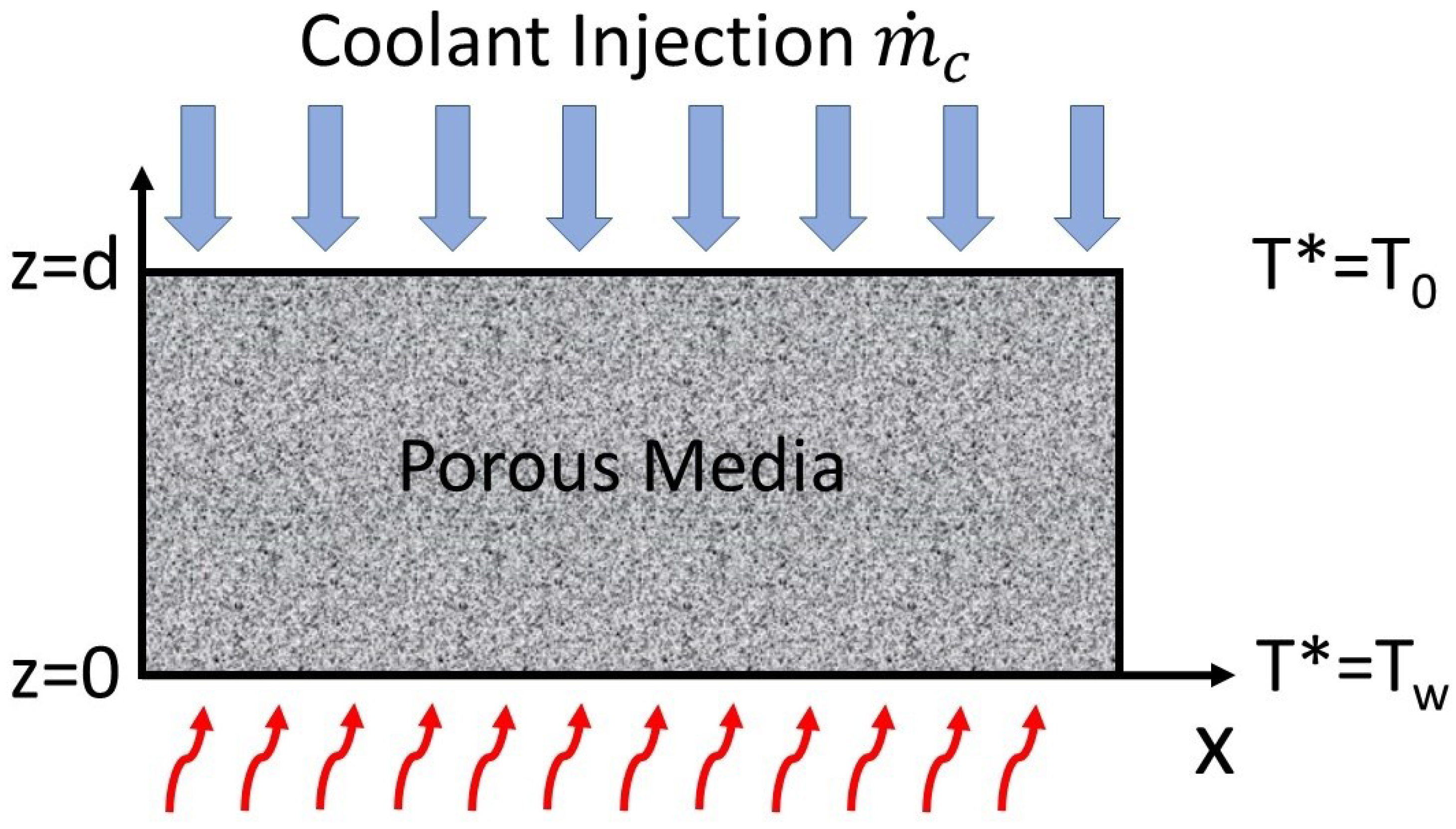
2. Mathematical Model
2.1. Governing Equations
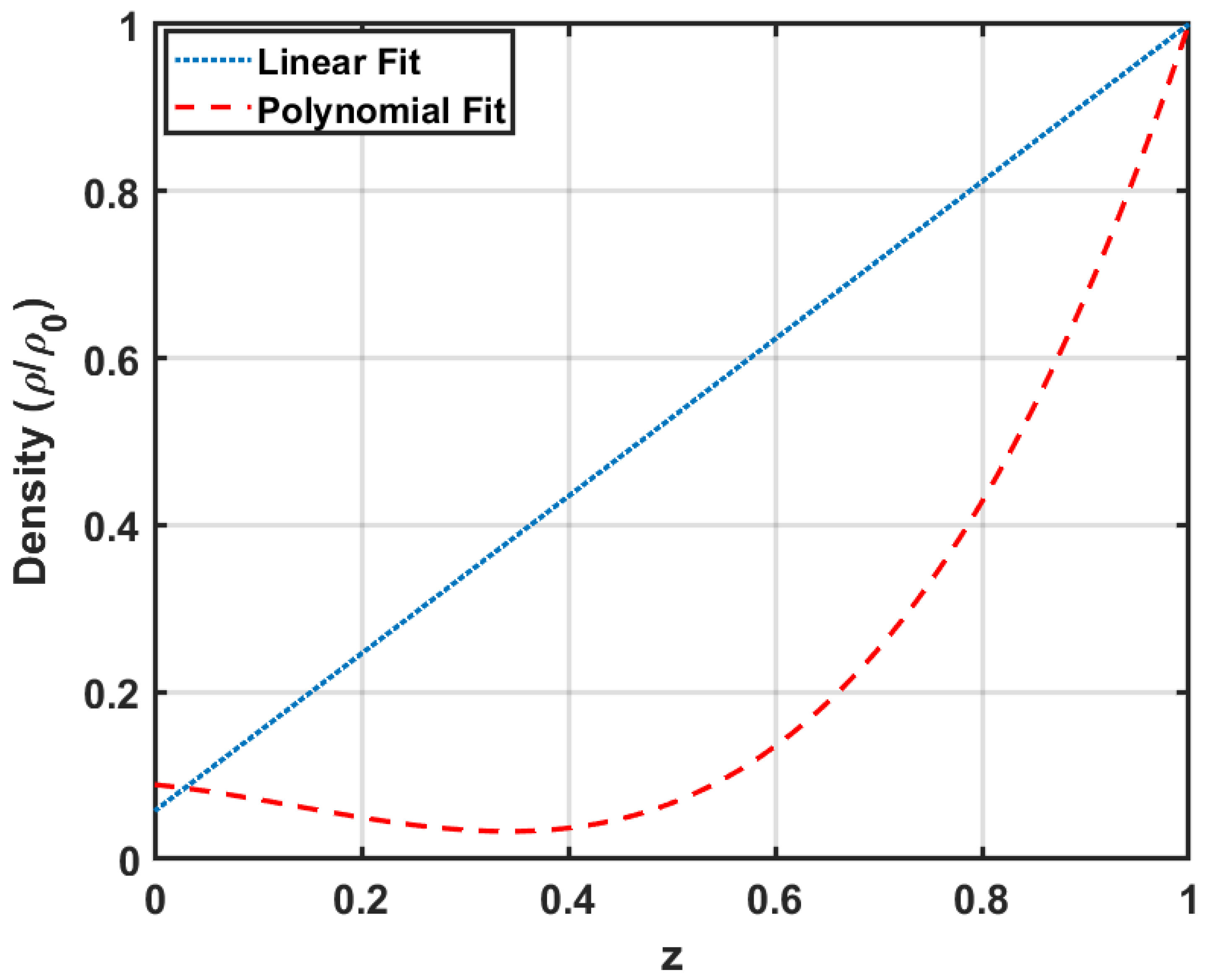
2.2. Base State
3. Linear Stability Analysis
4. Solution Techniques
4.1. Power Series
4.2. Chebyshev Method
4.3. Finite Difference Method
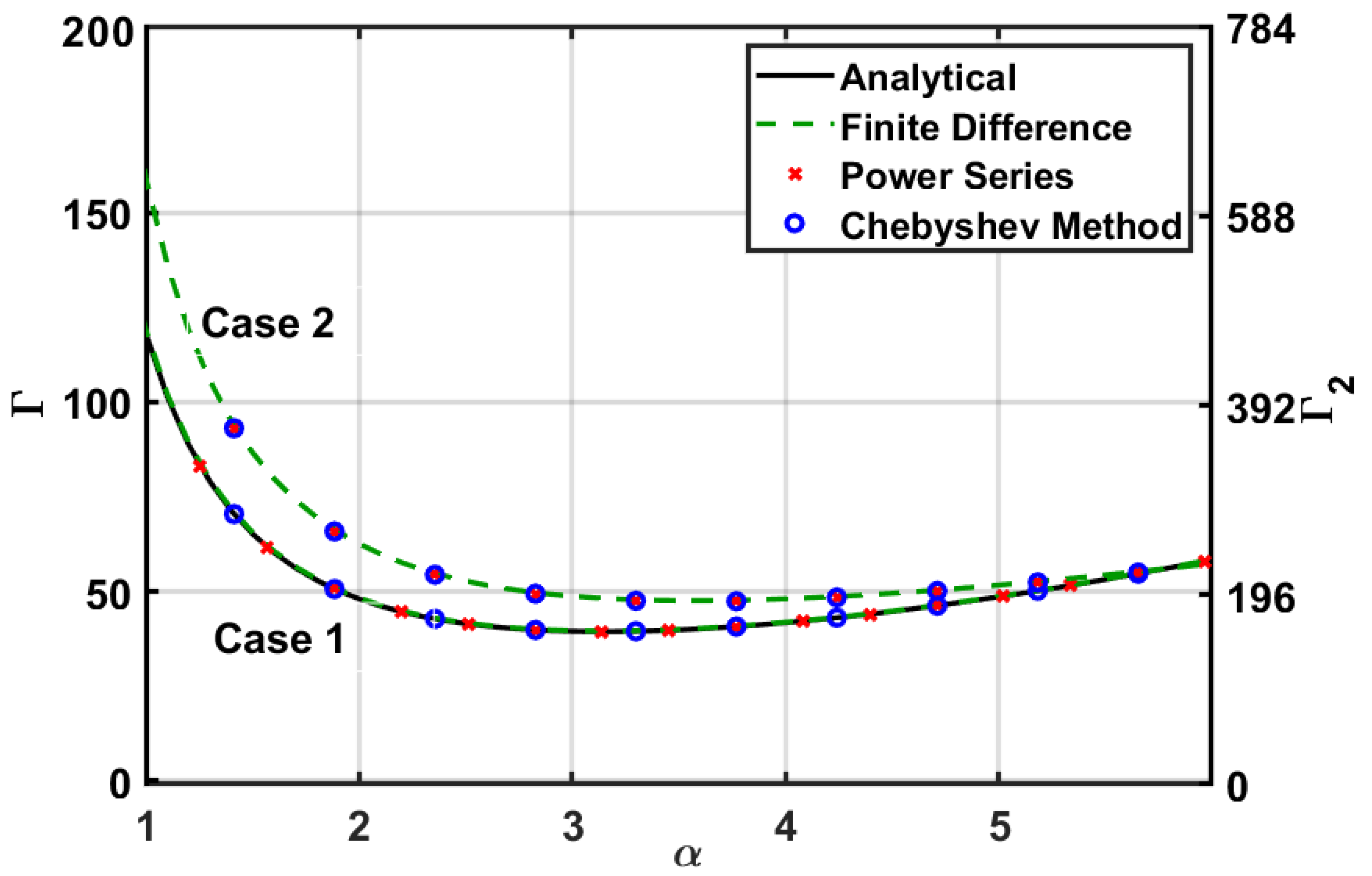
5. Results
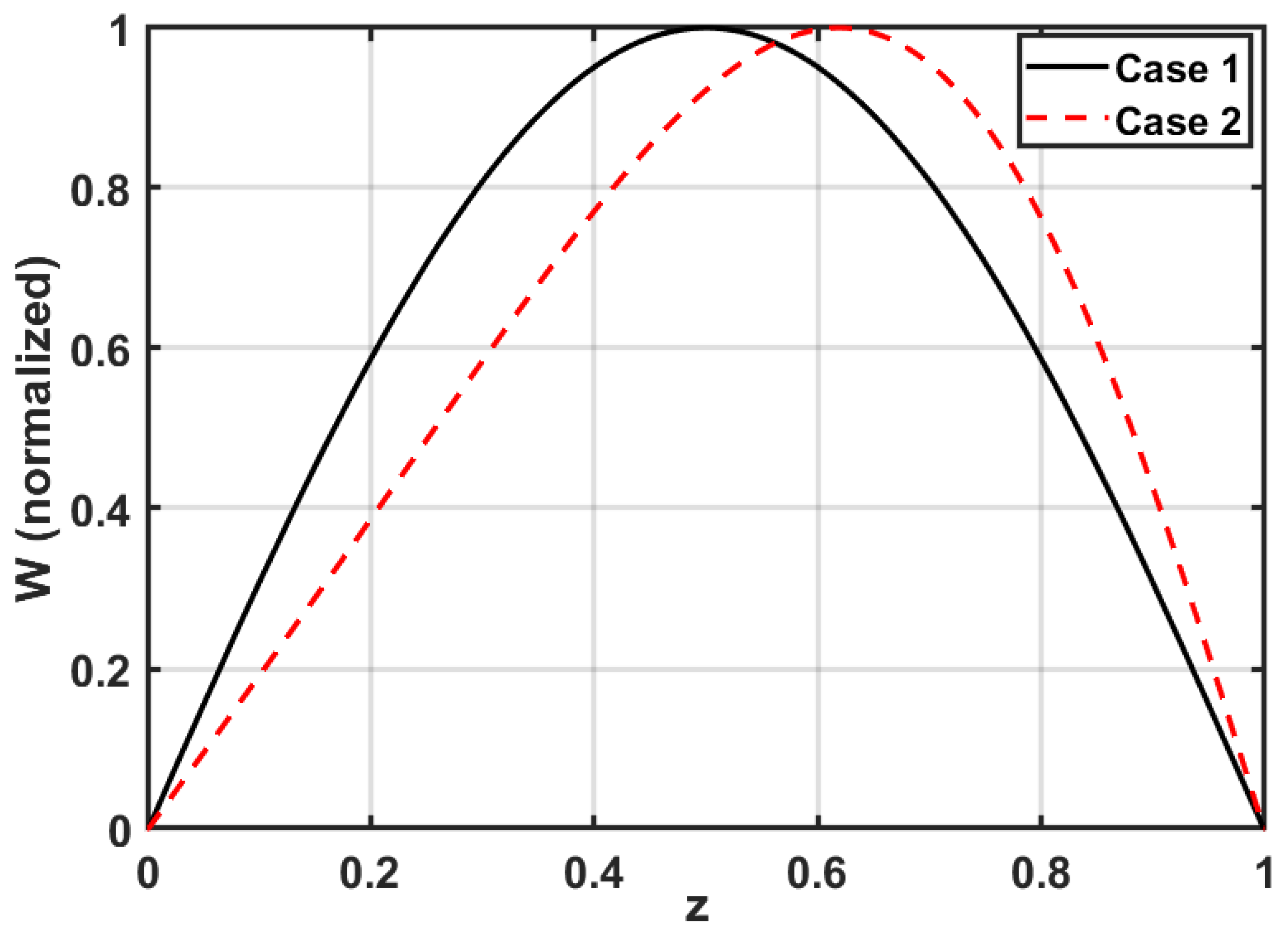
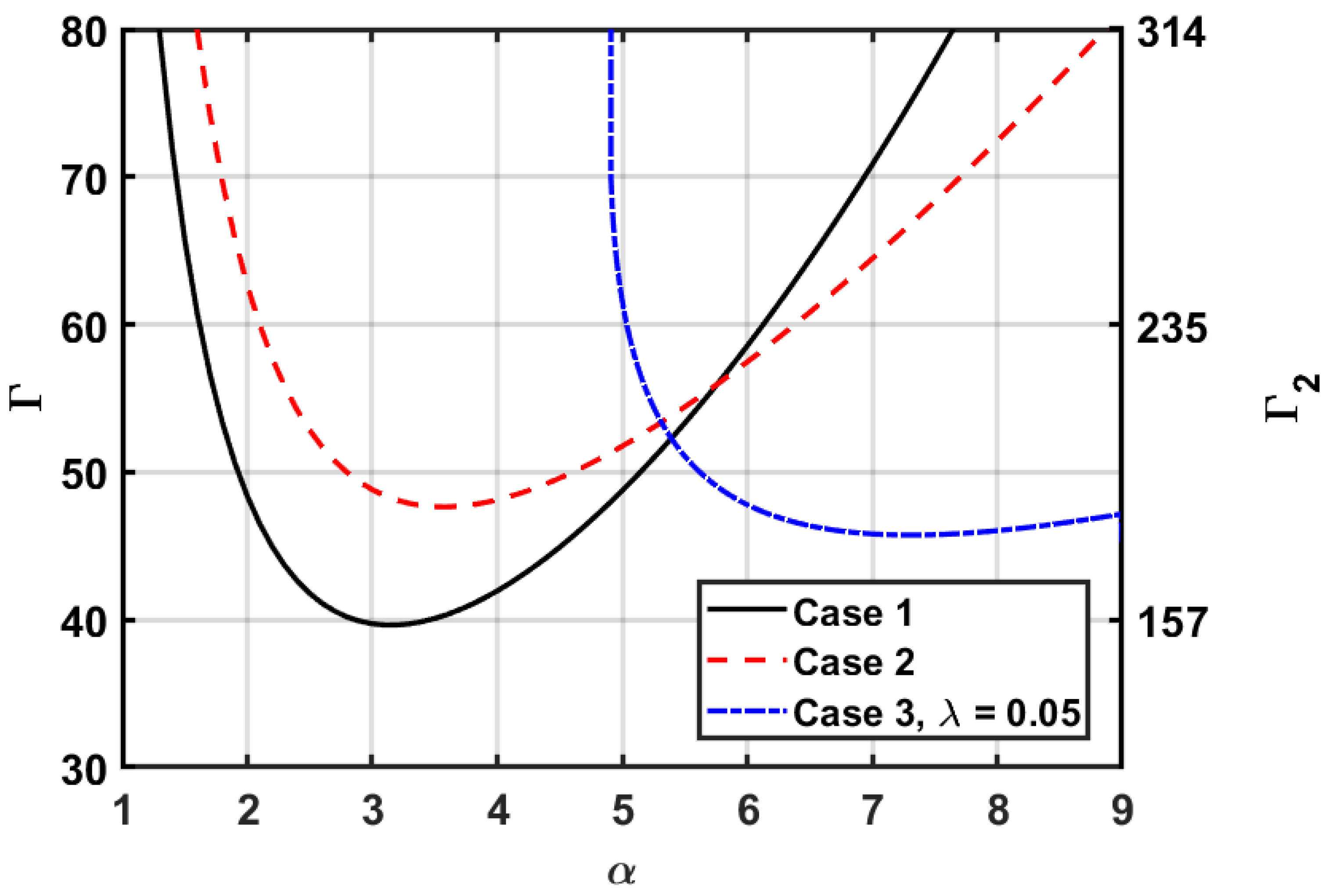
5.1. Case 1: and
5.2. Case 2: and
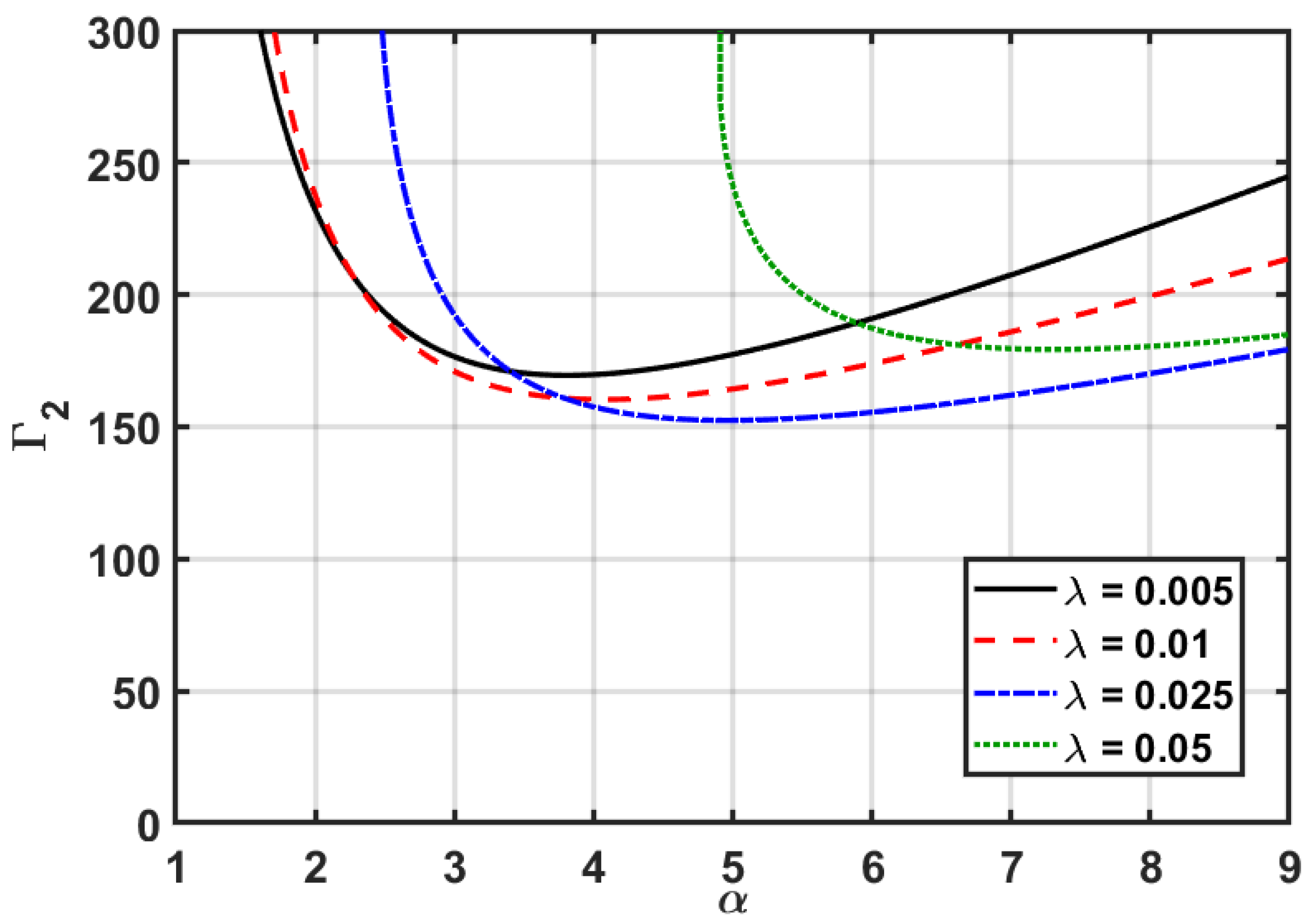
5.3. Case 3: and
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rannie, W.; Dunn, L.G.; Millikan, C.B. A Simplified Theory of Porous Wall Cooling; Technical Report; Jet Propulsion Laboratory, National Aeronautics and Space: Pasadena, CA, USA, 1947. [Google Scholar]
- Eckert, E.R.G.; Livingood, J.N. Comparison of Effectiveness of Convection-, Transpiration-, and Film-Cooling Methods with Air as Coolant; National Advisory Committee for Aeronautics, Lewis Flight Propulsion Laboratory: Cleveland, OH, USA, 1954; Volume 1182. [Google Scholar]
- Eckert, E.R.G.; Drake, R.M., Jr. Analysis of Heat and Mass Transfer; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Hermann, T.; McGilvray, M. Analytical solution of flows in porous media for transpiration cooling applications. J. Fluid Mech. 2021, 915, A38. [Google Scholar] [CrossRef]
- Choi, S.; Scotti, S.; Song, K.; Ries, H.; Choi, S.; Scotti, S.; Song, K.; Ries, H. Transpiring cooling of a scram-jet engine combustion chamber. In Proceedings of the 32nd Thermophysics Conference, Atlanta, GA, USA, 23–25 June 1997; p. 2576. [Google Scholar]
- Langener, T.; Von Wolfersdorf, J.; Steelant, J. Experimental investigations on transpiration cooling for scramjet applications using different coolants. AIAA J. 2011, 49, 1409–1419. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, S.; Zhao, R.; Jiang, P. Experimental investigation of flow coking and coke deposition of supercritical hydrocarbon fuels in porous media. Energy Fuels 2018, 32, 2941–2948. [Google Scholar] [CrossRef]
- Ifti, H.S.; Hermann, T.; McGilvray, M. Flow characterisation of transpiring porous media for hypersonic vehicles. In Proceedings of the 22nd AIAA International Space Planes and Hypersonics Systems and Technologies Conference, Orlando, FL, USA, 17–19 September 2018; p. 5167. [Google Scholar]
- Dahmen, W.; Gotzen, T.; Müller, S.; Rom, M. Numerical simulation of transpiration cooling through porous material. Int. J. Numer. Methods Fluids 2014, 76, 331–365. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Han, X. Numerical investigation of transpiration and ablation cooling. Heat Mass Transf. 2007, 43, 275–284. [Google Scholar] [CrossRef]
- Glass, D.E.; Dilley, A.D.; Kelly, H.N. Numerical analysis of convection/transpiration cooling. J. Spacecr. Rocket. 2001, 38, 15–20. [Google Scholar] [CrossRef] [Green Version]
- Horton, C.; Rogers, F., Jr. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Lapwood, E. Convection of a fluid in a porous medium. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1948; Volume 44, pp. 508–521. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Cham, Switzerland, 2006; Volume 3. [Google Scholar]
- Prats, M. The effect of horizontal fluid flow on thermally induced convection currents in porous mediums. J. Geophys. Res. 1966, 71, 4835–4838. [Google Scholar] [CrossRef]
- Barletta, A.; Celli, M.; Rees, D.A.S. Darcy–Forchheimer flow with viscous dissipation in a horizontal porous layer: Onset of convective instabilities. J. Heat Transf. 2009, 131, 072602. [Google Scholar] [CrossRef]
- Celli, M.; Impiombato, A.N.; Barletta, A. Buoyancy-driven convection in a horizontal porous layer saturated by a power-law fluid: The effect of an open boundary. Int. J. Therm. Sci. 2020, 152, 106302. [Google Scholar] [CrossRef]
- Barletta, A.; Celli, M. The Horton–Rogers–Lapwood problem for an inclined porous layer with permeable boundaries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180021. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wooding, R. Rayleigh instability of a thermal boundary layer in flow through a porous medium. J. Fluid Mech. 1960, 9, 183–192. [Google Scholar] [CrossRef]
- Sutton, F.M. Onset of convection in a porous channel with net through flow. Phys. Fluids 1970, 13, 1931–1934. [Google Scholar] [CrossRef]
- Homsy, G.M.; Sherwood, A.E. Convective instabilities in porous media with through flow. AIChE J. 1976, 22, 168–174. [Google Scholar] [CrossRef]
- Partha, M. Nonlinear convection in a non-Darcy porous medium. Appl. Math. Mech. 2010, 31, 565–574. [Google Scholar] [CrossRef]
- RamReddy, C.; Naveen, P.; Srinivasacharya, D. Influence of non-linear Boussinesq approximation on natural convective flow of a power-law fluid along an inclined plate under convective thermal boundary condition. Nonlinear Eng. 2019, 8, 94–106. [Google Scholar] [CrossRef]
- Lemmon, E.; Bell, I.H.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- May, L.; Burkhardt, W.M. Transpiration Cooled Throat for Hydrocarbon Rocket Engines; Technical Report; Aerojet Propulsion Div: Sacramento, CA, USA, 1991. [Google Scholar]
- Harfash, A. Numerical methods for solving some hydrodynamic stability problems. Int. J. Appl. Comput. Math. 2015, 1, 293–326. [Google Scholar] [CrossRef] [Green Version]

| Property | * | K | T | L | |||
|---|---|---|---|---|---|---|---|
| Units | K | mm | - | ||||
| Value | 0.05–0.15 | 500–1000 | 1–5 | 650 | 0.003 | 5–10 | 5–20 |
| Reference | [6] | [6] | current work | [25] | [24] | [6] | [6] |
| Power Series | Chebyshev | Finite Difference | |
|---|---|---|---|
| Maximum Error [%] | 1.92 | 0.74 | |
| RMS Error [%] | 0.44 |
| Power Series | Finite Difference | |
|---|---|---|
| Maximum Error [%] | 4.6 | |
| RMS Error [%] |
| 3.81 | 43.24 | |
| 4.07 | 40.90 | |
| 4.96 | 38.89 | |
| 7.31 | 45.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wanstall, C.T.; Johnson, P.R. The Role of Buoyancy Induced Instability in Transpirational Cooling Applications. Appl. Sci. 2021, 11, 11766. https://doi.org/10.3390/app112411766
Wanstall CT, Johnson PR. The Role of Buoyancy Induced Instability in Transpirational Cooling Applications. Applied Sciences. 2021; 11(24):11766. https://doi.org/10.3390/app112411766
Chicago/Turabian StyleWanstall, C. Taber, and Phillip R. Johnson. 2021. "The Role of Buoyancy Induced Instability in Transpirational Cooling Applications" Applied Sciences 11, no. 24: 11766. https://doi.org/10.3390/app112411766
APA StyleWanstall, C. T., & Johnson, P. R. (2021). The Role of Buoyancy Induced Instability in Transpirational Cooling Applications. Applied Sciences, 11(24), 11766. https://doi.org/10.3390/app112411766





