Abstract
Accurately measuring the lower extremities and L5/S1 moments is important since L5/S1 moments are the principal parameters that measure the risk of musculoskeletal diseases during lifting. In this study, protocol that predicts lower extremities and L5/S1 moments with an insole sensor was proposed to replace the prior methods that have spatial constraints. The protocol is hierarchically composed of a classification model and a regression model to predict joint moments. Additionally, a single LSTM model was developed to compare with proposed protocol. To optimize hyperparameters of the machine learning model and input feature, Bayesian optimization method was adopted. As a result, the proposed protocol showed a relative root mean square error (rRMSE) of 8.06~13.88% while the single LSTM showed 9.30~18.66% rRMSE. This protocol in this research is expected to be a starting point for developing a system for estimating the lower extremity and L5/S1 moment during lifting that can replace the complex prior method and adopted to workplace environments. This novel study has the potential to precisely design a feedback iterative control system of an exoskeleton for the appropriate generation of an actuator torque.
1. Introduction
More than 40% of workers suffer from work-related musculoskeletal disorders (WMSD) annually due to manual materials handling (MMH) tasks despite efforts to improve the work environment [1]. It has been reported that 52% of WMSDs are caused by lifting tasks, of which 62% are low-back musculoskeletal disorders [2]. The high mechanical load applied to the lumbar spine during lifting is considered a major risk factor for back pain. Studies have been conducted to measure the risk factor by calculating low-back loading [3]. Internal moments to a body segment are caused by a combined action of muscle strength within the joint or tensile force of the skin, joint capsule, and ligaments [4]. By calculating external joint moments, internal moments acting within each joint can be estimated. The L5/S1 moment tends to increase according to the weight of the object. Repetitive moment is one of the risk factors that can increase the incidence of low-back musculoskeletal disorders [5]. The lower extremity and L5/S1 moment are also used as evaluation parameters for lifting posture [6]. Therefore, the moment is being studied as a major parameter to determine the risk of musculoskeletal disorders during lifting [3,6,7,8].
Optical 3D motion tracking system (OTS) is a method of calculating the lower extremity and L5/S1 moments [9]. The OTS acquires optical marker trajectory and ground reaction force based on optical camera, force plate, and the subject’s anthropometric information. It then calculates the moment of each joint using the acquired optical marker trajectory, ground reaction force, and inverse dynamic method [10]. Calculating moments using an OTS is considered as the golden standard method. Many studies have been conducted to measure the lower extremity and L5/S1 moment during symmetric and asymmetric lifting [1,6,8,11,12]. However, the OTS has a disadvantage in that it is impossible to be utilized in a working environment due to spatial constraints [13,14]. To overcome a spatial limitation, methods using wearable sensors have been reported [15]. Wearable sensors such as inertial measurement unit (IMU), insole sensor, or portable force plate can be used to calculate joint moments [16,17]. In the case of an IMU sensor, the center of joint can be obtained by attaching it onto the body segment, with an insole sensor or portable force plate that can be worn on shoes to obtain ground reaction force data [18]. Previous studies suggest L5/S1 moment measurement system using 12–17 IMU sensors and 2 force shoes or insole sensors [18,19]. According to recent studies mentioned above, studies using human body modeling [16,17,18] based on wearable sensor data have shown the possibility of overcoming limitations of OTS using multiple wearable sensors. However, using multiple sensors showed a complicated application method, inducing unnatural movement and taking a longer time for detachment in a real working environment. In addition, a robust estimation of movement is difficult due to substantial movement variability and irregular data [20].
To overcome these limitations mentioned above, previous studies have been conducted to predict biomechanical parameters such as ground reaction force, joint torque, and joint moment by replacing it with artificial intelligence techniques [21,22]. Mundt et al. (2020) have conducted a study to estimate the angle and moment of lower extremity joints during gait using IMU sensors and machine learning techniques. Their research suggested a predictive model using long short-term memory (LSTM). The predicted moment and joint angle showed a normalized root mean square error (RMSE) of about 10% [23]. Additionally, Choi et al. (2019) have developed an LSTM model that predicts the inclination angle between the center of gravity and the center of pressure when walking using time-series data obtained from a single IMU sensor. Compared to an artificial neural network (ANN), the relative RMSE result of the LSTM model showed 6% reduction, indicating improved accuracy [24]. Previous studies have reported that the LSTM shows particularly high performance when predicting biomechanical parameters using motion sequenced sensor data while developing a machine learning model in the biomechanical field.
Therefore, in this study, we evaluated the performance of LSTM for predicting a joint moment based on plantar pressure data collected from a wearable insole sensor during a lifting task.
The purpose of this study is to propose a system that predicts lower extremities and L5/S1 joint moment using machine learning model and plantar pressures from an insole sensor system. In detail, we developed a new deep learning structure by combining classifier and regressor as one network to estimate the lower extremities and L5/S1 moments. Additionally, we evaluated the usefulness of the proposed machine learning model by applying to various lifting conditions.
2. Materials and Methods
2.1. Subjects, Apparatus, and Lifting Experiments
This experiment was conducted on 9 adult males (age: 23.1 ± 1.4 years, height: 176.6 ± 4.9 cm, weight: 69.3 ± 6.7 kg). The subjects were selected based on the questionnaires of the subjects considering general musculoskeletal diseases such as rheumatoid arthritis, osteoarthritis, and mechanical pain in the lower extremities and lumbar joints [25]. This experiment was approved by the local ethics committee. It was carried out following the guidelines of Sungkyunkwan University. In addition, written informed consent was obtained from all participants before the experiment.
As experimental equipment, six MCam2 cameras (VICON, Oxford Metrics, Oxford, UK) and 2 OR6-6-2000 ground reaction forces (AMTI Inc., Newton, MA, USA) were used. Each system was operated at sampling rates of 120 Hz and 1080 Hz, respectively [24,26,27]. Participants wore a Pedar-X insole system (Pedar Mobile, Novel Electronics Inc., GmbH, Munich, Germany). Data were acquired at 100 Hz [21,28]. The camera and ground reaction force data were time-series synchronized with a Vicon 460 system. The motion analysis system and the Pedar-X insole system were manually synchronized based on the instance when the subject lifted a box from the ground during a lifting task.
Optical markers were attached to 16 anatomical landmarks of the lumbar spine and lower extremity joints of each subject based on the modified Helen Hayes marker protocol [11,26]. In addition, one optical marker was attached to the box to distinguish the event of the lifting task. Each subject performed warm-up exercises before participating in this experiment. Preliminary movements were performed to adapt to the experimental environment. For the lifting motion, two postures were performed: squat and stoop. Each lifting motion was performed with boxes (Size: 32 × 40 × 25 cm3) having 3 different weights (4, 8, and 12 kg). The speed of the lifting task was set as normal, fast, or slow. Each speed indicated the normal, fast, and slow speed considered by the subject, respectively. Each subject performed the 54 times of lifting motions (3 repetitions for 18 types of lifting tasks: 2 postures × 3 weights × 3 speeds). Subjects are asked to lift boxes from ground to the knuckle height [5,29].
2.2. Data Processing
Optical marker trajectories obtained by OTS were filtered by 4th-order, low-pass Butterworth filter and cut-off frequency was set at 5 Hz [12]. Kinematic data of the lower extremities and L5/S1 moments were calculated using Euler angle and numerical differentiation methods. Based on the kinematic data, the ground reaction force data of 6 axes, and the subject’s anthropometric information, the lower extremities and L5/S1 moments of sagittal plane were calculated. These calculations were performed using kinematic and kinetic models developed in the Biomedical Engineering Laboratory of Sungkyunkwan University [8,30]. During the lifting task, pressure data obtained from the insole sensor were filtered with 3rd Butterworth, zero-lag low-pass filter and the frequency was set at 7 Hz [31]. The event of the lifting task was segmented based on the optical marker attached to the box. The time when the box was moved from the ground was marked as the starting point and the time when the box reached the highest point was marked as end of task. The amplitude of moment obtained from the OTS and 99 pressure data collected from the insole system were normalized by dividing the subject’s body weight (BW). In addition, the length of moment and pressure data were normalized to 100% for each trial [27]. In the proposed model, each posture was labeled for motion classification where the squat posture was labeled as 0 and the stoop posture was labeled as 1. The total insole pressure, lower extremities, and L5/L1 moments dataset was 480.
2.3. Neural Network Architecture
In this study, an architecture hierarchically composed of a classification model and a regression model was proposed to predict lower extremities and L5/S1 moments during symmetric lifting using plantar pressure obtained from the insole sensor. In order to classify the lifting motion, the following three machine learning techniques commonly used as classification models in previous studies [32,33] were used: ANN, Support Vector Machine (SVM), Random Forest (RF). The LSTM model showing relatively high performance on a time-series data set [34,35,36,37] was used as a regression model for predicting joint moment. Figure 1 presents the structure of the proposed architecture and the overall flow chart to predict lower extremities and L5/S1 moments on sagittal plane.
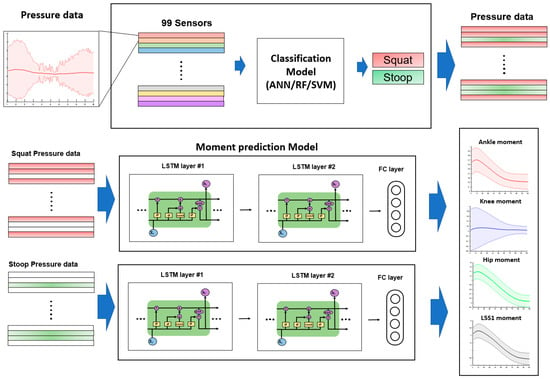
Figure 1.
Flow chart of joint moment prediction using insole pressure data developed in this study.
The proposed architecture consisted of 1 classification model that could classify the lifting posture, and 2 regression models for the lower extremities and L5/S1 moments. For each classification model, pre-processed pressure data acquired from the left insole of the Pedar-X were used as input values, and the labeled index for lifting posture was used as an output value [6]. Based on results of the classification model, dataset was classified into squat data and stoop data. Pressure values and lower extremities and L5/S1 moments were used as input and output for each regression model, respectively.
To evaluate the performance of the proposed model, a single machine learning model composed of single LSTM was constructed, and the input and output values were as follows. The pressure data obtained from the left insole of Pedar-X were used as input data, and the predicted values were the sagittal moment of the left ankle, left knee, left hip, and L5/S1 was used.
In this study, performance was evaluated through a 10-fold cross-validation. The ratio of training, validation, and testing data was 80:10:10 (the number of training data set: 384, the number of validation data set: 48, the number of test data set: 48). All models were trained and tested using MATLAB R2020a version (The Mathworks, Inc., Natick, MA, USA) and RTX 2080 Ti GPU.
2.4. Hyperparameter Optimization
Hyperparameters of all models used in this study were optimized using the Bayesian optimization method, as an efficient method to find the optimal solution for a function with a large amount of computation based on the Gaussian probability [38]. As an optimization objective function of the proposed architecture, it is constructed based on the error rate of the classification model and the rRMSE of the regression model, which is shown in Equations (1) and (2). In addition, the single LSTM model used rRMSE as the objective function:
where f(x) is the optimization objective function and error is value calculated based on the error rate of the classification model and the rRMSE of the regression model. The x is the error rate of the classification model and y is the rRMSE of the regression model. In addition, and presented as the weighted values of the error rate of the classification model and the rRMSE value of the regression model, respectively. Weights are set as 0.7 and 0.3, respectively [39]. The maximum optimization iteration was set to 100. Table 1 presents the classification model’s hyperparameter and their ranges optimized by the Bayesian optimization method. Table 2 shows the LSTM model’s hyperparameters and ranges. Optimized results of the LSTM models are shown in Table 3.

Table 1.
The classification model’s optimized hyperparameter and their ranges by the Bayesian optimization method.

Table 2.
LSTM model’s hyperparameters and their structure selected by the Bayesian optimization method.

Table 3.
LSTM model’s structure and hyperparameters optimized by the Bayesian optimization method.
2.5. Data Analysis
The classification model of symmetric lifting posture was evaluated for classification accuracy rate. The performance of the regression model was evaluated with RMSE, Pearson correlation coefficient (R), and rRMSE using moments of the lower extremities and L5/S1 obtained from the OTS as a reference system. RMSE, rRMSE, and R are calculated with Equations (3)–(5), respectively:
where represents the actual value, represents the predicted value from the artificial intelligence model, and N represents the length of 1 trial. In Equation (2), R represents the value of the Pearson correlation coefficient. is the average of the actual values, is the average of the values predicted by the artificial intelligence model, is the maximum value in 1 trial, and is the minimum value in 1 trial. One-way analysis of variance (ANOVA) was performed to compare the accuracy of the single LSTM and the proposed artificial intelligence model. After the analysis, post hoc Tukey’s method was used. The significance level was set at p < 0.01. All statistics analyses were performed using PASW Statistics 18 (Ver. 18, SPSS Inc., Chicago, IL, USA).
For moments obtained from the proposed model and the reference system, the maximum value among absolute values of moments was extracted for each trial. The error rate between the extracted peak moment value of the proposed model and the reference system was calculated using the following Equation (6):
where was the peak value among absolute values of prediction values of the artificial intelligence model, and was the peak value among absolute values of the reference moment. meant the error rate between peak moment.
3. Results
Figure 2 presents results of feature selection on the number of sensors as input data using the Bayesian optimization method. For single LSTM, ANN-LSTM, RF-LSTM and SVM-LSTM models, 96, 96, 98 and 99 sensors were selected, respectively. Results of the objective function at the time when the sensor was selected were 14.49, 15.38, 6.53 and 4.94, respectively.
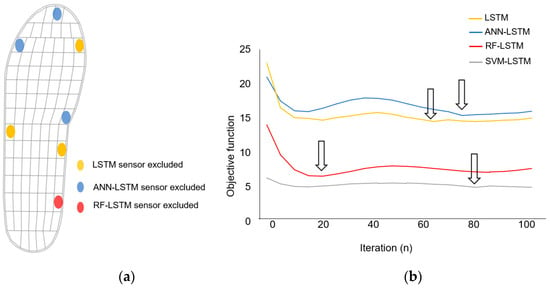
Figure 2.
(a) Selected optimal sensor location; (b) The progress of optimization using Bayesian optimization showing the objective function value for selecting optimal input feature.
Table 4 shows classification accuracies of ANN, RF, and SVM as motion classification models of the proposed algorithm. Based on confusion matrix results of 10-fold cross-validation, average accuracies of ANN, RF, and SVM were 83.54 ± 4.48, 91.67 ± 3.40, and 94.00 ± 2.43%, respectively. There was a significant difference (p < 0.01) between the accuracy of ANN, RF, and SVM models.

Table 4.
Symmetric lifting task posture classification accuracy for three classification models.
In Table 5, RMSE, rRMSE, and R of each model were calculated to evaluate the performance of single LSTM, ANN-LSTM, RF-LSTM, and SVM-LSTM models. With the squat posture, rRMSE (%) results of single LSTM, ANN-LSTM, RF-LSTM, and SVM-LSTM were 9.38~18.64, 8.81~20.35, 8.06~16.33 and 8.44~14.03, respectively. With the stoop posture, rRMSE (%) values were 9.26~18.70, 9.59~18.36, 7.91~15.36 and 8.02~13.73, respectively. In both squat and stoop lifting tasks, the knee showed the highest rRMSE and a low correlation coefficient while the hip joint showed the lowest rRMSE with a high correlation coefficient.

Table 5.
RMSE, rRMSE and R (correlation coefficients) values between calculated joint moment from optical tracking system and predicted joint moment with a hierarchical deep learning model.
Figure 3 shows performances of single LSTM, ANN-LSTM, RF-LSTM, and SVM-LSTM models by rRMSE. The SVM-LSTM model showed significant differences (p < 0.01) in ankle and L5S1 joints compared with single LSTM and ANN-LSTM models. In addition, for the knee joint, the SVM-LSTM model showed a significant difference (p < 0.01) compared with all other models. Compared to the single LSTM model, the SVM-LSTM model showed approximately 2.19%, 4.68%, 1.23% and 1.35% rRMSE reductions for the ankle, knee, hip, and L5/S1, respectively. In particular, the knee joint moment showed the largest decrease in rRMSE compared to other joints.
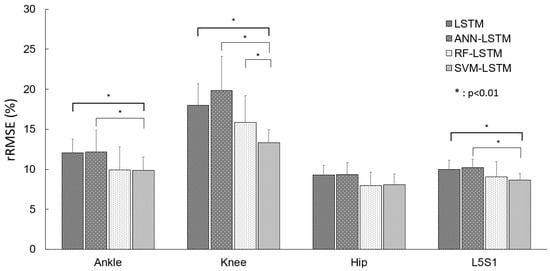
Figure 3.
Relative RMSE values between reference moment and predicted moment by deep learning models.
Figure 4 shows the moment predicted by the single LSTM model, the SVM-LSTM model and representative values of the reference moment classified according to posture. The x-axis is the time normalized to 100% during the lifting task and the y-axis is the moment normalized by the weight of each subject. (−) on the y-axis means flexion moment and (+) refers to the extension moment. During the lifting task, changes in the moment of the knee joint showed a different tendency from those of the ankle, hip joint, and lumbar joint. In the squat posture, the peak extension moment at the knee joint occurred at the beginning of the lifting motion and showed a pattern of decreasing close to zero. In stoop posture, the peak flexion moment occurred initially, and the flexion moment tended to decrease as the lifting task progressed.
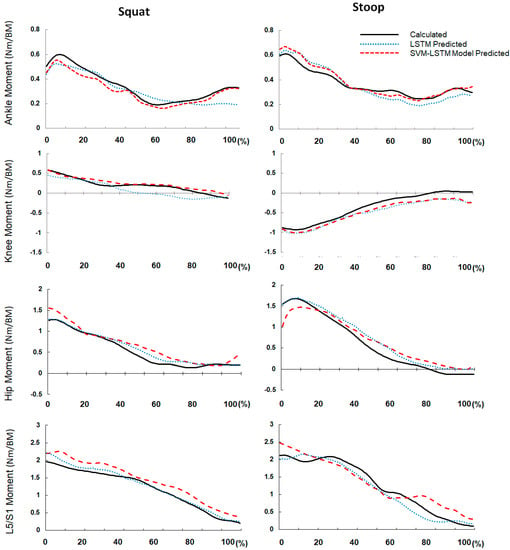
Figure 4.
Representative results of lower extremities and L5/S1 joint moment prediction (ankle, knee, hip and L5/S1) from the reference system and the SVM-LSTM model.
Table 6 shows the reference peak moment, the predicted peak value of the SVM-LSTM model, and the error rate of the peak moment of the lower extremity and L5/S1. Error rates were 5.20 ± 4.85 (%), 8.77 ± 6.45 (%), 3.20 ± 2.33 (%), and 5.19 ± 3.18 (%) for the ankle, knee, hip and L5/S1, respectively.

Table 6.
Reference peak moment calculated from OTS, peak moment predicted from SVM-LSTM model, and error rate between these values.
4. Discussion
In this study, a novel machine learning-based protocol was proposed to predict lower extremity and L5/S1 moments during symmetrical lifting using plantar pressure as an input. This study designed a structure that combines SVM, a classifier, and LSTM model, one of the time-series prediction deep learning models. The performance of the SVM-LSTM model showed rRMSE (%) of 8.06~13.88, and peak moment error rate (%) of 3.20~8.77 (Table 3 and Table 5).
Recently, cases of estimating the moment of the L5/S1 during lifting using wearable sensor data and human body modeling showed rRMSE of 8~10% and peak moment error rate of 5~10% by wearing 6~17 IMU sensors and two portable force plate or insole sensors [19,38]. These could be judged to have similar accuracy to results of this study, which estimated the lower extremity and L5/S1 moments during symmetrical lifting using 2 insole sensors and the SVM-LSTM hierarchical machine learning model. According to Matijevich (2020), the architecture presented in this study is a system that wears two insoles [17]. It is expected to show higher applicability to the working environment than a system that wears 6–19 wearable sensors (e.g., IMU sensors) [17]. Kipp et al. (2018) developed a model that predicts the lower extremity moment during weightlifting operation using artificial intelligence and optical marker trajectories. As a result, the error rate of peak moment was about 5 to 16% [40]. Considering the similarity between weightlifting and symmetric lifting, the deep learning-based model proposed in this study showed similar results with a small number of sensors, indicating that the model proposed in this study could be more applicable to the field in terms of convenience than models proposed in previous studies (Table 3).
The proposed deep learning-based moment prediction model consists of a hierarchical structure, which is a step of classifying posture (stop and square) and a step of estimating the moment. Collected data were analyzed by dividing the lifting operation into three types of conditions (speed, weight, and posture). As a result, the foot pressure which was the input of the proposed model showed a clear difference according to posture in the cumulative pressure distribution of 1 trial based on the result classification model composed the posture among three types of conditions as the output of the classification model [41]. According to results of this study, the knee joint showed a high rRMSE (4.68%) reduction compared to other joints for the predicted moment between the SVM-LSTM model and the single LSTM model. Khashei et al. (2012) have reported that the hierarchical architecture is highly likely to improve the performance due to reduced data complexity [42]. However, in the case of the ANN-LSTM model compared with the single LSTM model, rRMSE and correlation coefficient showed no significant performance improvement. This was because classification accuracy of ANN was 83.5 ± 4.5%, which was low compared to accuracies of other RF and SVM classification models. This might be due to the accumulation of errors due to misclassification of the ANN classification model. Hierarchical architecture can be applied as a method to improve performance when a single model does not show high performance due to complexity of input/output data. However, errors can accumulate depending on the performance of the classification model. Thus, it is necessary to consider the performance of the classification model.
In this study, Bayesian optimization was used to obtain the optimal sensor location information from the acquired 99 pressure sensor data. According to a previous study, the main change direction of the pressure center of the foot during symmetric lifting was the anterior/posterior direction, and a constraint was given to select the number of at least 1 sensor in each area to select the sensor position for the entire range of the foot [43]. When the subject wears an insole sensor, the position and absolute value at which the sensor is pressed are different depending on the position of the sensor and the size of the foot. Thus, a large number of sensors was selected. Additionally, in this study, the area of the foot was divided into 3 zones (forefoot, midfoot, rearfoot) and the sensor position was extracted for each area. In the case of a different task, for example, an asymmetric lifting, it is necessary to consider a method of selecting an optimal position by setting the region differently according to the position of the pressed sensor. As an objective function, the error rate of the classification model and the rRMSE of the regression model were calculated by giving 7 and 3 weights, respectively. This is because, in the case of a model using a hierarchically structured protocol such as in this study, the error in the classification model has a structure in which the error in the subsequent regression model can be accumulated. To minimize the misclassification rate, the ratio of 7 to 3 was chosen. However, if weights of the objective function for the classification model and the regression model are different, the selection of features might be different.
The purpose of this study is to propose a system that can predict the joint moments of the lower extremities and L5/S1 in the workplace. The proposed system is meaningful in overcoming the spatial constraints of existing studies. It is considered that this system can be applied to workers who are engaged in an irregular working environment. For example, paramedics show a 13 times higher risk of musculoskeletal disorders than other medical workers, mainly due to frequent lifting of patients [44]. In addition, agricultural workers are also exposed to musculoskeletal disorders caused by lifting work, carrying heavy objects, or improper posture [45,46]. Based on the system proposed in this study, a prediction of the lower extremities and L5/S1 joint moment might provide a continuous health notification for workers who do not have an irregular working environment. Therefore, the risk of musculoskeletal disorders can be reduced by applying the health notification which includes the system proposed in this research.
This study has several limitations. First, the data used for training the model consisted of only the data of young adult males. However, to the best of our knowledge, this is the first study to predict moments of the lower extremities and lumbar spine during work-related lifting motions using insole sensors and machine learning. In future research, it is necessary to include the various age groups in order to increase the usefulness of the model. Second, a model was constructed for limiting the lifting task. In this study, models were constructed for the squat and stoop posture during symmetric lifting. In future research, it is necessary to construct a generalized model for lifting tasks by adding data to symmetric lifting posture such as free lifting, semi-squat, and asymmetric lifting tasks. Lastly, a limitation of this study is that it was conducted with limited number of healthy adults. The subjects’ musculoskeletal disorders were defined by their opinion without any medical history confirmation. Consequently, laterality or underlying physical condition was not considered. In future study, obtaining more data while considering laterality and medical history is necessary to construct a more robust machine learning model.
In conclusion, we proposed an architecture that could predict the lower extremity and L5/S1 moments as plantar pressure during symmetric lifting. In order to improve the performance of the machine learning model, a hierarchical architecture was presented and the performance was evaluated by comparing with the reference value. The accuracy between the single LSTM model and each proposed architecture was then compared. The hierarchical architecture was divided into two stages. The first stage consists of classifying the posture by constructing a motion classification model and the second stage predicted the lower extremity and L5/S1 moment using the data classified by posture. Among classification models of the proposed architecture, SVM showed the highest classification accuracy and the SVM-LSTM model showed an rRMSE of 8.06~13.88%, and an error rate of a peak moment of 3.20~8.77%. This is similar to the case of estimating the moment using a wearable system. Therefore, the protocol for estimating the lower extremity and L5/S1 moment during lifting using the insole system and artificial intelligence proposed in this study provides a starting point for developing a system for estimating the lower extremity and L5/S1 moment during lifting that can be applied to future workplace environments. This novel study has the potential to precisely design feedback iterative control system of an exoskeleton for the appropriate generation of an actuator torque.
Author Contributions
Conceptualization, S.C. and A.C.; methodology, S.C., T.H.K. and A.C.; investigation, H.J. and K.K.; writing—original draft preparation, S.C. and A.C.; writing—review and editing, S.C. and T.H.K.; supervision, K.K. and J.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out with the support of “Cooperative Research Program for Agriculture Science and Technology Development (Project No. PJ01531103)” Rural Development Administration, Republic of Korea.
Institutional Review Board Statement
This study was approved by the Institutional Review Board of Institute of Biotechnology and Bioengineering, Sungkyunkwan University.
Informed Consent Statement
Written informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Der Have, A.; Van Rossom, S.; Jonkers, I. Squat lifting imposes higher peak joint and muscle loading compared to stoop lifting. Appl. Sci. 2019, 9, 3794. [Google Scholar] [CrossRef] [Green Version]
- Bernard, B. Musculoskeletal Disorders (MSDs) and Workplace Factors; US Department of Health and Human Services: Cincinnati, OH, USA, 1997.
- Kingma, I.; De Looze, M.P.; Toussaint, H.M.; Klijnsma, H.G.; Bruijnen, T.B.M. Validation of a full body 3-D dynamic linked segment model. Hum. Mov. Sci. 1996, 15, 833–860. [Google Scholar] [CrossRef]
- Shimokochi, Y.; Yong Lee, S.; Shultz, S.J.; Schmitz, R.J. The relationships among sagittal-plane lower extremity moments: Implications for landing strategy in anterior cruciate ligament injury prevention. J. Athl. Train. 2009, 44, 33–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lavender, S.A.; Andersson, G.B.J.; Schipplein, O.D.; Fuentes, H.J. The effects of initial lifting height, load magnitude, and lifting speed on the peak dynamic L5/S1 moments. Int. J. Ind. Ergon. 2003, 31, 51–59. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, Y.; Kim, Y. Lower extremity joint kinetics and lumbar curvature during squat and stoop lifting. BMC Musculoskelet. Disord. 2009, 10, 15. [Google Scholar] [CrossRef] [Green Version]
- Faber, G.S.; Kingma, I.; van Dieën, J.H. Effect of initial horizontal object position on peak L5/S1 moments in manual lifting is dependent on task type and familiarity with alternative lifting strategies. Ergonomics 2011, 54, 72–81. [Google Scholar] [CrossRef]
- Choi, A.R.; Yun, T.S.; Lee, K.S.; Min, K.K.; Hwang, H.; Lee, K.Y.; Oh, E.C.; Mun, J.H. Asymmetric loading of erector spinae muscles during sagittally symmetric lifting. J. Mech. Sci. Technol. 2009, 23, 64–74. [Google Scholar] [CrossRef]
- Li, G.; Buckle, P. Current techniques for assessing physical exposure to work-related musculoskeletal risks, with emphasis on posture-based methods. Ergonomics 1999, 42, 674–695. [Google Scholar] [CrossRef] [PubMed]
- Schreven, S.; Beek, P.J.; Smeets, J.B.J. Optimising filtering parameters for a 3D motion analysis system. J. Electromyogr. Kinesiol. 2015, 25, 808–814. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, S.; Kotowski, S.; Davis, K.G.; Mark, C.; Compton, C.S.; Huston, R.L.; Connelly, J. External L5–S1 joint moments when lifting wire mesh screen used to prevent rock falls in underground mines. Int. J. Ind. Ergon. 2009, 39, 828–834. [Google Scholar] [CrossRef]
- Kuijer, P.P.F.M.; van Oostrom, S.H.; Duijzer, K.; Van Dieen, J.H. Maximum acceptable weight of lift reflects peak lumbosacral extension moments in a functional capacity evaluation test using free style, stoop and squat lifting. Ergonomics 2012, 55, 343–349. [Google Scholar] [CrossRef]
- Hlucny, S.D.; Novak, D. Characterizing human box-lifting behavior using wearable inertial motion sensors. Sensors 2020, 20, 2323. [Google Scholar] [CrossRef]
- David, G.C. Ergonomic methods for assessing exposure to risk factors for work-related musculoskeletal disorders. Occup. Med. 2005, 55, 190–199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Wang, N.; Ho, S.-C.; Chen, X.; Pan, M.; Song, G. Design of a novel wearable sensor device for real-time bolted joints health monitoring. IEEE Internet Things J. 2018, 5, 5307–5316. [Google Scholar] [CrossRef]
- Faber, G.S.; Chang, C.C.; Kingma, I.; Dennerlein, J.T.; Van Dieën, J.H. Estimating 3D L5/S1 moments and ground reaction forces during trunk bending using a full-body ambulatory inertial motion capture system. J. Biomech. 2016, 49, 904–912. [Google Scholar] [CrossRef] [Green Version]
- Matijevich, E.S.; Volgyesi, P.; Zelik, K.E. A promising wearable solution for the practical and accurate monitoring of low back loading in manual material handling. Sensors 2021, 21, 340. [Google Scholar] [CrossRef]
- Conforti, I.; Mileti, I.; Panariello, D.; Caporaso, T.; Grazioso, S.; Del Prete, Z.; Lanzotti, A.; Di Gironimo, G.; Palermo, E. Validation of a novel wearable solution for measuring L5/S1 load during manual material handling tasks. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT (IEEE2020), Roma, Italy, 3–5 June 2020; pp. 501–506. [Google Scholar] [CrossRef]
- Faber, G.S.; Kingma, I.; Chang, C.C.; Dennerlein, J.T.; Van Dieen, J.H. Validation of a wearable system for 3D ambulatory L5/S1 moment assessment during manual lifting using instrumented shoes and an inertial sensor suit. J. Biomech. 2020, 102, 109671. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, D.A.; Ferris, D.P. Estimation of ground reaction forces and ankle moment with multiple, low-cost sensors. J. NeuroEng. Rehabil. 2015, 12, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sim, T.; Kwon, H.; Oh, S.E.; Joo, S.-B.; Choi, A.; Heo, H.M.; Kim, K.; Mun, J.H. Predicting complete ground reaction forces and moments during gait with insole plantar pressure information using a wavelet neural network. J. Biomech. Eng. 2015, 137, 091001. [Google Scholar] [CrossRef]
- Mundt, M.; Johnson, W.R.; Potthast, W.; Markert, B.; Mian, A.; Alderson, J. A Comparison of Three Neural Network Approaches for Estimating Joint Angles and Moments from Inertial Measurement Units. Sensors 2021, 21, 4535. [Google Scholar] [CrossRef]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of lower limb joint angles and moments during gait using artificial neural networks. Med. Biol. Eng. Comput. 2020, 58, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Choi, A.; Jung, H.; Mun, J.H. Single inertial sensor-based neural networks to estimate COM-COP inclination angle during walking. Sensors 2019, 19, 2974. [Google Scholar] [CrossRef] [Green Version]
- Jin, Z.; Wang, D.; Zhang, H.; Liang, J.; Feng, X.; Zhao, J.; Sun, L. Incidence trend of five common musculoskeletal disorders from 1990 to 2017 at the global, regional and national level: Results from the global burden of disease study 2017. Annals of the rheumatic diseases. Ann. Rheum. Dis. 2020, 79, 1014–1022. [Google Scholar] [CrossRef]
- Choi, A.; Lee, I.K.; Choi, M.T.; Mun, J.H. Inter-joint coordination between hips and trunk during downswings: Effects on the clubhead speed. J. Sports Sci. 2016, 34, 1991–1997. [Google Scholar] [CrossRef]
- Choi, A.; Jung, H.; Lee, K.Y.; Lee, S.; Mun, J.H. Machine learning approach to predict center of pressure trajectories in a complete gait cycle: A feedforward neural network vs. LSTM network. Med. Biol. Eng. Comput. 2019, 57, 2693–2703. [Google Scholar] [CrossRef]
- Ramanathan, A.K.; Kiran, P.; Arnold, G.P.; Wang, W.; Abboud, R.J. Repeatability of the Pedar-X® in-shoe pressure measuring system. Foot Ankle Surg. 2010, 16, 70–73. [Google Scholar] [CrossRef]
- Chang, C.-C.; McGorry, R.W.; Lin, J.-H.; Xu, X.; Hsiang, S.M. Prediction accuracy in estimating joint angle trajectories using a video posture coding method for sagittal lifting tasks. Ergonomics 2010, 53, 1039–1047. [Google Scholar] [CrossRef]
- Choi, A.; Sim, T.; Mun, J.H. Quasi-stiffness of the knee joint in flexion and extension during the golf swing. J. Sports Sci. 2015, 33, 1682–1691. [Google Scholar] [CrossRef]
- Joo, S.-B.; Oh, S.E.; Sim, T.; Kim, H.; Choi, C.H.; Koo, H.; Mun, J.H. Prediction of gait speed from plantar pressure using artificial neural networks. Expert Syst. Appl. 2014, 41, 7398–7405. [Google Scholar] [CrossRef]
- Gholipour, A.; Arjmand, N. Artificial neural networks to predict 3D spinal posture in reaching and lifting activities; Applications in biomechanical models. J. Biomech. 2016, 49, 2946–2952. [Google Scholar] [CrossRef]
- Conforti, I.; Mileti, I.; Del Prete, Z.; Palermo, E. Measuring biomechanical risk in lifting load tasks through wearable system and machine-learning approach. Sensors 2020, 20, 1557. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.-C.; Chen, Y.-J.; Hsu, C.-S.; Wen, Y.-T.; Lee, Y.-J. Multiple inertial measurement unit combination and location for center of pressure prediction in gait. Front. Bioeng. Biotechnol. 2020, 8, 1252. [Google Scholar] [CrossRef] [PubMed]
- Zebin, T.; Sperrin, M.; Peek, N.; Casson, A.J. Human activity recognition from inertial sensor time-series using batch normalized deep LSTM recurrent networks. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18 July 2018; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Zaroug, A.; Garofolini, A.; Lai, D.T.H.; Mudie, K.; Begg, R. Prediction of gait trajectories based on the long short term memory neural networks. PLoS ONE 2021, 16, e0255597. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Moon, H.; Ha, H.; Lee, J.; Yu, J.; Chae, S.; Mun, J.; Choi, A. Can a deep learning model estimate low back torque during a golf swing? Int. J. Biotechnol. Sports Eng. 2021, 2, 59–65. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization b. J. Electron. Sci. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Zeiaee, A.; Soltani-Zarrin, R.; Langari, R.; Tafreshi, R. Kinematic Design Optimization of an Eight Degree-of-Freedom Upper-Limb Exoskeleton. Robotica 2019, 37, 2073–2086. [Google Scholar] [CrossRef]
- Kipp, K.; Giordanelli, M.; Geiser, C. Predicting net joint moments during a weightlifting exercise with a neural network model. J. Biomech. 2018, 74, 225–229. [Google Scholar] [CrossRef] [Green Version]
- Antwi-Afari, M.F.; Li, H.; Yu, Y.; Kong, L. Wearable insole pressure system for automated detection and classification of awkward working postures in construction workers. Autom. Constr. 2018, 96, 433–441. [Google Scholar] [CrossRef]
- Khashei, M.; Hamadani, A.Z.; Bijari, M. A novel hybrid classification model of artificial neural networks and multiple linear regression models. Expert Syst. Appl. 2012, 39, 2606–2620. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B. Influence of in-shoe heel lifts on plantar pressure and center of pressure in the medial–lateral direction during walking. Gait Posture 2014, 39, 1012–1016. [Google Scholar] [CrossRef]
- Friedenberg, R.; Kalichman, L.; Ezra, D.; Wacht, O.; Alperovitch-Najenson, D. Work-related musculoskeletal disorders and injuries among emergency medical technicians and paramedics: A comprehensive narrative review. Arch. Environ. Occup. Health 2020, 1–9, in press. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Choi, A.; Moon, J.; Chae, S.H.; Lee, K.; Kim, K.; Mun, J.H. Insole system-based neural network model to evaluate force risk in cube method: Application to pepper farming tasks. J. Med. Imaging Health Inform. 2020, 10, 1444–1451. [Google Scholar] [CrossRef]
- Mokarami, H.; Varmazyar, S.; Kazemi, R.; Taghavi, S.M.; Stallones, L.; Marioryad, H.; Farahmand, F. Low cost ergonomic interventions to reduce risk factors for work related musculoskeletal disorders during dairy farming. Work 2019, 64, 195–201. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).