Use of Deep Learning to Improve the Computational Complexity of Reconstruction Algorithms in High Energy Physics
Abstract
1. Introduction
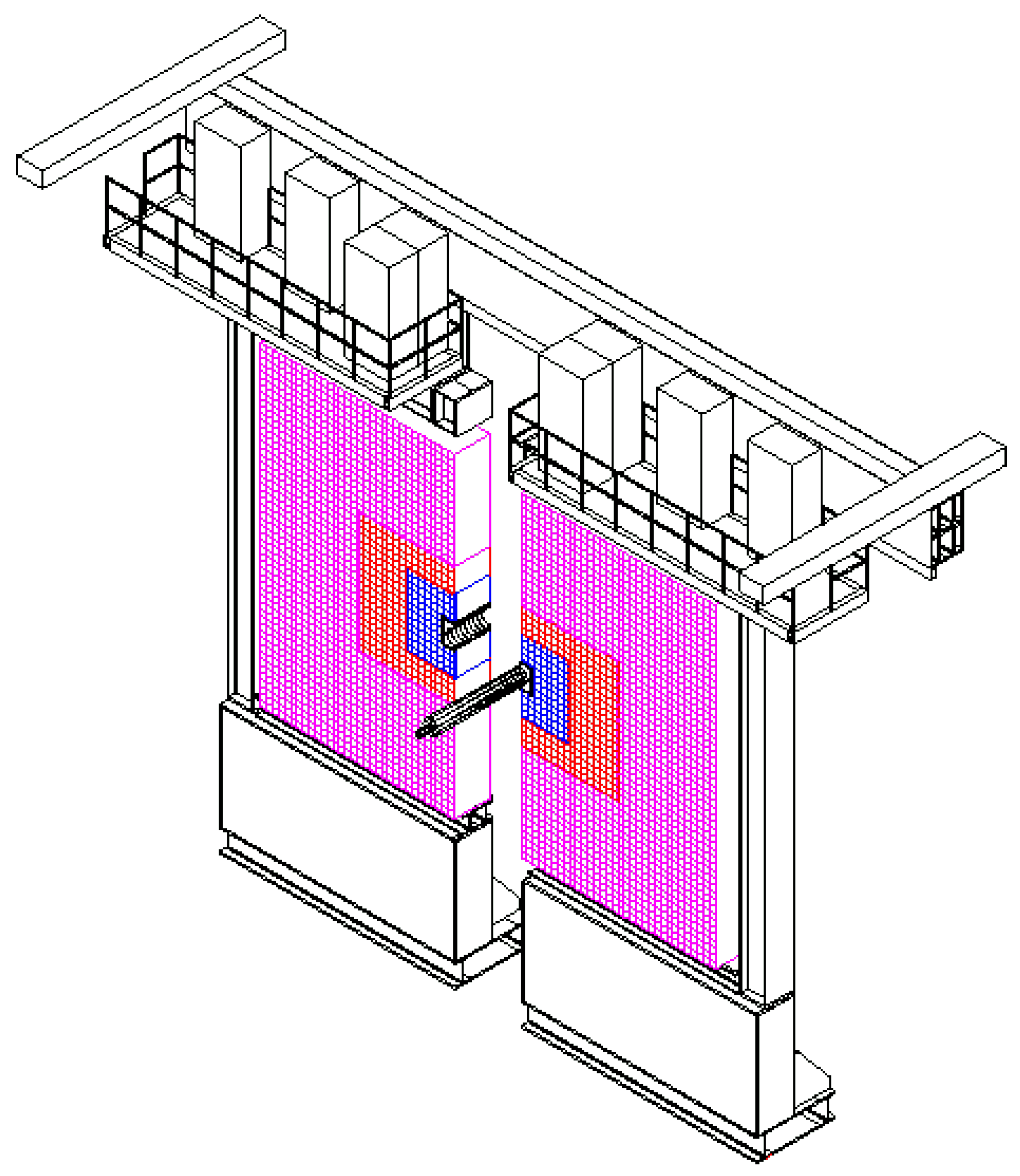
2. Overview of Data Processing in Modern Particle Detectors
3. Methods
3.1. Fundamentals
3.2. Local Maxima Formulation
- States: two. One (1) if the cell is a maximum and zero (0) otherwise.
- Neighborhood: eight cells. In order to check if it is a local maxima, the surrounding cells at distance one need to be checked. In a two-dimensional grid of cells, the number of distance one neighbors is eight.
- Ruleset function: in order to define the condition of a cell to be a maximum: (1) its value needs to be higher or equal to its neighbors. Although the equal condition is not obvious, it is needed to represent a specific pair of particles from a that strike the calorimeter at a very short distance. Therefore Equation (1) defines the ruleset, where stands for the value of each cell at time t and the case is excluded. The initial states of the grid cells concerning are the values of the calorimeter readout cells.
3.3. Clustering Formulation
- States: three. Since we need to identify three types of cells: cells that belong to one cluster (1), overlapping cells (−1), and the rest of them (0).
- Neighborhood: eight cells. In order to differentiate cells as overlapping or belonging to a cluster from the others, the neighborhood at one cell distance needs to be checked.
- Ruleset function: in order to identify the cell states, the algorithm needs to check how many local maxima are in the neighborhood of a cell. Cells that belong to a certain cluster are those that have a single local maximum in its neighborhood of distance one. In the same way, overlap cases are identified when there is more than one local maximum in its neighborhood. If there are no local maxima in a cell neighborhood then it is either a local maximum itself or not relevant for the clustering. This is formulated in Equation (2), where K is defined as the number of local maxima in the neighborhood of a cell.
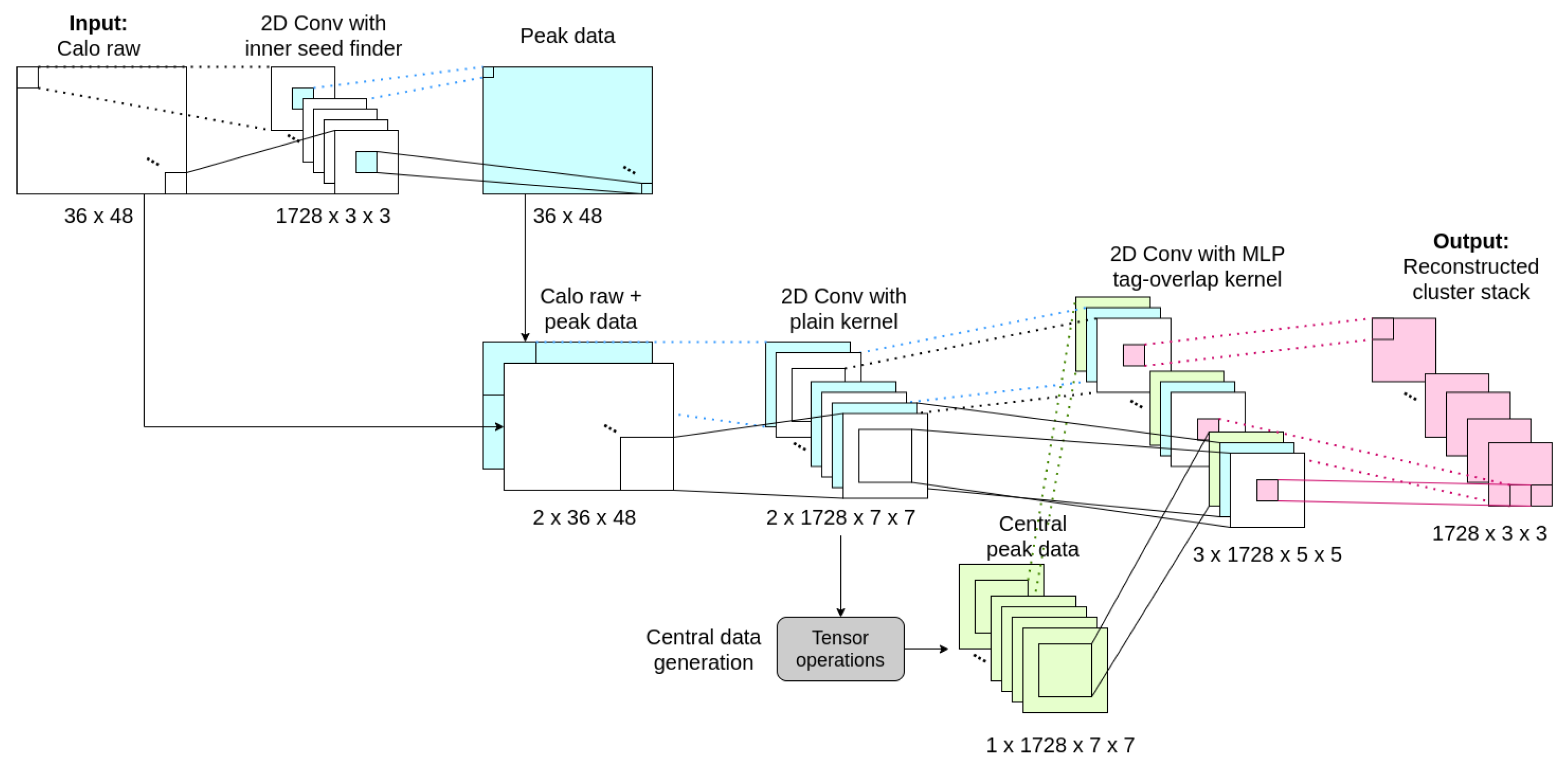
3.4. Clustering and Overlap Formulation
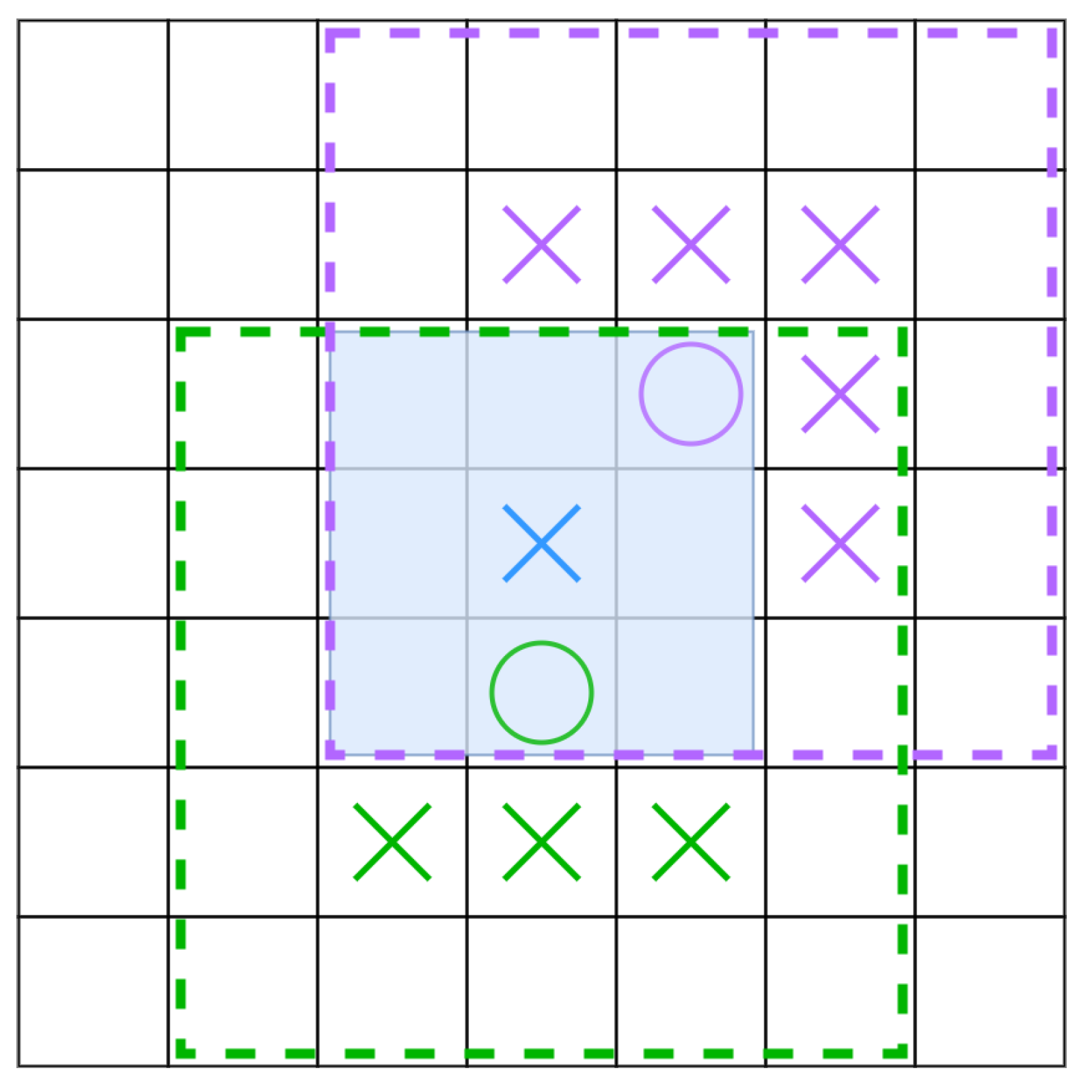
- The neighborhood window for this step needs to be big enough to identify all the cells belonging to the possible clusters causing overlap. This number corresponds with 24 neighbors inside a square window around the given cell, as can be seen in Figure 3.
- Extra information needs to be added to the window, indicating the cluster to which the energy fraction is going to be part of. Since each fraction of energy needs to be assigned to a certain cluster, in the overlap cases, the same window must be evaluated as many times as the number of clusters involved, but each time selecting a cluster that the fraction is going to contribute. This dominant cluster, within a window, will be called central cluster.
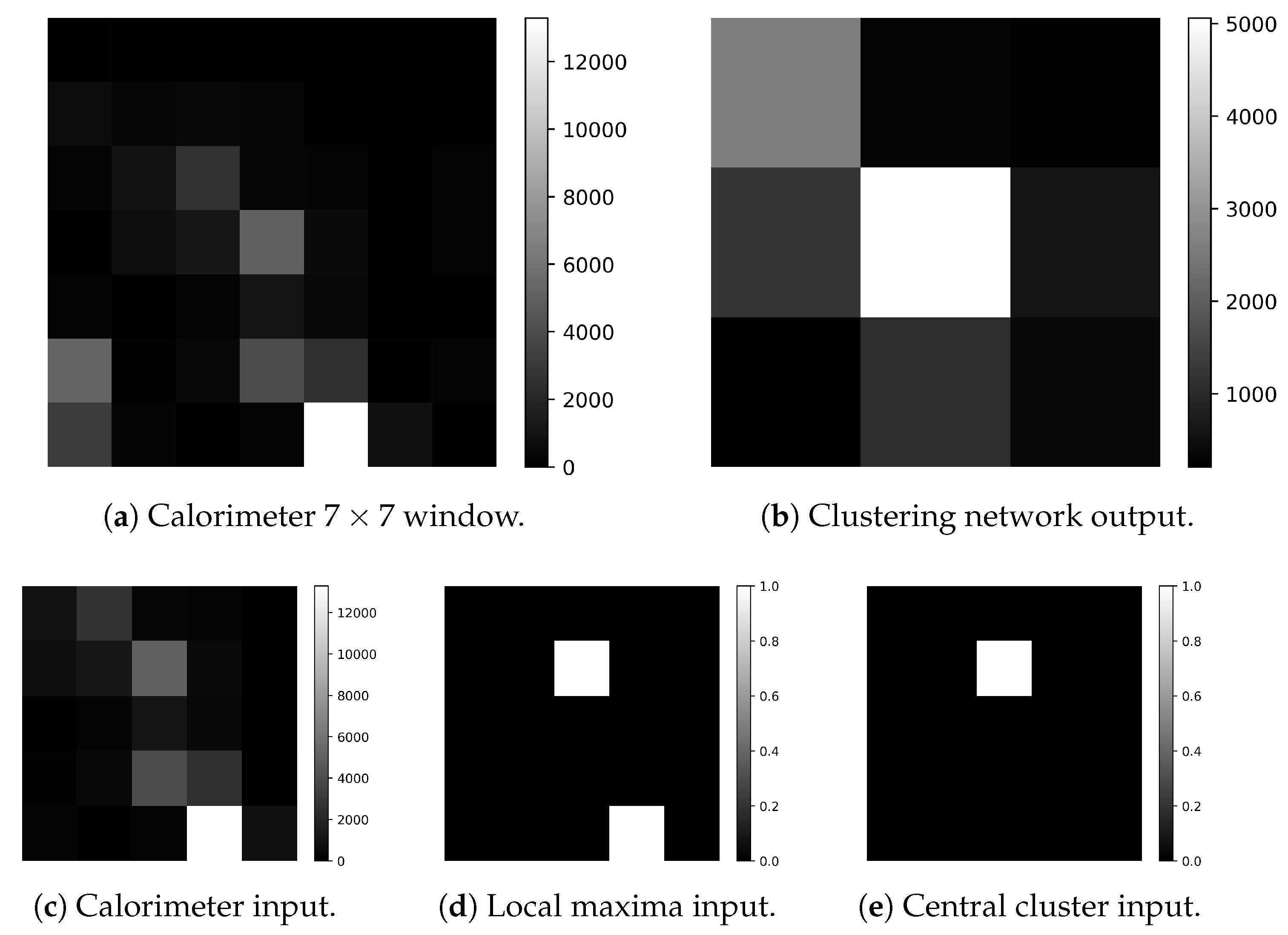
- States: 10,240. Since the algorithm needs to give, as output, a value concerning the energy of a cell, the CA must have enough states to model the full calorimeter sensitivity, which is of 12 bits on the ADC lecture with a gain of MeVs per ADC value ().
- Neighborhood: 24 cells. As explained above, the window around a cell to predict its value needs to be of cells.
- Ruleset function: at this point of the reconstruction, we have three streams of information:
- –
- Original data sample. Obtained from the calorimeter simulation with values from 0 to 10,240.
- –
- Local maxima information. Obtained from the output of the local maxima finder network. With values from 0 to 1.
- –
- Central cluster information. Obtained from the masking of the central cell on each window from the image. With values from 0 to 1.
At this point, the ruleset function for this step defines the fractioning of a cell’s energy in case of overlap in Equation (3). In the same equation, num_clusters refers to the number of local maxima that could be causing overlap. As an example, if we look at the purple circle in Figure 3 to account for num_clusters, the positions marked with a purple X should be checked.
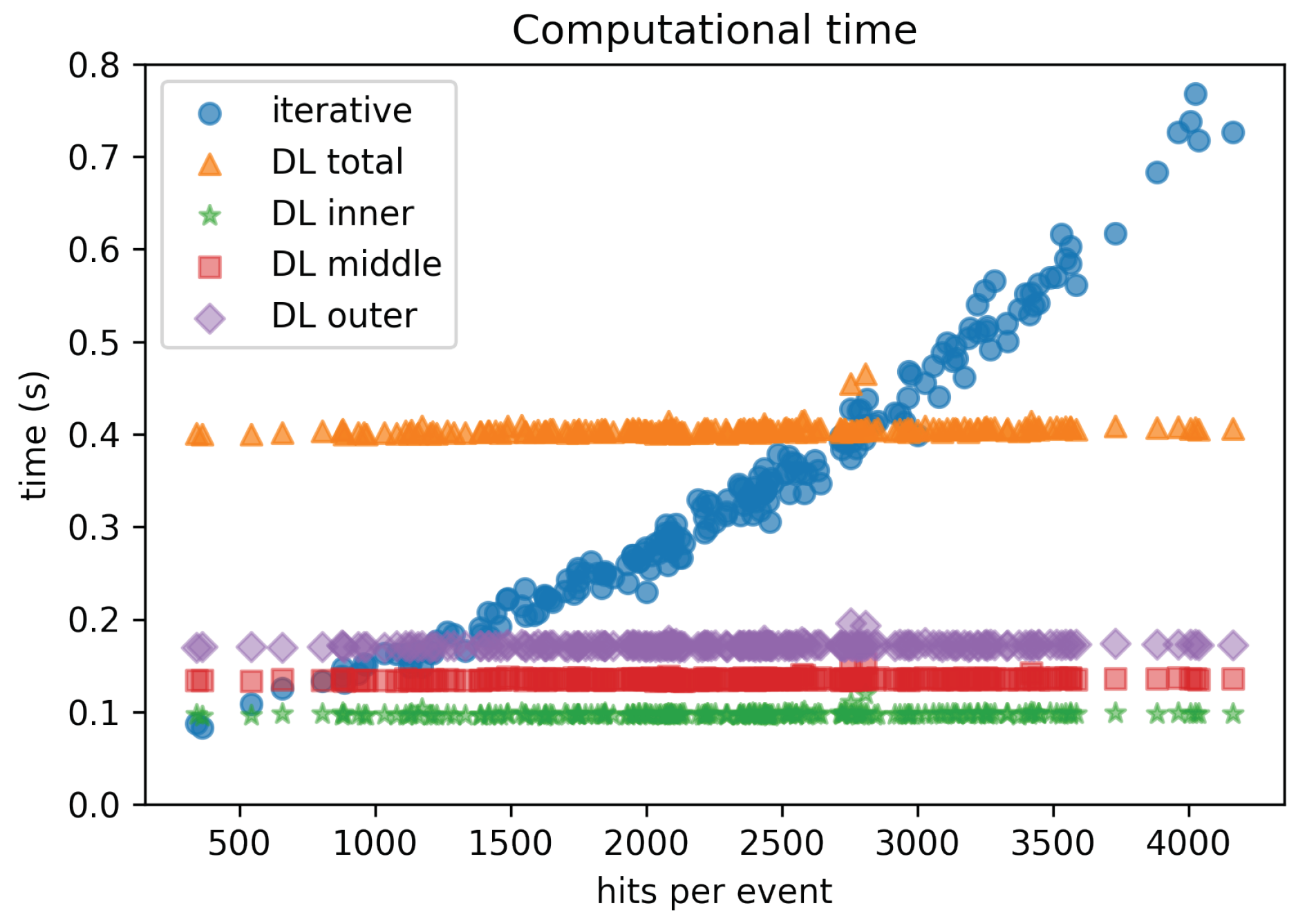
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alves, A.A., Jr.; Andrade Filho, L.; Barbosa, A.; Bediaga, I.; Cernicchiaro, G.; Guerrer, G.; Lima, H., Jr.; Machado, A.; Magnin, J.; Marujo, F.; et al. The LHCb detector at the LHC. J. Instrum. 2008, 3, S08005. [Google Scholar]
- Evans, L.; Bryant, P. LHC Machine. JINST 2008, 3, S08001. [Google Scholar] [CrossRef]
- Bediaga, I.; Torres, M.C.; De Miranda, J.; Gomes, A.; Massafferri, A.; Rodriguez, J.M.; dos Reis, A.; Aoude, R.; Amato, S.; Akiba, K.C.; et al. Physics case for an LHCb Upgrade II-Opportunities in flavour physics, and beyond, in the HL-LHC era. arXiv 2018, arXiv:1808.08865. [Google Scholar]
- LHCb Collaboration. Throughput and Resource Usage of the LHCb Upgrade HLT; Technical Report; LHCB-FIGURE-2020-007; CERN: Geneva, Switzerland, 2020. [Google Scholar]
- Omelaenko, O.; Dalpiaz, P.; Guzik, Z.; Spiridenkov, E.; Jarron, P.; Semenov, V.; Ocariz, J.; Khan, A.; Perret, P.; Schneider, O.; et al. LHCb Calorimeters: Technical Design Report; Technical Report; LHCb-TDR-002; CERN: Geneva, Switzerland, 2000. [Google Scholar]
- Breton, V.; Brun, N.; Perret, P. A Clustering Algorithm for the LHCb Electromagnetic Calorimeter Using a Cellular Automaton; Technical Report; CERN-LHCb-2001-123; CERN: Geneva, Switzerland, 2001. [Google Scholar]
- Breton, V.; Fonvieille, H.; Grenier, P.; Guicheney, C.; Jousset, J.; Roblin, Y.; Tamin, F. Application of neural networks and cellular automata to interpretation of calorimeter data. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 362, 478–486. [Google Scholar] [CrossRef]
- Casolino, M.; Picozza, P. A cellular automaton to filter events in a high energy physics discrete calorimeter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 364, 516–523. [Google Scholar] [CrossRef][Green Version]
- Denby, B. Neural networks and cellular automata in experimental high energy physics. Comput. Phys. Commun. 1988, 49, 429–448. [Google Scholar] [CrossRef]
- Baldanza, C.; Bisi, F.; Bruschi, M.; D’Antone, I.; Meneghini, S.; Rizzi, M.; Zuffa, M. A cellular neural network for peak finding in high-energy physics. In Proceedings of the 2000 6th IEEE International Workshop on Cellular Neural Networks and their Applications (CNNA 2000) (Cat. No. 00TH8509), Catania, Italy, 25 May 2000; pp. 443–448. [Google Scholar]
- Mazurek, M. Deep Learning Solutions for 2D Calorimetric Cluster Reconstruction at LHCb. In Proceedings of the 4th Inter-Experiment Machine Learning Workshop, Zürich, Switzerland, 19–23 October 2020. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Canudas, N.V.; Cardona, X.V.; Gómez, M.C.; Ribé, E.G. Deep Learning approach to LHCb Calorimeter reconstruction using a Cellular Automaton. EPJ Web Conf. EDP Sci. 2021, 251, 04008. [Google Scholar] [CrossRef]
- Abba, A.; Caponio, F.; Cusimano, A.; Geraci, A.; LHCb Collaboration. LHCb Particle Identification Upgrade: Technical Design Report; CERN: Geneva, Switzerland, 2013. [Google Scholar]
- Bediaga, I.; Chanal, H.; Hopchev, P.; Cadeddu, S.; Stoica, S.; Calvo Gomez, M.; T’Jampens, S.; Machikhiliyan, I.V.; Guzik, Z.; Alves, A.A., Jr.; et al. Framework TDR for the LHCb Upgrade: Technical Design Report; Technical Report; LHCb-TDR-012; CERN: Geneva, Switzerland, 2012. [Google Scholar]
- Neumann, J.; Burks, A.W. Theory of Self-Reproducing Automata; University of Illinois Press: Urbana, IL, USA, 1966; Volume 1102024. [Google Scholar]
- Gilpin, W. Cellular automata as convolutional neural networks. Phys. Rev. E 2019, 100, 032402. [Google Scholar] [CrossRef] [PubMed]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]

| Region | Image Shape | Training Samples | Neurons Per Layer | Parameters | Training Time | Accuracy |
|---|---|---|---|---|---|---|
| Outer | 10,000 | [20, 20, 20, 10, 2] | 1272 | 1354.7 s | 99.96% | |
| Middle | 10,000 | [20, 20, 20, 10, 2] | 1272 | 1052.3 s | 99.92% | |
| Inner | 10,000 | [10, 10, 10, 2] | 342 | 461.8 s | 99.93% |
| Case | Number of Clusters (K) | Overlap with Central Cell | Samples on 2k Events | RMSE |
|---|---|---|---|---|
| 1 | 0 | No | 153,519 | 96.281 |
| 2 | 1 | No | 121,316 | 135.616 |
| 3 | 2 | Yes (1 cluster) | 45,066 | 147.501 |
| 4 | 3 | Yes (2 clusters) | 9937 | 199.644 |
| 5 | 4+ | Yes (3+ clusters) | 1367 | 244.312 |
| 6 | >1 | Yes (energy difference of 1 order of magnitude) | 6816 | 181.693 |
| Region | Image Shape | Training Samples | Neurons Per Layer | Parameters | Training Time | RMSE |
|---|---|---|---|---|---|---|
| All | 270,000 | [64, 64, 64, 32] | 108,993 | 2130.4 s | 168.884 |
| Algorithms | Mean of Relative Error | STD of Relative Error |
|---|---|---|
| Deep Learning | 0.056 | 0.105 |
| Python version of LHCb algorithm | 0.079 | 0.159 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valls Canudas, N.; Calvo Gómez, M.; Golobardes Ribé, E.; Vilasis-Cardona, X. Use of Deep Learning to Improve the Computational Complexity of Reconstruction Algorithms in High Energy Physics. Appl. Sci. 2021, 11, 11467. https://doi.org/10.3390/app112311467
Valls Canudas N, Calvo Gómez M, Golobardes Ribé E, Vilasis-Cardona X. Use of Deep Learning to Improve the Computational Complexity of Reconstruction Algorithms in High Energy Physics. Applied Sciences. 2021; 11(23):11467. https://doi.org/10.3390/app112311467
Chicago/Turabian StyleValls Canudas, Núria, Míriam Calvo Gómez, Elisabet Golobardes Ribé, and Xavier Vilasis-Cardona. 2021. "Use of Deep Learning to Improve the Computational Complexity of Reconstruction Algorithms in High Energy Physics" Applied Sciences 11, no. 23: 11467. https://doi.org/10.3390/app112311467
APA StyleValls Canudas, N., Calvo Gómez, M., Golobardes Ribé, E., & Vilasis-Cardona, X. (2021). Use of Deep Learning to Improve the Computational Complexity of Reconstruction Algorithms in High Energy Physics. Applied Sciences, 11(23), 11467. https://doi.org/10.3390/app112311467






