Ensemble Voting-Based Multichannel EEG Classification in a Subject-Independent P300 Speller
Abstract
:1. Introduction
2. Overview of Classifiers
2.1. Linear Discriminant Analysis
2.2. Support-Vector Machine
2.3. k-Nearest Neighbors
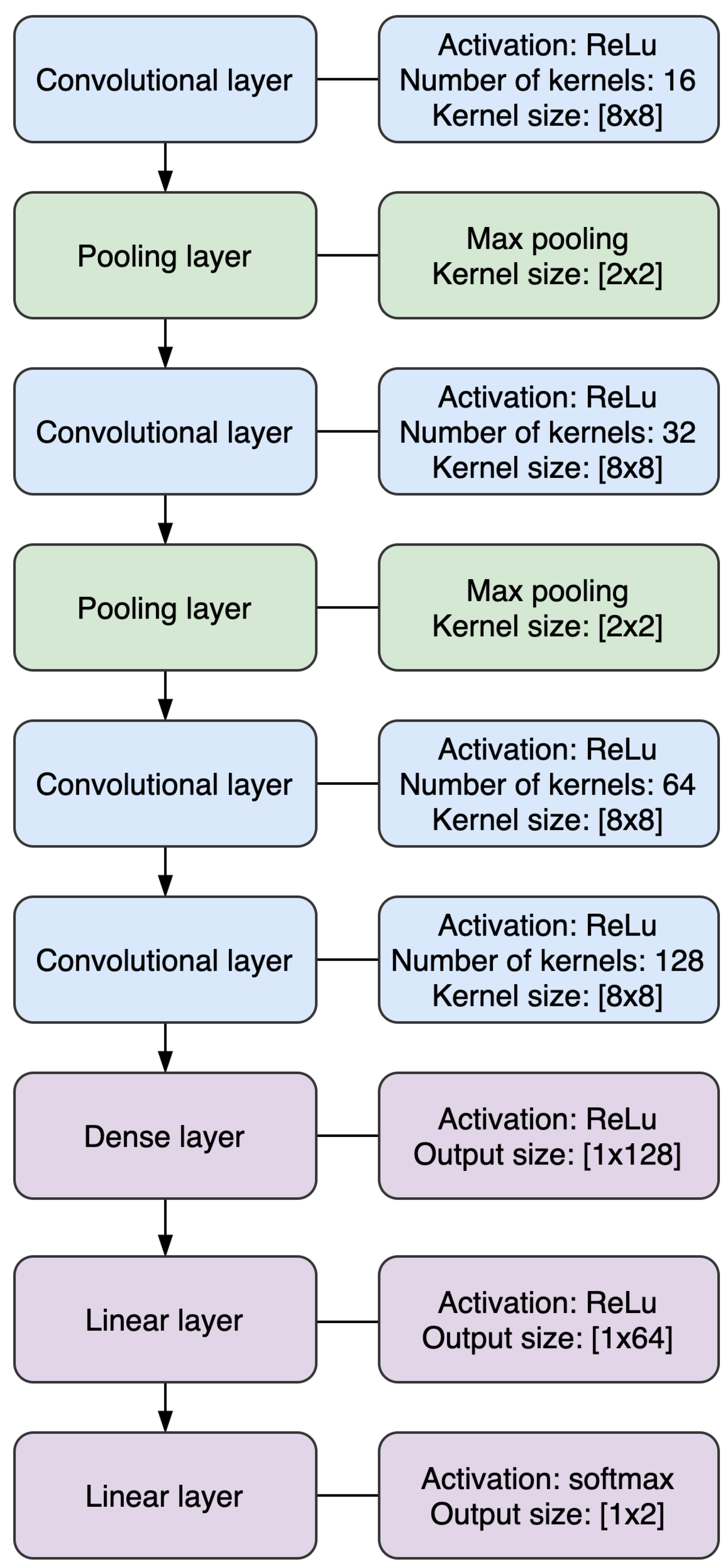
2.4. Convolutional Neural Network
3. Proposed Methodology
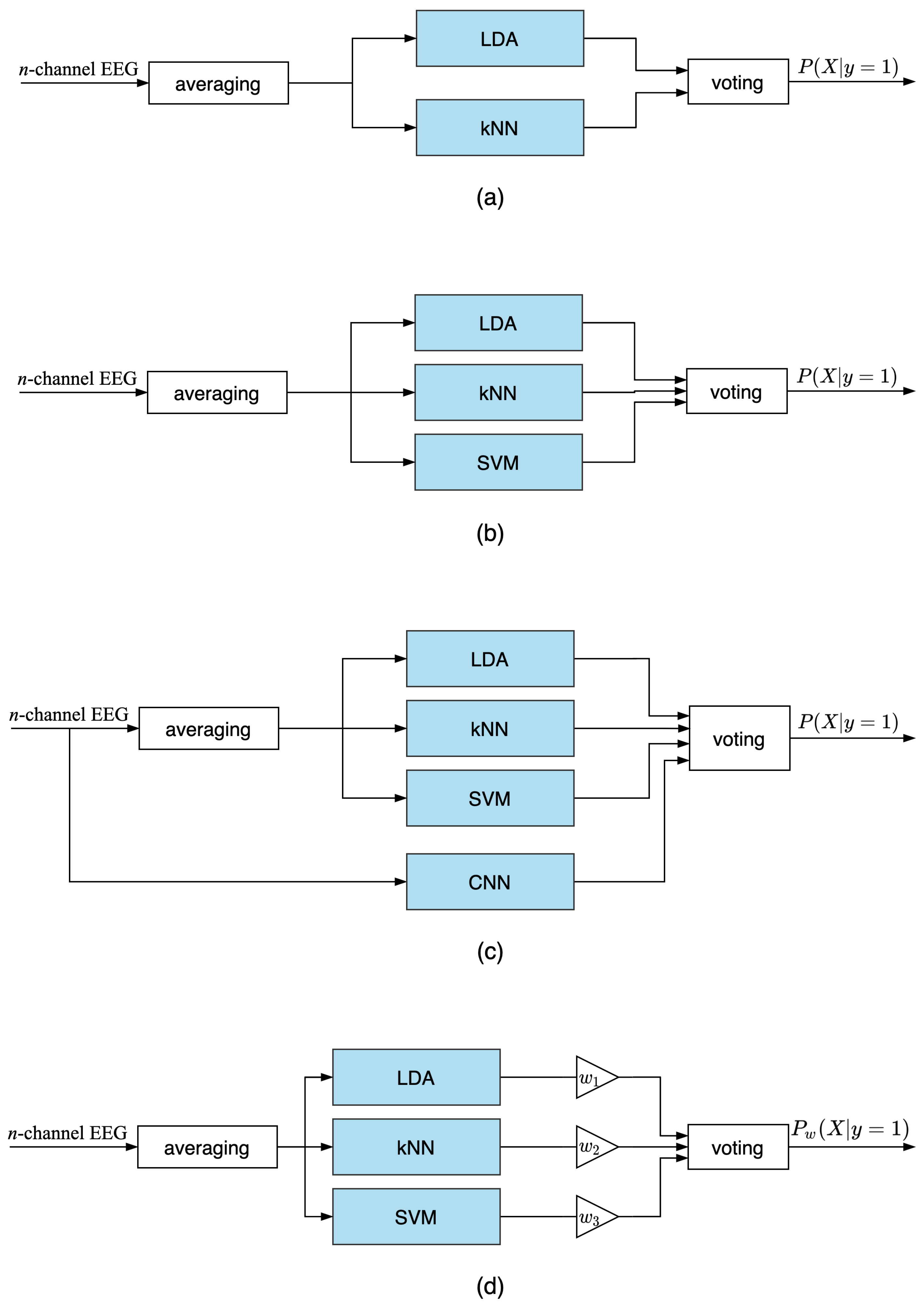
3.1. Training Approach
3.2. Ensemble Voting
4. Simulation Results
4.1. Experimental Settings
4.2. Intra-Subject Experiments
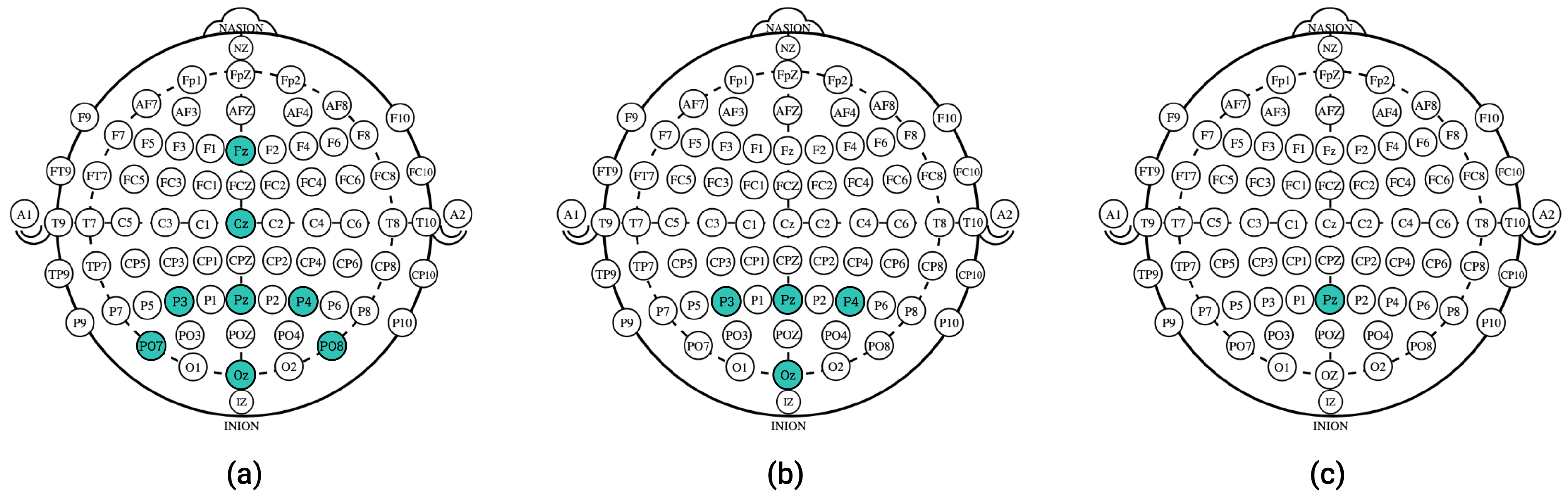
4.3. Eight-Channel Data Simulations
- LDA weight:
- SVM weight:
- kNN weight:
4.4. Four-Channel Data Simulations
4.5. Single-Channel Data Simulations
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| ALS | Amyotrophic lateral sclerosis |
| BCI | Brain–computer interface |
| CNN | Convolutional neural network |
| ED | Eigenvalue decomposition |
| EEG | Electroencephalography |
| EOG | Electrooculography |
| ERP | Event-related potential |
| ERSP | Event-related spectral power |
| GUI | Graphical user interface |
| kNN | k-nearest neighbors |
| LDA | Linear discriminant analysis |
| LSS | Least squares solution |
| LSTM | Long-short term memory |
| PCA | Principal component analysis |
| ReLU | Rectified linear unit |
| SVD | Singular value decomposition |
| SVM | Support vector machine |
References
- McFarland, D.J.; Wolpaw, J.R. EEG-based brain–computer interfaces. Curr. Opin. Biomed. Eng. 2017, 4, 194–200. [Google Scholar] [CrossRef]
- Nicolas-Alonso, L.; Gomez-Gil, J. Brain computer interfaces, a review. Sensors 2012, 12, 1211. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Zhao, S.; Lou, W. Identification of early vascular dementia patients with EEG signal. IEEE Access 2019, 7, 68618–68627. [Google Scholar] [CrossRef]
- Qin, Y.; Zheng, H.; Chen, W.; Qin, Q.; Han, C.; Che, Y. Patient-specific seizure prediction with scalp EEG using convolutional neural network and extreme learning machine. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 7622–7625. [Google Scholar] [CrossRef]
- Colombo, R.; Pisano, F.; Micera, S.; Mazzone, A.; Delconte, C.; Carrozza, M.; Dario, P.; Minuco, G. Robotic techniques for upper limb evaluation and rehabilitation of stroke patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 311–324. [Google Scholar] [CrossRef]
- Rebsamen, B.; Burdet, E.; Guan, C.; Zhang, H.; Teo, C.L.; Zeng, Q.; Laugier, C.; Ang, M.H. Controlling a wheelchair indoors using thought. IEEE Intell. Syst. 2007, 22, 18–24. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, B.; Wang, Y.; Xu, S.; Gao, X. Control of a 7-DOF robotic arm system with an SSVEP-based BCI. Int. J. Neural Syst. 2018, 28. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Liu, T.; Liu, L.; Yao, X.; Chen, L.; Fan, D.; Zhan, S.; Wang, S. Global variation in prevalence and incidence of amyotrophic lateral sclerosis: A systematic review and meta-analysis. J. Neurol. 2020, 267, 944–953. [Google Scholar] [CrossRef] [PubMed]
- Kameswara, T.; Rajyalakshmi, M.; Prasad, T. An exploration on brain computer interface and its recent trends. Int. J. Adv. Res. Artif. Intell. 2013, 1, 17–22. [Google Scholar] [CrossRef] [Green Version]
- Farwell, L.; Donchin, E. Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials. Electroenceph. Clin. Neurophysiol. 1998, 70, 510–523. [Google Scholar] [CrossRef]
- Picton, T. The P300 wave of the human event-related potential. J. Clin. Neurophysiol. 1992, 9, 456–479. [Google Scholar] [CrossRef]
- Lu, S.; Guan, C.; Zhang, H. Unsupervised brain computer interface based on intersubject information and online adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 135–145. [Google Scholar] [CrossRef]
- Speier, W.; Knall, J.; Pouratian, N. Unsupervised training of brain–computer interface systems using expectation maximization. In Proceedings of the 2013 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; pp. 707–710. [Google Scholar] [CrossRef]
- Grizou, J.; Iturrate, I.; Montesano, L.; Oudeyer, P.Y.; Lopes, M. Calibration-free BCI based control. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; Volume 2, pp. 1213–1220. [Google Scholar] [CrossRef]
- Gu, Z.; Yu, Z.; Shen, Z.; Li, Y. An online semi-supervised brain–computer interface. IEEE Trans. Biomed. Eng. 2013, 60, 2614–2623. [Google Scholar] [CrossRef] [PubMed]
- Dal Seno, B.; Matteucci, M.; Mainardi, L. A genetic algorithm for automatic feature extraction in P300 detection. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 3145–3152. [Google Scholar] [CrossRef]
- Kalaganis, F.; Laskaris, N.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. A Riemannian geometry approach to reduced and discriminative covariance estimation in brain computer interfaces. IEEE Trans. Biomed. Eng. 2019, 67, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.D.; Langley, P. Methods of conceptual clustering and their relation to numerical taxonomy. Artif. Intell. Stat. 1986, 18, 77–116. [Google Scholar]
- Vidaurre, C.; Kawanabe, M.; von Bünau, P.; Blankertz, B.; Müller, K.R. Toward unsupervised adaptation of LDA for brain–computer interfaces. IEEE Trans. Biomed. Eng. 2011, 58, 587–597. [Google Scholar] [CrossRef]
- Lee, M.H.; Williamson, J.; Won, D.O.; Fazli, S.; Lee, S.W. A high performance spelling system based on EEG-EOG signals with visual feedback. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1443–1459. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Y.; Liu, J.; Sun, J.; Cichocki, A.; Gao, F. Regularized group sparse discriminant analysis for P300-based brain–computer interface. Int. J. Neural Syst. 2019, 29, 1950002. [Google Scholar] [CrossRef]
- Naebi, A.; Feng, Z.; Hosseinpour, F.; Abdollahi, G. Dimension reduction using new bond graph algorithm and deep learning pooling on EEG signals for BCI. Appl. Sci. 2021, 11, 8761. [Google Scholar] [CrossRef]
- Diehl, C.P.; Cauwenberghs, G. SVM incremental learning, adaptation and optimization. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Portland, OR, USA, 20–24 July 2003; Volume 4, pp. 2685–2690. [Google Scholar] [CrossRef]
- Vo, K.; Pham, T.; Nguyen, D.N.; Kha, H.H.; Dutkiewicz, E. Subject-independent ERP-based brain–computer interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 719–728. [Google Scholar] [CrossRef] [Green Version]
- Kundu, S.; Ari, S. P300 based character recognition using convolutional neural network and support vector machine. Biomed. Signal Process. Control 2020, 55, 101645. [Google Scholar] [CrossRef]
- Platt, J.C. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Barsim, K.S.; Zheng, W.; Yang, B. Ensemble learning to EEG-based brain computer interfaces with applications on P300-spellers. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 631–638. [Google Scholar] [CrossRef]
- Lu, Z.; Li, Q.; Gao, N.; Wang, T.; Yang, J.; Bai, O. A convolutional neural network based on batch normalization and residual block for P300 signal detection of P300-speller system. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 2303–2308. [Google Scholar] [CrossRef]
- Ditthapron, A.; Banluesombatkul, N.; Ketrat, S.; Chuangsuwanich, E.; Wilaiprasitporn, T. Universal joint feature extraction for P300 EEG classification using multi-task autoencoder. IEEE Access 2019, 7, 68415–68428. [Google Scholar] [CrossRef]
- Kundu, S.; Ari, S. Fusion of convolutional neural networks for P300 based character recognition. In Proceedings of the 2019 International Conference on Information Technology (ICIT), Bhubaneswar, India, 19–21 December 2019; pp. 155–159. [Google Scholar] [CrossRef]
- Ledesma-Ramirez, C.; Bojorges-Valdez, E.; Yanez-Suarez, O.; Saavedra, C.; Bougrain, L.; Gentiletti, G. P300-speller public-domain database. In Proceedings of the 4th International BCI Meeting, Pacific Grov, CA, USA, 31 May–4 June 2010; p. 257. [Google Scholar]
- Riccio, A.; Simione, L.; Schettini, F.; Pizzimenti, A.; Inghilleri, M.; Olivetti Belardinelli, M.; Mattia, D.; Cincotti, F. Attention and P300-based BCI performance in people with amyotrophic lateral sclerosis. Front. Hum. Neurosci. 2013, 7, 732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, M.; Liu, J.; Chen, L.; Qi, H.; He, F.; Zhou, P.; Cheng, X.; Wan, B.; Ming, D. Inter-subject information contributes to the ERP classification in the P300 speller. In Proceedings of the 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, France, 22–24 April 2015; pp. 206–209. [Google Scholar] [CrossRef]
- Mussabayeva, A.; Jamwal, P.K.; Akhtar, M.T. Comparison of generic and subject-specific training for features classification in P300 speller. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 222–227. [Google Scholar]
- Takeichi, T.; Yoshikawa, T.; Furuhashi, T. Detecting P300 potentials using weighted ensemble learning. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 950–954. [Google Scholar] [CrossRef]
- Nuwer, M.R. 10-10 electrode system for EEG recording. Clin. Neurophysiol. 2018, 129, 1103. [Google Scholar] [CrossRef] [PubMed]
- Teplan, M. Fundamental of EEG measurement. Meas. Sci. Rev. 2002, 2, 1–11. [Google Scholar]
- He, H.; Wu, D. Transfer learning for brain–computer interfaces: A Euclidean space data alignment approach. IEEE Trans. Biomed. Eng. 2020, 67, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhang, H.; Chen, M.; Zhang, L. A boosting-based spatial-spectral model for stroke patients’ EEG analysis in rehabilitation training. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 169–179. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, U.; Garcia, G.; Vesin, J.; Diserens, K.; Ebrahimi, T. A boosting approach to P300 Detection with application to brain-computer interfaces. In Proceedings of the 2nd International IEEE EMBS Conference on Neural Engineering, Arlington, VA, USA, 16–19 March 2005; pp. 97–100. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Vijay, M.; Kashyap, A.; Nagarkatti, A.; Mohanty, S.; Mohan, R.; Krupa, N. Extreme gradient boosting classification of motor imagery using common spatial patterns. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Nashed, N.N.; Eldawlatly, S.; Aly, G.M. A deep learning approach to single-trial classification for P300 spellers. In Proceedings of the 2018 IEEE 4th Middle East Conference on Biomedical Engineering (MECBME), Tunis, Tunisia, 28–30 March 2018; pp. 11–16. [Google Scholar] [CrossRef]
- Lee, Y.R.; Lee, J.Y.; Kim, H.N. A reduced-complexity P300 speller based on an ensemble of SVMs. In Proceedings of the 2015 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 1173–1176. [Google Scholar] [CrossRef]
- Yu, T.; Yu, Z.; Gu, Z.; Li, Y. Grouped automatic relevance determination and its application in channel selection for P300 BCIs. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1068–1077. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Wei, H.; Yan, T.; Zhou, W. P300 detection with adaptive filtering and EEG spectrogram graph. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 1570–1575. [Google Scholar] [CrossRef]
- Qu, H.; Shan, Y.; Liu, Y.; Pang, L.; Fan, Z.; Zhang, J.; Wanyan, X. Mental workload classification method based on EEG independent component features. Appl. Sci. 2020, 10, 3036. [Google Scholar] [CrossRef]
- Makeig, S. Auditory event-related dynamics of the EEG spectrum and effects of exposure to tones. Electroenceph. Clin. Neurophysiol. 1993, 86, 283–293. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]

| Model | F-Score (%) | ||
|---|---|---|---|
| 8-Channel Data | 4-Channel Data | Single-Channel Data | |
| Gradient Boosting | 99.53 | 99.45 | 84.01 |
| XGBoost | 99.70 | 99.75 | 85.52 |
| LDA | 98.78 | 98.84 | 83.35 |
| kNN | 98.51 | 98.54 | 82.29 |
| SVM | 98.80 | 98.81 | 82.64 |
| CNN | 98.45 | 92.18 | - |
| LDA-kNN | 98.78 | 98.95 | 83.35 |
| LDA-SVM-kNN | 98.85 | 99.23 | 83.28 |
| LDA-SVM-kNN-CNN | 98.75 | 93.56 | - |
| W-LDA-kNN-SVM | 99.45 | 99.37 | 83.51 |
| Model | Accuracy (%) | Recall (%) | F-Score (%) | Time Elapsed (s) |
|---|---|---|---|---|
| Gradient Boosting | 98.21 | 80.45 | 81.91 | 16.25 |
| XGBoost | 99.90 | 97.01 | 97.89 | 4.88 |
| LDA | 98.82 | 98.98 | 98.79 | 0.61 |
| kNN | 97.23 | 96.82 | 97.01 | 0.16 |
| SVM | 99.55 | 99.20 | 99.12 | 3.79 |
| CNN | 88.45 | 83.14 | 84.33 | 2686.98 |
| LDA-kNN | 99.92 | 99.90 | 99.08 | 0.72 |
| LDA-SVM-kNN | 99.94 | 99.25 | 99.13 | 3.83 |
| LDA-SVM-kNN-CNN | 88.17 | 83.15 | 81.29 | 2687.57 |
| W-LDA-SVM-kNN | 99.93 | 99.20 | 99.12 | general: 3.91 weights search: 41.58 |
| Model | Accuracy (%) | Recall (%) | F-Score (%) |
|---|---|---|---|
| Gradient Boosting | 85.01 | 83.56 | 85.98 |
| XGBoost | 89.95 | 87.42 | 88.21 |
| LDA | 78.09 | 77.48 | 77.02 |
| kNN | 82.52 | 82.21 | 82.15 |
| SVM | 83.98 | 84.01 | 83.79 |
| CNN | 68.26 | 65.13 | 64.49 |
| LDA-kNN | 84.79 | 81.00 | 82.95 |
| LDA-SVM-kNN | 84.20 | 84.97 | 83.99 |
| LDA-SVM-kNN-CNN | 76.04 | 73.89 | 74.45 |
| W-LDA-SVM-kNN | 85.36 | 83.97 | 86.00 |
| Model | Accuracy (%) | Recall (%) | F-Score (%) |
|---|---|---|---|
| Testing on healthy subjects | |||
| Gradient Boosting | 97.65 | 96.11 | 97.03 |
| XGBoost | 99.53 | 99.05 | 99.21 |
| LDA | 98.32 | 98.19 | 98.19 |
| kNN | 97.64 | 96.99 | 97.57 |
| SVM | 98.56 | 98.05 | 98.51 |
| CNN | 71.20 | 70.98 | 70.55 |
| LDA-kNN | 99.33 | 98.80 | 98.71 |
| LDA-SVM-kNN | 98.52 | 97.69 | 97.99 |
| LDA-SVM-kNN-CNN | 78.04 | 71.81 | 73.77 |
| W-LDA-SVM-kNN | 98.52 | 97.69 | 97.99 |
| Testing on ALS patients | |||
| Gradient Boosting | 89.92 | 87.45 | 88.59 |
| XGBoost | 92.51 | 91.87 | 92.09 |
| LDA | 84.17 | 82.47 | 81.24 |
| kNN | 87.46 | 87.92 | 85.21 |
| SVM | 87.56 | 87.01 | 87.34 |
| CNN | 60.61 | 60.08 | 60.52 |
| LDA-kNN | 89.33 | 89.12 | 89.17 |
| LDA-SVM-kNN | 90.02 | 88.93 | 88.88 |
| LDA-SVM-kNN-CNN | 65.00 | 61.39 | 62.93 |
| W-LDA-SVM-kNN | 91.34 | 90.08 | 90.73 |
| Model | Accuracy (%) | Recall (%) | F-Score (%) |
|---|---|---|---|
| Testing on healthy subjects | |||
| Gradient Boosting | 90.17 | 89.32 | 89.97 |
| XGBoost | 91.68 | 91.51 | 92.80 |
| LDA | 89.15 | 88.99 | 89.06 |
| kNN | 86.58 | 86.42 | 87.10 |
| SVM | 87.51 | 87.21 | 87.49 |
| LDA-kNN | 91.51 | 91.12 | 91.40 |
| LDA-SVM-kNN | 91.10 | 90.90 | 91.00 |
| W-LDA-SVM-kNN | 91.24 | 90.91 | 91.17 |
| Testing on ALS patients | |||
| Gradient Boosting | 78.02 | 77.01 | 77.46 |
| XGBoost | 79.95 | 78.93 | 79.59 |
| LDA | 73.15 | 72.89 | 73.11 |
| kNN | 70.58 | 70.53 | 70.05 |
| SVM | 76.98 | 77.82 | 77.09 |
| LDA-kNN | 77.86 | 76.93 | 77.37 |
| LDA-SVM-kNN | 77.98 | 77.36 | 77.42 |
| W-LDA-SVM-kNN | 78.74 | 78.15 | 78.62 |
| Type of Data | LDA-kNN | LDA-SVM-kNN | LDA-SVM-kNN-CNN | W-LDA-SVM-kNN |
|---|---|---|---|---|
| 8-channel data | 84.79% | 84.20% | 76.04% | 85.36% |
| 4-channel data | 89.33% | 90.02% | 65.00% | 91.34% |
| single-channel data | 77.86% | 77.98% | - | 78.74% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mussabayeva, A.; Jamwal, P.K.; Akhtar, M.T. Ensemble Voting-Based Multichannel EEG Classification in a Subject-Independent P300 Speller. Appl. Sci. 2021, 11, 11252. https://doi.org/10.3390/app112311252
Mussabayeva A, Jamwal PK, Akhtar MT. Ensemble Voting-Based Multichannel EEG Classification in a Subject-Independent P300 Speller. Applied Sciences. 2021; 11(23):11252. https://doi.org/10.3390/app112311252
Chicago/Turabian StyleMussabayeva, Ayana, Prashant Kumar Jamwal, and Muhammad Tahir Akhtar. 2021. "Ensemble Voting-Based Multichannel EEG Classification in a Subject-Independent P300 Speller" Applied Sciences 11, no. 23: 11252. https://doi.org/10.3390/app112311252
APA StyleMussabayeva, A., Jamwal, P. K., & Akhtar, M. T. (2021). Ensemble Voting-Based Multichannel EEG Classification in a Subject-Independent P300 Speller. Applied Sciences, 11(23), 11252. https://doi.org/10.3390/app112311252






