1. Introduction
Path and trajectory planning and generation are the most important parts of navigating in autonomous vehicles and mobile robots. In an autonomous driving system, a feasible path is referred to as the geometric construction, and the global plan is used to map out the curve moving from point A to point B while taking into account the avoidance of obstacles or overcoming complex mazes. Meanwhile, the trajectory is a piece in a path, or trajectories of the path, and are designed locally including specified velocities in each position. All trajectories must be joined smoothly, or a trajectory must be designed in account to connect the two adjunction trajectories smoothly and continuously. This paper provides some discrete mathematic polynomial methods to map out feasible trajectories from a given starting position to a given destination position subject to the vehicle’s physical and environmental limitations.
The main aim of this paper is to develop a real-time trajectory planning for an autonomous vehicle based on the global path given from the GPS positioning and LIDAR detecting systems. The generation of feasible and the optimal trajectories is based on the online calculation of the vehicle’s updated information such as the position, velocity, and steering angular speed, etc. In this paper, we assumed that the vehicle steering wheel is designed based on the vehicle dynamics in [
1]. A typical passenger vehicle is selected with a steering ratio of 15.0 and a maximum turn on the right and left of the steering wheel of +/−675 degrees. Therefore, the front wheel angles will be limited to +/−45 degrees. From now on, the vehicle steering angle is considered as the front wheel angle and has a physical limitation of +/−45 degrees.
The body of literature for recent autonomous vehicle paths and trajectory generation is enormous. This paper reviews some update information on the model predictive controls, optimal iterative calculations for real-time control of autonomous ground vehicles, auto-driving, and auto-parking systems. Basic mathematic functions to determine feasible trajectories were presented in [
2], in which the authors introduced different mathematical methods for generating optimal paths. The vehicle was controlled and simulated moving on its feasible paths, including forward and reverse velocity, into and out of parking places. However, Authors in [
2] lacked the generation of continuing trajectories and online calculations for feasible and optimal trajectories subject to the vehicle’s dynamic constraints.
Vehicle steering dynamic control and simulation are referred to in [
3]. In [
3], the author provided analyses and simulations of sideslips and the steering angle depending on the vehicle velocity and the environmental limitations. The vehicle steering angle in forward and reverse speeds were also analyzed and simulated. Fundamental parameters of vehicles regarding the position of the gravity center, the stiffness of front and rear wheels, under-steering and over-steering conditions, as well as the sideslip dynamics were also included in the analyses and calculations. Therefore, data from [
3] is useful for generating the vehicle trajectories subject to physical constraints.
Regarding the model predictive control for vehicles’ tracking setpoints, reference [
4] is considered. The authors in [
4] presented a fundamental new robust model of predictive control for uncertain and constrained systems. The tracking setpoints of the robust model predictive control for input-saturated and softened-state constraints were introduced. The softened-state constraints showed higher superiority since, in many cases, the autonomous vehicle might be allowed to violate certain constraints while being subject to heavy penalty conditions. After this, the control system will find it easier to determine the optimal solution and minimize the tracking error.
Recent studies on vehicle trajectory generation and tracking control are referred as following: Reference [
5] introduced the problem of tracking trajectories under certain traffic conditions. The design of feasible paths was performed step by step based on the traffic environments. The closed-loop control was determined by a Proportional Integral Derivative (PID) controller. The trajectory generation and the tracking path controller were feasible but lacked optimal calculation and were not subject to vehicle constraints. A new study on vehicle trajectory generation for autonomous systems subject to emergency situations was referred to in [
6]. Reference [
6] presented an efficient solution to improve the vehicle control subject to emergency situations from the autonomous decision support. However, authors in [
6] did not provide mathematic calculations for generating the vehicle optimal trajectory.
Recent research references on vehicle trajectory generation are investigated, most of which presented new mathematic functions for generating online feasible trajectories. The authors in [
7] updated the prediction and generation of vehicle trajectory in non-linear programming with consideration of the long short-term memory and generative adversarial networks. The authors in [
8] presented trajectory generation for a vehicle changing lanes automatically with nonlinear mathematical functions while taking into account the public traffic laws. The authors in [
9] introduced a new method for robust trajectory generation based on neuromorphic research and robotic control. The authors in [
10] introduced a new model of predictive control for autonomous vehicle tracking of any given path. The authors in [
11] presented a new approach for industrial robot trajectory generation based on motion modular technology. The authors in [
12] reviewed recent advances in the generation of trajectory planning methodologies. The authors in [
13] described the new method in motion planning for mobile robots with the use of jumping leap search with Bezier curves. The authors in [
14] highlighted robust and the efficient tool path generation for curving along low triangular mesh surfaces. The authors in [
15] presented research on trajectory generation optimization for robotics and autonomous systems. Finally, the authors References [
16,
17,
18,
19,
20] presented updated mathematical algorithms and information technologies applied for mapping out the feasible paths of autonomous vehicles. Updated references on vehicle trajectory generation and advanced autonomous vehicle control techniques are referred to in [
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31].
Online optimal trajectory generation subject to a vehicle’s physical constraints and environmental limitations remain a challenge. This paper proposes new methods of trajectory generations subject to those constraints. The optimal trajectory is selected based on three criteria: The shortest distance, the smoothest curve, and the smallest tracking error. The outline of this paper is as follows:
Section 2 outlines the conventional kinematic diagram and control model for the ground vehicle;
Section 3 introduces a basic method for trajectory generation;
Section 4 presents the selection of the optimal trajectory subject to the vehicle constraints and environmental limitations;
Section 5 introduces a new method for quartic polynomial trajectory generation;
Section 6 presents a new method for symmetric polynomial function;
Section 7 reviews the performances comparison of all three methods; and
Section 8 includes conclusions and recommendations.
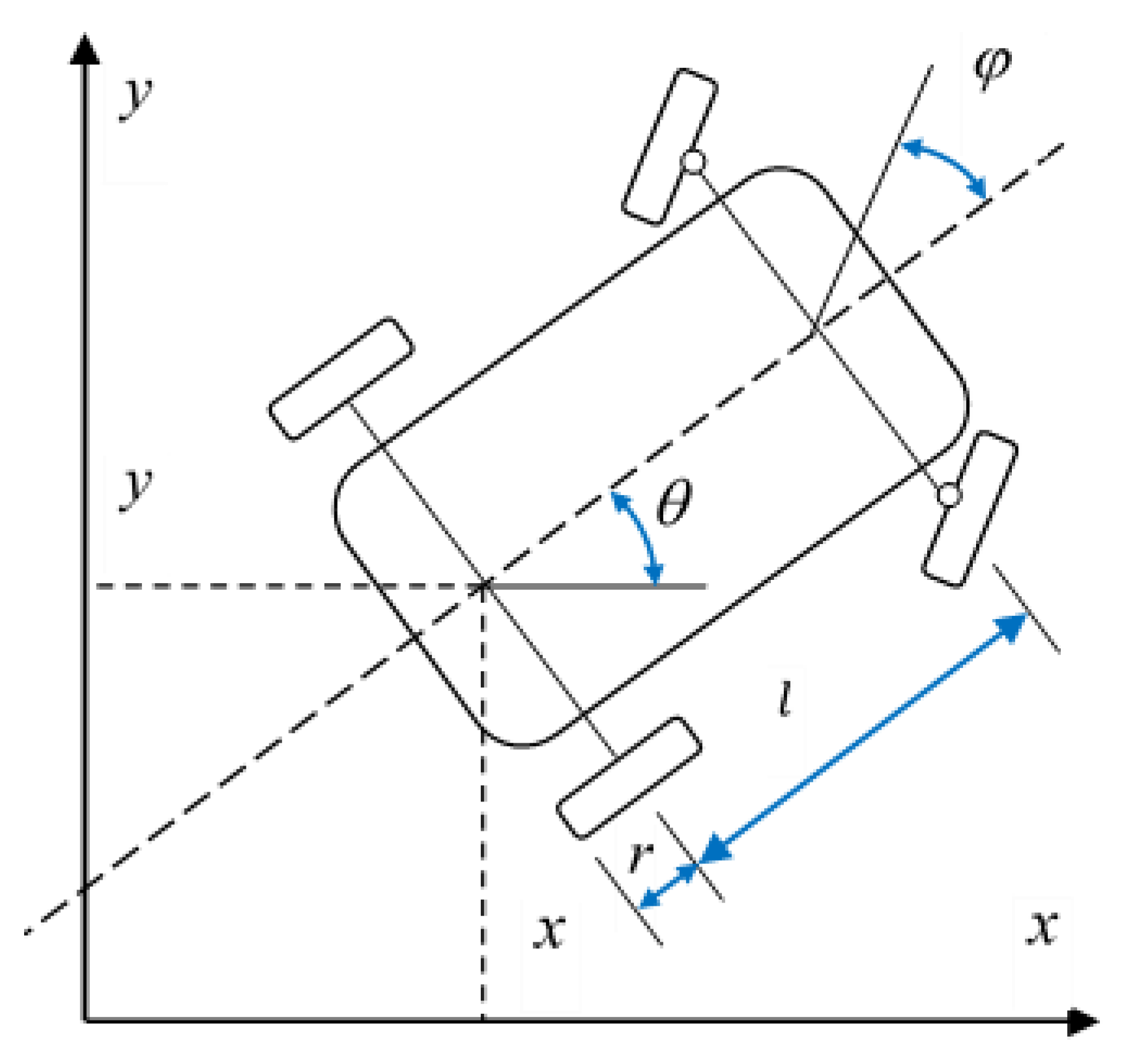
2. Vehicle Kinematic Model
A typical passenger vehicle can be modelled as a simple draw of four wheels, where two front wheels are connected to the steering system,
, and rotate in a maximum angle range of +/−45° (degrees) to the vehicle body. The distance between the center of the front wheels and the center of the rear wheels is called the vehicle wheelbase (
l). In our model, we select the wheelbase length of
l = 2 m. The wheel radius of four wheels is assumed to be
r = 0.25 m. The vehicle position (
x and
y) is identified at the center of the rear wheels. The vehicle body angle,
, is also identified along the axe
x. It is assumed that the vehicle position is always identical to the GPS and LIDAR systems with exact
x and
y coordinates. The vehicle body angle
θ and the steering angle
ψ are assumed to also always be identical to the 3D sensors. The kinematic model of a vehicle is shown in
Figure 1.
The vehicle moves forward and reverses and is controlled by the engine angular and steering angular velocity. A vehicle driven by the rear wheels and moving forward is presented in Equation (1):
The vehicle driven by the rear wheels and moving in reverse is obtained in Equation (2), where the vehicle speed is assigned in a negative sign:
The vehicle driven by the front wheels is formulated in Equation (3):
where
are the state and output variables. The two control inputs are
and
, where
is the angular speed of the driven wheels, therefore
is the vehicle speed (km/h); and
is the steering angular speed in revolutions per minute (rpm). The two models in Equations (1) and (2) are mainly used to calculate and simulate the vehicle performances. The next part presents a basic method for trajectory generation.
3. Position Quintic Polynomial for Trajectory Generation
A basic position quintic polynomial for trajectory generation can be achieved from the nonlinear vehicle movement curve along the
x and
y axes on the flat system as referred to in [
21]. Then, the control input
can be identified as:
The vehicle body angle,
, along the
x axis can be formulated:
Then, the vehicle body angular velocity,
, will always be identical:
The vehicle steering angle and the body angle in Equations (5) and (6) can be formulated directly from , , and , . Similarly, all state variables and inputs can be represented by the output coordinates x and y.
It is assumed that the vehicle moves from the starting point at time
t = 0 to the destination point at
t =
T for
x(0),
y(0) and
x(
T),
y(
T) from
t = 0
at the starting point of
x(
t) =
x(0):
and at the starting point of
y(
t) =
y(0)
At the destination point
y(
t) =
y(
T)
It is assumed that
, then the trajectory of
x(
t) can be chosen by the following Equation:
Then,
y(
t) can be chosen as
where
,
, and
; and
, in which:
Then, the vehicle body angle,
, is
and the vehicle steering angle,
, is
The vehicle velocity and acceleration can be re-formulated from (10) and (11) as
and
and for variable
x:
and
The vehicle velocity can be identified from Equations (14)–(17):
Or another way to calculate
, then:
is re-formulated from Equation (6):
To calculate
, from Equation (13), when
,
Then, the second input
is:
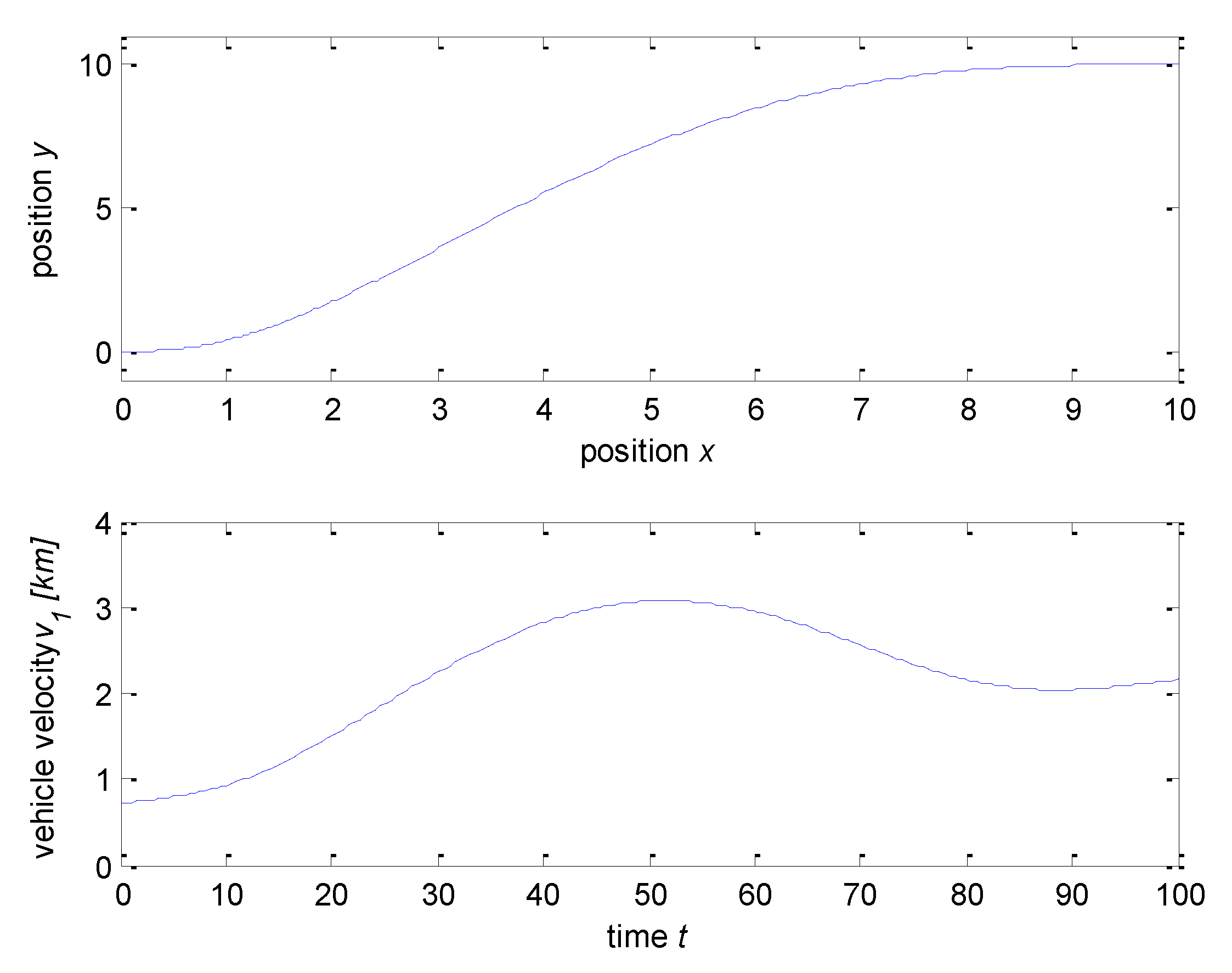
Simulations for this method were conducted with the above vehicle parameters of
,
,
,
, and
(
T is calculated for 100 discrete time intervals from
t = 0
). The trajectory generation for
x,
y,
,
,
, and
is obtained from Equations (12)–(22) and shown in
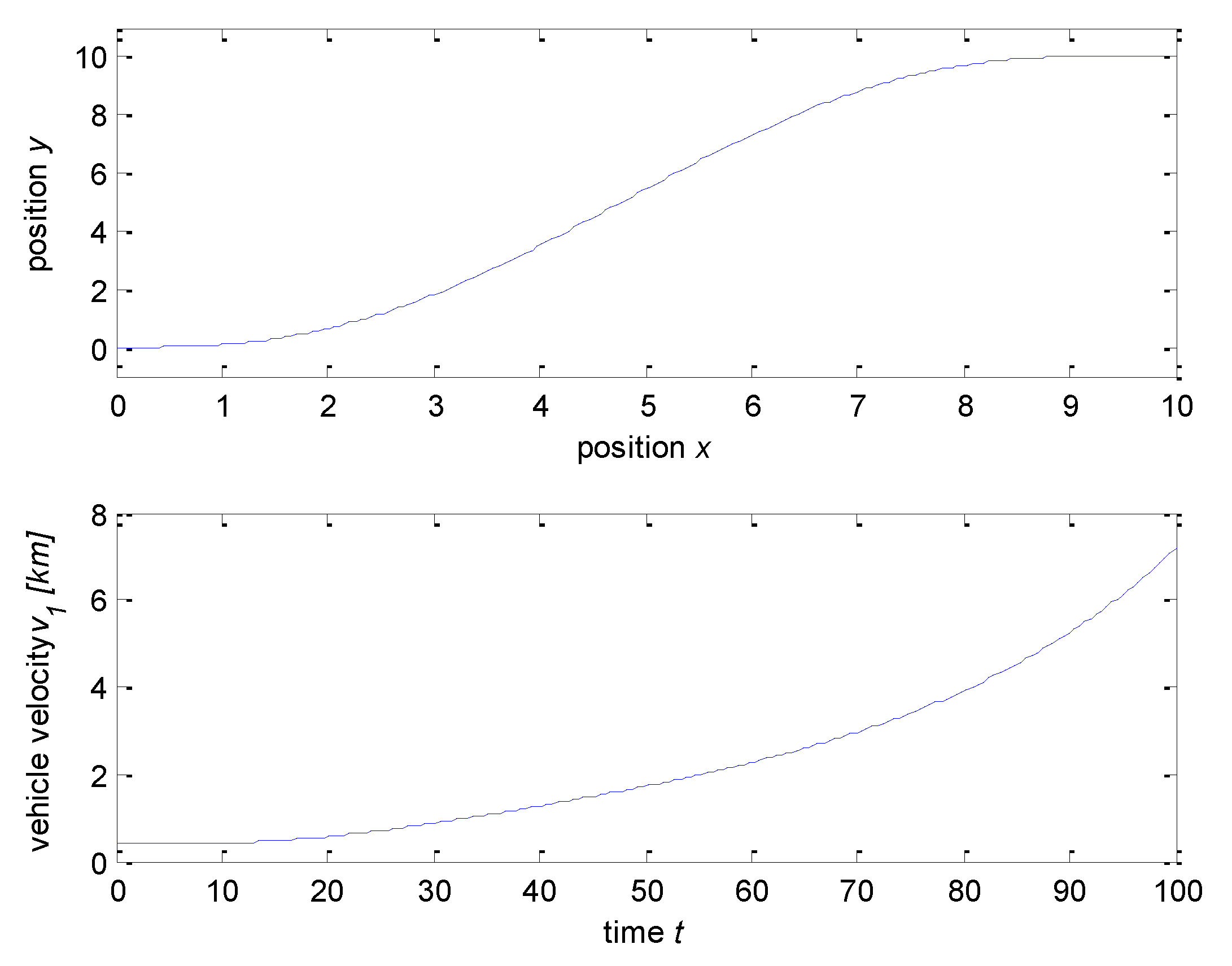
Figure 2 and
Figure 3.
Figure 3 shows the maximum steering angle,
radians or 62.87° (degrees). This value violated the constraint for the vehicle steering angle
. This trajectory, therefore, is infeasible because the distance from x°, y° to x
T and y
T is too short, causing the steering angle to be too large. The next part presents the method to achieve feasible and optimal trajectories subject to vehicle constraints and environmental limitations.
4. Trajectory Generation Subject to Constraints
For a real vehicle, the steering angle is always limited from
Once the vehicle moves from to , it is assumed that the initial conditions of are given and the final conditions cannot be changed. The vehicle violates the constraint because the distance from to is too short. By using iterations from computer programming, it is easy to determine the feasible trajectories with lower values of and or the vehicle will move on smoother and safer curves.
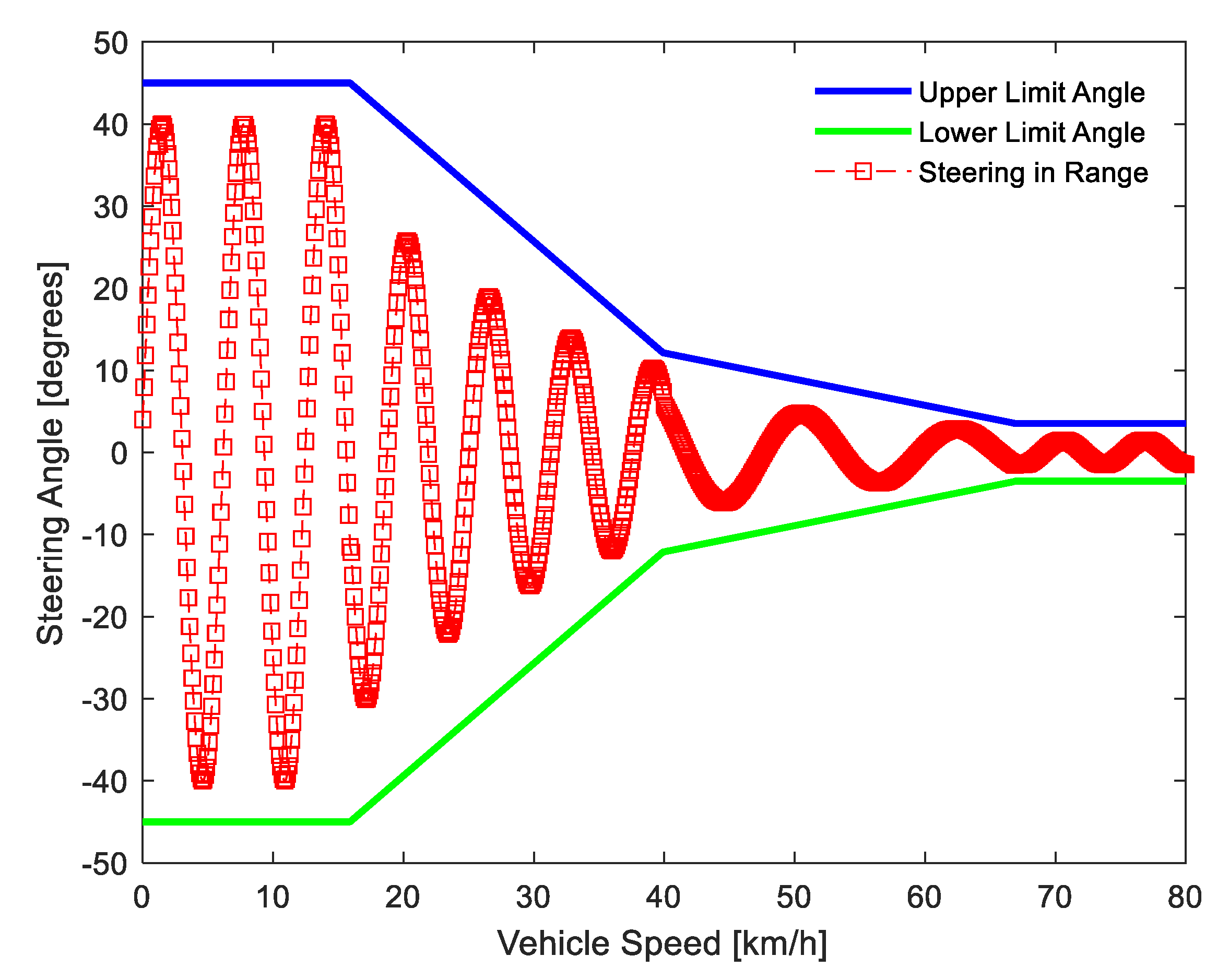
As mentioned in [
1], the front wheel angle always has hard constraints. At a low vehicle velocity of less than 16 km/h, the vehicle can be driven with the maximum steering angle. However, in higher speeds, the steering angles allowed will be reduced from +/−45 to +/−12 degrees when the vehicle velocity reaches 40 km/h. At a vehicle speed higher 67 km/h, the steering angle is restricted to less than only +/−3.5 degrees as shown in
Figure 4.
The vehicle speed always has to be controlled in a strict function of the steering angle due to safety purposes, therefore this paper proposes a new method for generating the vehicle’s feasible trajectories subject to the hard steering angular constraints and the environmental conditions as follows:
The feasible trajectories
x(
t) and
y(
t) from starting points
x(0) and
y(0) to the destination point
x(
T) and
y(
T) for
t = 0 ÷
T subject to Equation (23) and other constraints in [
1] generated from Equations (10) and (11) can be modified by adding iterations to lengthen the trajectory distance. The programming calculation for each feasible trajectory must be verified online and then the steering angle
and other variables must be re-calculated to satisfy the objective constraints. If certain constraints are violated, the distance from the starting point to the destination point is too short to generate a safe and feasible trajectory. In this case, we must lengthen the trajectory distance,
to a new, longer distance with a small amplification coefficient
:
Several iterations,
are required until the steering and other condition constraints are satisfied. Then, the new destination position of the vehicle will be:
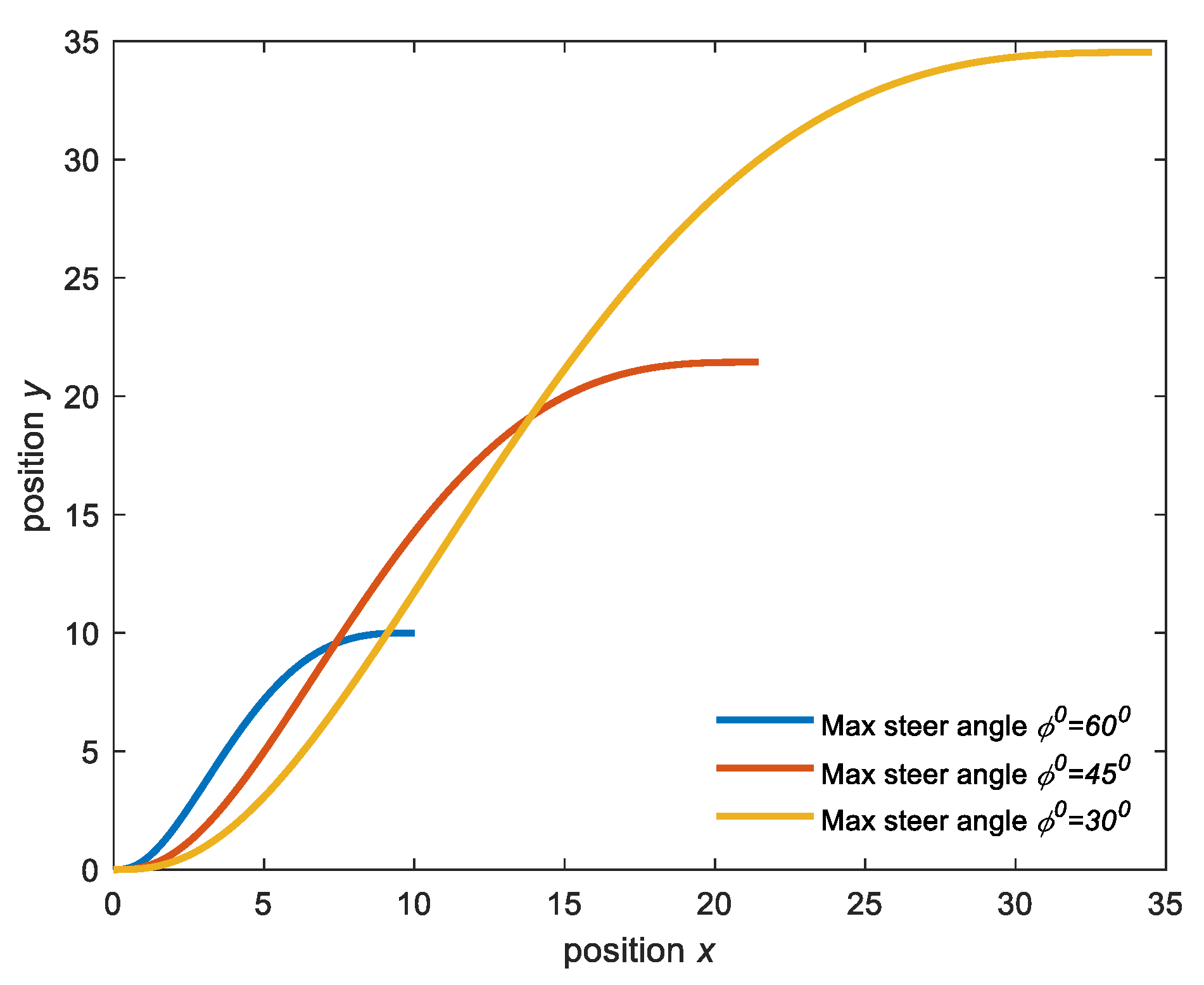
The following simulations are conducted with
, and the vehicle parameters are the same as in previous simulations. By adding constraint (23) and other vehicle dynamic constraints, feasible trajectories are obtained in
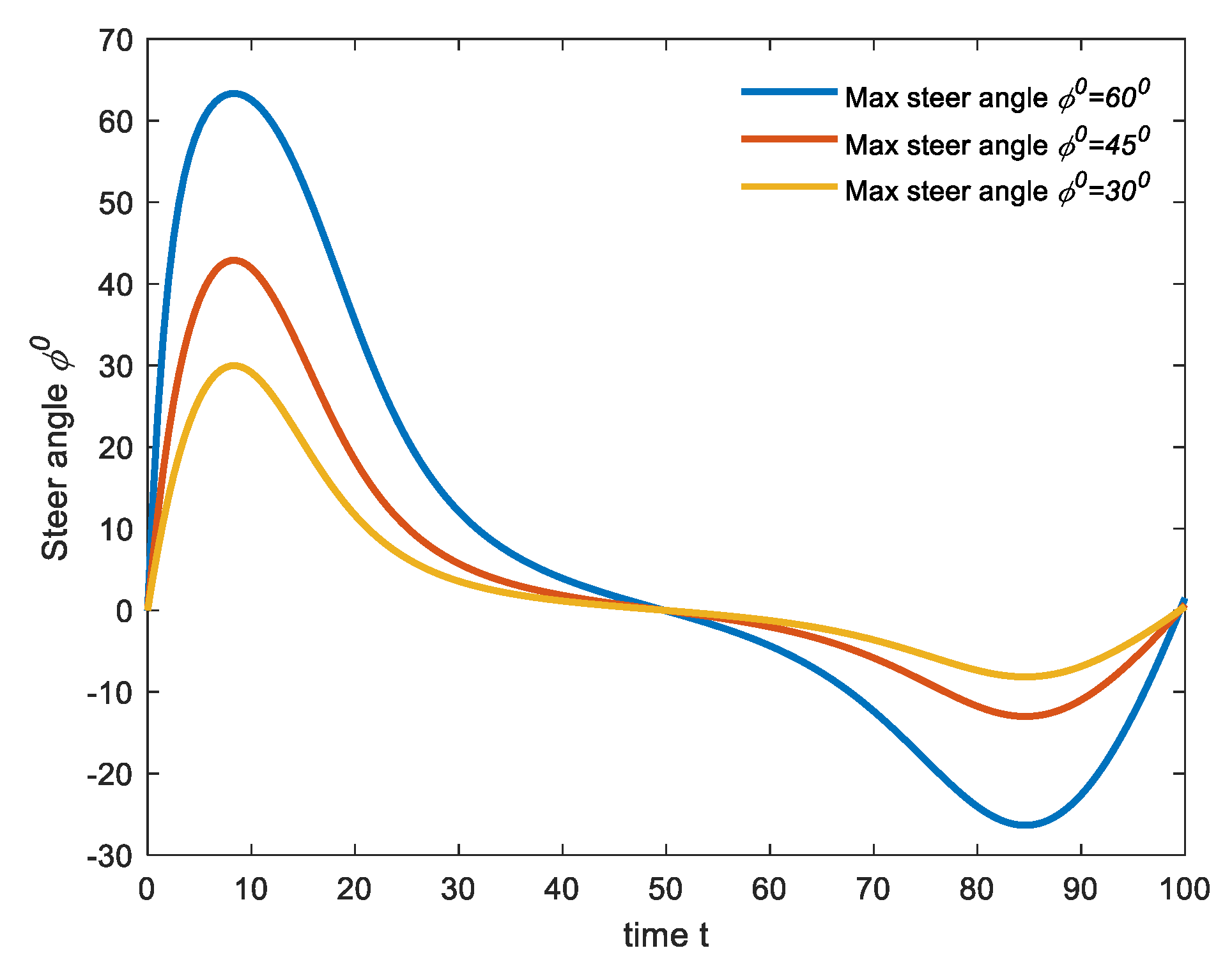
Figure 5. The steering angles are assumed to be limited to 60°, 45°, or 30° according to the vehicle and environment safety requirements. The minimum lengths of corresponding feasible trajectories are 15.0910 m, 32.3490 m, and 52.0983 m corresponding to the new destination points of
x(
T) =
y(
T) = 10.000, 23.579, and 34.5227, respectively.
Figure 6 shows the steering angles during the time that the vehicle is moving along different trajectories with different maximum steering angles. The lower and smoother steering angles will lead to safer trajectories. According to the environmental limitations, the optimal trajectory can be selected based on the safest steering angle, the shortest distance, and the smallest tracking error, etc.
Once we have calculated and selected an optimal feasible trajectory subject to constraints, we can again determine the steering angle by the vehicle velocity moving along this trajectory.
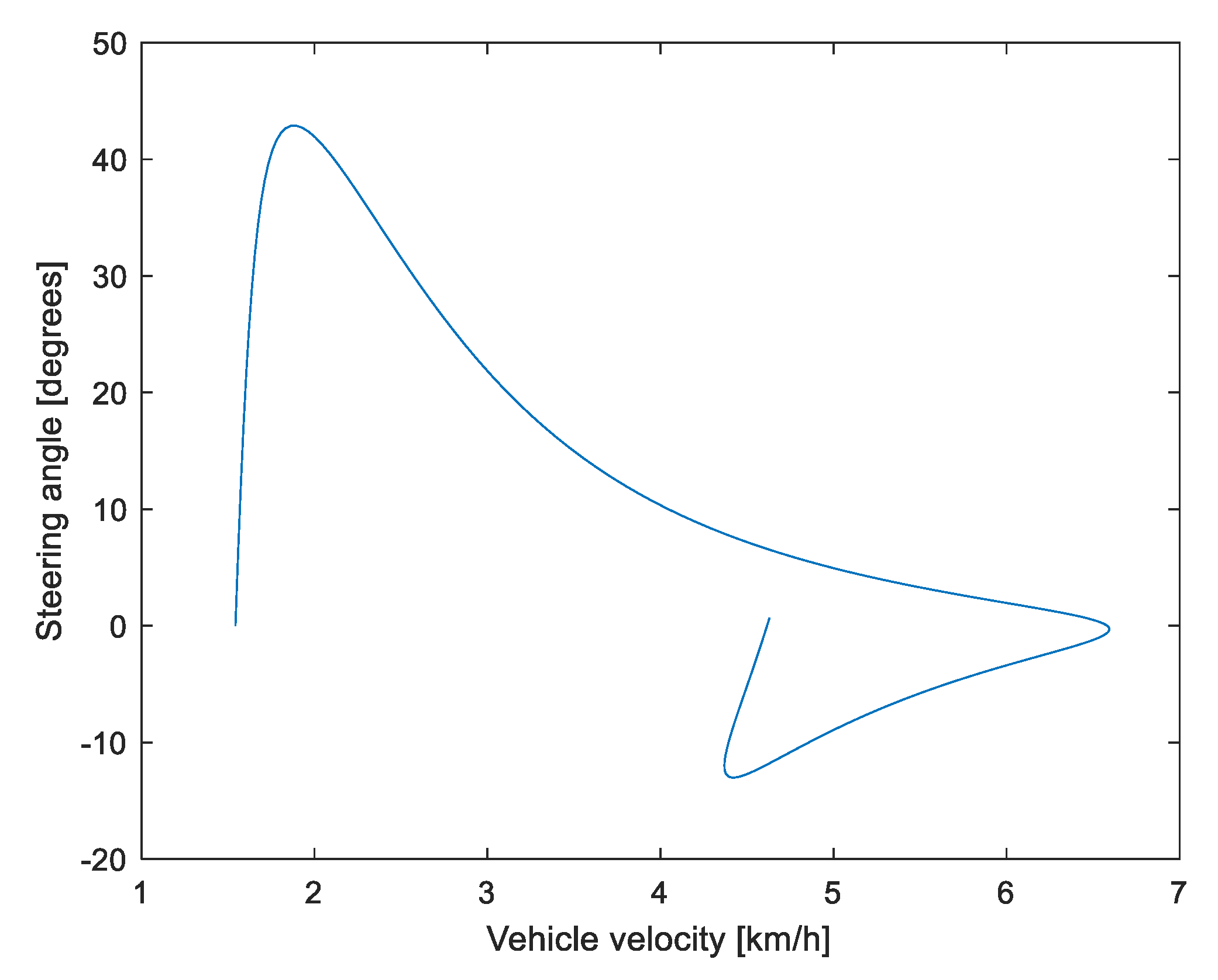
Figure 7 shows the graphic of the vehicle steering angle vs. the vehicle velocity subject to the hard constraint for the steering angle less than 45°. In this case, the vehicle moves along this trajectory with the maximum steering angle of 42.8547°. The new destination of the vehicle is
and this feasible trajectory is found after four interactions with
trials in (24) and (25).
The next part proposes a new quartic polynomial trajectory generation.
5. Speed Quartic Polynomial Trajectory Generation
From reference [
22] of trajectory generation for a nonholonomic system, for faster and smoother feasible trajectory generation, we propose a quartic function for generating the vehicle feasible trajectory:
The vehicle dynamics in Equation (1) can be separated into four variables,
,
,
, and
.
The vehicle travels from the starting point at time to the destination point at time similarly to the system in (26) from the new starting point at to the new destination point at .
For
, the identification of
is:
and
and
and
in which,
and
, and
The new trajectory will be achieved from Equations (35)–(42):
and
and
and
and
and
and from Equation (27)
Figure 8 shows the new trajectory of the vehicle and the vehicle velocity.
Figure 9 shows the steering angle,
, and the vehicle body angle,
, corresponding to the angular velocity
, and
.
As shown in
Figure 9, this feasible trajectory requires a maximum steering angle of
and satisfied the steering angle constraint,
. Thus, this method is better than the previous method in part 3 with
that violated the vehicle steering angle constraint. However, in this method, the vehicle velocity is increasing and not in a smooth curve. In reality, the speed of vehicle must be controlled under smooth changes. The next part proposes another method, which can generate smoother velocity changes.
6. Symmetric Polynomial Trajectory Generation
This part presents a new method of symmetric trajectory generation for smoother, safer, and easier to control for autonomous vehicle tracking on its trajectory. This method is based on the optimal motion planning in [
23]. The vehicle moving from the start point to the destination point with the travelling time
can be now reformulated based on a symmetric polynomial function:
and the position of
y is:
The velocity of
:
and the velocity of
:
Then, the acceleration of
and the acceleration of
At the starting point
:
At the destination point
:
From Equations (49) and (50), for simplicity, we assumed that the coefficients of velocity at the start and destination points,
, then
and similarly
Simulation of this method is conducted with the same vehicle parameters in previous examples and shown in
Figure 10 and
Figure 11. The velocity coefficients are set at
. Other parameters regarding the vehicle angular velocity,
, the vehicle body angle,
, the vehicle body angular velocity,
, the vehicle steering angle,
, and the vehicle steering angular velocity,
are calculated using the following Equations:
and
and
and
and
The results of this method were observed to be better than previous methods: The vehicle trajectory is smoother. The vehicle speed also increases smoothly from the starting point and reaches the maximum speed in the middle of the trajectory. Then, the speed is reduced as the vehicle moves to the destination point, as is shown in
Figure 10.
This method appears to be more realistic and controls the vehicle tracking in its trajectory more easily. The body and steering angle and the angular velocity are shown in
Figure 11.
As shown in
Figure 11, the maximum steering angle for this method is
and is better than the method in part 5 with
. Therefore, the trajectory in
Figure 10 is smoother and safer than the previous methods. The next part presents the performance comparisons of all three methods.
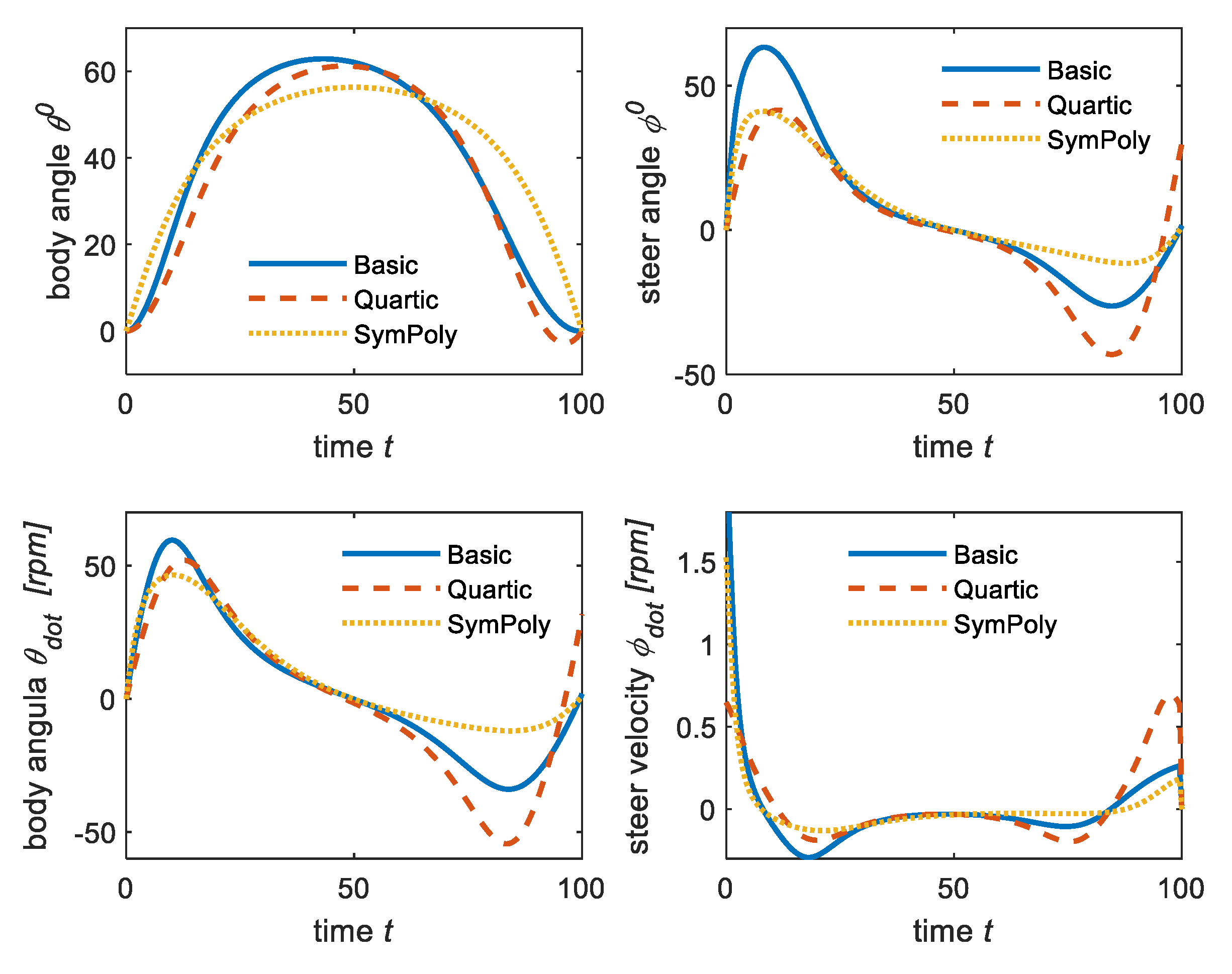
7. Performances Comparison
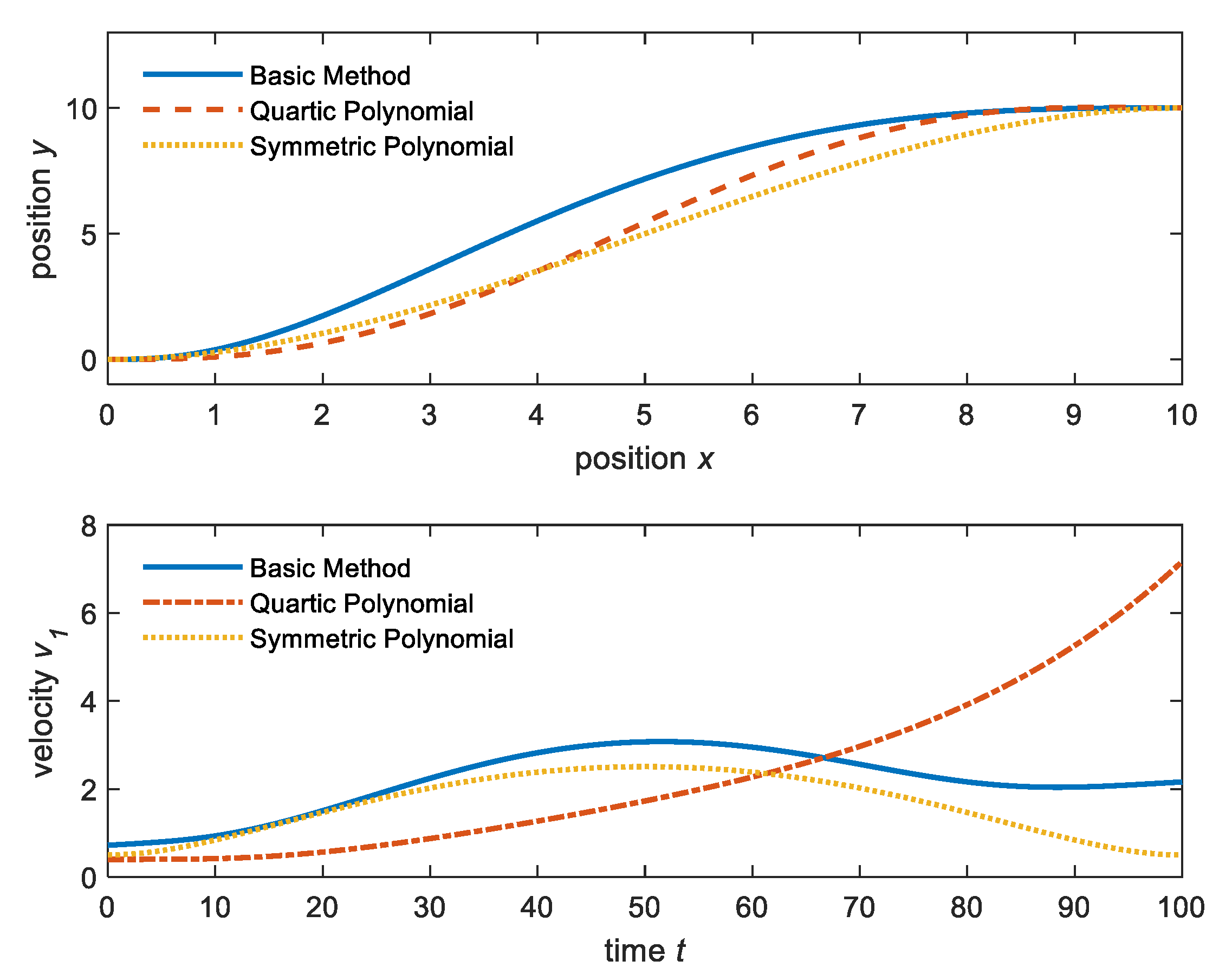
The comparison of performances for all three methods is shown in
Figure 12 and
Figure 13 for trajectory curves, velocities, the steering angle/velocity, and the body angle/velocity.
Figure 12 shows the feasible trajectory of the symmetric polynomial method is the smoothest, and the velocity of this method is also symmetrical, increasing from 0 and reducing to 0. Therefore, this method is useful in the application of auto-parking systems.
Figure 13 shows the comparison of the body and steering angles and angular velocity. This symmetric method also provides the smoothest curve of the body and steering angles and velocity.
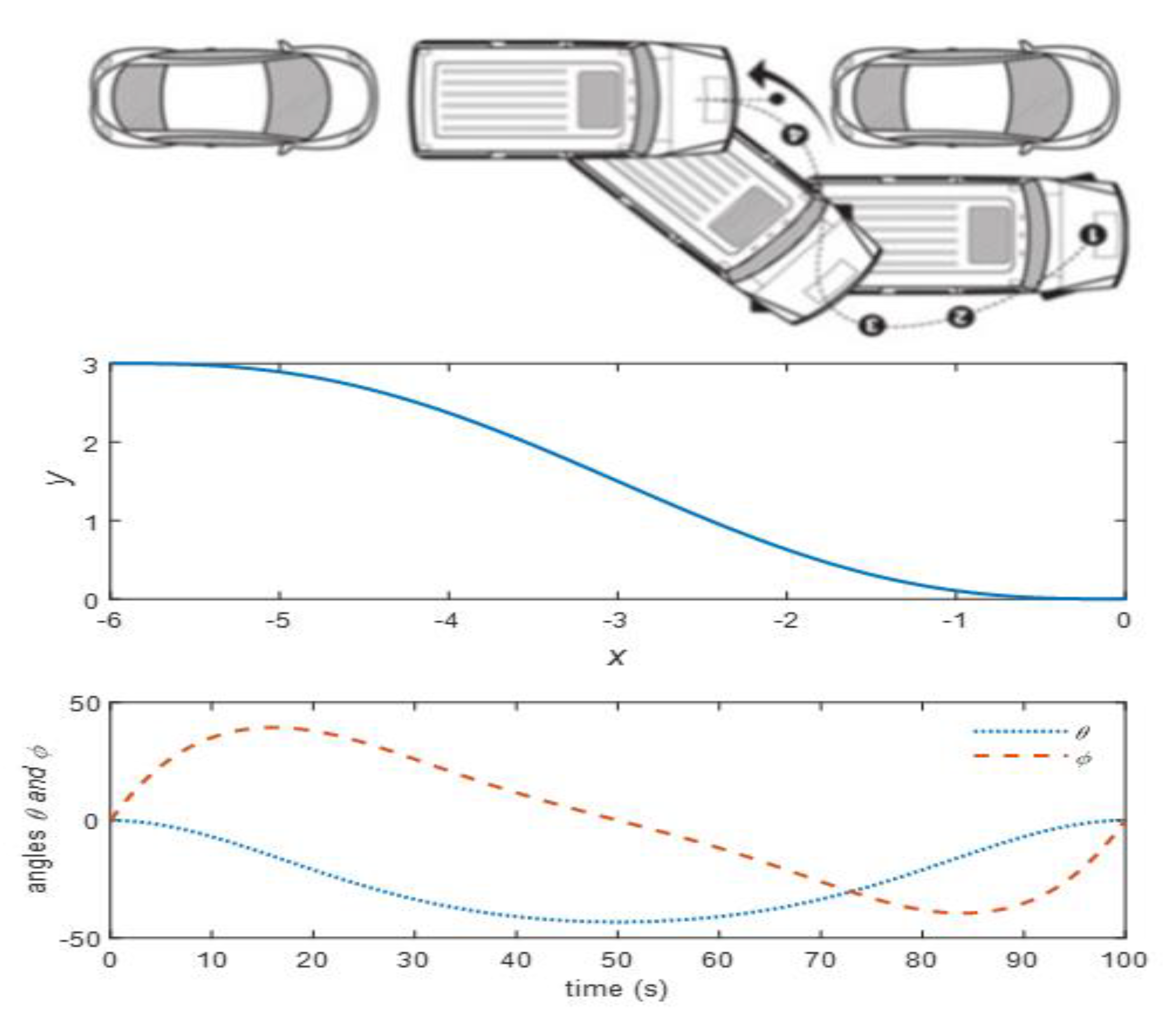
A vehicle’s feasible trajectories are the continuous segments connected to each other along the vehicle’s feasible path. All trajectories are required to join each other smoothly and continuously. The control of vehicle tracking along its feasible trajectories is performed by the control of the vehicle velocity and the steering angle. The following are the simulations of a vehicle’s auto-parking performance with the symmetric polynomial trajectory generated from a starting point of
x(0),
y(0) to a destination point of
x(−6),
y(3).
Figure 14 shows the vehicle moving in reverse and the steering angle
moving from positive to negative and returning to 0 position. The steering angle,
, satisfied the constraint as per the vehicle dynamic moving in reverse in Equation (2).
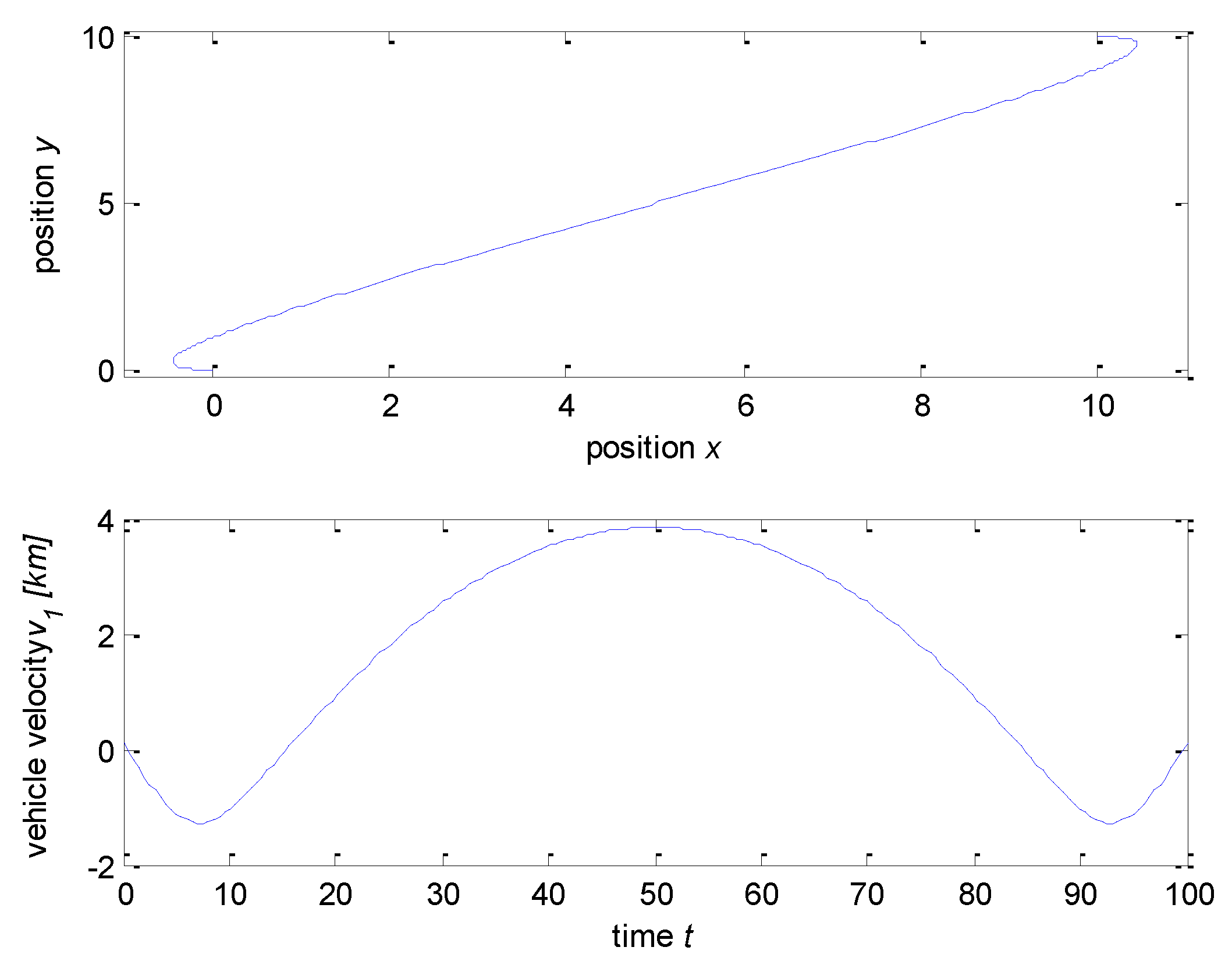
Simulations for the vehicle moving in reverse speeds are also displayed in
Figure 15. As mentioned in Equation (2), the reverse speed is a negative sign. Then the velocity coefficients in Equations (51) and (52) must be negative values. Simulations for the vehicle in reverse speeds are conducted with the symmetric polynomial method. The velocity coefficients are assigned for
.
Since this simulation assigns the vehicle reversing at the start, for
, and at the destination, for
,
Figure 15 shows the vehicle reversing at the starting point then moving forward to the destination, then reversing to the destination. The vehicle velocities change the sign three times accordingly.
All three methods of feasible trajectory generation subject to vehicle constraints and environmental limitations are presented and illustrated with simulations. The next part outlines the conclusions and recommendations drawn from this paper.