Novel Beam Scan Method of Fabry–Perot Cavity (FPC) Antennas
Abstract
:Featured Application
Abstract
1. Introduction
- A predictable beam-scan direction based on a newly introduced design formula;
- A wide beam-scan range with a well-maintained high gain;
- A continuously changeable beam-scan direction.
2. Materials and Methods
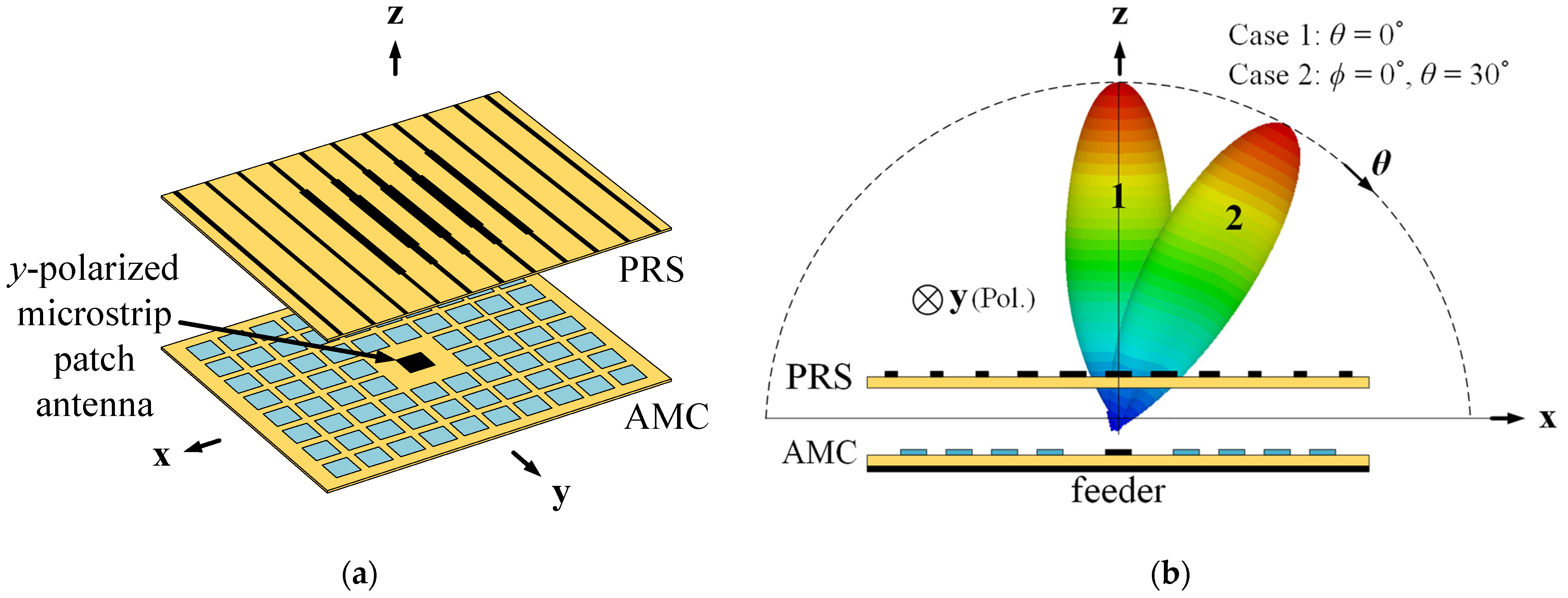
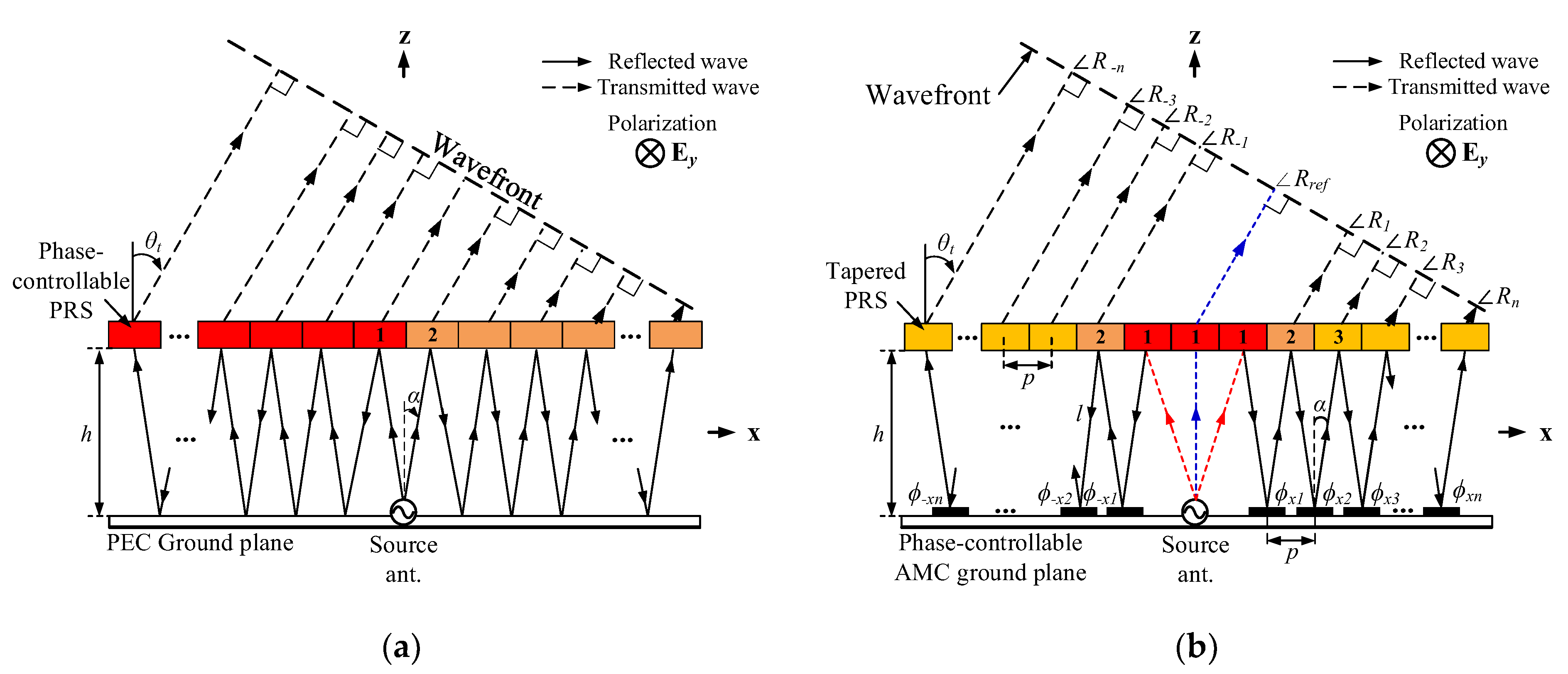
2.1. Operation Principle of the Proposed Antenna
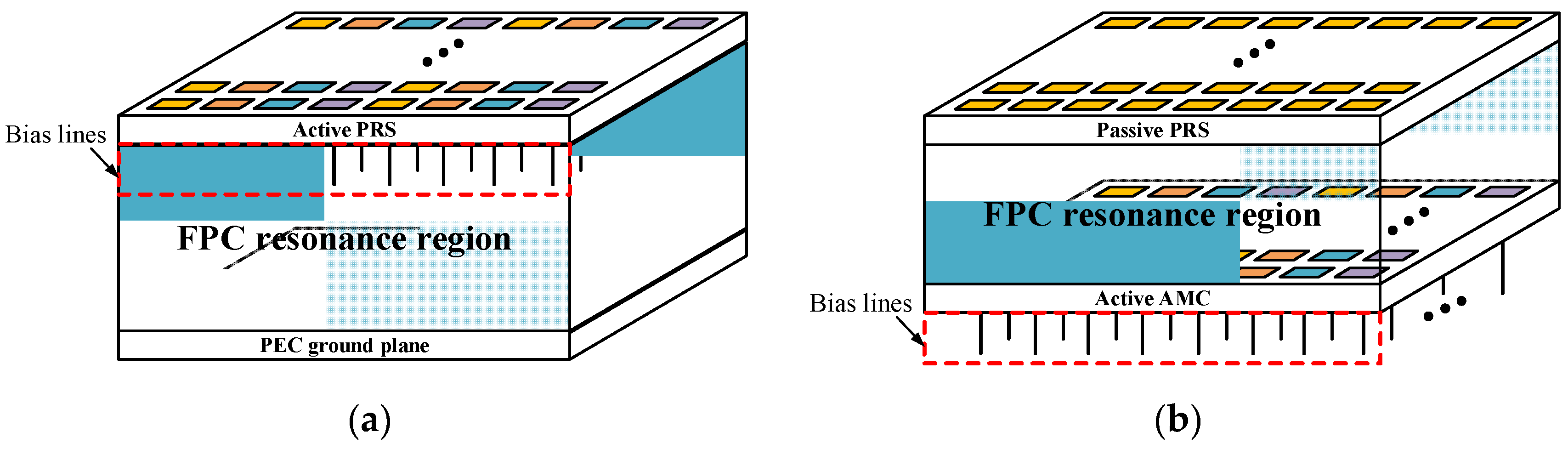
2.2. Deployment of a PRS Superstrate and an AMC Ground Plane
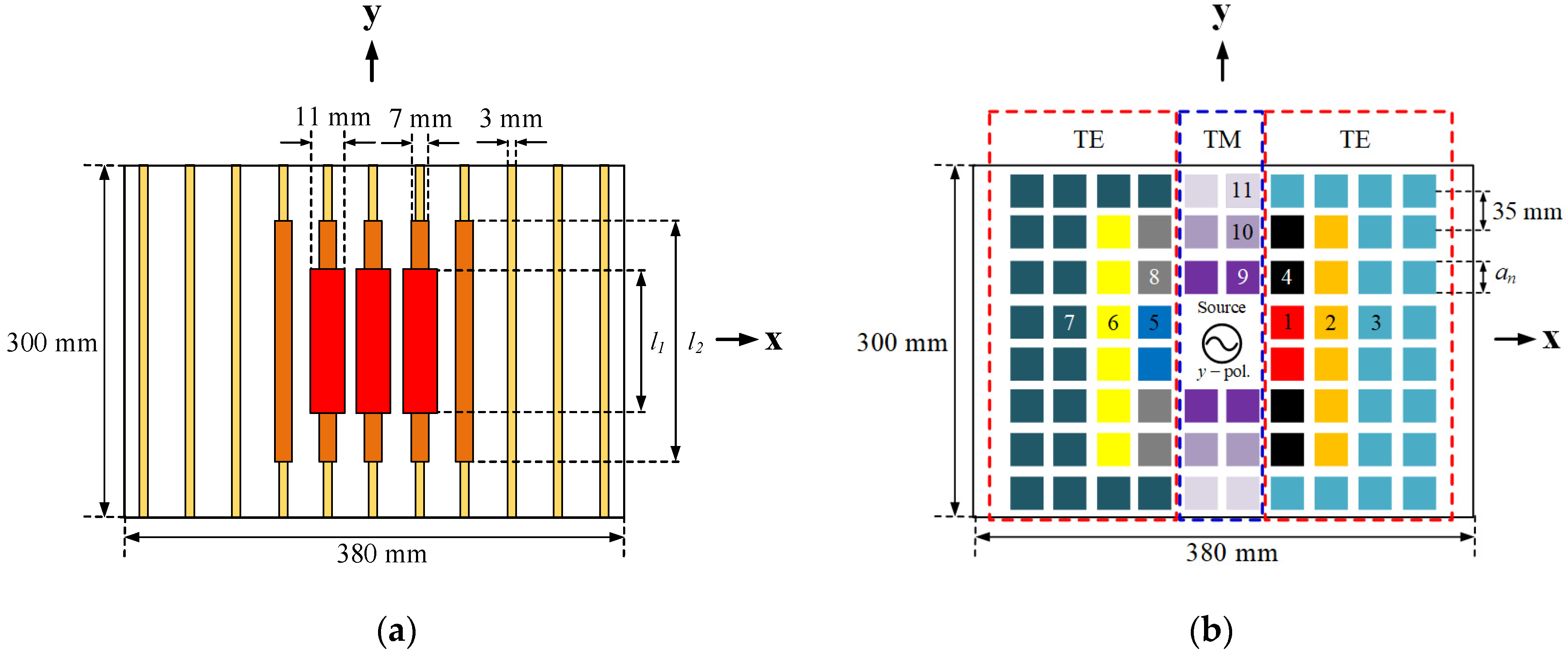
2.3. Design of the AMC and the PRS Unit Cell
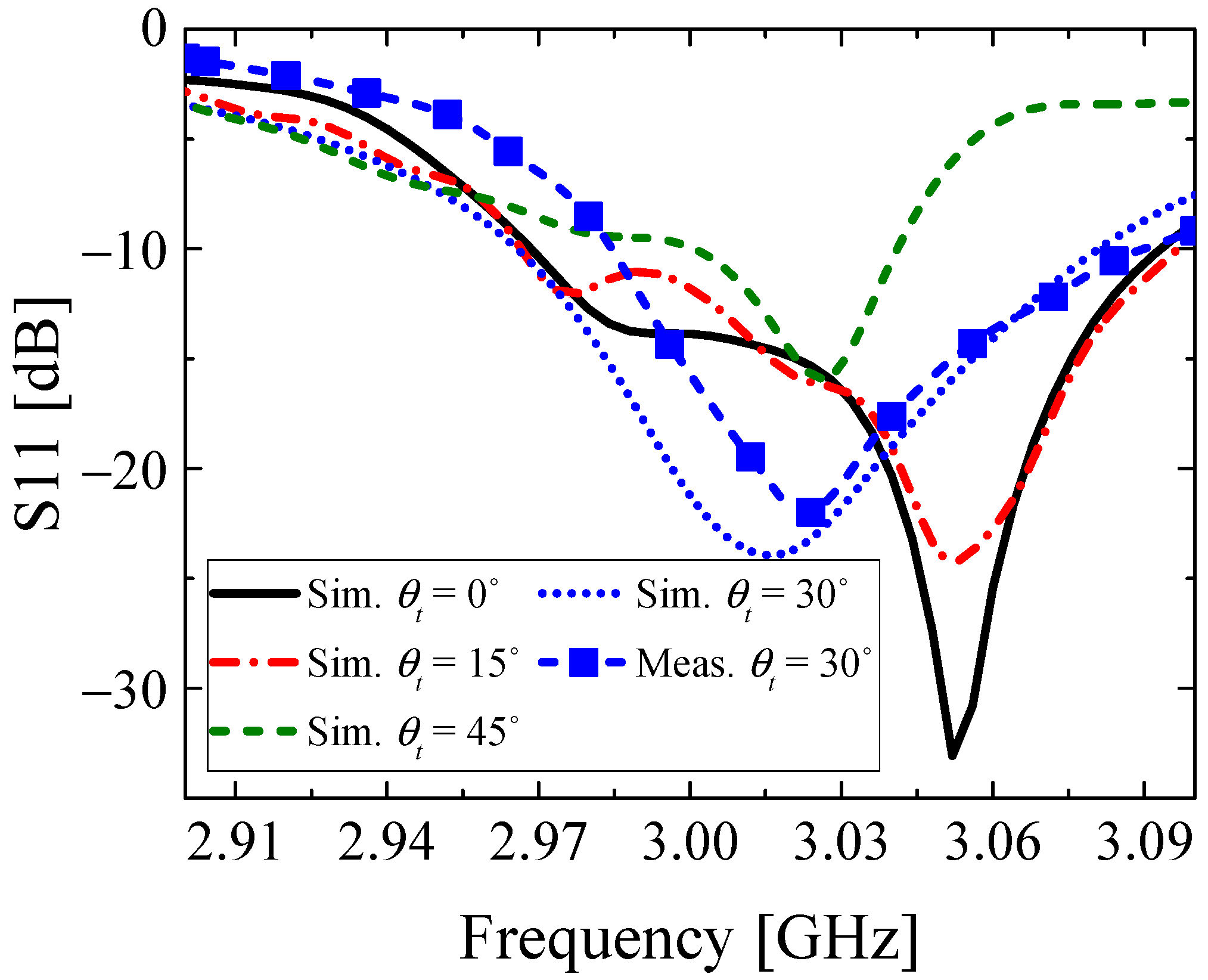
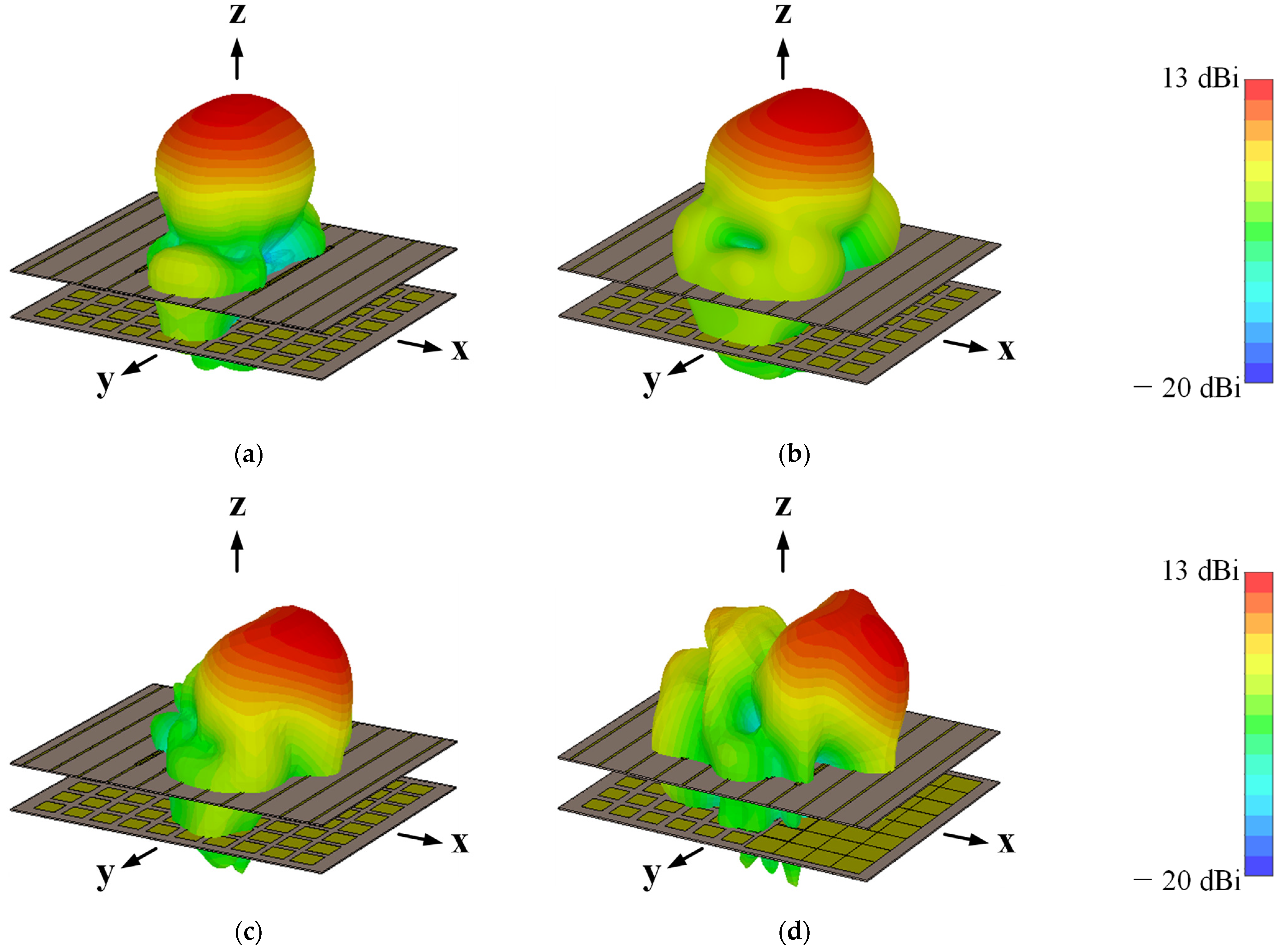
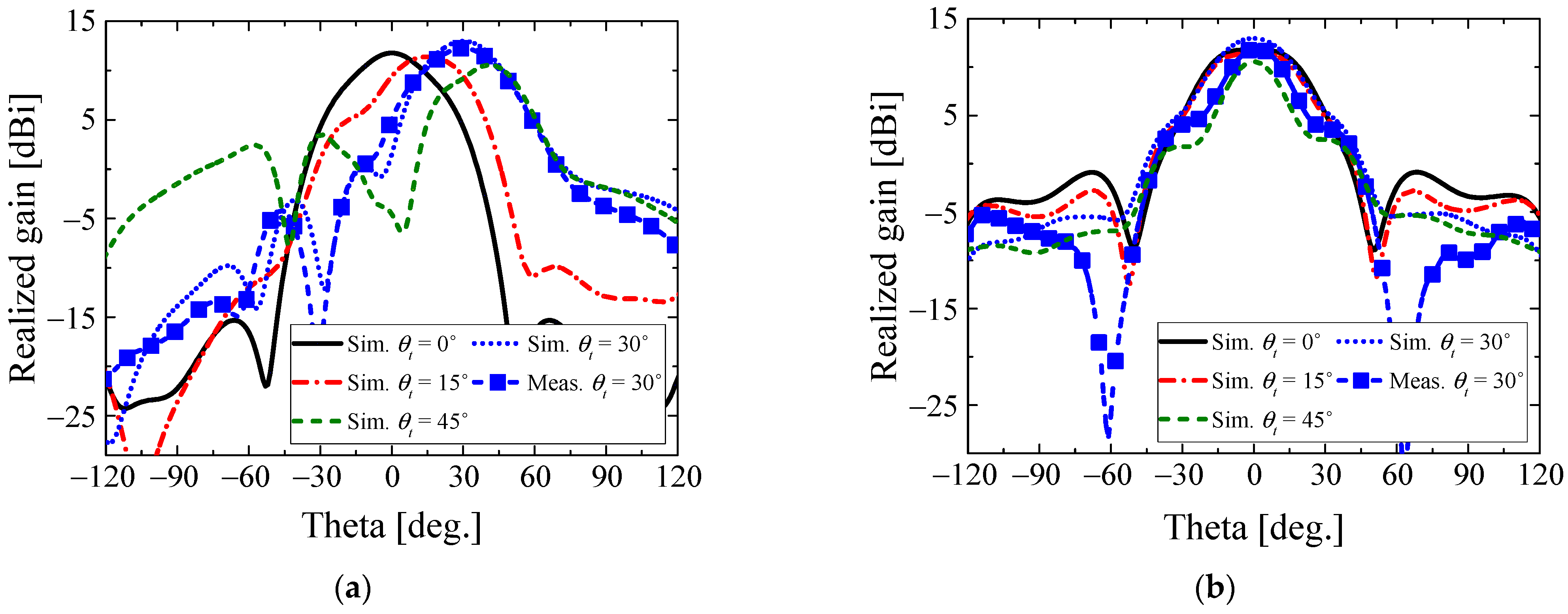
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.O.; Yoon, W.S.; Han, S.M. Frequency-Selective Beamforming Array Antenna Systems with Frequency-Dependent Phase Shifters. J. Electromagn. Eng. Sci. 2019, 19, 259–265. [Google Scholar] [CrossRef] [Green Version]
- Mao, C.; Gao, S.; Wang, Y. Broadband High-Gain Beam-Scanning Antenna Array for Millimeter-Wave Applications. IEEE Trans. Antennas Propag. 2017, 65, 4864–4868. [Google Scholar] [CrossRef]
- Nayeri, P.; Yang, F.; Elsherbeni, A.Z. Beam-Scanning Reflectarray Antennas: A technical overview and state of the art. IEEE Trans. Antennas Propag. Mag. 2015, 57, 32–47. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J.A. Reflectarray Antennas, 1st ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sievenpiper, D.F.; Schaffner, J.H.; Song, H.J.; Loo, R.Y.; Tangonan, G. Two-dimensional beam steering using an electrically tunable impedance surface. IEEE Trans. Antennas Propag. 2003, 51, 2713–2722. [Google Scholar] [CrossRef] [Green Version]
- Trentini, G.V. Partially reflecting sheet arrays. IRE Trans. Antennas Propag. 1956, 4, 666–671. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Esselle, K.P. Directivity improvement of a Fabry-Perot cavity antenna by enhancing near field characteristic. In Proceedings of the 17th International Symposium on Antenna Technology and Applied Electromagnetics, Montreal, QC, Canada, 10–13 July 2016; pp. 1–2. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. Low-Cost Nonuniform Metallic Lattice for Rectifying Aperture Near-Field of Electromagnetic Bandgap Resonator Antennas. IEEE Trans. Antennas Propag. 2020, 68, 3328–3335. [Google Scholar] [CrossRef]
- Lee, J.G. Compact and robust Fabry-Perot cavity antenna with PEC wall. J. Electromagn. Eng. Sci. 2021, 21, 184–188. [Google Scholar] [CrossRef]
- Guo, Q.-Y.; Lin, Q.W.; Wong, H. A High Gain Millimeter-Wave Circularly Polarized Fabry–Pérot Antenna Using PRS-Integrated Polarizer. IEEE Trans. Antennas Propag. 2021, 69, 1179–1183. [Google Scholar] [CrossRef]
- Afzal, M.U.; Matekovits, L.; Esselle, K.P.; Lalbakhsh, A. Beam-Scanning Antenna Based on Near-Electric Field Phase Transformation and Refraction of Electromagnetic Wave Through Dielectric Structures. IEEE Access 2020, 8, 199242–199253. [Google Scholar] [CrossRef]
- Naqvi, A.H.; Lim, S. A Beam-Steering Antenna with a Fluidically Programmable Metasurface. IEEE Trans. Antennas Propag. 2019, 67, 3704–3711. [Google Scholar] [CrossRef]
- Xie, P.; Wang, G.; Li, H.; Liang, J. A Dual-Polarized Two-Dimensional Beam-Steering Fabry–Pérot Cavity Antenna with a Reconfigurable Partially Reflecting Surface. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2370–2374. [Google Scholar] [CrossRef]
- Ji, L.; Guo, Y.J.; Qin, P.; Gong, S.; Mittra, R. A Reconfigurable Partially Reflective Surface (PRS) Antenna for Beam Steering. IEEE Trans. Antennas Propag. 2015, 63, 2387–2395. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, Z.; Liu, N. A Two-Dimensional Beam-Steering Partially Reflective Surface (PRS) Antenna Using a Reconfigurable FSS Structure. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1076–1080. [Google Scholar] [CrossRef]
- Jopek, Ł.; Hausman, S.; Di Barba, P. Optimization of an Artificial Magnetic Conductor Geometry Using a Paretian Approach. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Niaz, M.W.; Yin, Y.; Zheng, S.; Zhao, Z. Dual-polarized low sidelobe Fabry-Perot antenna using tapered partially reflective surface. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22070. [Google Scholar] [CrossRef]
- CST Microwave Studio. Available online: http://www.cst.com/ (accessed on 17 November 2021).
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L.; Zeb, B.A. Single-Dielectric Wideband Partially Reflecting Surface with Variable Reflection Components for Realization of a Compact High-Gain Resonant Cavity Antenna. IEEE Trans. Antennas Propag. 2019, 67, 1916–1921. [Google Scholar] [CrossRef]
- Abdelrahman, A.H.; Elsherbeni, A.Z.; Yang, F. Transmission Phase Limit of Multilayer Frequency-Selective Surfaces for Transmitarray Designs. IEEE Trans. Antennas Propag. 2014, 62, 690–697. [Google Scholar] [CrossRef]
- Dewan, R.; Rahim, M.K.A.; Hamid, M.R.; Yusoff, M.F.M.; Samsuri, N.A.; Murad, N.A.; Kamardin, K. Artificial magnetic conductor for various antenna applications: An overview. Int. J. RF Microw. Comput. Aided Eng. 2017, 27, e21105. [Google Scholar] [CrossRef]
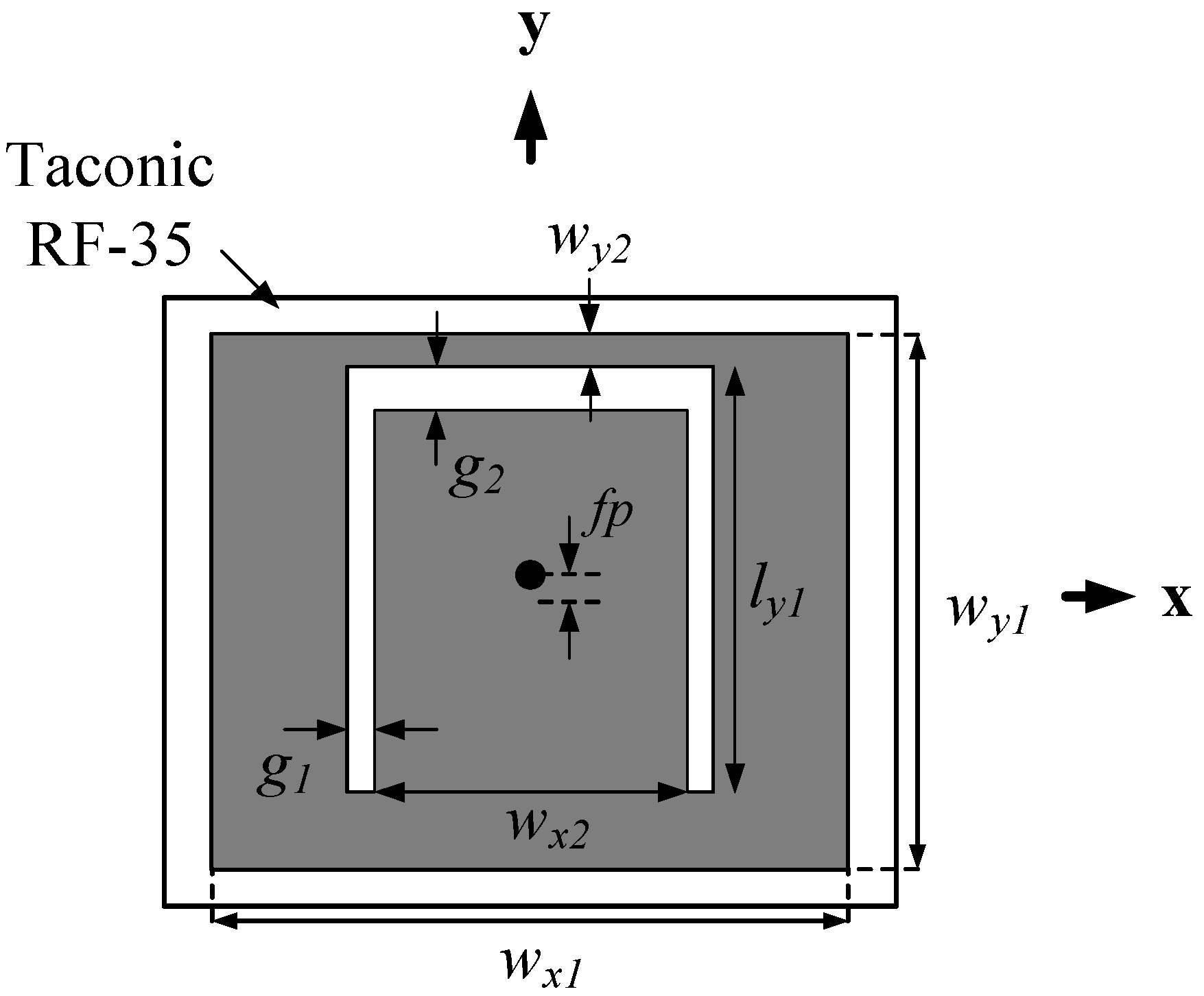
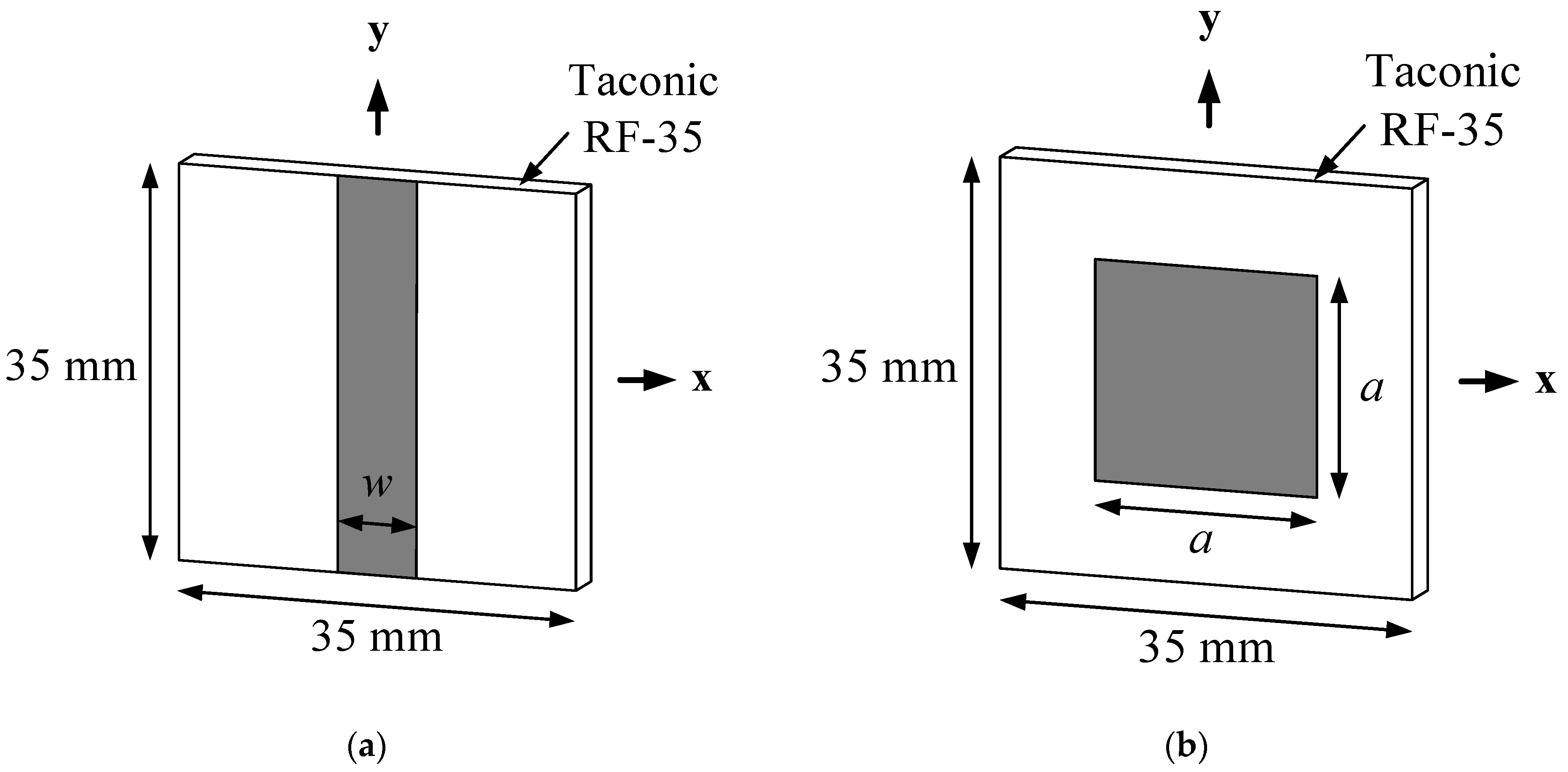
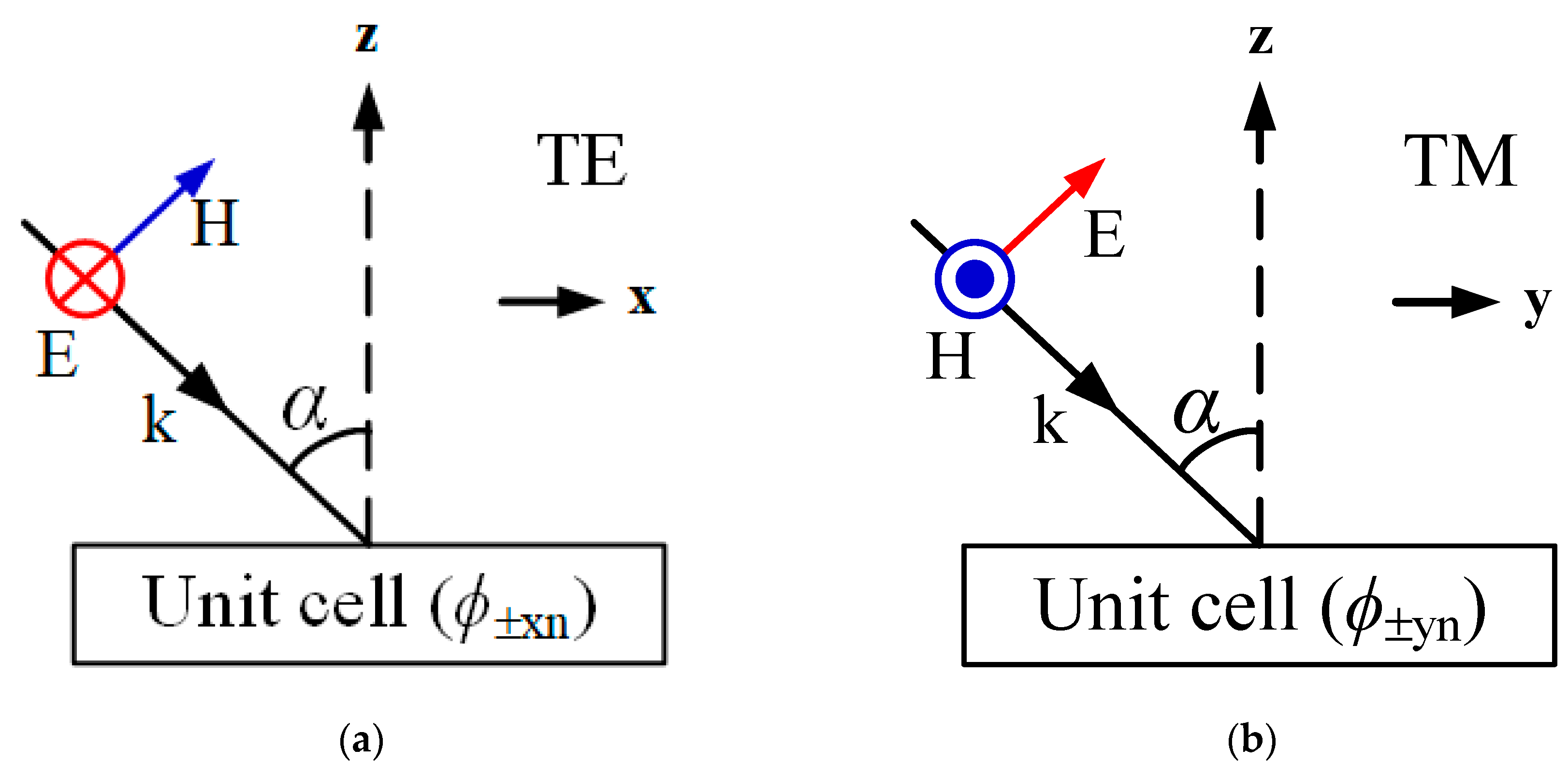
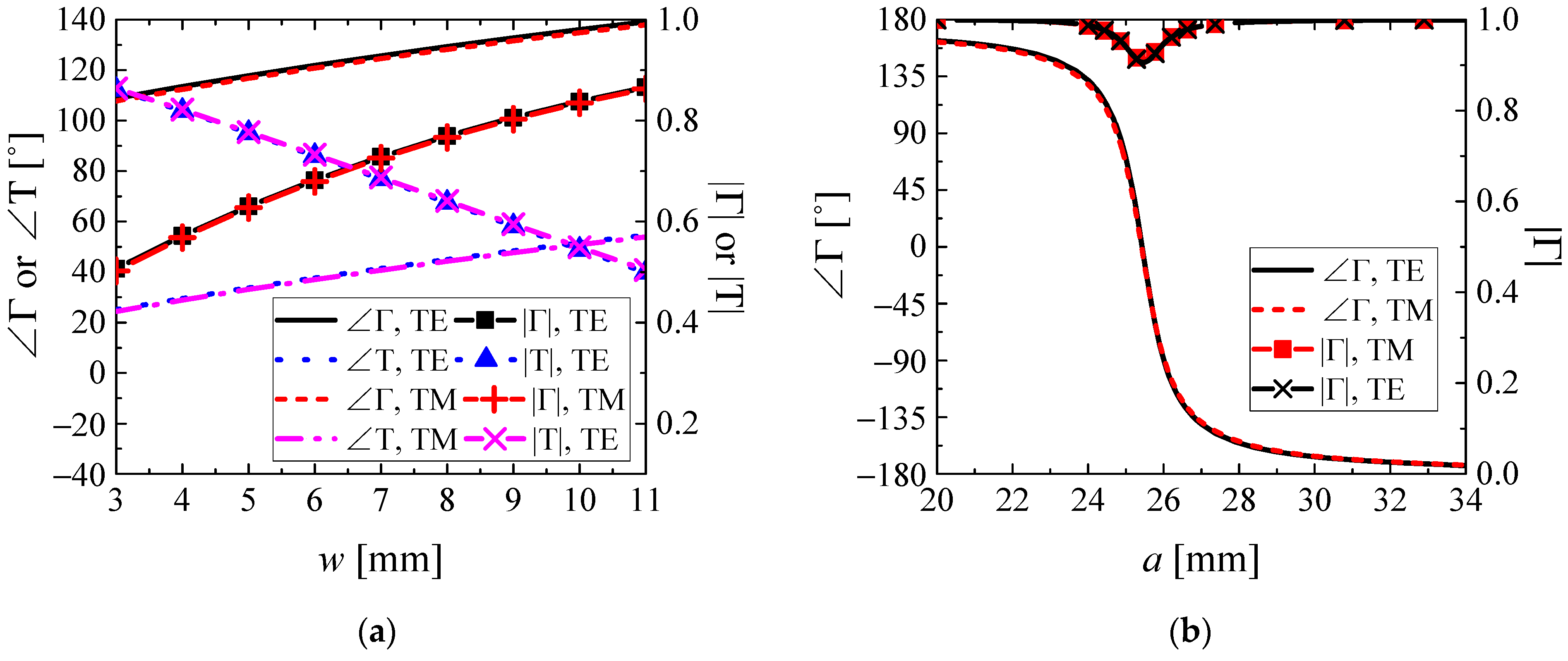

| nth AMC Cell | Length [mm] |
|---|---|
| 1 | 22.53 |
| 2 | 27.61 |
| 3 | 27.57 |
| 4 | 27.24 |
| 5 | 25.88 |
| 6 | 25.56 |
| 7 | 25.56 |
| 8 | 25.53 |
| 9 | 25.84 |
| 10 | 25.99 |
| 11 | 25.98 |
| Beam Scanning Angle [°] | Realized Gain [dBi] | Sidelobe Level [dB] | Half-Power Beamwidth [°] | ||
|---|---|---|---|---|---|
| E-Plane | H-Plane | E-Plane | H-Plane | ||
| 0° | 11.8 | −14.1 | −19.2 | 45 | 36 |
| 15° | 11.4 | −13.1 | −18.3 | 43 | 36 |
| 30° | 13 | −18.1 | −12.8 | 34 | 34 |
| 41° | 10.6 | −8 | −7.1 | 23 | 40 |
| Ref. # 1 | Beam Scanning Type | Beam Scanning Angle 2 [°] | Gain [dBi] |
|---|---|---|---|
| [11] | Continuous | 1–39 | 12.2–16.0 |
| [12] | Continuous | ±20 | 4.67–8.53 |
| [13] | Discrete | 0, ±10 | 11.9–12.0 |
| [14] | Discrete | 0, ±15 | 11.7–16.3 |
| [15] | Discrete | 0, ±22 | 9.6–10.4 |
| This work | Continuous | ±41 | 10.6–13.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, W.; Jeon, Y.-g.; Maeng, H.-j.; Kim, J.; Kim, D. Novel Beam Scan Method of Fabry–Perot Cavity (FPC) Antennas. Appl. Sci. 2021, 11, 11005. https://doi.org/10.3390/app112211005
Jang W, Jeon Y-g, Maeng H-j, Kim J, Kim D. Novel Beam Scan Method of Fabry–Perot Cavity (FPC) Antennas. Applied Sciences. 2021; 11(22):11005. https://doi.org/10.3390/app112211005
Chicago/Turabian StyleJang, Wook, Yeong-geun Jeon, Han-jun Maeng, Jongyeong Kim, and Dongho Kim. 2021. "Novel Beam Scan Method of Fabry–Perot Cavity (FPC) Antennas" Applied Sciences 11, no. 22: 11005. https://doi.org/10.3390/app112211005
APA StyleJang, W., Jeon, Y.-g., Maeng, H.-j., Kim, J., & Kim, D. (2021). Novel Beam Scan Method of Fabry–Perot Cavity (FPC) Antennas. Applied Sciences, 11(22), 11005. https://doi.org/10.3390/app112211005






