Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity
Abstract
1. Introduction
2. Physical Model and Numerical Method
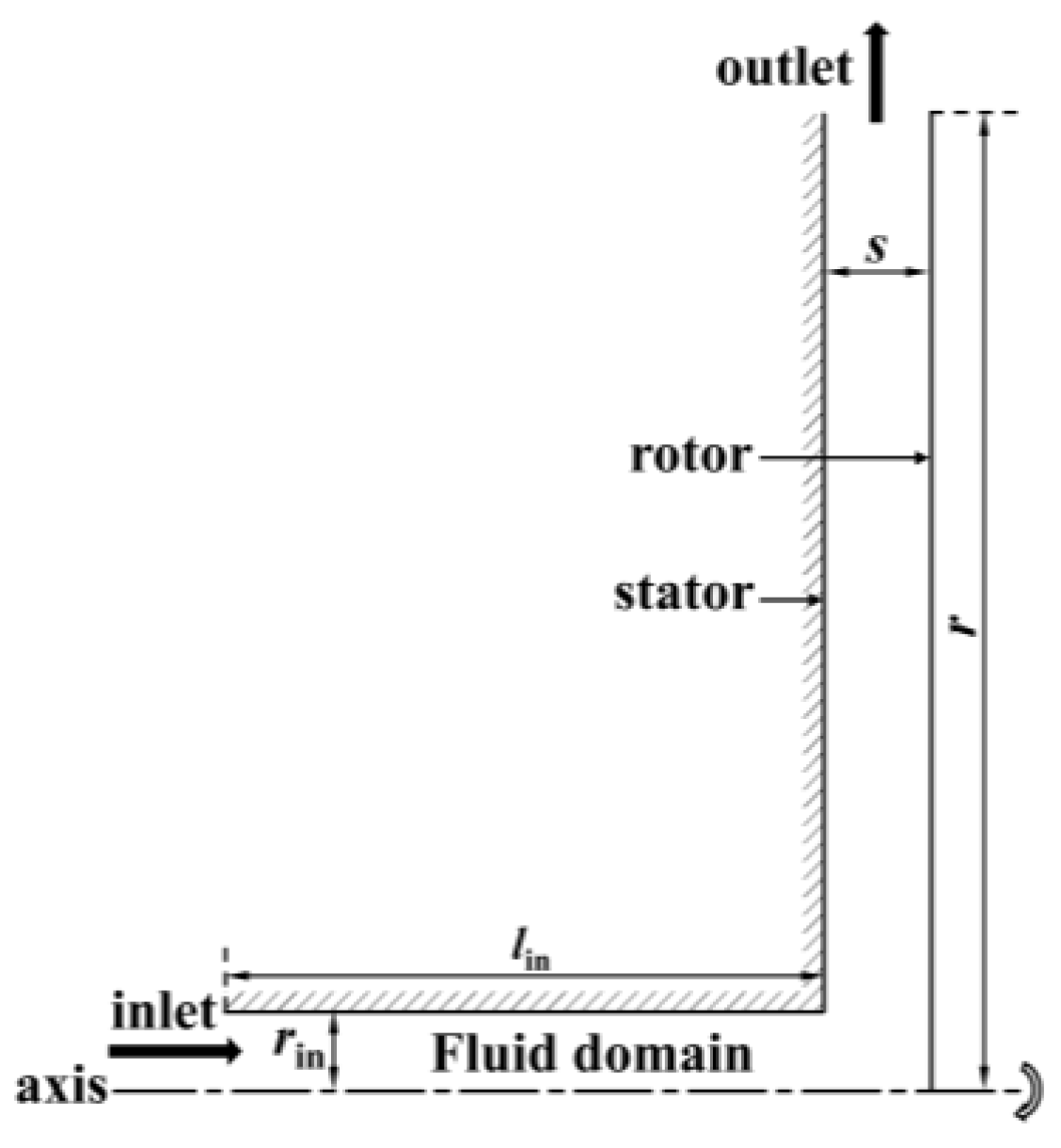
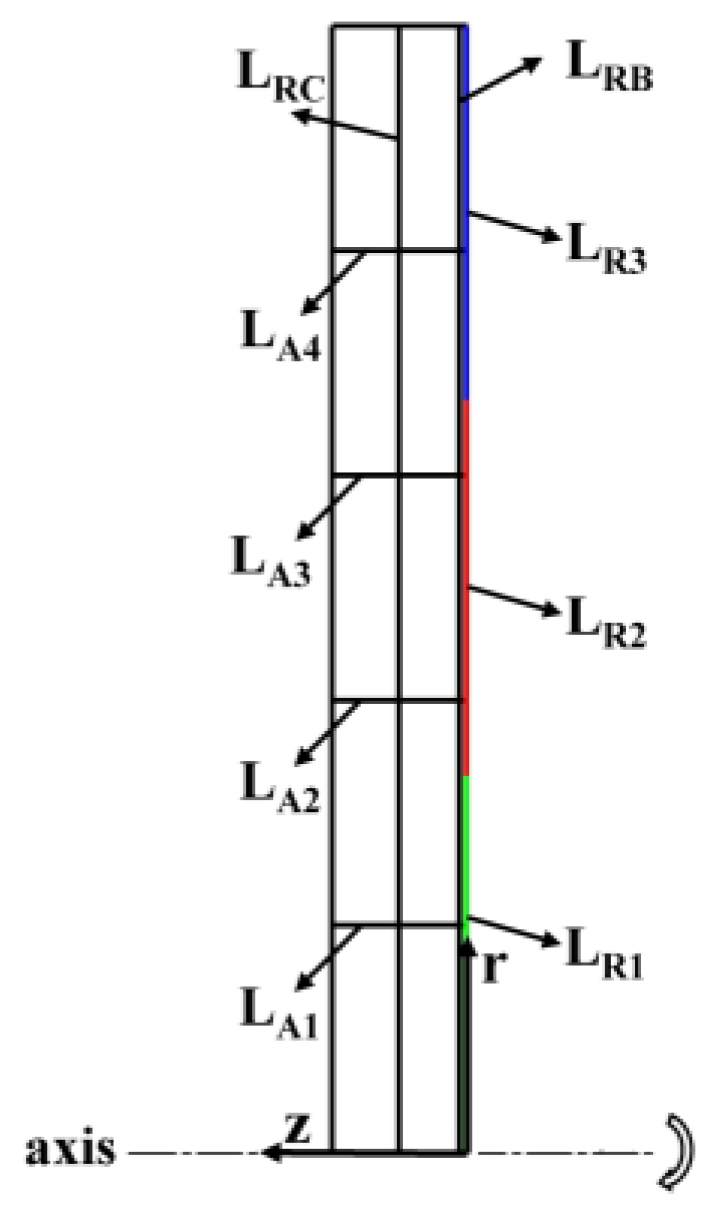
2.1. Physical Model and Computational Domain
2.2. Turbulence Model
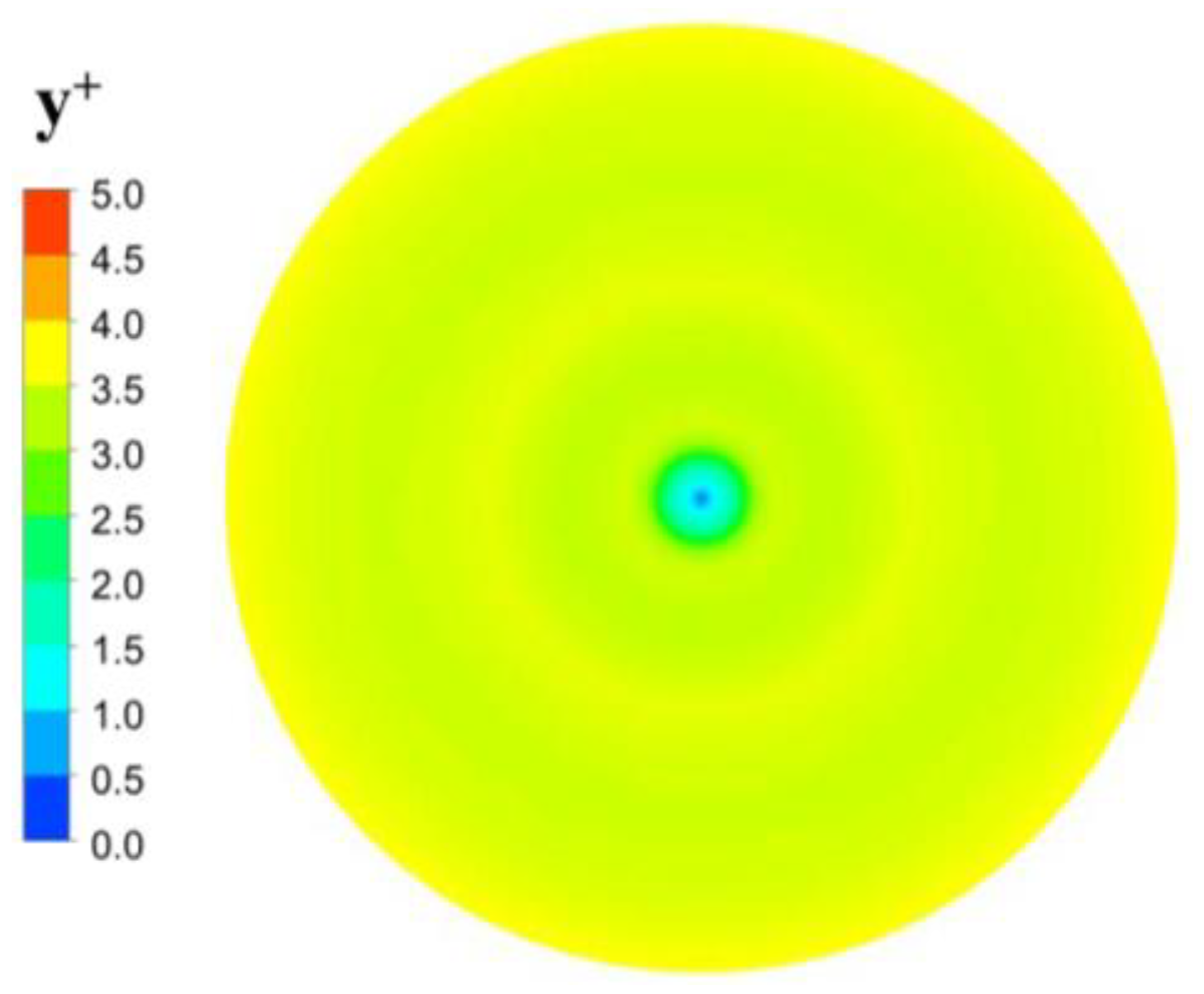
2.3. Computational Setup
3. Results and Discussion
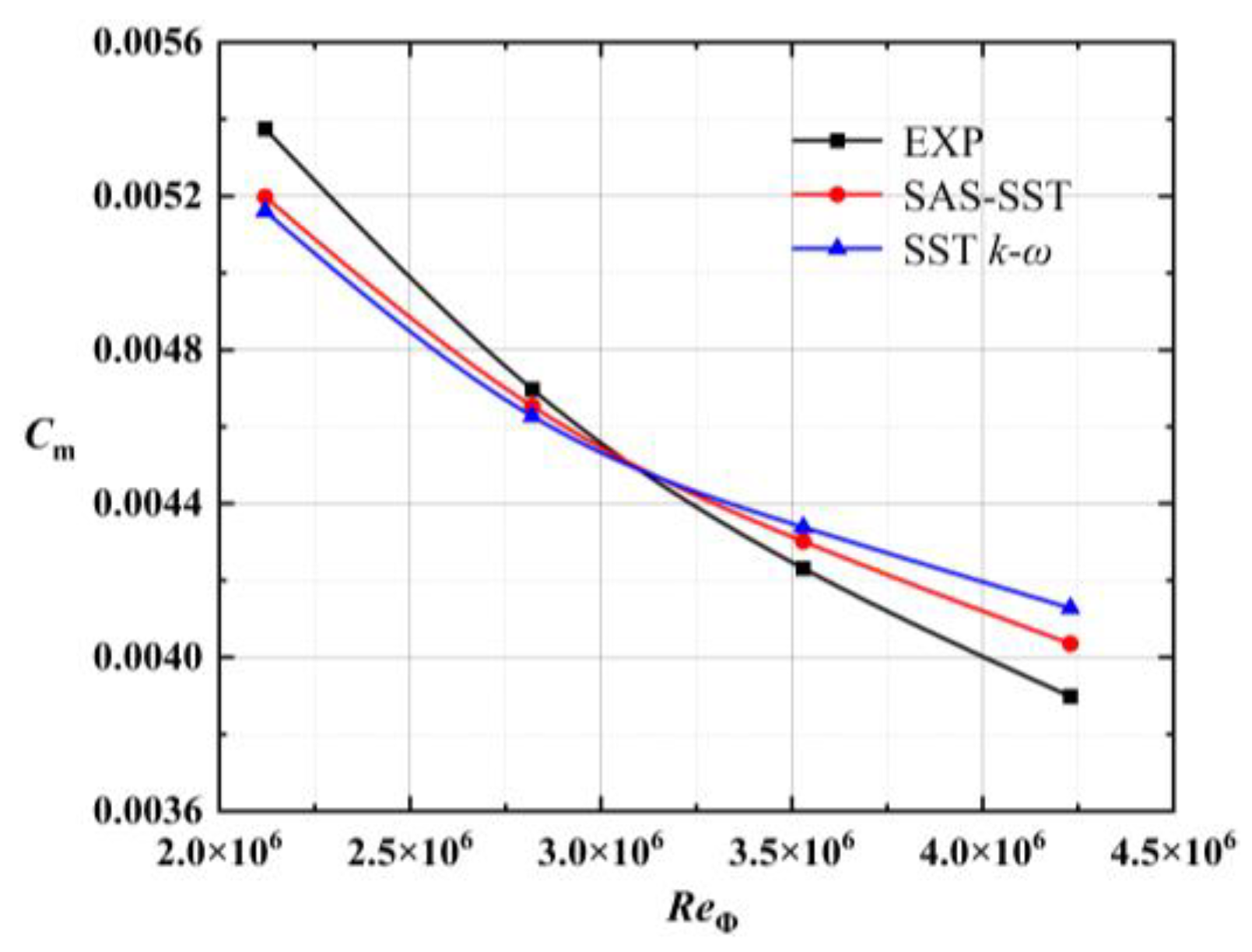
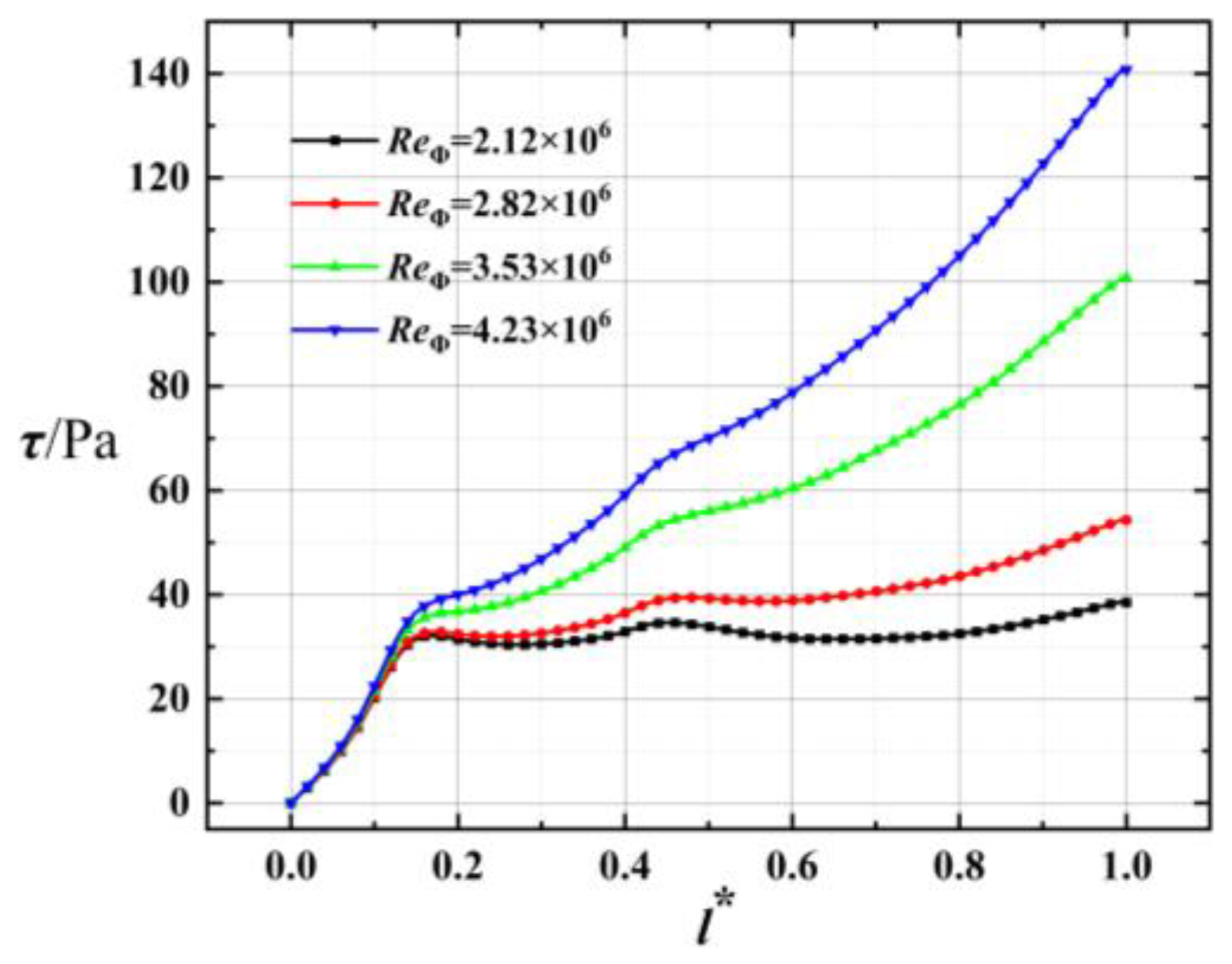
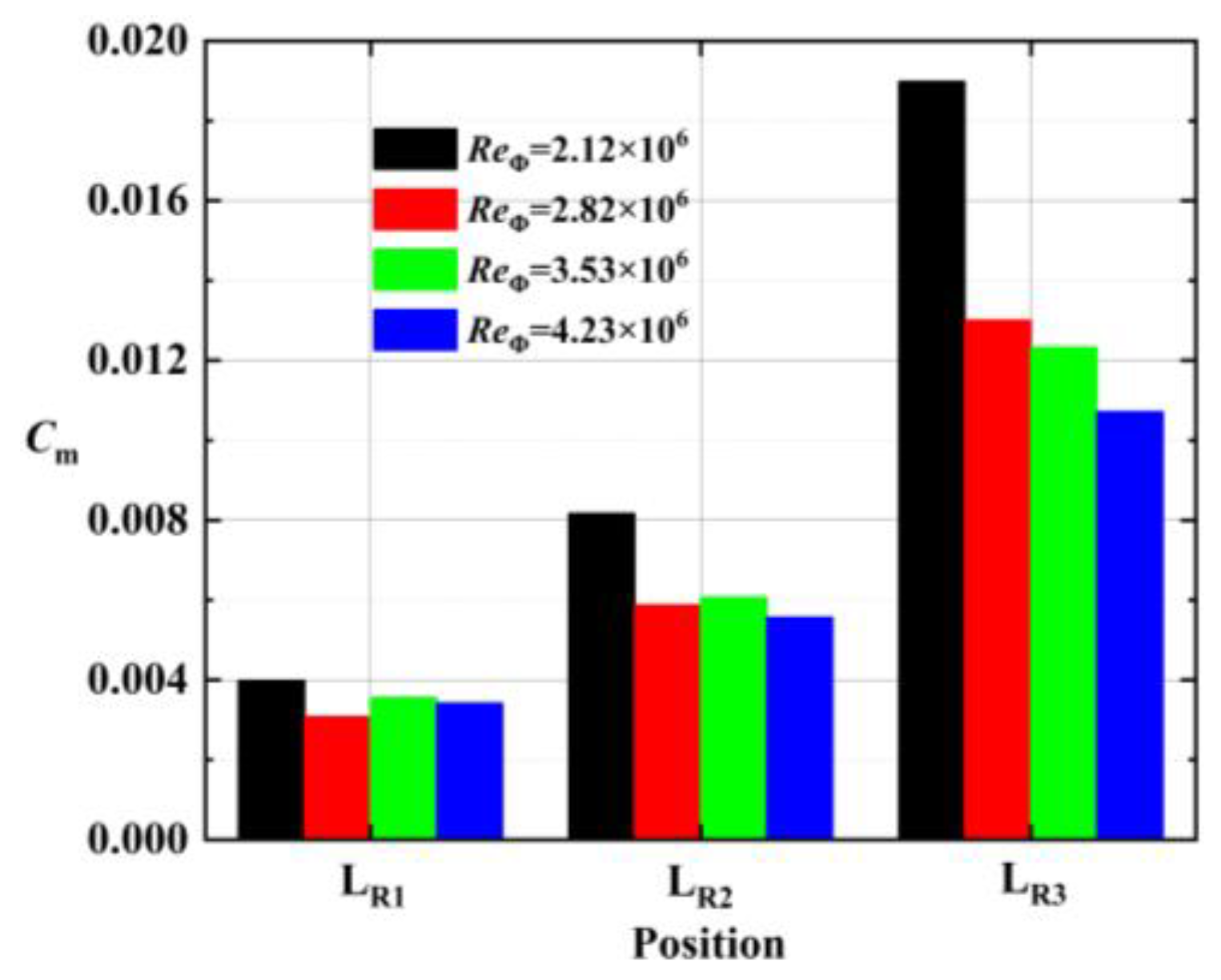
3.1. Torque Distribution Characteristics of the Rotor Wall
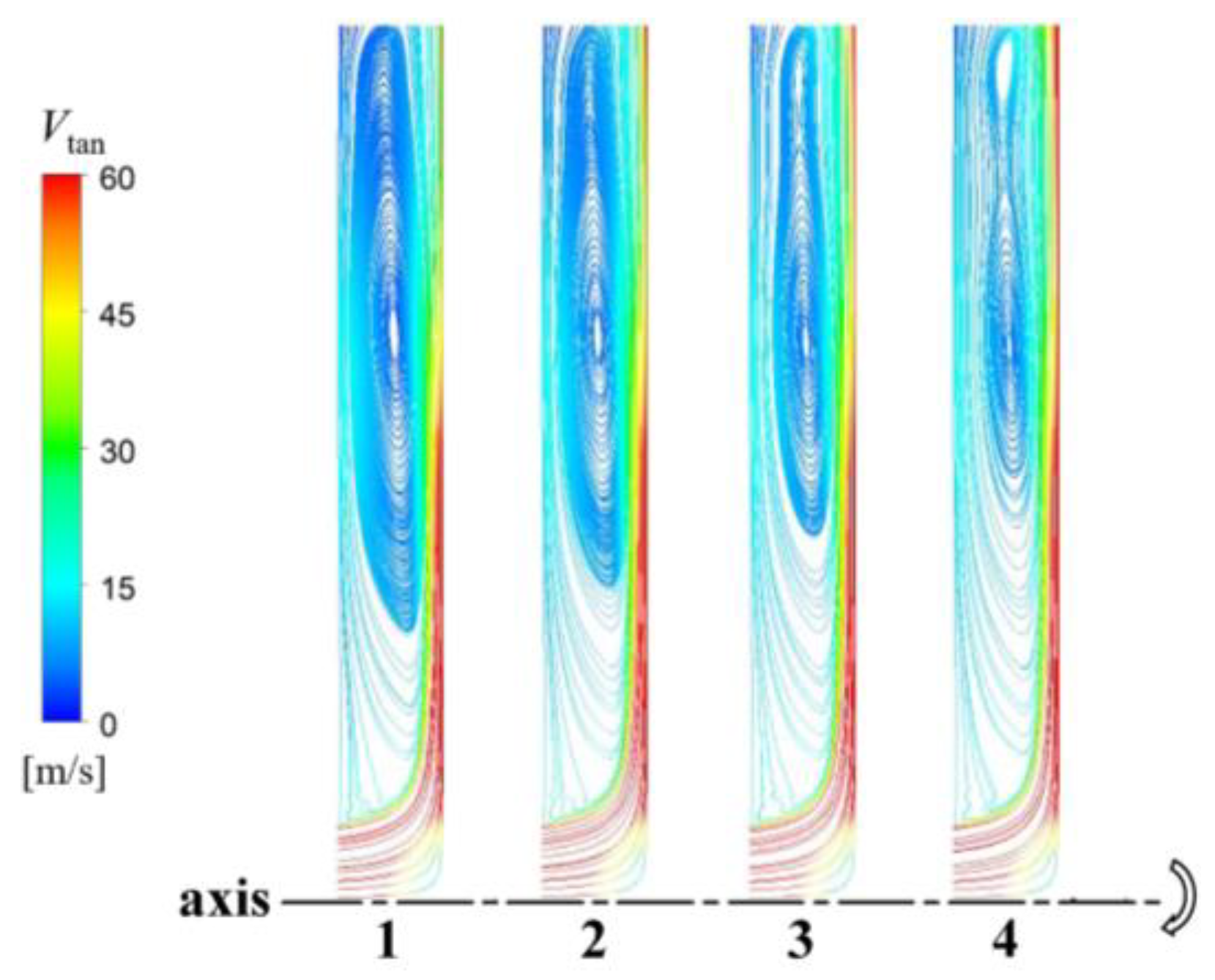
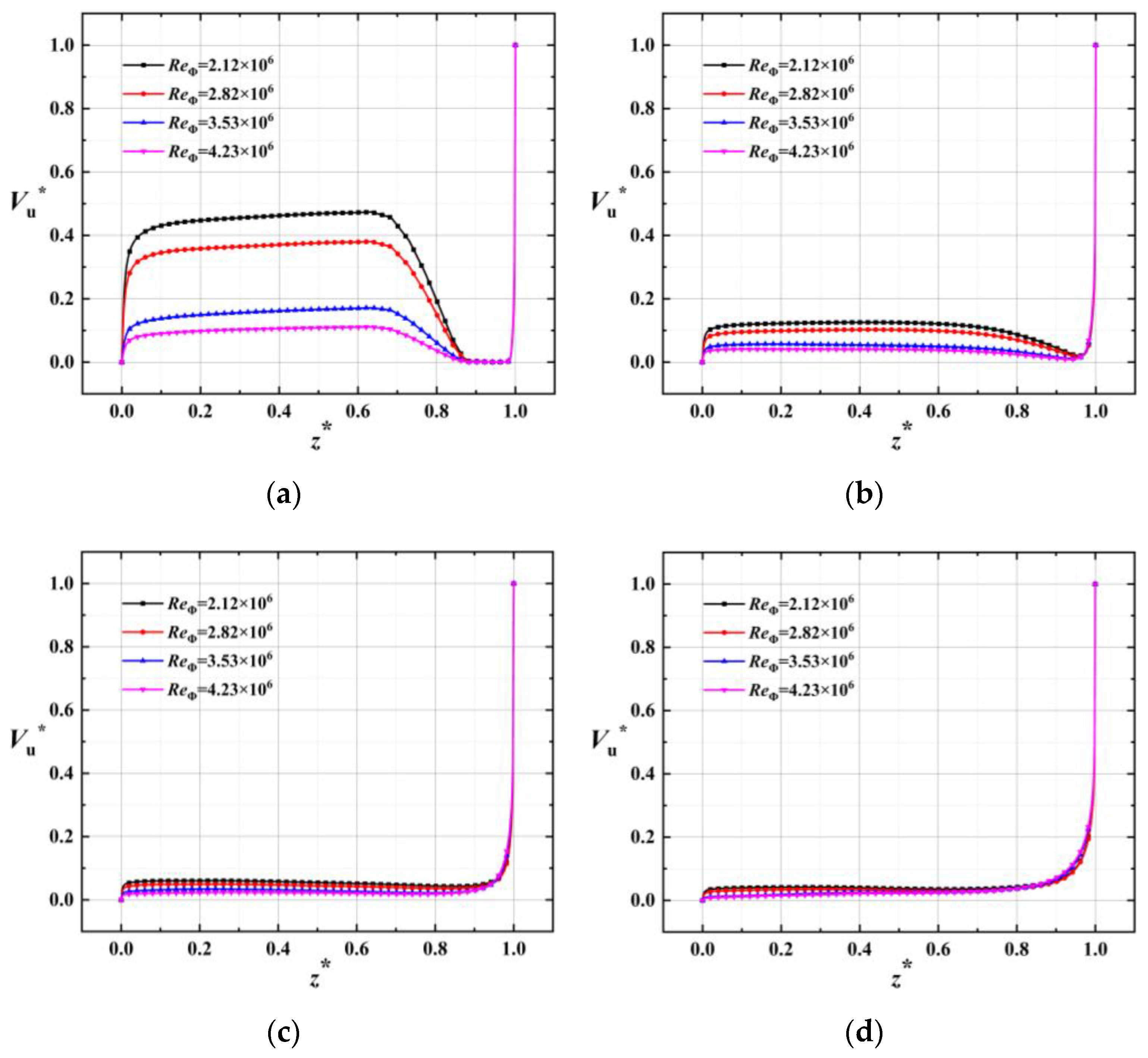
3.2. Flow Field Distribution Characteristics
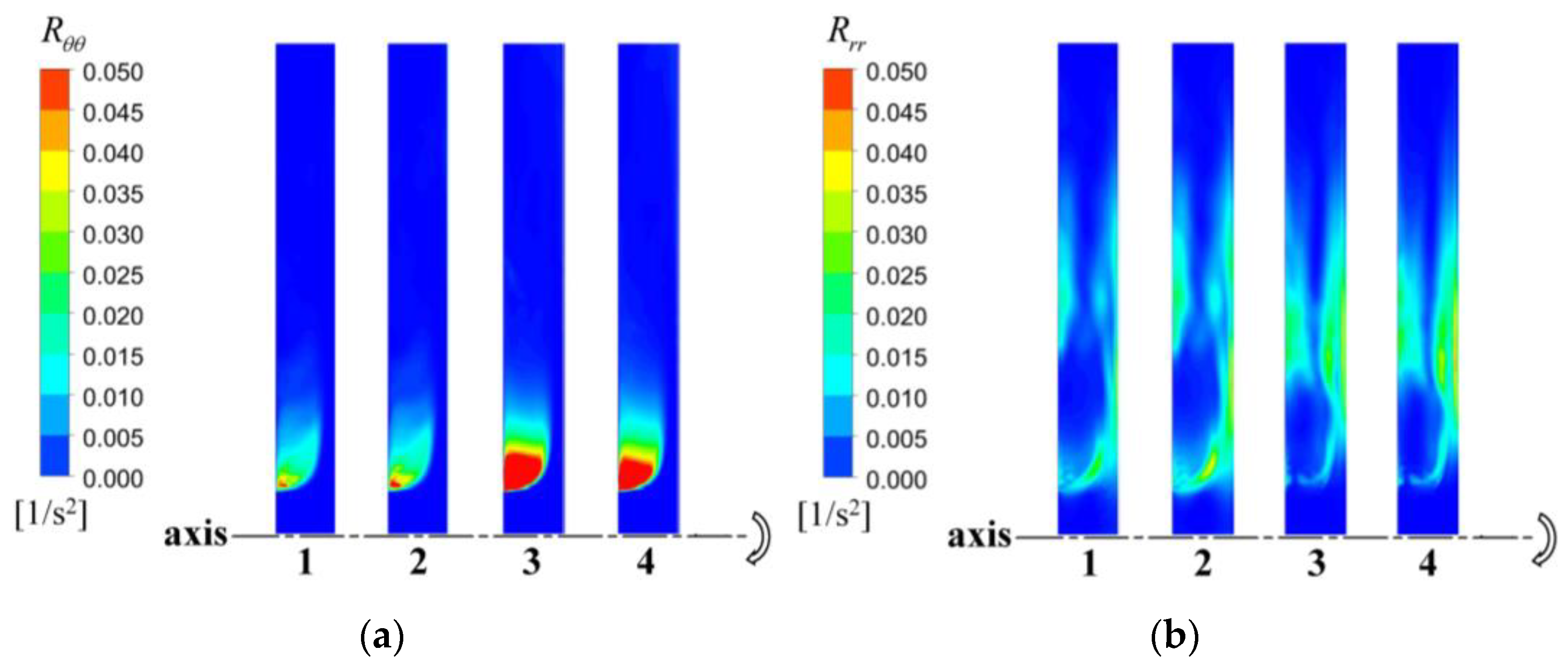
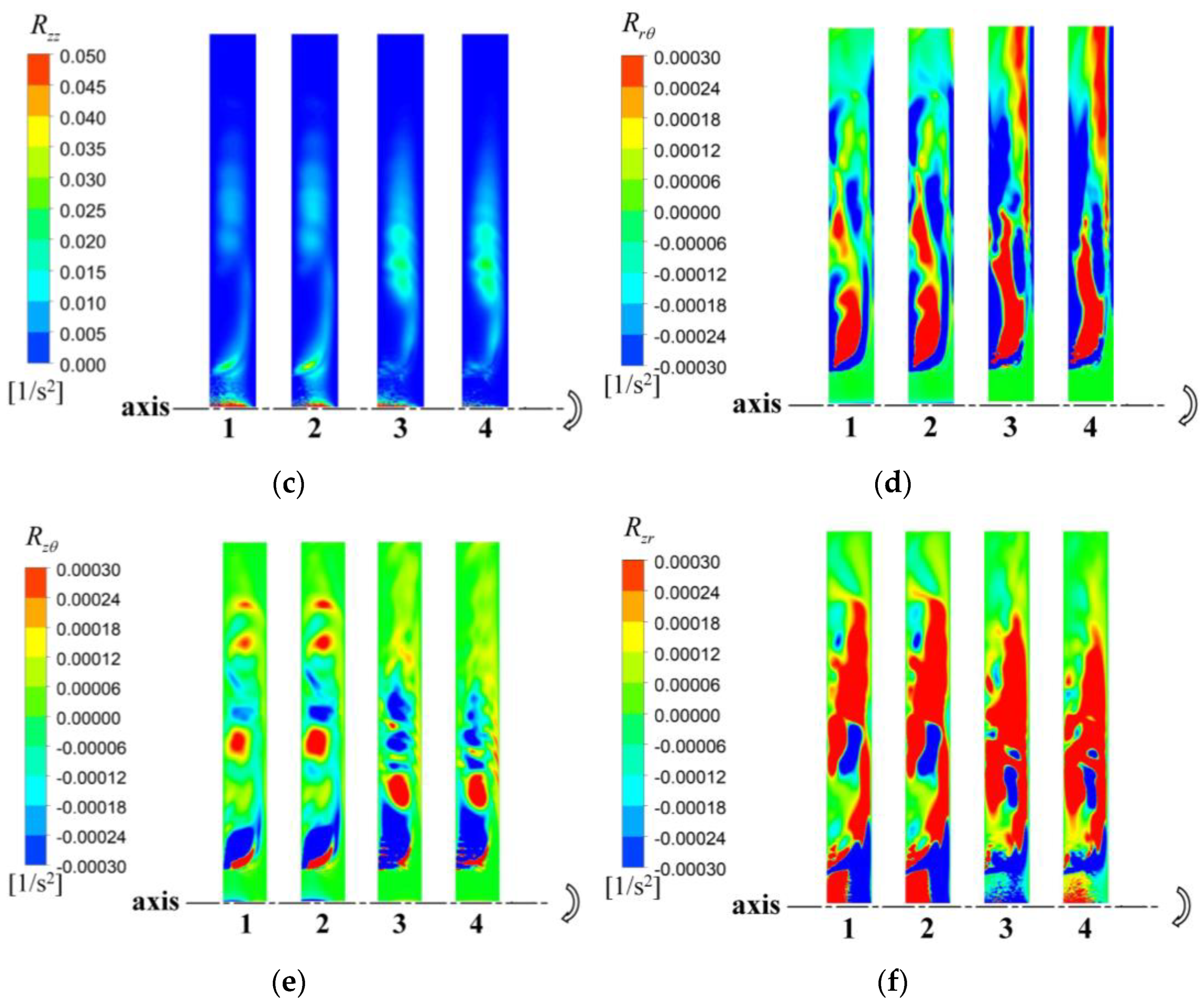
3.3. Reynolds Stress Analysis
3.4. Vortex Structure Characteristics
4. Conclusions
- In a rotor-stator system, the torque on the rotor wall is mainly produced by shear stress. With an increase in the Reynolds number, the shear stress on the rotor wall increases, and the torque coefficient Cm decreases.
- In the range of the rotating Reynolds number selected for calculation, the main vortex separation occurs because of the inertial force of the fluid in the cavity, and the critical rotating Reynolds number at which separation begins is ReΦ = 3.53 × 106.
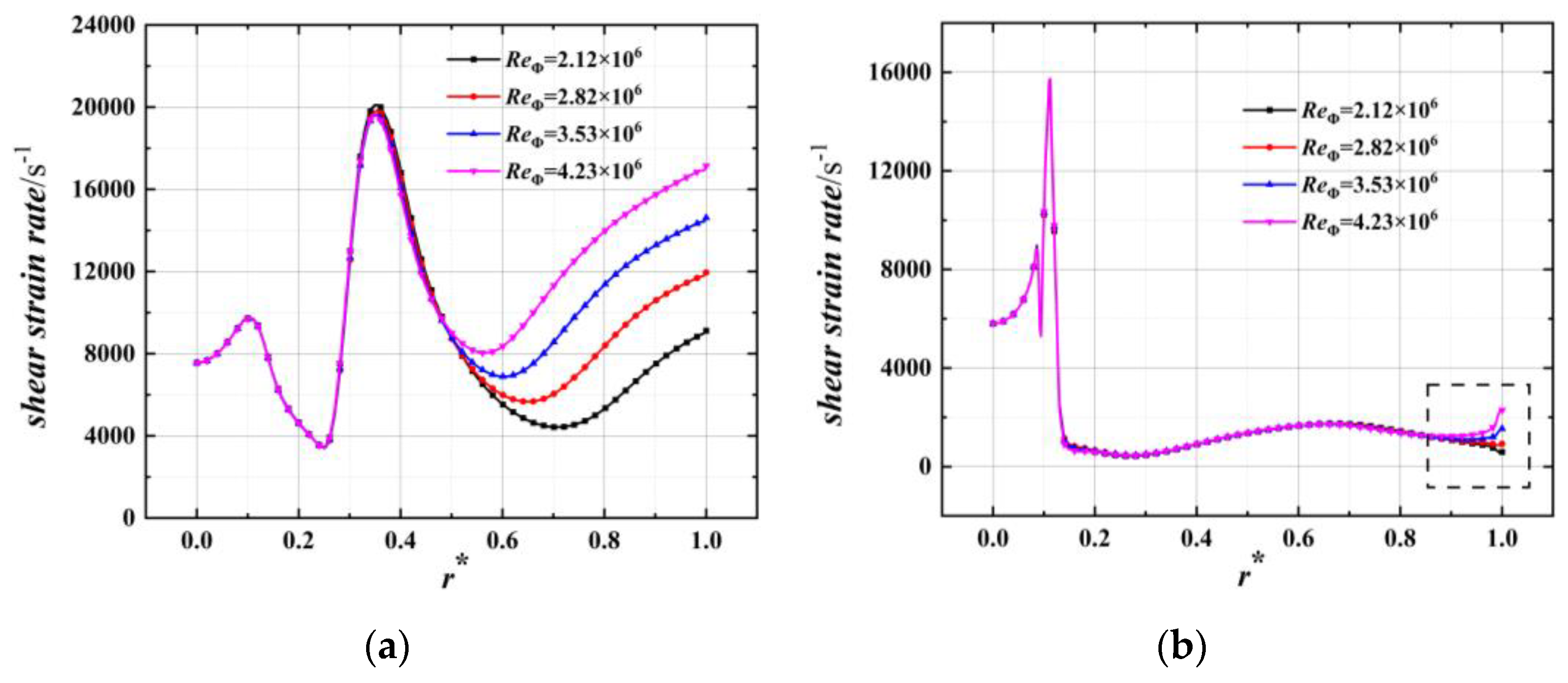
- The radial change in the shear strain rate in the rotor turbulent boundary layer is affected by different factors, and there is a turning point at r* = 0.5–0.7. At this point, the change in the shear strain rate is transformed from the leading role of the inertial force of the inlet flow to the leading role of the rotor rotation on the fluid adhesion.
- The order of torque on the rotor under different rotating Reynolds numbers is as follows: Case 4 > Case 3 > Case 2 > Case 1. In addition to fluid adhesion, the Reynolds stress also contributes partly to the rotor wall torque.
- The vortex structure of the rotor-stator system cavity mainly includes the main vortex, return vortex, secondary vortex, and vortex in the turbulent boundary layer. With an increase in the rotating Reynolds number, the intensity of the vortex in the turbulent boundary layer decreases, but the number of vortex cores increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faller, A.J. An experimental study of the instability of the laminar Ekman boundary layer. J. Fluid Mech. 1963, 15, 560. [Google Scholar] [CrossRef]
- Bayley, F.J.; Owen, J.M. Flow between a Rotating and a Stationary Disc. Aeronaut. Q. 1969, 20, 333–354. [Google Scholar] [CrossRef]
- Owen, J.M. Flow and Heat Transfer in Rotating-Disc Systems; John Wiley Sons Inc.: New York, NY, USA, 1989; Volume 90, pp. 81–103. [Google Scholar] [CrossRef]
- Serre, E.; Del Arco, E.C.; Bontoux, P. Annular and spiral patterns in flows between rotating and stationary discs. J. Fluid Mech. 2001, 434, 65–100. [Google Scholar] [CrossRef]
- Amirante, D.; Hills, N.J. Large-Eddy Simulations of Wall Bounded Turbulent Flows Using Unstructured Linear Reconstruction Techniques. J. Turbomach. 2015, 137, 051006. [Google Scholar] [CrossRef]
- Yim, E.; Chomaz, J.M.; Martinand, D.; Serre, E. Transition to turbulence in the rotating disk boundary layer of a rotor–stator cavity. J. Fluid Mech. 2018, 848, 631–647. [Google Scholar] [CrossRef]
- Appelquist, E.; Schlatter, P.; Alfredsson, P.H.; Lingwood, R.J. Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 2015, 765, 612–631. [Google Scholar] [CrossRef]
- Appelquist, E.; Schlatter, P.; Alfredsson, P.H.; Lingwood, R.J. On the global nonlinear instability of the rotating-disk flow over a finite domain. J. Fluid Mech. 2016, 803, 332–355. [Google Scholar] [CrossRef]
- Oguic, R.; Poncet, S.; Viazzo, S. High-Order Direct numerical simulations of a turbulent round impinging jet onto a rotating heated disk in a highly confined cavity. Int. J. Heat Fluid Flow 2016, 61, 366–378. [Google Scholar] [CrossRef]
- Davies, C.; Thomas, C.; Carpenter, P.W. Global stability of the rotating-disk boundary layer. J. Eng. Math. 2007, 57, 219–236. [Google Scholar] [CrossRef]
- Pitz, D.B.; Chew, J.W.; Marxen, O.; Hills, N.J. Direct Numerical Simulation of Rotating Cavity Flows Using a Spectral Element-Fourier Method. J. Eng. Gas. Turbines Power-Trans. ASME 2017, 139, 10. [Google Scholar] [CrossRef]
- Darvish Damavandi, M.; Nejat, A. Numerical investigation of fluid flow in a rotor–stator cavity with curved rotor disk. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 180. [Google Scholar] [CrossRef]
- Luo, X.; Han, G.; Wu, H.; Wang, L.; Xu, G. Experimental investigation of pressure loss and heat transfer in a rotor–stator cavity with two outlets. Int. J. Heat Mass Transf. 2014, 78, 311–320. [Google Scholar] [CrossRef]
- Healey, J.J. Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 2010, 663, 148–159. [Google Scholar] [CrossRef]
- Geis, T.; Ebner, J.; Kim, S.; Wittig, S. Flow Structures Inside a Rotor-Stator Cavity. Int. J. Rotating Mach. 2014, 7, 285–300. [Google Scholar] [CrossRef]
- Poncet, S.; Chauve, M.P.; Schiestel, R. Batchelor versus Stewartson flow structures in a rotor-stator cavity with throughflow. Phys. Fluids 2005, 17, 253–668. [Google Scholar] [CrossRef]
- Makino, S.; Inagaki, M.; Nakagawa, M. Laminar-Turbulence Transition over the Rotor Disk in an Enclosed Rotor-Stator Cavity. Flow Turbul. Combust. 2015, 95, 399–413. [Google Scholar] [CrossRef]
- Abadi, A.M.E.; Sadi, M.; Farzaneh-Gord, M.; Ahmadi, M.H.; Chau, K.W. A numerical and experimental study on the energy efficiency of a regenerative Heat and Mass Exchanger utilizing the counter-flow Maisotsenko cycle. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1–12. [Google Scholar] [CrossRef]
- Gu, Y.; Pei, J.; Yuan, S.; Zhang, J. A Pressure Model for Open Rotor–Stator Cavities: An Application to an Adjustable-Speed Centrifugal Pump With Experimental Validation. J. Fluids Eng. 2020, 142, 101301. [Google Scholar] [CrossRef]
- Ghalandari, M.; Bornassi, S.; Shamshirband, S.; Mosavi, A.; Chau, K.W. Investigation of submerged structures’ flexibility on sloshing frequency using a boundary element method and finite element analysis. Eng. Appl. Comput. Fluid Mech. 2019, 13, 519–528. [Google Scholar] [CrossRef]
- Wang, C.; Zeng, Y.; Yao, Z.; Wang, F. Rigid vorticity transport equation and its application to vortical structure evolution analysis in hydro-energy machinery. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1016–1033. [Google Scholar] [CrossRef]
- Yuan, C.; Zhu, L.; Du, Z.; Liu, S. Numerical investigation into the cavitating jet inside water poppet valves with varied valve seat structures. Eng. Appl. Comput. Fluid Mech. 2021, 15, 391–412. [Google Scholar] [CrossRef]
- Jiao, Z.; Fu, S. Investigations of an enclosed annular rotor-stator system with LES method. Sci. China Phys. Mech. Astron. 2018, 61, 54–64. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, D.; Xu, G.Q. Experimental study on windage torque in unshrouded rotor-stator system with central inflow. Tuijin Jishu/J. Propuls. Technol. 2015, 36, 1199–1205. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. Aiaa J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Mulu, B.G.; Cervantes, M.J.; Devals, C.; Vu, T.C.; Guibault, F. Simulation-based investigation of unsteady flow in near-hub region of a Kaplan Turbine with experimental comparison. Eng. Appl. Comput. Fluid Mech. 2015, 9, 139–156. [Google Scholar] [CrossRef][Green Version]
- Darvish Damavandi, M.; Nejat, A. Flow Characteristics of Curved Rotor Stator Systems Using Large Eddy Simulation. Flow Turbul. Combust. 2019, 103, 111–140. [Google Scholar] [CrossRef]
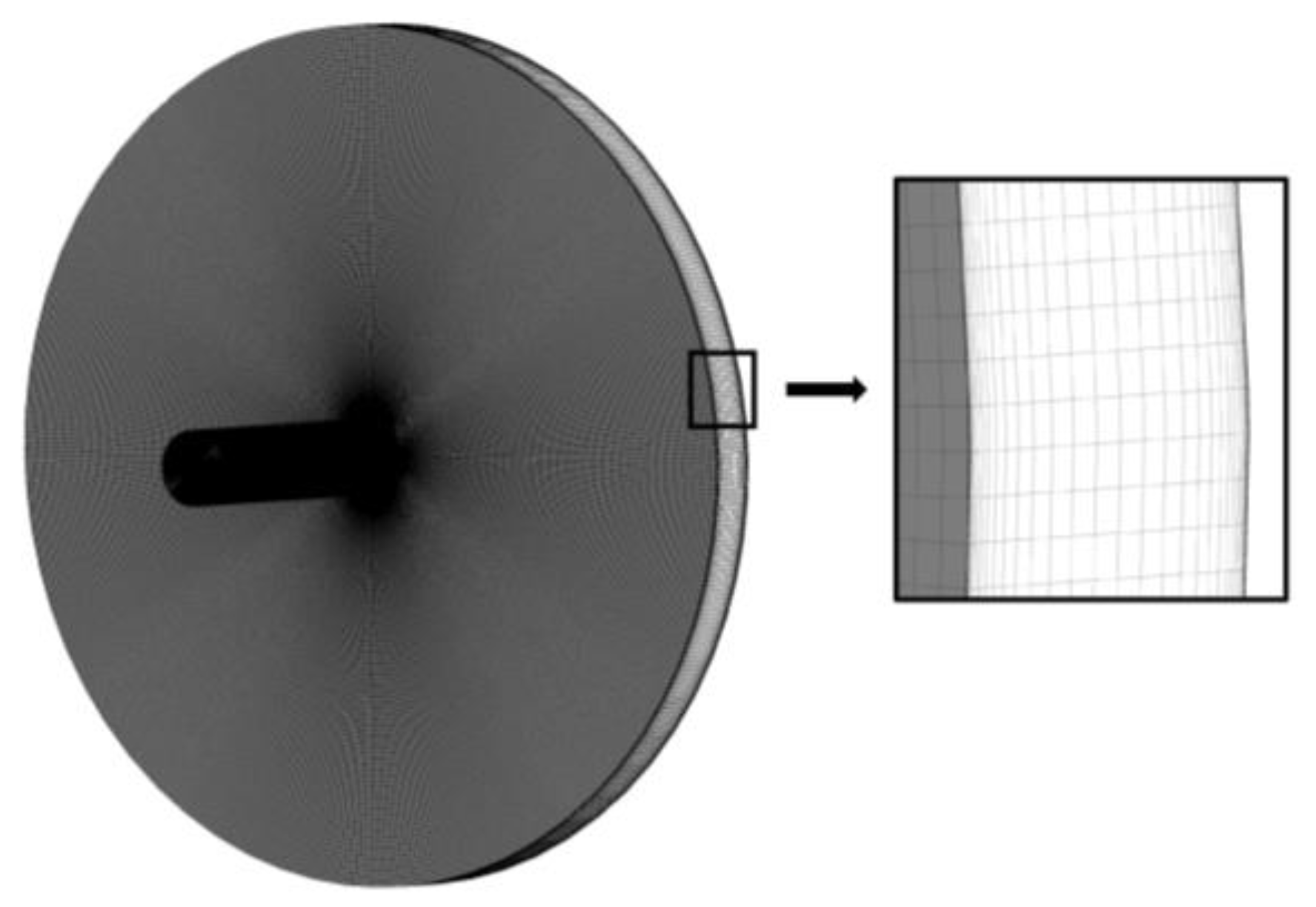
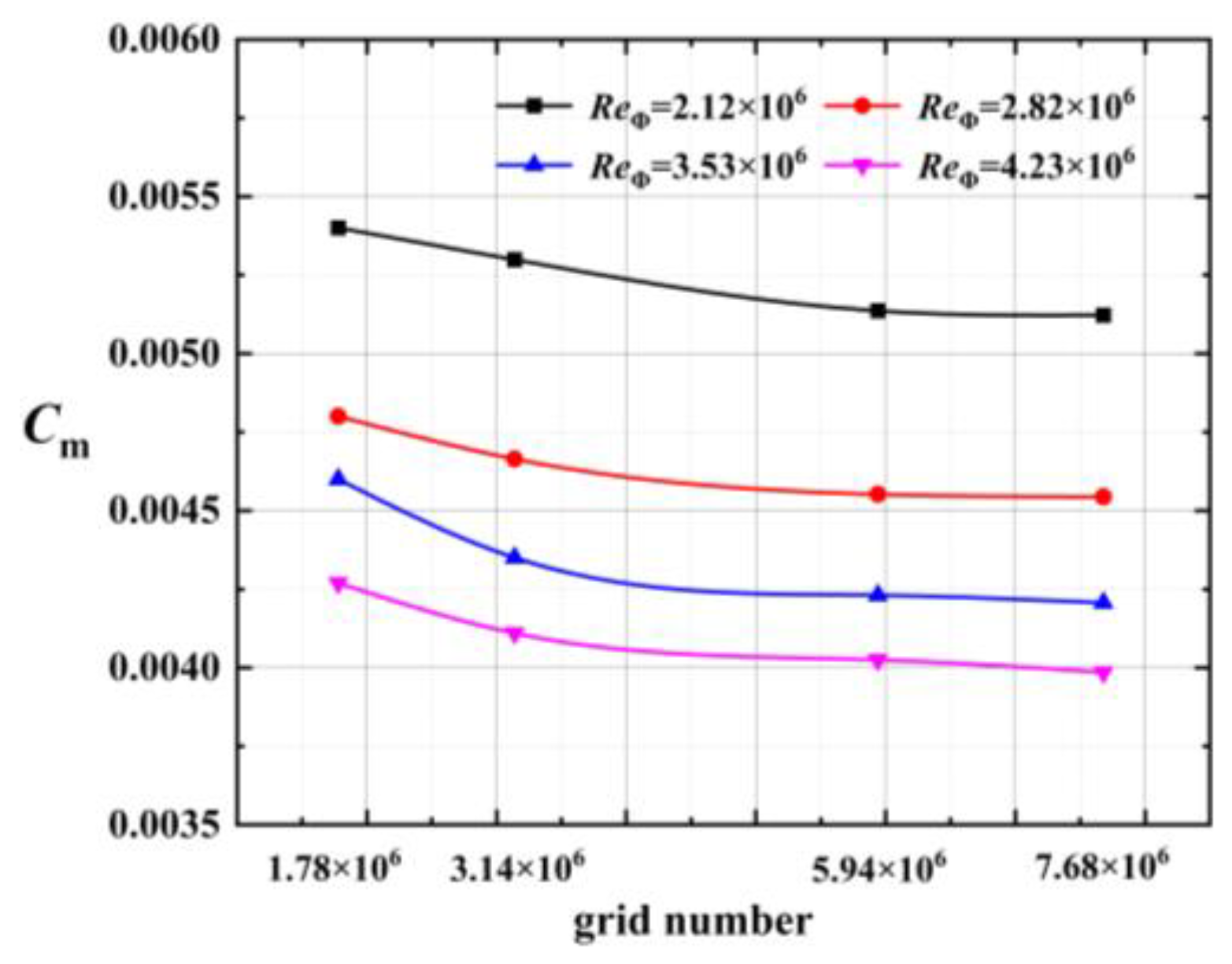

| Component | Total Elements | Min Angle (°) | Max Aspect Ratio | Quality (3 × 3 × 3) | GCI (%) |
|---|---|---|---|---|---|
| 1 | 1.78 × 106 | 45 | 19 | 0.68 | 9.30 |
| 2 | 3.14 × 106 | 45 | 64 | 0.65 | 3.26 |
| 3 | 5.94 × 106 | 45 | 349 | 0.58 | 1.84 |
| 4 | 7.68 × 106 | 45 | 558 | 0.49 | 1.67 |
| Case | G | ReΦ/106 | Cw/104 |
|---|---|---|---|
| 1 | 0.12 | 2.12 | 3.41 |
| 2 | 0.12 | 2.82 | 3.41 |
| 3 | 0.12 | 3.53 | 3.41 |
| 4 | 0.12 | 4.23 | 3.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Song, W.; Jin, Y.; Lu, J. Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity. Appl. Sci. 2021, 11, 11000. https://doi.org/10.3390/app112211000
Zhao Z, Song W, Jin Y, Lu J. Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity. Applied Sciences. 2021; 11(22):11000. https://doi.org/10.3390/app112211000
Chicago/Turabian StyleZhao, Zhizhou, Wenwu Song, Yongxin Jin, and Jiaxing Lu. 2021. "Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity" Applied Sciences 11, no. 22: 11000. https://doi.org/10.3390/app112211000
APA StyleZhao, Z., Song, W., Jin, Y., & Lu, J. (2021). Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity. Applied Sciences, 11(22), 11000. https://doi.org/10.3390/app112211000






