Sparse-View Neutron CT Reconstruction Using a Modified Weighted Total Difference Minimization Method
Abstract
:1. Introduction
2. Methods
2.1. Weighted Total Difference Minimization
2.2. Median Root Prior
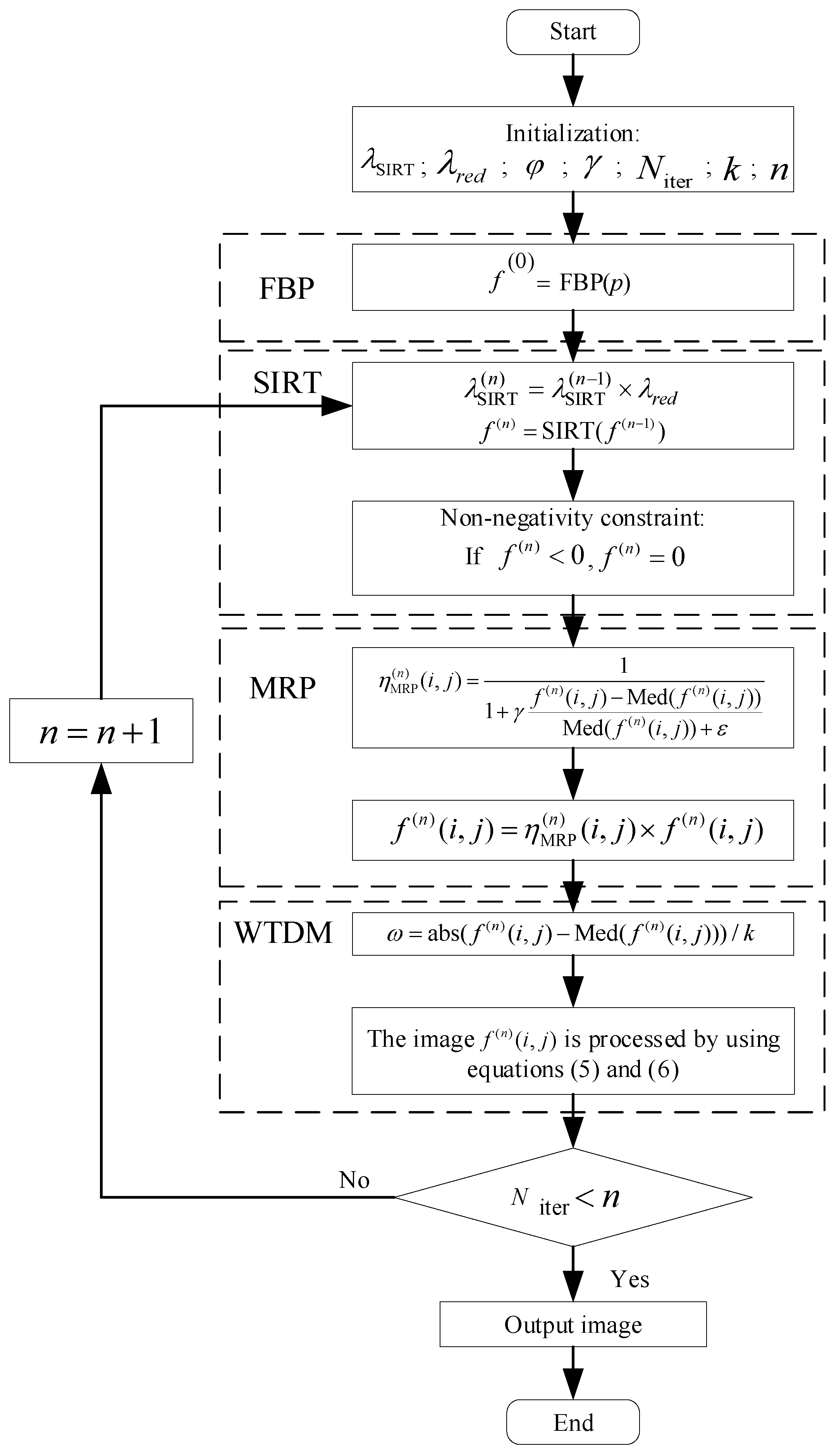
2.3. The SIRT-MWTDM Iterative Algorithm
| Algorithm 1. The organizational scheme of the SIRT-MWTDM |
| Initialization: ; ; ; ; ; ; |
| FBP reconstruction: |
| for to do |
| SIRT updating: |
| Non-negativity constraint: |
| If , |
| MRP: |
| Calculate about image according to Equation (8) |
| Calculate according to Equation (9) |
| WTDM: |
| Calculate adaptive threshold according to Equation (7) |
| Solve equation (4) according to Equations (5) and (6) |
| Image updating and next loop |
| end |
3. Experiment
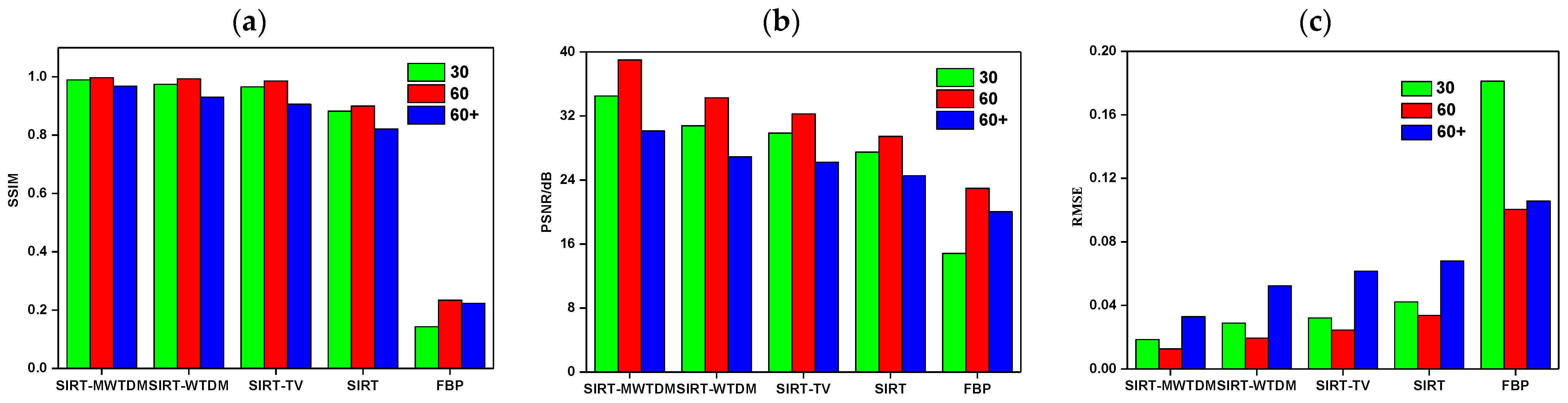
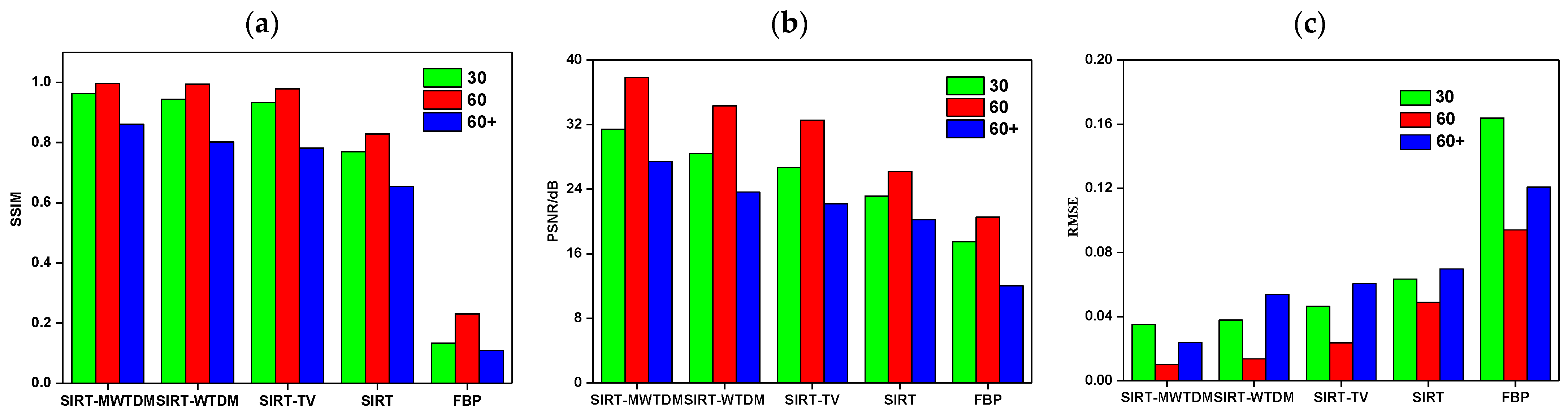
3.1. Quantitative Evaluation Index
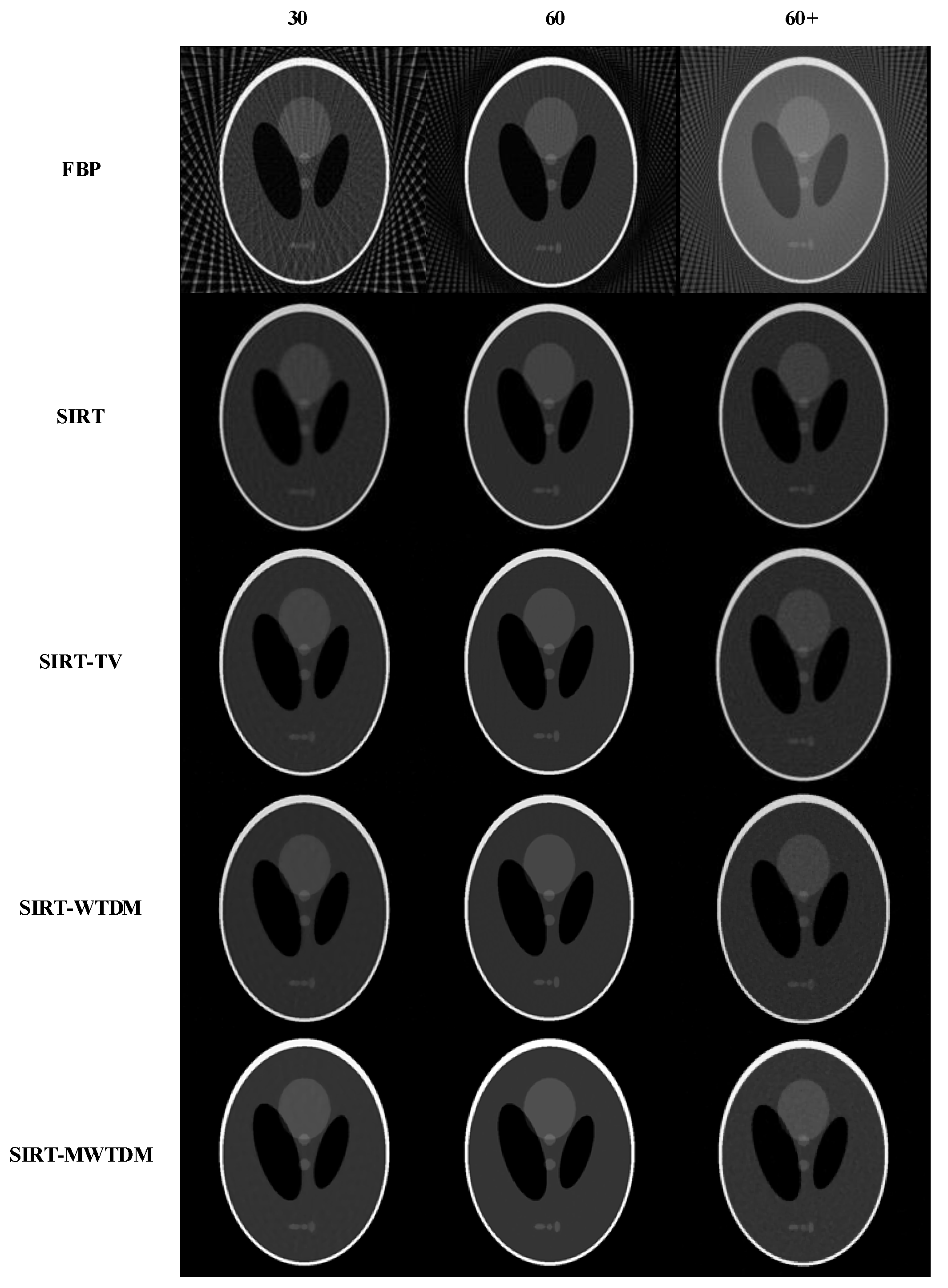
3.2. Simulation Experiment
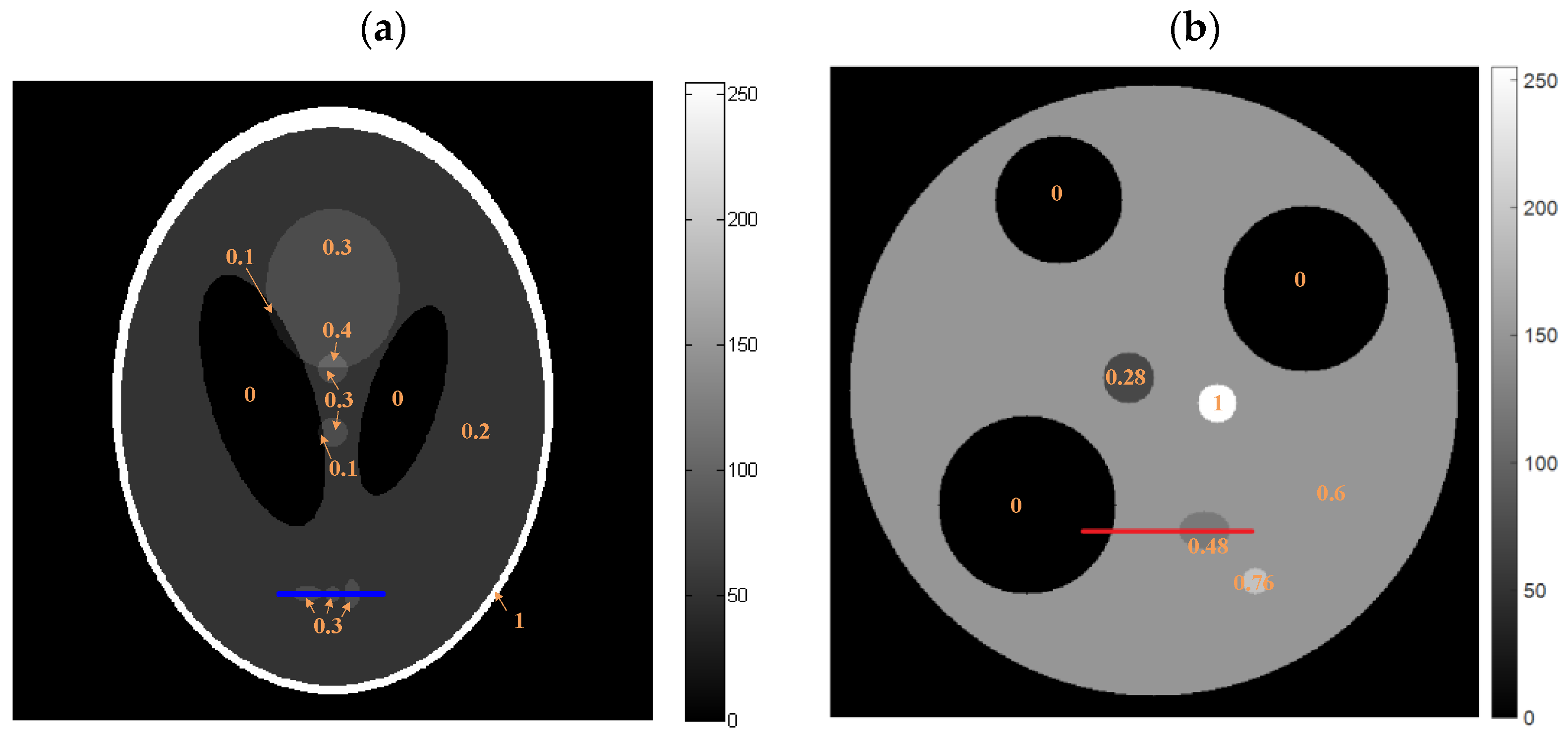
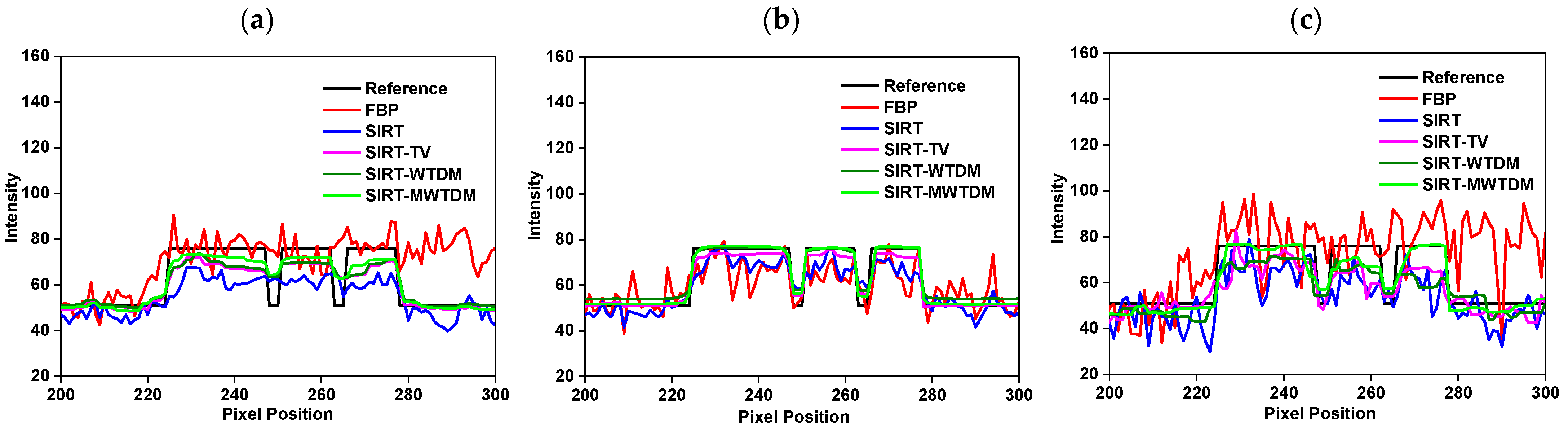
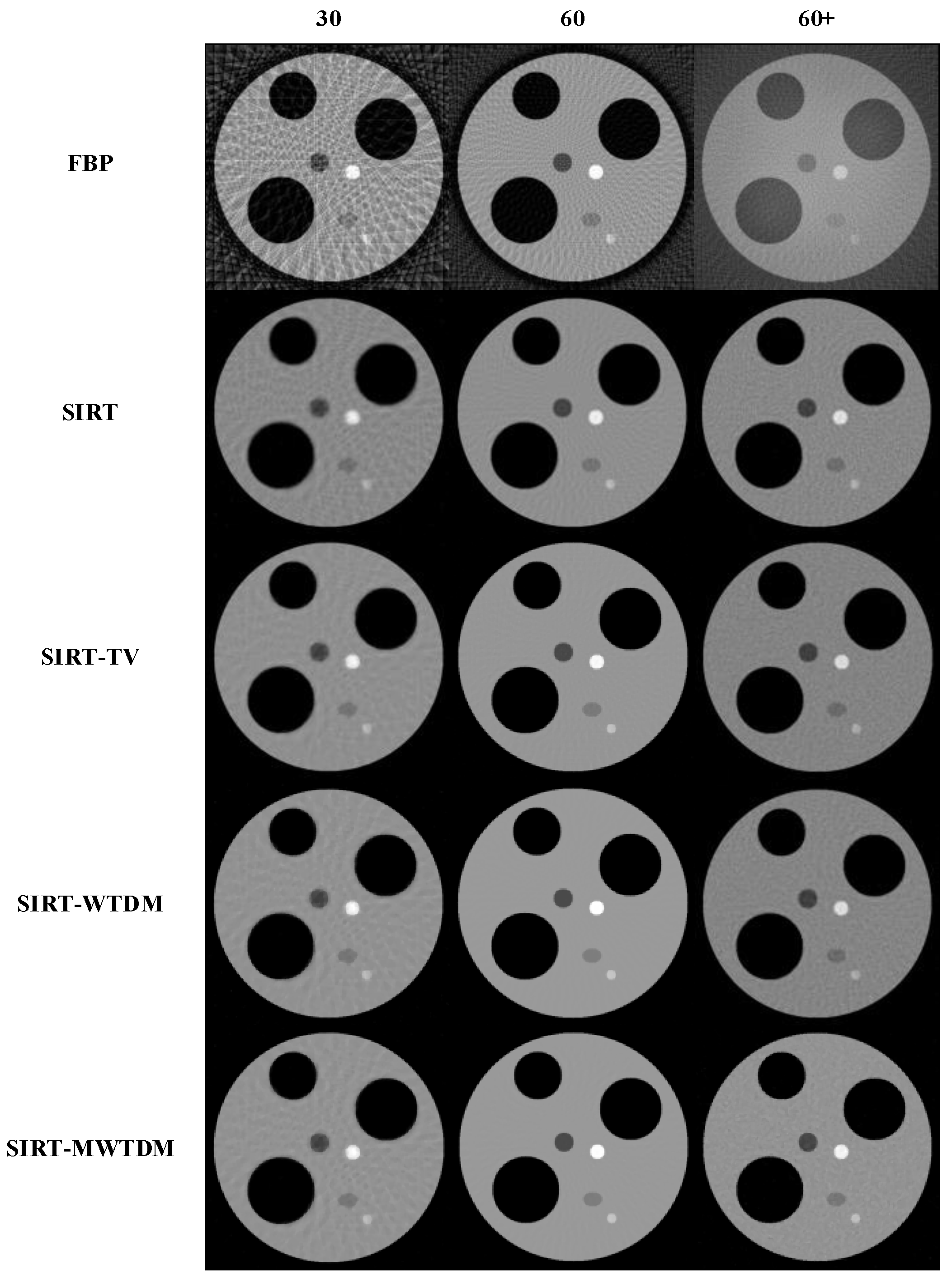
3.2.1. Shepp–Logan Phantom
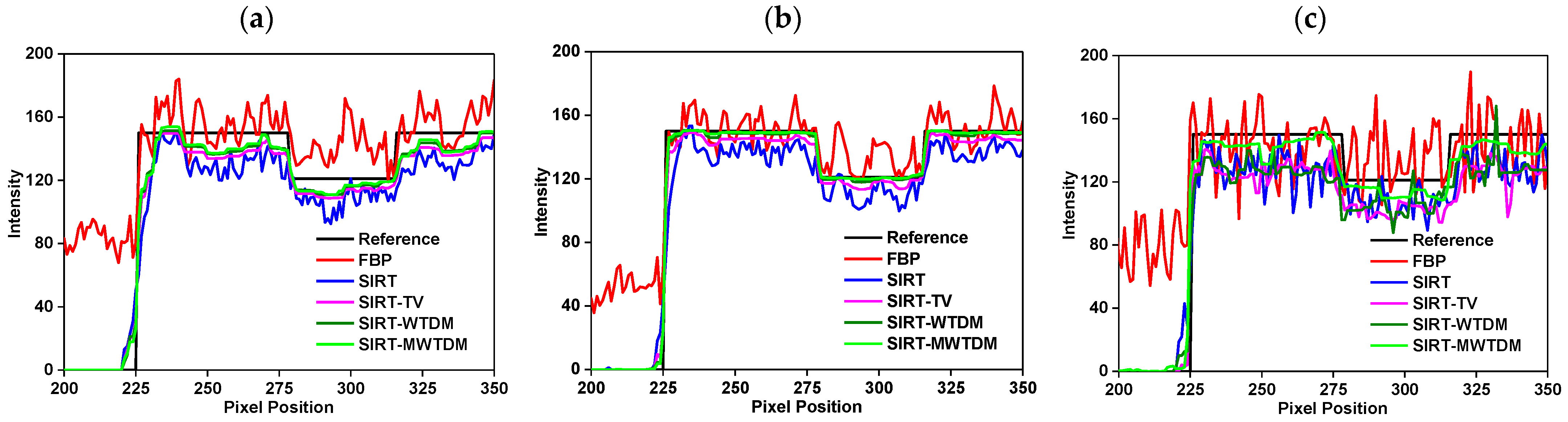
3.2.2. Circular Phantom
3.3. Neutron Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Juan, W.; Sulan, Z.; Qingjun, Z. The relationship of renewable energy consumption to financial development and economic growth in China. Renew. Energy 2021, 170, 897–904. [Google Scholar]
- Firoz, A.; Rashid, S.; Harun, C. Nuclear power plants in emerging economies and human resource development: A review. Energy Procedia. 2019, 160, 3–10. [Google Scholar]
- Smith, K.; Gieré, R. Why Some Nations Choose Nuclear Power, Kleinman Centre for Energy Policy, Newsletter. 2017. Available online: https://kleinmanenergy.upenn.edu/policy-digests/why-some-nations-choose-nuclear-power (accessed on 17 June 2021).
- Kim, D.; Park, J.; Lee, N. Nuclear Plant Accident and Change of the Nuclear Power Regime: Cases of the Three Mile Island and the Chernobyl Accidents. J. West. Hist. 2016, 55, 83–120. [Google Scholar] [CrossRef]
- Vladimir, D. Radiation Exposure to the Thyroid after the Chernobyl Accident. Front. Endocrinol. 2021, 11, 569041. [Google Scholar]
- Makoto, H.; Michio, M.; Yoshitake, T. Social Capital Enhanced Disaster Preparedness and Health Consultations after the 2011 Great East Japan Earthquake and Nuclear Power Station Accident. Int. J. Environ. Res. Public Health 2018, 15, 516. [Google Scholar]
- Hsiao, W.T.; Kuo, W.C.; Lin, H.H.; Lai, L.H. Assessment and Feasibility Study of Lemon Ripening Using X-ray Image of Information Visualization. Appl. Sci. 2021, 11, 3261. [Google Scholar] [CrossRef]
- Qiang, L.; Min, Y.; Fanyong, M.; Liang, S.; Bin, T. Calibration method of center of rotation under the displaced detector scanning for industrial CT. Nucl. Inst. Methods Phys. Res. A 2019, 922, 326–335. [Google Scholar]
- Min, Y.; Jianhai, Z.; Maodan, Y.; Xingdong, L.; Wenli, L.; Fanyong, M.; Sungjin, S.; Dongbo, W. Calibration method of projection coordinate system for X-ray cone-beam laminography scanning system. NDTE Int. 2012, 52, 16–22. [Google Scholar]
- Muhammad, A.; Fahima, I.; Daniel, W.; Hyoung-Koo, L. Sparse-view neutron CT reconstruction of irradiated fuel assembly using total variation minimization with Poisson statistics. J. Radioanal. Nucl. Chem. 2016, 307, 1967–1979. [Google Scholar]
- Kudo, H.; Suzuki, T.; Rashed, E. Image reconstruction for sparse-view CT and interior CT-introduction to compressed sensing and differentiated back projection. Quant. Imaging Med. Surg. 2013, 3, 147–161. [Google Scholar]
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Gilbert, P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol. 1972, 36, 105–117. [Google Scholar] [CrossRef]
- Andersen, A.; Kak, A. Simultaneous algebraic reconstruction technique (SART): A superior implementation of the ART algorithm. Ultrason. Imaging 1984, 6, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Zhanli, H.; Juan, G.; Na, Z.; Yongfeng, Y.; Xin, L.; Hairong, Z.; Dong, L. An improved statistical iterative algorithm for sparse-view and limited-angle CT image reconstruction. Sci. Rep. 2017, 7, 10747. [Google Scholar]
- Hongxiao, L.; Xiaodong, C.; Yi, W.; Zhongxing, Z.; Qingzhen, Z.; Daoyin, Y. Sparse CT reconstruction based on multi-direction anisotropic total variation (MDATV). BioMedical Eng. OnLine 2014, 13, 92. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Kao, C.M.; Pan, X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J. X-ray Sci. Technol. 2006, 14, 119–139. [Google Scholar]
- Sidky, E.Y.; Pan, X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 2008, 53, 4777–4807. [Google Scholar] [CrossRef] [Green Version]
- Ailong, C.; Linyuan, W.; Hanming, Z.; Bin, Y.; Lei, L.; Xiaoqi, X.; Jianxin, L. Edge guided image reconstruction in linear scan CT by weighted alternating direction TV minimization. J. X-ray Sci. Technol. 2014, 22, 335–349. [Google Scholar]
- Yuanjun, W.; Zeyao, Q. A new adaptive-weighted total variation sparse-view computed tomography image reconstruction with local improved gradient information. J. X-ray Sci. Technol. 2018, 26, 957–975. [Google Scholar]
- Gerardo, G.; Ville, K.; Aku, S. Isotropic and anisotropic total variation regularization in electrical impedance tomography. Comput. Math. Appl. 2017, 74, 564–576. [Google Scholar]
- Yumeng, G.; Li, Z.; Jiaxi, W.; Zhaoqiang, S. Image reconstruction method for exterior circular cone-beam CT based on weighted directional total variation in cylindrical coordinates. J. Inverse Ill-Posed Probl. 2020, 28, 155–172. [Google Scholar]
- Hui, Z.; Yanzhou, L.; Cheng, H.; Tianlong, W. Hybrid-Weighted Total Variation and Nonlocal Low-Rank-Based Image Compressed Sensing Reconstruction. IEEE Access 2020, 8, 23002–23010. [Google Scholar]
- Zhaoyan, Q.; Xiaojie, Z.; Jinxiao, P.; Ping, C. Sparse-view CT reconstruction based on gradient directional total variation. Meas. Sci. Technol. 2019, 30, 055404. [Google Scholar]
- Hengyong, Y.; Ge, W. A soft-threshold filtering approach for reconstruction from a limited number of projections. Phys. Med. Biol. 2010, 55, 3905–3916. [Google Scholar]
- Xianbiao, S.; Narendra, A. Hybrid compressive sampling via a new total variation TVL1. In European Conference on Computer Vision (ECCV 2010); Part VI; Paragios, N., Ed.; Springer: Berlin, Heidelberg, 2010; pp. 393–404. [Google Scholar]
- Sangang, L.; Zhengyun, D.; Quan, G.; Jing, S.; Qi, Y. An adaptive regularized iterative FBP algorithm with high sharpness for irradiated fuel assembly reconstruction from few projections in FNCT. Ann. Nucl. Energy 2020, 145, 107515. [Google Scholar]
- Alenius, S.; Ruotsalainen, U. Bayesian image reconstruction for emission tomography based on median root prior. Eur. J. Nucl. Med. 1997, 24, 258–265. [Google Scholar]
- Yu, W.; Zeng, L. A novel weighted total difference based image reconstruction algorithm for few-view computed tomography. PLoS ONE 2014, 9, e109345. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Jing, F.; Fei, F.; Huimin, Q.; Qian, W. PWLS-PR: Low-dose computed tomography image reconstruction using a patch-based regularization method based on the penalized weighted least squares total variation approach. Quant Imaging Med. Surg. 2021, 11, 2541–2559. [Google Scholar]
- Xiaoguang, L.; Linfeng, H.; Meimei, W.; Guohai, W.; Zhengyao, L.; Yuqing, L.; Kai, L.; Xuesheng, J. Development of Indirect Neutron CT Experimental Platform for Nuclear Fuel Elements. At. Energy Sci. Technol. 2021, 55, 939–944. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Yang, M.; He, L.; Lin, Q.; Wu, M.; Li, Z.; Li, Y.; Liu, X. Sparse-View Neutron CT Reconstruction Using a Modified Weighted Total Difference Minimization Method. Appl. Sci. 2021, 11, 10942. https://doi.org/10.3390/app112210942
Wu Y, Yang M, He L, Lin Q, Wu M, Li Z, Li Y, Liu X. Sparse-View Neutron CT Reconstruction Using a Modified Weighted Total Difference Minimization Method. Applied Sciences. 2021; 11(22):10942. https://doi.org/10.3390/app112210942
Chicago/Turabian StyleWu, Yapeng, Min Yang, Linfeng He, Qiang Lin, Meimei Wu, Zhengyao Li, Yuqing Li, and Xiaoguang Liu. 2021. "Sparse-View Neutron CT Reconstruction Using a Modified Weighted Total Difference Minimization Method" Applied Sciences 11, no. 22: 10942. https://doi.org/10.3390/app112210942
APA StyleWu, Y., Yang, M., He, L., Lin, Q., Wu, M., Li, Z., Li, Y., & Liu, X. (2021). Sparse-View Neutron CT Reconstruction Using a Modified Weighted Total Difference Minimization Method. Applied Sciences, 11(22), 10942. https://doi.org/10.3390/app112210942






