Forecasting the Daily Maximal and Minimal Temperatures from Radiosonde Measurements Using Neural Networks
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.1.1. Radiosonde Measurements
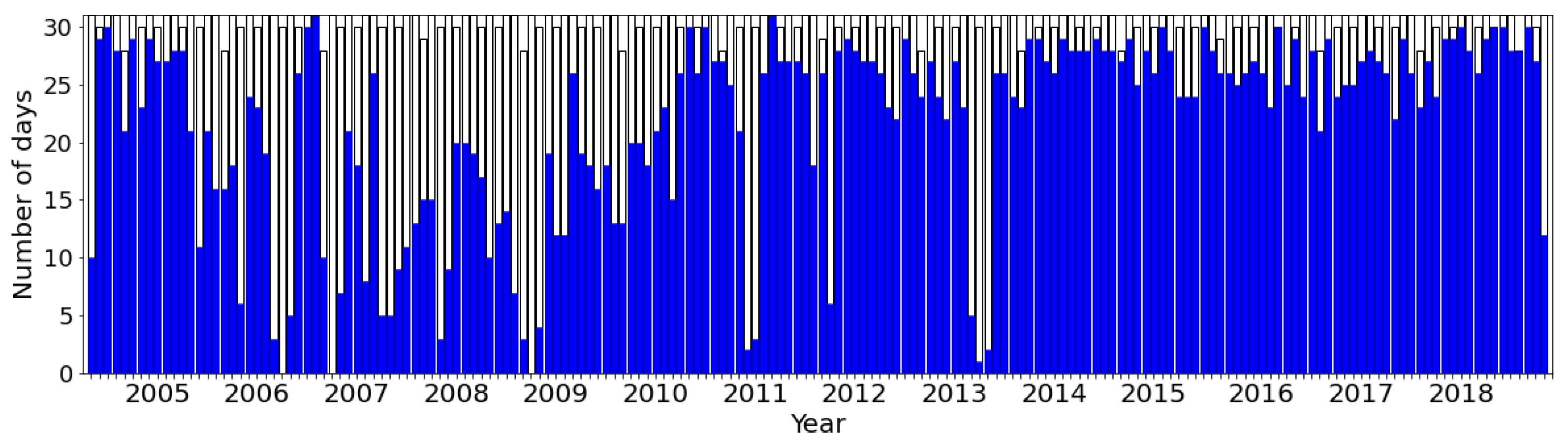
2.1.2. Daily Maximum and Minimum Temperature
2.2. Methods
2.2.1. Neural Network Setup
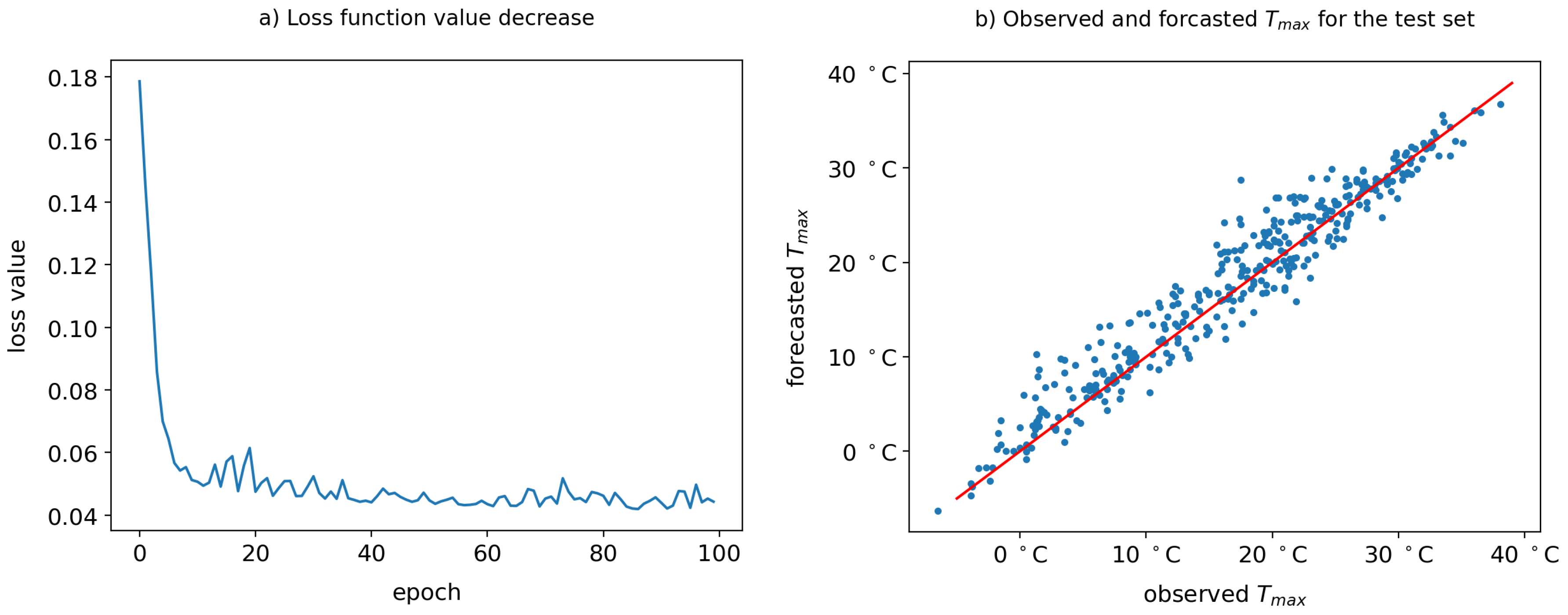
2.2.2. Forecast Performance Evaluation
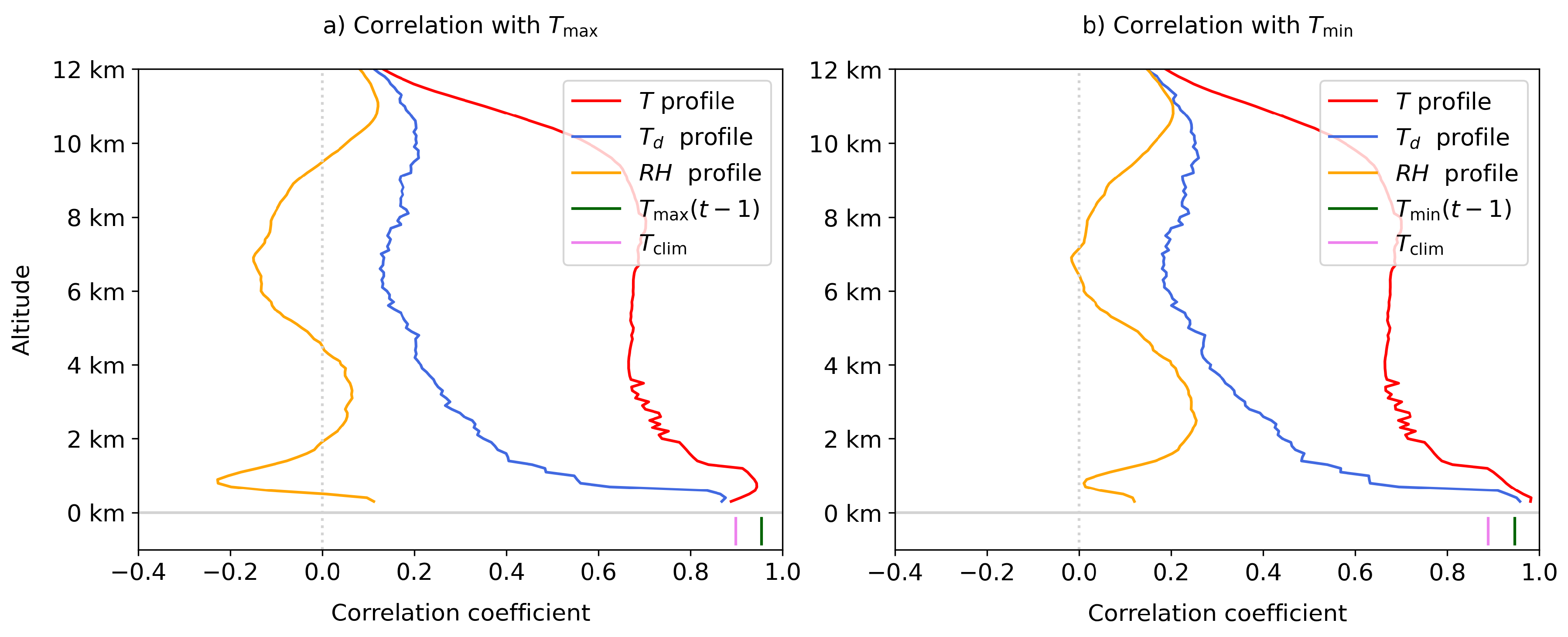
2.2.3. Neural Network Interpretation
3. Simplistic Sequential Networks
4. Dense Sequential Networks
4.1. Network Setup
| Name | Neurons in Layers | Input Variables |
|---|---|---|
| Setup X | 35,35,35,5,3,3,1 | 354 variables: T profile, profile, RH profile |
| Setup Y | same as Setup X | 355 variables: same as Setup X + |
| Setup Z | same as Setup X | 356 variables: same as Setup X + , |
| Setup Q | 3,3,5,3,1 | 1 variable: |
| Setup R | same as Setup Q | 2 variables: , |
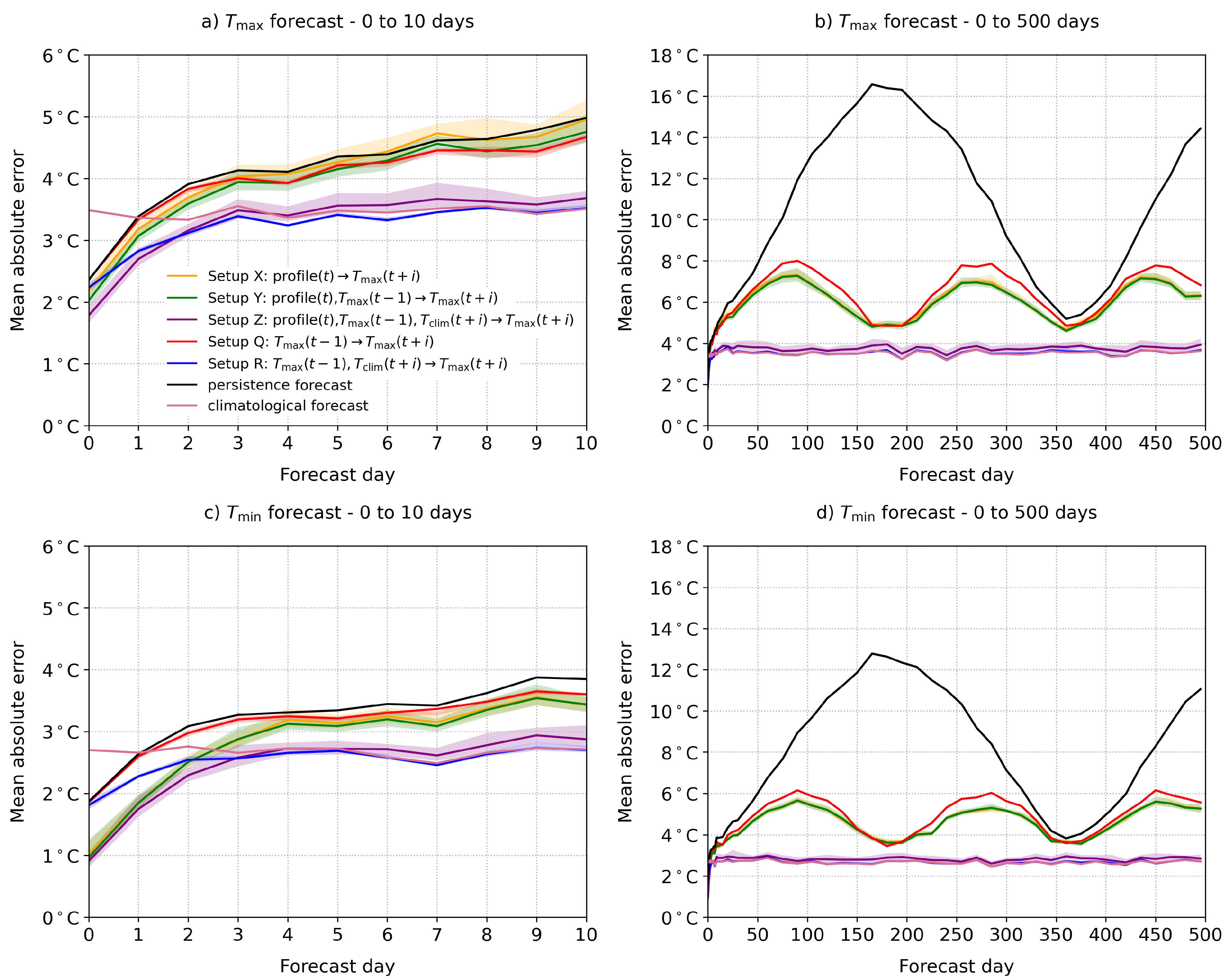
4.2. Forecast Performance
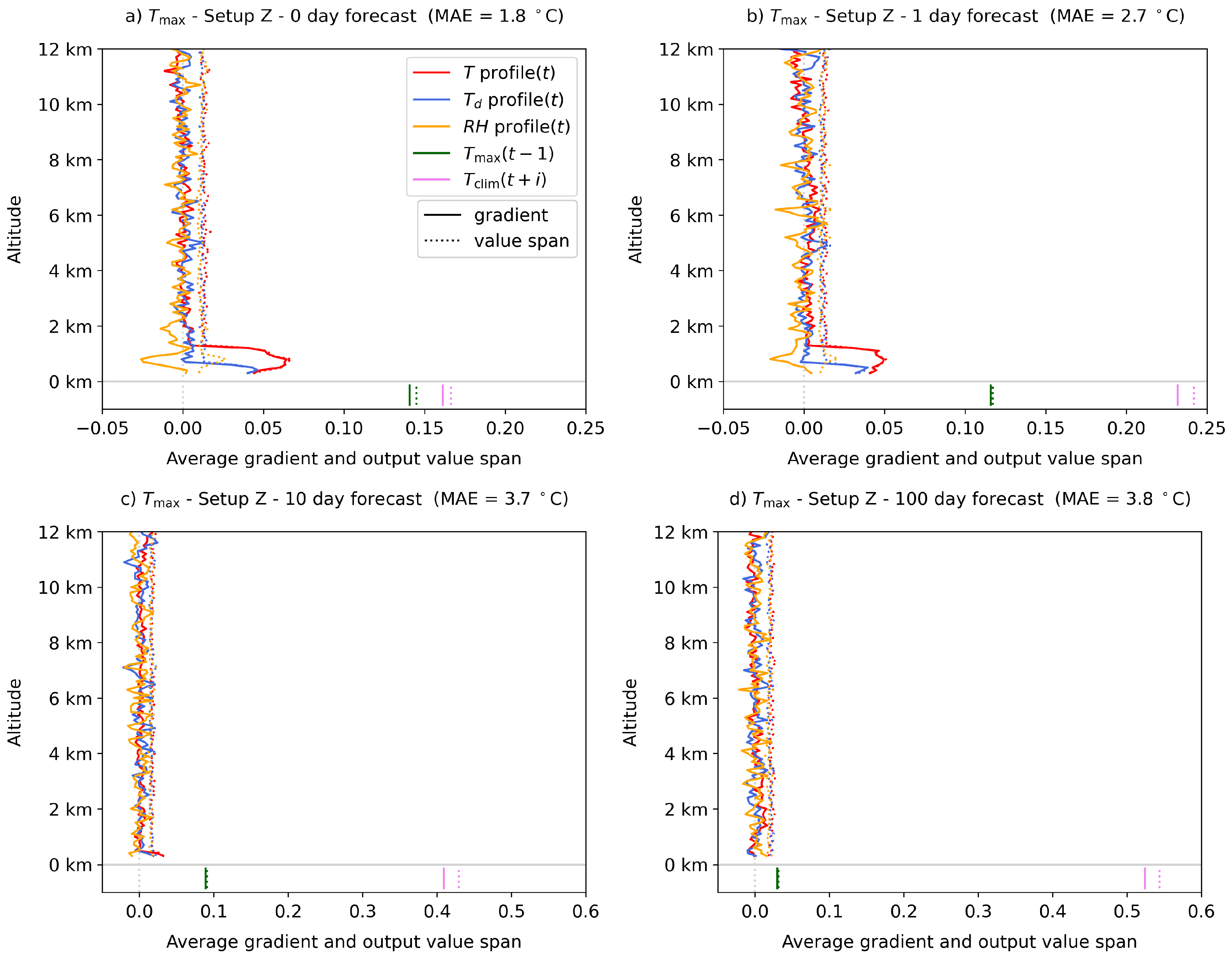
4.3. Network Interpretation
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T. A Vision for Numerical Weather Prediction in 2030. arXiv 2020, arXiv:2007.04830. [Google Scholar]
- Schultz, M.G.; Betancourt, C.; Gong, B.; Kleinert, F.; Langguth, M.; Leufen, L.H.; Mozaffari, A.; Stadtler, S. Can deep learning beat numerical weather prediction? Philos. Trans. R. Soc. A 2021, 379, 20200097. [Google Scholar] [CrossRef] [PubMed]
- Krasnopolsky, V.M.; Fox-Rabinovitz, M.S.; Chalikov, D.V. New Approach to Calculation of Atmospheric Model Physics: Accurate and Fast Neural Network Emulation of Longwave Radiation in a Climate Model. Mon. Weather Rev. 2005, 133, 1370–1383. [Google Scholar] [CrossRef] [Green Version]
- Brenowitz, N.D.; Bretherton, C.S. Prognostic Validation of a Neural Network Unified Physics Parameterization. Geophys. Res. Lett. 2018, 45, 6289–6298. [Google Scholar] [CrossRef]
- Chantry, M.; Hatfield, S.; Dueben, P.; Polichtchouk, I.; Palmer, T. Machine Learning Emulation of Gravity Wave Drag in Numerical Weather Forecasting. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002477. [Google Scholar] [CrossRef]
- Hatfield, S.; Chantry, M.; Dueben, P.; Lopez, P.; Geer, A.; Palmer, T. Building tangent-linear and adjoint models for data assimilation with neural networks. J. Adv. Model. Earth Syst. 2021, e2021MS002521. [Google Scholar] [CrossRef]
- Rodrigues, E.R.; Oliveira, I.; Cunha, R.; Netto, M. DeepDownscale: A deep learning strategy for high-resolution weather forecast. In Proceedings of the IEEE 14th International Conference on eScience, e-Science 2018, Amsterdam, The Netherlands, 29 October–1 November 2018; pp. 415–422. [Google Scholar] [CrossRef] [Green Version]
- Rasp, S.; Lerch, S. Neural Networks for Postprocessing Ensemble Weather Forecasts. Mon. Weather Rev. 2018, 146, 3885–3900. [Google Scholar] [CrossRef] [Green Version]
- Grönquist, P.; Yao, C.; Ben-Nun, T.; Dryden, N.; Dueben, P.; Li, S.; Hoefler, T. Deep learning for post-processing ensemble weather forecasts. Philos. Trans. R. Soc. A 2021, 379. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Hassanzadeh, P.; Pasha, S. A test case for application of convolutional neural networks to spatio-temporal climate data: Re-identifying clustered weather patterns. arXiv 2018, arXiv:1811.04817. [Google Scholar] [CrossRef]
- Lagerquist, R.; McGovern, A.; Gagne, D.J., II. Deep Learning for Spatially Explicit Prediction of Synoptic-Scale Fronts. Weather Forecast. 2019, 34, 1137–1160. [Google Scholar] [CrossRef]
- Liu, Y.; Racah, E.; Prabhat; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Can Machines Learn to Predict Weather? Using Deep Learning to Predict Gridded 500-hPa Geopotential Height From Historical Weather Data. J. Adv. Model. Earth Syst. 2019, 11, 2680–2693. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Improving Data-Driven Global Weather Prediction Using Deep Convolutional Neural Networks on a Cubed Sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109. [Google Scholar] [CrossRef]
- Rasp, S.; Dueben, P.D.; Scher, S.; Weyn, J.A.; Mouatadid, S.; Thuerey, N. WeatherBench: A Benchmark Data Set for Data-Driven Weather Forecasting. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002203. [Google Scholar] [CrossRef]
- Rasp, S.; Thuerey, N. Data-Driven Medium-Range Weather Prediction With a Resnet Pretrained on Climate Simulations: A New Model for WeatherBench. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002405. [Google Scholar] [CrossRef]
- Scher, S. Toward Data-Driven Weather and Climate Forecasting: Approximating a Simple General Circulation Model With Deep Learning. Geophys. Res. Lett. 2018, 45, 12616–12622. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Jia, Q.S.; Guan, X. Review of wind power forecasting methods: From multi-spatial and temporal perspective. In Proceedings of the Chinese Control Conference, CCC 2017, Dalian, China, 26–28 July 2017; pp. 10576–10583. [Google Scholar] [CrossRef]
- Grover, A.; Kapoor, A.; Horvitz, E. A deep hybrid model for weather forecasting. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; Association for Computing Machinery: New York, NY, USA, 2015; Volume 2015, pp. 379–386. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. MetNet: A Neural Weather Model for Precipitation Forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar]
- American Meteorological Society. 2021: Radiosonde. Glossary of Meteorology. Available online: https://glossary.ametsoc.org/wiki/Radiosonde (accessed on 8 November 2021).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2016, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier: Oxford, UK, 2011; Volume 59, p. 627. [Google Scholar] [CrossRef]
- Samek, W.; Müller, K.R. Towards Explainable Artificial Intelligence. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer: Cham, Switzerland, 2019; pp. 5–22. [Google Scholar] [CrossRef] [Green Version]
- Hechtlinger, Y. Interpretation of Prediction Models Using the Input Gradient. arXiv 2016, arXiv:1611.07634. [Google Scholar]
- Bannister, R.N. A review of forecast error covariance statistics in atmospheric variational data assimilation. I: Characteristics and measurements of forecast error covariances. Q. J. R. Meteorol. Soc. 2008, 134, 1951–1970. [Google Scholar] [CrossRef]
- Cohen, J.; Coumou, D.; Hwang, J.; Mackey, L.; Orenstein, P.; Totz, S.; Tziperman, E. S2S reboot: An argument for greater inclusion of machine learning in subseasonal to seasonal forecasts. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10, e00567. [Google Scholar] [CrossRef] [Green Version]
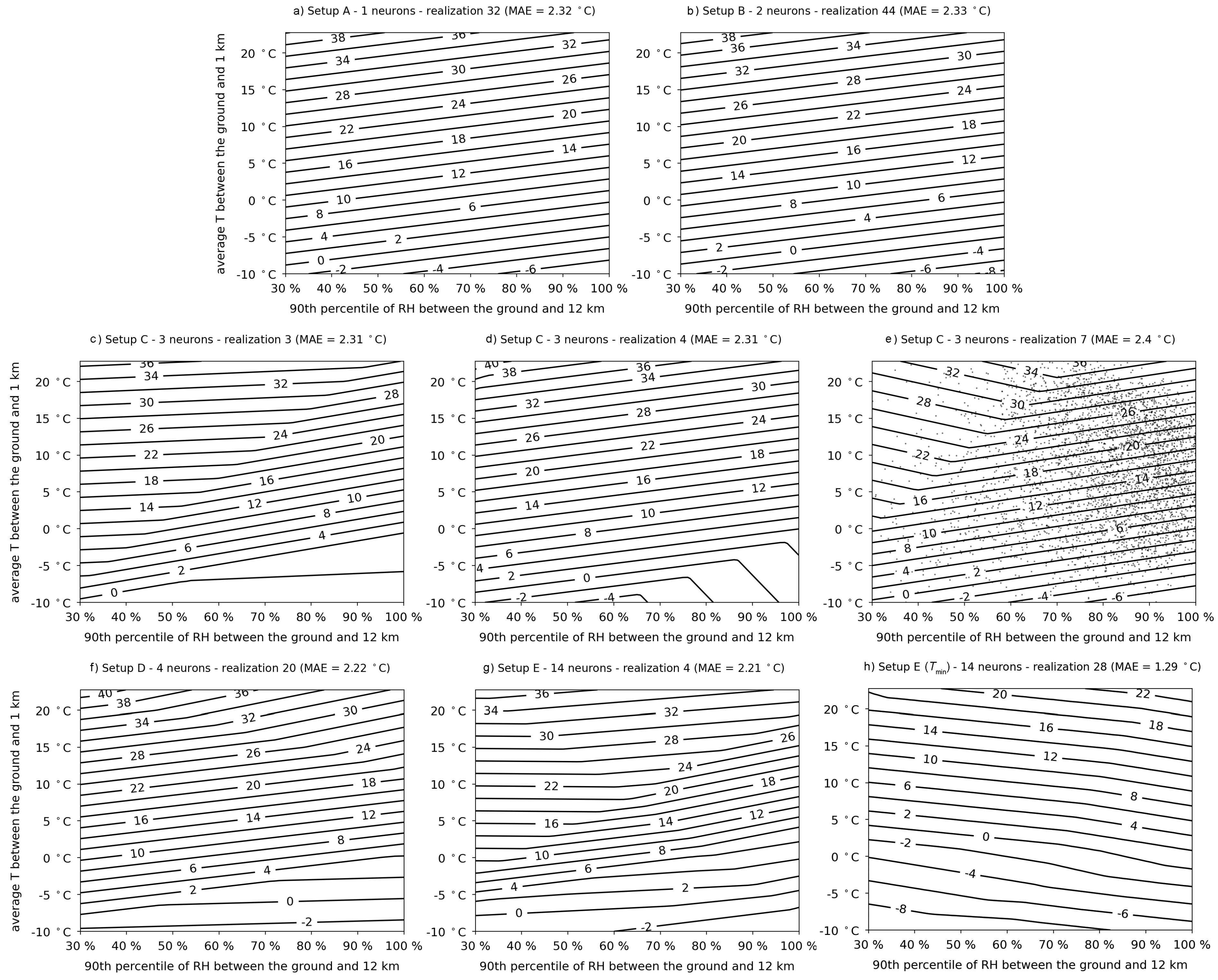

| Name | Neurons in Layers | MAE avg. [10th perc., 90th perc.] |
|---|---|---|
| Setup A | 1 | 2.32 [2.32, 2.33] °C |
| Setup B | 1,1 | 2.32 [2.29, 2.34] °C |
| Setup C | 2,1 | 2.31 [2.26, 2.39] °C |
| Setup D | 3,1 | 2.31 [2.26, 2.38] °C |
| Setup E | 5,5,3,1 | 2.27 [2.22, 2.31] °C |
| gradient | value span | gradient | value span | |
| avg. T in the lowest 1 km | 1.05 | 1.01 | 0.97 | 0.96 |
| 90th percentile of RH | −0.16 | 0.16 | 0.17 | 0.18 |
| Batch Size (Number of Epochs = 100) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | |
| MAE avg. | 2.03 | 2.08 | 2.06 | 2.05 | 2.01 | 1.99 | 2.02 | 2.01 | 2.03 | 2.06 | 2.15 | 2.21 |
| MAE 10th perc. | 1.89 | 1.91 | 1.90 | 1.89 | 1.89 | 1.88 | 1.89 | 1.89 | 1.93 | 1.98 | 2.05 | 2.09 |
| MAE 90th perc. | 2.31 | 2.42 | 2.28 | 2.33 | 2.11 | 2.13 | 2.22 | 2.14 | 2.22 | 2.15 | 2.31 | 2.35 |
| execution time | 916 s | 504 s | 260 s | 131 s | 67 s | 35 s | 19 s | 11 s | 7.3 s | 5 s | 3.6 s | 2.6 s |
| Number of Epochs (Batch Size = 256) | ||||||||||||
| 1 | 2 | 5 | 10 | 15 | 20 | 50 | 100 | 150 | 200 | 500 | 1000 | |
| MAE avg. | 8.84 | 7.82 | 5.54 | 3.31 | 2.53 | 2.34 | 2.11 | 2.01 | 1.99 | 1.98 | 1.97 | 1.99 |
| MAE 10th perc. | 7.30 | 6.59 | 3.25 | 2.36 | 2.16 | 2.10 | 1.99 | 1.91 | 1.90 | 1.87 | 1.88 | 1.90 |
| MAE 90th perc. | 10.00 | 8.91 | 7.36 | 6.05 | 2.91 | 2.65 | 2.28 | 2.22 | 2.14 | 2.17 | 2.11 | 2.07 |
| execution time | 0.4 s | 0.5 s | 0.7 s | 1.0 s | 1.4 s | 1.7 s | 3.8 s | 7.3 s | 11 s | 14 s | 35 s | 70 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skok, G.; Hoxha, D.; Zaplotnik, Ž. Forecasting the Daily Maximal and Minimal Temperatures from Radiosonde Measurements Using Neural Networks. Appl. Sci. 2021, 11, 10852. https://doi.org/10.3390/app112210852
Skok G, Hoxha D, Zaplotnik Ž. Forecasting the Daily Maximal and Minimal Temperatures from Radiosonde Measurements Using Neural Networks. Applied Sciences. 2021; 11(22):10852. https://doi.org/10.3390/app112210852
Chicago/Turabian StyleSkok, Gregor, Doruntina Hoxha, and Žiga Zaplotnik. 2021. "Forecasting the Daily Maximal and Minimal Temperatures from Radiosonde Measurements Using Neural Networks" Applied Sciences 11, no. 22: 10852. https://doi.org/10.3390/app112210852
APA StyleSkok, G., Hoxha, D., & Zaplotnik, Ž. (2021). Forecasting the Daily Maximal and Minimal Temperatures from Radiosonde Measurements Using Neural Networks. Applied Sciences, 11(22), 10852. https://doi.org/10.3390/app112210852






