Dynamic Wind Turbine Blade Inspection Using Micro-Polarisation Spatial Phase Shift Digital Shearography
Abstract
:1. Introduction
2. Methodology
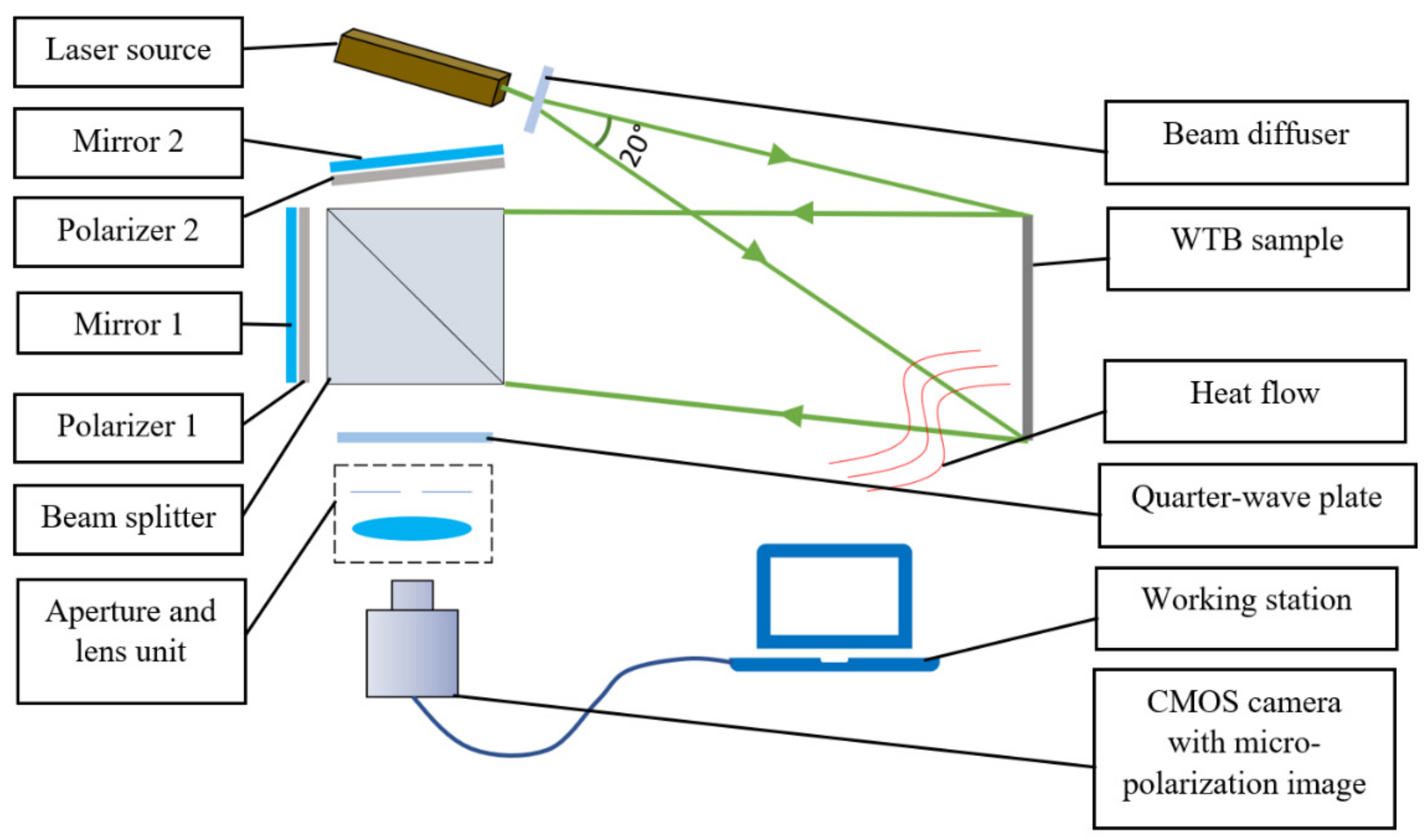
2.1. System Principle and Setup
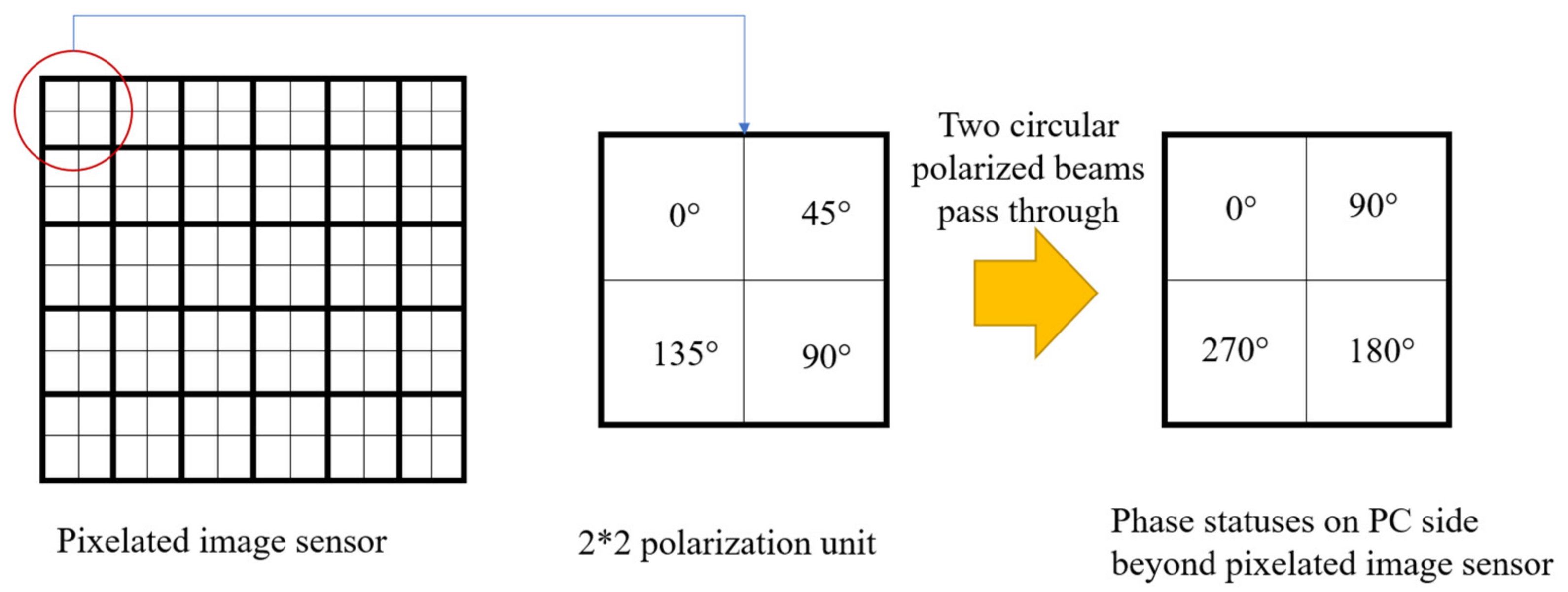
2.2. Carrier Mask Modulation and Window Selection Phase Map Retrieval
2.3. Filtering Algorithms and Phase Sequence Retrieval
2.4. Steps of the Proposed Method
- S1
- Set up the proposed SPS-DS system described in Section 2.1 and use a heating gun to heat up the area of the WTB surface where there is known defect at the subsurface.
- S2
- Record a sequence of the speckle patterns at the heated area. Decompose the recorded video into frame-by-frame images.
- S3
- From the initial frame at time to time , generate carrier masks at four phase values in different pixels and form a large mask to modulate the whole image, as expressed in Equation (2).
- S4
- Transform the modulated speckle patterns from time to time into 2D in the frequency domain and select the central speckle rings in each speckle pattern as described above with denoting the lower frequency in Equation (4). Transform the derived frequency domain patterns into the original domain using inverse 2D Fourier transform to form the complex terms from to .
- S5
- Multiply the derived at time with conjugates of that at time , as described in Equation (7), and calculate the phase map at time , as in Equation (8).
- S6
- In each of the initial phase maps derived at , adopt the WFF algorithm in their complex domain and obtain a new filtered phase .
- S7
- Form the sequence from time to time , as described in Equation (9), produce the dynamic phase map series, and develop the defect variation along with the temperature change due to the dynamic thermal loading as a video sequence.
3. Experiments and Discussion
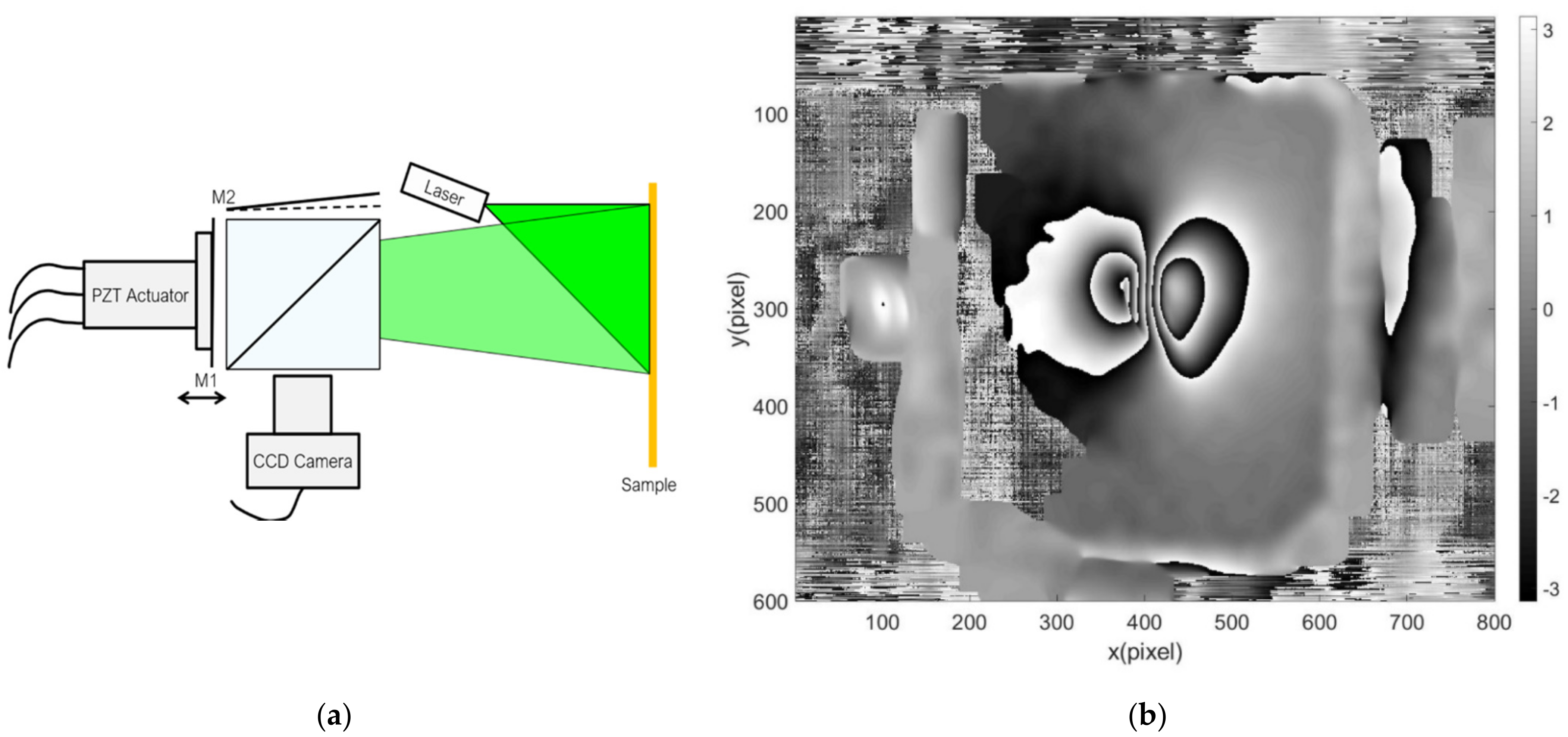
3.1. Pre-Test Using a Composite Sample
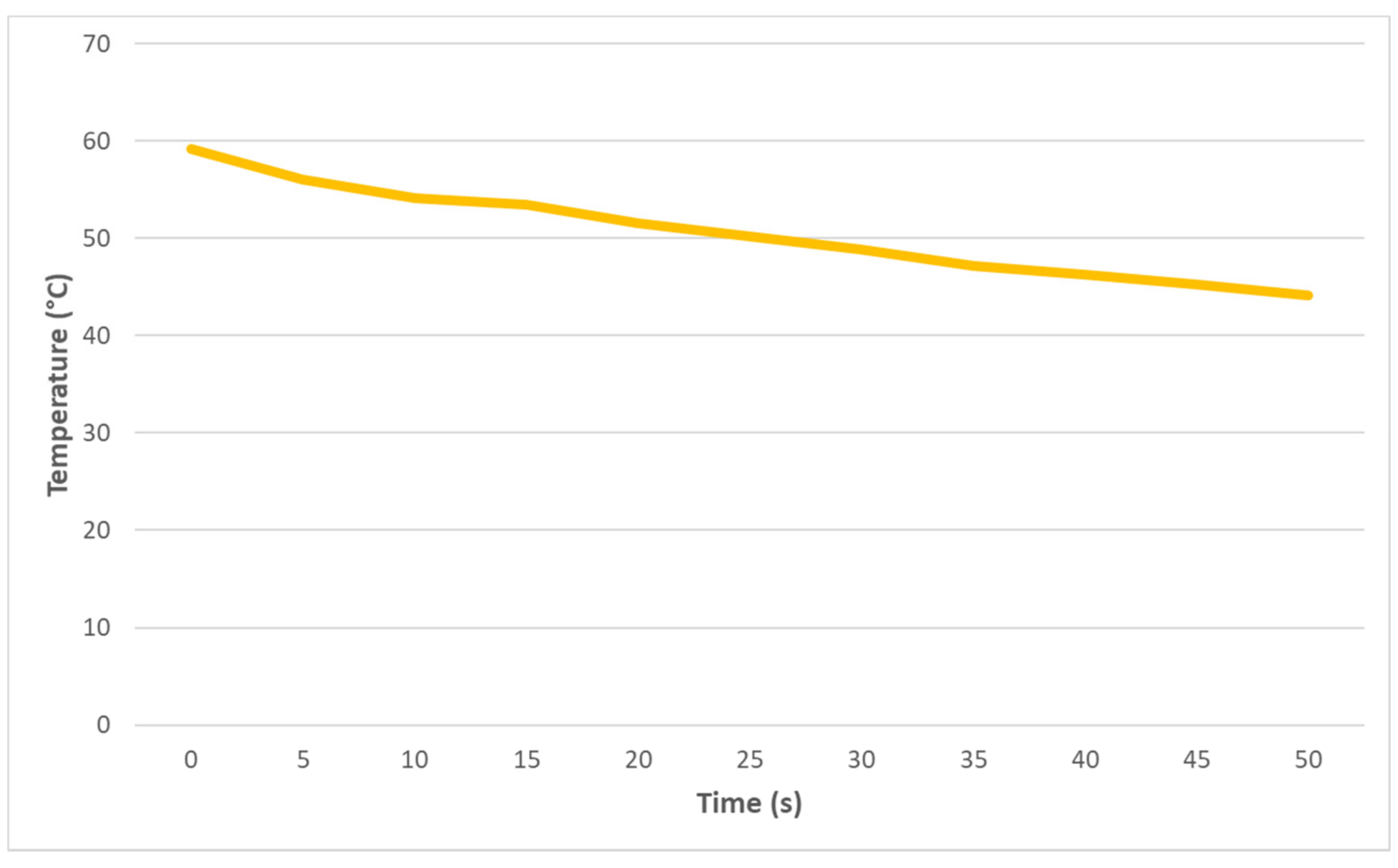
3.2. Test on the WTB with Known Defects
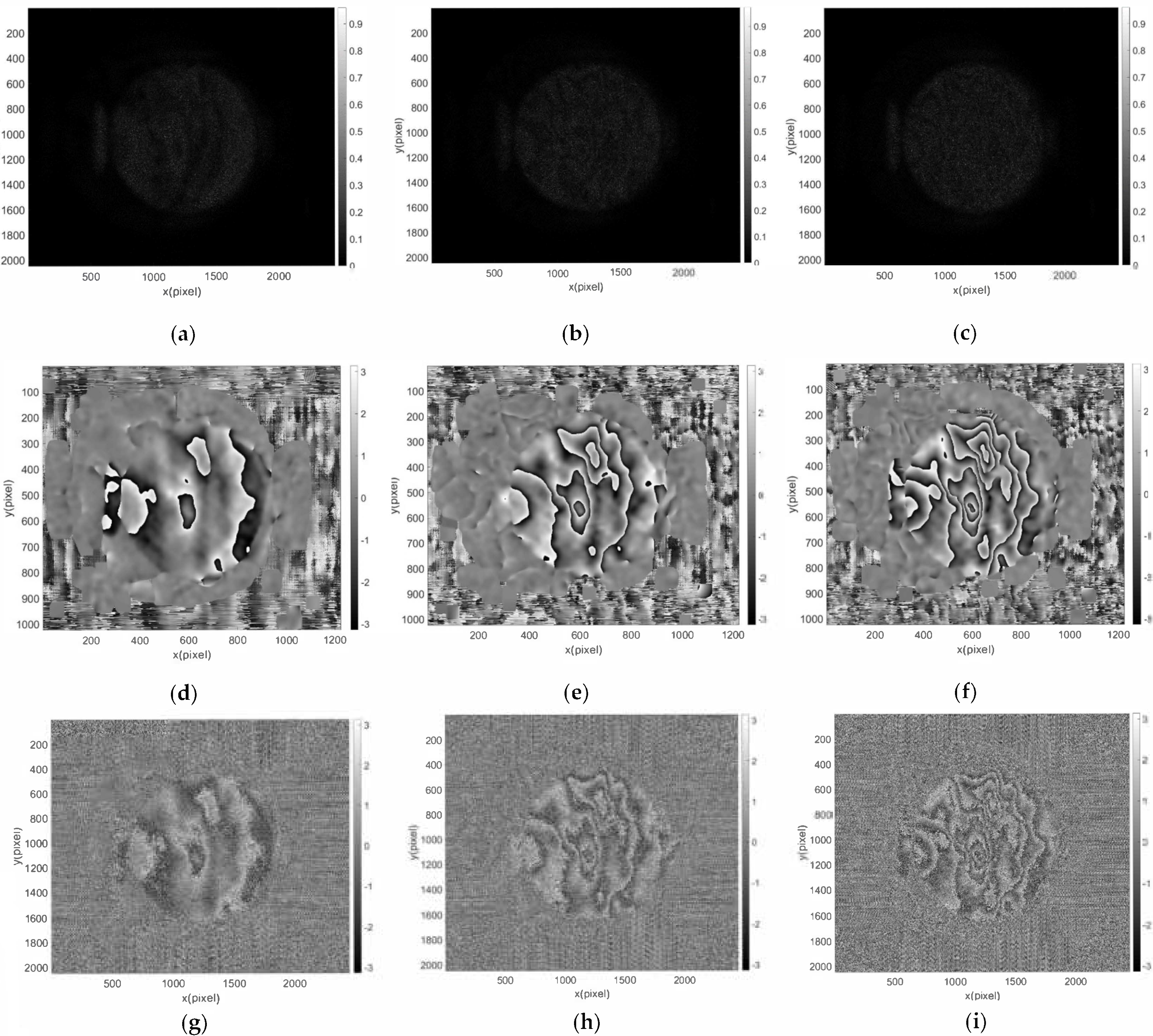
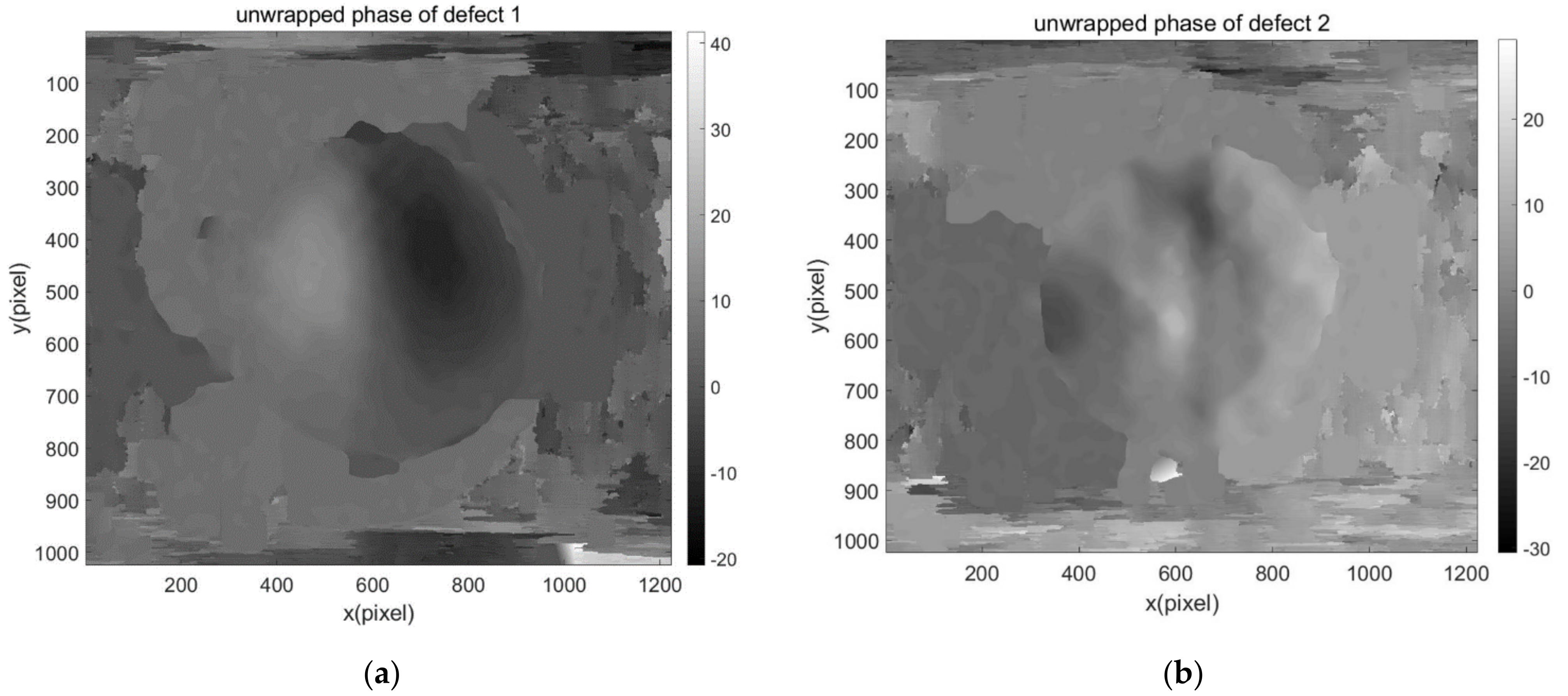
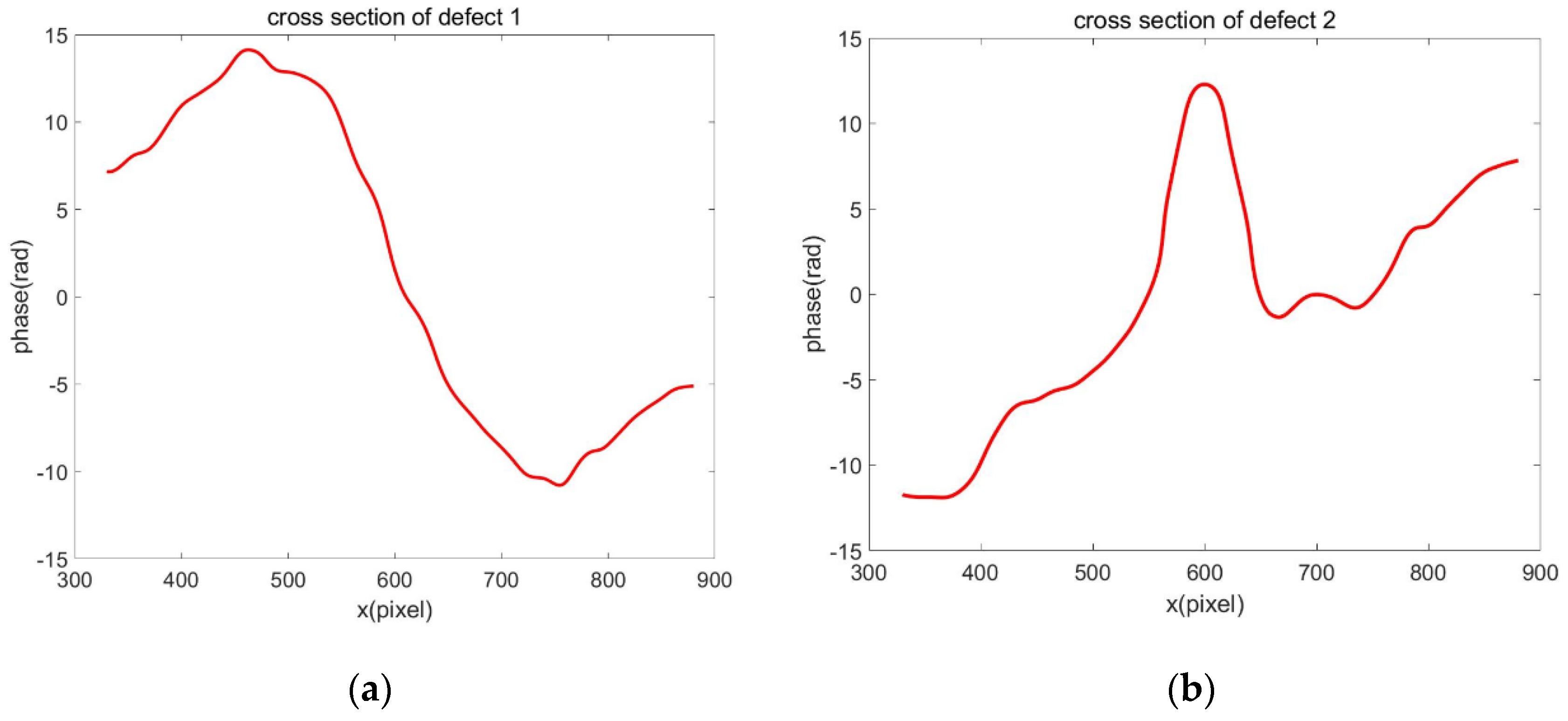
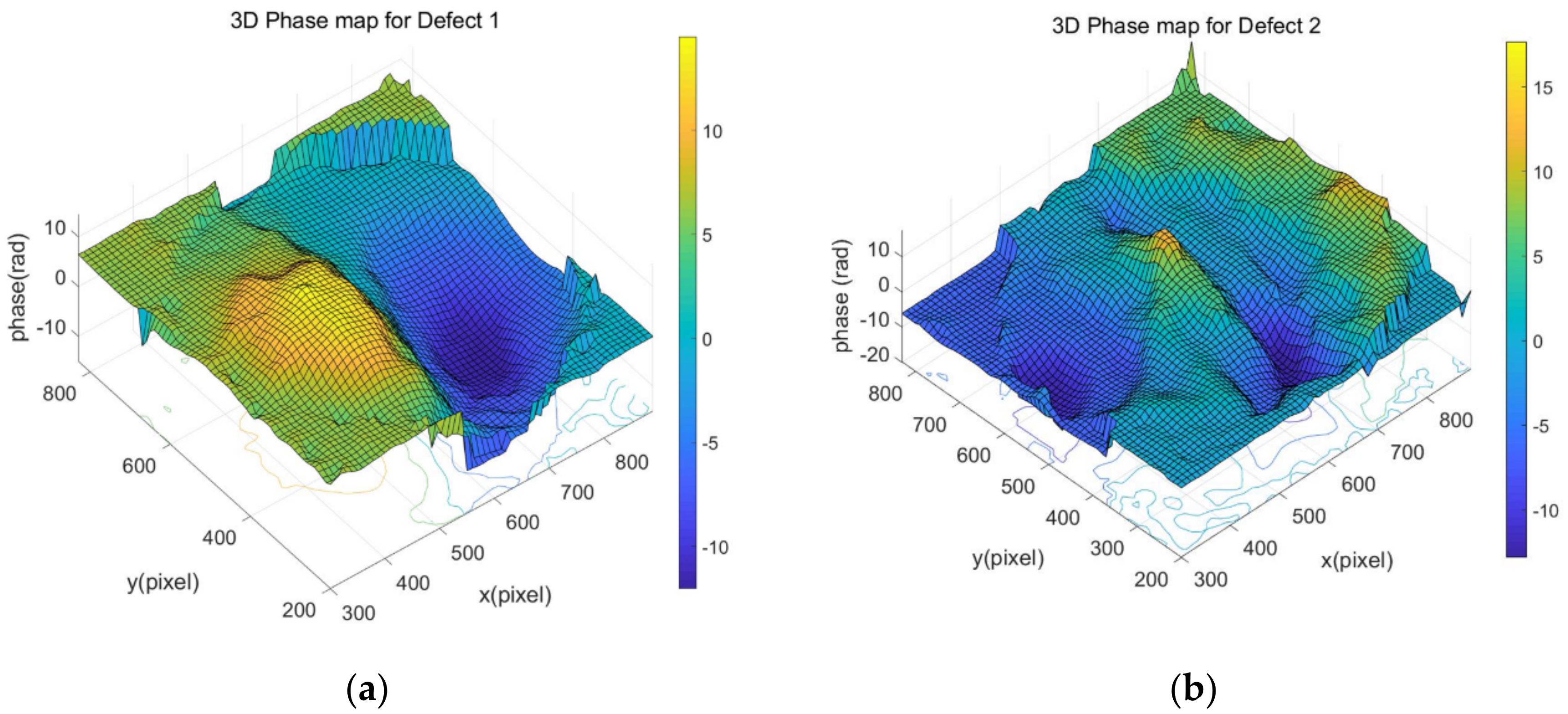
3.3. Phase Maps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, J. CORDIS|European Commission 31 May 2014. Available online: https://cordis.europa.eu/project/id/283533/reporting (accessed on 28 January 2021).
- London South Bank University. LSBU Researchers Are Developing Robots to Inspect wind Turbines. 21 May 2019. Available online: http://lsbu.staging.squizedge.net/stories/robots-inspect-wind-turbines (accessed on 28 January 2021).
- Zhao, Q.; Dan, X.; Sun, F.; Wang, Y.; Wu, S.; Yang, L. Digital Shearography for NDT: Phase Measurement Technique and Recent Developments. Appl. Sci. 2018, 8, 2662. [Google Scholar] [CrossRef] [Green Version]
- Carré, P. Installation et utilisation du comparateur photoélectrique et interférentiel du Bureau International des Poids et Mesures. Metrologia 1966, 2, 13–23. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef]
- Creath, K. Phase-shifting speckle interferometry. Appl. Opt. 1985, 24, 3053–3058. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, T.E.; Wei, A. Phase evaluation of speckle patterns during continuous deformation by use of phase-shifting speckle interferometry. Appl. Opt. 2000, 39, 2628–2637. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.H.; Ng, S.P.; Liu, L.; Chen, Y.S.; Hung, M.Y.Y. Shearographic phase retrieval using one single specklegram: A clustering approach. Opt. Eng. 2008, 47, 054301. [Google Scholar] [CrossRef]
- Kreis, T.M.; Jueptner, W.P.O. Fourier transform evaluation of interference patterns: Demodulation and sign ambiguity. In Laser Interferometry IV: Computer-Aided Interferometry; SPIE: Paris, France, 1992. [Google Scholar] [CrossRef]
- Vargas, J.; Quiroga, J.A.; Belenguer, T. Phase-shifting interferometry based on principal component analysis. Opt. Lett. 2011, 36, 1326–1328. [Google Scholar] [CrossRef] [Green Version]
- Vargas, J.; Quiroga, J.A.; Sorzano, C.O.S.; Estrada, J.C.; Carazo, J.M. Two-step demodulation based on the Gram-Schmidt orthonormalization method. Opt. Lett. 2012, 37, 443–445. [Google Scholar] [CrossRef]
- Vargas, J.; Sorzano, C.O.S. Quadrature Component Analysis for interferometry. Opt. Lasers Eng. 2013, 51, 637–641. [Google Scholar] [CrossRef]
- Van Haasteren, A.J.P.; Frankena, H.J. Real-time displacement measurement using a multicamera phase-stepping speckle interferometer. Appl. Opt. 1994, 33, 4137–4142. [Google Scholar] [CrossRef]
- Xie, X.; Yang, L.; Xu, N.; Chen, X. Michelson interferometer based spatial phase shift shearography. Appl. Opt. 2013, 52, 4063–4071. [Google Scholar] [CrossRef]
- Millerd, J.E.; Brock, N.J.; Hayes, J.B.; North-Morris, M.B.; Novak, M.; Wyant, J.C. Pixelated phase-mask dynamic interferometer. In Interferometry XII: Techniques and Analysis; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Serrano-Garcia, D.I.; Otani, Y. Dynamic phase measurements based on a polarization Michelson interferometer employing a pixelated polarization camera. Adv. Opt. Technol. 2017, 6, 47–51. [Google Scholar] [CrossRef]
- Aranchuk, V.; Lal, A.; Hess, C.F.; Trolinger, J.D. Pulsed spatial phase-shifting digital shearography based on a micropolarizer camera. Opt. Eng. 2018, 57, 024109. [Google Scholar] [CrossRef]
- Trillo, C.; Doval, Á.F.; Mendoza-Santoyo, F.; Pérez-López, C.; Ibarra, M.H.D.L.T.; Deán, J.L. Multimode vibration analysis with high-speed TV holography and a spatiotemporal 3D Fourier transform method. Opt. Express 2009, 17, 18014–18025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ri, S.; Wang, Q.; Xia, P.; Tsuda, H. Spatiotemporal phase-shifting method for accurate phase analysis of fringe pattern. J. Opt. 2019, 21, 095702. [Google Scholar] [CrossRef]
- Yan, P.; Liu, X.; Wu, S.; Sun, F.; Zhao, Q.; Wang, Y. Pixelated Carrier Phase-Shifting Shearography Using Spatiotemporal Low-Pass Filtering Algorithm. Sensors 2019, 19, 5185. [Google Scholar] [CrossRef] [Green Version]
- Servin, M.; Estrada, J.C. Error-free demodulation of pixelated carrier frequency interferograms. Opt. Express 2010, 18, 18492–18497. [Google Scholar] [CrossRef]
- Sony Semiconductor Solutions Group. Products|Image Sensor: Polarization Image Sensor|Products|Sony Semiconductor Solutions Group. 2019. Available online: https://www.sony-semicon.co.jp/e/products/IS/industry/product/polarization.html (accessed on 15 March 2021).
- Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef]
- Kai, L.; Kemao, Q. Dynamic phase retrieval in temporal speckle pattern interferometry using least squares method and windowed Fourier filtering. Opt. Express 2011, 19, 18058–18066. [Google Scholar] [CrossRef]
- Kemao, Q. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Kemao, Q.; Wang, H.; Gao, W. Windowed Fourier transform for fringe pattern analysis: Theoretical analyses. Appl. Opt. 2008, 47, 5408–5419. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Tokhi, M.O.; Marks, R.; Zheng, H.; Zhao, Z. Dynamic Wind Turbine Blade Inspection Using Micro-Polarisation Spatial Phase Shift Digital Shearography. Appl. Sci. 2021, 11, 10700. https://doi.org/10.3390/app112210700
Li Z, Tokhi MO, Marks R, Zheng H, Zhao Z. Dynamic Wind Turbine Blade Inspection Using Micro-Polarisation Spatial Phase Shift Digital Shearography. Applied Sciences. 2021; 11(22):10700. https://doi.org/10.3390/app112210700
Chicago/Turabian StyleLi, Zhiyao, Mohammad Osman Tokhi, Ryan Marks, Haitao Zheng, and Zhanfang Zhao. 2021. "Dynamic Wind Turbine Blade Inspection Using Micro-Polarisation Spatial Phase Shift Digital Shearography" Applied Sciences 11, no. 22: 10700. https://doi.org/10.3390/app112210700
APA StyleLi, Z., Tokhi, M. O., Marks, R., Zheng, H., & Zhao, Z. (2021). Dynamic Wind Turbine Blade Inspection Using Micro-Polarisation Spatial Phase Shift Digital Shearography. Applied Sciences, 11(22), 10700. https://doi.org/10.3390/app112210700





