Intelligent Prediction of Aeroengine Wear Based on the SVR Optimized by GMPSO
Abstract
:1. Introduction
2. SVR Prediction Model
3. Improved PSO Algorithm
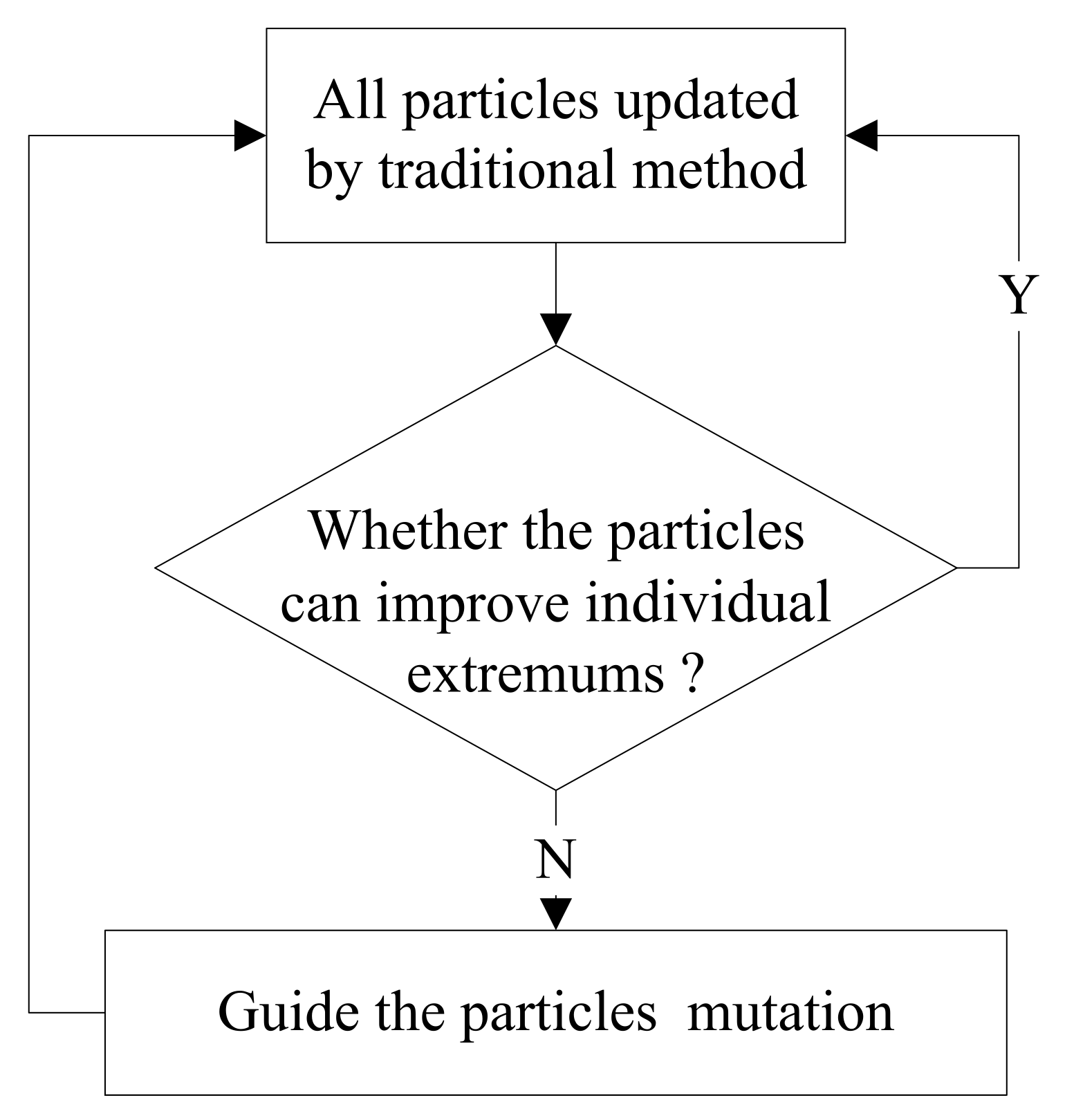
3.1. Guided Mutation Strategy
3.2. PSO Performance Verification
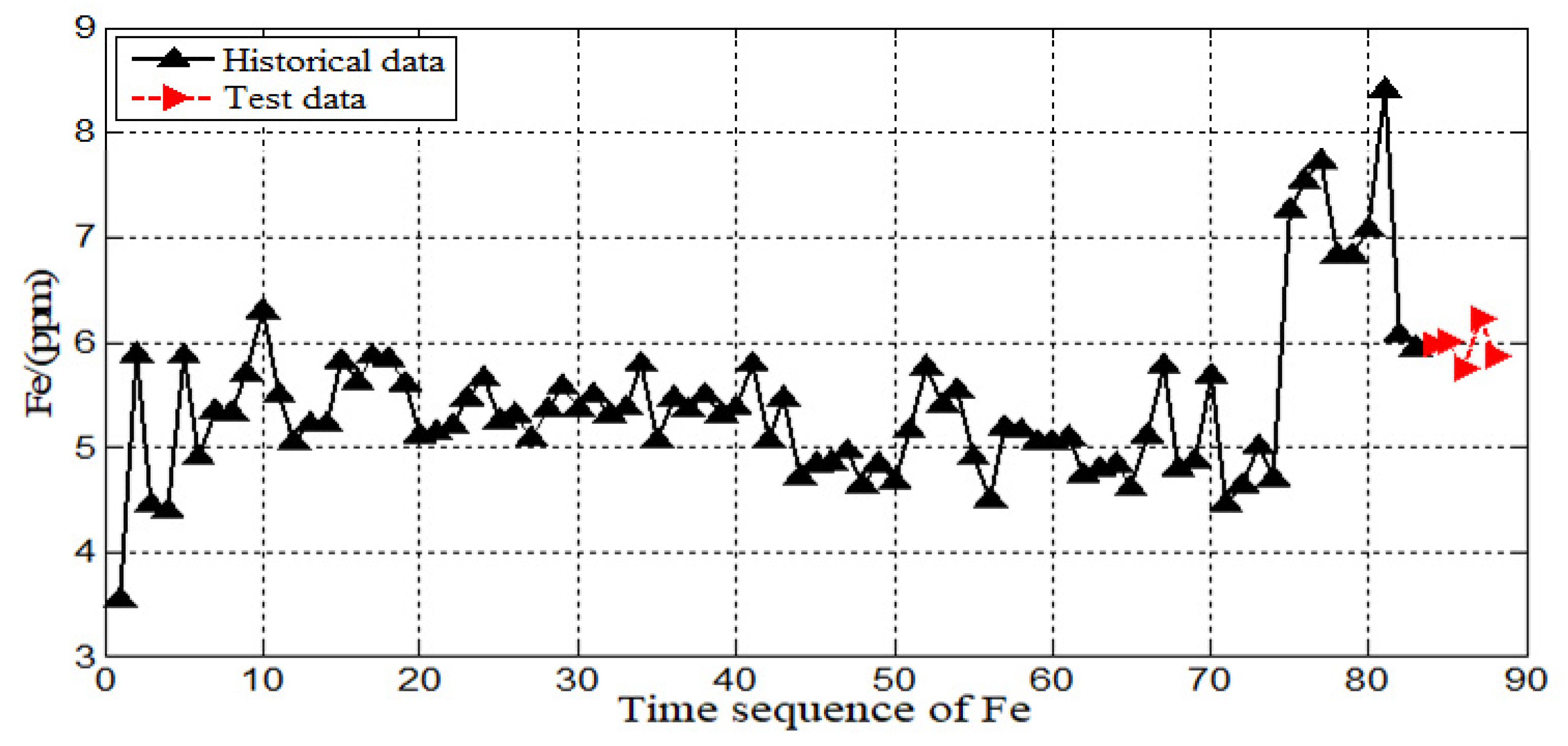
4. Aeroengine Wear Prediction Case
4.1. Multi-Step Prediction
4.2. Single-Step Prediction
4.3. Comparison with Other Methods
5. Conclusions
- (1)
- The guided mutation strategy can increase the diversity of particles and improve the global optimal performance. Therefore, GMPSO is basically better than other PSO variants.
- (2)
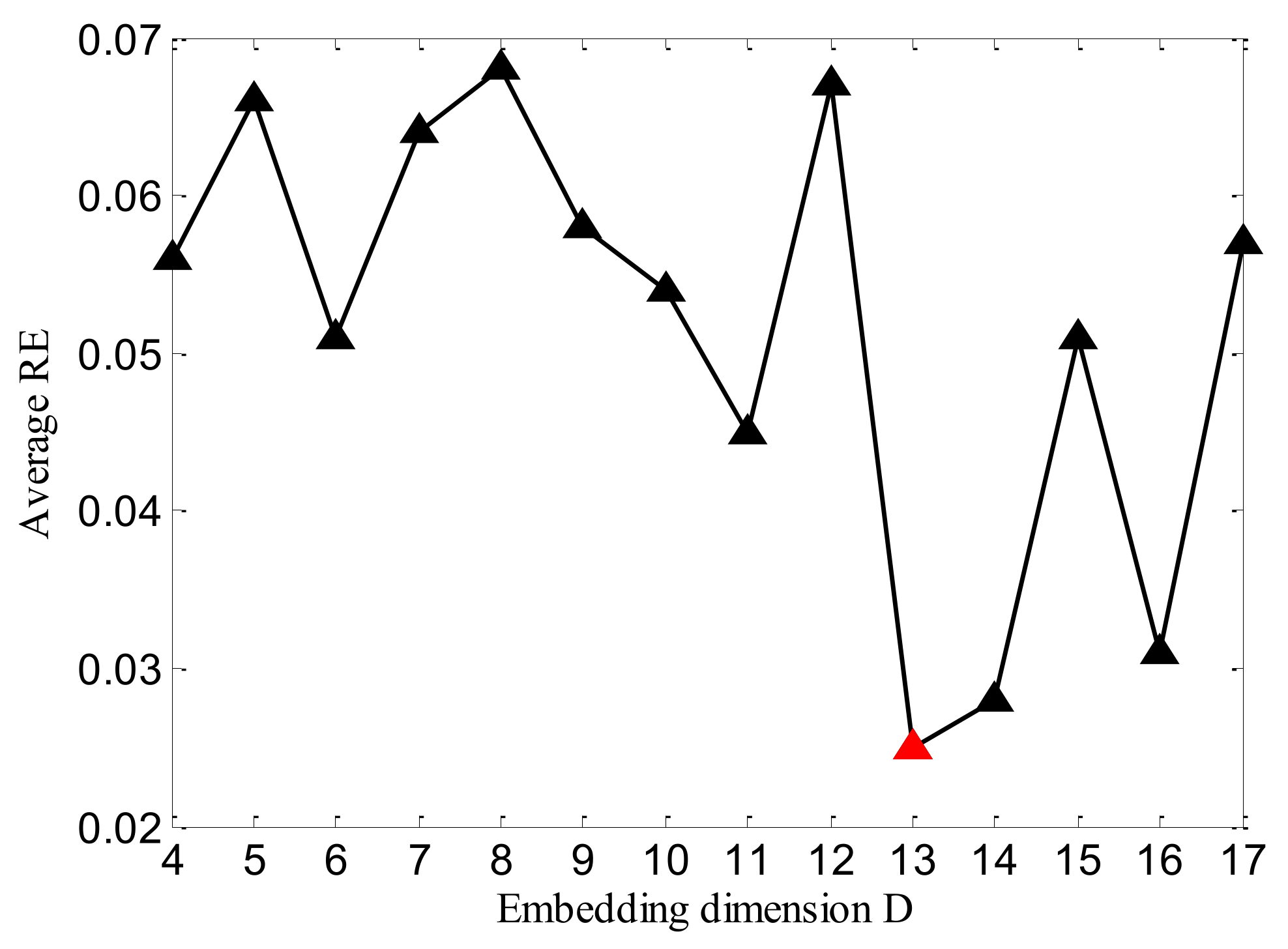
- The structure parameters and the embedding dimension have an obvious impact on the prediction accuracy; it is necessary to optimize them to improve the prediction accuracy of SVR.
- (3)
- Multi-step prediction has relatively lower accuracy than that of single-step prediction due to the error cumulative effect, but the time costs of the two forms exhibit the opposite trend.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Diaz, H.; Guedes Soares, C. A Failure Analysis of Floating Offshore Wind Turbines using AHP-FMEA Methodology. Ocean Eng. 2021, 234, 109261. [Google Scholar] [CrossRef]
- Schmidt, W.; Groche, P. Wear prediction for oscillating gear forming processes using numerical methods. Key Eng. Mater. 2018, 767, 283–289. [Google Scholar] [CrossRef]
- Zheng, B.; Ma, X. Application of improved Kohonen network in aeroengine classification fault diagnosis. Aeroengine 2020, 46, 23–29. [Google Scholar]
- Li, Y.; Chen, Y.; Zhong, J.; Huang, Z. Niching particle swarm optimization with equilibrium factor for multi-modal optimization. Inf. Sci. 2019, 494, 233–246. [Google Scholar] [CrossRef]
- Huang, C.G.; Huang, H.Z.; Li, Y.F. A bi-directional LSTM prognostics method under multiple operational conditions. IEEE Trans. Ind. Electron. 2019, 66, 8792–8802. [Google Scholar] [CrossRef]
- Lei, Y.G.; Jia, F.; Zhou, X.; Jing, L. A deep learning-based method for machinery health monitoring with big data. J. Mech. Eng. 2015, 51, 49–56. [Google Scholar] [CrossRef]
- Li, H.; Guedes Soares, C.; Huang, H.Z. Reliability analysis of a floating offshore wind turbine using Bayesian networks. Ocean Eng. 2020, 217, 107827. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H. Support vector machine method for developing ground motion models for earthquakes in western part of China. J. Earthq. Eng. 2021, 2021, 3086. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, H.Y.; Ma, X.; Zhang, X. Graph Partition Based on Dimensionless Similarity and Its Application to Fault Diagnosis. IEEE Access 2021, 9, 35573–35583. [Google Scholar] [CrossRef]
- Li, H.; Diaz, H.; Guedes Soares, C. A developed failure mode and effect analysis for floating offshore wind turbine support structures. Renew. Energy 2021, 164, 133–145. [Google Scholar] [CrossRef]
- Shailaja, K.; Anuradha, B. Improved face recognition using a modified PSO based self-weighted linear collaborative discriminant regression classification. J. Eng. Appl. Sci. 2017, 12, 7234–7241. [Google Scholar]
- Tanweer, M.R.; Suresh, S.; Sundararajan, N. Self regulating particle swarm optimization algorithm. Inf. Sci. 2015, 294, 182–202. [Google Scholar]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Particle swarm optimization with an aging leader and challengers algorithm for optimal power flow problem with FACTS devices. Electr. Power Energy Syst. 2015, 64, 1185–1196. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.C. A social learning particle swarm optimization algorithm for scalable optimization. Inf. Sci. 2015, 291, 43–60. [Google Scholar] [CrossRef]
- Zeng, B.; Liu, S.; Cuevas, C. A self-adaptive intelligence gray prediction model with the optimal fractional order accumulating operator and its application. Math. Methods Appl. Sci. 2017, 40, 7843–7857. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, F. Fault diagnosis method based on S-PSO classification algorithm. Acta Aeronaut. Astronaut. Sin. 2015, 36, 3640–3651. [Google Scholar]
- Zeng, R.; Wang, Y.Y. A chaotic simulated annealing and particle swarm improved artificial immune algorithm for flexible job shop scheduling problem. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 101–123. [Google Scholar] [CrossRef] [Green Version]
- Kalidindi, K.R.; Gottumukkala, P.S.V.; Davuluri, R. Derivative-based band clustering and multi-agent PSO optimization for optimal band selection of hyper-spectral images. J. Supercomput. 2020, 76, 5873–5898. [Google Scholar] [CrossRef]
- Li, H.; Diaz, H.; Guedes Soares, C. A two-stage failure mode and effect analysis of offshore wind turbines. Renew. Energy 2020, 162, 1438–1461. [Google Scholar] [CrossRef]
- Ziani, R.; Felkaoui, A.; Zegadi, R. Bearing fault diagnosis using multiclass support vector machines with binary particle swarm optimization and regularized Fisher’s criterion. J. Intell. Manuf. 2017, 28, 405–417. [Google Scholar] [CrossRef]
- Khorram, B.; Yazdi, M. A new optimized thresholding method using ant colony algorithm for MR brain image segmentation. J. Digit. Imaging 2019, 32, 162–174. [Google Scholar] [CrossRef] [PubMed]
- Ugalde, A.; Egozcue, J.J.; Ranero, C.R. A new autoregressive moving average modeling of H/V spectral ratios to estimate the ground resonance frequency. Eng. Geol. 2021, 280, 105957. [Google Scholar] [CrossRef]
| Test Function | Search Range | Dimension | Optimal Solution | Optimal Extremum |
|---|---|---|---|---|
| Sphere: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Schaffer: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Griewank: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Ackley: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Rastrigin: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Rosenbrock: | [−100, 100] | 50 | (1, 1,…,1)50 | 0 |
| SDPF: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| RHEF: | [−100, 100] | 50 | (0, 0,…,0)50 | 0 |
| Function | SRPSO | ALCPSO | SLPSO | IWPSO | SFPSO | DNPSO | SAPSO | MAPSO | GMPSO |
|---|---|---|---|---|---|---|---|---|---|
| fSph | 0.00025 | 8.4617 | 4174.53 | 474.278 | 1956.71 | 0.1176 | 132.214 | 0.0042 | 3.98 × 10−68 |
| fSch | 0.4481 | 0.4548 | 0.4928 | 0.4451 | 0.4886 | 0.4995 | 0.4455 | 0.3816 | 6.67 × 10−11 |
| fGri | 0.0055 | 0.3550 | 2.0718 | 1.1099 | 1.4751 | 0.0105 | 0.9869 | 0.0041 | 0 |
| fAck | 21.1626 | 19.2621 | 18.6374 | 19.7884 | 20.6655 | 20.0057 | 19.4486 | 18.8497 | 0 |
| fRas | 193.353 | 950.846 | 4564.84 | 1124.34 | 2613.14 | 471.213 | 1176.23 | 204.646 | 0 |
| fRos | 155.083 | 5219.32 | 8819.17 | 5891.12 | 2059.34 | 168.554 | 2634.42 | 148.853 | 47.3102 |
| fSDPF | 3.15 × 108 | 1.22 × 1024 | 6.12 × 1052 | 1.48 × 1038 | 1.43 × 1039 | 0.1566 | 9.66 × 1035 | 7.84 × 107 | 1.77 × 10−101 |
| fRHEF | 917.416 | 1033.42 | 9612.11 | 10436.4 | 6855.24 | 675.486 | 2506.73 | 1258.76 | 4.37 × 10−56 |
| True Values | GMPSO-SVR | PSO-SVR | ||||||
|---|---|---|---|---|---|---|---|---|
| Exp.No1 | Exp.No2 | Exp.No1 | Exp.No2 | |||||
| Prediction | RE | Prediction | RE | Prediction | RE | Prediction | RE | |
| 5.98 | 5.9842 | 0.07% | 5.9842 | 0.07% | 6.1838 | 3.41% | 6.1387 | 2.65% |
| 6.02 | 6.0338 | 0.23% | 6.0338 | 0.23% | 5.9301 | 1.49% | 6.0604 | 0.67% |
| 5.75 | 5.9962 | 4.28% | 5.9962 | 4.28% | 5.7172 | 0.57% | 5.9905 | 4.18% |
| 6.23 | 5.8659 | 5.85% | 5.8659 | 5.85% | 5.6559 | 9.21% | 5.8062 | 6.8% |
| 5.88 | 5.7425 | 2.34% | 5.7425 | 2.34% | 5.4062 | 8.06% | 5.7914 | 0.15% |
| (C, γ, ε, D)best | (0.1, 13.5887, 0.01, 13) | (0.1, 13.5887, 0.01, 13) | (100, 0.01, 0.01, 11) | (0.1, 11.8511, 0.01, 11) | ||||
| Fitness value | 0.049% | 0.049% | 0.053% | 0.051% | ||||
| Average RE | 2.55% | 2.55% | 4.55% | 2.89% | ||||
| True Values | Multi-Step GMPSO-SVR | Single-Step GMPSO-SVR | ||||
|---|---|---|---|---|---|---|
| Prediction | RE | (C, γ, ε, D)best | Fitness Value | Prediction | RE | |
| 5.98 | 5.9842 | 0.07% | (0.1, 13.5887, 0.01, 13) | 0.049% | 5.9842 | 0.07% |
| 6.02 | 6.0338 | 0.23% | (0.1, 11.6259, 0.01, 13) | 0.052% | 6.0213 | 0.022% |
| 5.75 | 5.9962 | 4.28% | (0.1, 4.9941, 0.01, 16) | 0.056% | 5.7554 | 0.094% |
| 6.23 | 5.8659 | 5.85% | (0.1, 54.7909, 0.01, 26) | 0.0489% | 6.2236 | 0.103% |
| 5.88 | 5.7425 | 2.34% | (0.1, 16.4312, 0.01, 3) | 0.0442% | 5.8819 | 0.032% |
| Average RE | 2.55% | 0.064% | ||||
| Elapsed time | 70.32 s | 358.35 s | ||||
| True Values | Multi-Step GMPSO-SVR | Single-Step GMPSO-SVR | BP Network | ARMA | ||||
|---|---|---|---|---|---|---|---|---|
| Prediction | RE | Prediction | RE | Prediction | RE | Prediction | RE | |
| 5.98 | 5.9842 | 0.07% | 5.9842 | 0.07% | 5.6074 | 6.23% | 5.5091 | 7.87% |
| 6.02 | 6.0338 | 0.23% | 6.0213 | 0.022% | 6.3361 | 5.25% | 5.5980 | 7.01% |
| 5.75 | 5.9962 | 4.28% | 5.7554 | 0.094% | 5.8454 | 1.66% | 6.2631 | 8.92% |
| 6.23 | 5.8659 | 5.85% | 6.2236 | 0.103% | 5.9702 | 4.17% | 4.7603 | 23.59% |
| 5.88 | 5.7425 | 2.34% | 5.8819 | 0.032% | 5.8382 | 0.71% | 3.8466 | 34.58% |
| Average RE | 2.55% | 0.064% | 3.60% | 16.39% | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, B.; Gao, F.; Ma, X.; Zhang, X. Intelligent Prediction of Aeroengine Wear Based on the SVR Optimized by GMPSO. Appl. Sci. 2021, 11, 10592. https://doi.org/10.3390/app112210592
Zheng B, Gao F, Ma X, Zhang X. Intelligent Prediction of Aeroengine Wear Based on the SVR Optimized by GMPSO. Applied Sciences. 2021; 11(22):10592. https://doi.org/10.3390/app112210592
Chicago/Turabian StyleZheng, Bo, Feng Gao, Xin Ma, and Xiaoqiang Zhang. 2021. "Intelligent Prediction of Aeroengine Wear Based on the SVR Optimized by GMPSO" Applied Sciences 11, no. 22: 10592. https://doi.org/10.3390/app112210592
APA StyleZheng, B., Gao, F., Ma, X., & Zhang, X. (2021). Intelligent Prediction of Aeroengine Wear Based on the SVR Optimized by GMPSO. Applied Sciences, 11(22), 10592. https://doi.org/10.3390/app112210592






