Using Optimisation Meta-Heuristics for the Roughness Estimation Problem in River Flow Analysis
Abstract
:1. Introduction
- the ‘physical’ parameters are those describing the properties of materials—these are usually constant values;
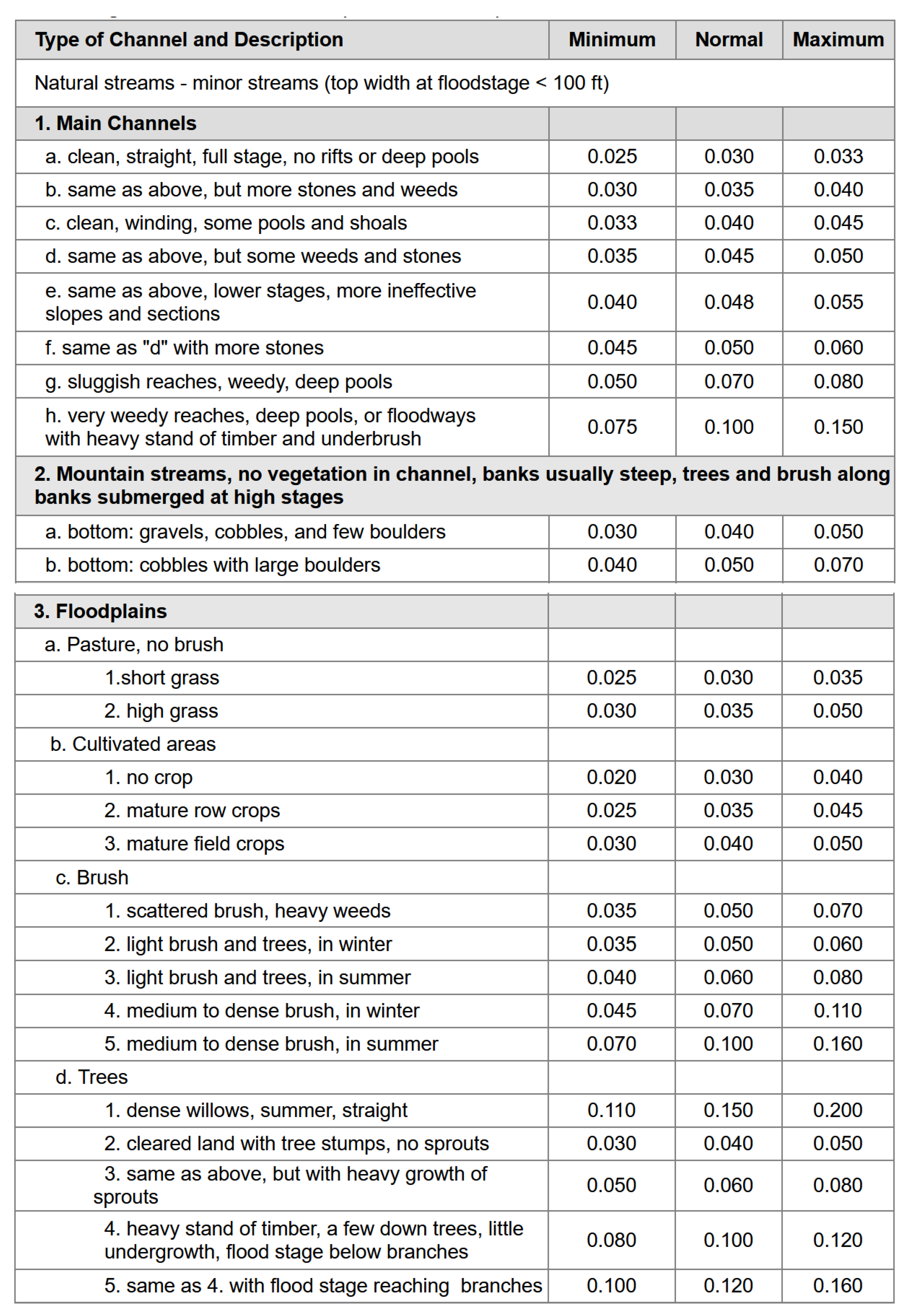
- the empirical parameters are those added to deal with the complexity and the variability of specific aspects characterising hydraulic properties of a channel. Amongst these, the so-called ‘roughness’ coefficient, which indicates the resistance to flood flows in both channels and flood plains, is one of the most important. Other empirical parameters are the vegetation, the alignment of the channel and its irregularities, shape and size, stage and discharge, suspended sediment load and bed sediment loads. These have to be calculated mathematically through analytical models [16].
- Section 2 introduces the designed objective function which allows formulating the coefficient estimation as an optimisation problem;
- Section 3 describes the hydrodynamic computational model which is used as a blackbox component inside the designed objective function;
- Section 4 briefly recalls the five meta-heuristic considered in this work to optimise the proposed objective function;
- Section 5 presents two case studies and describes the set-up of the conducted experiments;
- Section 6 analyses the experimental results;
- Finally, conclusions are drawn in Section 7 where future lines of research are also depicted.
2. Formulating the Optimisation Problem
- (i)
- a candidate solution , having the previously described structure, must be produced and fed to the HEC-RAS simulator;
- (ii)
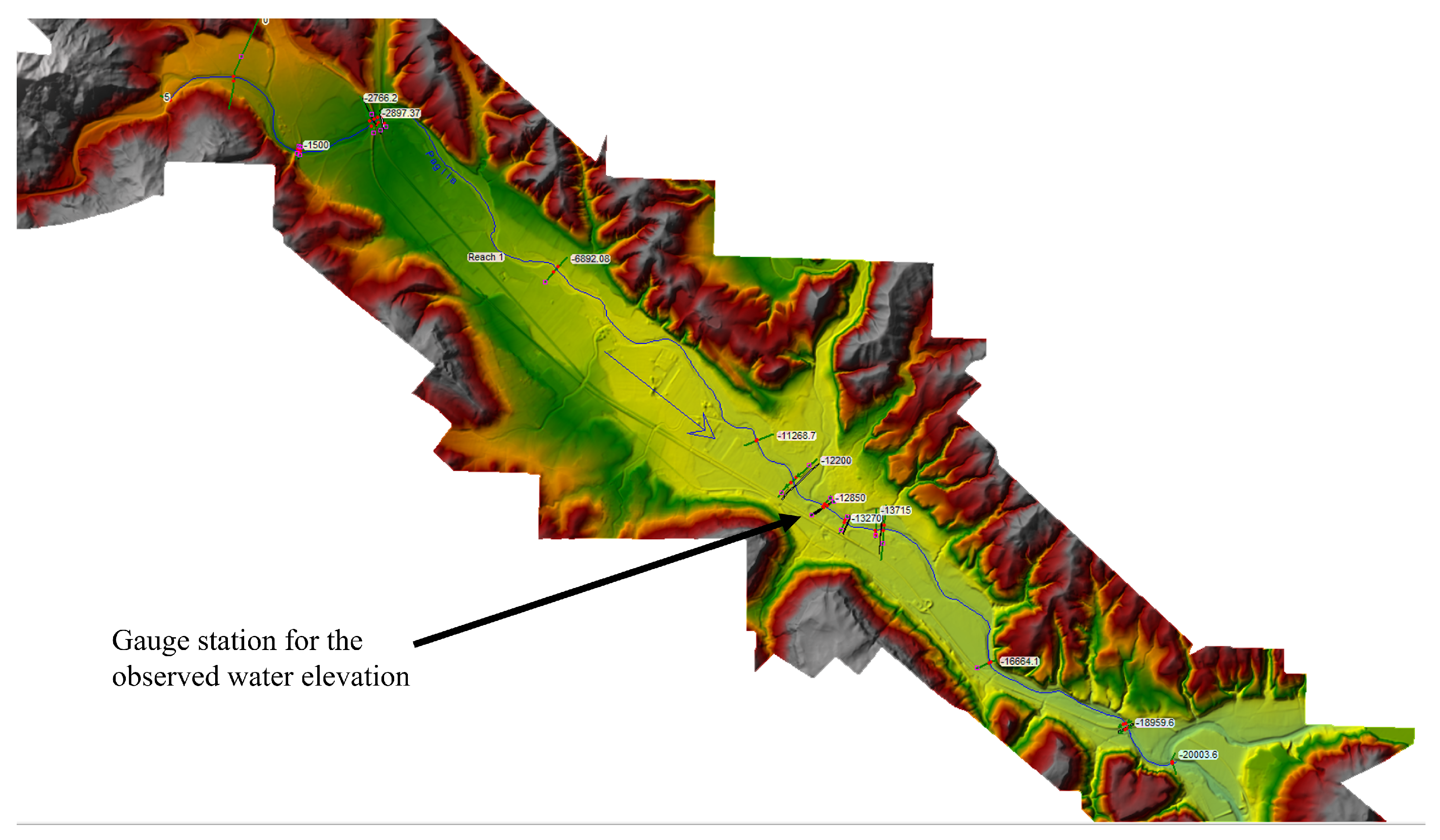
- HEC-RAS is set with Manning’s coefficients from the candidate solution and a simulation is run to obtain the expected depth of the water at the gauge station deployed along the river—this value is referred here to as ;
- (iii)
- the absolute difference between , i.e., the simulated depth, and , i.e., the true depth observed at the gauge station, is calculated to obtain the loss score as shown below in Equation (1):
3. Hydrodynamic River Flows Analysis
3.1. Mathematical Formulation and Software Settings for Implementing the Model
- z indicates the bottom elevation of the river;
- h is the river’s water depth;
- v is the water’s mean velocity in the channel cross-section at hand;
- the so-called St. Venant coefficient is a correction factor that takes into consideration undesired effects due to e.g., non-uniformity of the water’s velocity in the considered profile of the river;
- g is the universal gravitational constant.
4. The Employed Optimisation Methods
4.1. (1 + 1)-ES
4.2. Differential Evolution
4.3. Covariance Matrix Adaptation Evolution Strategy
4.4. Particle Swarm Optimisation
4.5. Bayesian Optimisation
5. Experimental Set-up
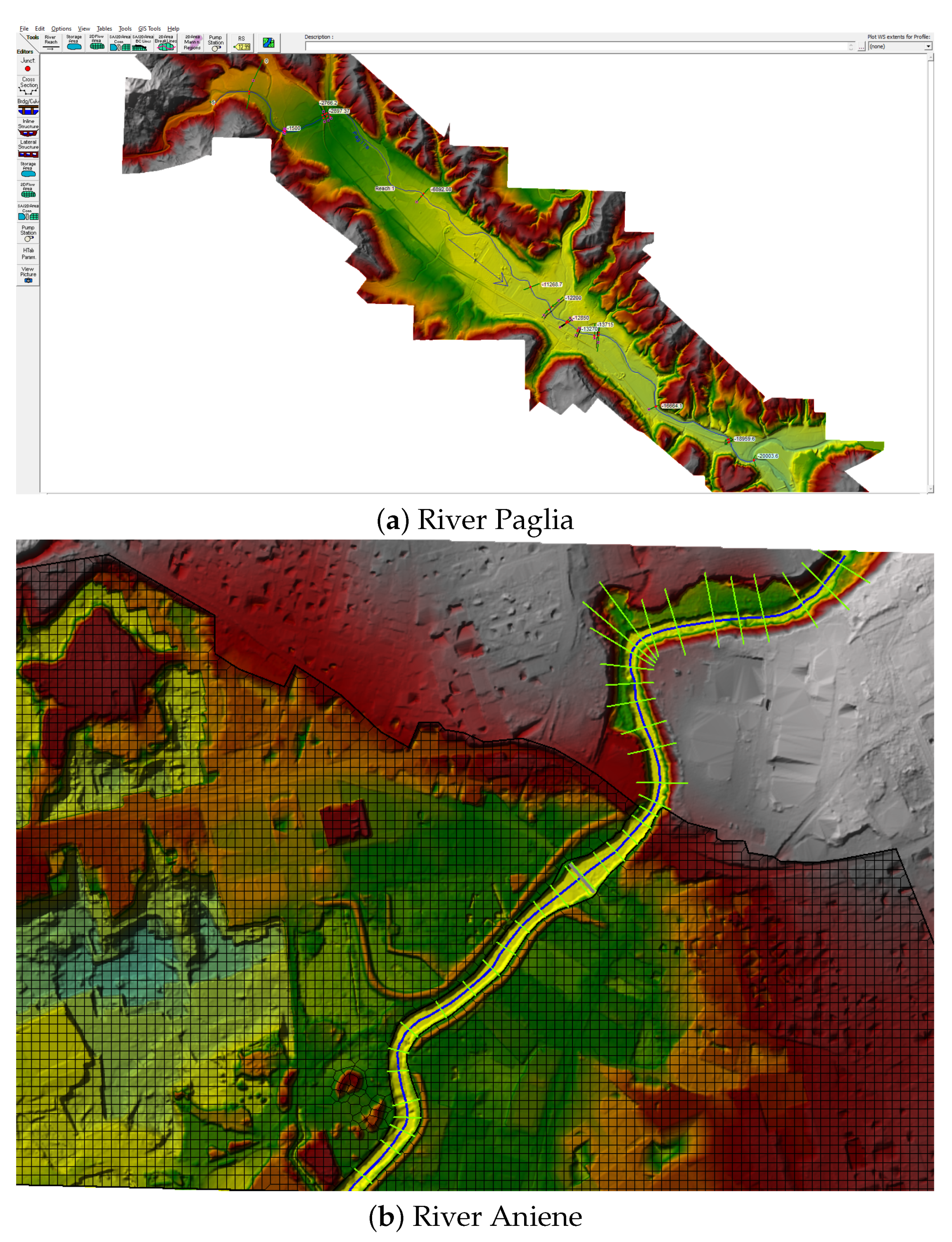
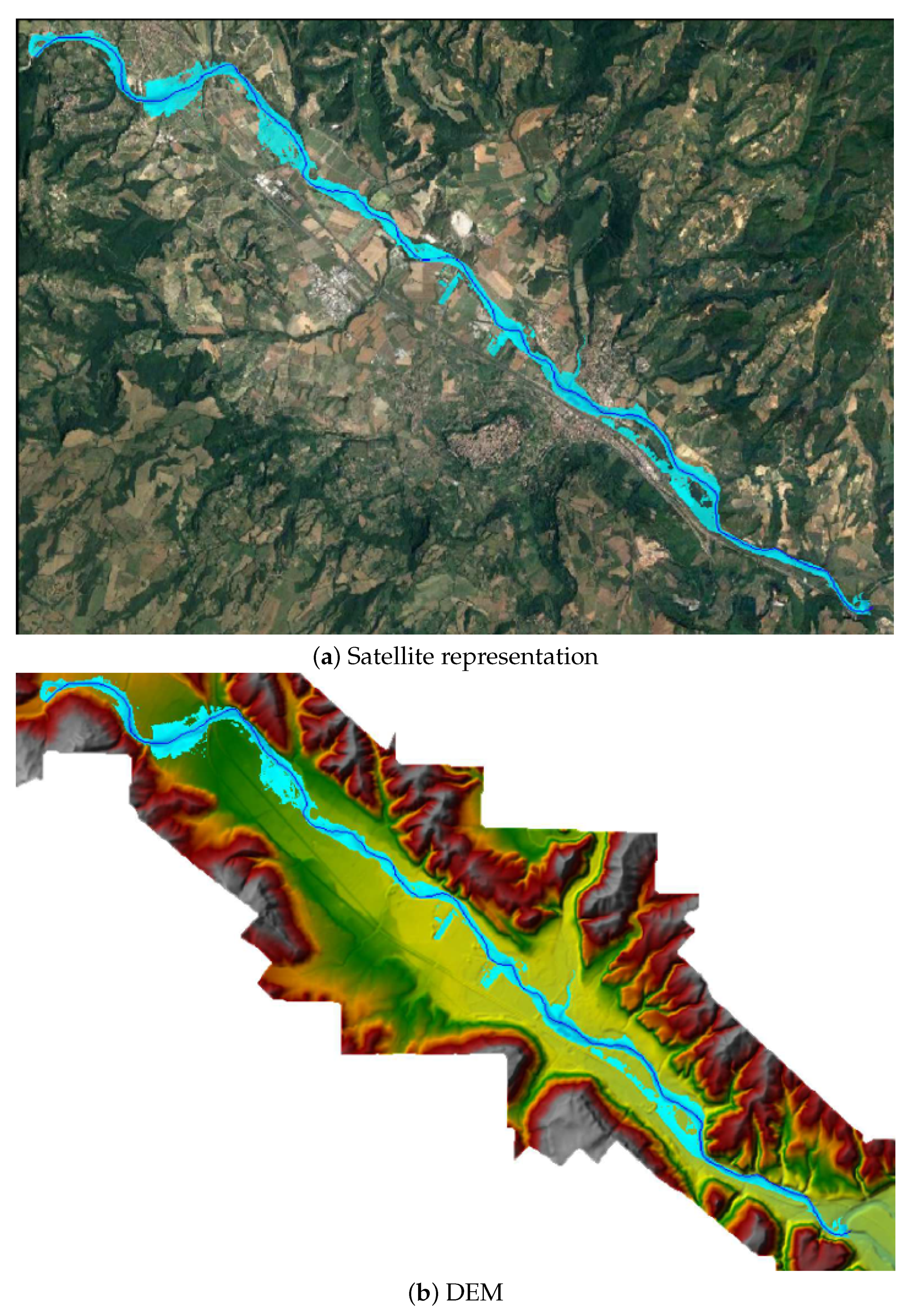
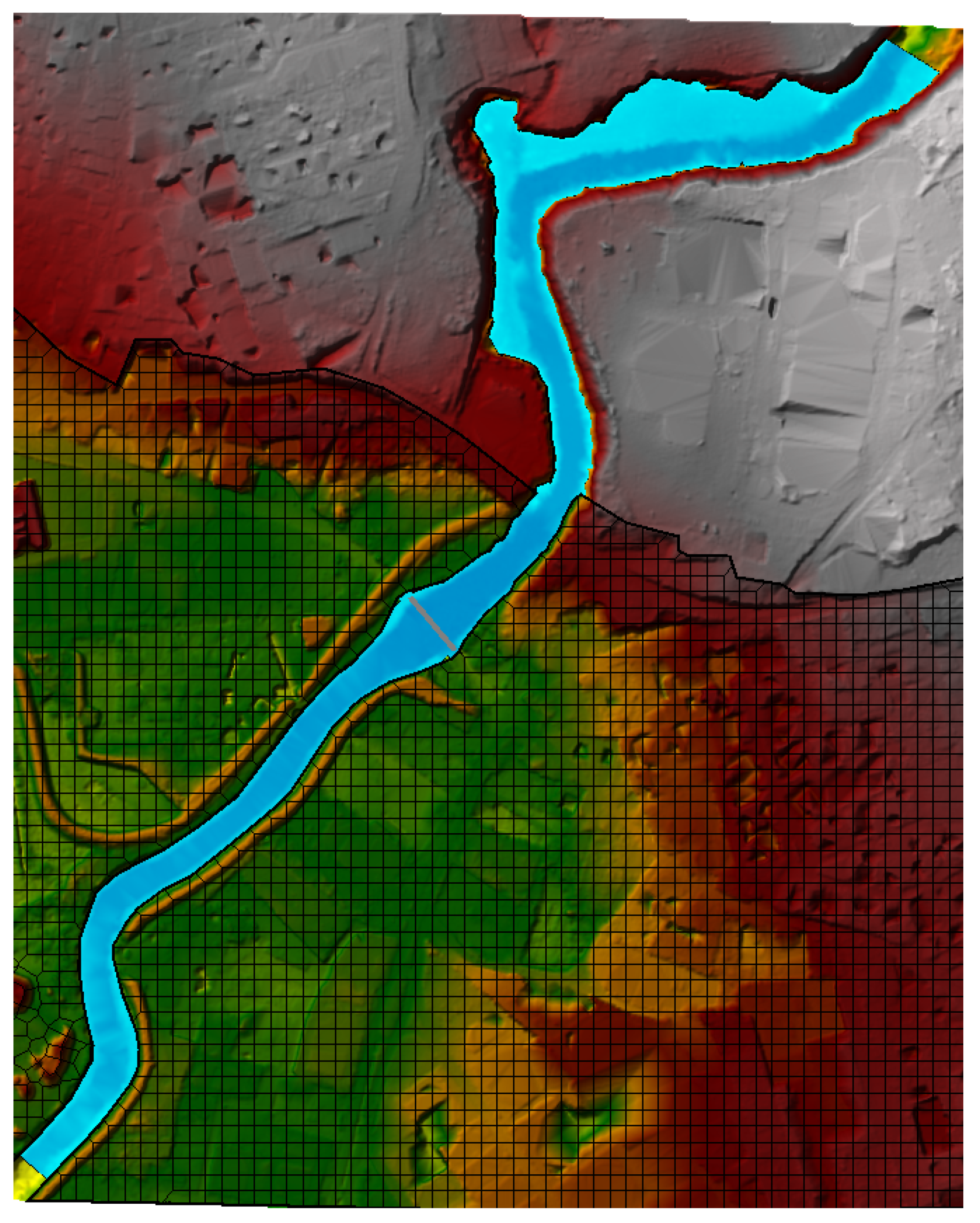
5.1. Case Study 1—The River Paglia
5.2. Case Study 2—The River Aniene
6. Experimental Results
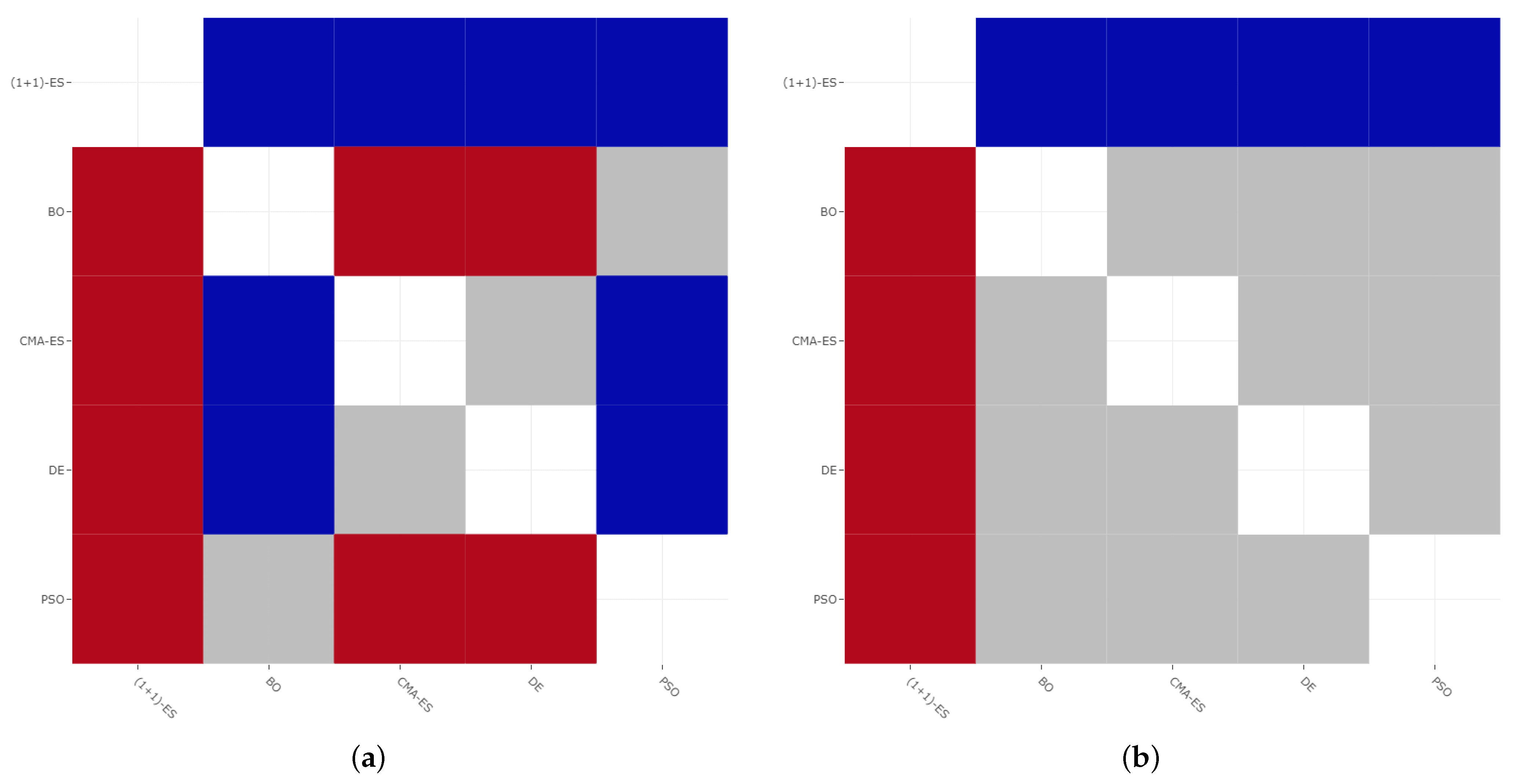
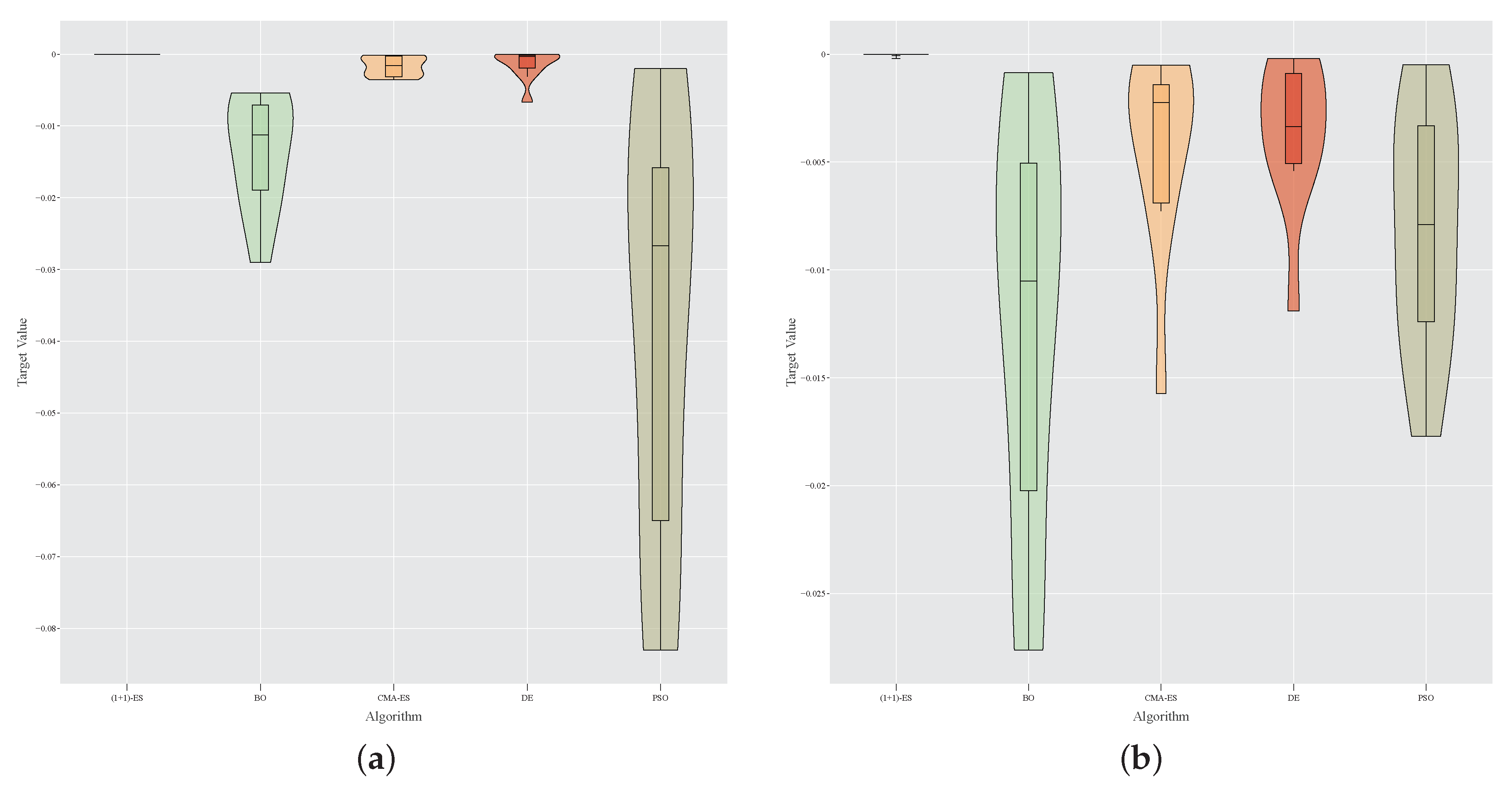
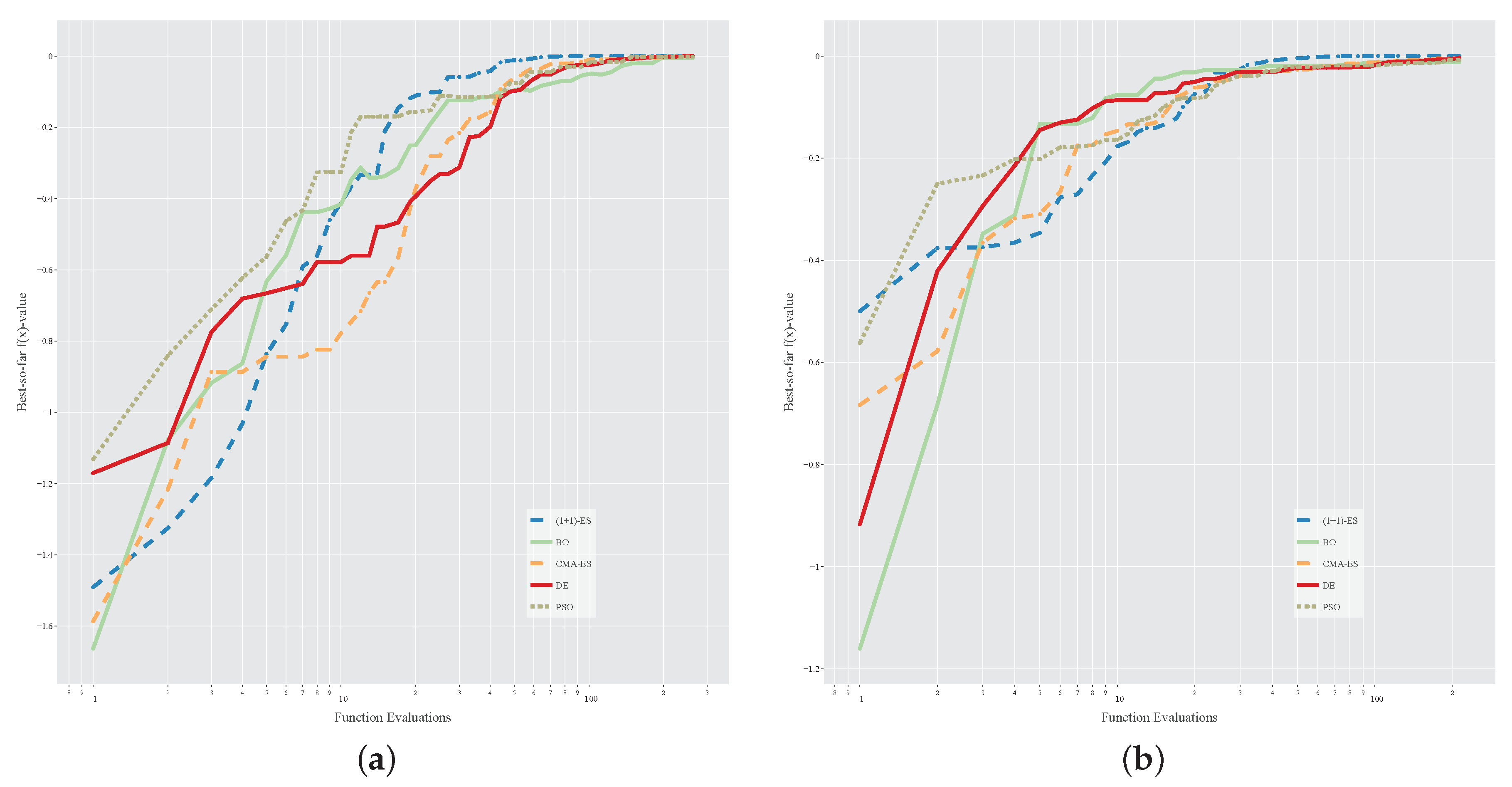
- DE and CMA-ES look, in general, to be preferable to PSO and BO;
- BO is not competitive enough in both case studies and, in particular, its effectiveness deteriorates in the larger case study, probably because BO is not good enough for large dimensionalities (indeed, it is generally used to tune the few hyper-parameters of machine learning models [30]);
- regarding robustness, (1 + 1)-ES is clearly the most robust algorithm;
- the high variance for the results of the PSO algorithm may indicate the presence of a considerable amount of local optima in the fitness landscape, given that PSO is prone to prematurely converge to local optima [56];
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ortigara, A.; Kay, M.; Uhlenbrook, S. A Review of the SDG 6 Synthesis Report 2018 from an Education, Training, and Research Perspective. Water 2018, 10, 1353. [Google Scholar] [CrossRef] [Green Version]
- Koskinen, K.T.; Leino, T.; Riipinen, H. Sustainable development with water hydraulics-possibilities and challenges. Proc. JFPS Int. Symp. Fluid Power 2008, 2008, 11–18. [Google Scholar] [CrossRef] [Green Version]
- Yusof, A.A.; Wasbari, F.; Zakaria, M.S.; Ibrahim, M.Q. Slip flow coefficient analysis in water hydraulics gear pump for environmental friendly application. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazan, Russia, 25–27 September 2013; Volume 50, p. 012016. [Google Scholar]
- Martınez-Vilalta, J.; Piñol, J.; Beven, K. A hydraulic model to predict drought-induced mortality in woody plants: An application to climate change in the Mediterranean. Ecol. Model. 2002, 155, 127–147. [Google Scholar] [CrossRef]
- Zischg, A.P.; Mosimann, M.; Bernet, D.B.; Röthlisberger, V. Validation of 2D flood models with insurance claims. J. Hydrol. 2018, 557, 350–361. [Google Scholar] [CrossRef] [Green Version]
- Kachiashvili, K.; Melikdzhanian, D. Software realization problems of mathematical models of pollutants transport in rivers. Adv. Eng. Softw. 2009, 40, 1063–1073. [Google Scholar] [CrossRef]
- Pinar, E.; Paydas, K.; Seckin, G.; Akilli, H.; Sahin, B.; Cobaner, M.; Kocaman, S.; Atakan Akar, M. Artificial neural network approaches for prediction of backwater through arched bridge constrictions. Adv. Eng. Softw. 2010, 41, 627–635. [Google Scholar] [CrossRef]
- Di Francesco, S.; Biscarini, C.; Manciola, P. Numerical simulation of water free-surface flows through a front-tracking lattice Boltzmann approach. J. Hydroinform. 2015, 17, 1–6. [Google Scholar] [CrossRef]
- Di Francesco, S.; Biscarini, C.; Manciola, P. Characterization of a flood event through a sediment analysis: The Tescio River case study. Water 2016, 8, 308. [Google Scholar] [CrossRef] [Green Version]
- Shen, D.; Jia, Y.; Altinakar, M.; Bingner, R.L. GIS-based channel flow and sediment transport simulation using CCHE1D coupled with AnnAGNPS. J. Hydraul. Res. 2016, 54, 567–574. [Google Scholar] [CrossRef]
- Horritt, M.; Bates, P. Evaluation of 1D and 2D Numerical Models for Predicting River Flood Inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Violante, C.; Biscarini, C.; Esposito, E.; Molisso, F.; Porfido, S.; Sacchi, M. The consequences of hydrological events on steep coastal watersheds: The Costa d’Amalfi, eastern Tyrrhenian Sea. IAHS Publ. 2009, 327, 102. [Google Scholar]
- Drake, J.; Bradford, A.; Joy, D. Application of HEC-RAS 4.0 temperature model to estimate groundwater contributions to Swan Creek, Ontario, Canada. J. Hydrol. 2010, 389, 390–398. [Google Scholar] [CrossRef]
- Rodriguez, L.B.; Cello, P.A.; Vionnet, C.A.; Goodrich, D. Fully conservative coupling of HEC-RAS with MODFLOW to simulate stream–aquifer interactions in a drainage basin. J. Hydrol. 2008, 353, 129–142. [Google Scholar] [CrossRef]
- Xing, Y.; Shao, D.; Yang, Y.; Ma, X.; Zhang, S. Influence and interactions of input factors in urban flood inundation modeling: An examination with variance-based global sensitivity analysis. J. Hydrol. 2021, 600, 126524. [Google Scholar] [CrossRef]
- Atanov, G.A.; Evseeva, E.G.; Meselhe, E.A. Estimation of Roughness Profile in Trapezoidal Open Channels. J. Hydraul. Eng. 1999, 125, 309–312. [Google Scholar] [CrossRef]
- Dooge, J.C. The Manning formula in context. In Channel Flow Resistance: Centennial of Manning’s Formula; Water Resources Publications, LLC.: Highlands Ranch, CO, USA, 1992; pp. 136–185. [Google Scholar]
- Perry, B. Open-Channel Hydraulics. Science 1960, 131, 1215. [Google Scholar] [CrossRef]
- Becker, L.; Yeh, W.W.G. Identification of parameters in unsteady open channel flows. Water Resour. Res. 1972, 8, 956–965. [Google Scholar] [CrossRef]
- Di Francesco, S.; Zarghami, A.; Biscarini, C.; Manciola, P. Wall roughness effect in the lattice Boltzmann method. In Proceedings of the AIP Conference. American Institute of Physics, 11th International Conference of Numerical Analysis and Applied Mathematics-ICNAAM, Rhodes, Greece, 21–27 September 2013; Volume 1558, pp. 1677–1680. [Google Scholar]
- Kiczko, A.; Romanowicz, R.J.; Napiorkowski, J.J. A Study of Flow Conditions Aimed at Preserving Valuable Wetland Areas in the Upper Narew Valley Using GSA-GLUE Methodology. In Environmental Informatics and Systems Research; Hryniewicz, O., Studzinski, J., Romaniuk, M., Eds.; Shaker Verlag: Aachen, Germany, 2007. [Google Scholar]
- Romanowicz, R.; Kiczko, A.; Napiórkowski, J. Stochastic transfer function model applied to combined reservoir management and flow routing. Hydrol. Sci. J.—J. Des Sci. Hydrol. 2010, 55, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.; Manning, L.; Hankin, R. Bayesian calibration of a flood inundation model using spatial data. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Romanowicz, R.; Beven, K. Dynamic real-time prediction of flood inundation probabilities. Hydrol. Sci. J. 1998, 43, 181–196. [Google Scholar] [CrossRef] [Green Version]
- Becker, L.; Yeh, W.W.G. Identification of multiple reach channel parameters. Water Resour. Res. 1973, 9, 326–335. [Google Scholar] [CrossRef]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computation; Springer: Berlin, Germany, 2003. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm Intelligence. In Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies; Springer: Boston, MA, USA, 2006; pp. 187–219. [Google Scholar] [CrossRef]
- Caraffini, F.; Santucci, V.; Milani, A. Evolutionary Computation & Swarm Intelligence; MDPI: Basel, Switzerland, 2020. [Google Scholar]
- Frazier, P.I. A tutorial on bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Yeoh, J.M.; Caraffini, F.; Homapour, E.; Santucci, V.; Milani, A. A clustering system for dynamic data streams based on metaheuristic optimisation. Mathematics 2019, 7, 1229. [Google Scholar] [CrossRef] [Green Version]
- Brunner, W.G. HEC River Analysis System (HEC-RAS); No. 147; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 1994.
- Dubin, J.R. On gradually varied flow profiles in rectangular openchannels. J. Hydraul. Res. 1999, 37, 99–106. [Google Scholar] [CrossRef]
- Beyer, H.G.; Schwefel, H.P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Caraffini, F.; Kononova, A.V.; Corne, D. Infeasibility and structural bias in differential evolution. Inf. Sci. 2019, 496, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Brabazon, A.; O’Neill, M.; McGarraghy, S. Natural Computing Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Santucci, V. Is Algebraic Differential Evolution Really a Differential Evolution Scheme? In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Krakow, Poland, 28 June–1 July 2021; pp. 9–16. [Google Scholar]
- Santucci, V.; Baioletti, M.; Di Bari, G.; Milani, A. A Binary Algebraic Differential Evolution for the MultiDimensional Two-Way Number Partitioning Problem. In Proceedings of the 2019 European Conference on Evolutionary Computation in Combinatorial Optimisation, Leipzig, Germany, 24–26 April 2019; pp. 17–32. [Google Scholar]
- Caraffini, F.; Neri, F. A study on rotation invariance in differential evolution. Swarm Evol. Comput. 2019, 50, 100436. [Google Scholar] [CrossRef]
- Santucci, V.; Baioletti, M.; Milani, A. An algebraic framework for swarm and evolutionary algorithms in combinatorial optimization. Swarm Evol. Comput. 2020, 55, 100673. [Google Scholar] [CrossRef]
- Santucci, V.; Baioletti, M.; Di Bari, G. An improved memetic algebraic differential evolution for solving the multidimensional two-way number partitioning problem. Expert Syst. Appl. 2021, 178, 114938. [Google Scholar] [CrossRef]
- Meunier, L.; Doerr, C.; Rapin, J.; Teytaud, O. Variance reduction for better sampling in continuous domains. In Proceedings of the 16th International Conference on Parallel Problem Solving from Nature, Leiden, The Nederlands, 5–9 September 2020; pp. 154–168. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Caraffini, F.; Neri, F.; Picinali, L. An analysis on separability for Memetic Computing automatic design. Inf. Sci. 2014, 265, 1–22. [Google Scholar] [CrossRef]
- Beyer, H.G.; Sendhoff, B. Covariance Matrix Adaptation Revisited—The CMSA Evolution Strategy. In Parallel Problem Solving from Nature—PPSN X; Rudolph, G., Jansen, T., Beume, N., Lucas, S., Poloni, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 123–132. [Google Scholar] [CrossRef]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:cs.LG/1604.00772. [Google Scholar]
- Rapin, J.; Teytaud, O. Nevergrad—A Gradient-Free Optimization Platform. 2018. Available online: https://GitHub.com/FacebookResearch/Nevergrad (accessed on 1 September 2021).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Santucci, V.; Milani, A.; Caraffini, F. An optimisation-driven prediction method for automated diagnosis and prognosis. Mathematics 2019, 7, 1051. [Google Scholar] [CrossRef] [Green Version]
- Rapin, J.; Bennet, P.; Centeno, E.; Haziza, D.; Moreau, A.; Teytaud, O. Open source evolutionary structured optimization. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancun, Mexico, 8–12 July 2020; pp. 1599–1607. [Google Scholar]
- Gray, D.N.; Hotchkiss, J.; LaForge, S.; Shalit, A.; Weinberg, T. Modern languages and Microsoft’s component object model. Comm. ACM 1998, 41, 55–65. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 751. [Google Scholar]
- Kim, J.; Scott, C.D. Robust kernel density estimation. J. Mach. Learn. Res. 2012, 13, 2529–2565. [Google Scholar]
- Larsen, R.B.; Jouffroy, J.; Lassen, B. On the premature convergence of particle swarm optimization. In Proceedings of the 2016 European Control Conference, Aalborg, Denmark, 29 June–1 July 2016; pp. 1922–1927. [Google Scholar]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Chhantyal, K.; Hoang, M.; Viumdal, H.; Mylvaganam, S. Flow Rate Estimation using Dynamic Artificial Neural Networks with Ultrasonic Level Measurements. In Proceedings of the 9th EUROSIM Congress on Modelling and Simulation, Oulu, Finland, 12–16 September 2016. [Google Scholar] [CrossRef] [Green Version]

| Algorithm | Final Fitness Values for the River Paglia | |||
|---|---|---|---|---|
| Average | Minimum | Maximum | St.Dev. | |
| (1 + 1)-ES | <10 | 0 | 0.00005 | <10 |
| DE | 0.00147 | 0.00004 | 0.00665 | 0.00211 |
| CMA-ES | 0.00167 | 0.00013 | 0.00355 | 0.00139 |
| BO | 0.01364 | 0.00538 | 0.02898 | 0.00807 |
| PSO | 0.03719 | 0.00199 | 0.08304 | 0.03013 |
| Std Method | 1.63000 | |||
| Algorithm | Final Fitness Values for the River Aniene | |||
|---|---|---|---|---|
| Average | Minimum | Maximum | St.Dev. | |
| (1 + 1)-ES | 0 | 0.00021 | ||
| DE | 0.00362 | 0.00020 | 0.01190 | 0.00333 |
| CMA-ES | 0.00431 | 0.00051 | 0.01572 | 0.00442 |
| PSO | 0.00815 | 0.00048 | 0.01770 | 0.00532 |
| BO | 0.01212 | 0.00085 | 0.02762 | 0.00914 |
| Std Method | 1.78000 | |||
| Cross Section | Std Dev. of the Manning’s Values for River Paglia | ||
|---|---|---|---|
| Left Channel | Main Channel | Right Channel | |
| 1 | 0.007826 | 0.007999 | 0.009895 |
| 5 | 0.008051 | 0.007276 | 0.008452 |
| 10 | 0.007449 | 0.008903 | 0.006296 |
| 15 | 0.003794 | 0.008512 | 0.008731 |
| 20 | 0.006102 | 0.008623 | 0.008709 |
| Cross Section | Std Dev. of the Manning’s Values for River Aniene | ||
|---|---|---|---|
| Left Channel | Main Channel | Right Channel | |
| 1 | 0.006855 | 0.006383 | 0.006739 |
| 10 | 0.007071 | 0.006672 | 0.006709 |
| 20 | 0.006489 | 0.006073 | 0.006354 |
| 30 | 0.006764 | 0.006162 | 0.006629 |
| 40 | 0.008475 | 0.005951 | 0.007752 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agresta, A.; Baioletti, M.; Biscarini, C.; Caraffini, F.; Milani, A.; Santucci, V. Using Optimisation Meta-Heuristics for the Roughness Estimation Problem in River Flow Analysis. Appl. Sci. 2021, 11, 10575. https://doi.org/10.3390/app112210575
Agresta A, Baioletti M, Biscarini C, Caraffini F, Milani A, Santucci V. Using Optimisation Meta-Heuristics for the Roughness Estimation Problem in River Flow Analysis. Applied Sciences. 2021; 11(22):10575. https://doi.org/10.3390/app112210575
Chicago/Turabian StyleAgresta, Antonio, Marco Baioletti, Chiara Biscarini, Fabio Caraffini, Alfredo Milani, and Valentino Santucci. 2021. "Using Optimisation Meta-Heuristics for the Roughness Estimation Problem in River Flow Analysis" Applied Sciences 11, no. 22: 10575. https://doi.org/10.3390/app112210575
APA StyleAgresta, A., Baioletti, M., Biscarini, C., Caraffini, F., Milani, A., & Santucci, V. (2021). Using Optimisation Meta-Heuristics for the Roughness Estimation Problem in River Flow Analysis. Applied Sciences, 11(22), 10575. https://doi.org/10.3390/app112210575










