Anomaly Detection in Automotive Industry Using Clustering Methods—A Case Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Clustering Algorithms
2.1. K-Means
2.2. K-Medoids
2.3. Fuzzy C-Means (FCM)
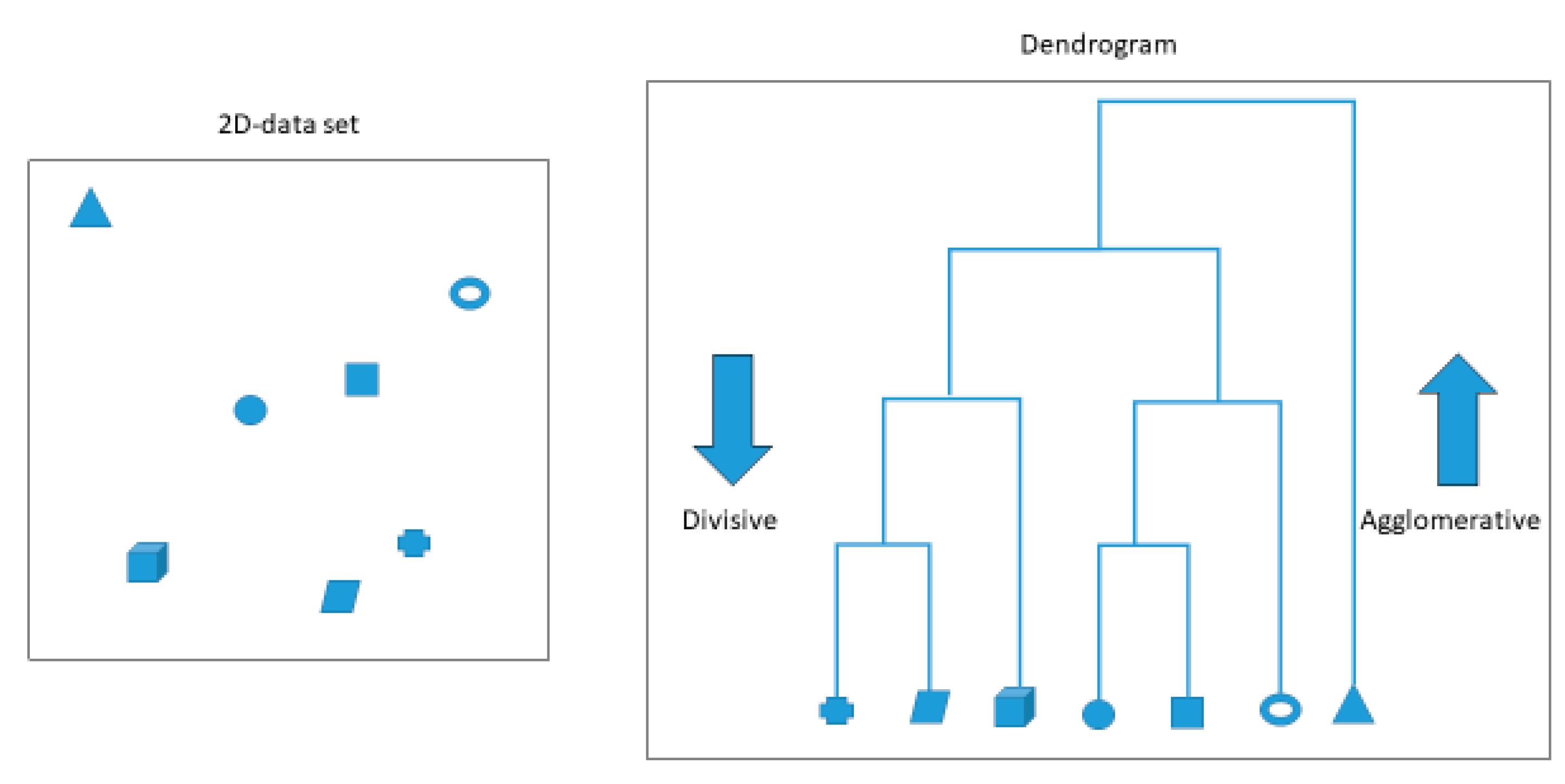
2.4. Hierarchical Clustering
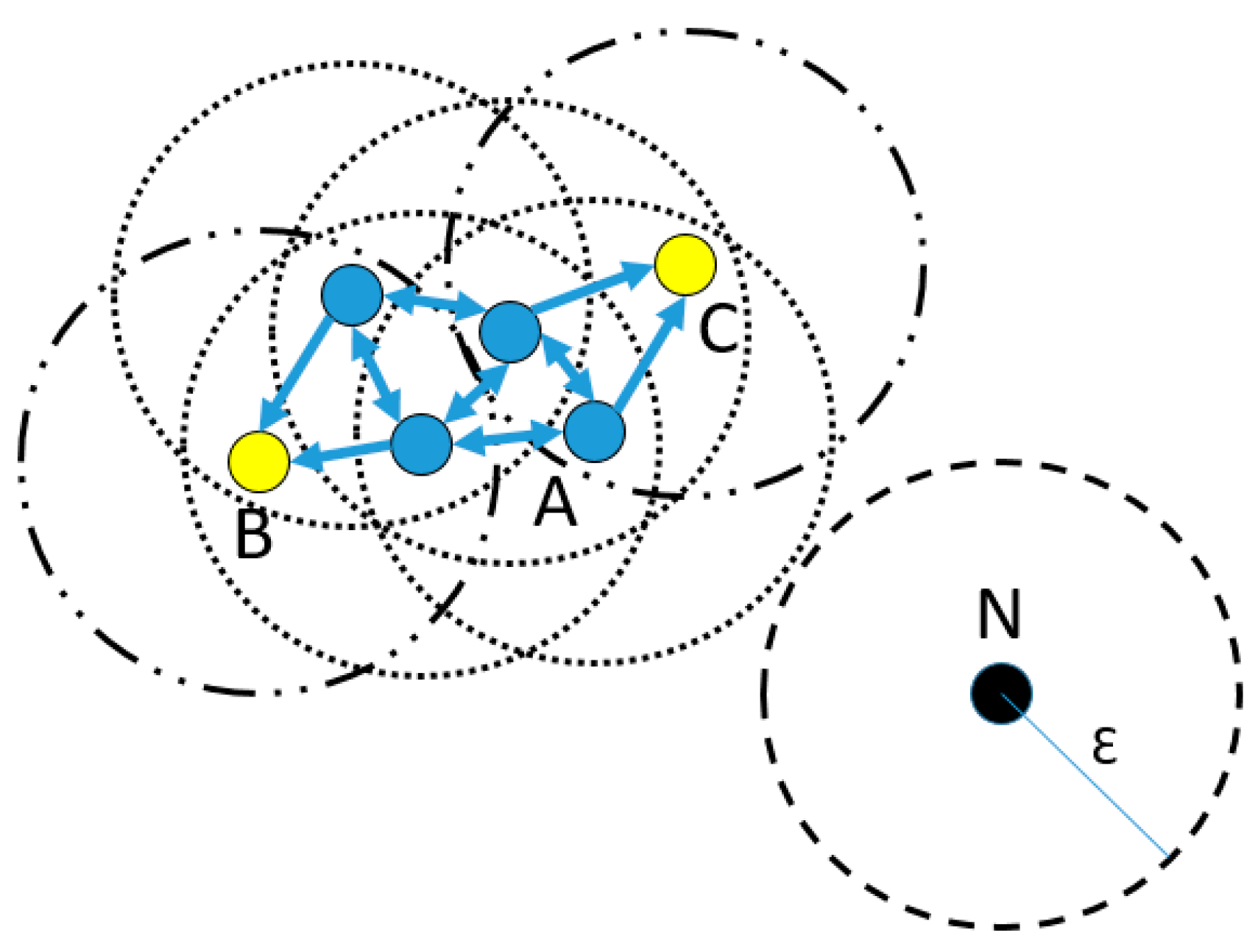
2.5. Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
2.6. Self Organizing Maps (SOM)
2.7. Particle Swarm Optimization (PSO)
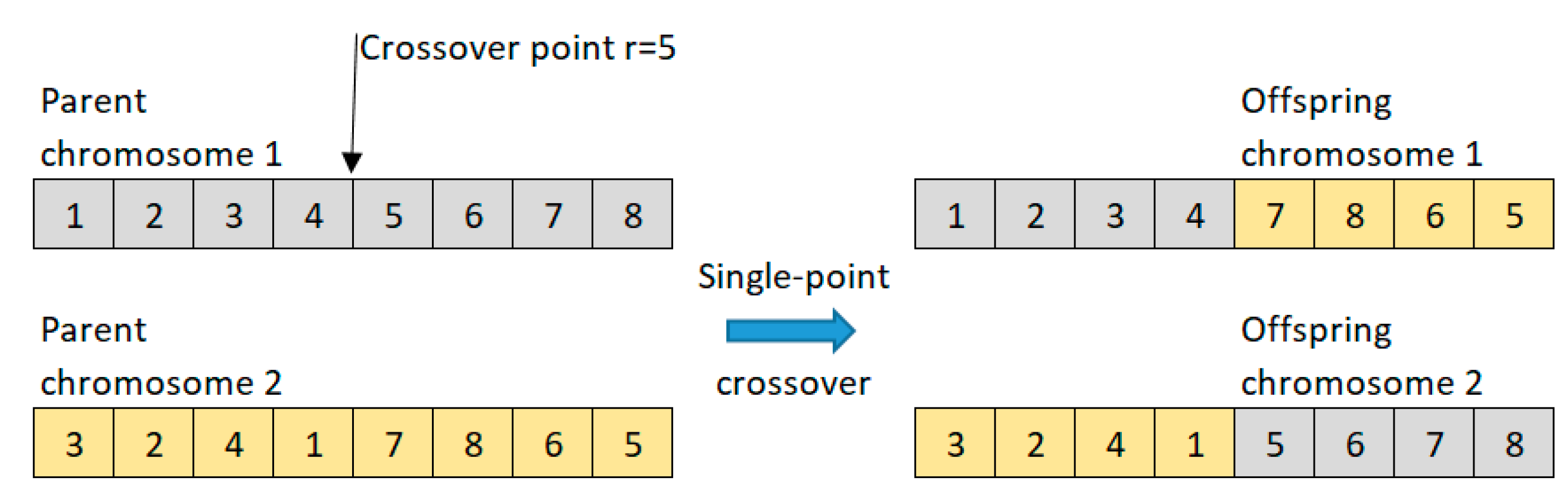
2.8. Genetic Algorithm (GA)
2.9. Differential Evolution (DE)
3. Clustering Metrics
3.1. Sum of Squared Errors (SSE)
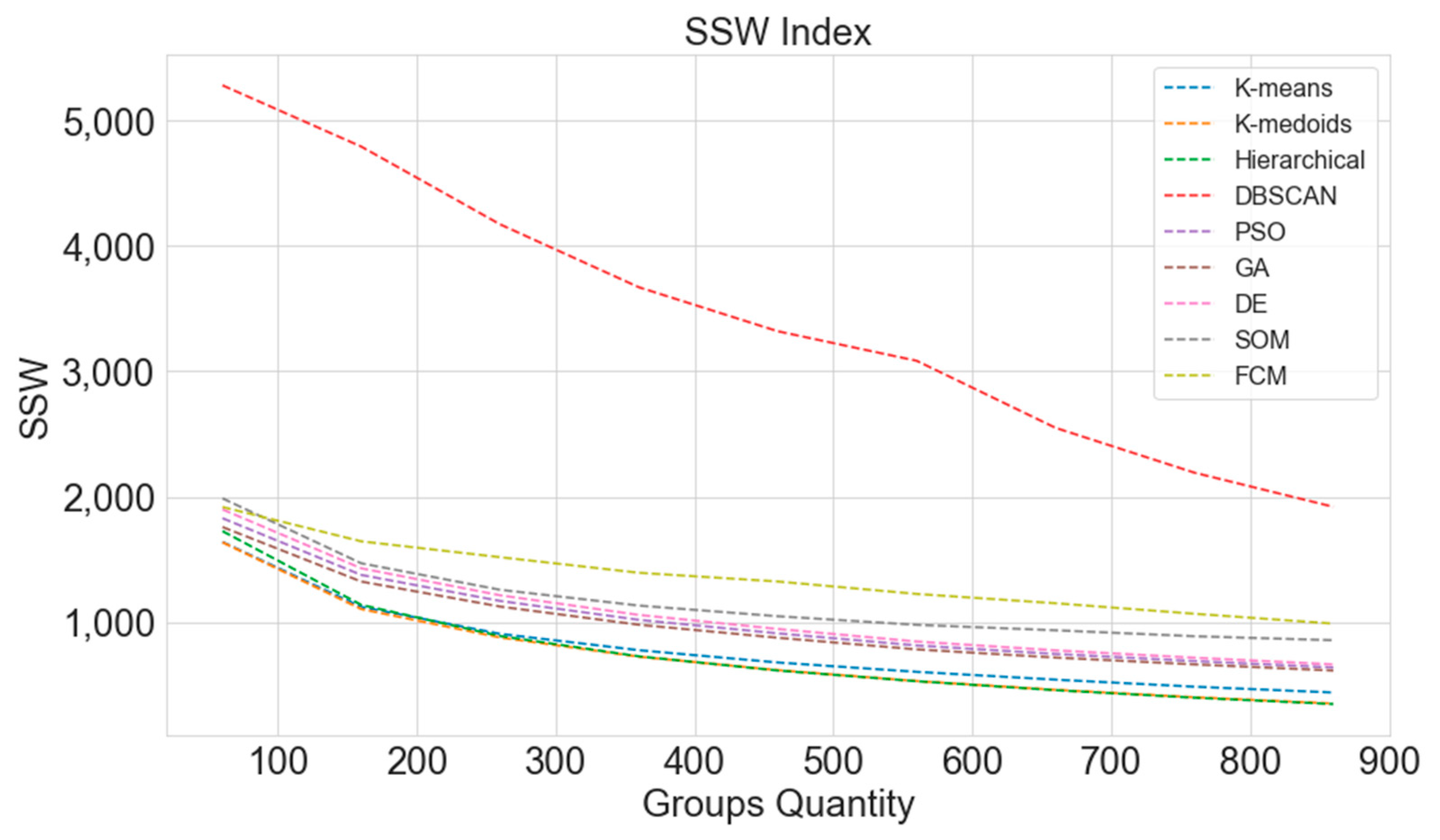
3.2. Sum of Squares within Clusters (SSW)
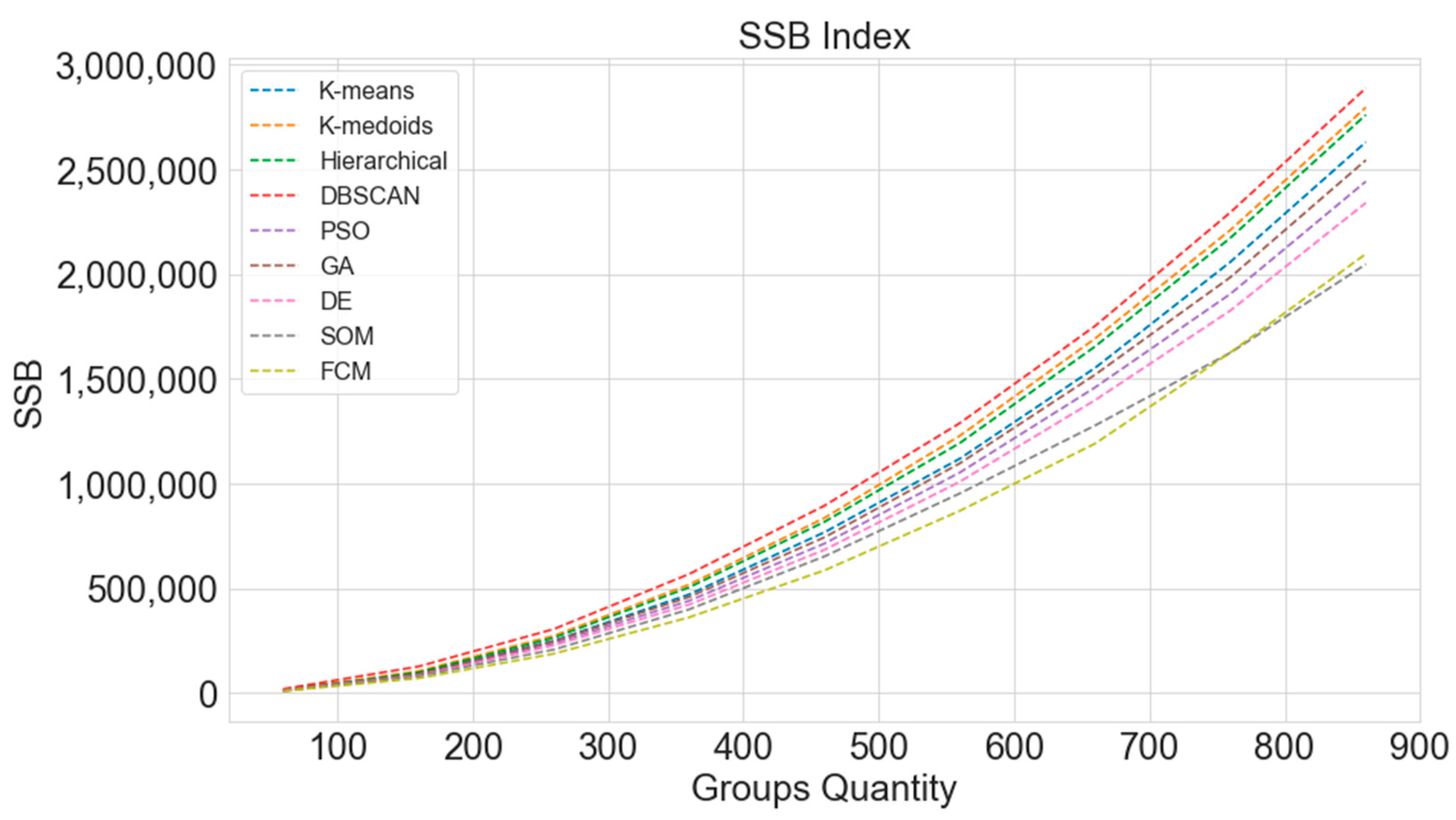
3.3. Sum of Squares between Clusters (SSB)
3.4. Calinski-Harabasz Index (CH)
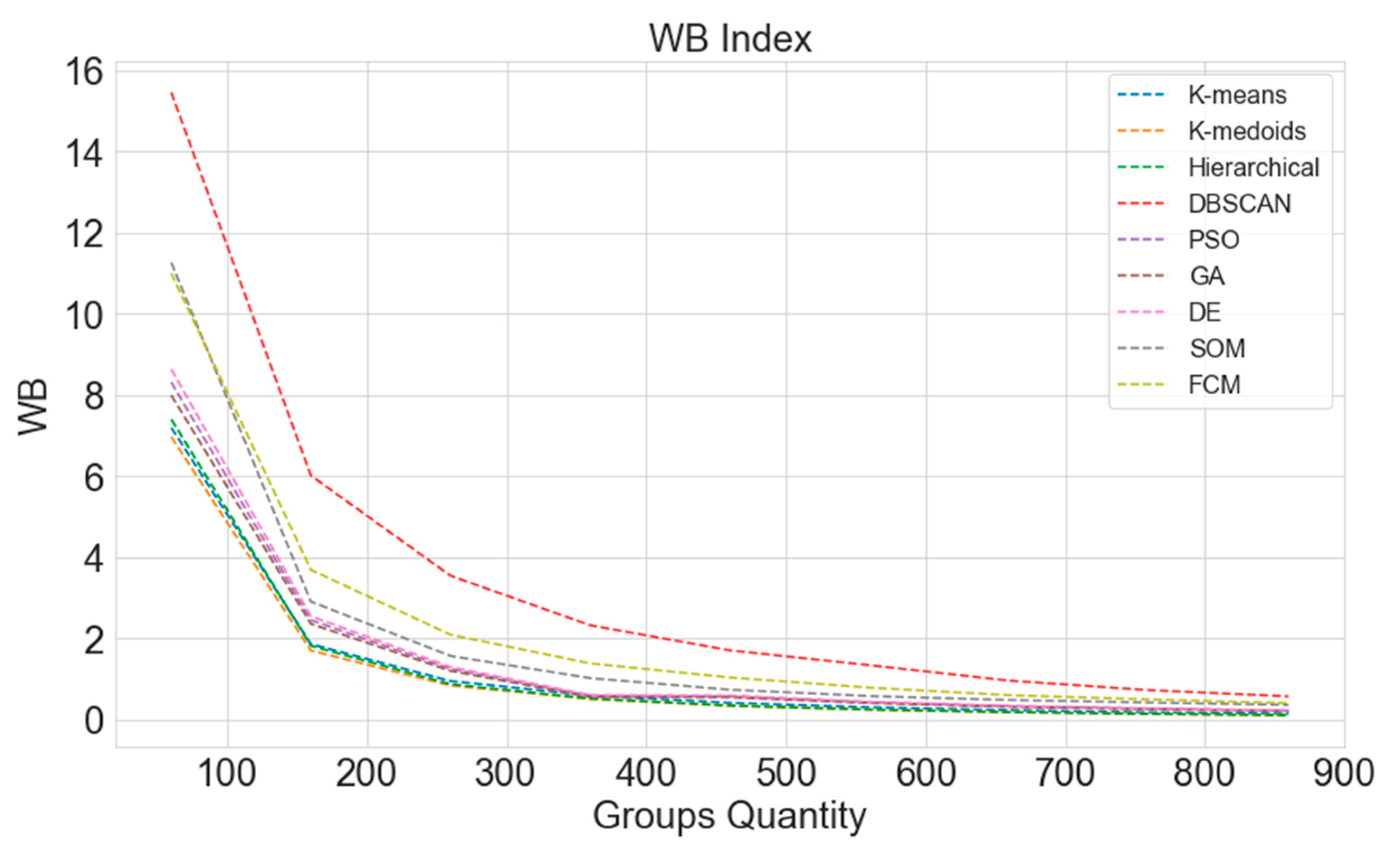
3.5. WB Index
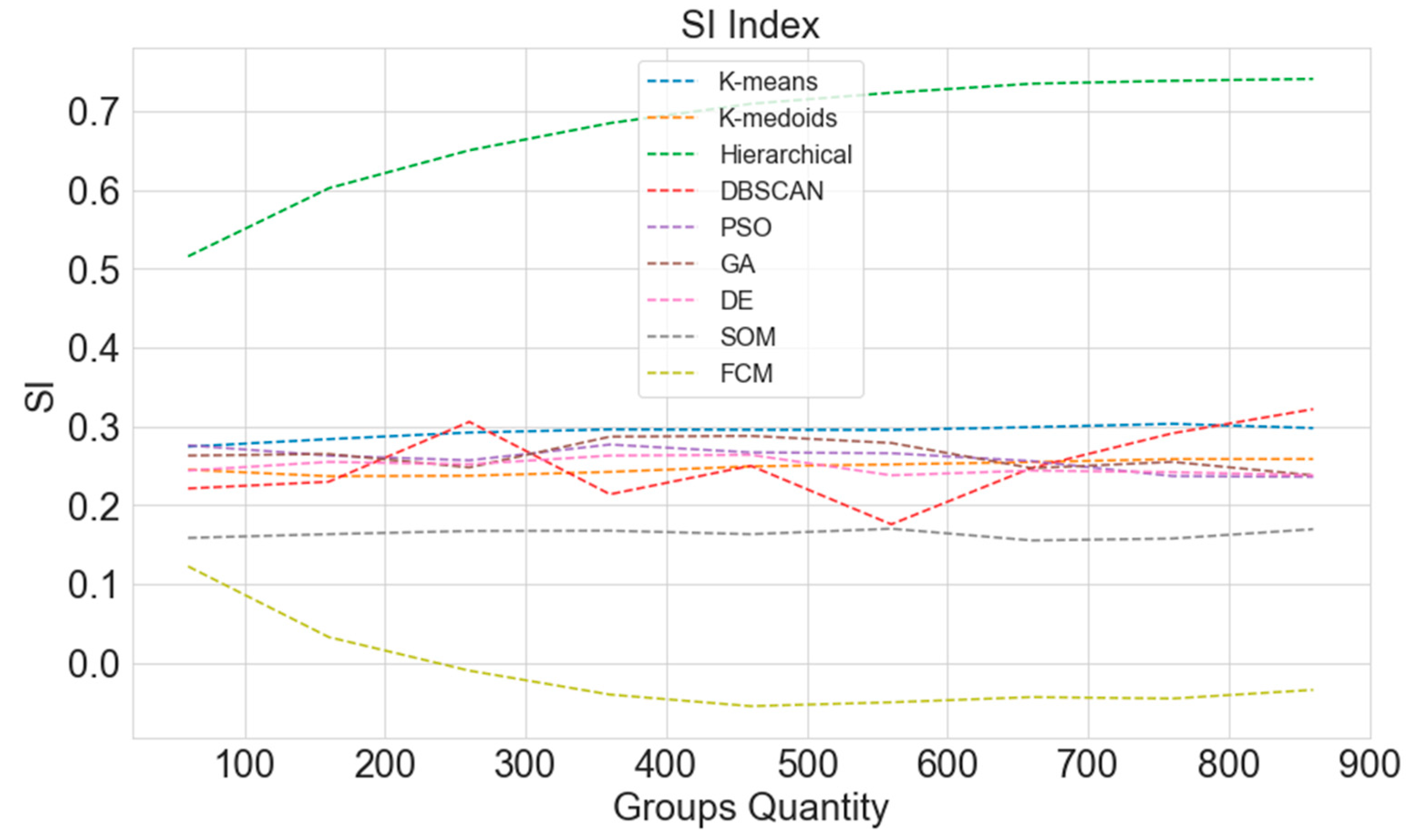
3.6. Silhouette Index (SI)
4. Case Study, Results, and Discussions
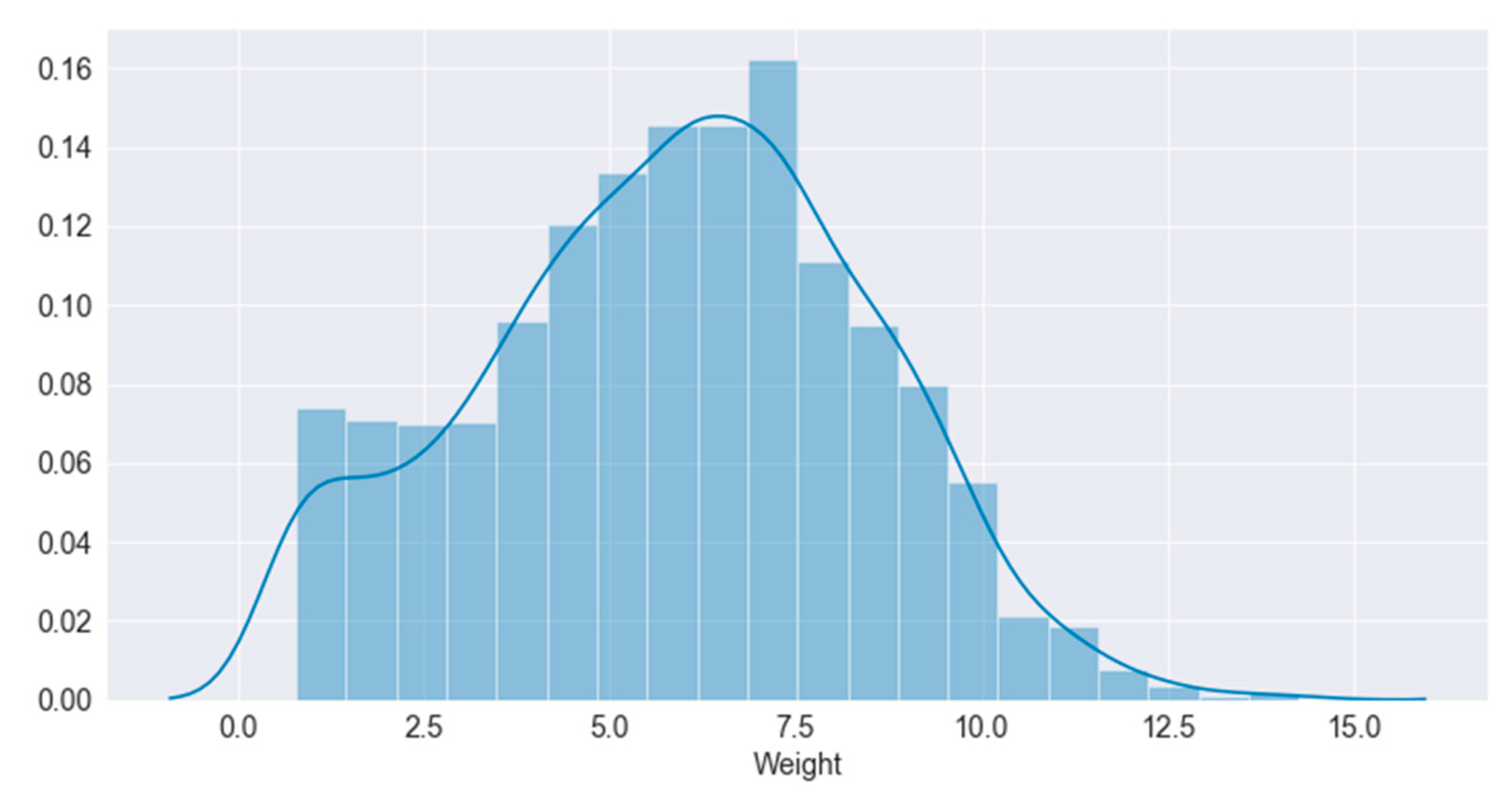
4.1. Industry Data
4.2. Pre Processing Stages
- (a)
- Four dimensions sepal length, sepal width, petal length, and petal width without PCA application;
- (b)
- PCA application using only the first principal components;
- (c)
- PCA application using only the first and second principal components.
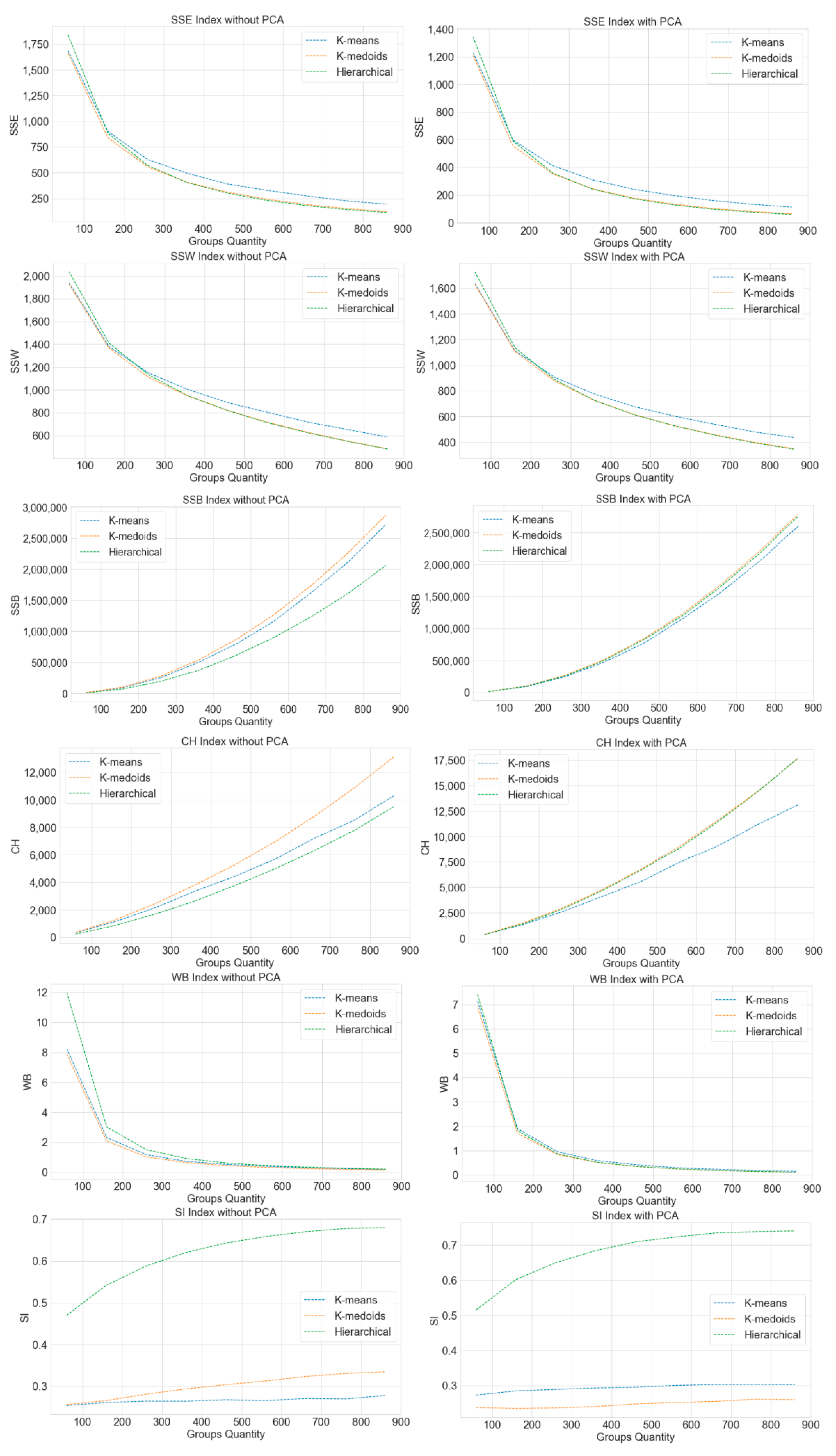
4.3. Computational Results
4.4. PCA Assessment for the Best Algorithms
4.5. Company Feedback on Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Holtewert, P.; Bauernhansl, T. Optimal configuration of manufacturing cells for high flexibility and cost reduction by component substitution. Procedia CIRP 2016, 41, 111–116. [Google Scholar] [CrossRef]
- Krappe, H.; Rogalski, S.; Sander, M. Challenges for handling flexibility in the change management process of manufacturing systems. In Proceedings of the 2006 IEEE International Conference on Automation Science and Engineering, Shanghai, China, 8–10 October 2006; pp. 551–557. [Google Scholar]
- Argoneto, P.; Renna, P. Capacity sharing in a network of enterprises using the Gale–Shapley model. Int. J. Adv. Manuf. Technol. 2013, 69, 1907–1916. [Google Scholar] [CrossRef]
- Hansen, J.O.; Kampker, A.; Triebs, J. Approaches for flexibility in the future automobile body shop: Results of a comprehensive cross-industry study. Procedia CIRP 2018, 72, 995–1002. [Google Scholar] [CrossRef]
- Elmaraghy, H.A. Changeable and Reconfigurable Manufacturing Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gameros, A.; Lowth, S.; Axinte, D.; Nagy-Sochacki, A.; Craig, O.; Siller, H. State-of-the-art in fixture systems for the manufacture and assembly of rigid components: A review. Int. J. Mach. Tools Manuf. 2017, 123, 1–21. [Google Scholar] [CrossRef]
- Greska, W.; Franke, V.; Geiger, M. Classification problems in manufacturing of sheet metal parts. Comput. Ind. 1997, 33, 17–30. [Google Scholar] [CrossRef]
- Flath, C.M.; Stein, N. Towards a data science toolbox for industrial analytics applications. Comput. Ind. 2018, 94, 16–25. [Google Scholar] [CrossRef]
- Santos, P.; Macedo, M.; Figueiredo, E.; Santana, C.J.; Soares, F.; Siqueira, H.; Maciel, A.; Gokhale, A.; Bastos-Filho, C.J.A. Application of PSO-based clustering algorithms on educational databases. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI 2017), Arequipa, Peru, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Figueiredo, E.; Macedo, M.; Siqueira, H.V.; Santana, C.J., Jr.; Gokhale, A.; Bastos-Filho, C.J. Swarm intelligence for clustering—A systematic review with new perspectives on data mining. Eng. Appl. Artif. Intell. 2019, 82, 313–329. [Google Scholar] [CrossRef]
- Bang, S.H.; Ak, R.; Narayanan, A.; Lee, Y.T.; Cho, H. A survey on knowledge transfer for manufacturing data analytics. Comput. Ind. 2019, 104, 116–130. [Google Scholar] [CrossRef]
- Cohen, S.; de Castro, L. Data clustering with particle swarms. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1792–1798. [Google Scholar]
- Alam, S.; Dobbie, G.; Koh, Y.S.; Riddle, P.; Rehman, S.U. Research on particle swarm optimization based clustering: A systematic review of literature and techniques. Swarm Evol. Comput. 2014, 17, 1–13. [Google Scholar] [CrossRef]
- José-García, A.; Gómez-Flores, W. Automatic clustering using nature-inspired metaheuristics: A survey. Appl. Soft Comput. 2016, 41, 192–213. [Google Scholar] [CrossRef]
- Pan, W.; Lu, W.F. A kinematics-aware part clustering approach for part integration using additive manufacturing. Robot. Comput. Manuf. 2021, 72, 102171. [Google Scholar] [CrossRef]
- Zhong, X.; Xu, X.; Pan, B. A non-threshold consensus model based on the minimum cost and maximum consensus-increasing for multi-attribute large group decision-making. Inf. Fusion 2022, 77, 90–106. [Google Scholar] [CrossRef]
- Kong, T.; Seong, K.; Song, K.; Lee, K. Two-mode modularity clustering of parts and activities for cell formation problems. Comput. Oper. Res. 2018, 100, 77–88. [Google Scholar] [CrossRef]
- Bodendorf, F.; Merkl, P.; Franke, J. Intelligent cost estimation by machine learning in supply management: A structured literature review. Comput. Ind. Eng. 2021, 160, 107601. [Google Scholar] [CrossRef]
- Chan, S.L.; Lu, Y.; Wang, Y. Data-driven cost estimation for additive manufacturing in cybermanufacturing. J. Manuf. Syst. 2018, 46, 115–126. [Google Scholar] [CrossRef]
- De Abreu Batista, R.; Bagatini, D.D.; Frozza, R. Classificação automática de códigos NCM utilizando o algoritmo naïve bayes. iSys-Rev. Bras. Sist. Inf. 2018, 11, 4–29. [Google Scholar]
- Macedo, L.C.L. Direito Tributário no Comércio Internacional; Edições Aduaneiras: Sao Paulo, Brazil, 2005. [Google Scholar]
- Fattalla, F.C. Proposta de Metodologia Para Classificação Fiscal de Mercadorias Têxteis na Nomenclatura Comum do Mercosul. Doctoral Dissertation, Universidade de São Paulo, São Paulo, Brazil, 2016. [Google Scholar]
- Pandove, D.; Goel, S.; Rani, R. Systematic review of clustering high-dimensional and large datasets. ACM Trans. Knowl. Discov. Data 2018, 12, 1–68. [Google Scholar] [CrossRef]
- Hancer, E.; Karaboga, D. A comprehensive survey of traditional, merge-split and evolutionary approaches proposed for determination of cluster number. Swarm Evol. Comput. 2017, 32, 49–67. [Google Scholar] [CrossRef]
- Nanda, S.J.; Panda, G. A Survey on Nature Inspired Metaheuristic Algorithms for Partitional Clustering. Swarm Evol. Comput. 2014, 16, 1–18. [Google Scholar] [CrossRef]
- Yoo, Y. Data-driven fault detection process using correlation based clustering. Comput. Ind. 2020, 122, 103279. [Google Scholar] [CrossRef]
- Xu, Z.; Dang, Y.; Zhang, Z.; Chen, J. Typical short-term remedy knowledge mining for product quality problem-solving based on bipartite graph clustering. Comput. Ind. 2020, 122, 103277. [Google Scholar] [CrossRef]
- Dogan, A.; Birant, D. Machine learning and data mining in manufacturing. Expert Syst. Appl. 2021, 166, 114060. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S.; Coelho, C.A.C. Survey of multiobjective evolutionary algorithms for data mining: Part II. IEEE Trans. Evol. Comput. 2013, 18, 20–35. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Park, H.-S.; Lee, J.-S.; Jun, C.-H. A K-means-like algorithm for K-medoids clustering and its performance. Proc. ICCIE 2006, 102–117. [Google Scholar]
- Velmurugan, T.; Santhanam, T. Computational complexity between K-means and K-medoids clustering algorithms for normal and uniform distributions of data points. J. Comput. Sci. 2010, 6, 363. [Google Scholar] [CrossRef] [Green Version]
- Mohd, W.M.B.W.; Beg, A.; Herawan, T.; Rabbi, K. An improved parameter less data clustering technique based on maximum distance of data and lioyd K-means algorithm. Procedia Technol. 2012, 1, 367–371. [Google Scholar] [CrossRef] [Green Version]
- Sood, M.; Bansal, S. K-medoids clustering technique using bat algorithm. Int. J. Appl. Inf. Syst. 2013, 5, 20–22. [Google Scholar] [CrossRef]
- Arora, P.; Varshney, S. Analysis of K-means and K-medoids algorithm for big data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.S.; Chauhan, N.C. K-means v/s K-medoids: A comparative study. In Proceedings of the National Conference on Recent Trends in Engineering & Technology, Anand, India, 13–14 May 2011; Volume 13. [Google Scholar]
- Zhao, R.; Gu, L.; Zhu, X. Combining fuzzy C-means clustering with fuzzy rough feature selection. Appl. Sci. 2019, 9, 679. [Google Scholar] [CrossRef] [Green Version]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy C-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Filho, T.S.; Pimentel, B.A.; Souza, R.; Oliveira, A. Hybrid methods for fuzzy clustering based on fuzzy c-means and improved particle swarm optimization. Expert Syst. Appl. 2015, 42, 6315–6328. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Mai, N.-L. A new soft computing model for estimating and controlling blast-produced ground vibration based on hierarchical K-means clustering and cubist algorithms. Appl. Soft Comput. 2019, 77, 376–386. [Google Scholar] [CrossRef]
- Alam, S.; Dobbie, G.; Rehman, S.U. Analysis of Particle Swarm Optimization Based Hierarchical Data Clustering Approaches. Swarm Evol. Comput. 2015, 25, 36–51. [Google Scholar] [CrossRef]
- Anderberg, M.R. The broad view of cluster analysis. In Cluster Analysis for Applications; Elsevier: Amsterdam, The Netherlands, 1973; pp. 1–9. [Google Scholar]
- Giacoumidis, E.; Lin, Y.; Jarajreh, M.; O’Duill, S.; McGuinness, K.; Whelan, P.F.; Barry, L.P. A blind nonlinearity compensator using DBSCAN clustering for coherent optical transmission systems. Appl. Sci. 2019, 9, 4398. [Google Scholar] [CrossRef] [Green Version]
- Comesaña-Cebral, L.; Martínez-Sánchez, J.; Lorenzo, H.; Arias, P. Individual tree segmentation method based on mobile backpack LiDAR point clouds. Sensors 2021, 21, 6007. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining KDD-96, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Abu-Mahfouz, I.; Banerjee, A.; Rahman, E. Evaluation of clustering techniques to predict surface roughness during turning of stainless-steel using vibration signals. Materials 2021, 14, 5050. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. TODS 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Juntunen, P.; Liukkonen, M.; Lehtola, M.; Hiltunen, Y. Cluster analysis by self-organizing maps: An application to the modelling of water quality in a treatment process. Appl. Soft Comput. 2013, 13, 3191–3196. [Google Scholar] [CrossRef]
- Alhoniemi, E.; Hollmén, J.; Simula, O.; Vesanto, J. Process monitoring and modeling using the self-organizing map. Integr. Comput. Eng. 1999, 6, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. Overture. In Self-Organizing Neural Networks; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–12. [Google Scholar]
- Hong, Y.-S.; Rosen, M.R. Intelligent characterisation and diagnosis of the groundwater quality in an urban fractured-rock aquifer using an artificial neural network. Urban Water 2001, 3, 193–204. [Google Scholar] [CrossRef]
- Liukkonen, M.; Havia, E.; Leinonen, H.; Hiltunen, Y. Quality-oriented optimization of wave soldering process by using self-organizing maps. Appl. Soft Comput. 2011, 11, 214–220. [Google Scholar] [CrossRef]
- Liukkonen, M.; Hiltunen, T.; Hälikkä, E. Modeling of the fluidized bed combustion process and NOx emissions using self-organizing maps: An application to the diagnosis of process states. Environ. Model. Softw. 2011, 26, 605–614. [Google Scholar] [CrossRef]
- Ghaseminezhad, M.; Karami, A. A novel self-organizing map (SOM) neural network for discrete groups of data clustering. Appl. Soft Comput. 2011, 11, 3771–3778. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer-using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- De Castro, L.N. Fundamentals of Natural Computing: Basic Concepts, Algorithms, and Applications; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Booker, L.B.; Goldberg, D.E.; Holland, J.H. Classifier systems and genetic algorithms. Artif. Intell. 1989, 40, 235–282. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zou, P.; Rajora, M.; Liang, S. Multimodal optimization of permutation flow-shop scheduling problems using a clustering-genetic-algorithm-based approach. Appl. Sci. 2021, 11, 3388. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Bhattacharjya, R.K. Introduction to Genetic Algorithms; Indian Institute of Technology Guwahati (IIT Guwahati): Guwahati, India, 2012; Volume 12. [Google Scholar]
- Jayaprakash, S.; Nagarajan, M.D.; de Prado, R.P.; Subramanian, S.; Divakarachari, P.B. A systematic review of energy management strategies for resource allocation in the cloud: Clustering, optimization and machine learning. Energies 2021, 14, 5322. [Google Scholar] [CrossRef]
- Lee, G.M.; Gao, X. A hybrid approach combining fuzzy C-means-based genetic algorithm and machine learning for predicting job cycle times for semiconductor manufacturing. Appl. Sci. 2021, 11, 7428. [Google Scholar] [CrossRef]
- Senthilkumar, P.; Vanitha, N.S. A stride towards developing efficient approaches for data clustering based on evolutionary programming. Int. J. Emerg. Technol. Comput. Sci. Electron. 2013, 3, 27–32. [Google Scholar]
- Ramadas, M.; Abraham, A.; Kumar, S. FSDE-forced strategy differential evolution used for data clustering. J. King Saud Univ.—Comput. Inf. Sci. 2019, 31, 52–61. [Google Scholar] [CrossRef]
- Su, T.; Dy, J. A deterministic method for initializing K-means clustering. In Proceedings of the 16th IEEE International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 15–17 November 2005; pp. 784–786. [Google Scholar]
- Thinsungnoena, T.; Kaoungkub, N.; Durongdumronchaib, P.; Kerdprasopb, K.; Kerdprasopb, N. The clustering validity with silhouette and sum of squared errors. In Proceedings of the International Conference on Industrial Application Engineering 2015, Kitakyushu, Japan, 28–31 March 2015. [Google Scholar] [CrossRef] [Green Version]
- Fränti, P.; Sieranoja, S. K-means properties on six clustering benchmark datasets. Appl. Intell. 2018, 48, 4743–4759. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. In Communications in Statistics—Theory and Methods; Taylor & Francis: Abingdon, UK, 1974; pp. 1–27. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Medina, J.-L.; Villarreal, S.; Vanderdonckt, J. A gesture elicitation study of nose-based gestures. Sensors 2020, 20, 7118. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Xu, M.; Fränti, P. Sum-of-Squares Based Cluster Validity Index and Significance Analysis; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 313–322. [Google Scholar]
- Ozturk, C.; Hancer, E.; Karaboga, D. Improved clustering criterion for image clustering with artificial bee colony algorithm. Pattern Anal. Appl. 2015, 18, 587–599. [Google Scholar] [CrossRef]
- Kraiem, H.; Aymen, F.; Yahya, L.; Triviño, A.; Alharthi, M.; Ghoneim, S.S.M. A comparison between particle swarm and grey wolf optimization algorithms for improving the battery autonomy in a photovoltaic system. Appl. Sci. 2021, 11, 7732. [Google Scholar] [CrossRef]
- Srinivas, T.; Madhusudhan, A.K.K.; Manohar, L.; Pushpagiri, N.M.S.; Ramanathan, K.C.; Janardhanan, M.; Nielsen, I. Valkyrie—Design and development of gaits for quadruped robot using particle swarm optimization. Appl. Sci. 2021, 11, 7458. [Google Scholar] [CrossRef]
- Belotti, J.T.; Castanho, D.S.; Araujo, L.N.; Silva, L.V.; Antonini Alves, T.; Tadano, Y.S.; Stevan, S.L., Jr.; Correa, F.C.; Siqueira, H.V. Air pollution epidemiology: A simplified generalized linear model approach optimized by bio-inspired metaheuristics. Environ. Res. 2020, 191, 110106. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Lucas, R.; Ferreira, F.R.V.; Siqueira, H.V.; Kaster, M.S. Gaussian adaptive PID control optimized via genetic algorithm applied to a step-down DC-DC converter. In Proceedings of the 12th IEEE International Conference on Industry Applications (INDUSCON), Curitiba, Brazil, 20–23 November 2016; pp. 1–6. [Google Scholar]



| Algorithm | (a) | (b) | (c) |
|---|---|---|---|
| GA | 89.78% | 92.00% | 88.67% |
| FCM | 89.78% | 89.33% | 91.33% |
| K-Medoids | 89.78% | 89.33% | 91.33% |
| K-Means | 89.78% | 89.33% | 91.33% |
| Hierarchical | 89.78% | 89.33% | 90.00% |
| PSO | 89.11% | 90.00% | 88.67% |
| DE | 89.11% | 90.00% | 88.67% |
| SOM | 85.33% | 85.33% | 85.33% |
| DBSCAN | 67.78% | 68.00% | 67.33% |
| Algorithm | SSE | SSW | SSB | WB | CH | SI | Total |
|---|---|---|---|---|---|---|---|
| Hierarchical | 8 | 8 | 7 | 8 | 8 | 9 | 48 |
| K-Medoids | 9 | 9 | 8 | 9 | 9 | 3 | 47 |
| K-Means | 7 | 7 | 6 | 7 | 7 | 8 | 42 |
| GA | 6 | 6 | 5 | 6 | 6 | 7 | 36 |
| PSO | 5 | 5 | 4 | 5 | 5 | 6 | 30 |
| DE | 4 | 4 | 3 | 4 | 4 | 4 | 23 |
| DBSCAN | 1 | 1 | 9 | 1 | 1 | 5 | 18 |
| SOM | 3 | 3 | 2 | 3 | 3 | 2 | 16 |
| FCM | 2 | 2 | 1 | 2 | 2 | 1 | 10 |
| Algorithm | SSE | SSW | SSB | WB | CH | SI | Total | |
|---|---|---|---|---|---|---|---|---|
| With PCA | K-Medoids | 3 | 3 | 3 | 3 | 3 | 1 | 16 |
| Hierarchical | 2 | 2 | 2 | 2 | 2 | 3 | 13 | |
| K-Means | 1 | 1 | 1 | 1 | 1 | 2 | 7 | |
| Without PCA | K-Medoids | 3 | 3 | 3 | 3 | 3 | 2 | 17 |
| Hierarchical | 2 | 2 | 1 | 1 | 1 | 3 | 10 | |
| K-Means | 1 | 1 | 2 | 2 | 2 | 1 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerreiro, M.T.; Guerreiro, E.M.A.; Barchi, T.M.; Biluca, J.; Alves, T.A.; de Souza Tadano, Y.; Trojan, F.; Siqueira, H.V. Anomaly Detection in Automotive Industry Using Clustering Methods—A Case Study. Appl. Sci. 2021, 11, 9868. https://doi.org/10.3390/app11219868
Guerreiro MT, Guerreiro EMA, Barchi TM, Biluca J, Alves TA, de Souza Tadano Y, Trojan F, Siqueira HV. Anomaly Detection in Automotive Industry Using Clustering Methods—A Case Study. Applied Sciences. 2021; 11(21):9868. https://doi.org/10.3390/app11219868
Chicago/Turabian StyleGuerreiro, Marcio Trindade, Eliana Maria Andriani Guerreiro, Tathiana Mikamura Barchi, Juliana Biluca, Thiago Antonini Alves, Yara de Souza Tadano, Flávio Trojan, and Hugo Valadares Siqueira. 2021. "Anomaly Detection in Automotive Industry Using Clustering Methods—A Case Study" Applied Sciences 11, no. 21: 9868. https://doi.org/10.3390/app11219868
APA StyleGuerreiro, M. T., Guerreiro, E. M. A., Barchi, T. M., Biluca, J., Alves, T. A., de Souza Tadano, Y., Trojan, F., & Siqueira, H. V. (2021). Anomaly Detection in Automotive Industry Using Clustering Methods—A Case Study. Applied Sciences, 11(21), 9868. https://doi.org/10.3390/app11219868









