Abstract
A modular steel structure building has obvious advantages in reducing construction period and protecting the environment due to its unique construction method, so it is widely used in modern construction. However, the modular building connection design and modeling are mostly based on the traditional connection research results. To address this issue, the paper developed a component-based model for novel modular connections with an inbuild component. First of all, the comprehensive parameter study was implemented using elaborate finite element models. Then the component-based model for novel modular connections was developed, and the force-deformation response of each component was determined using the finite element method. Thirdly, assembly of all components to overall rotational joint and the simplified finite element model of modular connections was obtained. Finally, comparison between simplified and refined finite element was conducted, the results showed that the proposed model can predict the mechanical behavior of modular building connections within the acceptable margin of error.
1. Introduction
Modular building can maximize the prefabrication of building factories and improve the efficiency of building construction. In recent years, modular building has gradually replaced the traditional prefabricated building structure system in developed countries in North America, Japan and Europe, and it has been widely used in engineering construction [1,2]. The structural framework, maintenance wall panels and pipelines of the modular units are all prefabricated in the factory and transported to the site for assembly as shown in Figure 1. This process ensures the construction quality of modular units but also makes the modular connections become the most critical factor to ensure the overall structural stability and robustness. A state-of-the-art review conducted by Wahid Ferdous [3] pointed out that the development of multi-story modular buildings still faces the challenge of lack of design guidelines and reliable connection systems. In addition, a same conclusion can be drawn from the research of E. Brunesi [4,5] in seismic property of cast-in-place structure.
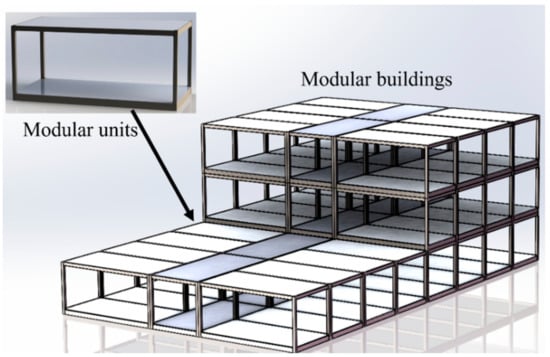
Figure 1.
Assembling process of modular construction.
In recent years, many scholars have proposed new modular connections to meet the requirements of modular structural strength and stiffness. The mechanical properties were studies mainly based on the experiment and finite element method. Chen et al. [6,7] developed a plug-in connection system that could connect modular units horizontally and vertically at the same time. The test results showed that the beam–beam connection reduces the shear deformation at the corner of the module. The results of finite element modeling show that the upper and lower intramodule connection exhibit independent mechanical behavior. Dhanapal et al. [8] proposed a plug-in cast steel connection system for modular corner connection. The experimental results show that the joints remain elastic under the design load. The weight of cast steel connectors will affect the compressive strength of the connectors, while the position of bolts will affect the tensile strength of the connectors. The finite element method was conducted to optimize bolt position and thickness of steel castings to achieve high strength and low weight. A self-locking connection system was proposed by Xiao-Meng Dai et al. [9]. When the studs are inserted, the joints can be self-locked by modular units’ weight, eliminating the need for construction space during installation. The experimental results show that the self-locking joint has better pulling capacity and no obvious slip before failure.
In addition to the mechanical properties of modular connections, some scholars have studied the mechanical behavior of connections in the structural system. The simplified connection FEM model is the key point of system analysis because the experiment and fine FEM need high time and financing cost. C.D. Annan et al. [10] invented a simplified model for studying the seismic behavior of modular buildings. The model uses rigid links between beams and columns, and a one-side hinge connector between upper and lower columns. Sultana and Youssef [11] provided a spring-based model for intermodule connection using super elastic shape memory alloy bolts. The model considers the rigid link inside the modular unit and semi-rigid link between upper and lower columns using spring groups. Based on the work of C.D. Annan [10], Fathieh and Mercan [12] extended the model to three dimensions. The horizontal joint between modular units was considered as a bolted steel plate, and the elastic behavior was assumed by modeling the connection as an element with strength in bending and shear 30% greater than the adjacent beam section. Gunawardena [13] developed a combined horizontal and vertical connection model. The vertical intermodule connections were modeled by beam element with consideration of the possible positions of plastic hinge. Spring models were placed between horizontal modular units to transfer lateral load. The spring stiffness was determined as the shear stiffness of the adjacent intermodule connection.
According to the above analysis, intramodule connections are usually considered to be rigid. The selection of stiffness and strength parameters of intermodule connections mainly depends on traditional design assumptions and experience. Moreover, due to the construction complexity of modular connections, it is difficult to relate the mechanical properties of real connections to the simplified model. The component method that adopted in Eurocode 3 [14] and Eurocode 4 [15], also known as mechanical model or spring model. It describes the mechanical behavior of connections through a series of rigid and elastic elements. This method has wide applicability and can be extended to all connection structures theoretically. Considering the flexibility of the component method, many researchers have been dedicated to developing a component method for different types of connections [16,17,18]. Some of the studies have also investigated connection mechanical properties under various complex loading conditions using the component method, such as cyclic loading [19], axial load-bending moment interaction [20,21] and fire [22]. However, there are a few component method studies for modular connections in the present study.
The aim of this paper is to develop a component-based model for novel modular connections with superimposed beams shown in Figure 2. The novel modular connection eliminated gaps between ceiling and floor beams in order to ensure more continuous force transmission between modular units. The basic mechanical properties of joints [23] and superimposed beams [24,25,26] were previously studied. In this paper, a more comprehensive parameter study was fist implemented using elaborate finite element models. We then followed the component method procedure:
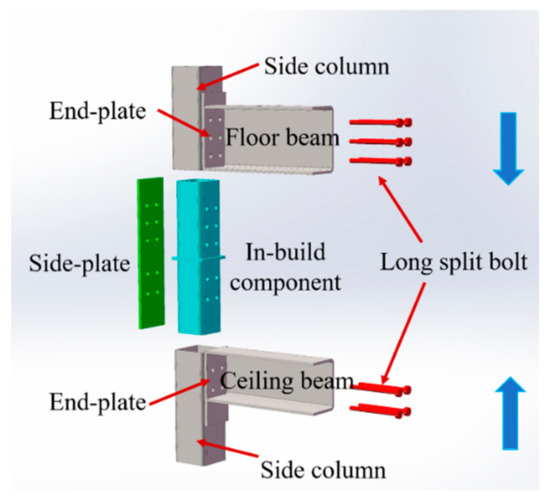
Figure 2.
The novel modular connection with inbuild component.
- (1)
- the component-based model for novel modular connections was developed based on parameter analysis results.
- (2)
- the force-deformation response of each component was determined with the help of the finite element method.
- (3)
- assembly of all components to overall rotational joint. At last, the results of the simplified model were compared with the results of the elaborate finite element model.
2. Parameter Analysis
2.1. Establishment and Validation of FEM
To ensure the logical integrity of the study, the finite element modeling procedure and validation were reviewed briefly. Three full-scale connections experiments were carried out to investigate the basic mechanical behavior. The dimension details and relevant number of specimens were shown in Figure 3 and summarized in Table 1. The reasonable modeling process is the premise to ensure the accuracy of the numerical model. According to E. Brunesi [27,28], a refined nonlinear solid FE model, accounting for the influence of friction, preload of bolts, relative slippage of components, could well reproduce the test result. The typical finite element model was shown in Figure 4a; the loading and support condition were exactly the same as the experiment (Figure 4b). All degrees of freedom on the top and bottom were constrained to achieve a fixed state. A z-direction constraint plane was set at the twin beams to simulate the out-of-plane restraint device in experiment. The bolts and nuts are simplified into cylinders of the same volume, and the pre-tightening force is applied using the “bolt load” method in the Abaqus. All contacts between components are modeled using the “surface-to-surface” algorithm. Normal contact is simulated by “hard contact” to ensure complete pressure transfer and allow separation after contact. Tangential contact is simulated by “penalty” with a friction coefficient of 0.3. All welded parts are modeled as solid units and “tie” to surrounding components. To ensure that the model can accurately simulate the local buckling behavior of the web and the flange of the beam, at least two layers of mesh are set in the direction of the thickness of all the member plates. The model was meshed using the C3D8R element with the size of 10 mm at the connection domain and 20 mm in other areas to speed up the calculation while ensuring accuracy. The model contained 94,594 elements and 143,067 nodes. The geometrical nonlinearities were considered through switching “nlgeom” on in Abaqus. Material nonlinearities were considered by plastic function in “material manger” in Abaqus. For more detailed material parameters, one can refer to the author’s previous articles [23]. In the experiment, the load was applied to test specimens through a particular steel bracket. It ensured that the upward displacement of floor and ceiling were equal. In the numerical model, the upward displacement was applied at the bottom flange of the floor beam to achieve the same effect as the experiment.
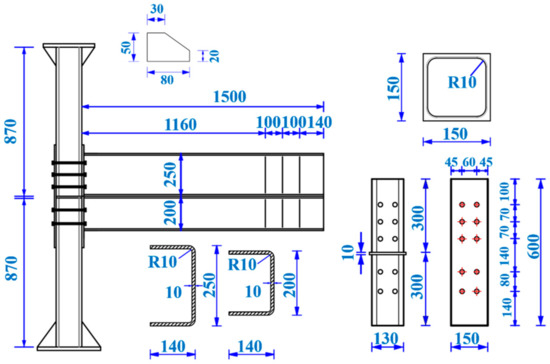
Figure 3.
Geometric configuration of tested specimens (units: mm).

Table 1.
Structural members of the tested specimens.
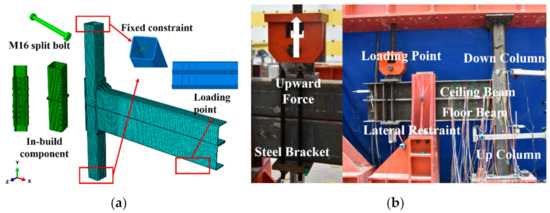
Figure 4.
Loading and support condition of novel modular connections: (a) Finite element model; (b) Test specimens.
The moment of global modular connection was obtained through the force at loading point multiply by the length of twin beams. The overall rotation was equal to the beam rotation minus column rotation. The comparison of moment-rotation curves between the finite element and the experiment were shown in Figure 5. For T1 connection, the curve of the finite element fits well in the elastic range with that of the experiment. When the moment reaches about 225 kNm, two curves began to separate. The finite element curve is slightly higher than the experimental curve. For T2 and T3 connections, the finite element curves are in good agreement with the test curves within the whole loading stage. In general, the finite element can accurately predict the mechanical properties of joints.
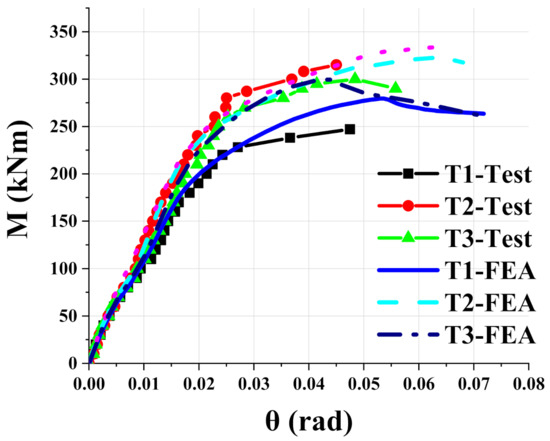
Figure 5.
Validation of finite element model.
2.2. Parameter Setting
The parameters of novel modular connections were shown in Figure 6. According to the experimental results, the bending stiffness of floor and ceiling beams has great influence on the initial stiffness, ultimate strength and continuity of modular connections. In parameter analysis, models were named by F and C followed by beam heights. The reserved construction error between the build-in component and the column leads to the discontinuity of the upper and lower intramodule connections, which is one of the important sources of modular connection deformation between modular units. In the model, the size is represented by G followed by a number. The inbuild component is the main part of the intermodule connection, which can not only locate the position but also enhance the strength of joint panels during construction. The height and thickness of internal inserts are denoted by letters H and P, respectively. After inserting the inbuild component into the side column, the modular connection needs to be tightened by the side plate and split bolts. The thickness of the side sealing plate and the bolt pre-tightening force are respectively represented by S and BL. The beam and column inside the modular unit are welded together through an end plate, which will affect the mechanical properties of the global connections by affecting the strength of the intramodule connection. The thickness of the end plate is represented by D.
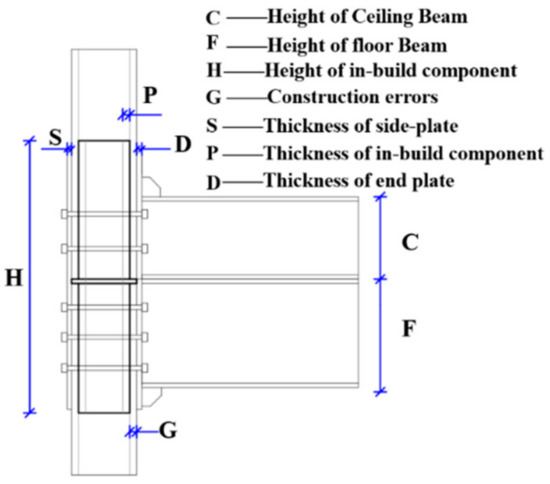
Figure 6.
Parameters setting of finite element model.
In the experiment, the stiffeners can not only prevent the welding failure in advance, but also play a positive role in the mechanical properties of the whole connection. Therefore, stiffeners were set at intramodule connections in all models. The bilinear constitutive model was adopted for the material properties and all members are made of Q345b steel with nominal yield stress 345 MPa (E = 210,000 MPa, ν = 0.3). The simplification of material properties would facilitate the development of subsequent theoretical model research. In the experiment, the construction error was set up to ensure the smooth connection between intramodule connections, and it is considered as one of the parameters in the finite element parameter analysis. Hence, the reference of parameter analysis is based on T3, and the construction error was eliminated. According to the above parameter expression rules, the reference model can be named as F250C200H600G0S12P10D12.
The moment-rotation curve directly expressed the mechanical properties of the joint, and can be used as the basis for the design of the joint. For modular building connections, the deformation was more complicated than that of traditional connections. Therefore, in addition to the basic moment-rotation curve, two groups of curves for joint deformation between modular units were defined as shown in Figure 7. Firstly, the relationship between relative dislocation and the bending moment between upper and lower module side columns are shown in Figure 7a. The dislocation between upper and lower columns was defined as g. When the modular units were stacked vertically, the relative dislocation between the side columns will cause additional bending moment to the bottom units. Secondly, the relation between bending moment and relative rotation of upper and lower columns is shown in Figure 7b. The relative rotation between upper and lower columns was defined as CI. The rotation between modular units was related to the story drift, which affected the seismic performance of the building system. Moreover, excessive rotation and translational deformation may cause premature failure of intermodule connection, and then lead to system disintegration and failure.
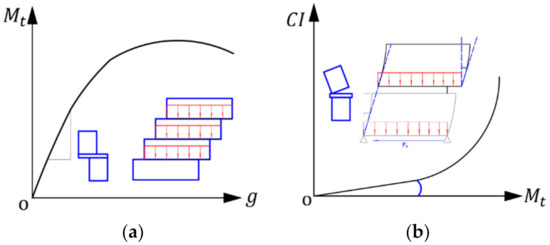
Figure 7.
Parameters setting of finite element model: (a) Relative dislocation between units; (b) Relative rotation between units.
2.3. Parameter Analysis Results
2.3.1. Thickness of Side Plate and Bolts Preload
The thickness of the side plate was selected from 6 mm to 16 mm with an interval of 2 mm, and the preload of split bolts was selected from 80 kN to 120 kN with an interval of 20 kN. The moment-rotation curves were shown in Figure 8. There was no obvious difference among all curves, indicating that the side plate thickness and bolts preload have little influence on the mechanical properties of modular connections.
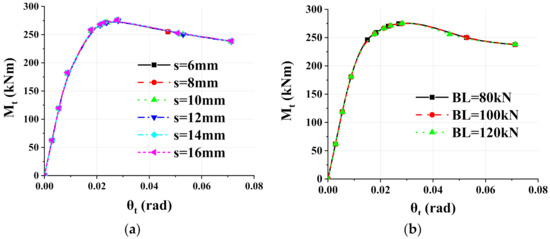
Figure 8.
Moment-rotation curves: (a) Thickness of side plate; (b) Bolts preload.
The influence rule of side plate thickness and bolts preload on relative dislocation between upper and lower columns were shown in Figure 9. When the moment is below 200 kNm, the curves almost coincide and increase linearly, indicating that the thickness of the side plate has little influence on the relative dislocation of the upper and lower columns in the elastic stage. When the bending moment reaches 200 kNm, curves entered into the elastic–plastic stage and began to separate. The higher the thickness of the side plate, the smaller the relative dislocation of the side columns. There is no significant difference between the curves with different bolt preload.
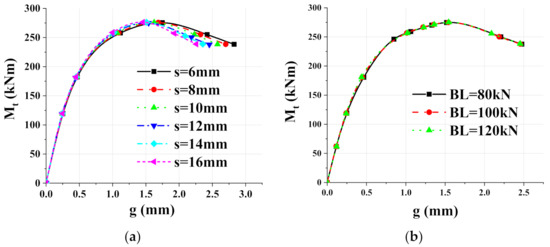
Figure 9.
Moment-relative dislocation curves of connections: (a) Thickness of side plate; (b) Bolts preload.
The influence rule of side plate thickness and bolts preload on continuity index were shown in Figure 10. As the thickness of side plate increases, the curve is closer to the horizontal axis, which means that the rotation difference between the upper and lower columns is smaller. For bolt preload influence, the connections with higher bolt preload have better continuity in the elastic stage, but there was no obvious difference in elastic–plastic range.
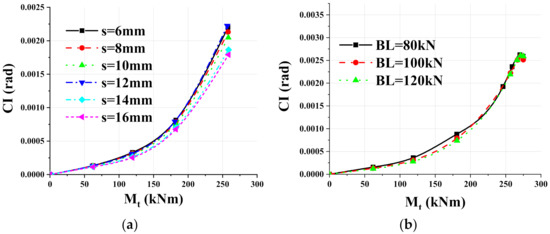
Figure 10.
Continuity index-moment curves of connections: (a) Thickness of side plate; (b) Bolts preload.
In general, the thickness of the side plate has little influence on the overall moment-rotation curve of connections but plays a positive role in enhancing the continuity between modules. The Mises stress distribution of side plates with thickness of 6 mm and 16 mm is shown in Figure 11. The yield area of S16 was obviously smaller than that of S6, indicating that the plate with larger stiffness can prevent the relative dislocation of the lower and upper columns more effectively. The bolt preload has little effect on the global mechanical properties of the connection, but it can improve the continuity index in the elastic stage. However, if the bolt preload is too high, the column flange will enter the yield stage before vertical force is formally applied, as shown in Figure 12.
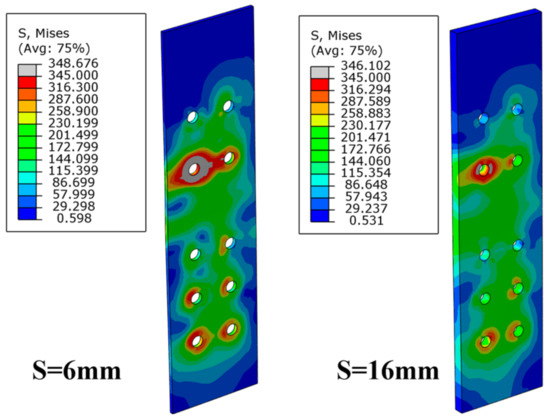
Figure 11.
Stress distribution of side plates.
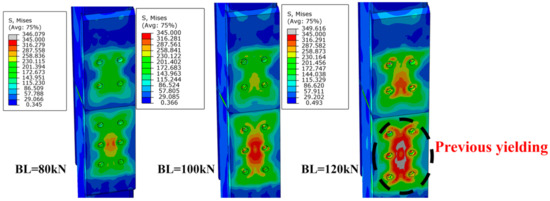
Figure 12.
Stress distribution of columns with different bolt preload.
2.3.2. Thickness of Beam End Plate
In order to understand the influence of beam end plates on mechanical properties of new modular building joints in a more comprehensive way, end plates with thickness of 6 mm to 16 mm (2 mm interval) were selected for parameter analysis based on the reference model. Among them, D6 and D8 were used to study the mechanical properties of joints with end-plate thickness less than or equal to column flange thickness, respectively. D12 to D16 were used to study the effect to modular connections when the thickness of end plate was greater than that of column flange. Figure 13 shows the influence of the thickness change of the end plate on the moment-rotation curve. The overall trend is that the connection with higher thickness of the high-end plate has better mechanical properties. For D6 and D8, the initial stiffness of connections was reduced by 11.0% and 6.7%, and the ultimate moment resistance capacity was reduced by 4.7% and 2.9%, respectively, as compared to the reference model. When the end plate thickness is increased (D14, D16), the initial stiffness was increased by 3% and 7.2%, and the ultimate moment resistance strength was increased by 1.1% and 2.2%, as compared to the reference model.
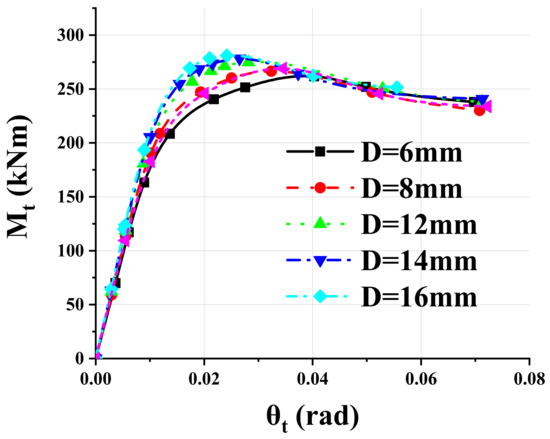
Figure 13.
Moment-rotation curves of connections with different end plate thickness.
The influence rule of end plate thickness on relative dislocation between upper and lower columns is shown in Figure 14. When the bending moment reached 225 kNm, the D6 and D8 models showed an obvious elastic–plastic stage, while the D12 to D16 models did not. When the maximum bending moment was reached, the horizontal displacement differences of D12, D14 and D16 were 1.54 mm, 1.39 mm and 1.24 mm, respectively, while those of D6 and D8 were 2.70 mm and 2.12 mm, respectively. After the connection reached the maximum bending moment, the curves of D12, D14 and D16 models showed a smooth descending section, while those of D6 and D8 models showed a slightly divergent state.
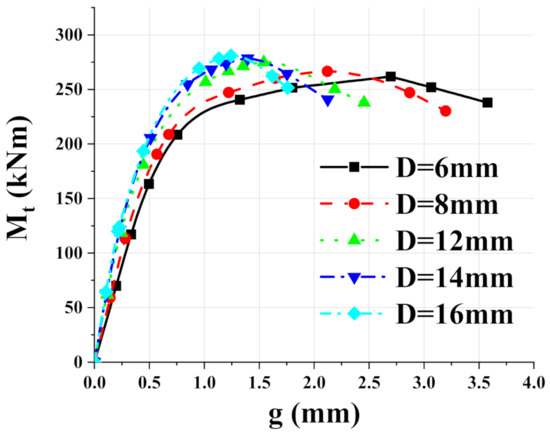
Figure 14.
Moment-relative dislocation curves of connections with different end plate thickness.
The continuity index curves of different end plate thicknesses were shown in Figure 15. It can be seen that the continuity index of D12, D14 and D16 models was significantly stronger than that of D6 and D8 models. Moreover, the curves of D12, D14 and D16 almost coincide, indicating that increasing the end plate thickness on the basis of the reference model have little impact on the continuity of connections.
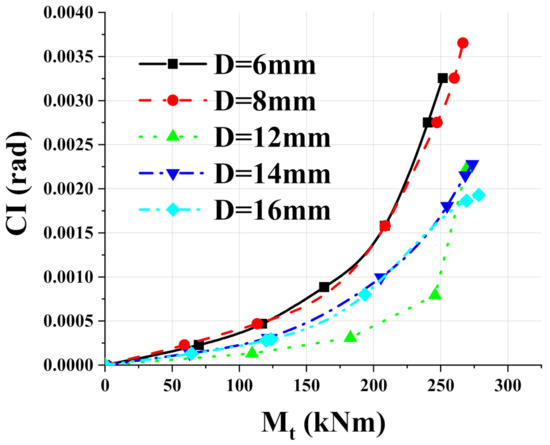
Figure 15.
Continuity index-moment curves of connections with different end plate thickness.
According to the above analysis, increasing the thickness of the beam end plate can improve the mechanical behavior and continuity of the connection. Mises stress distribution of D6, D12 and D16 models at the final loading stage was shown in Figure 16a, and the parts of stress over 345 MPa were indicated in gray. The yield area of the end plate with high thickness is small, which improves the ultimate bearing capacity of the joint. The stress distribution in the joint panel of D6 and D16 models at maximum moment is shown in Figure 16b. The end plate is connected with the column flange by welding. Increasing the thickness of the end plate is equivalent to improving the strength of the beam–column connection, and the initial stiffness of the global modular connection is improved by reducing the deformation of the column flange. At the same time, higher thickness of the end plate can better protect the inbuild component from local buckling under the ultimate load, thus improving the continuity of intermodule connection.
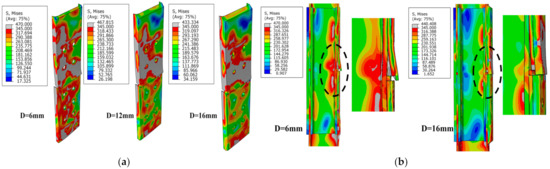
Figure 16.
Mises stress distribution of modular connections: (a) Beam end plate; (b) Joint panel.
2.3.3. The Height and Thickness of the Inbuild Component
The inbuild component is made by bending a steel plate. Considering bending and drilling difficulty of steel plate, the thickness parameter range was set by 2 mm interval from 6 mm to 14 mm. Two additional models with the inbuild component height of 650 mm and 700 mm are selected on the basis of 600 mm of the reference model. The moment-rotation curves with different inbuild component height were shown in Figure 17a; the initial stiffness amplitude of H600, H650 and H700 models was within 0.58%, and the ultimate bending capacity was 275 kNm, indicating that the height of the internal plug-in has little effect on the global mechanical behavior of the modular connection. Figure 17b showed the influence of the inbuild component thickness on the moment-rotation curves. There was little difference between each curve in the elastic stage, but obvious separation occurs in the elastic–plastic stage. Compared to the reference model P10, the initial stiffness of the P6 model and the P8 model decreased by 7.1% and 5.9%, respectively, while that of the P12 model and the P14 model increased by 5.4% and 5.7%. One can conclude that the initial stiffness of joints can be improved by increasing the thickness of the inbuild component. The ultimate moment of P6 to P12 models was between 274 kNm and 275 kNm, indicating that the thickness change of the inbuild component has little effect on the ultimate bearing capacity of connections.
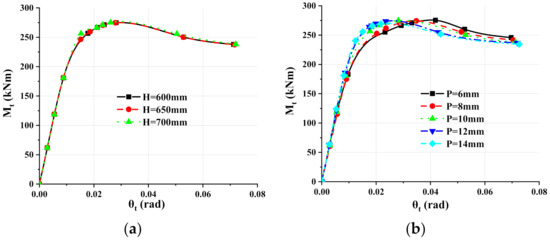
Figure 17.
Moment-rotation curves: (a) The height of inbuild component; (b) The thickness of inbuild component.
The moment-dislocation curves of different inbuild component heights and thicknesses were shown in Figure 18. For H600 to H700, the curves almost coincide with each other, which indicates that the height change has little influence on the relative dislocation between the upper and lower columns. For the P6 to P14 models, curves of the P10 to P14 models were significantly higher than that of the P6 and P8 models. When the bending moment reached 225 kNm, the curves of the P6 and P8 models showed an obvious elastic–plastic stage, and the relative displacement of the side column increases rapidly. However, the curves of the P10, P12 and P14 models have no obvious elastic–plastic stage. When the bending moment reached the maximum value, the dislocation of P6 and P8 was around 2.5 mm, which was 40% higher than that of reference model P10 (1.5 mm). The dislocation of P12 and P14 was 1.0 mm and 1.4 mm, respectively, which is 33.0% and 6% lower than that of reference model P10. Hence, the dislocation between upper and lower columns can be reduced by increasing the thickness of inbuild component.
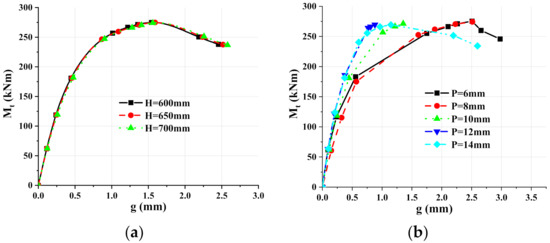
Figure 18.
Moment-relative dislocation t curves of connections: (a) The height of inbuild component; (b) The thickness of inbuild component.
The rotation difference moment curves with different inbuild component heights are shown in Figure 19a, indicating that the variation of inbuild component heights has little effect on the connection continuity index. Figure 19b showed the rotation difference-bending moment curves of different inbuild component thicknesses. At the initial stage (bending moment less than 100 kNm), the difference between curves was not obvious. When the bending moment reached 150 kNm, the curve began to separate, and the higher the thickness of the inner plug is, the better the continuity of the node. When the bending moment reached 250 kNm, the curves of the P6 and P8 models began to rise sharply and diverge, while the values of the P10 to P14 models remained at a low level.
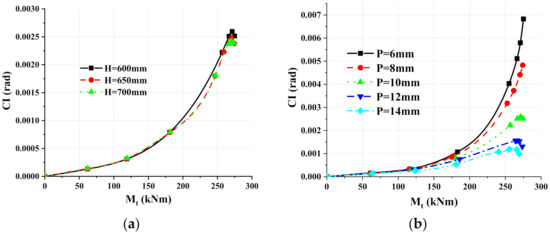
Figure 19.
Continuity index-moment curves of connections: (a) The height of inbuild component; (b) The thickness of inbuild component.
The above analysis showed that the inbuild component thickness had greater influence on the connection mechanical properties than the height. The Mises stress distribution of inbuild component in models P6 to P14 was shown in Figure 20. The stress concentration area was mainly distributed at the junction of the upper and lower columns. The inbuild component wall of model P6 and model P8 revealed obvious depression in the stress concentration area, which could not continue to constrain the relative dislocation of upper and lower columns to improve the continuity of joints. The yield area of P12 and P14 was significantly smaller than that of the P6 and P8 models. The internal inbuild component still had potential to limit the relative deformation between columns.
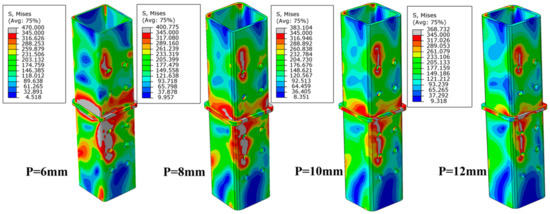
Figure 20.
Stress distribution of inbuild component with different thickness.
2.3.4. Allowable Construction Errors
In order to guide the design of joints accurately, it is necessary to analyze the influence degree of different construction errors on mechanical properties of connections. In this section, 1 mm, 2 mm and 3 mm were selected as the control group based on the reference model of 0 mm construction error. The moment-rotation curves of connections with different construction errors were shown in Figure 21. Compared to the reference model G0, the initial stiffness of G1, G2 and G3 models decreased by 29.8%, 41.7% and 48.7%, respectively, and the ultimate bending capacity decreased by 1.1%, 1.5% and 2.2%, respectively. Increasing the construction error had a great effect on the initial stiffness of the connection but had almost no effect on the ultimate bearing capacity.
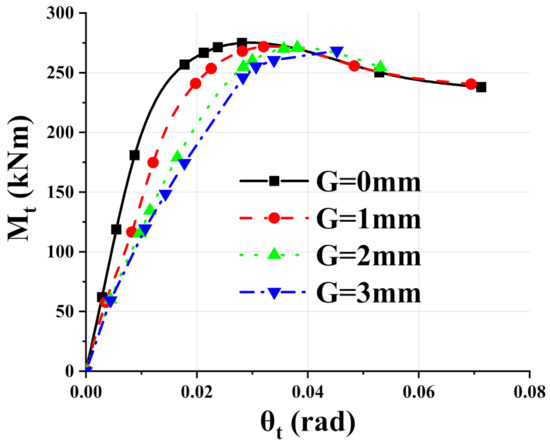
Figure 21.
Moment-rotation curves of connections with different construction errors.
Figure 22 showed moment-dislocation (M-g) curves with different allowable errors, and there were significant morphological differences among the curves. In the initial stage of the G0 model (moment was less than 200 kNm), dislocation grows almost linearly and slowly. The curve of the G1 model increased linearly in the initial stage, and the slope was about 78% lower than that of the G0 model. When the bending moment reached 80 kNm, a slip segment of about 0.5 mm appeared in the curve, and then the curve continued to maintain a linear growth before 200 kNm. A 1 mm horizontal slip segment appears at around 80 kNm of the G2 model, and then the curve changes back to a linear growth mode. The G3 model curve almost overlaps with the G2 model in the initial stage. When the bending moment reached 100 kNm, the curve showed a slip segment of about 3 mm. The dislocation of the G1, G2 and G3 models were 2.9 mm, 4.4 mm and 6.2 mm at ultimate moment, which were 86.6%, 185.5% and 305.3% higher than that of the reference model G0, respectively. The construction error has a significant effect on the relative displacement of the upper and lower columns.
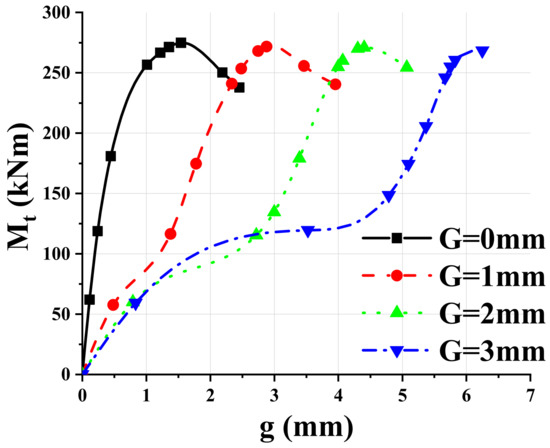
Figure 22.
Moment-relative dislocation curves of connections with different construction errors.
Rotation difference-moment curves of the G0 to G3 models were shown in Figure 23. Before 100 kNm, the curves of the G1, G2 and G3 models almost coincide and are higher than those of the G0 model, indicating that the continuity of connections with construction errors in the elastic stage was similar and weaker than that of the model without admissible errors. When the bending moment was greater than 200 kNm, the curves of the G2 model and the G3 model showed a divergent trend, and the rotation difference continued to increase, while the G0 model and the G1 model remained at a low level. Through the above analysis, it is found that the construction error has great influence on the initial stiffness, the dislocation and the continuity of the connection. Mises stress distribution at each connection was shown in Figure 24 at the moment of 100 kNm. For the G0 model, the inbuild component was closely attached to the column wall, which increases the strength of the joint panel and thus improves the initial stiffness of the node. For the G1 to G3 models however, the stress distribution still remains in a low level, indicating that the connection was in a “slip” stage.
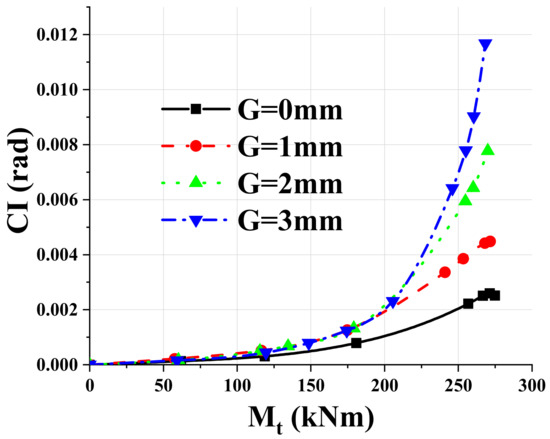
Figure 23.
Continuity index-moment curves of connections with different construction errors.
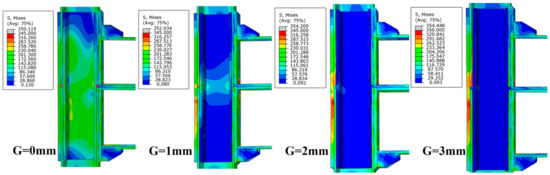
Figure 24.
Stress distribution of connections with different construction errors.
2.3.5. Dimension of Floor and Ceiling Beams
Different from traditional assembly joints, modular building joints consist of two beams. Many studies proved that the height ratio between floor beam and ceiling beam has significant influence on the mechanical properties of modular connections and systems. In order to better understand the influence of geometric dimensions of double beams on mechanical properties of joints, six groups of finite element models were set up under the premise that geometric dimensions of floor beams were no less than that of ceiling beams. F200C200, F225C200, F225C225, F250C200, F250C225 and F250C250 were considered, among which F250C200 was the reference model. The result moment-rotation curves were shown in Figure 25. Compared to the reference, the initial stiffness of F250C225 and F250C250 models increased by 16.6% and 19.9%, respectively, and the ultimate moment bearing capacity increased by 3.63% and 12.7%, respectively. F225C200 and F200C200 models reduce the height of floor beams on the basis of the reference model. The initial stiffness was reduced by 2.4% and 18.2%, respectively, and the ultimate bearing capacity was reduced by 10.9% and 18.9%, respectively.
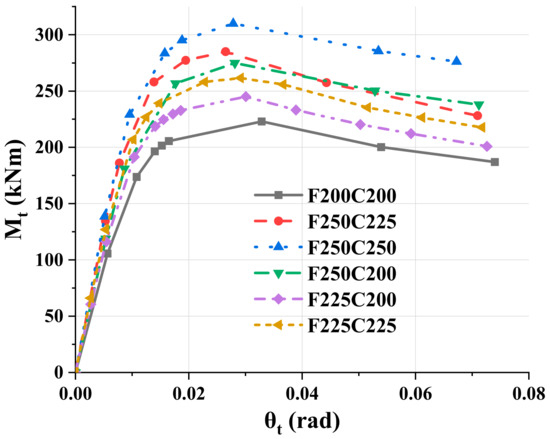
Figure 25.
Moment-rotation curves of connections with different beams height.
The moment-dislocation curves were shown in Figure 26. The curves were overlapped in the elastic stage and began to separate when the moment reached 125 kNm. Under the same bending moment, the higher the joint of double beam, the smaller the dislocation between columns. The relative displacement of the F250C225 model and the F250C250 model was 1.73 mm and 2.38 mm, respectively, at maximum moment, which was 12.3% and 54.5% higher than that of the F250C200 model. The relative displacement of the F225C200 model and the F200C200 model was 1.41 mm and 1.31 mm, respectively, when the bending moment reaches the maximum value, which was reduced by 8.4% and 14.9%, as compared to the reference model. The rotation difference-bending moment curves were shown in Figure 27. The curves of the F200C200 model, F225C225 model and F250C250 model which had the same height of floor beam and ceiling beam were significantly lower than those of other models. The inflection points of the F200C200 model, F225C225 model and F250C250 model appeared at about 200 kNm, 230 kNm and 260 kNm, respectively. The inflection points of the F250C200 model, F225C200 model and F250C225 model appeared at 150 kNm, 175 kNm and 225 kNm, respectively, and the curves diverged upward after reaching the inflection point, indicating that the rotation difference between upper and lower columns further expanded.
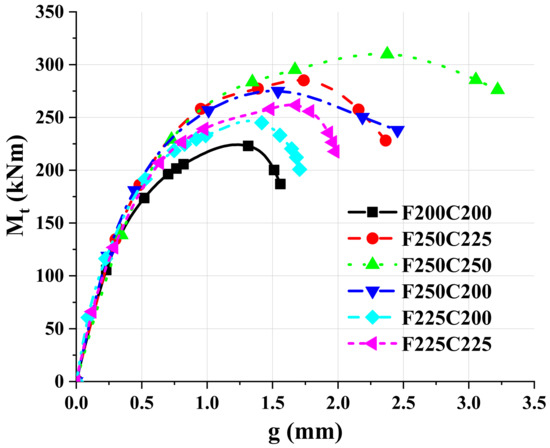
Figure 26.
Moment-relative dislocation curves of connections with different beam height.
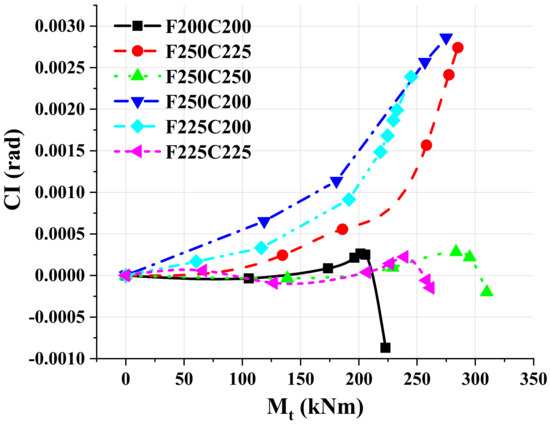
Figure 27.
Continuity index-moment curves of connections with different beam height.
The stress distribution along x direction of the twin beams and the Mises stress distribution of connections were shown in Figure 28 and Figure 29, respectively. By comparing F200C200, F225C200 and F250C200, it can be concluded that increasing the height of the floor beam can reduce the stress concentration area and then improved the stiffness and strength of upper intramodule connection. The same conclusion can be drawn by comparing F250C200, F250C225 and F250C250 for lower intramodule connection. For models with equal height of twin beams (F250C250, F225C225, F200C200), the strain was symmetrically distributed with respect to the interface of twin beams. The force transmitted from the double beams was equal to the intermodule connection, so the continuity of the joints is better than that of the joints with unequal heights of the double beams.
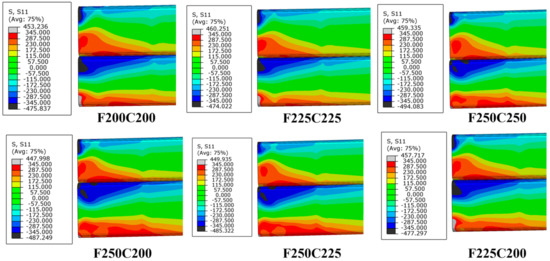
Figure 28.
Stress distribution of twin beams with different height.
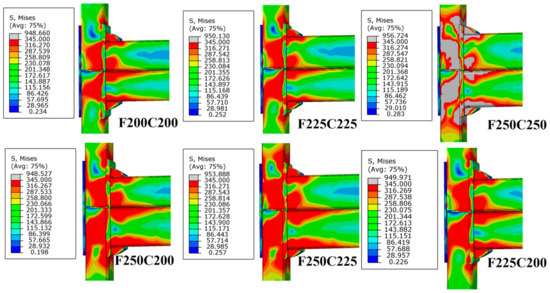
Figure 29.
Mises stress distribution of connections with different height.
3. Component-Based Model
3.1. Component Identification
According to the parameter analysis, the significant factors affecting the mechanical properties of modular connections were the geometric dimension of twin beams and admissible construction errors reserved between the inbuild component and columns. In reference to the classical studies on the component method and the three-dimensional macro model on Yukihiro Harada et al. [29,30], the model for novel modular connections was built (shown in Figure 30).
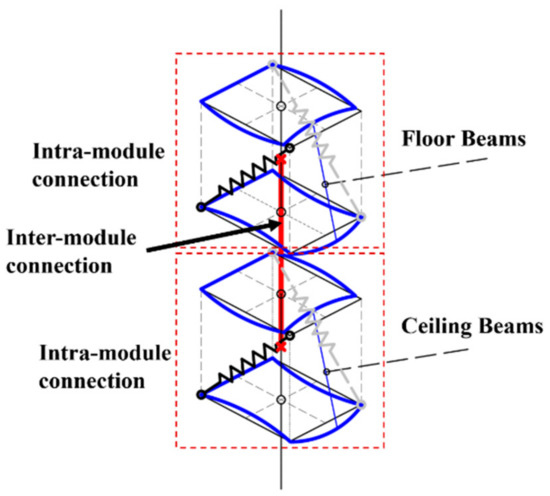
Figure 30.
Three-dimensional component model for the novel modular connection.
The advantage of the model was that it can distinguish the deformation of intramodule connections and intermodule connections that are shown in Figure 31. The skeleton (a) consists of several horizontal rigid rods and five vertical rigid rods. The plane composed of horizontal rods defines the deformation location of the converging section component (b) deformations. The space formed by vertical rods defines the region of intramodule connections. Converged section components (b) consist of the compression and tension deformations in column main face and side walls. It covers the interaction mechanism between columns and the inbuild component as well. Diagonal springs (c) located between the pair of converged section components represent the shear deformation of the intrajoint panel. Ceiling beams or floor beams were connected to a pair of converged section components through a rigid bar (d). The beam element (e) connected the geometrical center of the upper and lower skeleton to represent the behavior of intermodule connection. It can be concluded from the model that the mechanical properties of global modular connection could be obtained through superposing that of intramodule connections and intermodule connections. Moreover, for each intramodule connection, the key component was the joint panel and converged section component. The model needs to be based on the following assumptions:
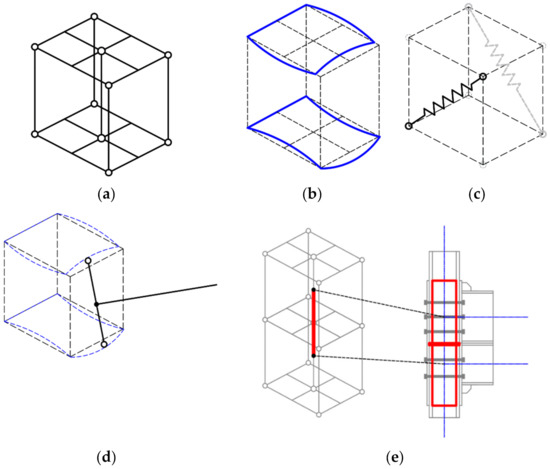
Figure 31.
The component deformation mode of novel modular connections: (a) The skeleton; (b) Converging section component; (c) Diagonal springs; (d) Beam connection; (e) The beam element (intermodule connection).
- (1)
- The rigid body assumption was made to beam end plate.
- (2)
- The allowable construction errors and relative dislocation between the upper and lower column were considered as the mechanical properties of intramodule connections (will be discussed in Section 3.2.3).
- (3)
- Based on assumption (2), only rotational deformation will be considered in intermodule connections.
- (4)
- The enhancement stiffeners’ effect on connections was neglected.
3.2. Characteristics of Components
3.2.1. Joint Panel (Shear Behavior)
A typical shear-load-displacement diagram of a steel plate was shown in Figure 32. When there was no support inside the column, the shear stiffness and the strength within the elastic range of the joint can be calculated by the following formula:
where z is the force arm (), β is the conversion parameter (β ≈ 1), is the shear area of the joint panel. In addition, the double shear sectional area should be considered in a square steel column.
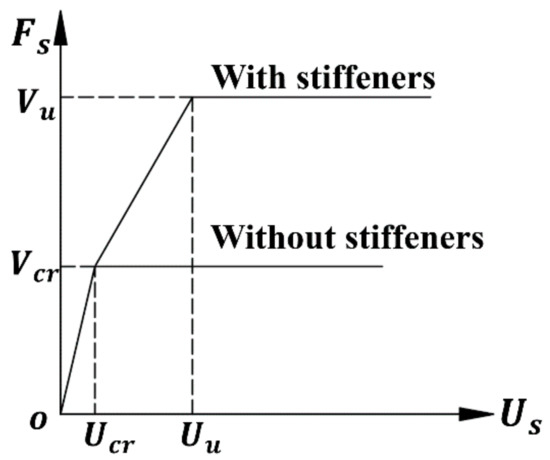
Figure 32.
Shear-load-displacement diagram.
During the assembly of the proposed novel modular connection, an inbuild component was inserted into the side column, which played the same role as transverse stiffeners. Hence the shear resistance could be increased by (shown in Figure 33).
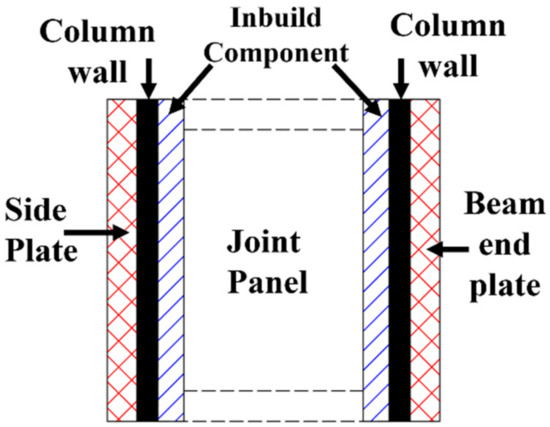
Figure 33.
The reinforcement of inbuild component to joint panel.
is the plastic moment resistance of column flanges. The dimension variable in all expressions was shown in Figure 34.
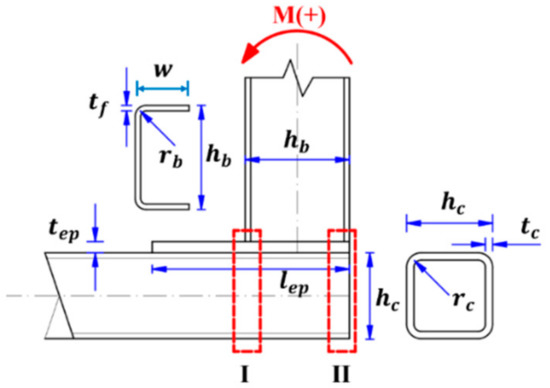
Figure 34.
Dimensions and geometric construction of intramodule connection.
3.2.2. Converged Section Component
The dimension of “L” type intramodule connection was shown in Figure 34. The converged section components were marked as red dashed lines which are located at the column corresponding to the top and bottom flanges of the beam. For the sake of easy description, the component near the column end was named “II” and the other side was named “I”. The moment direction from “II” to “I” was defined as positive. The deformation mode of the converged section component was shown in Figure 35; represents the vertical deformation caused by bending of the main column surface, and represents the vertical deformation caused by tension or compression of the column side wall. The total displacement of the converged section component can be obtained with plus .
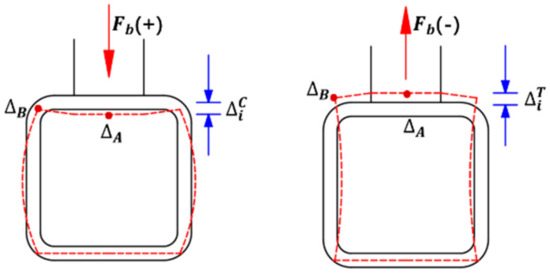
Figure 35.
Deformation model of converged section component.
According to the previous parameter analysis and the research in RHS joints [31] area, the main factors affecting the mechanical properties of the converged section component include the height () and thickness () of the column, the thickness of the beam end plate (), the length of the loading area (beam flange width ()). Moreover, one of the main features of intramodule connection is that the joint panel is very close to the column open end. It will lead to the distance (d) between the converged section model and the column end becoming an important influencing parameter. Based on the above reasons, this paper used the fitting method to obtained the force–displacement relationship of the converged section component.
The reference finite element model was shown in Figure 36. The length of the model was six times the height. The model was meshed by the “S4” shell element in Abaqus. The material properties are the same as the refined finite element model in Section 2.3. It was found that the force–displacement relationship of the converged section component can be expressed as
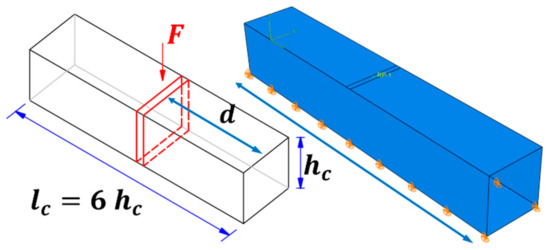
Figure 36.
Reference finite element model.
and are the shape parameters. As approaches infinity, is equal to . As is equal to 0, the slope of the functions is . It illustrates that and reflect the initial stiffness and ultimate strength of the converged section component to a certain extent. Therefore, studying the influence of various factors on the mechanical properties of the component section area is equivalent to studying that of various factors on and . The relationship between (, ) and (, ) was first studied. Using the control variable method, the thickness of the beam end plate () was set as 0, and the width of the beam flange (w) was equal to the height of the ring region . Finite element modeling was carried out for square columns with a height of 100 mm to 500 mm in Appendix 1 of “Cold formed Hollow Steel for Structure” [28], and 79 groups of numerical models were built. The force–displacement curves of 79 models were fitted according to the rules of (5), and 79 groups of (, ) were obtained. Constructing and represents the relation between and with (, ), respectively. After a tentative fitting, it is found that and conform to “Poly2D” and “Plane” functions, respectively:
When setting the ratio of the thickness of the main column surface ( + ) to the thickness of the column side wall () as α, the influence of the beam end plate on the mechanical properties of the converged section component can be expressed as a function of α. In order to simplify the calculation and the number of models, columns with a height of 150 mm and α thickness of 8 mm were taken as the basic model. The value of α range from 1 to 3.75 with an interval of 0.25. Following the same fitting procedure of (, ), 20 groups of (, ) were obtained. The ratio of (, ) with beam end plates to (, ) without the beam end plate was calculated, and the results were fitted with α. The influence of the beam end plate on the mechanical properties of the converged section component were obtained, which were defined as and corresponding to that of and , respectively.
Define the ratio of beam flange width (w) and distance (d) to column height () as and , respectively. Set the column with a height of 150 mm, thickness of 8 mm and α value of 2.5 as the reference model . The value of β ranges from 0.5 to 1.0, with an interval of 0.05. The value of ranges from to 2.0, where the interval between 0 and 1.0 was 0.1 and between 1.0 and 2.0 was 0.25. A total of 165 models were built. The effect of β and η on (, ) was obtained by fitting the force–displacement relation of 165 models and then dividing by the of the reference model, which was set as and , respectively.
The parameter values and of all fitting curves were summarized in Table 2. The final force ()-displacement () relationship expressions of the converged section component were as follows:

Table 2.
Summary of fitting coefficients.
3.2.3. Interaction Mechanism
During the assembly of modular units, inbuild components were inserted and secured by side plates and long bolts. According to the parameter analysis in Section 2, it was found that the thickness of the inbuild component has a positive effect on the rotational stiffness of the novel modular connection. The potentiation mechanism of the inbuild component can be reflected in the converged section component as shown in Figure 37. When the converged section component was under compression, the inbuild component would constrain the vertical displacement, leading to the improvement of mechanical properties. When the converged section component was under tension, the inbuild component was separated from the column face. Although the mechanical properties could still be improved by constraints on the column side walls, the extent of improvement was significantly lower than that under compression, obviously.
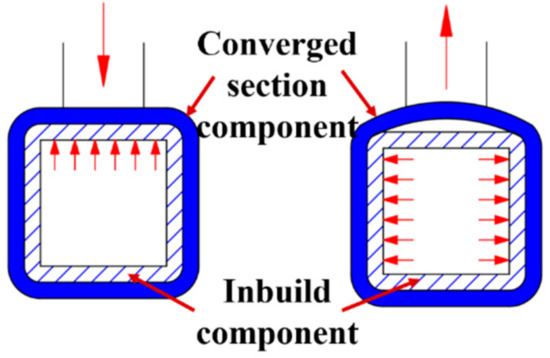
Figure 37.
The potentiation mechanism of inbuild component to section component.
Taking the allowable construction errors into consideration, the interaction mechanism was shown in Figure 38. The deformation mode can be divided into three stages. In the initial stage, the column face was bent under the action of compression force, but it had not contacted the inbuild component, so the mechanics of the component coincide with that without the inbuild component. In the second stage, the deformation of the column wall reached the construction error G; the inbuild component began to provide support for the converged section components. In the third stage of stress, the column face and the inbuild component were cooperating to deform. The inbuild component continued to provide support for the column.
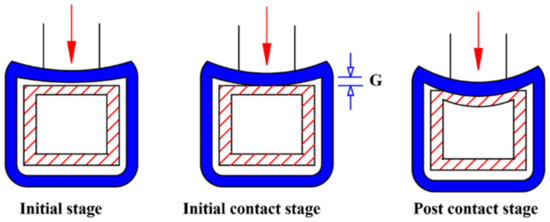
Figure 38.
The deformation mode of converged section component considering construction errors.
From above analysis, the interaction mechanism under compression between the converged section and the inbuild component was conformed to parallel springs as shown in Figure 39. The ( = I, = II) represents the force–displacement relationship between “I” and “II”, which conforms to (12). The represents the force–displacement relationship of the inbuild component which conforms to (15) without the influence of . and were the shape parameters of the inbuild component. and were the height and thickness of the inbuild component.
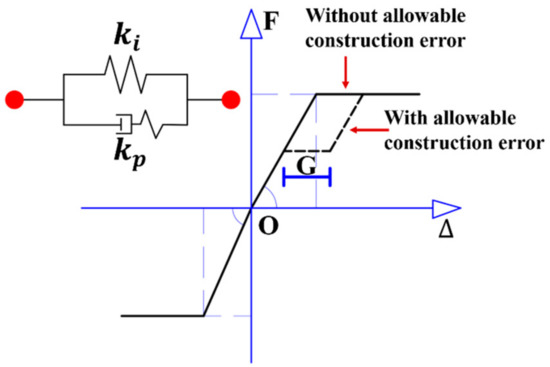
Figure 39.
Spring model for understanding interaction mechanism between inbuild component and converged section component.
3.3. Component Identification
Based on the above analysis and the research of L.M. Gil-Martín [31], the calculation model of intramodule connection was shown in Figure 40. When considering the independent mechanical properties of intramodule connections, the spring of inbuild component () needs to be removed. The significance of discussing the independent intramodule connection lies in the design of mechanical properties of modular units before assembly (such as transportation and hoisting et al.). According to the simplified rule of spring in series and parallel, the spring group in I area can be simplified to a single spring with stiffness of and ultimate resistance of ; the spring group in II area can be simplified to a single spring with a stiffness of and ultimate resistance of . Therefore, the initial rotational stiffness and ultimate bending moment of intramodule can be expressed as
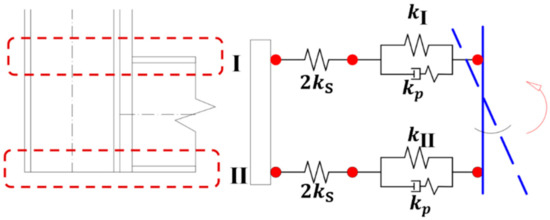
Figure 40.
Spring-based model for intramodule connections.
4. Validation
4.1. Intramodule Connections
The simplified finite element model of the intramodular connection was shown in Figure 41a. The floor beam (or ceiling beam) was modeled by the B31OS element in Abaqus, while the column was modeled by the B31 element. A rotational spring was placed at the intersection point between beam and column, which were modeled as connectors with “join and revolution” in Abaqus. The moment–rotation relationship of the spring was calculated through the method described in Section 3. To verify the accuracy of the simplified model, more refined models were built using a shell element as shown in Figure 41b. The column bottom face was pinned to the ground, and the material properties were consistent with the model in Section 2. The letter B followed by a number indicates the height of the beam, the letter P indicates whether the influence of inbuild component was considered, the letter G followed by a number represents the allowable error and values were considered, and the letter M means the simplified model. The thickness of inbuild component () was 10 mm. The other dimension details were the same as the refined finite element model in Section 2.
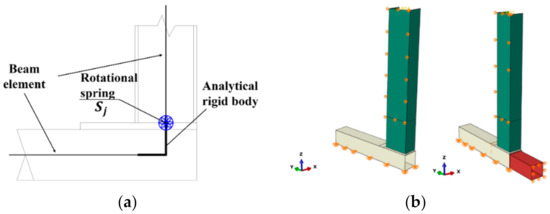
Figure 41.
Finite element model of intramodule connection for validation. (a) Simplified finite element model; (b) Refined finite element model.
The comparison results between simplified and refined finite element model were shown in Figure 42. Figure 42a shows the moment-rotation curves without setting the inbuild component. When the connection was subjected to the positive bending moment, the “I” region was in compression and the “II” region was in tension. “II” had low mechanical properties as compare to “I” due to its proximity to the column open end. Therefore, the failure mode of the connection was the tension failure at the “I”, and the beam had not reached its ultimate bearing capacity. The same conclusion can be deduced when the connections were subjected to negative bending moment but with the compression failure at “II”. The curves of the simplified and refined finite element mode were almost coincided in elastic stage. In the nonlinear stage, the curve of the simplified model was slightly higher than that of the refined finite element method. Figure 42b shows the results of connections enhanced by the inbuild component under the positive bending moment. The inbuild component enhanced the stiffness and strength of the “I” part but had little effect to the “II” region, so the failure mode of the connection was still the tension failure of the “II” region. The results of simplified model were in good agreement with those of the refined finite element in linear stages. In the plastic stage, the curves of the simplified model were close to horizontal, while the curve of the refined finite element model showed a trend of slow decline. Figure 42c showed the comparison results under the negative bending moment with the inbuild component. The simplified model agreed well with the refined finite element model in the elastic stage. There was no obvious elastic–plastic stage in the mechanical model, and the ultimate bending moment in the plastic stage is slightly lower than that predicted by the refined finite element method. Under the negative bending moment, the “I” region was in the tension state, and the “II” region was in the compression state. The existence of the inbuild component greatly enhances the compressive stiffness and strength of the “II” region, and thus it improves the initial stiffness and ultimate bearing capacity of the connection (Figure 37). Therefore, the failure mode of the joint was that the plastic hinge was formed at the joint beam. When there was construction error between the inner plug-in and the node column, the moment-rotation curves under the negative bending moment were shown in Figure 42d. The curves with construction error were between that without the inbuild component (B250) and without construction error (B250-P), which can be regarded as the lower limit and upper limit. The shape of the curve can be explained by the interaction mechanism between the inbuild component and the converged section component (Figure 38). According to the value of the allowable construction error, the “II” region will be strengthened at different rotational degrees, hence there will be a “slip” phenomenon on the curves. The slip length predicted by the simplified model was slightly lower than that by the refined finite element method. After the intramodule connections were strengthened by inbuild component, the failure mode was a plastic hinge formed at the beam. Because the beam height used in the model was all 250 mm, the ultimate bending capacity of the connections was the same. The prediction results of the simplified finite element model at this stage are slightly lower than that of the refined finite element model. The quantitative comparison of mechanical properties of intramodule connection was summarized in Table 3. In general, the simplified finite element model could accurately predict the mechanical properties and behavior of intramodule connections.
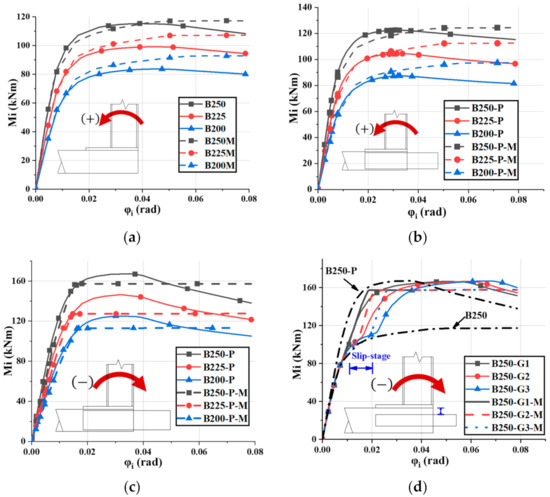
Figure 42.
Moment-rotation curves of intramodule connections: (a) Under positive bending moment without inbuild component; (b) Under positive bending moment with inbuild component; (c) Under negative bending moment with inbuild component; (d) Under negative bending moment with inbuild component and take construction errors into consideration.

Table 3.
The comparison between simplified and finite element model.
4.2. Global Connections
The global simplified finite element model of novel modular connections was shown in Figure 43. It consists of two simplified intramodule connection models and a beam element to represent the intermodule connection. The mechanical properties of intermodule connection should cover all the bending deformation between the upper and lower intramodule connections, such as upper and lower columns, the inbuild component, side plates and the beam-end plate. However, for the novel modular connections, it was obvious that the inbuild component was the main part to transfer the bending moment. Therefore, the cross-section characteristics of the beam can be determined according to the inbuild component dimension. The length of intramodule connection was the distance between the geometric centerline of floor beams and ceiling beams. In this paper, the twin beams were in direct contact, hence the was half of the total height of the ceiling and the floor beams. The intermodule beam was rigidly connected with the upper and lower intramodule connections to simulate the fixing effect of the long-split bolts. In the simplified model, equal vertical displacement was applied to the ends of the floor and ceiling beams simultaneously to ensure that the loading condition was equivalent to that of the refined model in the finite element parameter analysis.
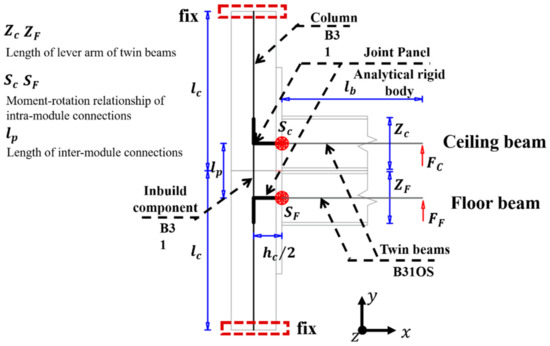
Figure 43.
Simplified finite element model of global novel modular connections.
According to the research results of intramodule connection, a slip stage would appear in the moment-rotation curves when there was construction allowable error. This result was obtained when the geometric centerline of the inbuild component coincides perfectly with that of the side column. However, in the process of the global modular connection deformation, it was difficult to determine the exact relative position between the inbuild component with the upper and lower columns. Therefore, the conservative estimation method as shown in Figure 44 was used to calculate the moment-rotation curve when the allowable error of construction was considered in global modular connections.
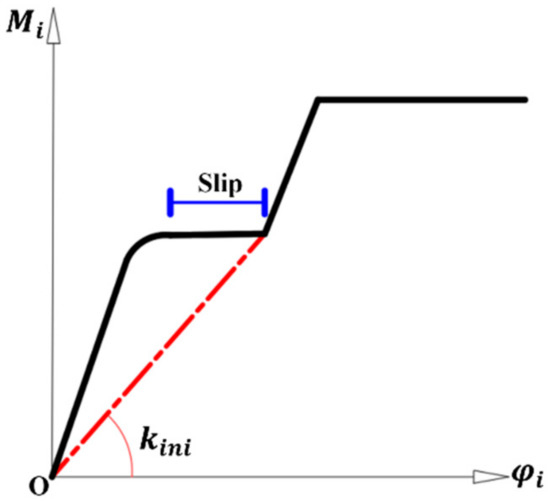
Figure 44.
Estimated initial stiffness considering allowable construction errors.
Thus, the initial stiffness and ultimate bearing capacity of the global modular connections can be obtained, which are summarized in Table 4. When the construction error was 1 mm, the predicted initial stiffness of the simplified finite element model was 2.12% higher than that of the refined finite element model. The predicted initial stiffness of the other models was lower than that of the refined finite element model, and the error of F225C200 model was slightly more than 10%. The average error of the simplified finite element model about initial stiffness was 3.9%. The prediction value of the ultimate bending capacity of the joints by the simplified mechanical model was low, with an error range of 7.0% to 11.2% and an average error of 9.3%. In general, the proposed model can well predict the mechanical behavior of novel modular building connections.

Table 4.
Comparison between the simplified model and the finite element model of novel modular connections.
5. Conclusions
- (1)
- Bolt preload, side plate thickness and inbuild component height had little influence on mechanical properties of novel modular connections. The thickness of the inbuild component affected the initial stiffness and continuity of the connection but had no effect on the ultimate bending capacity of the joint. The allowable construction error mainly affected the initial stiffness of the joint but did not change the ultimate bending strength of the joint. The height of twin beams was proportional to the initial stiffness and ultimate bending capacity of the novel modular building connections. When the height of the floor beam was equal to that of the ceiling beam, the continuity index of the connections was better. When the height of floor beam was larger than the ceiling height, the rotational difference between upper and lower columns increased and the continuity of connections decreased.
- (2)
- A component-based model for novel modular connections was established. The advantage of the model was that it can describe the deformation of intramodule connections and intermodule connections, respectively. The key factor of the model was the converged section component, and its force–displacement relationship under various parameters was obtained by the fitting method. The interaction mechanism between inbuild component and columns was analyzed. It was found that the inbuild component improved the mechanical properties of the converged section component under compression but had little effect on the mechanical properties under tension. Taking the allowable construction errors into consideration, the deformation mode can be divided into three stages which would cause a “slip” in moment-rotation curves of a related model.
- (3)
- A simplified finite element model of intramodule connection was built and compared with the finite element model meshed by “shell element”. For connections without the inbuild component, the failure mode was the tension (compression) failure at the column open end (called “II” region in the paper). The inbuild component can improve the mechanical properties of the intramodule connection under negative bending moment by protecting the “II” from compression failure. When the connection was under positive bending moment, the initial stiffness was increased by improving the mechanical properties of “I” region, but the failure mode remained unchanged. The curves with construction error were between that without the inbuild component and without construction error. In general, the simplified finite element model could accurately predict the mechanical properties and behavior of intramodule connections.
- (4)
- The simplified finite element model of global novel modular connections was built and compared with the refined finite element model. Length and section characteristics of the “beam” element that represented the intermodule connection was clearly stated. The conservative estimation method was proposed to evaluate the weakening effect of allowance construction error on initial stiffness of global modular connections. The average error of the simplified finite element model about initial stiffness and ultimate bending moment was 3.9% and 9.3%, respectively. In general, the proposed model can predict the mechanical behavior of novel modular building connections within the acceptable margin of error.
Author Contributions
Conceptualization, R.M. and J.X.; methodology, J.X.; software, R.M. and B.X.; validation, J.X. and H.C.; investigation, B.X.; writing—original draft preparation, R.M.; writing—review and editing, R.M.; supervision, J.X.; project administration, J.X.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52074270 and grant number 51978657. This research was funded by Doctoral Research Fund of JiangSu Collaborative Innovation Center for Building Energy Saving and Construction Technology, grant number SJXTBS1721.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors thank the reviewers for constructive comments and suggestions that have helped to improve our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.X.; Al-Hussein, M.; Lei, Z.; Ajwhen, Z. Risk identification and assessment of modular construction utilizing fuzzy analytic hierarchy process (AHP) and simulation. Can. J. Civ. Eng. 2013, 40, 1184–1195. [Google Scholar] [CrossRef]
- Lu, N.; Korman, T. Implementation of Building Information Modeling (BIM) in Modular Construction: Benefits and Challenges Na Lu1 and Thomas Korman2. Constr. Res. Congr. 2010, 1136–1145. [Google Scholar]
- Ferdous, W.; Bai, Y.; Ngo, T.D.; Manalo, A.; Mendis, P. New advancements, challenges and opportunities of multi-storey modular buildings—A state-of-the-art review. Eng. Struct. 2019, 183, 883–893. [Google Scholar] [CrossRef]
- Brunesi, E.; Peloso, S.; Pinho, R.; Nascimbene, R. Cyclic testing of a full-scale two-storey reinforced precast concrete wall-slab-wall structure. Bull. Earthq. Eng. 2018, 16, 5309–5339. [Google Scholar] [CrossRef]
- Brunesi, E.; Peloso, S.; Pinho, R.; Nascimbene, R. Cyclic testing and analysis of a full-scale cast-in-place reinforced concrete wall-slab-wall structure. Bull. Earthq. Eng. 2018, 16, 4761–4796. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Yu, Y. Experimental study on interior connections in modular steel buildings. Eng. Struct. 2017, 147, 625–638. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Yu, Y.; Zhou, C.; Yan, R. Experimental study of an innovative modular steel building connection. J. Constr. Steel Res. 2017, 139, 69–82. [Google Scholar] [CrossRef]
- Dhanapal, J.; Ghaednia, H.; Das, S.; Velocci, J. Structural performance of state-of-the-art VectorBloc modular connector under axial loads. Eng. Struct. 2019, 183, 496–509. [Google Scholar] [CrossRef]
- Dai, X.M.; Zong, L.; Ding, Y.; Li, Z.-X. Experimental study on seismic behavior of a novel plug-in self-lock joint for modular steel construction. Eng. Struct. 2019, 181, 143–164. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; El Naggar, M.H. Seismic overstrength in braced frames of modular steel buildings. J. Earthq. Eng. 2008, 13, 1–21. [Google Scholar] [CrossRef]
- Sultana, P.; Youssef, M.A. Seismic performance of modular steel-braced frames utilizing superelastic shape memory alloy bolts in the vertical module connections. J. Earthq. Eng. 2020, 24, 628–652. [Google Scholar] [CrossRef]
- Fathieh, A.; Mercan, O. Seismic evaluation of modular steel buildings. Eng. Struct. 2016, 122, 83–92. [Google Scholar] [CrossRef]
- Gunawardena, T. Behaviour of Prefabricated Modular Buildings Subjected to Lateral Loads. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2016. [Google Scholar]
- CEN. EN 1993-1-8: Eurocode 3: Design of Steel Structures–Part 1–8: Design of Joints; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- CEN. EN 1994-1-1: Eurocode 4: Design of Composite Steel and Concrete Structures-Part 1–1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Sadeghi, S.N.; Heidarpour, A.; Zhao, X.L.; Al-Mahaidi, R. A component-based model for innovative prefabricated beam-to-hybrid tubular column connections. Thin-Wall Struct. 2018, 132, 265–275. [Google Scholar] [CrossRef]
- Demonceau, J.F.; Weynand, K.; Jaspart, J.P.; Muller, C. Application of Eurocode 3 to steel connections with four bolts per horizontal row. In Proceedings of the SDSS’Rio 2010 Conference, Rio de Janeiro, Brazil, 8–10 September 2010; pp. 199–206. [Google Scholar]
- Málaga-Chuquitaype, C.; Elghazouli, A.Y. Component-based mechanical models for blind-bolted angle connections. Eng. Struct. 2010, 32, 3048–3067. [Google Scholar] [CrossRef] [Green Version]
- Alhasawi, A.; Guezouli, S.; Couchaux, M. Component-Based Model Versus Stress-Resultant Plasticity Modelling of Bolted End-Plate Connection: Numerical Implementation[C]//Structures; Elsevier: Amsterdam, The Netherlands, 2017; Volume 11, pp. 164–177. [Google Scholar]
- Stylianidis, P.M.; Nethercot, D.A. Modelling of connection behaviour for progressive collapse analysis. J. Constr. Steel Res. 2015, 113, 169–184. [Google Scholar] [CrossRef]
- Del Savio, A.A.; Nethercot, D.A.; Vellasco, P.; Andrade, D.A.L.; Martha, L.F. Generalised component-based model for beam-to-column connections including axial versus moment interaction. J. Constr. Steel Res. 2009, 65, 1876–1895. [Google Scholar] [CrossRef]
- Block, F.M.; Davison, J.B.; Burgess, I.W.; Plank, R.J. Principles of a component-based connection element for the analysis of steel frames in fire. Eng. Struct. 2013, 49, 1059–1067. [Google Scholar] [CrossRef]
- Ma, R.; Xia, J.; Chang, H.; Xu, B.; Zhag, L. Experimental and numerical investigation of mechanical properties on novel modular connections with superimposed beams. Eng. Struct. 2021, 232, 111858. [Google Scholar] [CrossRef]
- Bo, X.; Junwu, X.; Hongfei, C.; Renwei, M.; Lihai, Z. Flexural behaviour of pairs of laminated unequal channel beams with different interfacial connections in corner-supported modular steel buildings. Thin-Wall Struct. 2020, 154, 1–12. [Google Scholar]
- Bo, X.; Junwu, X.; Hongfei, C.; Renwei, M.; Lihai, Z. A comprehensive experimental-numerical investigation on the bending response of laminated double channel beams in modular buildings. Eng. Struct. 2019, 200, 1–15. [Google Scholar]
- Bo, X.; Junwu, X.; Renwei, M.; Jian, W.; Xiaomiao, C.; Hongfei, C.; Lihai, Z. Investigation on true stress-strain curves of flat and corner regions of cold-formed section using 3D digital image correlation method. Adv. Civ. Eng. 2019, 3138176, 1–18. [Google Scholar]
- Brunesi, E.; Nascimbene, R.; Rassati, G.A. Seismic response of MRFs with partially-restrained bolted beam-to-column connections through FE analyses. J. Constr. Steel Res. 2015, 107, 37–49. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Rassati, G.A. Response of partially-restrained bolted beam-to-column connections under cyclic loads. J. Constr. Steel Res. 2014, 97, 24–38. [Google Scholar] [CrossRef]
- Harada, Y.; da Silva, L.S. Three-dimensional macro-modeling of beam-to-rectangular hollow section column joints under cyclic loading. Part 1: Modeling of cyclic out-of-plane behavior of single isolated plate element. J. Constr. Steel Res. 2019, 162, 105713. [Google Scholar] [CrossRef]
- Harada, Y.; da Silva, L.S. Three-dimensional macro-modeling of beam-to-rectangular hollow section column joints under cyclic loading. Part 2: Modeling of beam-to-column joint by extended component-based approach. J. Constr. Steel Res. 2019, 162, 105714. [Google Scholar] [CrossRef]
- Garifullin, M. Component Method for High Strength Steel Rectangular Hollow Section T Joints; Tampere University: Tampere, Finland, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).