Abstract
We present the CFD based non-dimensional characterization of violent slosh induced energy dissipation due a tank under vertical excitation. Experimentally validated CFD is used for this purpose as an ideally suited and versatile tool. It is thus first demonstrated that a weakly compressible VoF based CFD scheme is capable of computing violent slosh induced energy dissipation with high accuracy. The resulting CFD based energy analysis further informs that the main source of energy dissipation during violent slosh is due liquid impact. Next, a functional relationship characterising slosh induced energy dissipation is formulated in terms of fluid physics based non-dimensional numbers. These comprised contact angle and liquid–gas density ratio as well as Reynolds, Weber and Froude numbers. The Froude number is found the most significant in characterising verticle violent slosh induced energy dissipation (in the absence of significant phase change). The validated CFD is consequently employed to develop scaling laws (curve fits) which quantify energy dissipation as a function of the most important fluid physics non-dimensional numbers. These newly developed scaling laws show for the first time that slosh induced energy dissipation may be expressed as a quadratic function of Froude number and as a linear function of liquid–gas density ratio. Based on the aforementioned it is postulated that violent slosh induced energy dissipation may be expressed as a linear function of tank kinetic energy. The article is concluded by demonstrating the practical use of the novel CFD derived non-dimensional scaling laws to infer slosh induced energy dissipation for ideal experiments (with exact fluid physics similarity to the full scale Aircraft) from (non-ideal) slosh experiments.
1. Introduction
The modelling of liquid–gas free-surface interaction (sloshing) within tanks and containers is an area of interest within the aerospace industry, impacting aerodynamic stability and aircraft control characteristics during flight, ground manoeuvres and loads. As such the EU H2020 SLOWD (SLOshing Wing Dynamics) [1] aims to characterise and model the impact of fuel sloshing on the damping characteristics of a wing structure due to vertical excitation where the direction of excitation is normal to the liquid free-surface. The preceding Protospace tests [2,3] proved that liquid sloshing provides significant energy dissipation (damping) to a cantilever based tank undergoing free-vibration due to an initial structural perturbation. In this case, the major frequency of excitation was found to remain constant. Note that the beam tip underwent geometrically linear motion (The verticle displacement is small compared to the beam length.). This article, therefore, focuses on non-dimensionally characterising the violent liquid slosh induced energy dissipation due vertical tank motion at a fixed frequency . The tank motion is therefore prescribed as a single-degree-of-freedom (SDOF) system. Further, it is assumed that the liquid density is orders of magnitude larger than that of the gas while the liquid may be assumed as incompressible while the gas is modelled via a weakly compressible formulation. Finally, the flow physics does not involve significant phase change.
Due to the laboratory scale of the cited experiments [2,3], increased understanding of the bias introduced by such geometric scaling is a key objective of this article. To this end we develop suitable similarity parameters to account for the effects introduced by non-ideal (practical) scaling such that the influence of sloshing on the structural dynamics of full scale aircraft wings may be quantified. Once validated, the use of CFD is key in such studies, as it allows for quantification of the influence of a wide range of parameters and their combinations on slosh induced damping. This is not possible experimentally if limited to available fluid properties. In this work, all CFD calculations are conducted with the multi-physics CFD code Elemental® [4,5,6,7,8].
It is widely accepted that non-dimensional analysis provides a powerful technique to characterise a complex physical system. This enables the study and quantification of the relative importance of various physical parameters/phenomena on such systems [9]. Despite the insights that non-dimensional analyses provide, limited studies of violent slosh through such techniques exist in literature. Thompson and Nein [10] successfully employed dimensional analysis as a method to predict the pressurisation requirements for space vehicles at launch. Summer [11] developed a generalisation of slosh force subject to several excitation frequency parameters for various tank geometries. The above cited work did not deal specifically with slosh induced energy dissipation.
Past work into the application and tuning of liquid damping systems has centred on structural design and civil engineering applications [12,13]. Previous aeroelastic studies into the influence of slosh damping focus on the general trends and changes in flutter boundaries due to various tank fill-level configurations [14]. These campaigns neglected the vertical motion of the tank, employing seismic shaking tables to provide the excitation to the structure.
This article furthers on existing work in a number of respects. First, weakly compressible volume of fluid (VoF) based CFD [15,16] is experimentally validated, predicting violent slosh induced energy dissipation to with-in of the experimental values. The CFD also uncovers that the main source of slosh induced energy dissipation is due liquid impact. Next, the SDOF system is non-dimensionalised such that slosh induced energy dissipation may for the first time be expressed accurately in terms of Froude number and liquid-gas ratio via CFD generated curve fits. These in turn for the first time point to the possibility that slosh induced energy dissipation may be expressed as a linear function of tank excitation kinetic energy. Finally, it is demonstrated how the newly fitted non-dimensional scaling laws may be used with ease to estimate the slosh induced damping of ideally scaled experiments. Note that the development of the aforementioned scaling laws is impossible via laboratory size experimental campaigns due to limitations in available fluids. As such, for this purpose we employ the rigorously validated Elemental® volume-of-fluid (VoF) CFD software.
This paper is organised as follows:
- We validate the accuracy of the CFD code Elemental® for modelling violent vertical slosh physics relevant to this article.
- We detail the CFD based energy budget used to quantify effects of scaling non-dimensional properties on the system.
- We present a non-dimensional analysis of a SDOF tank under vertical slosh, isolating the functional relationship characterising slosh induced energy dissipation.
- We define the non-dimensional parameter space of interest for the problem under consideration (to include both experimental and full scales).
- Finally, we develop novel scaling-laws which correlate the slosh induced energy dissipation as a function of the identified non-dimensional parameters. This is done via curve fitting of CFD generated data.
- The developed novel scaling laws are finally applied to quantify ideal (representative of full scale aircraft) experimental slosh induced energy dissipation.
2. Validation of CFD Model
The utilisation of VoF CFD within the study requires accurate, high-fidelity, mesh independent simulations. Specifically, the accuracy with regards to the predicted slosh force is critical as this is the key uncertainty when quantifying slosh induced energy dissipation in this work (see Equation (12)). This is due to this work involving prescribed tank motions (obtained from measurements). The VoF CFD code Elemental® has been employed extensively to model violent slosh [17,18]. Turbulence is modelled via Large-eddy simulation (LES) employing the Smagorinsky-Lilly model [19] and a weakly compressible gas model [15,16] is employed while the liquid-gas interface initialisation is performed to machine precision accuracy via the AGI tool [20].
The validation of Elemental® as an accurate tool for this work requires the comparison of the computed results against relevant experimental data. The modelling of the fill-level Protospace experiment [3] has been selected for this purpose as it was designed to be a small scale representation of wing-tank based slosh. The Protospace experiment involved the damped vibration (structural and slosh damping) of a cantilever beam mounted with a seven compartmental fuel tank, as shown in Figure 1. The experiment involved applying an initial deflection and then releasing the cantilever at followed by free vibration [3].

Figure 1.
Footage of interface regimes for the Protospace Experiment. (a) t = 0.0 s; (b) t = 0.12 s, liquid–solid impact; (c) t = 0.4 s, Aerated Flow Slosh; (d) t = 3 s, Reconstituted Free Surface.
Using the measured tank accelerations from the experiment as input, CFD simulations were performed on a range of different mesh spacings. For the coarsest mesh considered (), 2D and 3D simulations resulted in near identical computed slosh forces and therefore energy dissipation due to the definition of (see Equation (12)). In the interest of computational efficiency therefore, 2D was employed for all subsequent simulations. The 2D CFD predicted free-surface interface at various times is depicted in Figure 2. These may be compared to experimental footage (Figure 1). As shown, a range of different slosh regimes are present. These include liquid-solid impact (Figure 1b and Figure 2b), aerated flow Figure 1c and Figure 2c) and weakly linear slosh (Figure 1d and Figure 2d). Further, a reasonable agreement exists between predicted and experimental footage.
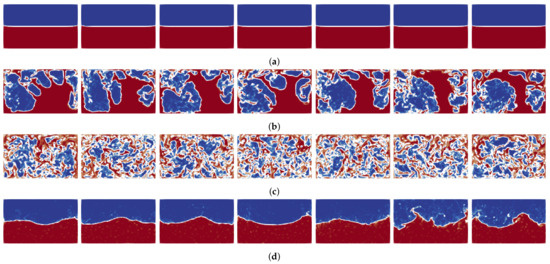
Figure 2.
CFD predicted interface regimes for the Protospace experimental case. (a) t = 0.0 s; (b) t = 0.12 s; (c) t = 0.4 s; (d) t = 3 s.
The use of LES to model turbulence required estimation of the Taylor micro-scale [21] as this informs mesh resolution. This was done as part of the SLOWD project [22] which yielded
where is the fluid kinematic viscosity, is kinetic energy dissipation rate and k is the turbulent kinetic energy. The above aided in informing suitable CFD mesh spacing as detailed next.
Figure 3 compares the measured and CFD predicted vertical slosh loads (See Equation (11)) for Cartesian meshes, namely and . Completing an error analysis and mesh sensitivity study provides Table 1 and Figure 4. This highlights engineering precision convergence for as the computed dissipated energy ( in Figure 5 computed via Equation (12)) is found to lie within of the experimental result. This validates the use of Elemental to predict violent slosh induced slosh loads and damping, provided that suitably fine meshes are employed. To ensure direct applicability, the SDOF slosh model used for our non-dimensional characterization will consist of one of the Protospace compartments and be modelled with a 2D Cartesian mesh with spacing .
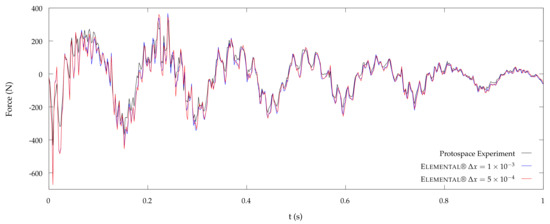
Figure 3.
Experimental vs. Elemental® Simulated Vertical Slosh Loads.

Table 1.
Error analysis.
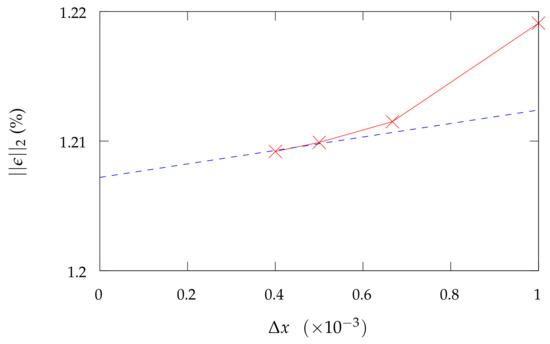
Figure 4.
Percentage difference between CFD predicted and experimentally derived slosh induced energy dissipation for various mesh resolutions.
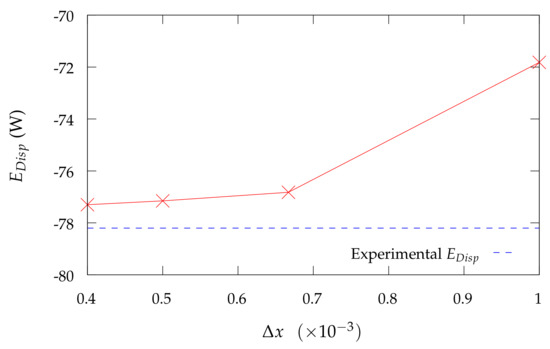
Figure 5.
Comparison of CFD predicted and experimentally derived slosh induced energy dissipation.
3. Energy Analysis
We next derive the relations employed to estimate slosh induced energy dissipation. For the system under consideration the mechanical energy budget is considered for this purpose. This is composed of the work done on the fluid by the domain boundary surfaces or surface work , deformation work , kinetic energy , potential energy , viscous dissipation , and surface tension energy . The full energy budget is defined by
where and includes losses due liquid impact (as described next).
Consider an enclosed fluid domain containing an immiscible liquid–gas mixture (gas is weakly compressible) undergoing a rigid body linear acceleration of . The resulting absolute fluid velocity (velocity relative to earth) can be defined as the sum of the domain velocity and the fluid velocity relative to the non-inertial reference frame (CFD mesh reference frame), therefore . The momentum conservation of the fluid is given by:
where p is pressure, t is time, is VoF volume fraction and the fluid properties are defined in Table 2. Mechanical energy conservation results from taking the dot product of Equation (3) with the volume averaged followed by integration over space and time (includes integration by parts of the pressure term):
where volume averaged quantities are defined as , is the surface of all mesh finite volumes , and is the outwards pointing normal. Further is the fluid domain bounding surface and due the domain being assumed rigid. The terms in Equation (4) quantify the different forms of energy:
where is the force from the tank onto the liquid and is the domain boundary viscous component included in (5). Therefore, the force is computed via the following expression,
which is used for the CFD load calculations.

Table 2.
Dimensional Matrix.
The reason for subtracting the kinetic energy term from the first integral in (8) is to account for the liquid impact related losses (we assume initial fluid velocities of ). These impact losses (liquid-liquid or liquid-wall) have been shown [23,24] to be accounted for by the liquid incompressible pressure-poisson fractional step [17] method employed in our solver. This is consistent with the accuracy achieved in the preceding section in computing slosh induced energy dissipation. Note that liquid impact was found to account for the dominant source of energy dissipation in this work. From the above, it is instructive to note that may also be approximated from experimentally measured data as follows:
where is the fluid mass in the tank and is the force of the tank on the fluid (which may be inferred from load cell measurements). This is provided that accurate tank position (displacement) data are available and noting it was found that accounts for less than of the energy budget.
4. Dimensional Analysis
The remainder of the article will consider a slosh system which is representative dimensionally of the Protospace experimental setup. As such we consider the vertical oscillation (SDOF) of a rectangular 2D tank (single Protospace compartment) supported by a mass-spring-damper system with a spring constant k and damper constant c. All simulations employ air at standard atmospheric conditions as the gas within the liquid-gas slosh system. Therefore the 14 parameters considered relevant to the dimensional analysis are presented in Table 2. Also included are entries of the dimensional matrix for the units of Mass (M), Length (L) and Time (T).
The rank 3 dimensional matrix employs the normalisation of length , mass and time respectively. A straightforward application of the Buckingham Pi Theorem leads to dimensionless groups:
We define the group as of the order solid to liquid mass ratio of the one-degree of freedom system. is the density ratio of the gas and liquid phase in the tank. groups 3 to 5 are well known flow physics related dimensionless numbers, namely Reynolds, Froude and Weber. Note that the v subscript is added to the latter to indicate that the standard definition based on the fluid speed was employed.
As we are interested in the energy dissipation of a tank which is supported by a spring-mass-damper system, the fluid non-dimensional numbers are to be written in terms of the resulting excitation. Considering harmonic motion at frequency enables expressing the reference flow velocity in terms of the slosh-mass-spring-damper system response as:
This is as in this work the magnitude of tank displacement is of a similar order to the tank height. To consolidate the validity of Equation (14) we note that from experimental observation the first two to three cycles of oscillation are representative of the slosh induced energy dissipation potential for the violent slosh under consideration. Hence only the first 3 excitation cycles are considered for the non-dimensional scaling calculations (to follow) as these are representative of peak loads and slosh induced dissipation. We can therefore modify groups 3 to 5 as follows
where , and are the excitation frequency-based Reynolds, Froude and Weber numbers, respectively. The Froude number as a function of the frequency parameter, therefore, infers a reduced frequency or a Strouhal number which represents the ratio of the characteristic time of the mechanical system and the fluid-characteristic time. Finally, the manipulation of and by combining with provides:
Here, we employ the standard definitions of the structural natural frequency of excitation and the structural damping ratio for harmonic oscillators, where:
and
Further, denotes the reduced frequency of the system (structure and slosh).
We are justified to choose h (tank height) as the characteristic length, as , and are derived by dividing all other relevant geometrical quantities by the characteristic length. The resulting is the tank aspect ratio, the liquid fill ratio and the dimensionless initial deflection of the mass-spring system. For the slosh case considered in this article, these quantities are and as a result the liquid centre of gravity displacements and wave height. The latter is a consequence of the slosh being within the physical bounds of the tank.
The derivation of a functional relationship to characterise the fluid-structure-system-damping will employ the resulting groups:
The total system damping can be decomposed into its two parts:
where and are the damping due the structure (dry) and slosh damping. To focus the analysis on the slosh induced damping via prescribed tank motion, we shall prescribe (the chosen value will be motivated when used in the relevant sections to follow) and such that the derivation of a functional relationship characterising the slosh damping results in the form:
From the above, we can identify three distinct groups of dimensionless numbers influencing the slosh damping within the SDOF system. The three groups are flow physics (fluid specific non-dimensional numbers such as , , , and ), fluid-structure interactions (FSI) and geometric non-dimensional factors. This paper employs high fidelity VoF CFD to investigate the influence of a range of flow physics parameters (As defined within Section 6) while the geometric numbers will remain unchanged and the FSI group will be selected such as to be consistent with the flow physics numbers. Specifically, will be dictated by the number.
5. Scaling of Violent Sloshing Systems
To provide a perfect scaled experiment requires complete mechanical similarity with the full scale system. This implies geometric, kinetic and dynamic similarity (identical force ratios for all terms in Equation (3)). While it is possible to achieve geometric and kinetic similarity, ensuring complete dynamic similarity is not practically feasible. This is as it requires identical non-dimensional numbers for all flow physics related ratios (, etc.) which is impossible using available fluids. As a result, experimental similarity of a single non-dimensional number is then targeted in industry, which in the case of slosh is the Froude number. Scaled slosh experiments are therefore designed by ensuring similar Froude numbers between experimental and real systems.
5.1. Froude Scaling Rules
For experimental scale, it is possible to achieve perfect geometric scaling , where is the tank height at full scale, and consequently that this scaling factor applies to all the geometric ratios. As noted above, slosh fluid physics is then commonly scaled using the Froude number:
hence,
Consequently, the Froude scaling for time t is
Ensuring geometrical and Froude similarity constrains two of the three fundamental units (length and time). The rule for mass is generally achieved by simply using a test fluid of the same density as the full scale (in fact when possible the same fluid is used). This assumption leads to
All other scaling rules then follow from those derived above for length, time and mass such that:
5.2. Practical Considerations
As a direct consequence of Table 3, using the same fluid for a reduced-scale experiment leads to differences in the Reynolds and Weber numbers to the full scale. In addition, there are no practical constraints in enforcing equality for the other groups.

Table 3.
Scaling Rules.
By way of example, for 1:5 scale (), Equation (26) imply viscous effects approximately ten times greater () and surface tension effects approximately twenty-five times greater () than those at full scale. An alternative could be to engineer a fluid with the same density as full scale and the appropriate scaling for viscosity and surface tension. The associated time and cost (if at all possible) however make the use of validated numerical models instead ideal.
In practice, even exact Froude scaling is not always feasible due to budget and time constraints. As shown in Table 4, the Protospace experiment did not achieve the required number. With the available materials, it was not possible to reach a closer similarity, as this would have required a bespoke cantilever design. The lower natural frequency of Hz would have implied a greater initial displacement of the free-end, possibly leading to a geometrically non-linear oscillation of the beam. Further, the fact that the characteristic velocity achieved is higher than that required by similarity could indicate that the dissipative effects due to liquid impact are overestimated experimentally if compared to an ideally Froude scaled experiment. All of the aforementioned point to the use of CFD to quantify the effect of the various non-dimensional numbers on all key physical characteristics (forces, damping, etc.) of interest. This will result in so-called non-dimensional scaling-laws, from which experimental data may be used to estimate the flow physics of the full-scale tank. This is the objective of the sections to follow and indeed a key contribution of this article.

Table 4.
Protospace Froude Similarity Parameters.
6. Non-Dimensional Property Parameter Space
The intended aim of the Protospace experiment [3] was to provide a Froude scaled aircraft wing with a geometry scaling of while employing water whereas the full-scale model makes use of cold kerosene. The calculated non-dimensional values for the Froude scaled Protospace (employing kerosene), actual Protospace (as achieved in the experimental campaign employing water) and the full-scale model are given in Table 5. Accordingly, the range of the non-dimensional parameter space for which to build the scaling-laws was chosen to contain both the Protospace and full-sized model non-dimensional values, as presented in Table 6. Note that the liquid–solid contact angle lower limit allowed by the software was and thus does not contain the value for kerosene. It was however found that (see next section) the key importance of contact angle lies in the initial meniscus, i.e., if the contact angle is or not. This is as the numbers are high while a contact angle results in the absence of Rayleigh–Taylor instability and therefore no violent slosh. Further, turbulence was found to be a minor contributor to energy dissipation (the major being liquid impact) and hence here implies the inviscid limit, i.e., .

Table 5.
Protospace vs Full Aircraft Non-dimensional Properties.

Table 6.
Non-dimensional property parameter space.
The CFD simulations to follow employ a single compartment tank undergoing a damped sinusoidal vertical acceleration where the vertical displacement is defined by,
where,
allowing an approximate acceleration definition such that,
Finally, as per the Protospace experiment m · s and for the non-dimensional number sensitivity study (next section). However, in computing the non-dimensional scaling graphs (later section) we set so as to focus on quantifying slosh induced damping.
7. Non-Dimensional Study Results and Analysis
To enable direct comparison (plotting on the same graph) of computed energy budget and slosh loads for different excitation frequencies and liquid masses, normalisation is required. Hence, the computed energy dissipated and work in are normalised to the maximum change in potential energy of a simulation . Further, computed vertical slosh force is normalised and oscillation count employed as follows:
Figure 6 and Figure 7 presents comparative ranges for the influence of fluid properties on the normalised sloshing fluid dissipation energy , surface work and vertical sloshing force . The influence range of each non-dimensional number on the aforementioned quantities are presented via the shaded region.
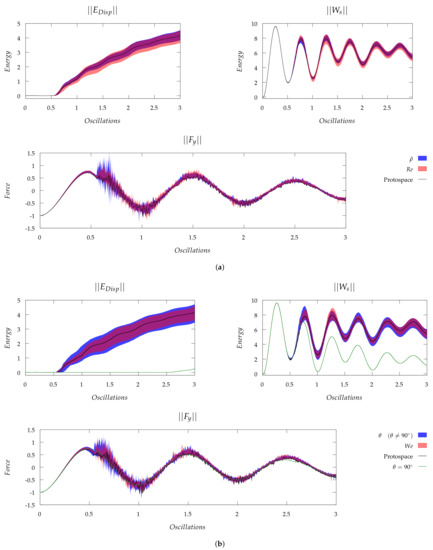
Figure 6.
Influence of flow physics on slosh induced damping, work and loads. (a) Density Ratio and Reynolds Number Scaling; (b) Fluid Surface Tension Properties.
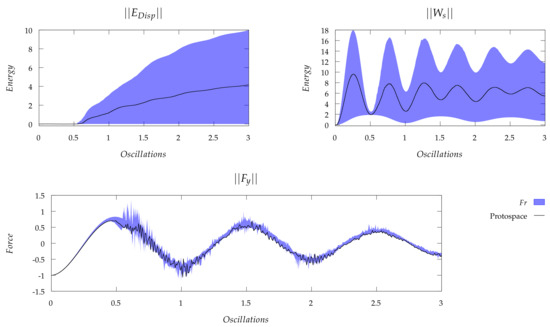
Figure 7.
Influence of flow physics on slosh induced damping, work and loads.
Table 7 lists the percentage root-mean-square difference due to the scaling of each non-dimensional property as compared to the actual Protospace values. The analysis reveals the relatively low influence of almost all fluid properties on where the RMSE and negligible on as RMSE . The exceptions are contact angle and number. The former is due a contact angle of resulting in no liquid–gas surface instability (Rayleigh–Taylor) and hence no slosh damping (note that the reported variation as opposed to is due numerically induced free-surface instability which occurs late in the analysis). At this point in the scaling analysis, the choice of Froude scaling (as opposed to etc.) is vindicated (and consistent with industrial practice) as all other fluid properties are shown to have a relatively small effect. This was further also demonstrated by a recent experimental campaign [25].

Table 7.
RMS Variation due to fluid property scaling relative to the actual Protospace (%).
We finally consider the effect that Froude scaling (via changing the excitation frequency) has on the system, with the results shown in Figure 7. Interestingly, for the Froude number range tested, the major effect is on slosh damping as shown, i.e., . This concludes the important insight that slosh induced dissipation is highly sensitive to Froude number, and to a far greater degree as compared to slosh forces.
8. Dissipated Energy Scaling Laws
We next focus on quantifying the change in slosh induced dissipation as a function of the fluid physics non-dimensional numbers. As mentioned before, we now set resulting in a vertical displacement and acceleration as defined by:
where it is instructive to note that the magnitude of tank displacement . It is important that this value remain fixed when varying the fluid physics non-dimensional numbers. Setting simplifies the calculation of slosh induced dissipation to:
The % change in computed slosh induced dissipation energy due a change in a non-dimensional parameter (from the Protospace value ) is expressed as:
Figure 8 depicts the discrete values for individually scaled non-dimensional numbers as well as the resulting trend line. Also delineated on the figures are the properties for the Protospace (black line) and full aircraft (green line). While no statistical trend was found for and (as a result not shown), the following cubic trend for was found around :
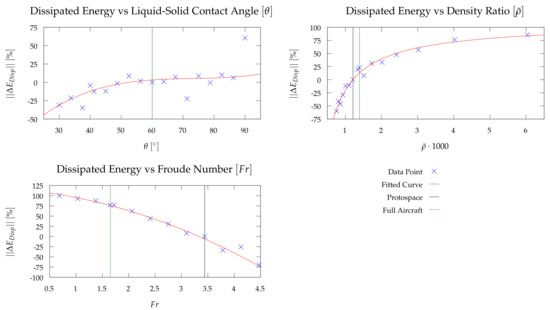
Figure 8.
Change in Dissipated Energy due to Scaling of Non-dimensional Properties.
Here, is the weighted sum of the squares of the difference between the fitted curve and the data such that with being a perfect fit. Outliers to this trend occur due to lack of Rayleigh Taylor instability for which leads to , while an enlarged meniscus results as (to be investigated in future work).
A very well-defined trend can however be found for the scaling of as:
Similarly, a very well defined trend is visible for the effect of the Froude number on slosh induced dissipation. The resulting trend line reads:
which is clearly quadratic in nature. This quadratic relationship between slosh induced dissipation and number is indeed a new finding and a key contribution of this article. Also note that the difference in dissipated energy between the Protospace experiment number and that of the actual aircraft (or indeed ideal experiment) are by far the most significant of all quantities. This necessitates the need to use the scaling law to estimate the expected slosh induced damping for the full scale aircraft tank. This is dealt with the in next section.
From the above it is evident that scales circa linearly with (due Equation (36)) and with (due Equation (37)). The latter is as the maximum tank velocity due Equation (14). From this, we postulate that it is possible to express dissipated energy as a linear function of tank kinetic energy viz.
for the slosh under consideration.
We digress briefly to investigate the difference in fitted scaling curves for each of the three cycles of oscillation. This is to confirm that scaling laws obtained per cycle are consistent with the experimental observation that the slosh damping which occurs over the first two to three cycles of oscillation is representative of the energy dissipation potential. The resulting curves are shown in Figure 9 while similar correlations to previously were found in most cases (see equations to follow). Apart from the curves, there is a reasonable correlation between the curve fits obtained for the three cycles with the number curve fearing the best. The correlation is of less concern due is significantly lower influence on slosh induced damping while is the most important.
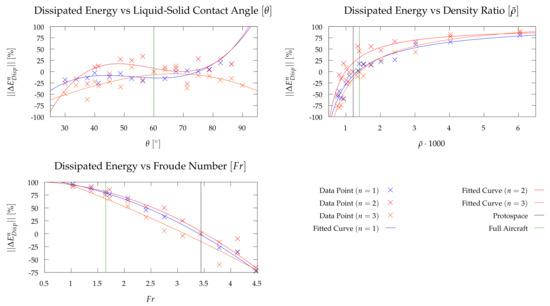
Figure 9.
Change in Dissipated Energy due to Scaling of Non-dimensional Properties for each oscillation n.
Cubic trends for the scaling of are found such that:
Better correlations were found for mass ratio:
The best trend was found throughout for number with all trend lines being quadratic in nature:
9. Scaling-Laws Application
The scaling between the full aircraft model and Protospace experiment employs an attempted Froude scaling due being limited by experimental design and fluid availability (as discussed previously). In contrast high-fidelity CFD enables the modelling of both the ideal (employing an ideal fluid which achieves perfect similarity for all physics non-dimensional numbers) and practical (employing kerosene) Froude scaled experiments. These are denoted as Protospace* and Protospace, respectively with the resulting non-dimensional numbers listed in Table 8. Note that by using kerosene (practical scaling or Protospace) both density ratio and numbers equal that of the full scale Aircraft tank. Further, by manipulating fluid properties in the CFD model it is possible to achieve perfect correlations for all shown non-dimensional numbers as shown for ideal scaling (Protospace*).

Table 8.
Fluid Properties due to Froude Scaling. (Nomenclature for scaling methods as defined above).
We now seek to quantify the difference in computed dissipated energy for the different cases and have two options in which to achieve this viz. CFD or using our scaling laws. Starting with CFD first, both practical and ideal scaled cases were simulated and the resulting computed dissipated energy compared in Table 9. As expected, the actual Protospace experiment overestimates the slosh induced dissipation while practical scaling (Protospace) yields a slosh induced dissipation which is within of the ideal experiment.

Table 9.
CFD simulated dissipated energy. (Nomenclature for scaling methods as defined above).
Considering finally the use of the scaling laws, we aim to scale the actual Protospace experiment to the ideal experiment. As both and are to be accounted for, a response surface of is created using Kriging interpolation which is shown in Figure 10. The resulting scaling computed dissipated power is which is within of the CFD computed value.
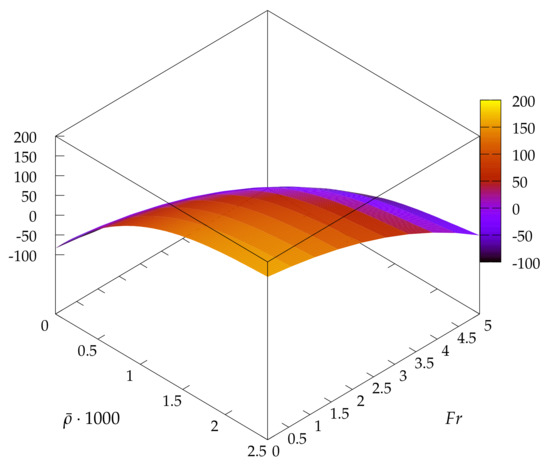
Figure 10.
Response surface of as a function of and .
Please note that the above derived scaling laws allow for scaling of a SDOF system with a geometric scaling . This is as the excitation velocity is affected directly by geometric scaling as per Table 3, i.e., velocity is expected to scale by . For a larger aircraft size tank this would increase the impact velocity of the slosh and hence also the energy dissipation.
10. Conclusions
This article presented the first ever volume of fluid (VoF) computational fluid dynamics (CFD) based non-dimensional analysis which characterises violent slosh induced energy dissipation of a tank under vertical excitation. This in the absence of significant phase change. The use of rigorously validated CFD for this purpose was essential as doing so via experimental means is not possible due limitations in available liquids. The work resulted in several new insights which are deemed of significant value to the field of liquid slosh modelling and liquid impact dynamics. Each of these key contributions are summarized next.
The VoF CFD software was first validated via modelling a representative slosh experiment. A sophisticated two phase model was employed which accounted for surface tension, turbulence and gas compressibility (via a weakly compressible formulation). The validation study concluded that the slosh induced energy dissipation is predicted to within of the experimental values. The CFD based mechanical energy budget also identified liquid impact as the major contributor to slosh induced energy dissipation. These constitute the first novel findings of this work.
Next a non-dimensional analysis was detailed. The specific emphasis was on developing a functional relationship between energy dissipation and fluid physics. The latter was characterised by Reynolds number, Weber number, contact angle, gas-liquid density ratio and Froude number. The validated CFD software was then used to estimate the influence of each of these non-dimensional numbers on slosh induced energy dissipation. As would be expected, Rayleigh–Taylor instability was found key to inducing liquid impact due purely verticle excitation. Hence, an appropriate contact angle is key to inducing violent verticle slosh induced energy dissipation. Apart from Froude number, all other non-dimensional numbers were for the first time found to have a small (circa ) influence on slosh induced energy dissipation. Hence, the Froude number was concluded to be the most important non-dimensional number in characterising slosh induced damping.
The validated CFD was then employed to characterise the change in slosh induced dissipation as a function of the most important non-dimensional numbers for the case of constant amplitude oscillatory tank excitation. Clear correlations (scaling laws) were found for both liquid–gas density ratio and Froude number. The latter scaling laws are linear and quadratic, respectively, which is deemed a significant new finding. From this it was postulated for the first time that violent slosh induced energy dissipation may be expressed as a linear function of tank kinetic energy. The final novel contribution of the article entailed demonstrating the application of the developed scaling laws for Froude number and density ratio to estimate slosh induced energy dissipation for an ideally scaled experiment. Thus, using the developed scaling laws, an accuracy of was achieved when compared to the CFD computed value.
Author Contributions
Conceptualization F.G., M.D.W., A.G.M.; methodology M.D.W., F.G., A.G.M.; software M.D.W., A.G.M.; validation M.D.W.; supervision A.G.M., F.G.; project administration A.G.M., F.G., funding acquisition A.G.M. visulisation M.D.W.; writing M.D.W., A.G.M., F.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This work is based on research supported by the National Research Foundation of South Africa (Grant Numbers: 89916). The opinions, findings and conclusions or recommendations ex-pressed are that of the authors alone, and the NRF accepts no liability whatsoever in this regard. The research leading to these results has also received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 815044, the SLOshing Wing Dynamics (SLOWD) project. The statements made herein do not necessarily have the consent or agreement of the SLOWD consortium and represent the opinion and findings of the author(s).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to use of IP protected software.
Acknowledgments
Computations were performed using facilities provided by the University of Cape Town’s ICTS High Performance Computing team: hpc.uct.ac.za, accessed on 29 October 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gambioli, F.; Chamos, A.; Jones, S.; Guthrie, P.; Webb, J.; Levenhagen, J.; Behruzi, P.; Mastroddi, F.; Malan, A.G.; Longshaw, S.; et al. Sloshing Wing Dynamics-Project Overview Sloshing Wing Dynamics—Project Overview. In Proceedings of the 8th Transport Research Arena TRA 2020, Helsinki, Finland, 27–30 April 2020. [Google Scholar]
- Titurus, B.; Cooper, J.E.; Saltari, F.; Mastroddi, F.; Gambioli, F. Analysis of a Sloshing Beam Experiment. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Savannah, GA, USA, 10–13 June 2019; pp. 1–18. [Google Scholar]
- Gambioli, F.; Usach, R.A.; Kirby, J.; Wilson, T.; Behruzi, P.; Dynamics, S. Experimental Evaluation of Fuel Sloshing Effects on Wing Dynamics. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Savannah, GA, USA, 10–13 June 2019; pp. 1–14. [Google Scholar]
- Lewis, R.W.; Malan, A.G. Continuum thermodynamic modeling of drying capillary particulate materials via an edge-based algorithm. Comput. Methods Appl. Mech. Eng. 2005, 194, 2043–2057. [Google Scholar] [CrossRef]
- Oxtoby, O.F.; Malan, A.G. A matrix-free, implicit, incompressible fractional-step algorithm for fluid-structure interaction applications. J. Comput. Phys. 2012, 231, 5389–5405. [Google Scholar] [CrossRef]
- Heyns, J.A.; Malan, A.G.; Harms, T.M.; Oxtoby, O.F. Development of a compressive surface capturing formulation for modelling free-surface flow by using the volume-of-fluid approach. Int. J. Numer. Methods Fluids 2013, 71, 788–804. [Google Scholar] [CrossRef]
- Suliman, R.; Oxtoby, O.F.; Malan, A.G.; Kok, S. An enhanced finite volume method to model 2D linear elastic structures. Appl. Math. Model. 2014, 38, 2265–2279. [Google Scholar] [CrossRef]
- Ilangakoon, N.A.; Malan, A.G.; Jones, B.W. A higher-order accurate surface tension modelling volume-of-fluid scheme for 2D curvilinear meshes. J. Comput. Phys. 2020, 420, 109717. [Google Scholar] [CrossRef]
- Gibbings, J.C. Dimensional Analysis; Springer Science & Business Media: Liverpool, UK, 2011; pp. 1–20. [Google Scholar] [CrossRef]
- Thompson, J.F.; Nein, M.E. Prediction of Propellant Tank Pressurization Requirements by Dimensional Analysis; NASA: Washington, DC, USA, 1966.
- Summer, I.E. Preliminary Experimental Investigation of Frequencies and Forces Resulting from Liquid Sloshing in Toroidal Tanks; NASA: Washington, DC, USA, 1963.
- Yu, J.K.; Wakahara, T.; Reed, D.A. A non-linear numerical model of the tuned liquid damper. Earthq. Eng. Struct. Dyn. 1999, 28, 671–686. [Google Scholar] [CrossRef]
- Tait, M.J. Modelling and preliminary design of a structure-TLD system. Eng. Struct. 2008, 30, 2644–2655. [Google Scholar] [CrossRef]
- Konopka, M.; De Rose, F.; Strauch, H.; Jetzschmann, C.; Darkow, N.; Gerstmann, J. Active slosh control and damping—Simulation and experiment. Acta Astronaut. 2019, 158, 89–102. [Google Scholar] [CrossRef]
- Heyns, J.A.; Malan, A.G.; Harms, T.M.; Oxtoby, O.F. A weakly compressible free-surface flow solver for liquid–gas systems using the volume-of-fluid approach. J. Comput. Phys. 2013, 240, 145–157. [Google Scholar] [CrossRef]
- Malan, A.G.; Jones, B.W.S.; Malan, L.C.; Wright, M.D. Accurate Prediction of Violent Slosh Loads via a Weakly Compressible VoF Formulation. In Proceedings of the 31st International Ocean and Polar Engineering Conference, Rhodes, Greece, 20–25 June 2021. Paper number ISOPE-I-21-3210. [Google Scholar]
- Oxtoby, O.F.; Malan, A.G.; Heyns, J.A. A computationally efficient 3D finite-volume scheme for violent liquid–gas sloshing. Int. J. Numer. Methods Fluids 2015, 79, 306–321. [Google Scholar] [CrossRef]
- Sykes, B.S.; Malan, A.G.; Gambioli, F. Novel nonlinear fuel slosh surrogate reduced-order model for aircraft loads prediction. J. Aircr. 2018, 55, 1004–1013. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007; pp. 102–104. [Google Scholar]
- Jones, B.W.; Malan, A.G.; Ilangakoon, N.A. The initialisation of volume fractions for unstructured grids using implicit surface definitions. Comput. Fluids 2019, 179, 194–205. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef] [Green Version]
- González-Gutiérrez, L.M.; Calderon-Sanchez, J.; Martinez-Carrascal, J.; Colagrossi, A.; Marrone, S. Report on Single-Phase, Multi-Phase SPH Model and Simulations; Technical Report; Universidad Politécnica de Madrid & Consiglio Nazionale delle Ricerche, Istituto di Ingegneria del Mare: Madrid, Spain, 2021. [Google Scholar]
- Antuono, M.; Marrone, S.; Colagrossi, A.; Bouscasse, B. Energy balance in the δ-SPH scheme. Comput. Methods Appl. Mech. Eng. 2015, 289, 209–226. [Google Scholar] [CrossRef]
- Marrone, S.; Colagrossi, A.; Di Mascio, A.; Le Touzé, D. Prediction of energy losses in water impacts using incompressible and weakly compressible models. J. Fluids Struct. 2015, 54, 802–822. [Google Scholar] [CrossRef]
- Calderon-Sanchez, J.; Martinez-Carrascal, J.; Gonzalez-Gutierrez, L.M.; Colagrossi, A. A global analysis of a coupled violent vertical sloshing problem using an SPH methodology. Eng. Appl. Comput. Fluid Mech. 2021, 15, 865–888. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).