Abstract
The paper is focused on reliable modeling and analysis of axially symmetric radiators with a very narrow (throat) funnel-shaped radiation pattern. When such a diagram is formed, a wave analogue of Smith–Purcell coherent radiation is realized—the surface wave of a radial dielectric waveguide ‘sweeps out’ with its exponentially decaying part a concentric periodic grating, the fundamental spatial harmonic of which, propagating without attenuation in a direction close to the symmetry axis of the structure, generates a radiation field with the required characteristics.
1. Introduction
A plane, density-modulated electron beam flying at a constant speed over a one-dimensional periodic grating generates in the surrounding space uniform plane electromagnetic waves; their number, the length, and direction of propagation are determined by the flow’s velocity and modulation period, as well as by the length of the grating’s period. This is a ‘coherent’ Smith–Purcell radiation (SPR) [1,2,3]. The same flow, passing at a constant speed in a medium, where the speed of light is less than its speed, generates there two homogeneous plane electromagnetic waves, diverging in a wedge from the direction of movement of the flow. The length of these waves and the direction of their propagation are determined by the period of modulation of the flow, the ratio of its speed to the speed of light in the medium, and by the sign of the refractive index of the medium. This is ‘coherent’ Vavilov–Cherenkov radiation (VChR) [4,5,6]. In this electromagnetic scenario, the field of the flow of charged particles generates the field of plane waves, above or below the grating, or in a sufficiently optically dense medium. We observe the same type of radiation and with the same characteristics in the case when we replace the electron flow with an open guiding structure (dielectric waveguide, for example), which supports the propagation of its eigen surface wave with phase velocity coinciding with the electron flow velocity. Here, we have the implementation of wave analogs of SPR and VChR. The analogy here is almost complete, since the field of the electron density-modulated flow is practically identical to the field of the eigen surface wave of the open guide line. The differences may be in the polarization of the fields, but they cannot change the picture of what is happening.
In diffraction radiation antennas (or simply in diffraction antennas) [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], wave analogs of SPR and VChR are implemented. It is impossible to say that they were very widespread, but several dozen devices of this type, unique in their characteristics, have been constructed at O.Ya. Usikov’s Institute for Radiophysics and Electronics of the Academy of Sciences of Ukraine (Kharkiv) for radar and radiometric systems of various purposes. These devices enabled the discovery of the solution to several urgent and practically important problems of remote sensing of the Earth using aerospace carriers, problems of monitoring the airfield and protecting the perimeters of airports, problems of preventing collisions in automobile, river, and sea transport, problems of ‘blind’ landing of helicopters, and problems of short-range radar and radiometry.
The problems that have to be solved for creating efficiently operating diffraction radiation antennas are essentially the same as in the case of phased antenna arrays—it is necessary to ensure, first of all, the required amplitude–phase distribution of the field at sufficiently large (in relation to the size of the period of the used gratings) apertures. These problems have to be solved in different ways: in antenna arrays, each elementary emitter (usually, it is associated with one period of the grating) is excited according to a certain program, and in diffraction, antennas all such emitters are excited by the field of surface wave of an open guiding line; it is necessary to ensure that the phase velocity of this wave is not distorted, and that the amplitude decreases meet the required amplitude distribution of the field at the aperture. The costs of these solutions’ implementation differ significantly—with diffraction antennas, they are much lower.
In operating systems, mainly linear [7,9,12,16,18,19,20,21,22] and planar [7,10,11,13,14,15,16,17,24] antennas of diffraction radiation were used. In the radiator of a linear antenna, the grating width and the effective width of the open (dielectric) waveguide are from half to two wavelengths, and the length of the radiating aperture is from several tens to several hundred wavelengths. In planar antennas allowing electromechanical beam scanning in two planes, the effective width of the grating and the effective width of the open (dielectric) waveguide, as well as the length of the emitting aperture, are measured in tens and hundreds of wavelengths.
Axially symmetric emitters based on circular dielectric waveguides and Goubau lines have been studied well enough theoretically [17,22,25], but they were implemented only in laboratory models and in prototypes with short apertures—they were used to solve the problems of synthesizing antennas with full-size apertures. The axially symmetric structure considered in this work implements a wave analogue of Smith–Purcell radiation in the ‘radial dielectric waveguide—concentric periodic grating’ system and is capable, due to the specific geometry of such a system, to form a radiation field with a very narrow funnel-shaped directivity pattern near the throat. Antennas with such patterns are in demand when solving several specific radar problems.
We construct a numerical solution of model problems, providing simulation and analysis of all physical features of the processes of electromagnetic waves transformation in the structures under consideration, applying the method of exact absorbing conditions [25,26,27,28,29,30,31,32,33,34,35,36]. The results of works [31,36,37] convincingly testify to its reliability and efficiency.
We use SI, the International System of Units, for all physical parameters except the ‘time’ , which is the product of the natural time and the velocity of light in vacuum; thus, is measured in meters. In this paper, all dimensions are omitted. According to SI, all geometrical parameters (, etc.) are given in meters. However, this is obviously not a serious obstacle to extend the results to any other geometrically similar structure.
2. Models of the Method of Exact Absorbing Conditions Time Domain Representations
Axially symmetric emitters, excited by eigen - or - pulse wave , of circular or coaxial waveguide , coming on the virtual boundary (see Figure 1: the structures are homogeneous along the axis ) at time moments , are studied by solving the following model problem of the method of exact absorbing conditions [25,32,34]:
Here, is the - or - field component of the exciting - or - pulse waveguide wave; and are its space–time amplitude and transverse eigen function respectively; is the closure of ; in the case of -waves (, ) and for -waves (, ); and are the vectors of the electric and magnetic fields, respectively; and are the cylindrical and spherical coordinates, respectively; piecewise constant functions and specify a conductivity and relative permittivity of non-magnetic elements of the structure; is an impedance of free space; and are electric and magnetic vacuum constants, respectively. The surfaces of perfectly conducting elements of the structure and surfaces , where the constitutive parameters and are discontinuous, are assumed to be sufficiently smooth. Nonzero components of the electromagnetic field lying in the half-plane are determined by the expressions
in the case of -waves, and in the case of -waves, by relations
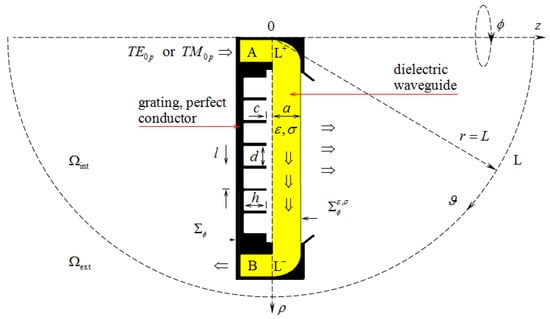
Figure 1.
Schematic representation of the geometry of an axially symmetric emitter ‘radial dielectric waveguide—concentric grating’ in a half-plane .
Computational domain of the problem (1) is a part of the plane , limited by contour , axis , virtual boundaries (input and output ports in the cross section of virtual waveguides and ) and by a ‘spherical’ boundary , separating from free space in . The arc of radius covers all scattering inhomogeneities of the domain .
Exact absorbing conditions , and for virtual boundaries are the ideal model for waves
traveling from domain into waveguides , , and domain [25,32,34]. Here, only in the case of coaxial waveguides and only for -waves; in all other cases .
Explicit analytic representations for transverse functions and the corresponding eigen values are well known [25,31,32,34]. For example, for -waves functions of coaxial waveguide ( is the radius of its inner conductor, is the radius of its outer conductor) have a form
and
for a circular waveguide. Here, и are cylindrical Bessel and Neumann functions.
The transverse functions
( are associated Legendre functions) have relevant eigen values , [32,34].
The works [25,26,27,28,29,30,31,32,33,34,35,36,37] are devoted to the theory and construction of exact absorbing conditions for open initial-boundary value problems in computational electrodynamics. It is possible to find there, in particular, such analytical representations for integro-differential operators and of the problem (1) (presume—see Figure 1—that virtual boundaries lie in the plane ):
( are Legendre polynomials).
Systems of transverse functions and are complete and orthonormal (with a certain weight) on the corresponding intervals of and variation. Spatial–temporal amplitudes , for the values and , corresponding to the boundaries and , are determined from the solution to the problem (1). Values of , , required for constructing the radiation pattern of the emitter, are obtained from , using the so-called ‘transport operators’ [31,34,38,39,40]. Function and its derivative with respect to on the boundary must be given by their space–time amplitudes and in order to meet the condition (8). Making a choice for the values of the function on a finite interval ( is the upper limit of the observation time), we have no restrictions. This choice is imposed mainly by the specifics of the problem and the conditions of the computational experiment. However, the function determining the normal derivative of the function on cannot be chosen arbitrarily. The causality principle requires the strict correspondence of a pair of functions
to eigen pulse wave (- or -), propagating along the waveguide in the direction of increasing values of . This requirement is fulfilled if the pair of functions (11) is connected by the relation
obtained in the same way as the exact absorbing conditions (8) and (9) [25,32,34].
3. Frequency Domain Representations
The solution to the problem (1) and (4) (we construct it by implementing the standard computational schemes of the finite difference method [41]) and the solution to the problem
are connected by integral transformation [25,32,34] (actually by integral transformation ; is an observation time in computational experiments). This transformation matches the characteristics of the time domain with the characteristics of the frequency domain —. Here, are cylindrical Hankel functions, in the case of monochromatic -waves and in the case of monochromatic -waves; is a wavenumber (frequency parameter or just frequency, is related with frequency by the ratio , where is a speed of light in vacuum), and
are longitudinal wavenumbers of - or - monochromatic eigen waves propagating in waveguides and with (if ) or without (if ) attenuation.
In Formula (13b,c), the term with the complex amplitude corresponds to the monochromatic wave arriving at the boundary , and the terms with the amplitudes, , , and , to the waves of the secondary field , , and , both in the waveguides , and in a free space. If we compare representations (13b–d) and (4), it becomes obvious that
or, in another notation, , . Similarly, we obtain
In the boundary value problem (13), expressions (13b–d) represent the so-called ‘partial radiation conditions’ [38], corresponding to the physically grounded requirement of the absence in the field waves coming from infinity. An exception is possible only for the ‘incident’ wave. In our case, this wave is determined by the function
In the frequency domain, the structure under consideration is characterized (in part) by the reflection coefficients (the conversion coefficients of the -th incident from the waveguide wave into -th reflected wave) and the transmission coefficients (the conversion coefficients of the -th wave of the waveguide into the -th wave of the waveguide ). These coefficients, given by , , and values
( for -waves, and for -waves, ) determine [34] the relative fraction of the energy absorbed in non-ideal elements of the structure and directed to each of the waves propagating in the waveguides and . For any finite value ( is the wavelength in free space), the number , of such waves taking away the energy supplied to the axially symmetric structure is finite. It follows from (18) that the fraction of the energy emitted by the structure into free space through the virtual boundary (radiation efficiency) can be calculated by the formula
Normalized radiation pattern on the arc
determines the spatial orientation and ‘energy capacity’ of waves radiated into free space. Here, is a tangential (with respect to the spherical surface ) component of the monochromatic electric field . The value determines the zone (near, mid, far) where the diagram is calculated. We presume that the boundary of the near zone is given by equality , and the far zone is determined by such values of , further increase in which does not lead to significant changes in the function for all considered values .
The main lobe of the radiation pattern is directed at an angle such that . The width of the main lobe is defined as the angle between two ( and ) directions in the main lobe of the diagram for which the radiated power is halved in relation to the maximum, i.e., , where and .
For calculating the radiation pattern , it is necessary to solve the initial boundary value problem (1), and then, using the exact radiation condition [25,32,34], from which absorbing condition (10) follows, to determine, by the values of on the arc , the values of and ( for -waves or for -waves (see formulas (1.19) in [31]) on the arc , and, finally, to use the transformation .
4. Radial Emitters with a Narrow Funnel-Shaped Radiation Pattern
It is possible that the implementation of wave analogs of Smith–Purcell coherent radiation in axially symmetric structures, which is going to be considered below, is the only fairly simple and least expensive way to build antennas with a very narrow funnel-shaped radiation pattern. The principle remains the same as with previously designed linear and planar antennas: the eigen slow wave of an open guiding line ‘sweeps out’ the periodic structure, and spatial propagating harmonics create the radiation field. The peculiarity lies in the fact that the role of an open guiding line is assigned to a planar radial dielectric waveguide, and a grating with concentric guiding lines, determining its period , is put on a round disc installed on the axis . The synthesis of an emitter with a very narrow funnel-shaped radiation pattern is reduced to the search for such a periodic structure that could provide the required amplitude and phase distribution of the radiation field at its zero spatial harmonic if the condition
holds. Here, and are deceleration coefficient and propagation constant of the eigen surface wave of a radial dielectric waveguide, in which component (in the case of -waves) or (in the case of -waves) may be presented in the form ; are longitudinal (along ) wavenumbers of grating’s spatial harmonics of the number [42,43,44]. Connecting values and , we implement in a form suitable for our particular case the well-known fact about the ‘identity’ of the field of the eigen surface wave of a planar dielectric waveguide and the field of one of the evanescent spatial harmonics of the grating [17,25,45]. This identity is manifested in the fact that the secondary fields of periodic structures generated by the fields of these generally different waves are the same. This allows us, when solving problems of analysis and synthesis of diffraction radiation antennas, to proceed from the fact that the characteristic bursts of their radiation pattern functions, both in magnitude and in the corresponding values of the angular coordinate, correlate fairly well with the amplitudes and space orientation of the spatial harmonics of the secondary fields of infinite gratings excited by the corresponding evanescent spatial harmonic. The effectiveness and validity of the approach to the construction of diffraction radiation antennas based on such concepts have already been proven by all the previous experience of researchers working in this direction.
Condition (21) formally reflects all that discussed above. If, for some values of , , and , in the secondary field of an infinite grating excited by the first evanescent harmonic, only the fundamental harmonic (harmonic with a number ) is propagating, then, in the half-plane , it will go into free space at an angle [44]. The equality follows from the relations and [44]. Condition (21) allows for each given frequency value to determine the period of the grating , capable of forming, together with a radial dielectric waveguide, supporting the propagation of a surface wave with a deceleration coefficient , a radiation field with the main lobe of the directional pattern ‘pressed’ to the axis . The structure of the grating period or the value of the parameter at the local intervals of the coordinate variation, which add up to the interval of length , determining the real dimensions of the aperture of the synthesized device, can be changed and is selected in such a way as to fulfill the known requirements [46], which ensure the radiation pattern of the required quality and are related to the implementation of a certain amplitude distribution of the radiation field. Below, we restrict ourselves to considering prototypes of emitters with an aperture determined by a relatively small size of (the structure of the grating period and the parameter are constant) and focus on clarifying the question of whether it is possible, in principle, to form a very narrow funnel-shaped radiation pattern by structures with a radial arrangement of the main functional elements: a grating and a dielectric waveguide (Figure 2).
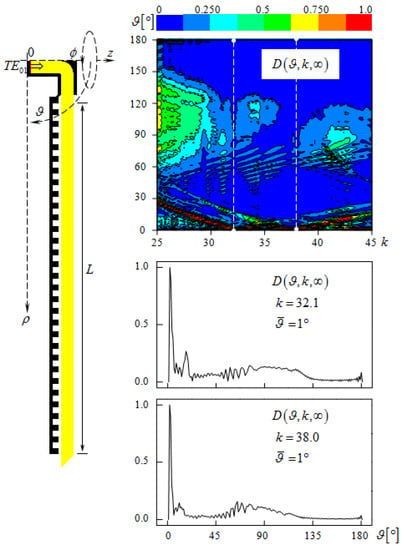
Figure 2.
Radial diffraction radiation antenna. Radiation pattern in the frequency band and at frequencies and . is a parameter that determines the size of the emitting aperture.
In the prototype shown in Figure 2 (the proportions in the image of the details of all analyzed structures are preserved), the circular feeder waveguide ( is its radius) moved into a radial waveguide and then into an open waveguide—a dielectric one (). A reflective grating with parameters , , and (width and depth of slots) was placed at a distance from the dielectric waveguide. The period length is determined from condition (21) after calculating the propagation constants of a surface wave excited in a radial dielectric waveguide by a -wave of a circular waveguide . Specifically, the value for the frequency () was taken into account. The values of we obtain by calculating the phase incursion of the field caused by the displacement of the observation point along the dielectric waveguide axis from the point to the point , [17,25]. According to the concepts discussed above, the considered emitter at frequencies close to should form a diagram, with one of the lobes directed practically along the axis . This is true in a flat representation. The rotation of this beam with variation of the coordinate generates a ‘funnel’ in space, which we would like to see in the field’s distribution emitted by the antenna.
The results of numerical simulation in the frequency band (in the waveguide , not more than two -waves are propagating: , , ; hereafter, the frequencies are the cut-off points of - and -waves in the waveguides and , i.e., ) confirmed the expectations (Figure 2). The main and well-pronounced lobes of the radiation patterns at frequencies close to and are oriented in the direction . However, instead of one arc in the plane associated with the zeroth spatial harmonic of the grating propagating without attenuation, we see two shifted relative to each other in frequency and intersecting in the region . This allows us to conclude that not one but two competing surface waves with close values are excited in a dielectric waveguide, and in our calculations, we determined their average value.
The considered model did not allow to determine the radiation efficiency in the directions of interest, since a significant part of the energy, as seen from Figure 2, leaves the open end of the radial dielectric waveguide into the corner sector . In other models presented in this section, we have corrected this drawback by adding a coaxial waveguide , removing the remained and not the radiated part of the primary -wave energy (Figure 3).
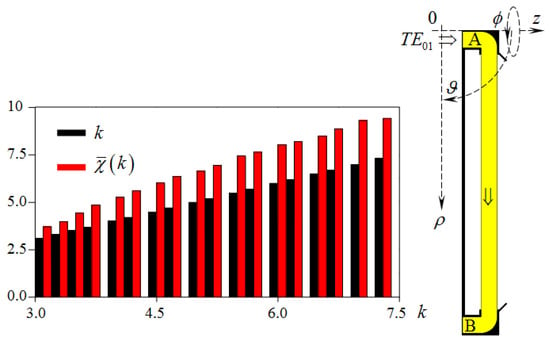
Figure 3.
Surface wave propagation constants of a radial dielectric waveguide.
The propagation constants of the radial dielectric waveguide were calculated for the structure (see Figure 3) with following parameters: the radii of the inner conductors of the coaxial waveguides and are equal to 0.12 and 15.84, respectively; the radii of their outer conductors are 1.0 and 16.72; and the thickness of the radial dielectric () waveguide is equal to 0.88. The cutoff points of the first three -waves in the waveguide are equal to , , and and in the waveguide , , , and . For the analysis, a frequency band , where no more than two -waves can propagate in each of these waveguides without attenuation, was chosen. At the frequency , the average for this range, , , and the value satisfying condition (21) is 0.9. Let us load an open dielectric waveguide with a reflective grating with defined above period and (aiming distance between the waveguide and the grating is ) and excite the structure with a pulsed -wave, such that
Here, is the Heaviside step function, is the central frequency of the pulse , and are its delay time and duration. The pulse occupies the frequency band [31,34]; in our case, this is a chosen for analysis interval .
The numerical results are presented in Figure 4. Directional properties of the emitter are much better than in the case considered above—sufficiently ‘powerful’ side lobes in the radiation pattern are almost completely absent. The minimum deviation of the beam corresponding to the zero spatial harmonic of the grating from the axis was, in this case, equal to .
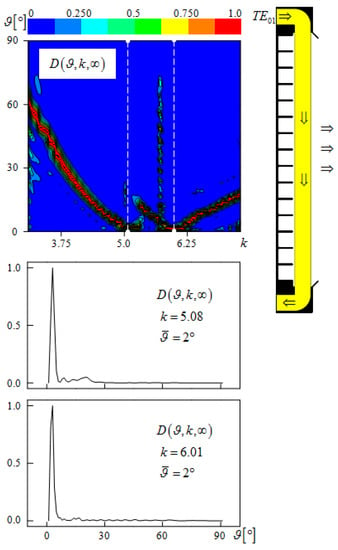
Figure 4.
Radial diffraction radiation antenna. Radiation pattern in the frequency band and at possible operating frequencies and ( and ).
The lower fragments of Figure 4 show the dependences at frequencies and ; the radiation efficiency here is, respectively, and . It is clear that, at least with the achieved value of and the selected type of periodic structure, one can count on a successful solution of the problem associated with the formation of the required amplitude distribution of the radiation field of the antenna, having an aperture size several times larger than the aperture size of the considered prototype [17,20,25].
The upper fragment of Figure 4 tells us that a decrease in frequency (transition to the range , where only -waves propagate without attenuation in feeder coaxial waveguides and ) will allow us to get rid of the ‘two arcs’ effect in the radiation pattern of the emitter, discussed earlier. This should also change the size of the period of the grating, directing its fundamental spatial harmonic at an angle close to zero. So, for the value , we obtain (see Figure 3), , and .
Having loaded the radial waveguide with a grating of a period (, the parameters and remain the same) and having excited the structure with a pulsed -wave , , , and , we arrive at the results presented in Figure 5. These results fully meet our expectations, but the minimum deviation of the beam corresponding to the zero spatial harmonic of the grating from the axis has increased to . Obviously, this is due to a decrease in the number of grating periods that fit into the length , determining the dimensions of the emitter aperture. With the transition to a full-size aperture of the synthesized antenna, this indicator can be significantly improved.
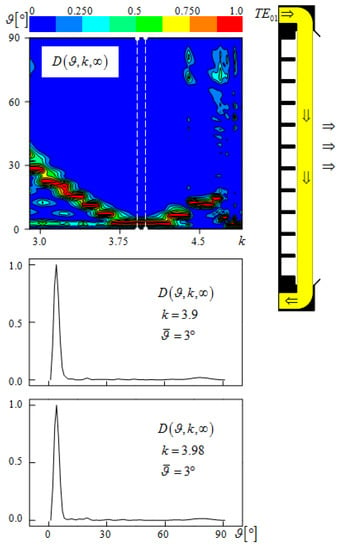
Figure 5.
Radial diffraction radiation antenna. Radiation pattern in the frequency band and at frequencies and ( and ).
As it has already been noted more than once [17,20,25], for the successful solution of the problem of synthesizing a real antenna of diffraction radiation, the energy parameters of prototype emitters and the ability to control their change by varying one of the parameters , , or , are important. In the case under consideration, at frequency , and at . Figure 6 shows how the radiation intensity changes with a change in the aiming distance , that is, the distance between the grating and the radial dielectric waveguide. When performing a specific technical task for the construction of a diffraction radiation antenna, similar dependences, calculated for all admissible (not leading to phase distortions of the surface wave field [17,20,25]) values should be taken into account.
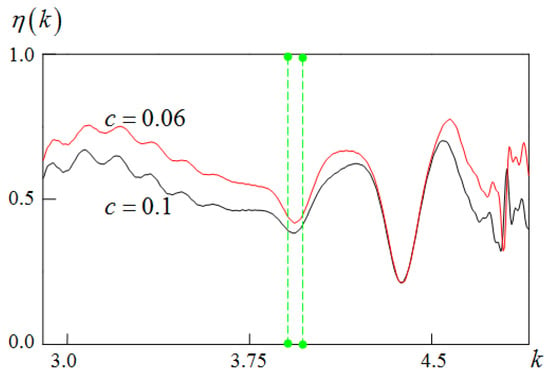
Figure 6.
Radiation efficiency of a radial antenna at aimed parameter values (see Figure 5) and .
An important issue in the construction of real antennas is the question of maximum simplification of their design without losses in the quality of the main electrodynamic characteristics of devices. In part, this also holds for the used periodic structures. The parameters of far from all gratings of classic geometry (gratings of the ‘comb’ type, for example) can be strictly maintained during their manufacture and operation in the wavelength ranges from 3.0 mm and less. A prototype of a diffractive radiation antenna, the main electrodynamic characteristics of which are presented in Figure 7 and Figure 8, can be proposed as one of the options allowing to effectively solve the above problems.
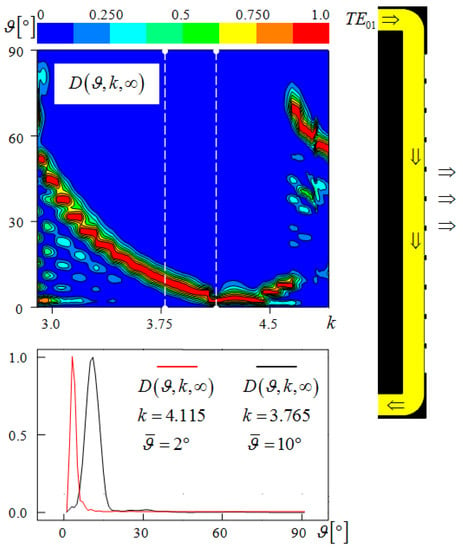
Figure 7.
Radiation pattern of emitter in the frequency band and at frequencies and ( and ).
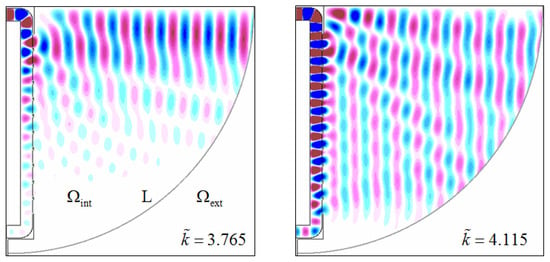
Figure 8.
Excitation of the radial antenna (see Figure 7) by a quasi-monochromatic -wave with a central frequency and . Distribution of values in the computational domain , .
In this prototype, one of the planes of the radial dielectric waveguide is metallized, and the second one contains a concentric grating of ‘thick’ () narrow (, ) metal strips—its propagating spatial harmonics mainly form the radiation field. The structure is excited by a pulsed -wave , , , , , covering the frequency range . For the expected value , the minimum deviation of the main lobe of the radiation pattern from the axis , equal to , is obtained for frequencies . The radiation pattern characteristic of this range is shown in the upper fragment of Figure 7. For , radiation efficiency is . The frequency corresponds to the maximum efficiency ; the corresponding radiation pattern is shown in the bottom fragment of Figure 7.
Figure 8 shows the spatial distribution of the radiation field at the instant , when the structure is excited by a quasi-monochromatic - pulse wave:
where is the central frequency of the signal and is its trapezoidal envelope, which equals unit for , and is zero for and The fronts of the radiated waves are practically flat (in the representation for values ) and the orientation of the relevant planes corresponds to the previously determined values (for ) and (for ). Obviously, the non-uniform (especially in the case ) distribution of the radiation field amplitude along the emitter aperture is connected, among other things, with a decrease in the spatial energy density carried by the surface wave of the radial waveguide as it moves along the axis . It will be necessary to consider the corresponding effect when creating actual antennas with a sufficiently large value of determining the size of their apertures.
5. Conclusions
The paper briefly describes rigorous models of the method of exact absorbing conditions, enabling the study and analysis of the effects of diffraction radiation (wave analogs of the effects of SPR) in axially symmetric electrodynamic structures such as ‘a finite segment of an open radial guiding line installed near a finite concentric reflective or semitransparent grating’. These mathematical models, implemented in a complex of original authentic algorithms and codes, were used to study the physics of the processes of transformation of eigen surface waves of the corresponding open waveguides into waves propagating infinitely far in free space. The primary attention was paid to emitters—prototypes of practical antennas, capable of forming a funnel-shaped radiation pattern with a very narrow ‘throat’. The results discussed in the paper confirm the possibility to construct such well-directed antennas, implementing the wave analog of the Smith–Purcell coherent radiation. The presented results also prove the correctness of our ideas about how, in what way, and due to what physical principals the proposed for implementing non-standard transformations of electromagnetic waves structure should work. It has been shown how and within what limits the characteristics of the corresponding devices can be changed in a controlled manner. In particular, this may be performed by the optimal selection of the parameters of the open waveguide line (due to the change in the parameters of the surface waves directed by such a line) and/or by choosing the geometric and material parameters of the grating, as only gratings propagating spatial harmonics determine all the features of the radiation field.
Author Contributions
Conceptualization, Y.S. and S.S.; methodology, Y.S.; software, M.S.; formal analysis, N.B. and A.B.; investigation, Y.S., S.S. and N.Y.; writing—original draft preparation, Y.S. and N.Y.; writing—review and editing, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan, grant number AP08855557. And The APC was funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan too.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- Smith, S.J.; Purcell, E.M. Visible light from localized surface charges moving across a grating. Phys. Rev. 1953, 92, 1069–1073. [Google Scholar] [CrossRef]
- Bolotovskiy, B.M.; Voskresenskiy, G.V. Radiation of charged particles in periodic structures. Usp. Fiz. Nauk. 1968, 94, 378–416. (In Russian) [Google Scholar] [CrossRef]
- Shestopalov, V.P. The Smith-Purcell Effect; Nova Science Publishes: New York, NY, USA, 1998. [Google Scholar]
- Cherenkov, P.A. Visible radiation produced by electrons moving in a medium with velocities exceeding that of light. Phys. Rev. 1937, 52, 378–379. [Google Scholar] [CrossRef]
- Jelley, J.V. Cherenkov Radiation and Its Applications; Pergamon Press: London, UK, 1958. [Google Scholar]
- Frank, I.M. Vavilov-Cherenkov Radiation; Nauka: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. A new trend in antenna array technology. Izv. VUZov. Radioelektron. 1996, 39, 54–61. (In Russian) [Google Scholar]
- Lee, J.W.; Eom, H.J.; Park, K.H.; Chun, W.J. TM-wave radiation from grooves in a dielectric-covered ground plane. IEEE Trans. Antennas Propag. 2001, 49, 104–105. [Google Scholar] [CrossRef]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. Optimization of the radiating system ‘dielectric waveguide—Grating’ for an automobile radar scanning antenna. Telecommun. Radio Eng. 2002, 57, 66–73. [Google Scholar] [CrossRef]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. The planar antenna array with a cosecant directional pattern for 8-mm waves. Elektromagn. Volny Elektron. Sist. 2003, 8, 52–58. (In Russian) [Google Scholar]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. A planar antenna with a combined beam swinging. Elektromagn. Volny Elektron. Sist. 2005, 10, 52–56. (In Russian) [Google Scholar]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. Millimeter wave radar scanning antennas for vehicle collision avoidance. Usp. Sovrem. Radioelektron. 2006, 70–79. (In Russian) [Google Scholar]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V. Antenna for 8-millimeter-range airfield control radar. Elektromagn. Volny Elektron. Sist. 2008, 13, 46–53. (In Russian) [Google Scholar]
- Melezhik, P.N.; Sidorenko, Y.B.; Provalov, S.A.; Andrenko, S.D.; Shilo, S.A. Planar antenna with diffraction radiation for radar complex of millimeter band. Radioelectron. Commun. Syst. 2010, 53, 233–240. [Google Scholar] [CrossRef]
- Yevdokymov, A.P.; Kryzhanovskiy, V.V.; Sirenko, Y.K. A planar diffraction antenna operating in EHF range. Elektromagn. Volny Elektron. Sist. 2011, 16, 53–61. (In Russian) [Google Scholar]
- Yevdokymov, A.P. Diffraction radiation antennas. Fiz. Osn. Priborostr. 2013, 2, 108–125. (In Russian) [Google Scholar]
- Sautbekov, S.S.; Sirenko, K.Y.; Sirenko, Y.K.; Yevdokimov, A.P. Diffraction radiation phenomena: Physical analysis and applications. Antennas Propag. Mag. IEEE. 2015, 57, 73–93. [Google Scholar] [CrossRef]
- Yevdokymov, A.P.; Mazur, V.Z.; Sirenko, K.Y.; Sirenko, Y.K. Diffraction radiation antennas based on a groove transmission line. Fiz. Osn. Priborostr. 2018, 7, 24–36. (In Russian) [Google Scholar]
- Sirenko, K.Y.; Sirenko, Y.K.; Yevdokymov, A.P. Diffraction antennas. A ridged dielectric waveguide. Telecommun. Radio Eng. 2018, 77, 839–852. [Google Scholar] [CrossRef]
- Sautbekov, S.S.; Sirenko, K.Y.; Sirenko, Y.K.; Yevdokymov, A.P. Diffraction antennas. Synthesis of radiating elements. Telecommun. Radio Eng. 2018, 77, 925–943. [Google Scholar] [CrossRef]
- Sirenko, Y.K.; Yevdokymov, A.P. Diffraction antennas. Linear structures on the basis of a ridged waveguide. Telecommun. Radio Eng. 2018, 77, 1203–1229. [Google Scholar] [CrossRef]
- Mazur, V.Z.; Sirenko, K.Y.; Sirenko, Y.K.; Yevdokymov, A.P. Diffraction antennas. Linear structures on the basis of a modified Goubau line. Telecommun. Radio Eng. 2018, 77, 1397–1408. [Google Scholar] [CrossRef]
- Melezhik, P.N.; Ney, M.; Sautbekov, S.S.; Sirenko, K.Y.; Sirenko, Y.K.; Vertiy, A.A.; Yashina, N.P. Cherenkov radiation based antenna with the funnel-shaped directional pattern. Electromagnetics. 2018, 38, 34–44. [Google Scholar] [CrossRef]
- Sirenko, K.Y.; Sirenko, Y.K.; Yevdokymov, A.P. Diffraction antennas. Planar structures with controllable beam positioning. Telecommun. Radio Eng. 2019, 78, 835–851. [Google Scholar] [CrossRef]
- Sirenko, Y.K.; Velychko, L.G. (Eds.) Electromagnetic Waves in Complex Systems: Selected Theoretical and Applied Problems; Springer: New York, NY, USA, 2016. [Google Scholar]
- Hagstrom, T. Radiation boundary conditions for the numerical simulation of waves. Acta Numer. 1999, 8, 47–106. [Google Scholar] [CrossRef]
- Perov, A.O.; Sirenko, Y.K.; Yashina, N.P. Explicit conditions for virtual boundaries in initial boundary value problems in the theory of wave scattering. J. Electromagn. Waves Appl. 1999, 13, 1343–1371. [Google Scholar] [CrossRef]
- Sirenko, Y.K. Exact ‘absorbing’ conditions in outer initial boundary value problems of the electrodynamics of nonsinusoidal waves. Part 2: Waveguide units and periodic structures. Telecommun. Radio Eng. 2002, 57, 1–31. [Google Scholar] [CrossRef]
- Sirenko, Y.K. Exact ‘absorbing’ conditions in outer initial boundary-value problems of the electrodynamics of nonsinusoidal waves. Part 3: Compact inhomogeneties in free space. Telecommun. Radio Eng. 2003, 59, 1–31. [Google Scholar] [CrossRef]
- Sirenko, K.Y.; Sirenko, Y.K. Exact ‘absorbing’ conditions in the initial boundary value problems of the theory of open waveguide resonators. Comput. Math. Math. Phys. 2005, 45, 490–506. [Google Scholar]
- Sirenko, Y.; Strom, S.; Yashina, N.P. Modeling and Analysis of Transient Processes in Open Resonant Structures. New Methods and Techniques; Springer: New York, NY, USA, 2007. [Google Scholar]
- Shafalyuk, O.S.; Sirenko, Y.K.; Smith, P. Simulation and Analysis of Transient Processes in Open Axially-Symmetrical Structures: Method of Exact Absorbing Boundary Conditions. In Electromagnetic Waves; Zhurbenko, V., Ed.; InTech: Rijeka, Croatia, 2011; pp. 99–116. [Google Scholar]
- Sirenko, K.Y.; Pazynin, V.L.; Sirenko, Y.K.; Bagci, H. An FFT-accelerated FDTD scheme with exact absorbing conditions for characterizing axially symmetric resonant structures. Prog. Electromagn. Res. 2011, 111, 331–364. [Google Scholar] [CrossRef] [Green Version]
- Kravchenko, V.F.; Sirenko, Y.K.; Sirenko, K.Y. Electromagnetic Wave Transformation and Radiation by the Open Resonant Structures. Modelling and Analysis of Transient and Steady-State Processes; Fizmathlit: Moscow, Russia, 2011. [Google Scholar]
- Sirenko, K.Y.; Sirenko, Y.K.; Bagci, H. Exact absorbing boundary conditions for periodic three-dimensional structures: Derivation and implementation in discontinuous Galerkin time-domain method. IEEE J. Multiscale Multiphysics Comput. Tech. 2018, 3, 108–120. [Google Scholar] [CrossRef] [Green Version]
- Sirenko, Y.K.; Pazynin, V.L.; Sirenko, K.Y.; Yashina, N.P. Exact absorbing conditions for initial boundary value problems of computational electrodynamics. Review. In A Closer Look at Boundary Value Problems; Avci, M., Ed.; Nova Science Publishers: New York, NY, USA, 2020; pp. 43–124. [Google Scholar]
- Pazynin, V.L.; Sautbekov, S.S.; Sirenko, K.Y.; Sirenko, Y.K.; Vertiy, A.A.; Yashina, N.P. Comparison of exact and approximate absorbing conditions for initial boundary value problems of the electromagnetic theory of gratings. Telecommun. Radio Eng. 2018, 77, 1581–1595. [Google Scholar] [CrossRef]
- Sirenko, Y.K. Simulation and Analysis of Transient Processes in Open Periodic, Waveguide, and Compact Resonators; EDENA: Kharkov, Ukraine, 2003. (In Russian) [Google Scholar]
- Sirenko, K.Y. Transport operators in the axially-symmetrical problems of the electrodynamics of pulsed waves. Elektromagn. Volny Elektron. Sist. 2006, 11, 15–26. (In Russian) [Google Scholar]
- Kravchenko, V.F.; Sirenko, K.Y.; Sirenko, Y.K. Transport operators and exact absorbing conditions in the plane problems of the electrodynamics of pulsed waves for compact open resonators with the waveguide feeder line. Elektromagn. Volny Elektron. Sist. 2009, 14, 4–19. (In Russian) [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Boston, MA, USA, 2000. [Google Scholar]
- Shestopalov, V.P.; Kirilenko, A.A.; Masalov, S.A.; Sirenko, Y.K. Resonance Wave Scattering. Volume 1. Diffraction Gratings; Naukova Dumka: Kiev, Ukraine, 1986. (In Russian) [Google Scholar]
- Shestopalov, V.P.; Sirenko, Y.K. Dynamic Theory of Gratings; Naukova Dumka: Kiev, Ukraine, 1989. (In Russian) [Google Scholar]
- Sirenko, Y.K.; Strom, S. (Eds.) Modern Theory of Gratings. Resonant Scattering: Analysis Techniques and Phenomena; Springer: New York, NY, USA, 2010. [Google Scholar]
- Shestopalov, V.P. Physical Foundation of the Millimeter and Sub Millimeter Waves Technique. Volume I. Open Structure; VSP Books Inc.: Utrecht, The Netherlands; Tokyo, Japan, 1997. [Google Scholar]
- Kuhn, R. Mikrowellen Antennen; VEB Verlag Technik: Berlin, Germany, 1964. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).