Abstract
Many real-world tasks require multiple agents to work together. When talking about multiple agents in robotics, it is usually referenced to multiple manipulators in collaboration to solve a given task, where each one is controlled by a single agent. However, due to the increasing development of modular and re-configurable robots, it is also important to investigate the possibility of implementing multi-agent controllers that learn how to manage the manipulator’s degrees of freedom (DoF) in separated clusters for the execution of a given application (e.g., being able to face faults or, partially, new kinematics configurations). Within this context, this paper focuses on the decentralization of the robot control action learning and (re)execution considering a generic multi-DoF manipulator. Indeed, the proposed framework employs a multi-agent paradigm and investigates how such a framework impacts the control action learning process. Multiple variations of the multi-agent framework have been proposed and tested in this research, comparing the achieved performance w.r.t. a centralized (i.e., single-agent) control action learning framework, previously proposed by some of the authors. As a case study, a manipulation task (i.e., grasping and lifting) of an unknown object (to the robot controller) has been considered for validation, employing a Franka EMIKA panda robot. The MuJoCo environment has been employed to implement and test the proposed multi-agent framework. The achieved results show that the proposed decentralized approach is capable of accelerating the learning process at the beginning with respect to the single-agent framework while also reducing the computational effort. In fact, when decentralizing the controller, it is shown that the number of variables involved in the action space can be efficiently separated into several groups and several agents. This simplifies the original complex problem into multiple ones, efficiently improving the task learning process.
1. Introduction
1.1. Context
Artificial intelligence and machine learning are quickly becoming core tools in the robotics domain, allowing incorporation of intelligence in robots, making them able to analyze, learn, and improve their behavior with minimum human intervention [1,2]. In particular, reinforcement learning (RL) [3] offers great potential to benefit from the experience to learn control tasks autonomously, as it is successfully shown in complex environments and scenarios [4,5]. However, reinforcement learning typically requires collecting a large number of samples to accumulate such an experience (i.e., training data), which still limits the application of RL in real physical systems such as robots, and pushes the current computer technology to the limit. Moreover, the control problems in robotics are best represented with high-dimensional matrices, continuous state, and action spaces, which actually make the application of this type of technique expensive even for highly efficient processors [6]. Therefore, it is important to consider new ways to simplify the learning problem, to reduce the computational efforts required by the RL. Recent works have considered ways to speed up the training process by learning contextual affordances [7], where the robot learns to perceive the effect of performing an action on an object using the current state. This is particularly important for learning vision-based manipulation skills since it greatly reduces the training time [8]. Some other works have instead focused on the explainability of RL agents, allowing a learning agent to explain the decision of selecting an action over other possible actions [9]. Exploration is another main challenge in RL agents that refers to the problem of choosing a policy that allows a learning agent to discover high-reward regions of the state space. In [10], the performance of different exploration strategies have been compared for on-policy and off-policy algorithms showing that the value-difference-based exploration strategy combined with softmax action selection improve the learning efficiency. Providing interactive feedback about the agent’s actions is another approach to deal with the exploration issue [11].
In this paper, a decentralized learning approach is proposed for the robot to learn to perform a target task in a simulation environment through the use of a multi-agent framework (being implemented as On or Off policy RL algorithms), and transfer such knowledge to the real robot for real-task execution. Results and achieved performance are then analyzed in terms of how this approach can improve the computational effort and learning curve speed, while processing the learning algorithms, by comparing the proposed multi-agent framework with a centralized learning schema (used as a baseline).
1.2. State of the Art and Related Works
Within the state-of-the-art methods related to robotic task learning, the two main learning approaches that can be identified are (i) reinforcement learning and (ii) learning from demonstration (LfD) or imitation learning. The main difference between these approaches is that RL discovers optimal behavior through trials, whereas LfD aims to learn the task based on the presented trajectories, such as in [12]. A combination of these approaches can be used as presented in [5], where an algorithm learned to play the game of Go and won against an international champion by first learning from playing games and later improving through RL. In order to implement autonomous task-learning approaches, RL is commonly adopted. Recent works have emerged in the use of deep RL techniques in robotic grasping as in [13], and more notably in [14]. In [15], deep RL is used in the execution of a robotic task in a continuous domain. This is of great importance, since most real-life robots are simulated in continuous space. In [16], major advancements in large convolutional neural networks used for deep RL are highlighted. These networks have been used to learn hand-eye coordination for robotic grasping from monocular images and can predict the probability of successful grasping using only camera images.
With the increasing complexity of systems and tasks, a new efficient learning method, decentralized RL, has been proposed [17]. Additional work in this field is presented in [18], where decentralized reinforcement learning is implemented in learning robot behavior. Within the field of multi-agent systems, ref. [19] provides a survey for cooperative multi-agent learning literature where the work is divided into two categories. These categories are applying a single learner to discover joint solutions to multi-agent problems (team learning), or using multiple simultaneous learners, often one per agent (concurrent learning). The complexity of continuous space made the first algorithms used in RL obsolete, presenting the need for creating new approaches. These new approaches include networks such as Hindsight Experience Replay, which uses deep Q-networks (DQN) and deterministic gradients (DDPG), which can be found in [20]. Another approach is a distributed Q-learning algorithm which was introduced in [21]. It is noted that by using this algorithm, agents might neglect a penalty due to non-coordination in their update. Ref. [22] points out the limitations of distributed Q-learning when dealing with stochastic environments, presenting a modified exploration strategy. Additionally, the Hysteretic Q-Learning algorithm [23] can be used for decentralized reinforcement learning. This algorithm is an extension of Q-learning and does not require any additional communication between the robots.
When studying multi-agent systems, the learning environment might be non-Markovian from an agent’s perspective. This property is explored in [24], where the multi-agent systems are investigated from an evolutionary dynamical perspective. In [25], some known intuitions about concurrent learning agents are formalized, providing formal conditions that make the environment non-Markovian from an independent (non-communicative) learner’s perspective. Cooperative control can be used to improve both the quality and speed of learning [26]. Additional parameterized control policies, which are used to reduce the computational load of high dimensional continuous state-action spaces, are presented in [27]. Ref. [28] combines deep learning with multi-agent systems, developing a deep multi-agent RL approach for decentralized continuous cooperative control. In [29], the distributed control of mobile robots is presented for environmental sensing applications. Closed-loop locomotion policies are learned for articulated mobile robots (snake and hexapod) using the multi-agent extension of asynchronous advantage actor-critic (A3C) algorithm [30]. The A3C algorithm acts as a global meta-agent storing a shared policy that multiple worker agents implement and improve in a distributed manner. Coordinating manipulation skills using two robots is also presented in [31], where a multi-agent approach using skill behavior diversification is implemented. The learning of skills is done separately and put together in order to achieve a complex task execution. In [32], a decentralized multi-arm motion planner is implemented using up to 10 robotic arms. The decentralized policy is trained to control one robot arm in the multi-arm system to reach its target end-effector position, given the observations of its workspace state.
1.3. Paper Contribution
The main objective of this work is to decentralize a centralized controlled system of a multi-DoF robotic arm. By decentralizing and splitting the actions into multiple separate agents, the proposed approach gives modularity to the system. Specifically, in the presented approach, two agents are used in the multi-agent system. The number of used agents, as well as the number of motors that a single agent controls, can be varied, providing flexibility and generalizible capabilities to the framework. Multiple variations of the recent RL algorithms (i.e., Proximal Policy Optimization—PPO—and Soft Actor-Critic—SAC) are used for the training. In the first case, the agents are coordinated by an overseer (a meta-agent), which gives importance to the actions of one of the two agents. In the other case, the agents are not coordinated, and instead, both the agents follow their own policy, either the PPO policy, the SAC policy, or the combination of both. In the uncoordinated case, the agents are not given any information about the output of the other agent, thus, not knowing that their actions affect the other agent and the overall system. In the final case, a single agent in a decentralized system is used. The manipulator’s action are divided into two parts, and a single agent following one policy is used to learn the task (as shown in [33]).
In order to evaluate the proposed multi-agent framework, a 7-DoF Franka EMIKA panda robot is employed to perform a grasping task. The robot is required to position the end-effector above the object to be grasped, grasp the object, and finally lift it off of the surface. The overall performance of the grasping task is compared with the centralized system proposed in [33]. In more detail, the decentralization of the system is done by splitting the motors of the system into two equal parts, and giving the control of one part of the system to one agent and the rest to the other agent. Specifically, one agent controls the first four motors of the manipulator, while the second agent controls the last three motors of the manipulator and the gripper. The information of the system is shared between the agents, each one following a specific policy, with four output control actions that affect the next state. Training with multiple agents demonstrates the modularity of the process. The learned behavior can then be transferred to the real robot, to execute the target task and prove the scalability of the algorithm.
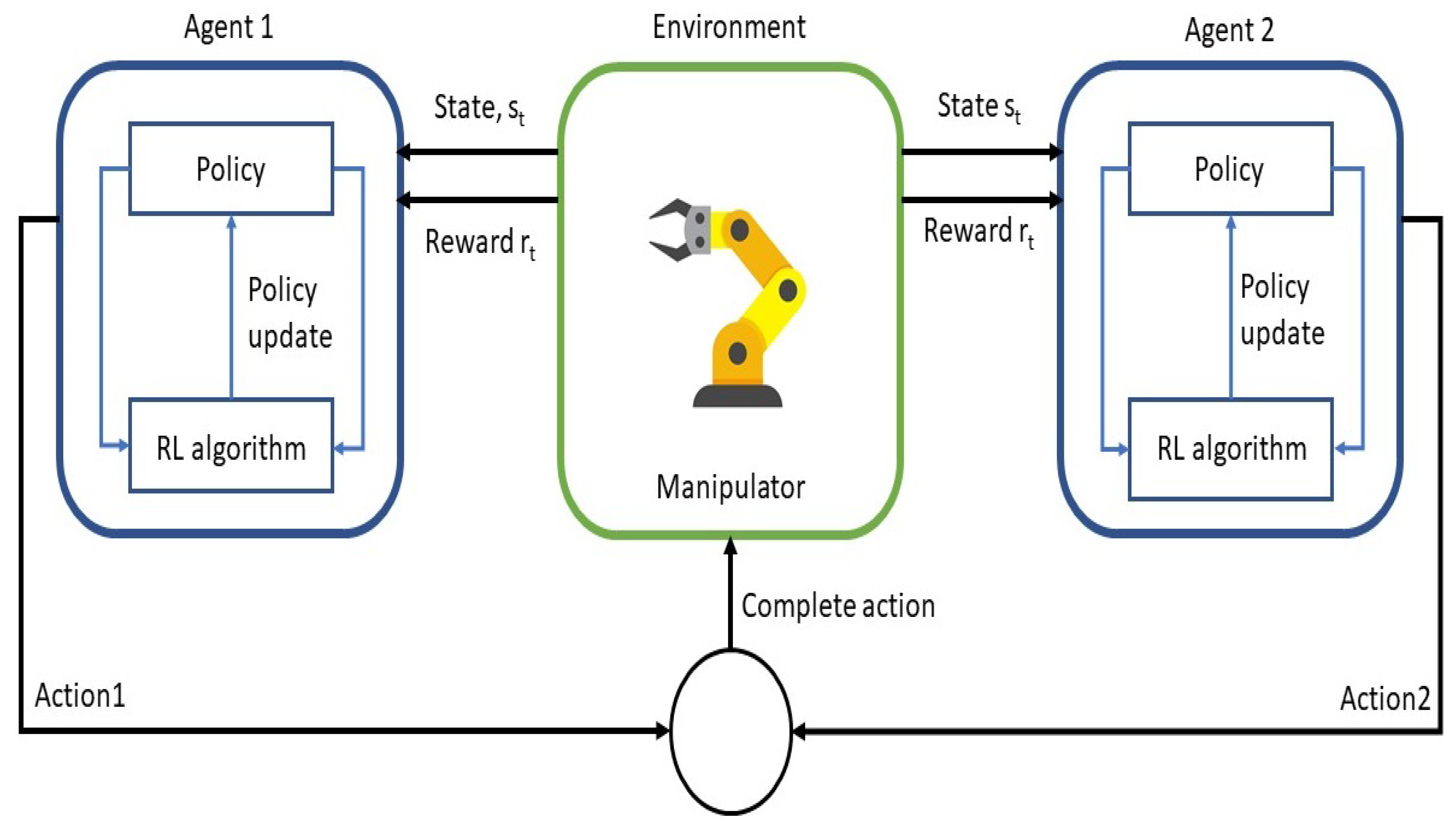
All of the achieved results show an acceleration in the learning process at the beginning of the episodes, even though the multi-agent approach leads to a stagnation of the learning curve. It is also shown that (with the correct setup of the reward function, the correct combination of On and Off policy algorithms, the correct number of agents, and the decentralization of the action space) a fewer amount of episodes are required to achieve the same reward of the baseline algorithm in [33] during the execution of the target manipulation task. This leads to an improvement of the overall training wall clock time, in combination with the efficiency gained for processing. The main scheme of the proposed multi-agent framework for the manipulator is shown in the Figure 1.
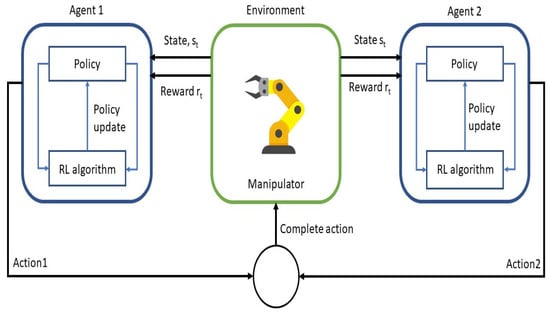
Figure 1.
Main conceptual scheme of the proposed approach using a multi-agent and decentralized reinforcement learning approach.
1.4. Paper Layout
The paper is organized as follows. In Section 2, the addressed problem is described and principal challenges faced in the paper are explained, along with a schematic representation of the developed solution. Section 3 serves as an introduction to the methodology behind some of the key concepts of the proposed multi-agent framework decentralizing the robots control action learning. It provides details about the multi-agent and decentralized RL, together with a more detailed scheme of the key algorithms that have been employed. Section 4 presents the implementation of the proposed solution, providing details related to the learning environment, the training, and the defined reward function. In Section 5, a deep analysis of the experimental evaluation is provided, comparing the decentralized and multi-agent approach with the centralized algorithm in [33], which has been used as a baseline. The obtained results are discussed in Section 6. Finally, Section 7 states the conclusions, highlighting the limitations of the proposed approach, together with further possible future works to address them.
2. Problem Description
The primary objective of this paper is two-fold: (1) to provide an approach for decentralizing a single manipulator into multiple parts to show the possibility of using multiple agents in modular robots, and (2) to compare the results of the decentralized framework with the centralized framework proposed in [33]. To do that, the robot needs to be simulated in continuous space, as most of the real-world robotics problems are represented in this way. For such a purpose, the Mujoco multiphysics simulation engine has been employed as it is better detailed in the following sections. Multiple variations of model-free reinforcement learning algorithms are employed in the learning process. The on-policy algorithm, Proximal Policy Optimization (PPO), off-policy algorithm, and Soft Actor-Critic (SAC) are proposed to train the robot controller. Another algorithm that is proposed is the use of a meta-controller that coordinates the multiple agents in the system.
In order to implement, validate, and test the proposed multi-agent framework, a manipulation task (i.e., grasping and lifting) has been considered. The target task is the same as in [33], to have a fair comparison between the centralized and decentralized approaches. In more detail, the task consists of the robot interacting with the object (a 6 cm cube) placed on a table. The goal is to successfully grasp and lift the cube off the table. The task can be split into several phases that need to be completed in a sequence in order to have a successful execution of the task. The phases are:
- Reaching: the agents receive a reward if the robot’s end-effector approaches the cube;
- Grasping: a grasping reward is given if both of the fingers of the gripper touch the cube, so that the grasping phase is fulfilled;
- Lifting: when the cube is lifted off the surface, the lifting reward is provided, and this constitutes a successful episode.
The complete task can be thought of as accomplishing the sub-tasks that lead to achieving the main objective.
3. Methodology
3.1. Preliminaries
In this paper, the RL problem is modeled as a discrete time-continuous Markov decision process (MDP). Markov decision processes are the mathematical foundation for RL [3,34]. A Markov decision process is a tuple , where S is a state set, P is the transition probability matrix, R is a reward function of the agent based on the current state and the chosen action, and A is a finite set of actions available to the agent. The objective of the agent is to learn a policy that maximizes the expected return, whilst achieving the maximum cumulative reward. A policy represents the description of behaviors of an agent. A stationary policy is a probability distribution over actions to be taken in each state. A deterministic policy has a probability of one for some action in a state.
Reinfocement learning methods can be divided into three main categories:
- Value-based methods, which learn a value function that is then used to derive a policy;
- Policy-based methods, which have a parameterized policy and directly search for the optimal policy;
- Actor-critic methods, which learn both the value function and the policy. The role of the critic is to judge the actions taken by the actor on the basis of the learned value function. The actor then updates its policy parameters based on the critic’s feedback [35].
In this paper, the actor-critic method is used to learn both the policy and the value function. Based on the way the algorithms generate and use experience data, a further classification can be made into On-policy and Off-policy algorithms. On-policy methods evaluate the same policy that is used to select actions; whereas, off-policy methods learn the target policy that is different from the behavioral policy used to generate experience. In this paper, two main algorithms are used, the on-policy PPO algorithm and the off-policy SAC algorithm. Further information on these algorithms can be found in [36,37].
3.2. Modular Framework for Decentralized Learning
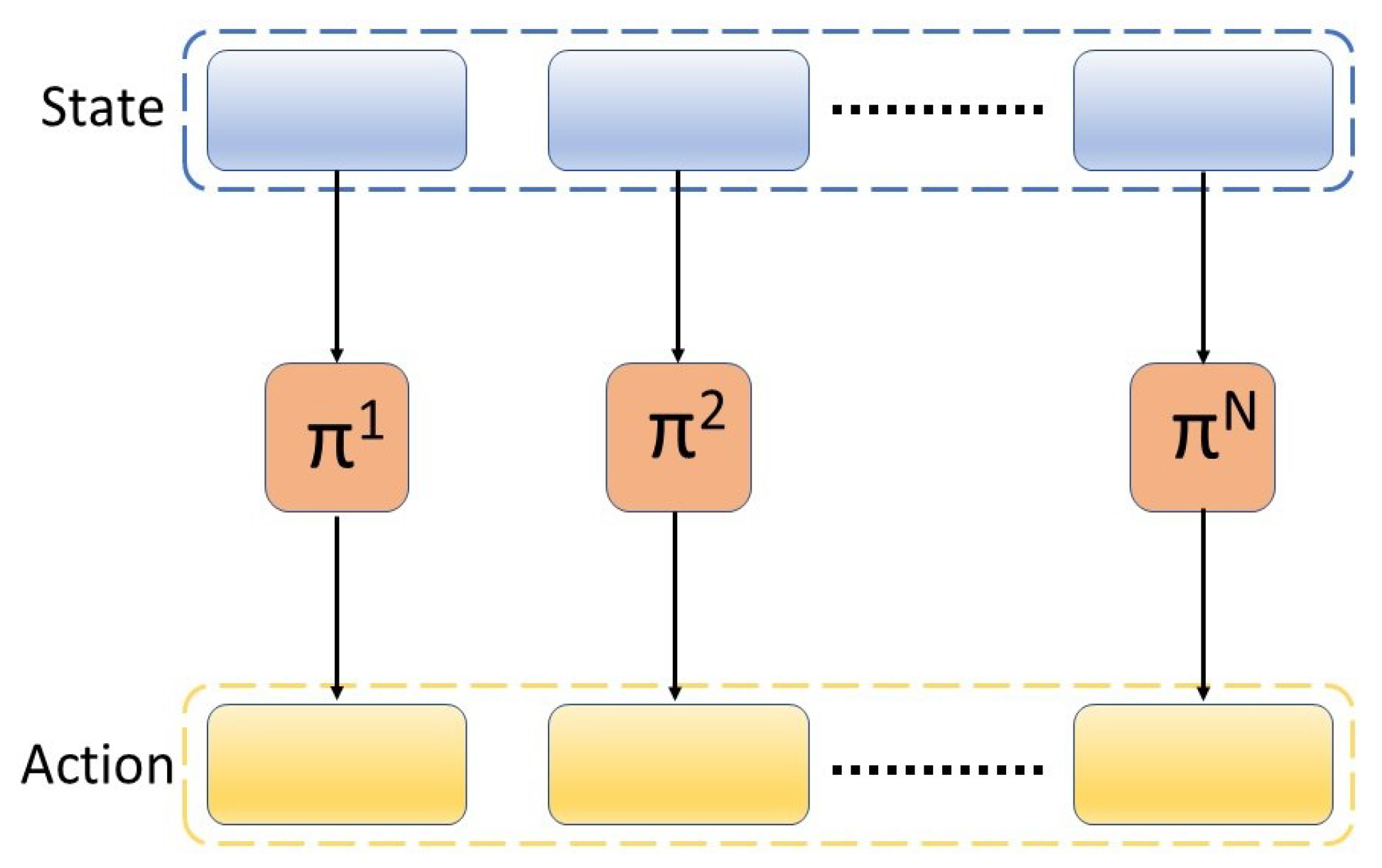
The multi-agent RL method (MARL) consists of N policies that operate on the state and actions of corresponding agents, as illustrated in Figure 2. Instead of having a single policy with the full observation and action space, multi-agent reinforcement learning (MARL) suggests an explicit split in the state and action space according to the agents (e.g., robots or end-effectors), which allows efficient low-level policy training as well as flexible skill composition [31]. The agents in the system can have information about the whole system (all the states) or just one part of the system (the states that the agent directly influences).
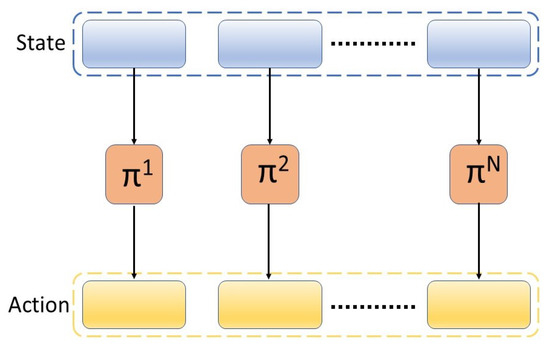
Figure 2.
Multi-agent reinforcement learning framework.
In this paper, a multi-agent RL method is proposed, where each of the N policies takes as input the observation of the whole system and outputs an action for the corresponding agent. Without a loss of generality, N = 2 policies are considered in this paper.
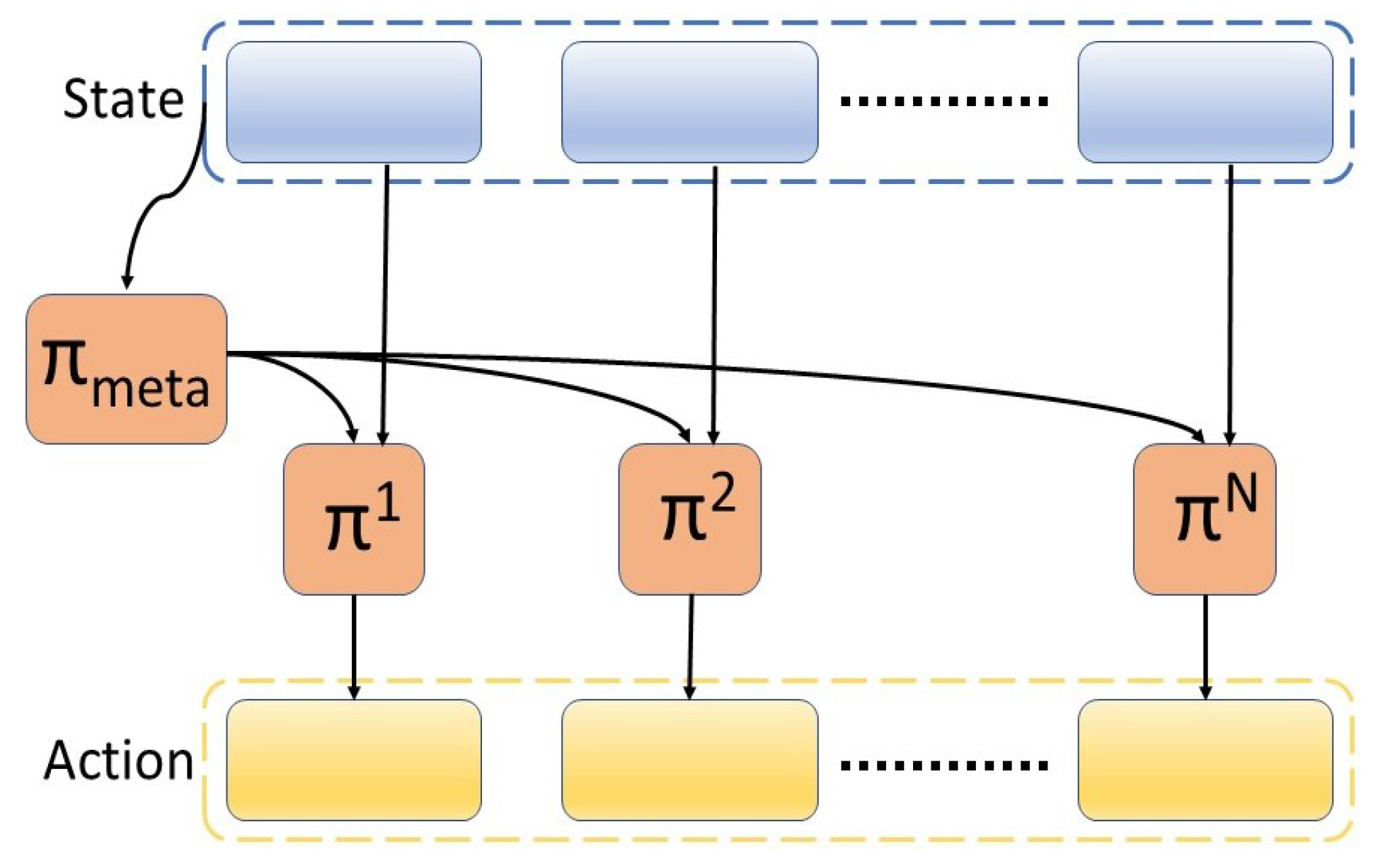
All policies share the global critic learned from a single task reward, as mentioned in [38]. The multi-agent system can be composed of an additional component, which is the meta-policy, as illustrated in Figure 3. This framework is comprised of a set of N agents and a meta-policy . In this configuration, the action of two low-level agents (PPO or SAC agents) learn to control the motors, each having an output of four (the control of the first or second part of the robot), and the meta-agent that oversees the process, gives importance to one of the agents. The meta-agent represents a high-level policy that decides which low-level policy to execute among a set of available policies. The low-level agents can first learn the primitive skills separately, which are then combined later on by a meta-agent to execute a complex task. In this paper, the low-level agents have not learned any specific primitive skills, such as positioning, orienting, or grasping. The learning process for both the low-level agents and the meta-agent is executed jointly. This choice is made in order to have comparable results with the single-agent system. In future work, the agent-specific tasks and rewards can first be learned by the primitive agents and later coordinated temporally by the meta-agent.
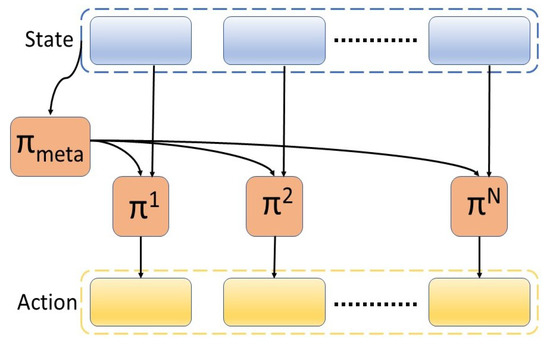
Figure 3.
Multi-agent reinforcement learning framework with a meta-agent.
4. Implementation of Proposed Approach
Reinforcement learning requires an interaction between the agent and the environment. In order for this interaction to be successful and for learning to be possible, the environment and task need to be completely defined. The environment is everything outside the agent. In the case of a robotic manipulator, the environment consists of the robot, the object that needs to be picked up, the table on which the object rests, and the full arena where the robot is placed. The other part that needs to be defined is the task. The task, in this case, is a pick-up task. The rewards that are given to the agent are associated with this task. This section presents a detailed description of the learning environment, the training details, and the network architectures. The final part of this section is used to explain the design of the reward function. This paper is based on the use of a MuJoCo multiphysics simulation engine [39] to model the environment and Pytorch library to train the agent.
4.1. Learning Environment
The learning environment was designed in MuJoCo physics engine in order to simulate the physical system. MuJoCo is a model-based optimization platform that allows fast and accurate simulations, including contact geometries. In order to speed up the simulation, MuJoCo allows the simulation without rendering. A comparison of simulation performance for multiple physics engines is presented in [40], showing that MuJoCo is the fastest environment for robotics-related tasks. The simulation of the robot being used is taken from [41]. With the combination of different models in the simulation, the simulation setup achieved is shown in Figure 4.

Figure 4.
Franka EMIKA panda robot employed in the target grasping task in the MuJoCo environment.
4.2. State-Space
The considered state space is continuous and consists of two main input modalities, the robot information and the target object information:
- Robot information: the data about the robot and its state is a 36-dimensional vector that contains the joint positions, velocities, gripper position, and the end-effector position, velocity, and orientation. The position of the joints is divided and represented by trigonometric functions, i.e., by sine and cosine representations. The robot has 7 DoFs, which gives a vector of 14 values for the position of each joint represented by a sin and cos function. The gripper is defined by a 2-dimensional vector that specifies the position of the left and right fingers. The joint velocities are represented by a single value for each joint, making a 7-dimensional vector. The end-effector data is represented by a 7-dimensional vector, where the position is represented in cartesian coordinates followed by a quaternion to represent the orientation. The end-effector’s state also includes a 6-dimensional vector specifying the linear and angular velocity.
- Object information: the data of the object that needs to be picked up is represented by the position and orientation in the world reference frame. In order to facilitate the reaching of the cube, a relative position vector between the object and the robot’s gripper is added. The object state, thus, makes a 10-dimensional vector.
4.3. Action Space
The action space consists of an 8-dimensional vector, which represents the 7 joints of the panda robot and the gripper. The last dimension of the action space represents the actuation control of the gripper and is mirrored to have a symmetrical action for the fingers. The action space is split into two equal parts. One part of the manipulator corresponds to the motors of the first 4 joints, while the second part corresponds to the last 3 joints and the gripper’s actuation. Dividing the action space in such a way allows for the decentralization of the system and shows the modularity of the robot. Joint velocities coming from the agents are fed into a controller that converts the desired joint velocities into joint torques. The robot is considered to be equipped with torque control compensating for the manipulator dynamics [42]:
In this equation, represents the robot inertia matrix, is the robot Coriolis vector, is the robot gravitational vector, is the robot joint friction vector, is the current joint position vector, and is the control torque vector. is the learned task-related control torque vector mapping the reference joint velocities to joint torques for the target task execution.
where and are the reference (i.e., the objective of the learning) and current joint velocities respectively, and:
is a diagonal matrix of fixed proportional gains for joint trajectory-tracking purposes. These control gains need to be tuned to allow the robot to track the reference joint velocities . The values that are selected are based on the variable impedance control [43], which results in accurate trajectory tracking performance. If needed, such control gains can be either learned or experimentally tuned to improve trajectory tracking performance.
4.4. Training Details
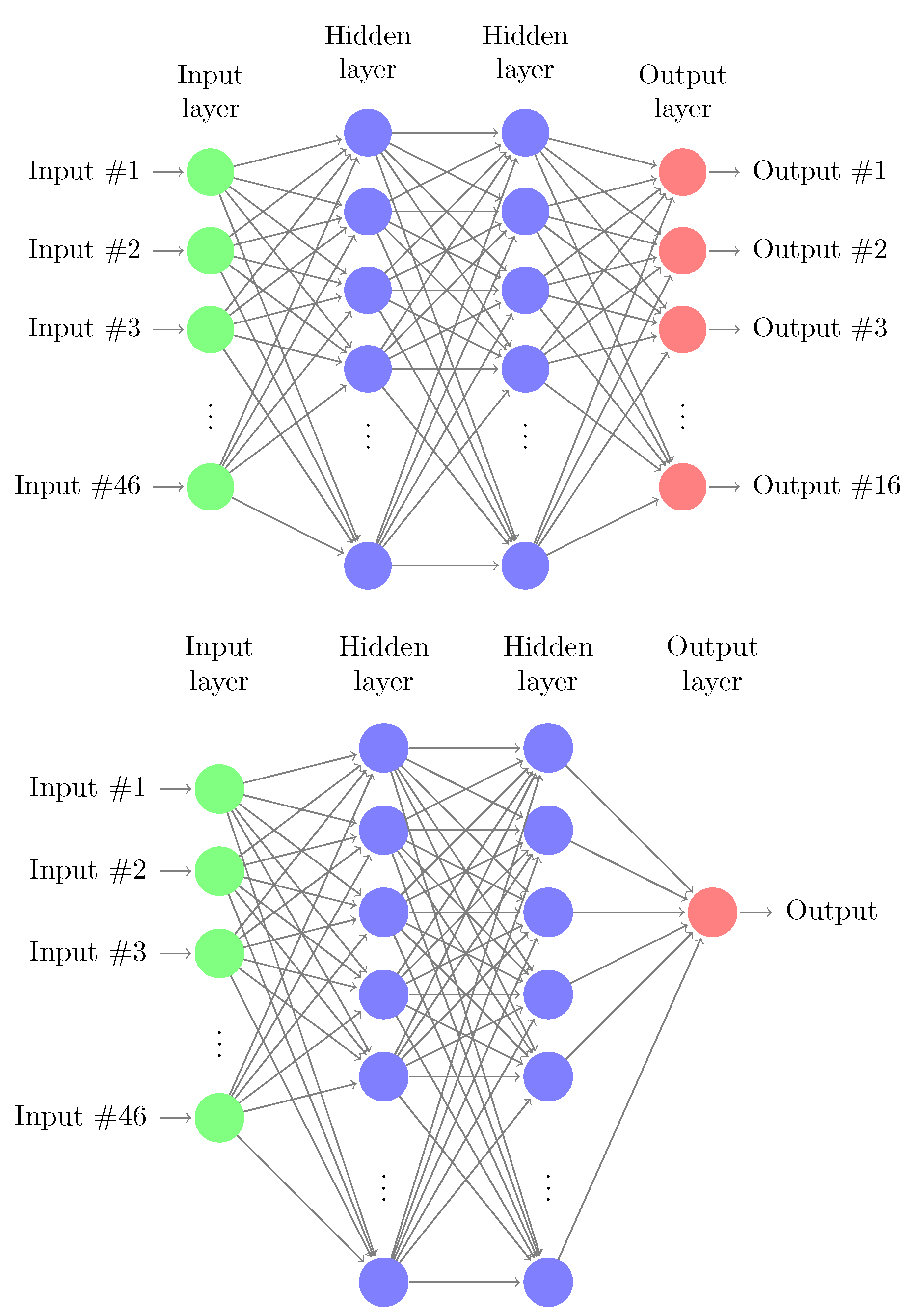
The algorithms described in Section 3 are used to train the target grasping task. The episodes are divided into 600 time-steps where each of them corresponds to roughly 0.1 s of real-time. At every step of the episode, the actions to be executed in the environment are sampled from Gaussian distributions parameterized by the mean and standard deviation for each action dimension. The agents use a replay buffer that stores the transition experience of the episodes. At every update iteration, random samples of a batch size of 512 are collected from the buffer to update the network parameters. While using a PPO agent, the buffer is cleared and the samples are discarded after performing each update because this is an on-policy algorithm. Both agents have the same parameters, the same state-space is fed into both of the agents, and both agents follow a given policy where the output of each agent is a vector of four values, each corresponding to the given motors. Each agent gives half of the output needed for the system and these outputs are combined and fed into the system. The policy network, as well as the value network, are encoded by MLP—multi-layer perceptron. The policy network consists of three layers and Rectified Linear Unit (ReLU) non-linearity. The input layer, representing the state of the system is 46-dim. The hidden layer size is of 64-dim and the output layer is 8-dim. The output layer of a policy network is two-fold, producing the mean and standard deviation (parametrizing the Gaussian distribution) for each action dimension. The value network outputs only a scalar value, which specifies the corresponding value function of the state. All inputs to the policy and value networks are normalized with running estimates of the mean and variance. Both the policy and value networks are shown in Figure 5.
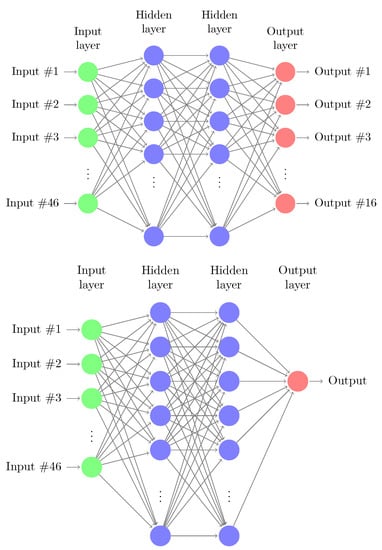
Figure 5.
Schematic representation of: (top) policy network with 46-dim input (environment states) and 8-dim output (actions); (bottom) value network with considered 46-dim input and 1-dim output.
4.5. Reward Shaping
The reward function helps the agents determine if their actions were desirable or not, thus allowing the agents to decide what they need to do. The dense reward signal guides the agent’s exploration process and enables efficient learning; however, shaping a reward function is an exhaustive process. Another approach to overcome the exploration issue is to provide an interactive feedback to the agent where the external teacher may overwrite the actions prescribed by the policy [44]. This approach is termed policy shaping, and allows the agent to learn even in the presence of binary reward signals. In this work, the reward shaping approach has been used to overcome the exploration issue for multi-agent learners in order to compare the results with a centralized single-agent that uses the same reward function. Shaping the multi-agent policies using interactive feedback, either from external human teachers or artificial trainers, is a promising direction for future work.
The reward function is divided into two phases, and a separate reward is given for each phase. The reward for the reaching phase is as follows:
In the above equation three different rewards are represented:
- : the distance reward which is computed using the relative position of the gripper w.r.t. the object;
- : the velocity reward that takes into account the end-effector velocity vector when approaching the object;
- : the gripper open reward depending upon the action of the gripper.
The combination of and incentivizes the agents to approach the object with an open gripper and a small velocity. All three contributions (, , ) are weighted with respective weights = 0.6, = 0.3, and = 0.1, and defined as:
where and denote the position vector of the gripper and the cube in the world reference frame; represents the velocity of the end-effector, which contains the linear and angular components of the velocity with ; specifies the action of the gripper with negative values indicating that the gripper is opening.
The lifting phase of the reward is initiated when the robot’s gripper is in close proximity to the object. The distance threshold for switching between the grip and lift rewards is set to cm. This is because the nominal cube measures 6 cm, and the robot should be able to grasp the cube when its grip site is within the cube boundaries. The reward for the lifting phase is defined as:
and consists of the following five contributions: and are the same as the previous equation; reward is now reversed so it gives a reward when the gripper closes in order to grasp the cube. This reward is weighted by = 0.1. Additional rewards are and . is given if both fingers of the gripper make contact with the walls of the cube and is an additional reward if the episode is successful, i.e., the task is completed. A successful episode constitutes if the gripper holds the cube at a certain height above the table. ; ; in the lifting case are defined as:
Different iterations were performed to set the values of the grasping reward and the success reward . In particular, setting higher values led to a very high variance in the reward, causing training inefficiency. The selected values encourage the learning agent to accumulate more reward in the lifting phase by accomplishing grasping and lifting of the cube, while avoiding too high of a variance in training results. The total reward is then computed as the accumulated sum of in Equation (4) and in Equation (6).
4.6. Software Implementation
The software implementation is available at the following GitHub repository [45].
5. Results
In this section, the algorithms used for the training are evaluated and compared with the centralized approach. The reward function presented in Section 4.5 has been shaped and optimized for the single-agent control. For the decentralized and multi-agent control, the same reward function is used to provide a proper comparison with the centralized approach. The following multi-agent algorithms are considered:
- One meta-PPO agent and two low level SAC agents;
- Two PPO agents;
- Two SAC agents;
- One PPO agent and one SAC agent.
In the first configuration, the two low-level agents learned to control the first or second part of the robot (each having an output of four), and the meta-agent oversees the process and gives importance to one of the agents. The other three configurations involve two separate agents, where each one controls one part of the action space, i.e., each controls four motors of the robot. The two agents do not communicate with each other, and each one strives to make the optimal decision knowing the observation space, but not knowing the actions of the other agent. The two agents follow either the PPO policy, the SAC policy, or the combination of both.
A final configuration is considered where only one agent is used, but the action space remains divided. Having the action space divided in such a way allows the agent to look at the actions it takes as two separate vectors. The output of the Policy network is thus two separate four-element vectors, each corresponding to the first and last four motors of the robot. In this way, only one agent is used, which looks at the action space in a decentralized way. The algorithms considered for decentralized single-agent control are the following:
- One SAC agent;
- One PPO agent.
A video showing the progress of the training employing the decentalized single-agent SAC controller is available at the GitHub link [45]. In the video, the improvements in the learning of the target task (i.e., grasping and lifting of the part) are shown, highlighting the capabilities of the method.
5.1. Decentralized Multi-Agent Approach
5.1.1. Meta-PPO Agent with Two Low Level SAC Agents
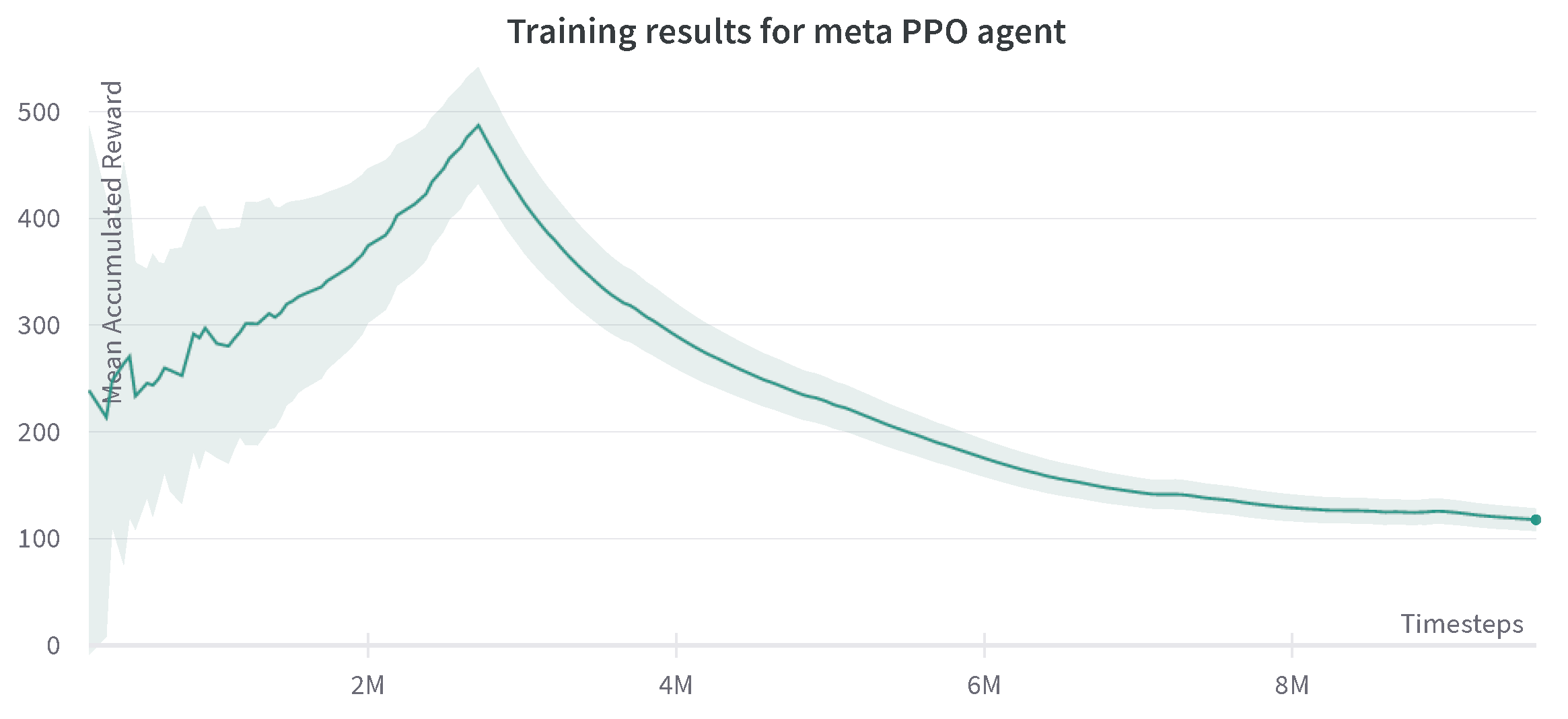
This type of baseline is a hierarchical framework that composes of a meta-policy that coordinates the two low-level agents, which control the robot joints following the SAC policy. In Figure 6, results are shown for the behavior of this algorithm. At the beginning of the training, a steady and relatively fast increase in the rewards is seen; this can be explained by the fact that everything in the experience is new to the robot, and the functional algorithms make the proper use of this experience for learning. However, after approximately three million time steps, the rewards plummet, and the agents enter a local minimum, which they do not escape, regardless of the number of iterations. The meta-agent’s interaction with the low-level agents comes to a point where it thinks the maximum successful reward has been achieved. This training has been run for 10 million time steps, and the reward stays in the same range of 50–100, without a successful episode.
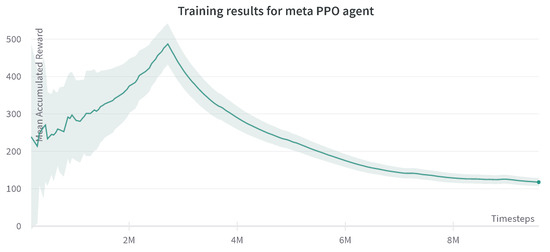
Figure 6.
Progression of mean accumulated reward for the meta-agent with two low-level SAC agents. Training results are reported for three experiments with different random seeds. The standard deviation of three runs is shown in the plot.
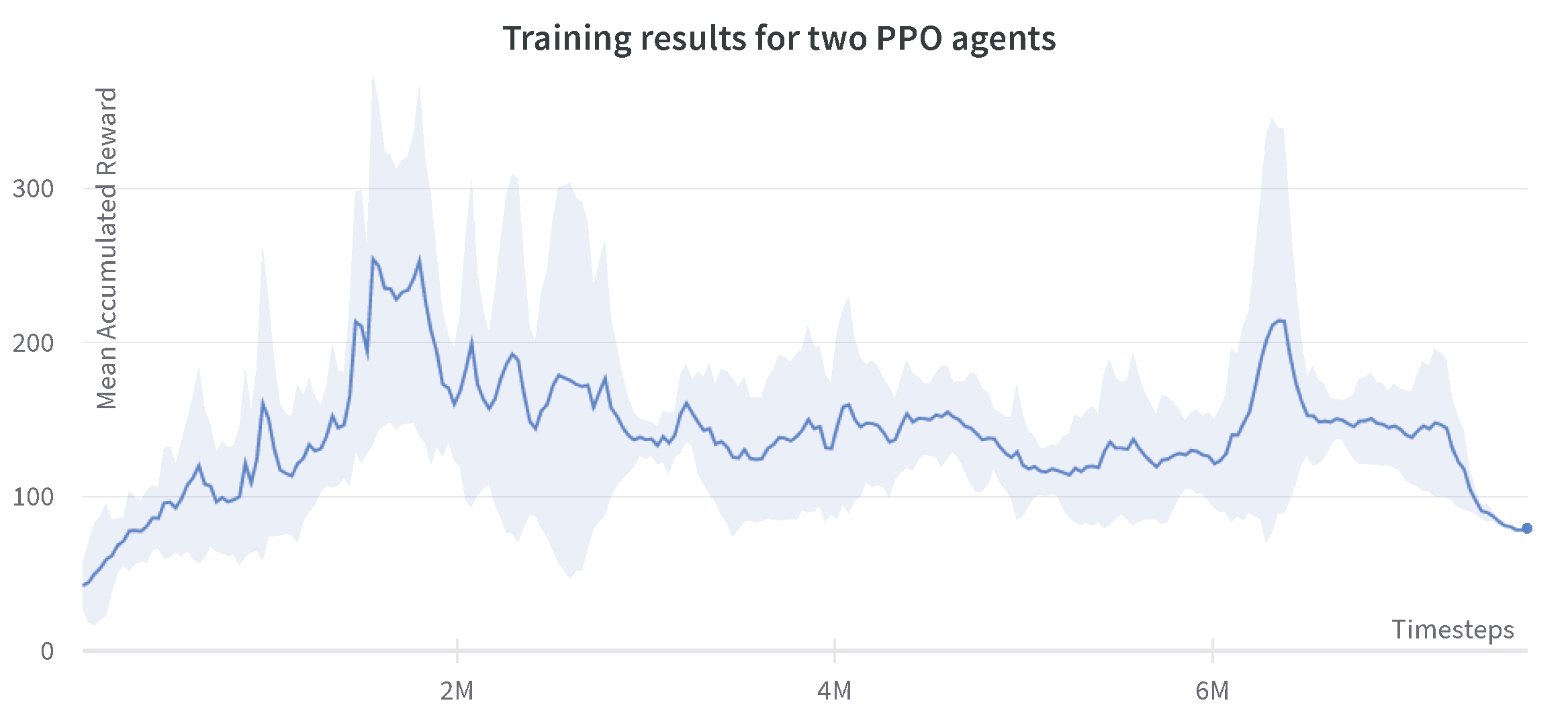
5.1.2. Two PPO Agents
The results for the case of two PPO agents are shown in Figure 7. As expected, the PPO agent has a more significant non-monotonic behavior. This experiment shows that a high reward of around 500 is achieved near the two million time steps, whereas the same algorithm, when used in the centralized single-agent setting, reaches the maximum reward of 250 at two million steps [46].
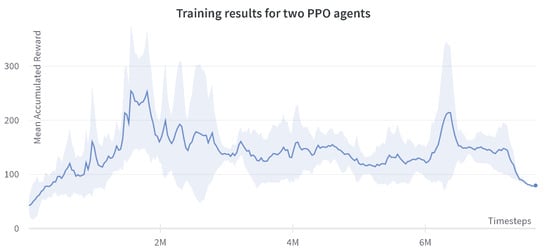
Figure 7.
Progression of mean accumulated reward for the two PPO agents.Training results are reported for four experiments with different random seeds. The standard deviation of four runs is shown in the plot.
At certain times before the two million steps, very high rewards can be seen. At these points, the robot manages to grasp the cube and the learning agent transitions to the second phase of the reward described in Section 4.5. However, unfortunately, it does not result in the lifting of the cube. This can be explained by the fact that the two agents prioritize the actions coming from their own policies instead of cooperating towards a common goal.
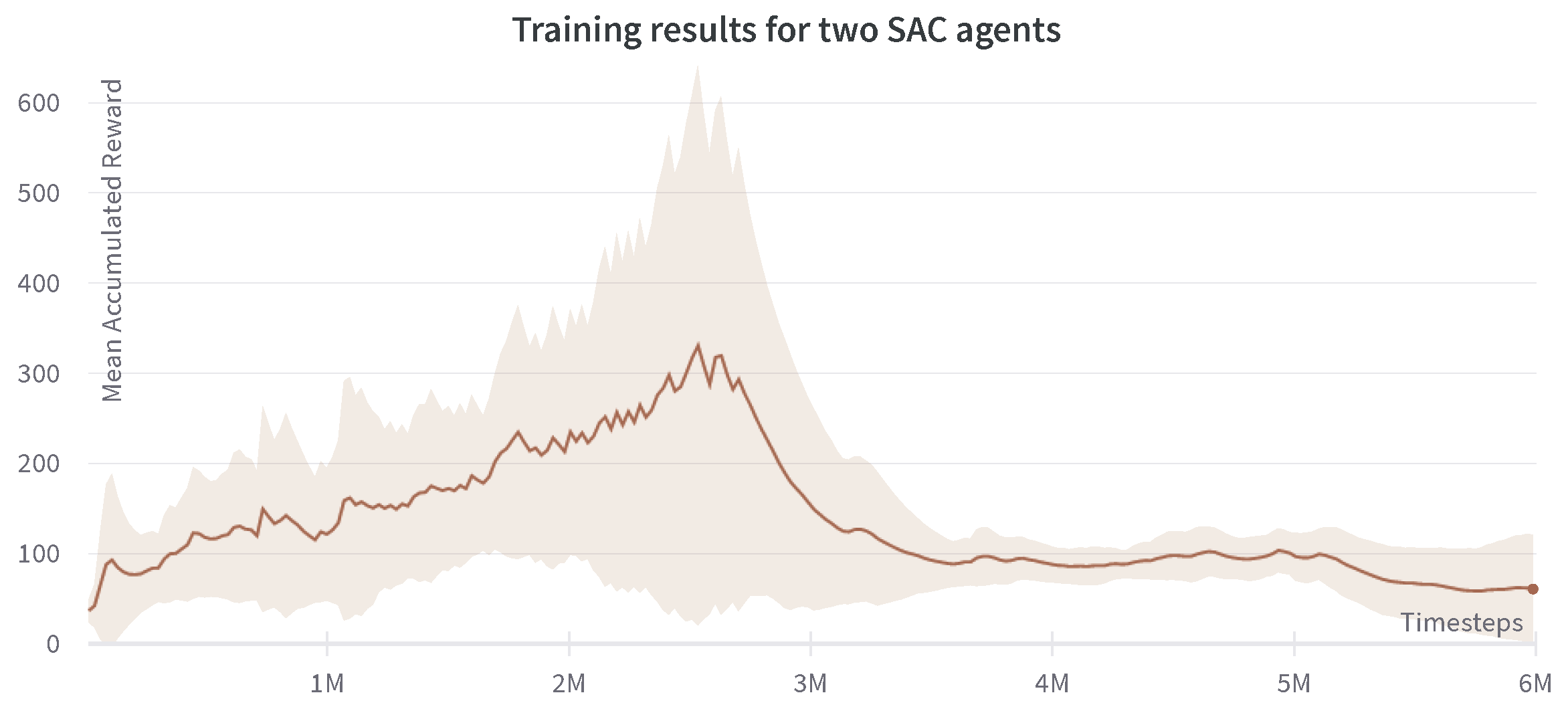
5.1.3. Two SAC Agents
In this configuration, two SAC agents are used in the multi-agent setting. The mean accumulated reward is plotted in Figure 8. A very similar conclusion can be inferred from the two SAC agents multi-agent controller. A clear rise in the total reward obtained can be read from the graph with a much more robust and monotonic increase, as expected to obtain an off-policy algorithm.
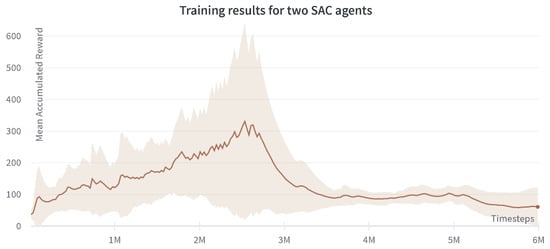
Figure 8.
Progression of mean accumulated reward for the two SAC agents. Training results are reported for four experiments with different random seeds. The standard deviation of four runs is shown in the plot.
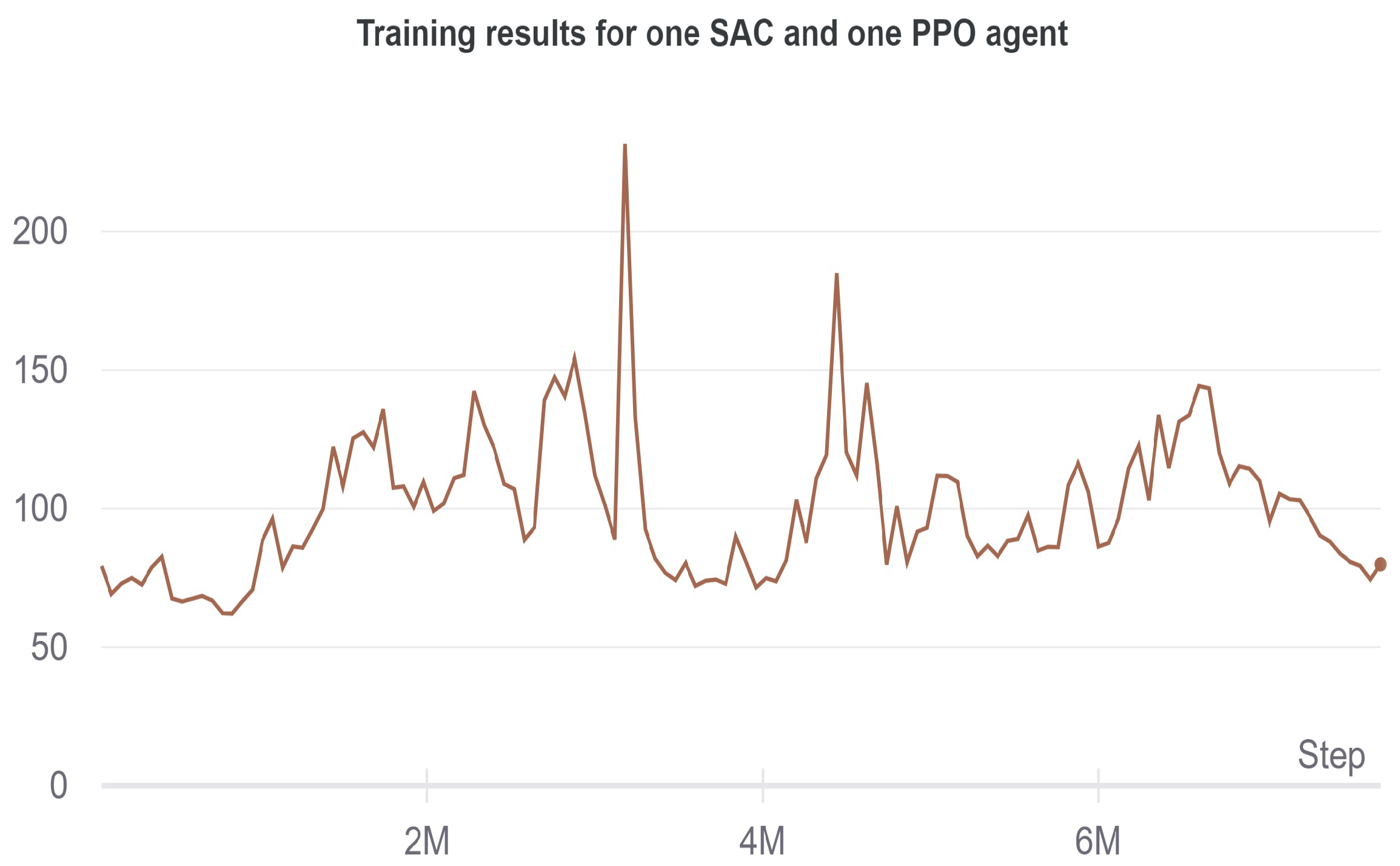
5.1.4. One SAC Agent One PPO Agent
In Figure 9, the training results for the combination of an SAC and PPO agent are shown. Using two separate algorithms, which follow two separate policies does not yield promising results. There is a slight uptrend in the reward at the beginning but the whole curve is relatively flat in the region of 50–150 for the duration of the whole run, which lasted for eight million timesteps.
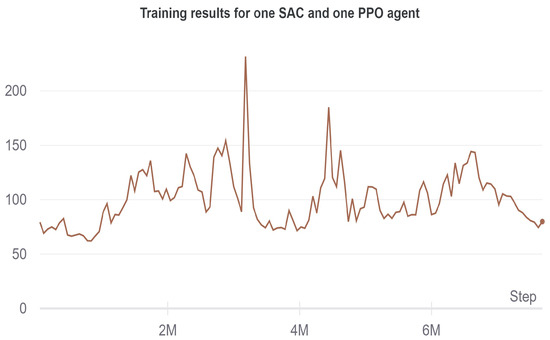
Figure 9.
Progression of the accumulated reward for one SAC and one PPO agent.
5.2. Decentralized Single-Agent
5.2.1. Decentralized Single-Agent SAC
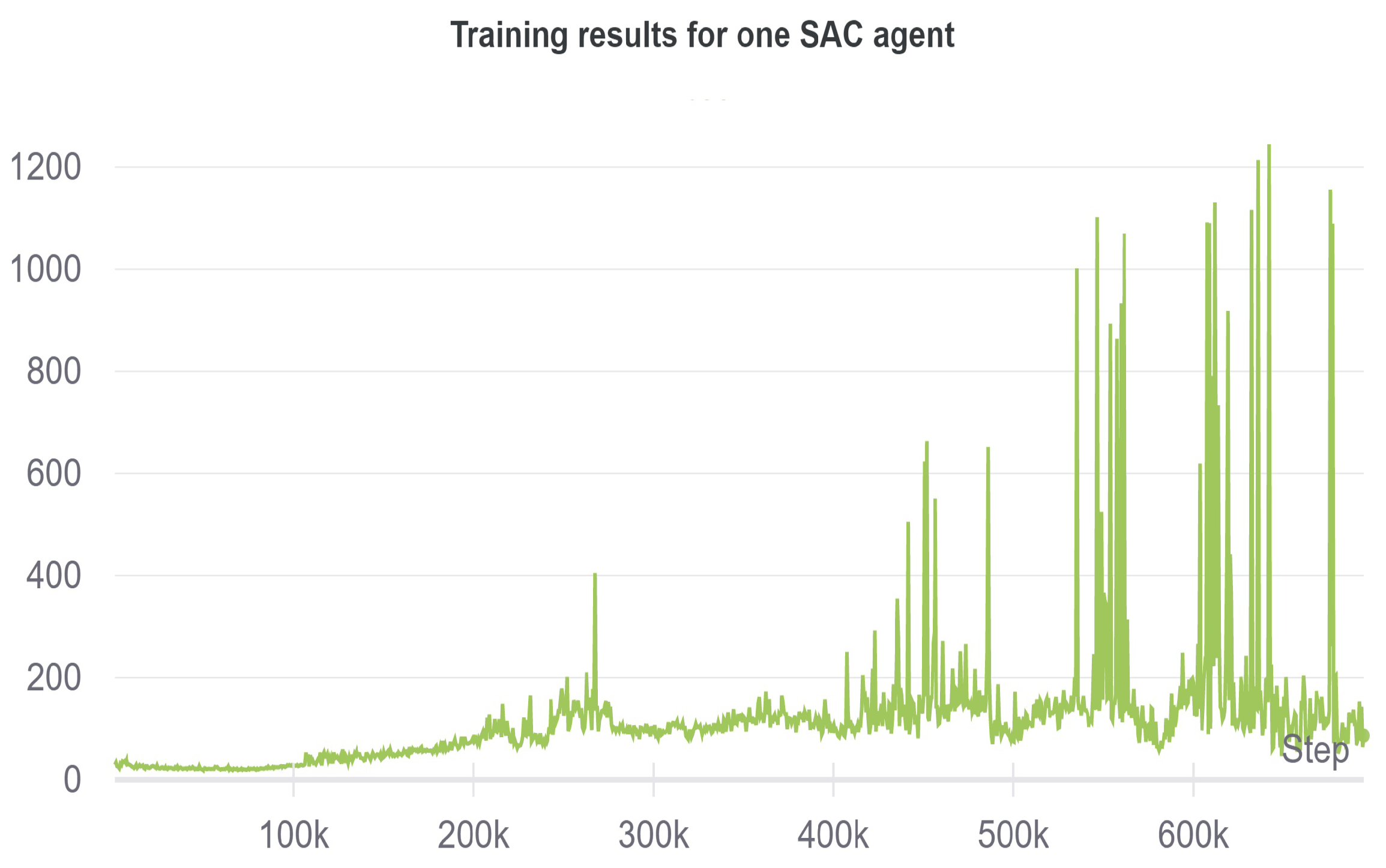
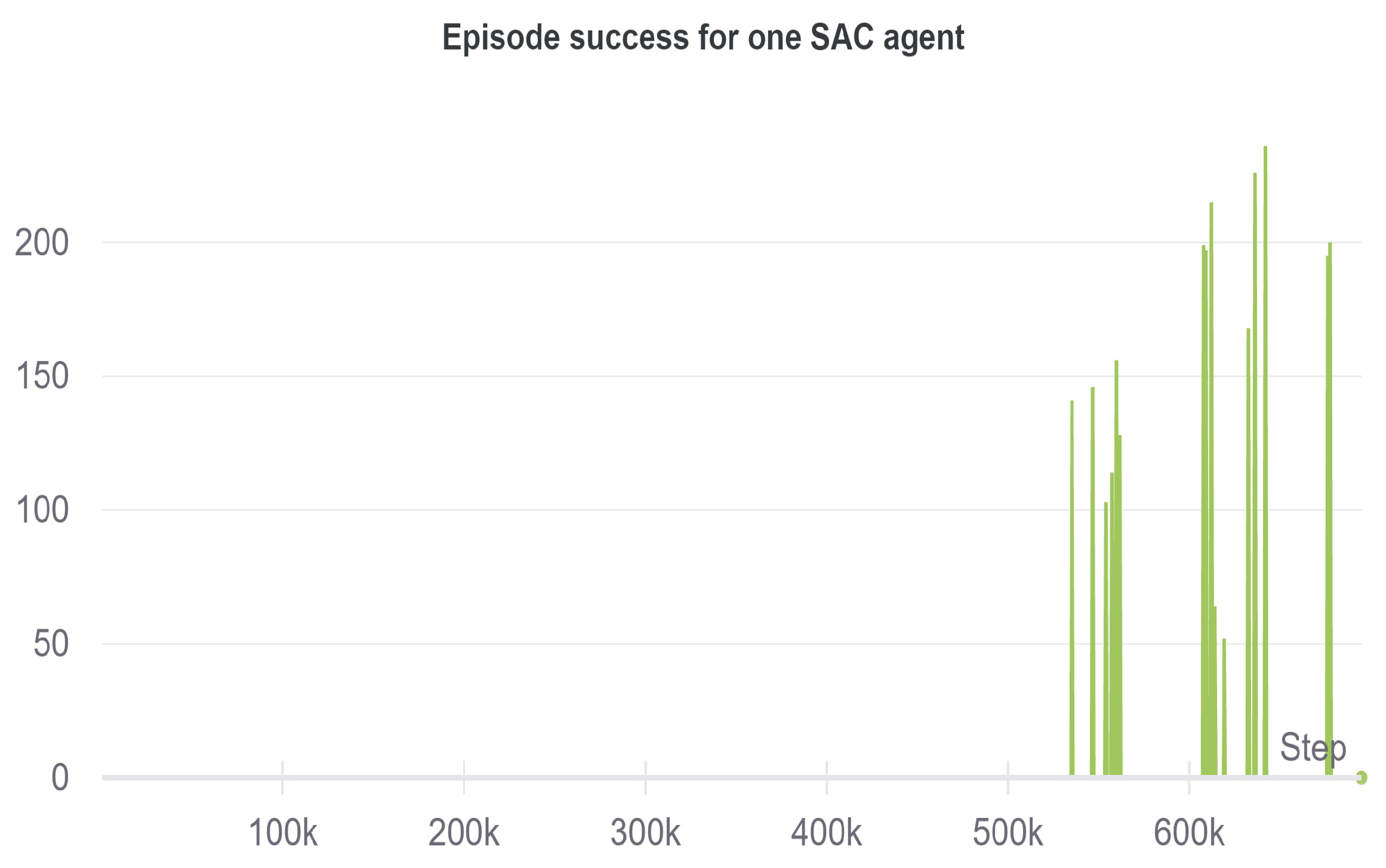
When using only one SAC agent with a divided action space, the following results achieved are shown in Figure 10 and Figure 11.
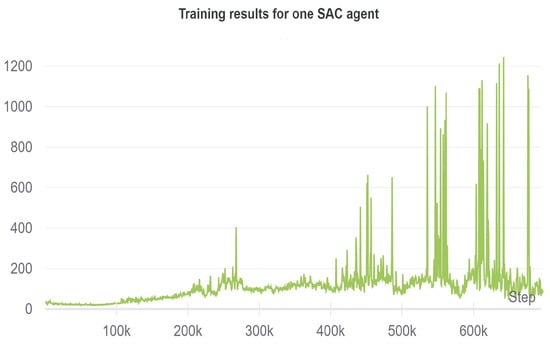
Figure 10.
Progression of the accumulated reward for the decentralized single-agent SAC.
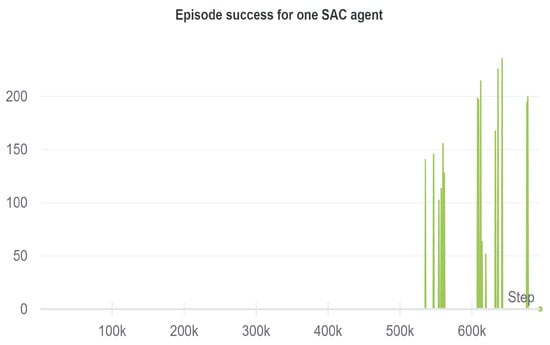
Figure 11.
Episode success rate for the decentralized single-agent SAC.
The figure shows a steady uptrend of the reward. At 400K timesteps, the robot learns to grasp the cube, while at 600K, the training results in a successful lifting of the cube. Comparing these results with the single-agent centralized approach in [46], the iterations needed for successful task completion are halved, achieving a reward of 1200 at 600K timesteps, leading to a much faster and efficient learning of the task. The division of the action space in single-agent helps to save the memory, and the training efficiency improves due to the fact that a common learning goal is shared through the same reward function, while the actions are redirected to the corresponding motors in a decentralized manner for the execution.
5.2.2. Decentralized Single-Agent PPO
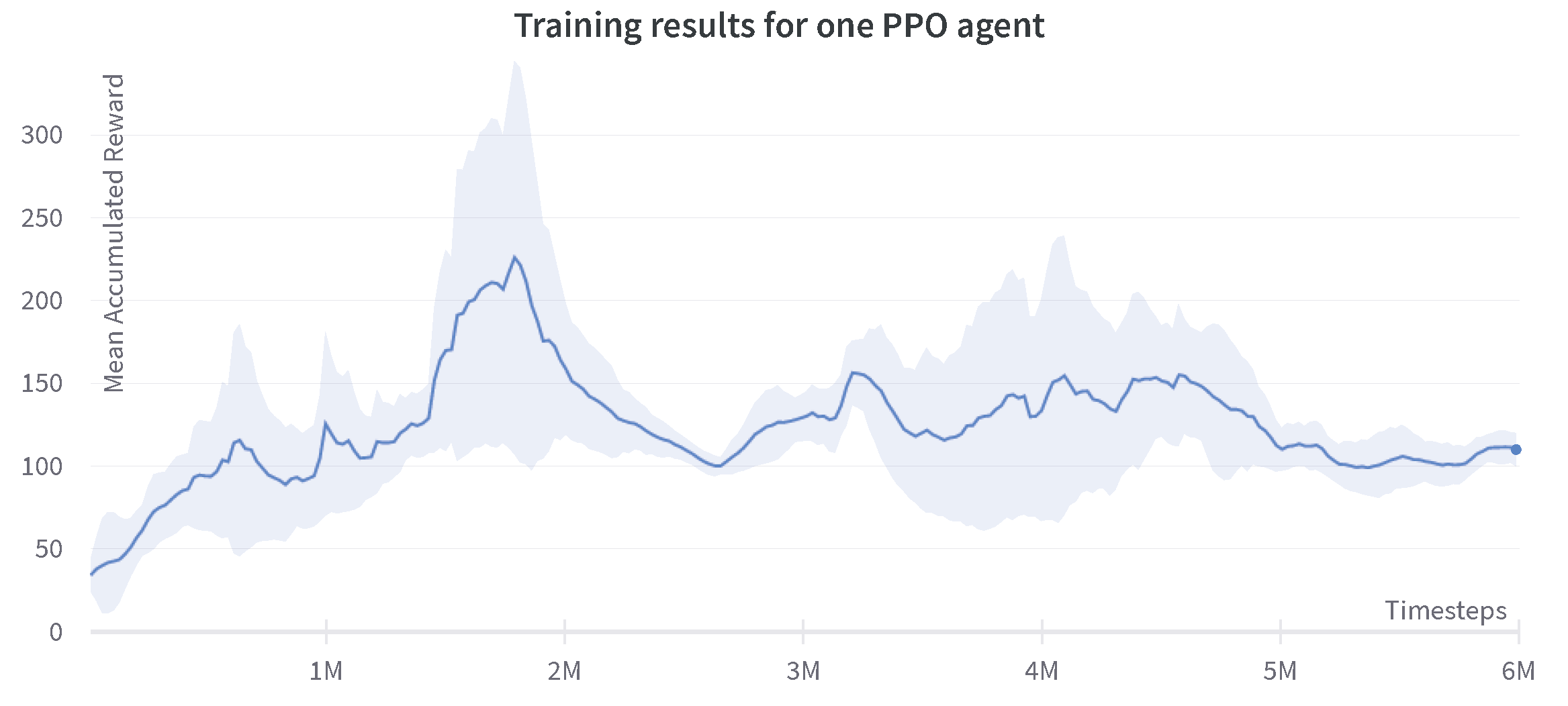
In this configuration, a single PPO agent is used with a decentralized action space and the results are shown in Figure 12.
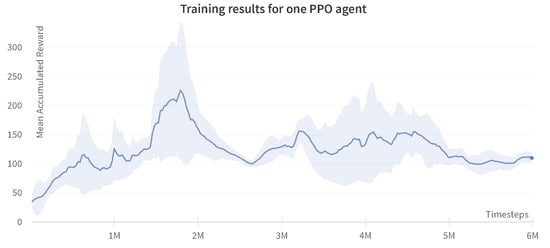
Figure 12.
Progression of the mean accumulated reward for the decentralized single-agent PPO. Training results are reported for three experiments with different random seeds. The standard deviation of three runs is shown in the plot.
The comparison of the results achieved through decentralized single-agent SAC and PPO is shown in Figure 13. It is shown that the decentralized PPO agent required more iterations in order to reach a successful episode in comparison to the SAC agent. The PPO agent also tends to stagnate at certain areas, which can be seen after the two million steps where the agent is performing positively, but later falls to a local minimum.
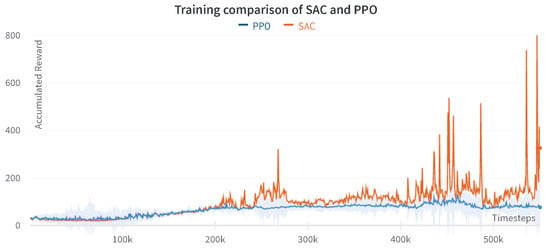
Figure 13.
Comparison of accumulated reward for the decentralized single-agent SAC and PPO.
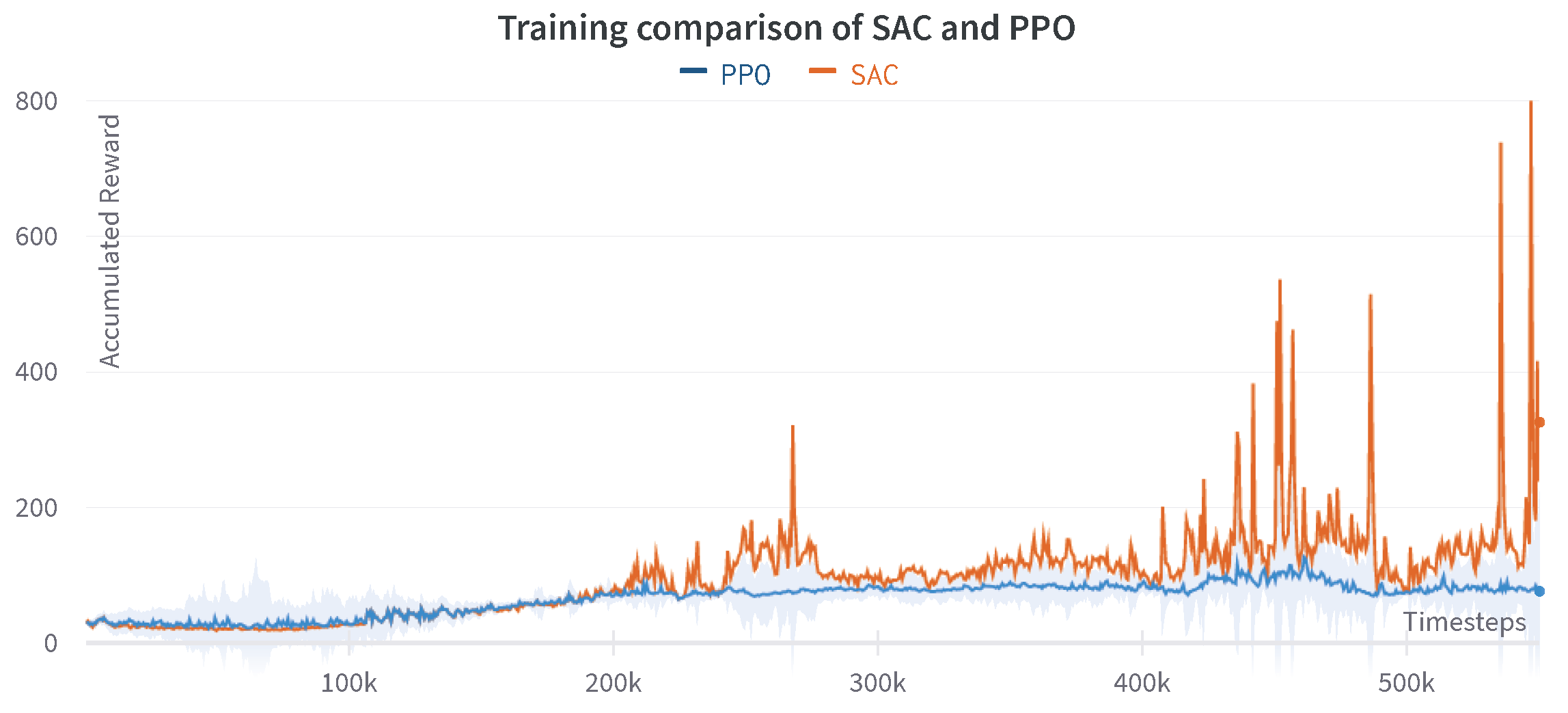
5.3. Comparison of Centralized and Decentralized Approach
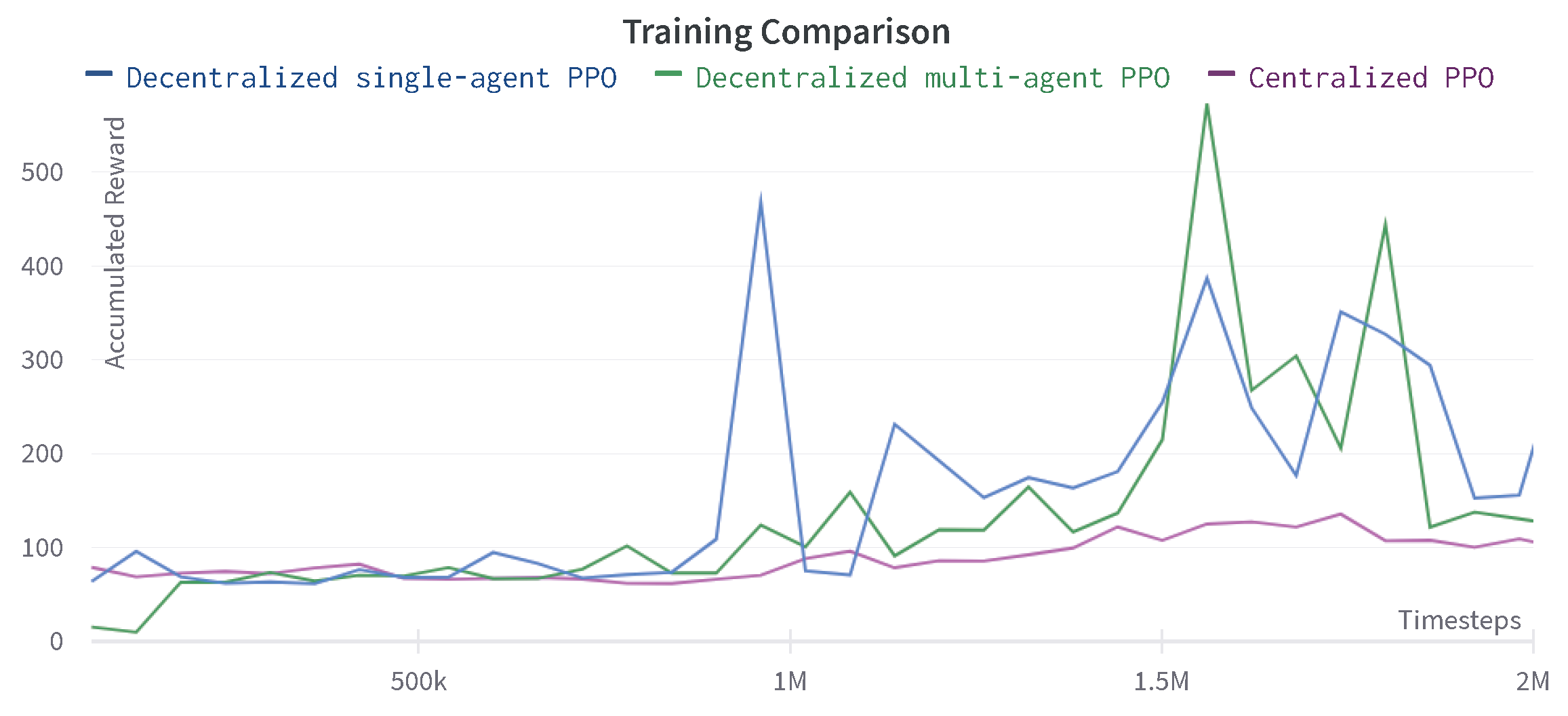
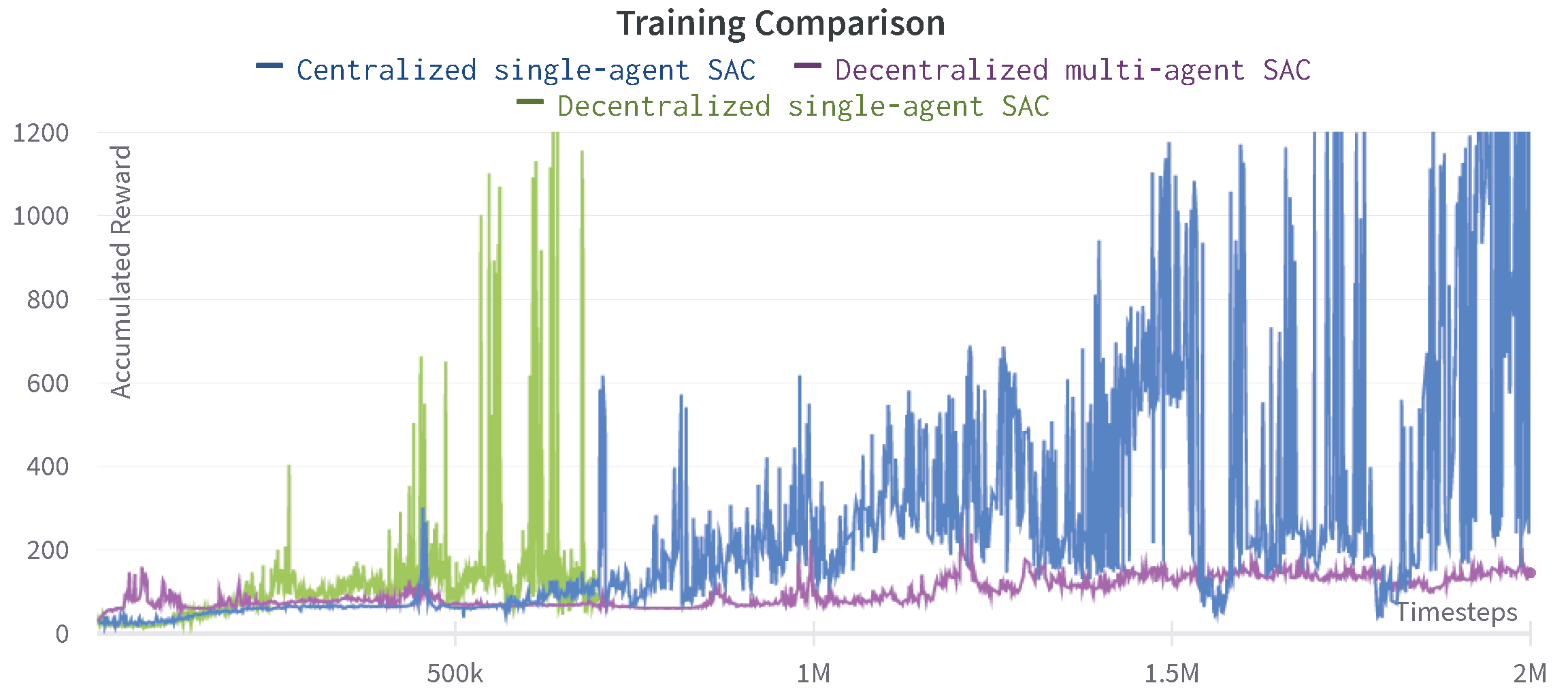
The training comparison between the centralized and decentralized approach for PPO and SAC agents is shown in Figure 14 and Figure 15. The decentralized PPO algorithm accumulates higher average reward than the centralized PPO; however, it also shows a non-monotonic behavior. Whereas, the learning curve of the centralized PPO agent is smooth, as demonstrated in Figure 14.
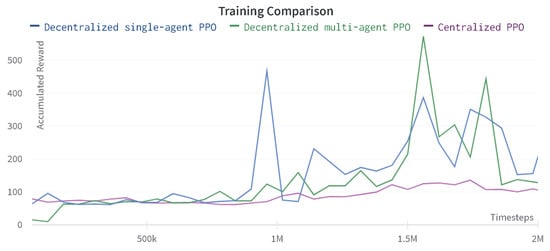
Figure 14.
Comparison of accumulated reward for the centralized and decentralized PPO agents.
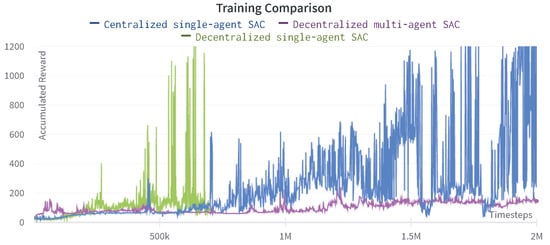
Figure 15.
Comparison of accumulated reward for the centralized and decentralized SAC agents.
On the other hand, the decentralized single-agent SAC in Figure 15 demonstrates a much faster and efficient learning process as it accumulates a very high average reward and shows the task success in just 600K timesteps while the centralized SAC agent needs at least 2M steps to reach success. The multi-agent SAC curve instead is relatively flat and does not reach any task success in the first 2M timesteps.
Table 1 summarizes the results of all analyzed approaches and shows the comparison of maximum accumulated reward achieved in an episode considering the first 2M steps of training. The decentralized single-agent SAC is the most efficient approach of all, since the agent accumulates the highest reward, while the combination of multi-agent SAC and PPO achieves the lowest reward. This might be due to the lack of coordination among agents in the multi-agent configuration as there are no explicit terms in the reward to encourage such coordination. Therefore, an interesting direction for the future work is to shape the reward function that encourages coordination among agents in a multi-agent setting.

Table 1.
Maximum accumulated reward in the first 2M time steps.
6. Discussion
Similar results and behaviors can be seen for all multi-agent approaches. The learning efficiency is improved at the beginning of the training before the stagnation of the learning curve. Therefore, the multi-agent division doesn’t improve the training efficiency for the completed task. However, it is still better from the computational point of view as the division of the action space provides modularity to the overall system, allowing to train the agents in a distributed manner. Moreover, larger expected rewards can be achieved by the off-policy SAC multi-agent compared to the PPO multi-agent, since it takes advantage of past data storage. The PPO agent is slower than the SAC agent in both the centralized and decentralized approach. Most of the higher rewards achieved during the multi-agent runs can be correlated with the gripper touching the cube with a good approaching velocity. Nevertheless, a lack of coordination and a sparse reward setup for the second phase in charge of lifting the cube prevents it from completing the task. In the reaching phase, a very high reward was achieved by the first agent that was, however, overturned in the lifting phase where the actions of the second agent had more significance. This sort of behavior can be attributed to the fact that the reward is shaped to accommodate the centralized single-agent learning. Since the reward is highly sensitive, and small variations can lead to the difference between a successful episode and an unsuccessful run, the reward function can be augmented with different aspects to accommodate the needs of multi-agent learning as was done for the centralized single-agent. In addition, having a separate reward function for each of the agents and augmenting the agents’ input with the information about prior sub-tasks could improve the performance of the decentralized multi-agent learning.
The video available at the GitHub link [45] shows the evolution of the learning process for the decentalized single-agent SAC controller, having the robot able to learn the target task (i.e., grasping and lifting of the target part). The policy of the training run with the highest accumulated reward is selected as the control actions to be applied to the robot to execute the learned task. As in [33], the learned control torques or joint positions/velocities can be transferred to the real robot to perform the given application.
7. Conclusions
In this paper, a decentralized and multi-agent approach has been formulated in the form of an RL problem, demonstrating the possibility of decentralizing a single manipulator controller by applying multiple agents in learning continuous actions. The idea of this paper has been to compare the feasibility of decentralization for a single robot to show the modularity in the joints, as well as the comparison between the centralized and decentralized approach. Results show that it is possible to decentralize the control action on the robot. Using multiple agents has shown the stagnation of the learning process when using the same reward function that is used for a single-agent. It is believed that this is due to the lack of communication between the agents and the generality of the reward when considering two agents. A sparser reward needs to be added to the system and agent specific rewards can be considered.
Future work will be devoted to deeper investigating of the proposed approaches, implementing improved methodologies based on the achieved results. A deeper investigation and analysis of the results (e.g., increasing the number of runs of each method to better highlight local minima issues, etc.) will also be conducted in order to provide further insights. In addition, the reward function will be tuned for each agent separately to improve the performance of the methods. Then, adding a sparse reward function, as well as agent-specific rewards, could result in a successful execution of the task using the decentralized approach. Meta-learning will be deeply investigated in order to further generalize the methodology. The transfer of the learned policies to manipulators (e.g., to the Franka EMIKA panda robot) will be performed to show the applicability of the proposed methods in real tasks.
Author Contributions
Conceptualization, L.R., A.A.S., J.S.V.S., D.P. (Damjan Pecioski) and D.P. (Dario Piga); methodology, L.R., A.A.S., J.S.V.S., D.P. (Damjan Pecioski) and D.P. (Dario Piga); software, J.S.V.S., D.P. (Damjan Pecioski) and A.A.S.; validation, J.S.V.S., D.P. (Damjan Pecioski), A.A.S. and L.R.; formal analysis, J.S.V.S., D.P. (Damjan Pecioski), A.A.S. and L.R.; investigation, L.R., A.A.S. and D.P. (Damjan Pecioski); resources, L.R.; data curation, J.S.V.S., D.P. (Damjan Pecioski) and A.A.S.; writing—original draft preparation, L.R., A.A.S., J.S.V.S., D.P. (Damjan Pecioski) and D.P. (Dario Piga); writing—review and editing, A.A.S. and L.R.; visualization, L.R., A.A.S., J.S.V.S., D.P. (Damjan Pecioski) and D.P. (Dario Piga); supervision, L.R., D.P. (Dario Piga) and F.B.; project administration, L.R.; funding acquisition, L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project ASSASSINN, funded from H2020 CleanSky 2, grant agreement n. 886977.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The software to replicate the achieved results can be found at the link in [45].
Acknowledgments
The work has been developed within the project ASSASSINN, funded from H2020 CleanSky 2 under grant agreement n. 886977.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rajan, K.; Saffiotti, A. Towards a Science of Integrated AI and Robotics. Artif. Intell. 2017, 247, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Van Roy, V.; Vertesy, D.; Damioli, G. AI and robotics innovation. In Handbook of Labor, Human Resources and Population Economics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–35. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 22447. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef] [Green Version]
- Cruz, F.; Parisi, G.I.; Wermter, S. Learning contextual affordances with an associative neural architecture. In Proceedings of the 24th European Symposium on Artificial Neural Networks, Bruges, Belgium, 27–29 April 2016; pp. 665–670. [Google Scholar]
- Yen-Chen, L.; Zeng, A.; Song, S.; Isola, P.; Lin, T.Y. Learning to See before Learning to Act: Visual Pre-training for Manipulation. arXiv 2021, arXiv:2107.00646. [Google Scholar]
- Cruz, F.; Dazeley, R.; Vamplew, P.; Moreira, I. Explainable robotic systems: Understanding goal-driven actions in a reinforcement learning scenario. Neural Comput. Appl. 2021, 1–18. [Google Scholar] [CrossRef]
- Cruz, F.; Wüppen, P.; Fazrie, A.; Weber, C.; Wermter, S. Action selection methods in a robotic reinforcement learning scenario. In Proceedings of the 2018 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Gudalajara, Mexico, 7–9 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Cruz, F.; Wüppen, P.; Magg, S.; Fazrie, A.; Wermter, S. Agent-advising approaches in an interactive reinforcement learning scenario. In Proceedings of the 2017 Joint IEEE International Conference on Development and Learning and Epigenetic Robotics (ICDL-EpiRob), Lisbon, Portugal, 18–21 September 2017; pp. 209–214. [Google Scholar] [CrossRef]
- Rahmatizadeh, R.; Abolghasemi, P.; Bölöni, L.; Levine, S. Vision-based multi-task manipulation for inexpensive robots using end-to-end learning from demonstration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 3758–3765. [Google Scholar]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Joshi, S.; Kumra, S.; Sahin, F. Robotic grasping using deep reinforcement learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1461–1466. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Busoniu, L.; De Schutter, B.; Babuska, R. Decentralized reinforcement learning control of a robotic manipulator. In Proceedings of the 2006 9th International Conference on Control, Automation, Robotics and Vision, Singapore, 5–8 December 2006; pp. 1–6. [Google Scholar]
- Leottau, D.L.; Ruiz-del Solar, J.; Babuška, R. Decentralized reinforcement learning of robot behaviors. Artif. Intell. 2018, 256, 130–159. [Google Scholar] [CrossRef] [Green Version]
- Panait, L.; Luke, S. Cooperative multi-agent learning: The state of the art. Auton. Agents Multi-Agent Syst. 2005, 11, 387–434. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Abbeel, P.; Zaremba, W. Hindsight experience replay. arXiv 2017, arXiv:1707.01495. [Google Scholar]
- Lauer, M.; Riedmiller, M. An algorithm for distributed reinforcement learning in cooperative multi-agent systems. In Proceedings of the Seventeenth International Conference on Machine Learning, Standord, CA, USA, 29 June–2 July 2000. [Google Scholar]
- Kapetanakis, S.; Kudenko, D. Reinforcement learning of coordination in heterogeneous cooperative multi-agent systems. In Adaptive Agents and Multi-Agent Systems II; Springer: Berlin/Heidelberg, Germany, 2004; pp. 119–131. [Google Scholar]
- Matignon, L.; Laurent, G.J.; Le Fort-Piat, N. Hysteretic q-learning: An algorithm for decentralized reinforcement learning in cooperative multi-agent teams. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 64–69. [Google Scholar]
- Tuyls, K.; Hoen, P.J.; Vanschoenwinkel, B. An evolutionary dynamical analysis of multi-agent learning in iterated games. Auton. Agents Multi-Agent Syst. 2006, 12, 115–153. [Google Scholar] [CrossRef]
- Laurent, G.J.; Matignon, L.; Fort-Piat, L. The world of independent learners is not Markovian. Int. J. Knowl.-Based Intell. Eng. Syst. 2011, 15, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Vidhate, D.; Kulkarni, P. Cooperative machine learning with information fusion for dynamic decision making in diagnostic applications. In Proceedings of the 2012 International Conference on Advances in Mobile Network, Communication and Its Applications, Bangalore, India, 1–2 August 2012; pp. 70–74. [Google Scholar]
- Theodorou, E.; Buchli, J.; Schaal, S. Reinforcement learning of motor skills in high dimensions: A path integral approach. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2397–2403. [Google Scholar]
- Kuba, J.G.; Wen, M.; Yang, Y.; Meng, L.; Gu, S.; Zhang, H.; Mguni, D.H.; Wang, J. Settling the Variance of Multi-Agent Policy Gradients. arXiv 2021, arXiv:2108.08612. [Google Scholar]
- Schwager, M.; Rus, D.; Slotine, J.J. Decentralized, adaptive coverage control for networked robots. Int. J. Robot. Res. 2009, 28, 357–375. [Google Scholar] [CrossRef] [Green Version]
- Sartoretti, G.; Paivine, W.; Shi, Y.; Wu, Y.; Choset, H. Distributed learning of decentralized control policies for articulated mobile robots. IEEE Trans. Robot. 2019, 35, 1109–1122. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Yang, J.; Lim, J.J. Learning to coordinate manipulation skills via skill behavior diversification. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Ha, H.; Xu, J.; Song, S. Learning a decentralized multi-arm motion planner. arXiv 2020, arXiv:2011.02608. [Google Scholar]
- Shahid, A.A.; Roveda, L.; Piga, D.; Braghin, F. Learning continuous control actions for robotic grasping with reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 4066–4072. [Google Scholar]
- Littman, M.L. Value-function reinforcement learning in Markov games. Cogn. Syst. Res. 2001, 2, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Lazaric, A.; Restelli, M.; Bonarini, A. Reinforcement learning in continuous action spaces through sequential monte carlo methods. Adv. Neural Inf. Process. Syst. 2007, 20, 833–840. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Todorov, E.; Erez, T.; Tassa, Y. Mujoco: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Erez, T.; Tassa, Y.; Todorov, E. Simulation tools for model-based robotics: Comparison of bullet, havok, mujoco, ode and physx. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4397–4404. [Google Scholar]
- Zhu, Y.; Wong, J.; Mandlekar, A.; Martín-Martín, R. robosuite: A Modular Simulation Framework and Benchmark for Robot Learning. arXiv 2020, arXiv:2009.12293. [Google Scholar]
- Massa, D.; Callegari, M.; Cristalli, C. Manual guidance for industrial robot programming. Ind. Robot Int. J. 2015, 42, 457–465. [Google Scholar] [CrossRef]
- Martín-Martín, R.; Lee, M.A.; Gardner, R.; Savarese, S.; Bohg, J.; Garg, A. Variable impedance control in end-effector space: An action space for reinforcement learning in contact-rich tasks. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1010–1017. [Google Scholar]
- Moreira, I.; Rivas, J.; Cruz, F.; Dazeley, R.; Ayala, A.; Fernandes, B. Deep Reinforcement Learning with Interactive Feedback in a Human–Robot Environment. Appl. Sci. 2020, 10, 5574. [Google Scholar] [CrossRef]
- Sesin, J.S.V.; Pecioski, D. GitHub Repository: Software for Decentralized and Multi Agent Control of Franka Emika Panda Robot. Available online: https://github.com/jvidals09/Decentralized-and-multi-agent-control-of-Franka-Emika-Panda-robot-in-continuous-task-execution (accessed on 29 September 2021).
- Shahid, A.A. Continuous Control Actions Learning with Performance Specifications through Reinforcement Learning. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2020. Available online: http://hdl.handle.net/10589/164660 (accessed on 3 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).