Design Method Using Response Surface Model for CFRP Corrugated Structure under Quasistatic Crushing
Abstract
:1. Introduction
2. Methods
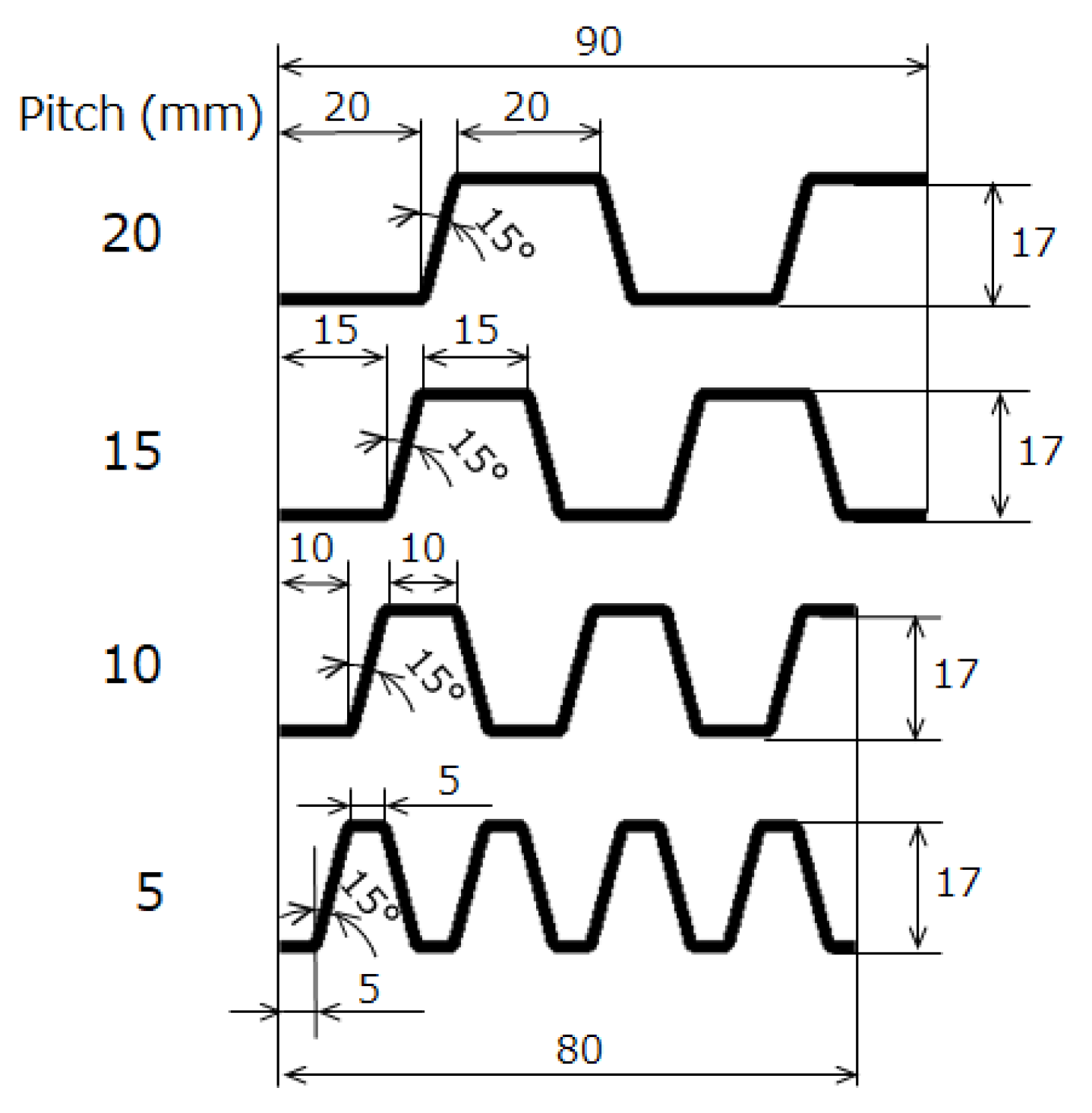
2.1. Material and Test Specimen
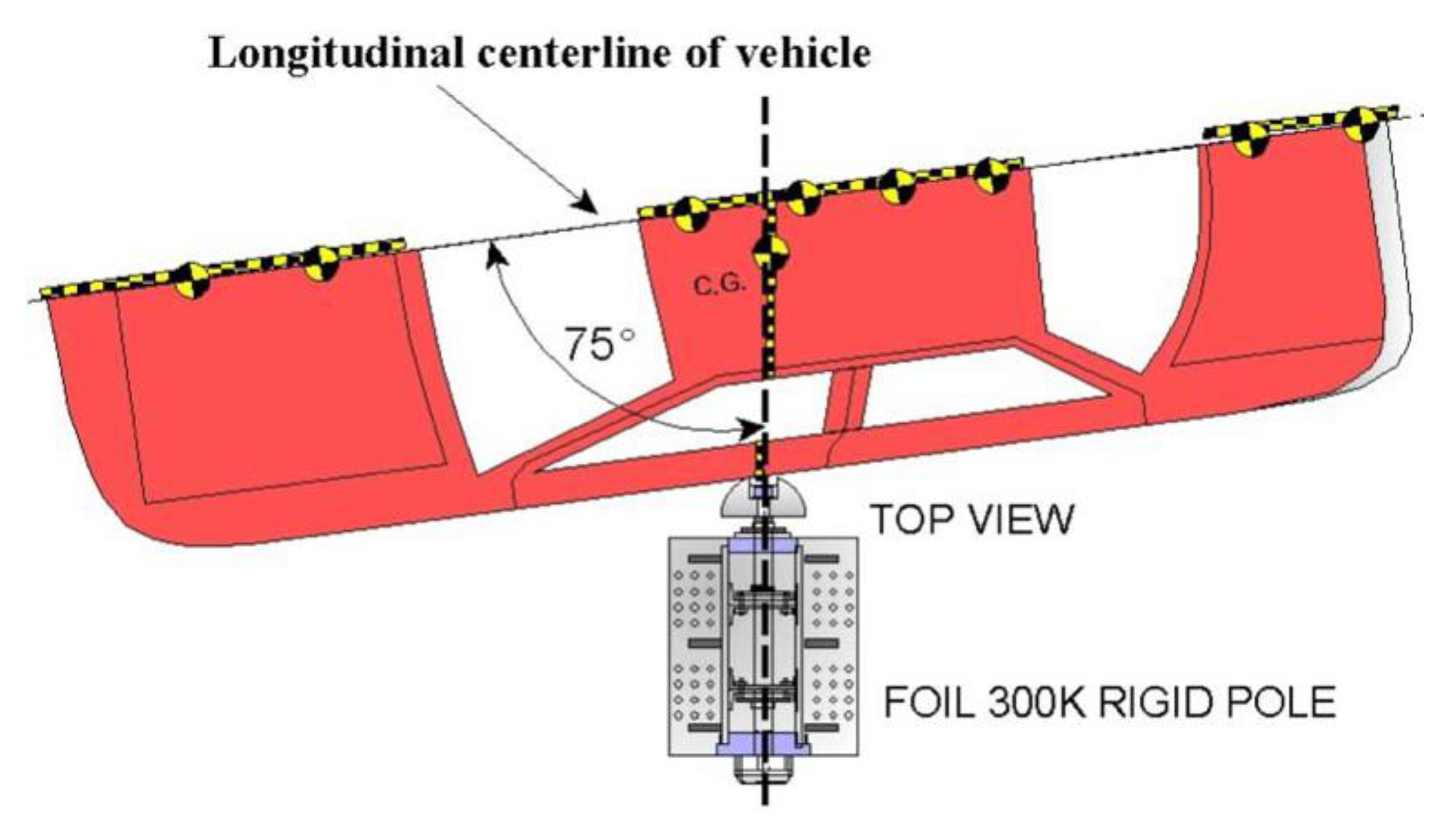
2.2. Quasistatic Compression Test
3. Test Results
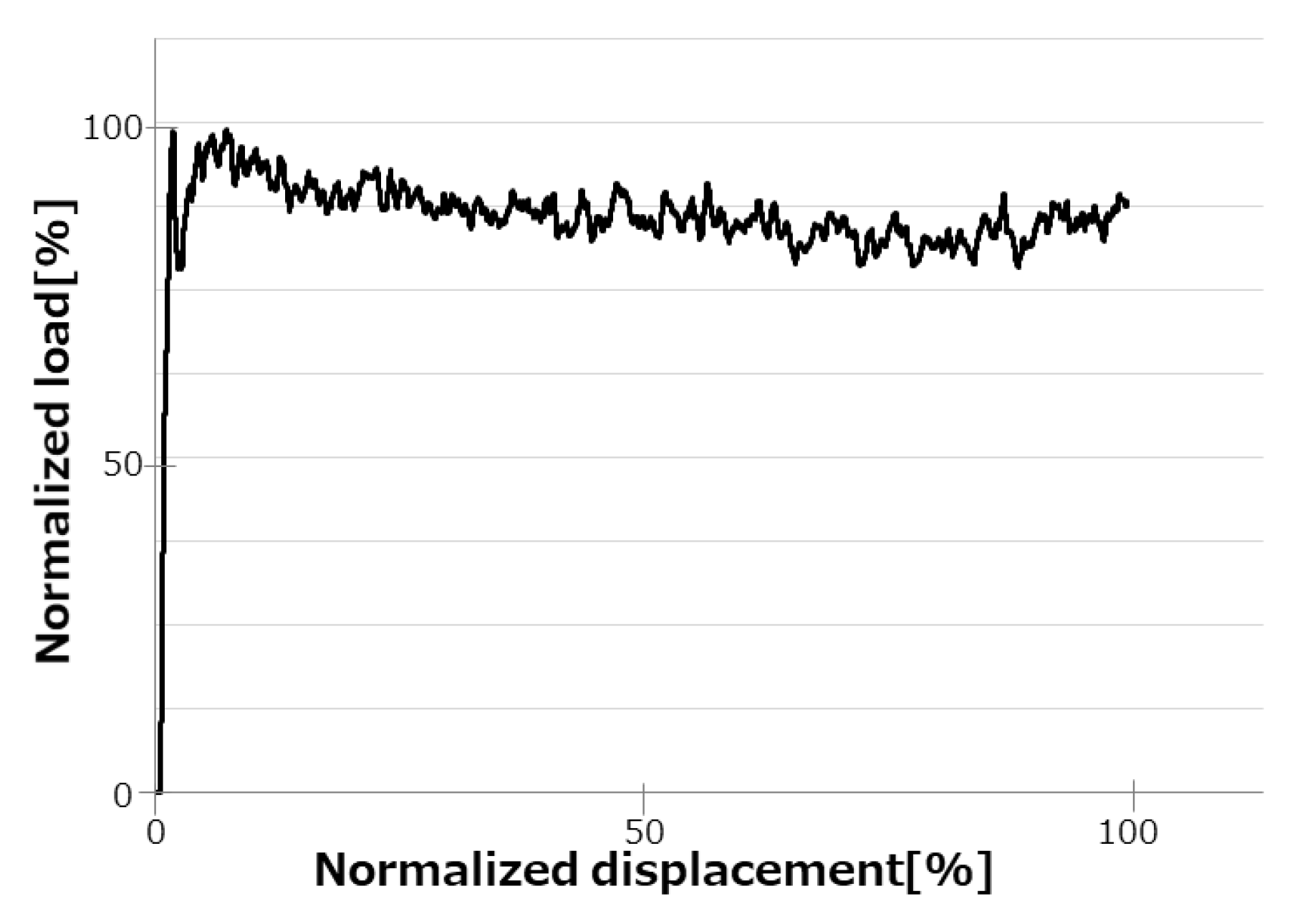
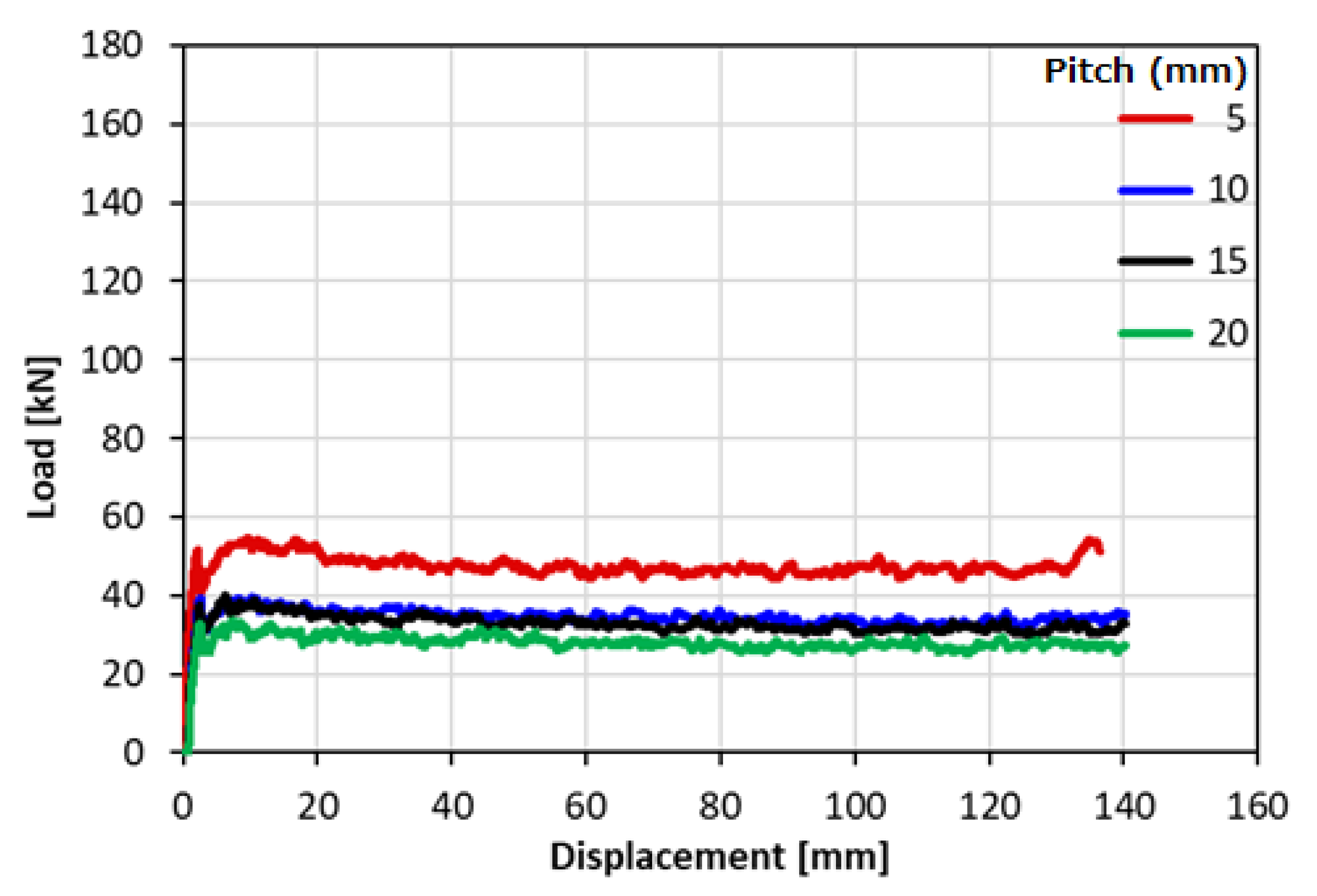
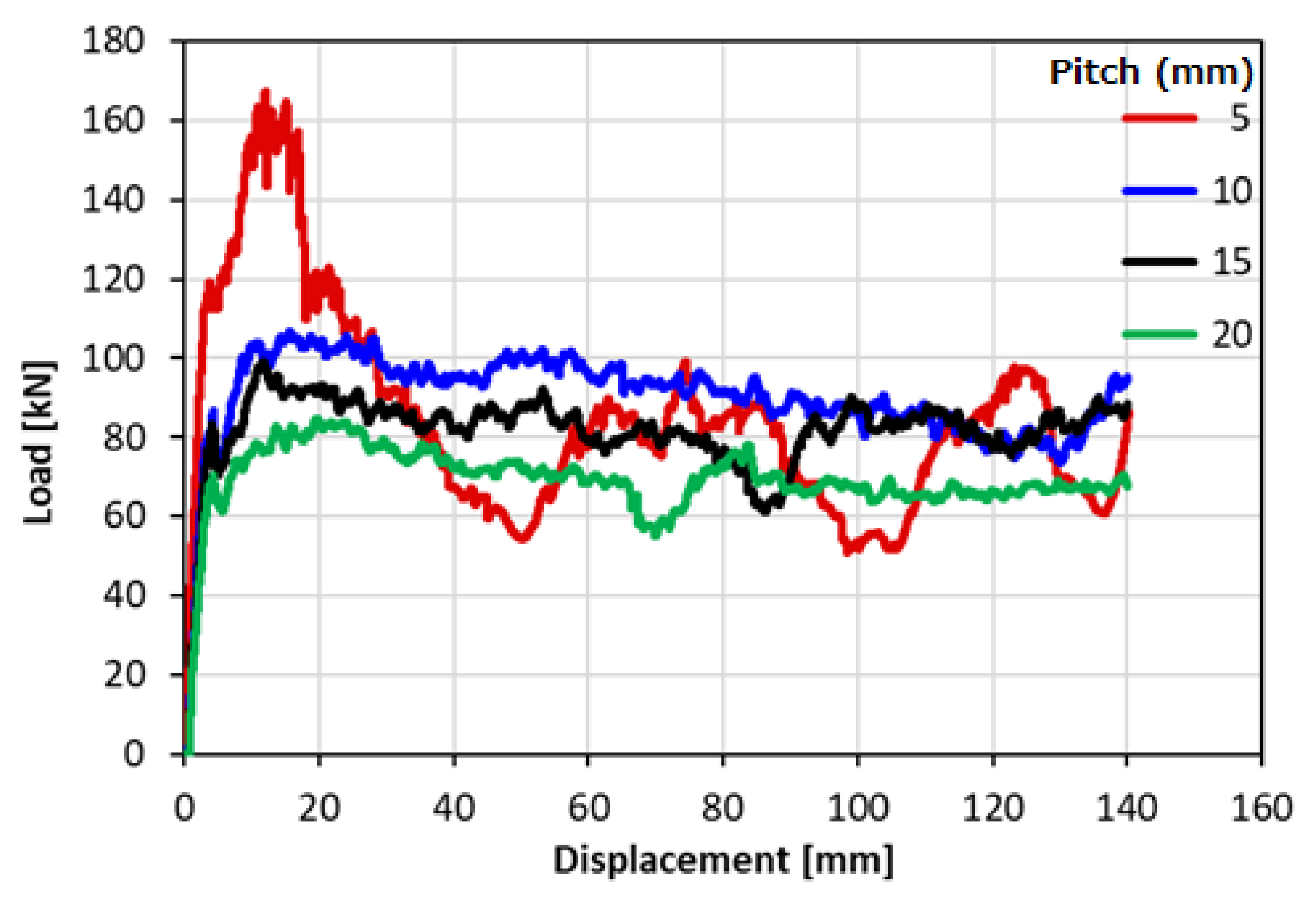
Specimen Load Characteristics and Observed Results
4. Analysis and Discussion
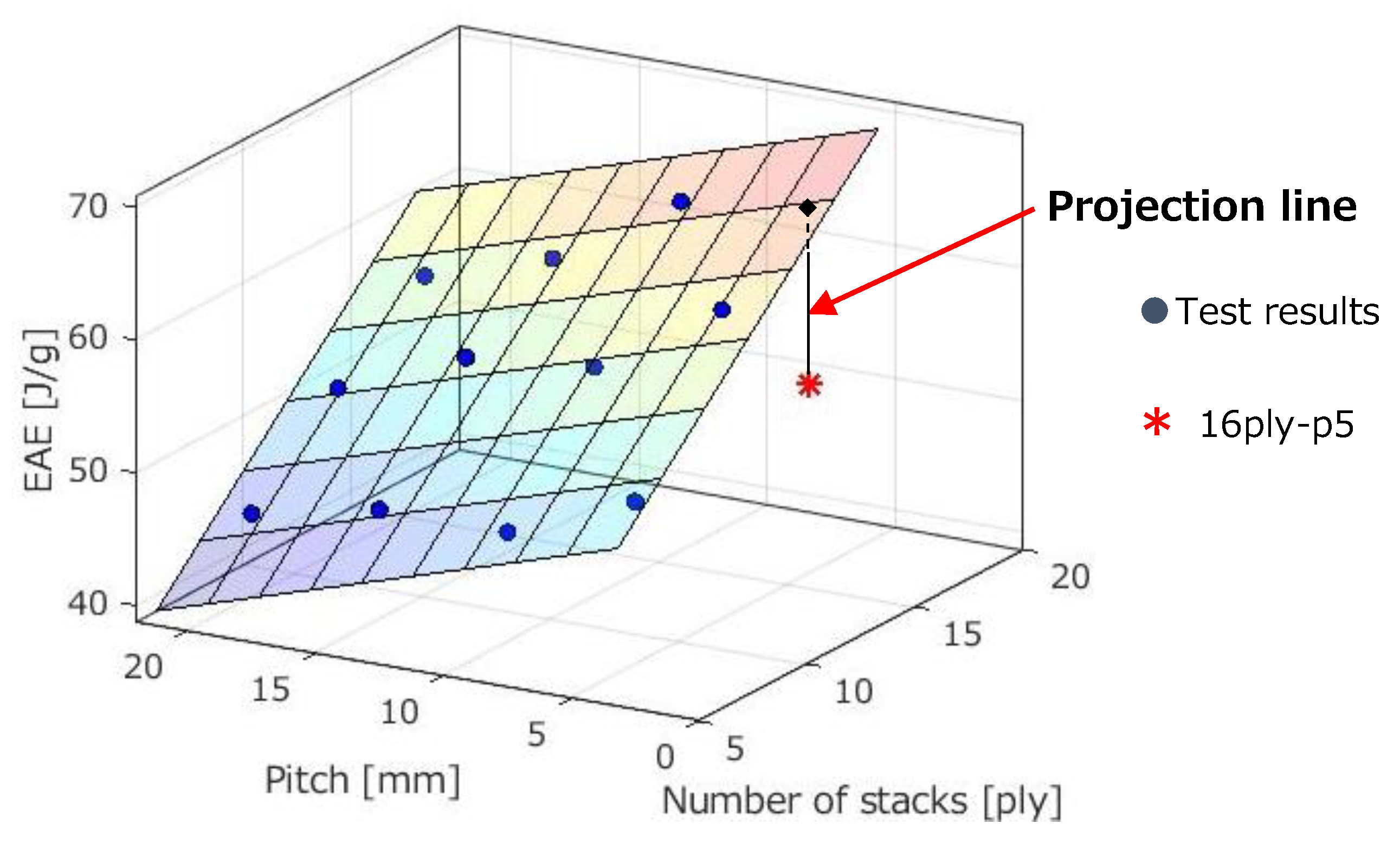
4.1. Mathematical Model of Energy Absorption Efficiency
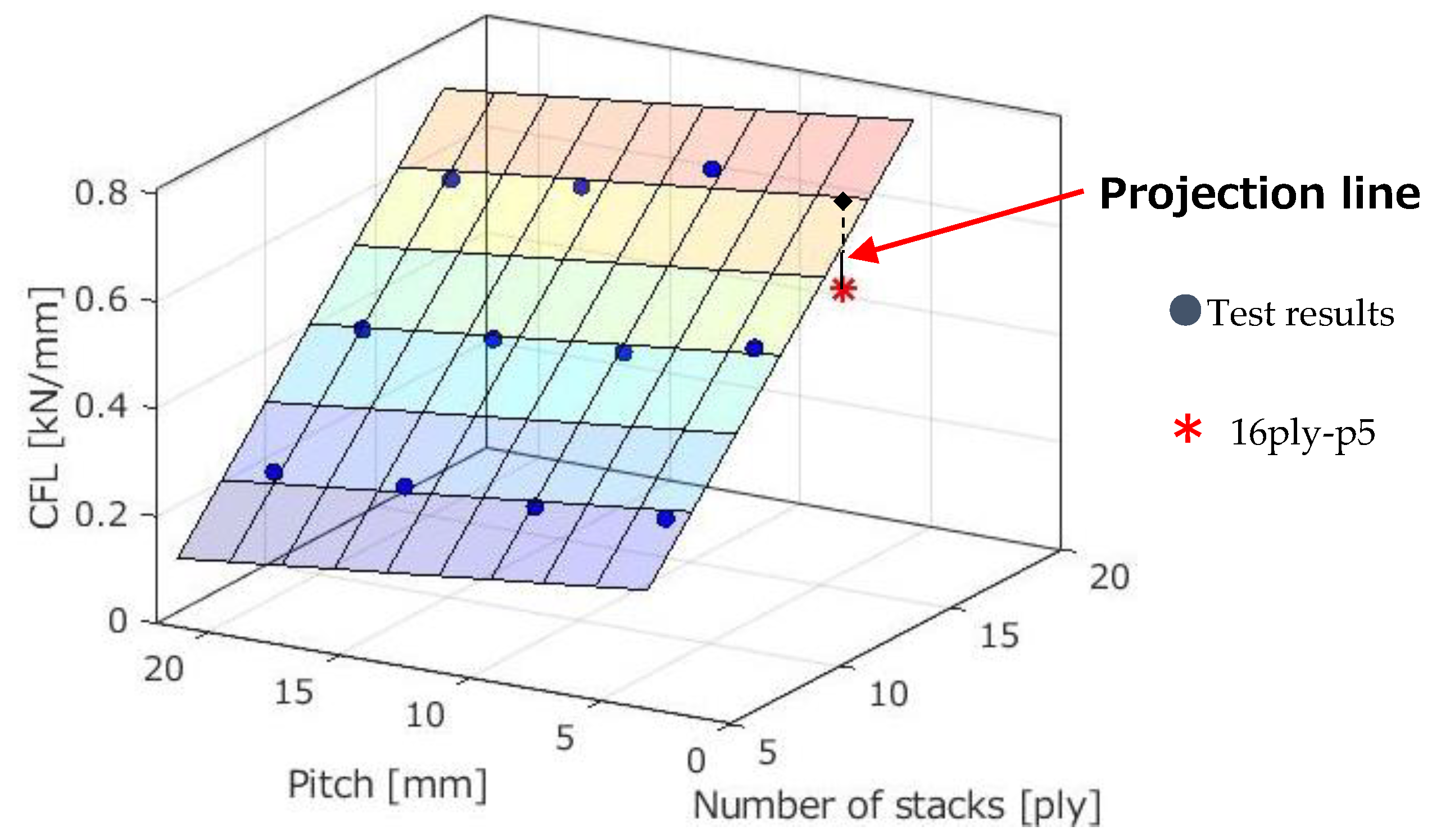
4.2. Mathematical Model of Crushing Force per Unit Length
4.3. Understanding the Phenomena Using the Stress Model of Corner Portions and Linear Portions
5. Conclusions
- In progressive crushing mode, EAE decreases with the increase in pitch.
- In progressive crushing mode, EAE increases with the increase in the number of stacks.
- In nonprogressive crushing mode, EAE significantly decreases.
- The energy absorption efficiency and average load generated in specimens with the varying number of stacks and pitch can be accurately represented by a linear response surface.
- As a result of examination by noting whether or not progressive crushing mode is observed, the corner portions largely contributed, with the predicted stress being 2.34 times larger than that of the linear portions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014; pp. 39–54.
- Lutsey, N. Review of Technical Literature and Trends Related to Automobile Mass-Reduction Technology; UCD-ITS-RR-10-10; Institute of Transportation Studies: Berkeley, CA, USA, 2010. [Google Scholar]
- Kiani, M.; Gandikota, I.; Rais-Rohani, M.; Motoyama, K. Design of lightweight magnesium car body structure under crash. J. Magnes. Alloys 2014, 2, 99–108. [Google Scholar] [CrossRef] [Green Version]
- 2019 Materials Annual Progress Report; U.S. Department of Energy: Washington, DC, USA, 2020.
- Hull, D. A unified approach to progressive crushing of fiber-reinforced composite tubes. Compos. Sci. Technol. 1991, 40, 377–421. [Google Scholar] [CrossRef]
- Asao, K.; Atsushi, Y.; Reika, A. Fracture mechanism analysis of FRP tube with continuous random fibers at initial stage. J. Soc. Mater. Sci. 2016, 65, 239–244. [Google Scholar]
- Zhi, X.; Fuhao, M.; Di, Z.; Yang, C. Experimental and numerical study of hat shaped CFRP structures under quasi-static axial crushing. Compos. Struct. 2020, 249, 112–465. [Google Scholar]
- Rouchon, J. Certification of large airplane composite structures, recent progress and new trends in compliance philosophy. In Proceedings of the 17th International Council of the Aeronautical Sciences (ICAS), Stockholm, Sweden, 9–14 September 1990. [Google Scholar]
- U.S. Department of Transportation National Highway Traffic Safety Administration Laboratory Test Procedure for FMVSS No. 214, Dynamic Side Impact Protection; NHTSA: Washington, DC, USA, 2012.
- New Car Assessment Program (NCAP) Side Impact Pole Test Honda Accord; NHTSA: Washington, DC, USA, 2018.
- Yokoyama, T.; Nakai, K.; Odamura, T. High Strain-Rate Compressive Characteristics of a Unidirectional Carbon/Epoxy Composite: Effect of Loading Directions. Exp. Anal. Nano Eng. Mater. Struct. 2007, 681–682. [Google Scholar]
- Yuan, J.; Takeda, N.; Song, D.-Y.; Waas, A.M. Experimental study on dynamic compressive failure of unidirectional CFRP composites. Mater. Sci. Res. Int. 1999, 5, 202–205. [Google Scholar] [CrossRef] [Green Version]
- Kowsika, M.V.; Mantena, P.R. Static and Low-Velocity Impact Response Characteristics of Pultruded Hybrid Glass-Graphite/Epoxy Composite Beams. J. Thermoplast. Compos. Mater. 1999, 12, 121–132. [Google Scholar] [CrossRef]
- Ma, Q.; Salim, M.S.A.; Rejab, M.R.M.; Otto-Ernst, B.; Yunus, N.A. Quasi-static crushing response of square hybrid carbon/aramid tube for automotive crash box application. Mater. Today Proc. 2020, 27, 683–690. [Google Scholar]
- Babbage, J.M.; Mallick, P.N. Static axial crush performance of unfilled and foam-filled aluminum-composite hybrid tubes. Compos. Struct. 2005, 70, 177–184. [Google Scholar] [CrossRef]
- Laananen, D.H.; Bolukbasi, A.O. Prediction of energy absorption in composite stiffeners. Compos. Struct. 1995, 32, 173–186. [Google Scholar] [CrossRef]
- Feraboli, P. Development of a Corrugated Test Specimen for Composite Materials Energy Absorption. J. Compos. Mater. 2008, 42, 229–256. [Google Scholar] [CrossRef]
- Tateishi, M.; Anayama, A.; Yokoyama, A.; Hamada, H. A numerical model for the crush-worthiness analysis designed for FRP materials with progressive crushing behavior. Zairyo 2002, 51, 506–511. [Google Scholar]
- Palanivelu, S.; Paepegem, W.V.; Degrieck, J.; Kakogiannis, D.; Ackeren, J.V.; Hemelrijck, D.V.; Wastiels, J. Numerical energy absorption study of composite tubes for axial impact loadings. In Proceedings of the 17th International Conference on Composite Materials (ICCM-17), Edinburgh, UK, 27–31 July 2009; pp. 27–31. [Google Scholar]
- Kiania, M.; Motoyama, K. Using experimental data to improve crash modeling for composite materials. Compos. Mater. Join. Technol. Compos. 2013, 7, 215–226. [Google Scholar]













| Mechanical Property | Values | |
|---|---|---|
| Density [g/cm3] | 1.50 | |
| Compression (SACMA SRM6) | Young’s modulus (GPa) | 59.49 |
| Ultimate strength (Mpa) | 671.20 | |
| Poisson’s ratio | 0.04 | |
| Tension (ASTM D 3039) | Young’s modulus (GPa) | 62.47 |
| Ultimate strength (Mpa) | 869.57 | |
| Poisson’s ratio | 0.04 | |
| Number of Stacks (ply) | Lay-Up | Thickness (mm) | Pitch (mm) |
|---|---|---|---|
| 8 | [0/90]8 | 1.82 | 5, 10, 15, 20 |
| 12 | [0/90]12 | 2.72 | Same |
| 16 | [0/90]16 | 3.63 | Same |
| Explanatory Variable | Response Variable | |
|---|---|---|
| Number of Stacks (ply) | Pitch (mm) | EAE (J/g) |
| 8 | 5 | 51.3 |
| 10 | 47.0 | |
| 15 | 47.1 | |
| 20 | 45.3 | |
| 12 | 5 | 62.1 |
| 10 | 56.0 | |
| 15 | 54.8 | |
| 20 | 51.3 | |
| 16 | 5 | 52.9 |
| 10 | 64.9 | |
| 15 | 58.5 | |
| 20 | 55.6 | |
| Item | Partial Regression Coefficient (β0, β1, β2) | p Value | Std. Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| Intercept | 42.6 *** | p < 0.001 | 5.14 | 31.0 | 54.2 |
| Number of stacks | 1.29 ** | 0.00564 | 0.356 | 0.481 | 2.09 |
| Pitch | −0.332 | 0.145 | 0.208 | −0.803 | 0.139 |
| Multiple R-squared (R2) | 0.634 | ||||
| Adjusted R-squared (R’2) | 0.553 | ||||
| Item | Partial Regression Coefficient (β0, β1, β2) | p Value | Std. Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| Intercept | 42.0 *** | p < 0.001 | 2.47 | 36.3 | 47.7 |
| Number of stacks | 1.71 *** | p < 0.001 | 0.187 | 1.28 | 2.14 |
| Pitch | −0.601 *** | p < 0.001 | 0.111 | −0.857 | −0.345 |
| Multiple R-squared (R2) | 0.925 | ||||
| Adjusted R-squared (R’2) | 0.906 | ||||
| Explanatory Variable | Response Variable | |
|---|---|---|
| Number of Stacks (ply) | Pitch (mm) | CFL (kN/mm) |
| 8 | 5 | 0.275 |
| 10 | 0.255 | |
| 15 | 0.249 | |
| 20 | 0.234 | |
| 12 | 5 | 0.506 |
| 10 | 0.456 | |
| 15 | 0.437 | |
| 20 | 0.412 | |
| 16 | 5 | 0.527 |
| 10 | 0.710 | |
| 15 | 0.635 | |
| 20 | 0.605 | |
| Item | Partial Regression Coefficient (β0, β1, β2) | p Value | Std. Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| Intercept | −0.0847 | 0.215 | 0.0635 | −0.228 | 0.0589 |
| Number of stacks | 0.0458 *** | p < 0.001 | 0.00440 | 0.0358 | 0.0557 |
| Pitch | −0.00181 | 0.500 | 0.00257 | −0.00762 | 0.00401 |
| Multiple R-squared (R2) | 0.923 | ||||
| Adjusted R-squared (R’2) | 0.906 | ||||
| Item | Partial Regression Coefficient (β0, β1, β2) | p Value | Std. Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| Intercept | −0.0919 ** | 0.00594 | 0.0248 | −0.149 | −0.0348 |
| Number of stacks | 0.0512 *** | p < 0.001 | 0.00188 | 0.0468 | 0.0555 |
| Pitch | −0.00528 ** | 0.00146 | 0.00111 | −0.00784 | −0.00271 |
| Multiple R-squared (R2) | 0.989 | ||||
| Adjusted R-squared (R’2) | 0.987 | ||||
| Case | Explanatory Variable | Response Variable | ||
|---|---|---|---|---|
| Number of Stacks (ply) | Pitch (mm) | Corner Area (CA) (mm2) | Straight-Line Area (LA) (mm2) | MCF (kN) |
| 8 | 5 | 72.4 | 242 | 48.8 |
| 10 | 45.2 | 204 | 35.7 | |
| 15 | 36.2 | 209 | 34.4 | |
| 20 | 27.1 | 196 | 29.3 | |
| 12 | 5 | 108.0 | 363 | 89.6 |
| 10 | 67.8 | 306 | 63.8 | |
| 15 | 54.3 | 313 | 60.2 | |
| 20 | 40.7 | 294 | 51.8 | |
| 16 | 10 | 90.5 | 408 | 99.4 |
| 15 | 72.4 | 418 | 87.5 | |
| 20 | 54.3 | 393 | 75.9 | |
| Item | Partial Regression Coefficient (β1, β2) | pValue | Std. Error | 95% Confidence Interval | |
| Lower | Upper | ||||
| Corner area (CA) | 0.163 | 0.196 | 0.118 | −0.0989 | 0.425 |
| Straight-line area (LA) | 0.171 *** | p < 0.001 | 0.0269 | 0.111 | 0.231 |
| Multiple R-squared (R2) | 0.987 | ||||
| Adjusted R-squared (R’2) | 0.985 | ||||
| Item | Partial Regression Coefficient (β1, β2) | p value | Std. Error | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
| Corner area (CA) | 0.332 * | 0.0234 | 0.122 | 0.0565 | 0.608 |
| Straight-line area (LA) | 0.142 *** | p < 0.001 | 0.0256 | 0.0843 | 0.200 |
| Multiple R-squared (R2) | 0.991 | ||||
| Adjusted R-squared (R’2) | 0.989 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomi, T.; Ayuzawa, S.; Urushiyama, Y.; Misaji, K.; Takahashi, S.; Motoyama, K.; Suzuki, K. Design Method Using Response Surface Model for CFRP Corrugated Structure under Quasistatic Crushing. Appl. Sci. 2021, 11, 10178. https://doi.org/10.3390/app112110178
Gomi T, Ayuzawa S, Urushiyama Y, Misaji K, Takahashi S, Motoyama K, Suzuki K. Design Method Using Response Surface Model for CFRP Corrugated Structure under Quasistatic Crushing. Applied Sciences. 2021; 11(21):10178. https://doi.org/10.3390/app112110178
Chicago/Turabian StyleGomi, Tetsuya, Shotaro Ayuzawa, Yuta Urushiyama, Kazuhito Misaji, Susumu Takahashi, Keiichi Motoyama, and Kosuke Suzuki. 2021. "Design Method Using Response Surface Model for CFRP Corrugated Structure under Quasistatic Crushing" Applied Sciences 11, no. 21: 10178. https://doi.org/10.3390/app112110178
APA StyleGomi, T., Ayuzawa, S., Urushiyama, Y., Misaji, K., Takahashi, S., Motoyama, K., & Suzuki, K. (2021). Design Method Using Response Surface Model for CFRP Corrugated Structure under Quasistatic Crushing. Applied Sciences, 11(21), 10178. https://doi.org/10.3390/app112110178







