Formal Chaos Existing Conditions on a Transmission Line Circuit with a Piecewise Linear Resistor
Abstract
:1. Introduction
2. Lossless Transmission Circuit Equations with Terminal Conditions
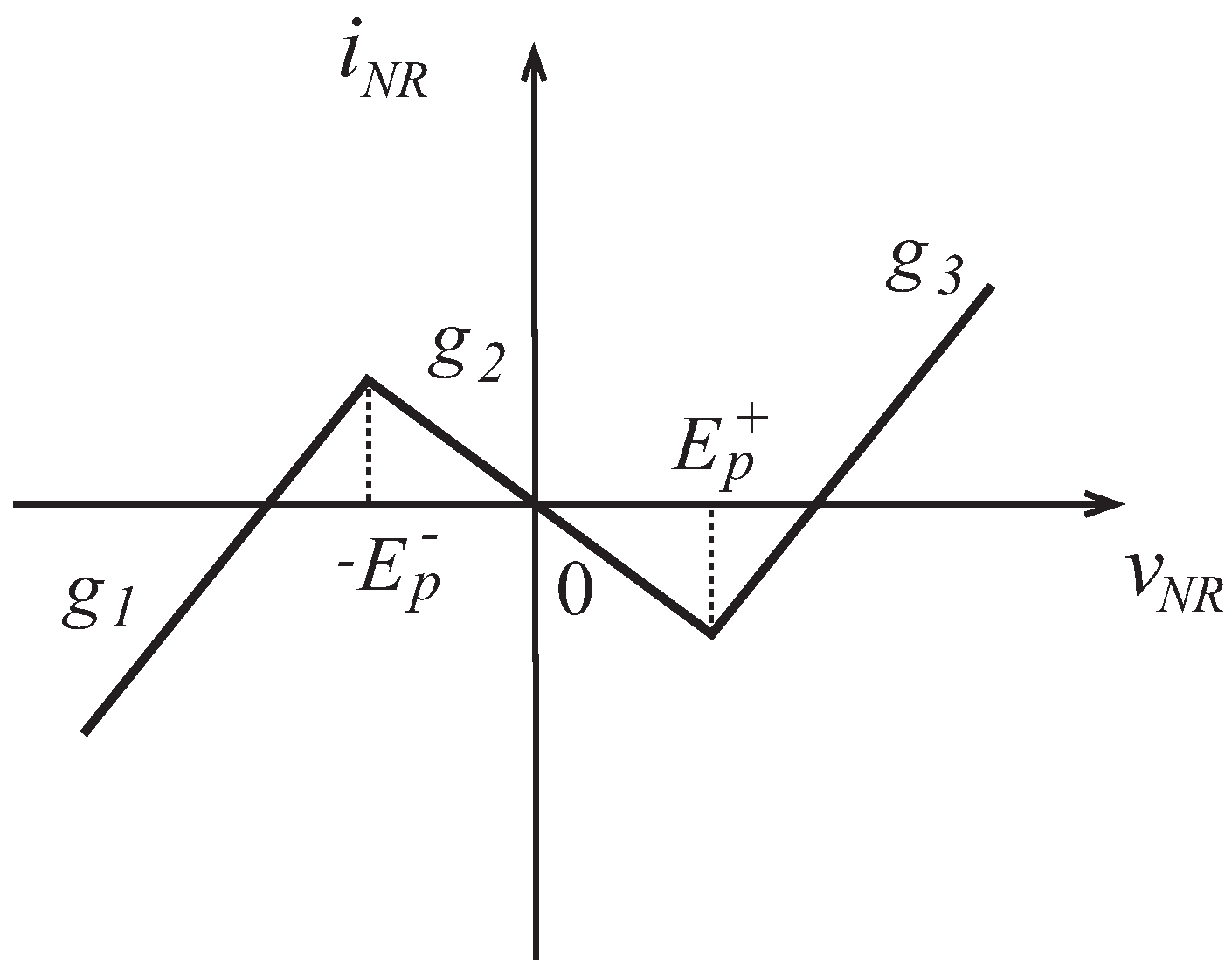
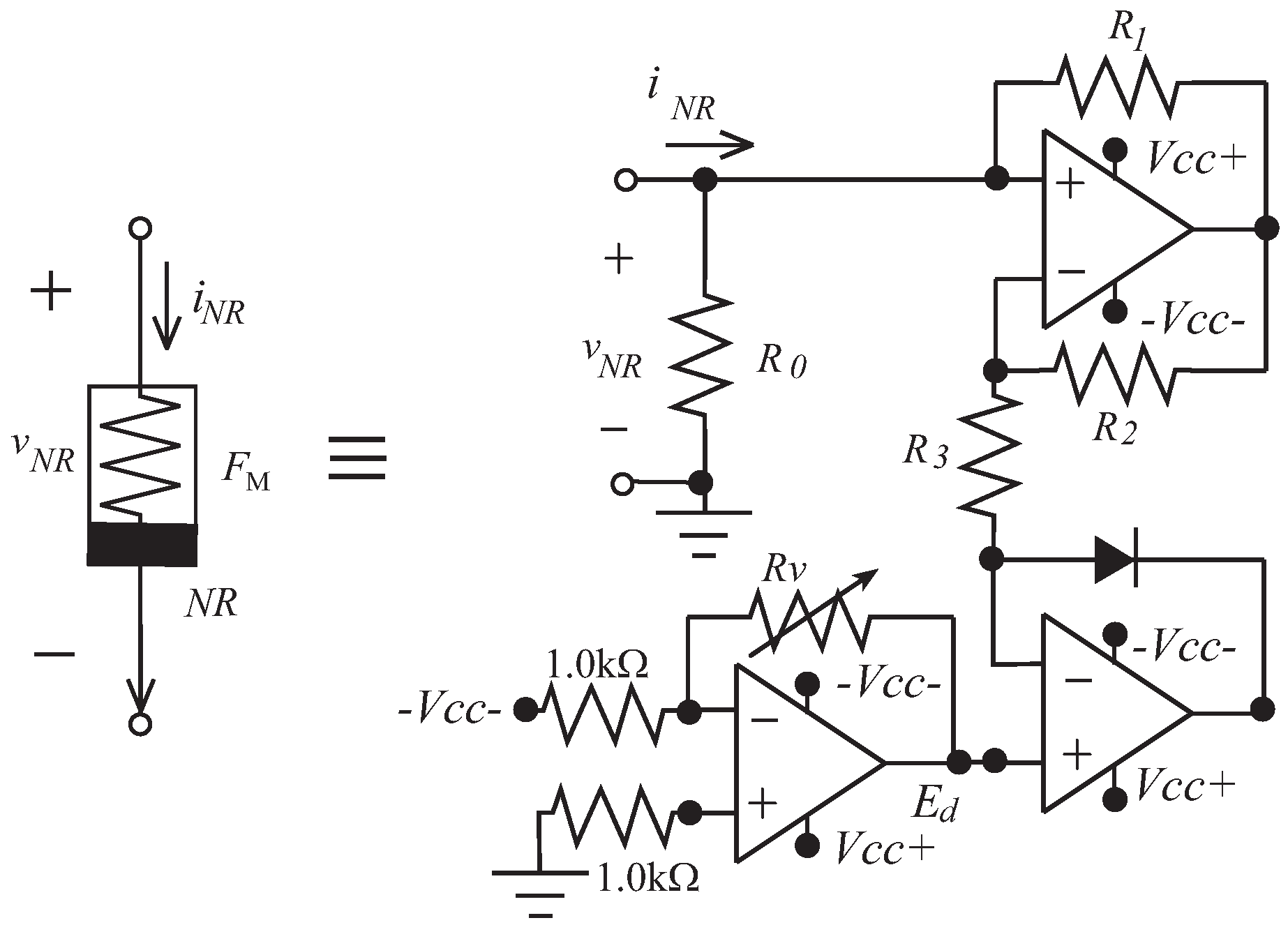
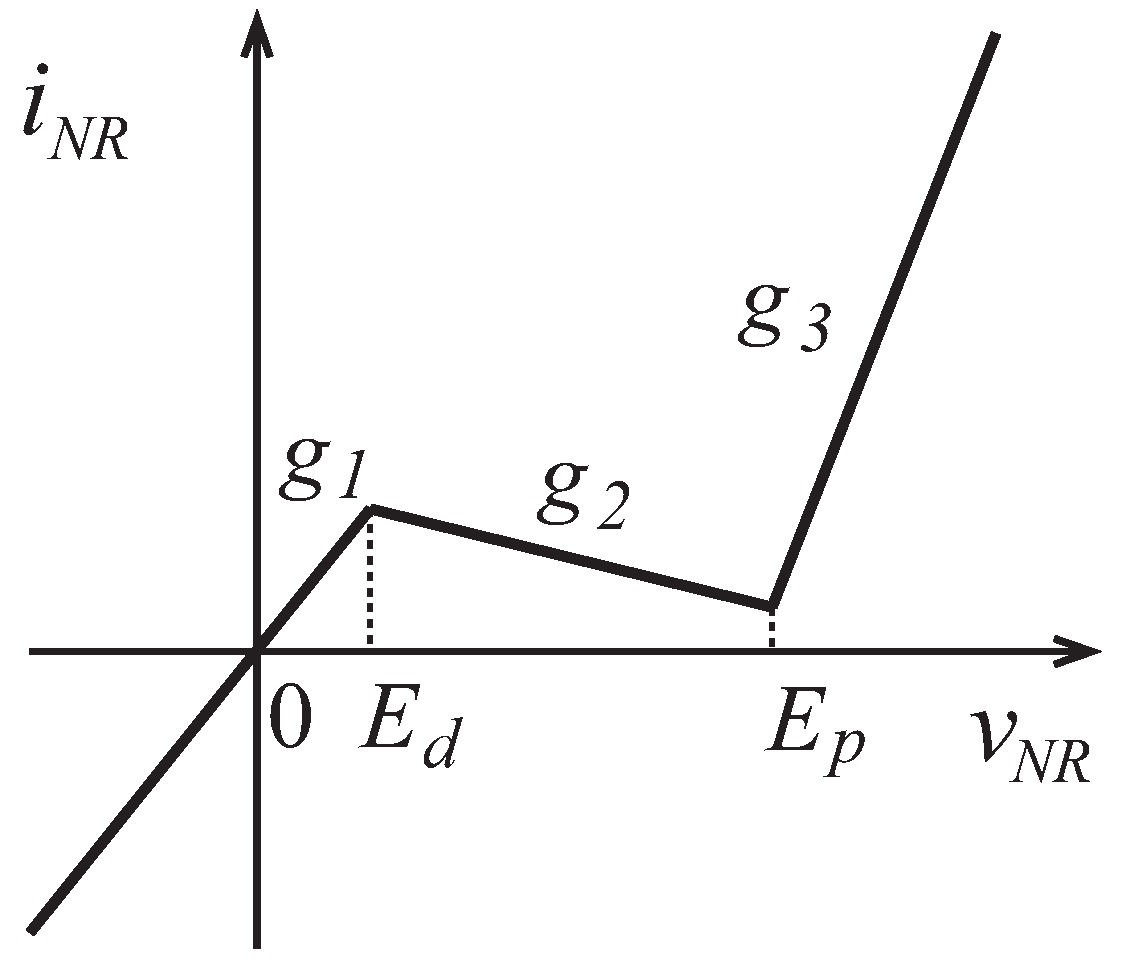
2.1. Three-Segment Piecewise Linear Resistor
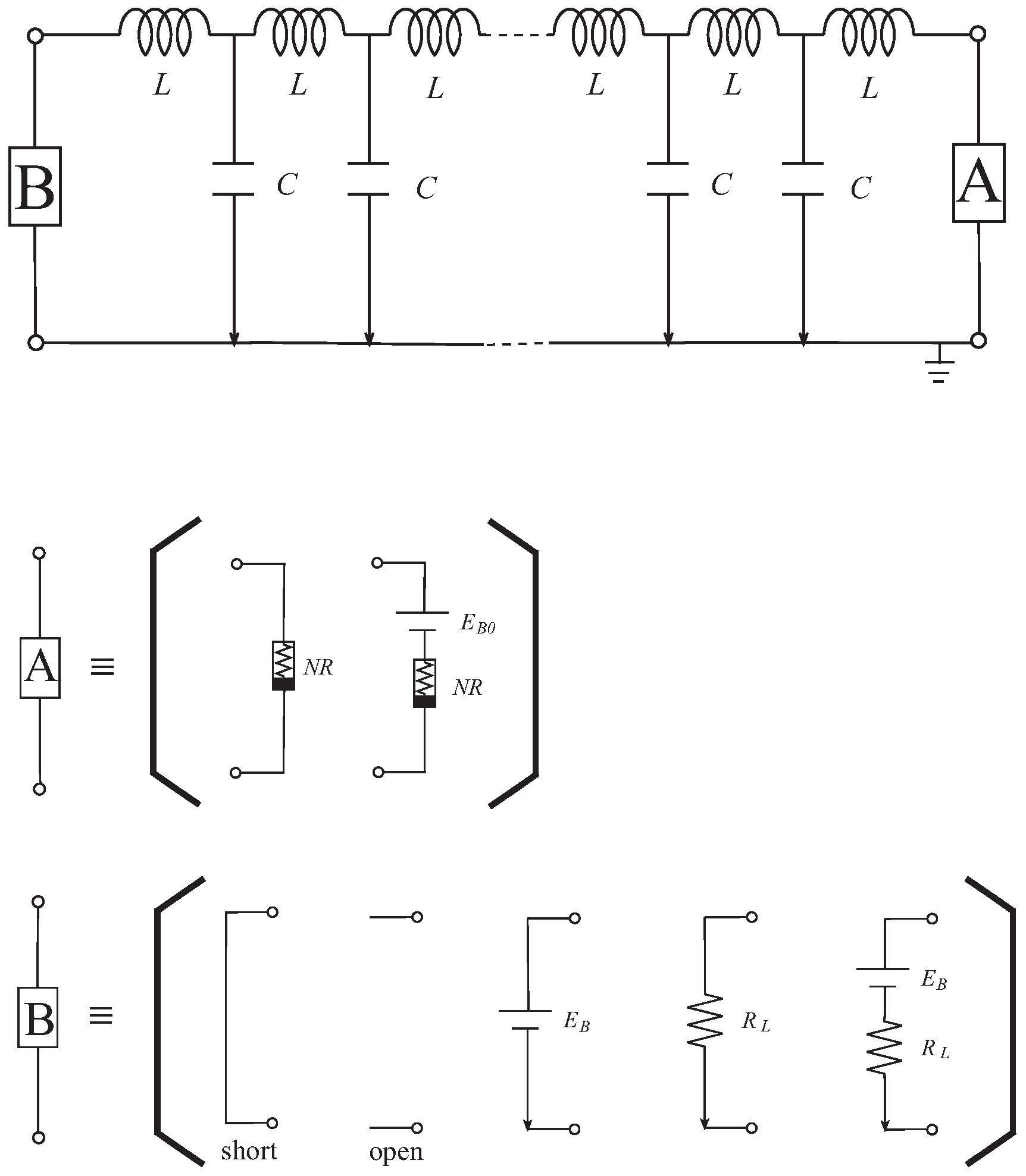
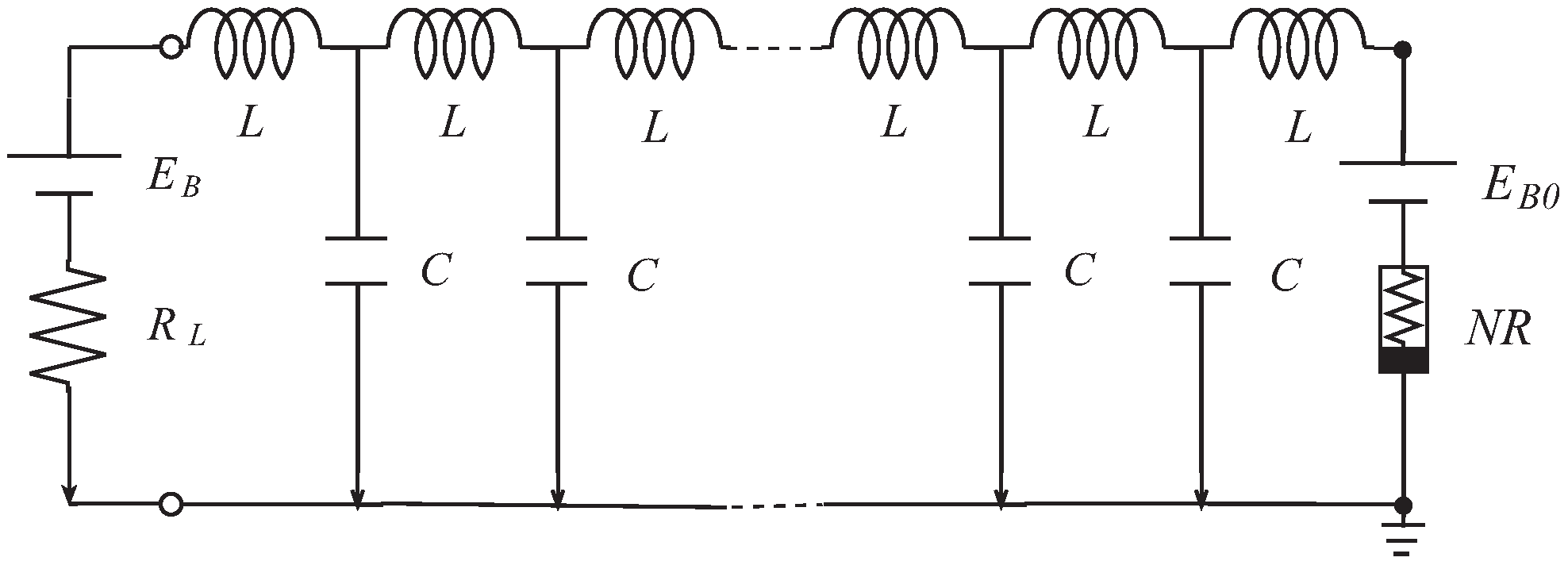
2.2. Transmission Line Circuit Equation
3. 1-D Map Describing the Behavior of the Transmission Line Circuit
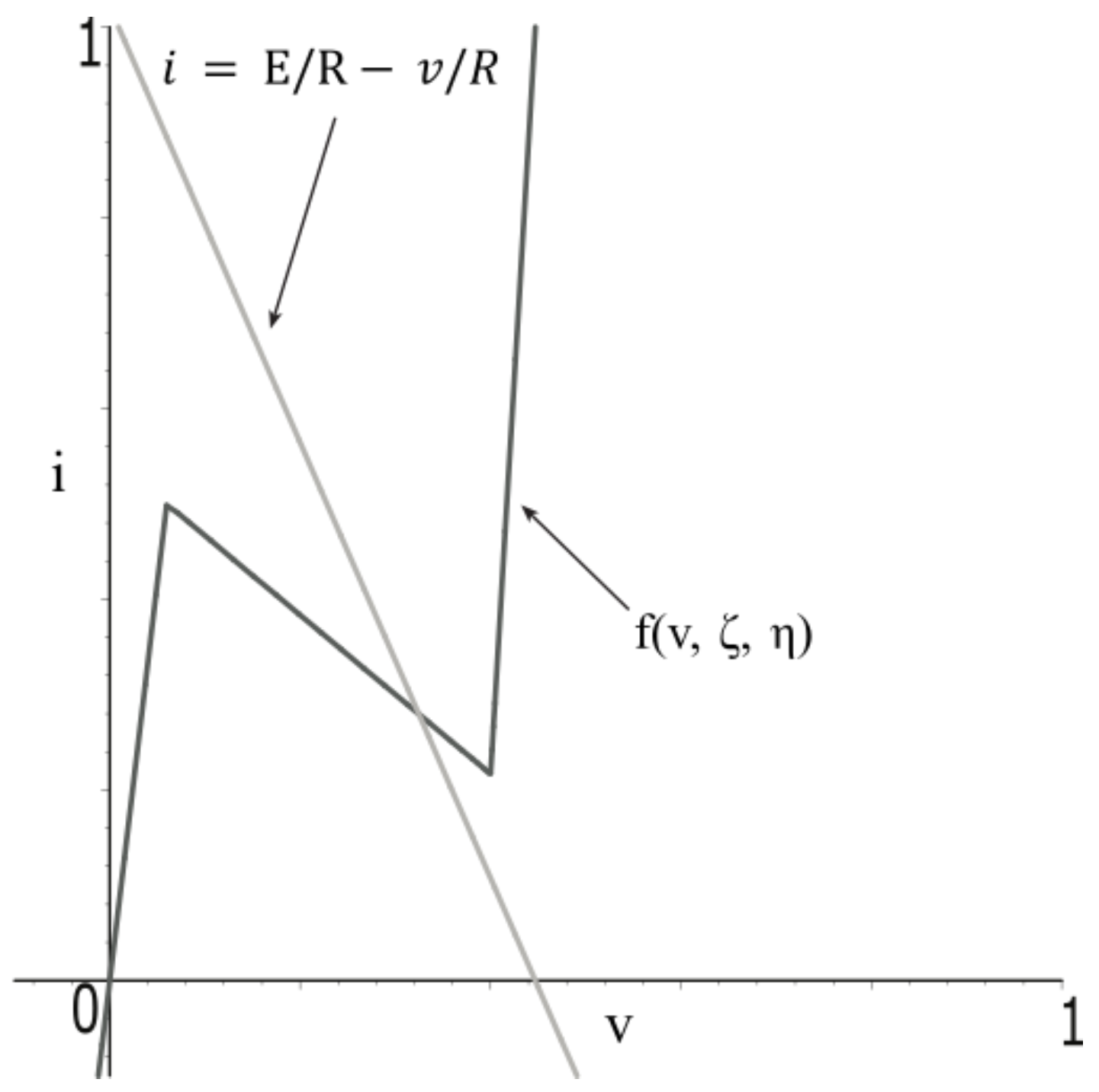
3.1. Derivation of 1-D Map
3.2. Global Behavior of 1-D Map
- The 1-D map has a unique unstable fixed point in the interval , where,.
- There exists an invariant interval such that and , where ,,,.
- For any , there exists jth iterate of such that , where denotes the jth iterate of , i.e., is the j-fold composition of with itself. is the set of non negative integers.
4. Formal Chaos Existing Conditions of 1-D Maps
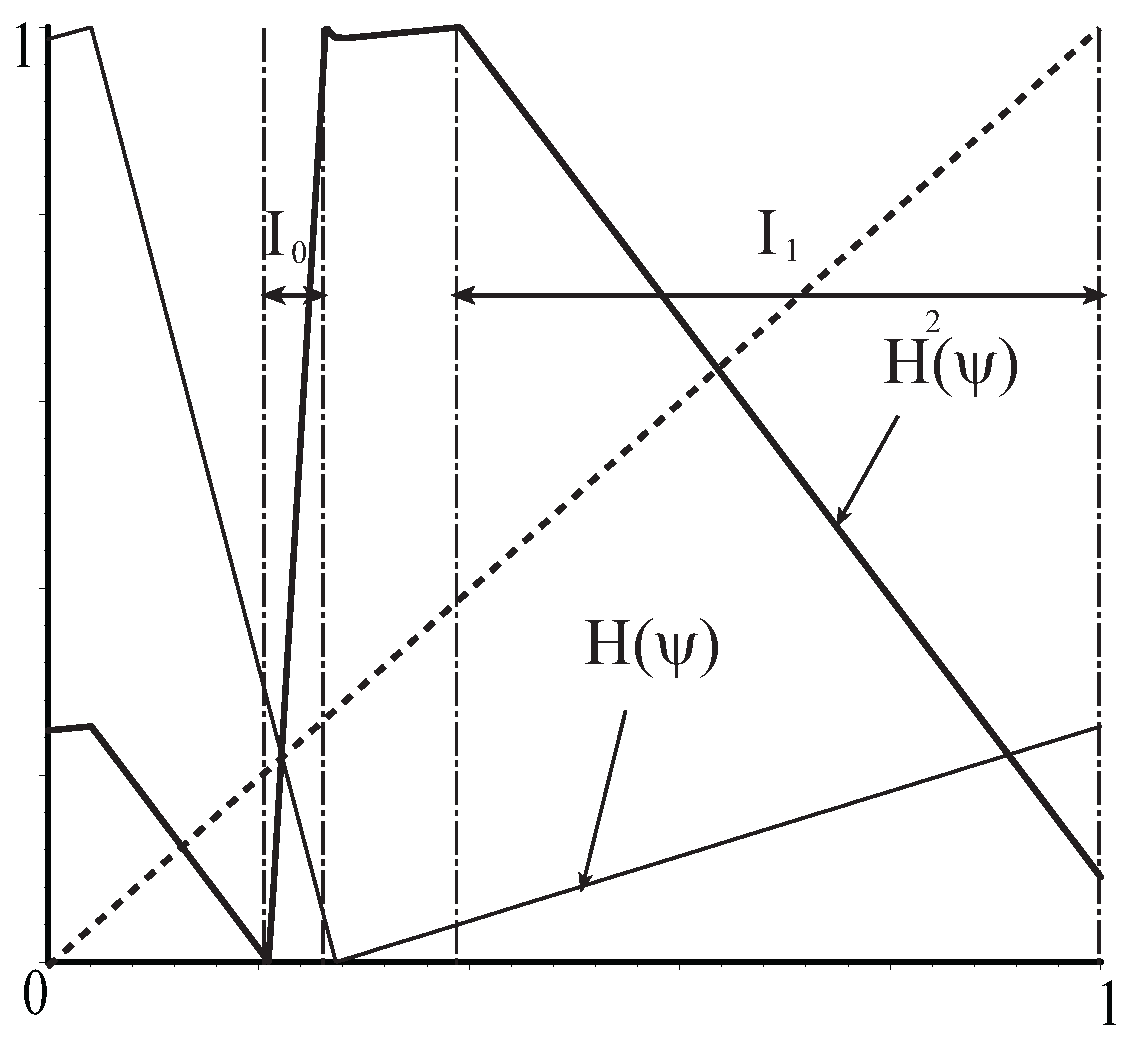
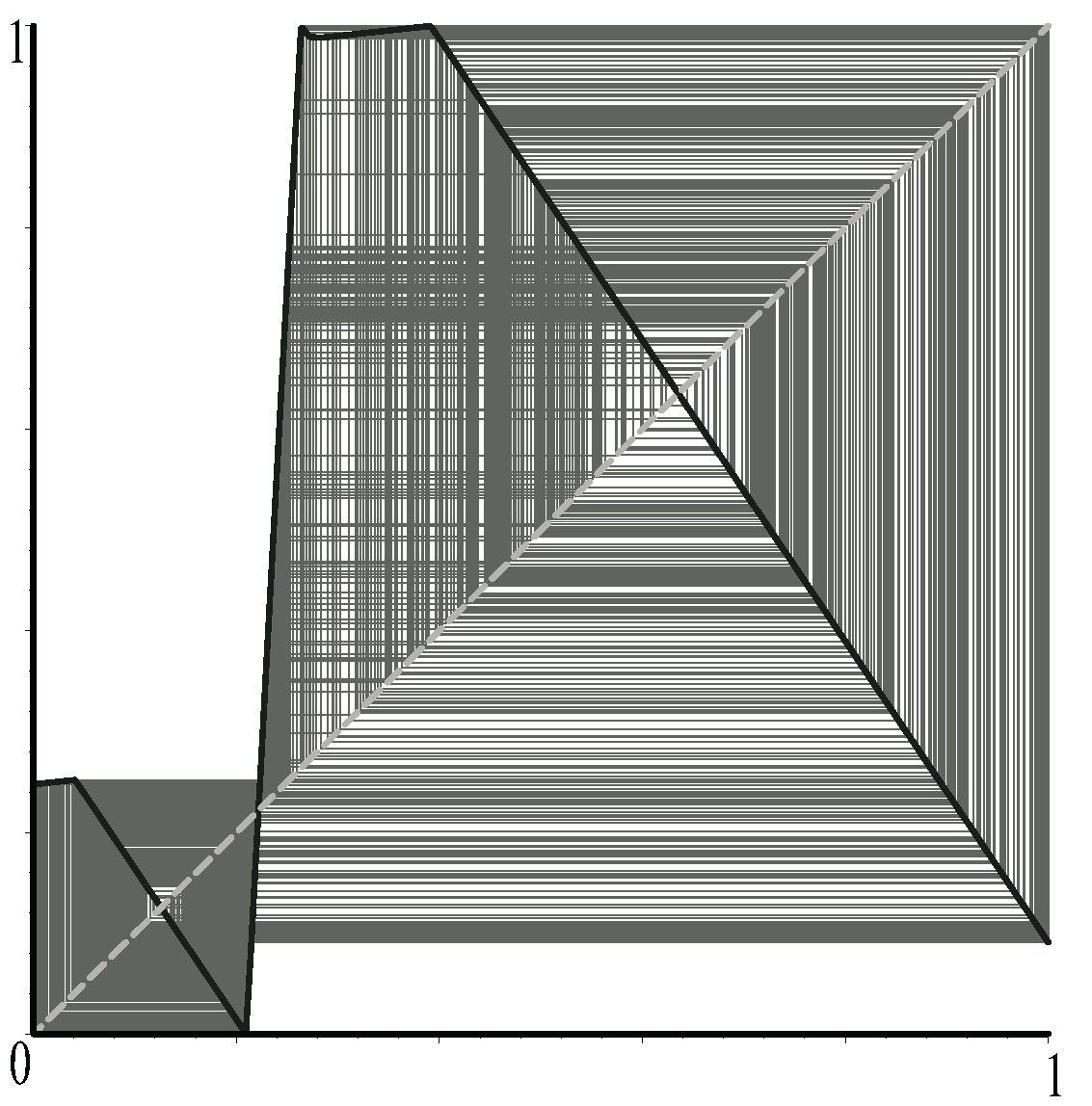
4.1. Formal Chaos Existing Conditions of a General 1-D Map
- There exist and disjoint closed subintervals in I such that and .
- holds for any x in . If f satisfies and , then the invariant set exists, and the 1-D map f on Λ is topologically conjugate to the shift dynamics with 2 symbols. The one-dimensional map f on Λ is mathematically chaotic.
4.2. Formal Chaos Existing Conditions of a 1-D Map Family
- There exist disjoint closed intervals and such that , , and holds for , where is the slope of .
- Invariant set exists, and on Λ is topologically conjugate to the shift dynamics with two symbols. on Λ is mathematically chaotic.
4.3. Formal Chaos Existing Conditions of 1-D Maps of Lossless Transmission Circuits
5. Formal Chaos Existence and Bifurcation Behavior of 1-D Maps by Using Maple
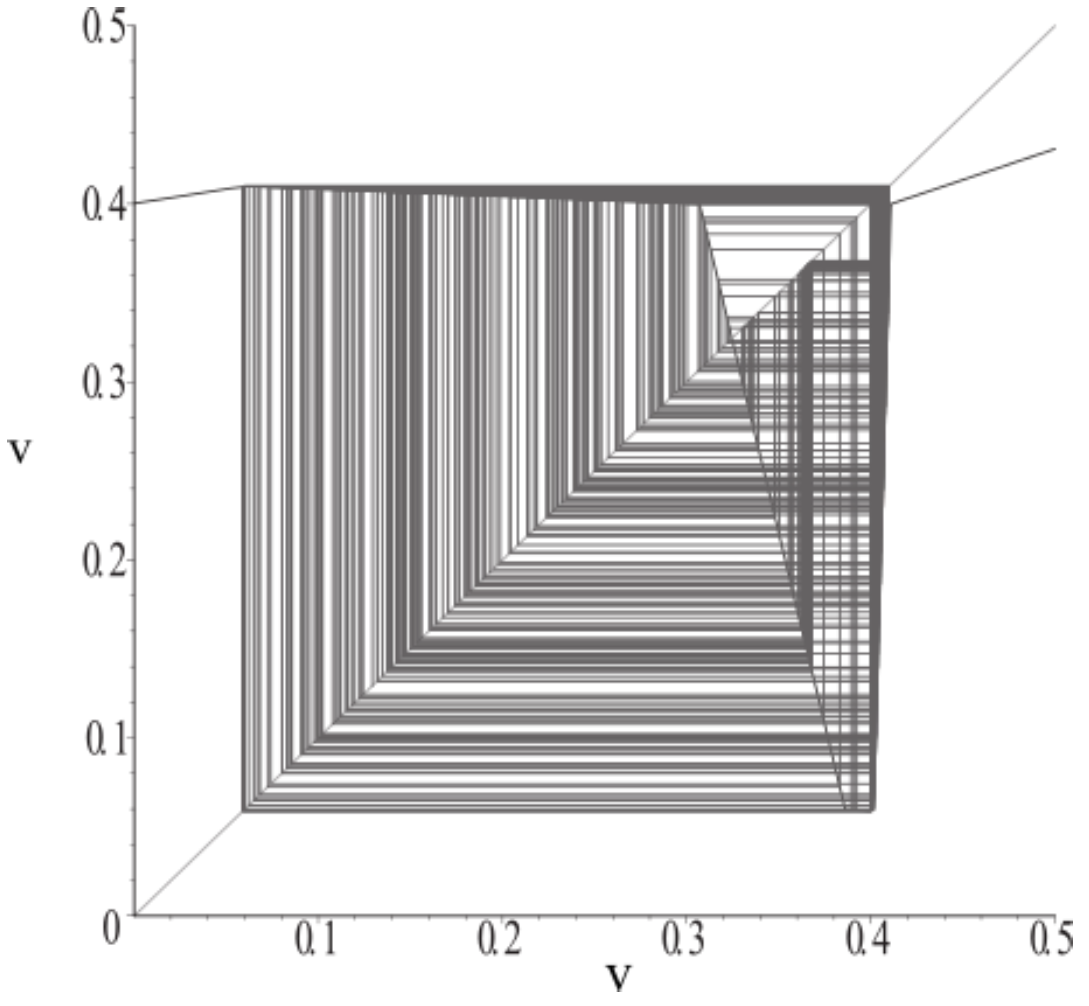
5.1. An Example of formal chaos Existence
- , , and hold;
- , and hold;
- , , , and hold;
- holds;
- holds;
- holds.
- holds.
- There exist disjoint intervals and such that , , and holds for , where is the slope of ;
- Invariant set exists, and on Λ is topologically conjugate to the shift dynamics with two symbols. on Λ is mathematically chaotic.
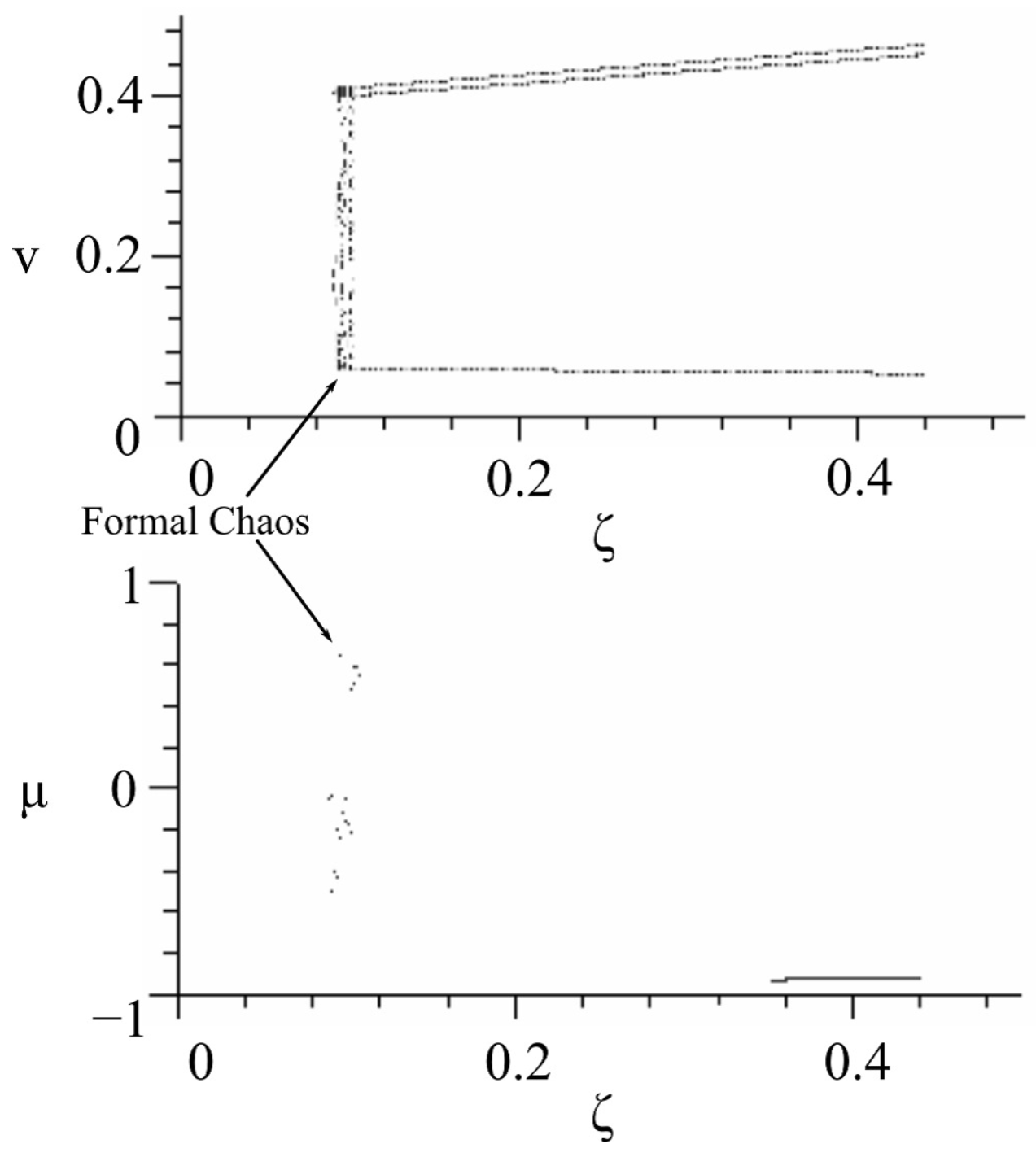
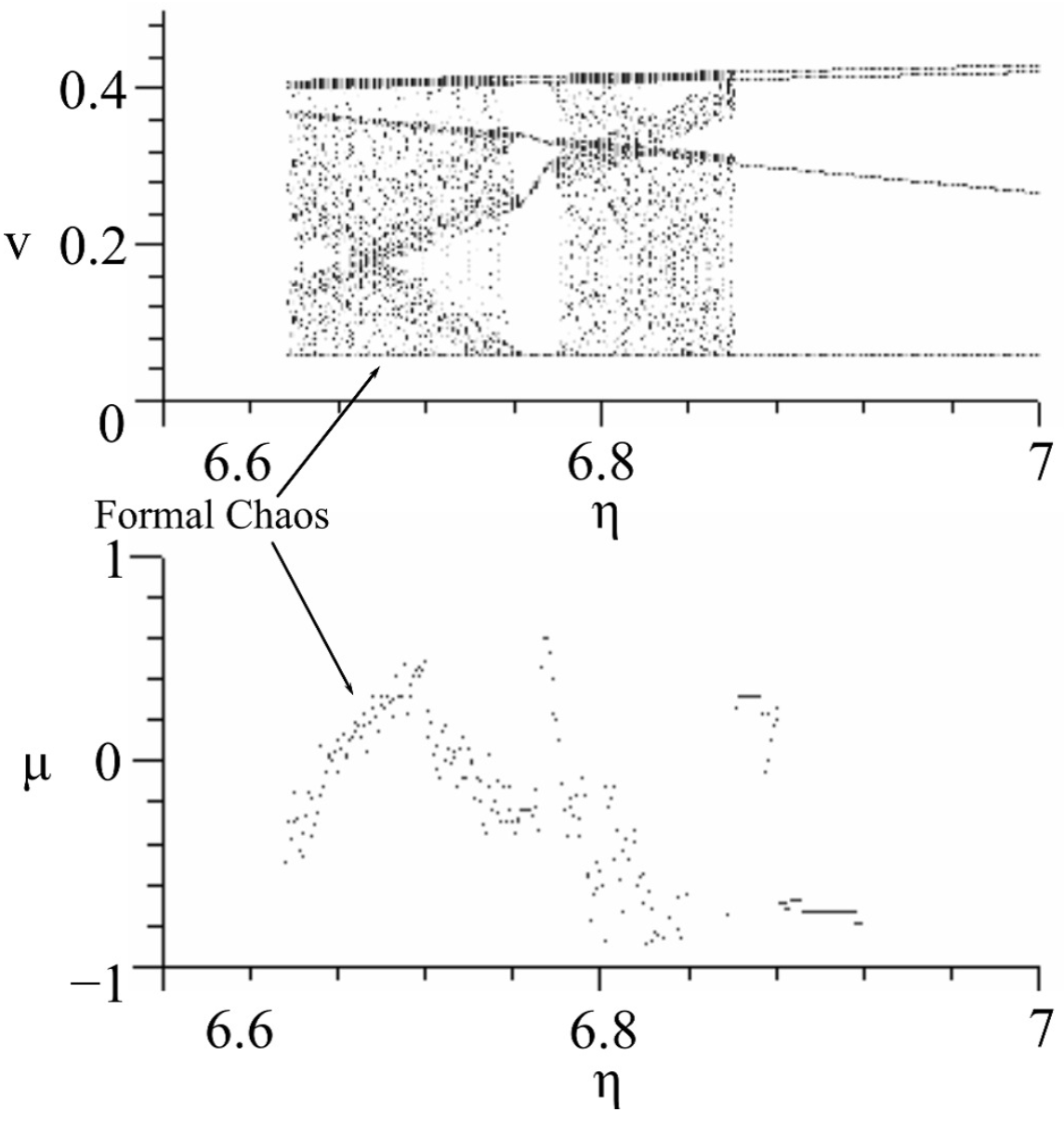
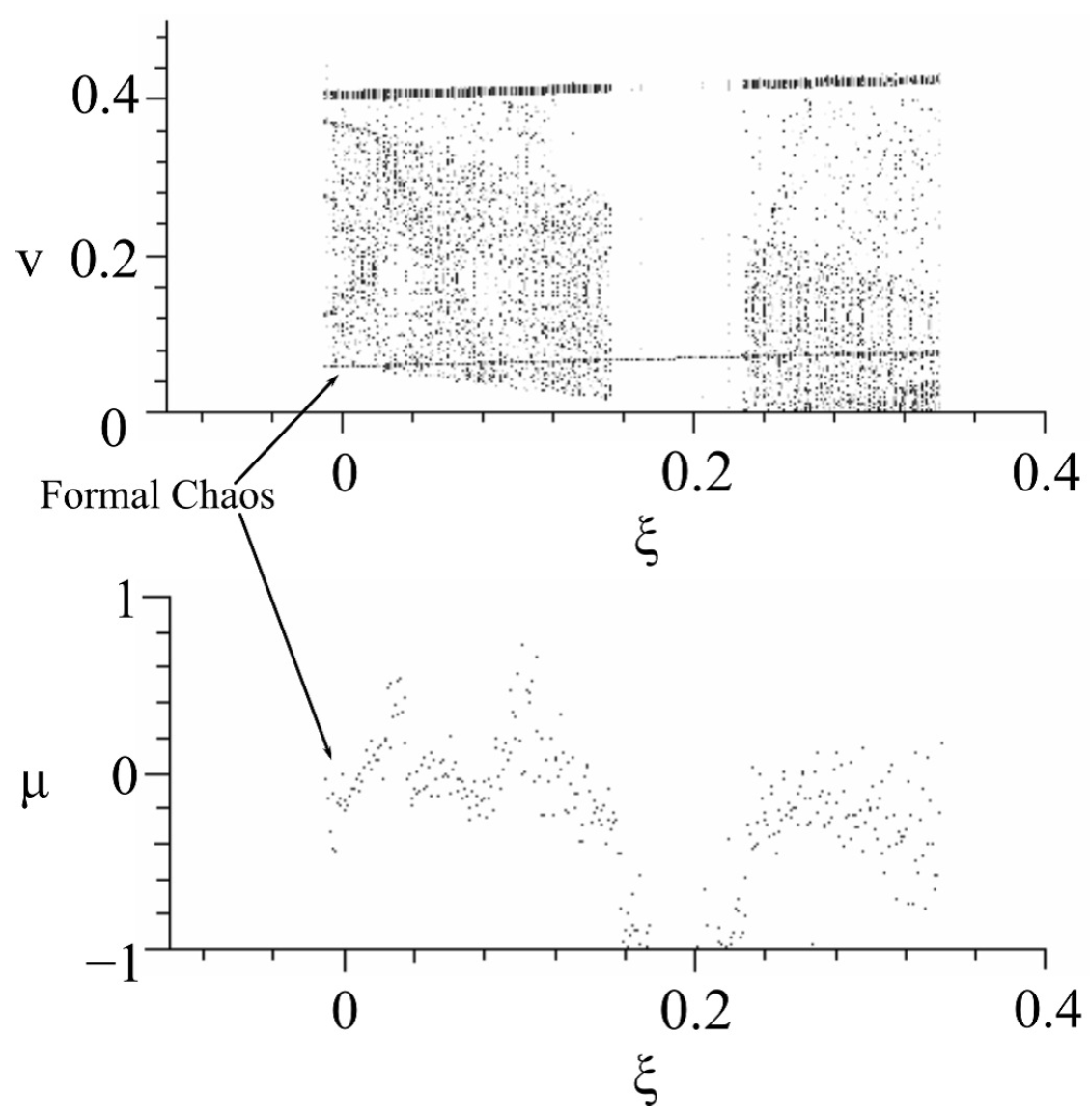
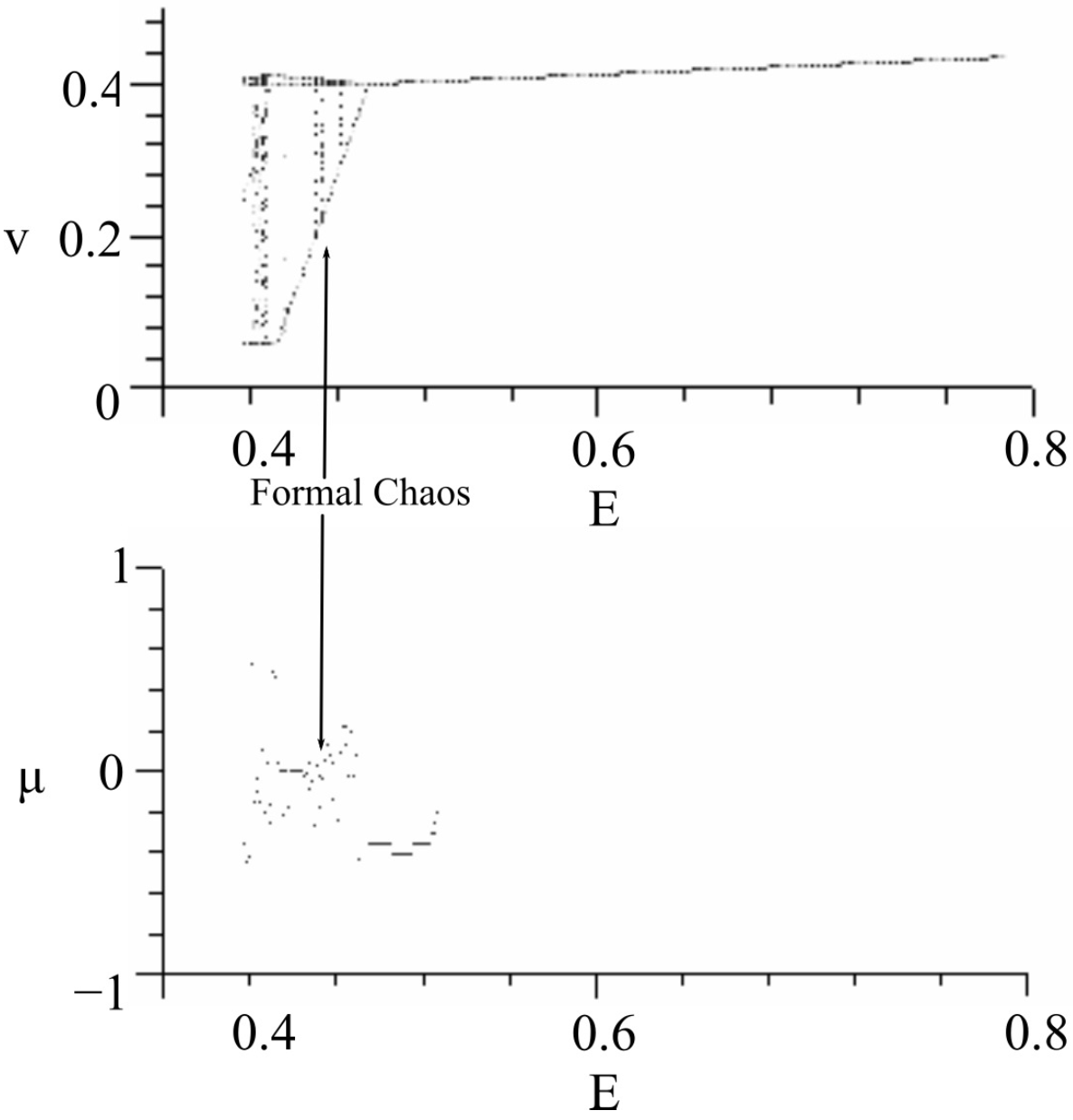
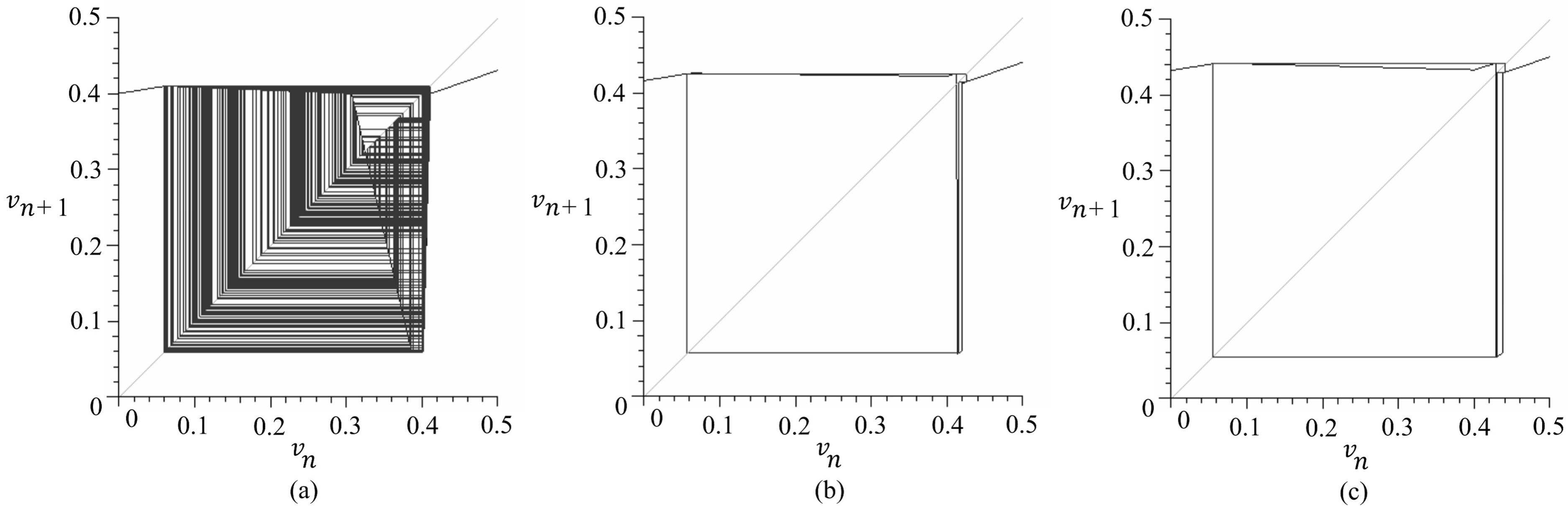
5.2. Several Examples of Bifurcation Behavior of 1-D Maps
- (1) bifurcation parameter:
- , ,, , .
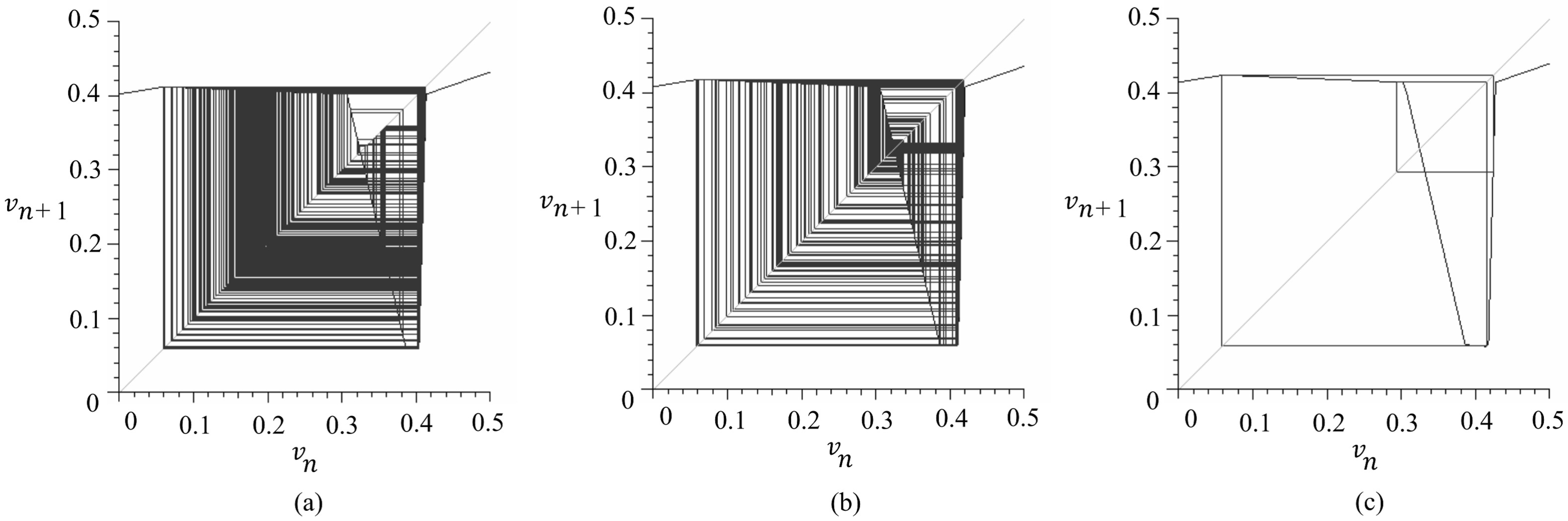
- (2) bifurcation parameter:
- , , , , .
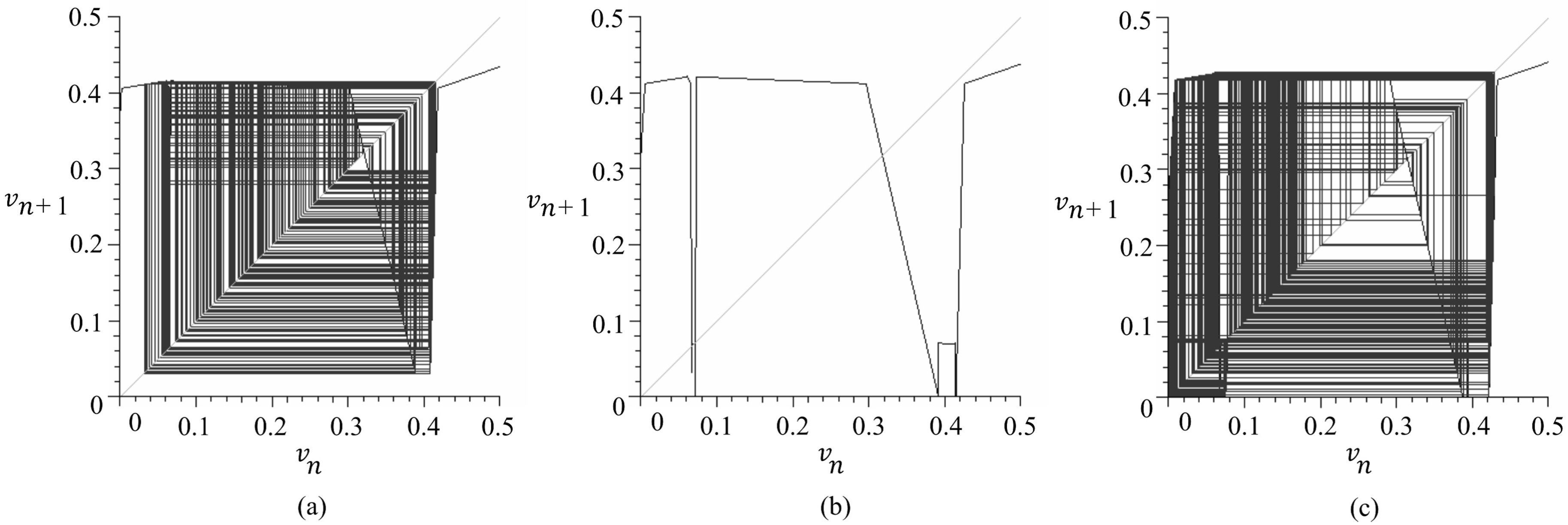
- (3) bifurcation parameter:
- , , , , .
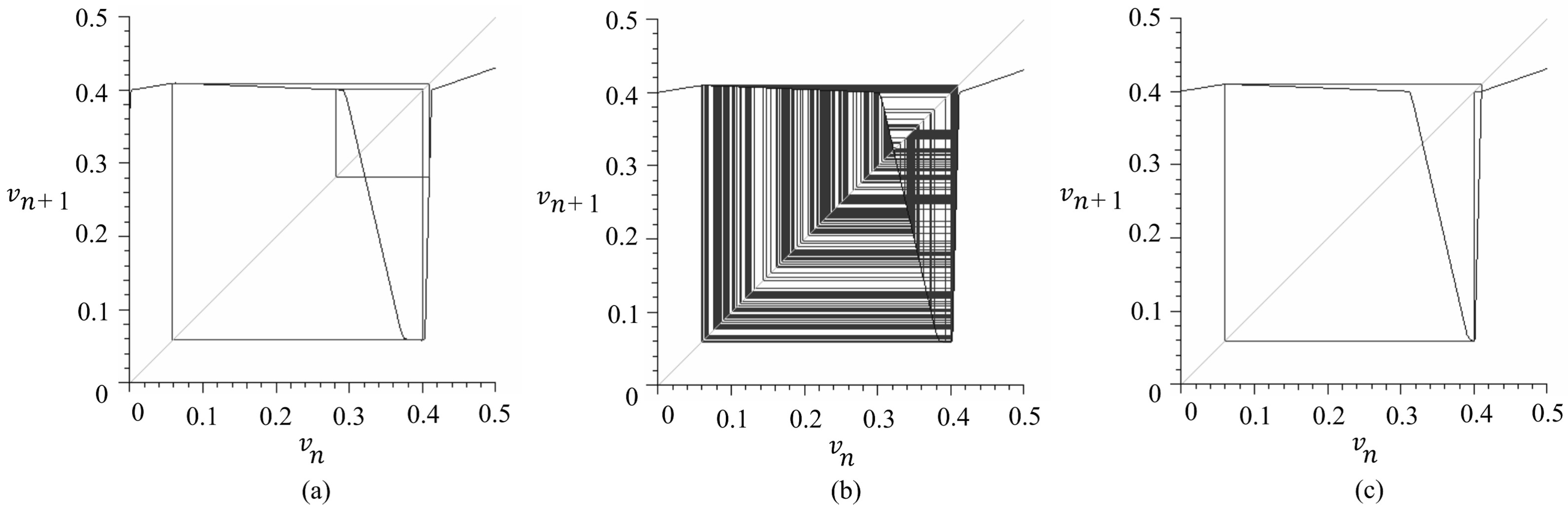
- (4) bifurcation parameter E:
- , , , , .
6. Conclusions
- We have described an implicit 1-D map of the incident and reflected waves that is derived from a lossless transmission line circuit with a dc bias voltage source in series with a load resistor at one side terminal and with a three-segment piecewise linear resistor at another side terminal.
- We have provided Theorem 1 establishing a 1-D map such as an incident wave: a reflected wave: ; Corollary 1 establishing 1-D map such as an incident wave: a reflected wave: ; and Corollary 2 establishing 1-D map such as a voltage: a voltage: in the case of Nagumo’s 3SPWL resistor or TD 3SPWL Resistor at the side terminal: .
- We have provided Theorem 3 such as an easy-to-use sufficient condition implying formal chaos existence in Definition 1.
- We have provided Theorem 2 to guarantee that for any initial point, every orbit by the iteration of the 1-D map ultimately penetrates in an invariant interval.
- We have provided Theorems 2 and 5 to guarantee that the dynamics of the second iterate map of the 1-D map on an invariant subset of the invariant interval has formal chaos.
- We have found that formal chaos exists under the condition such that [V], , , , , , , and .
- We have obtained the codimension of one type of four various bifurcation diagrams including the found formal chaos, with one of the bifurcation parameters: ζ, η, ξ, or E. From each bifurcation diagram with the Lyapunov exponent, the obsavability of the found formal chaos is considered to be rather high.
- As with the case of [12] such that the hidden dynamics of the circuit based on the integrated device has been unveiled on the basis of an analogy with the well-known Colpitts oscillator with the chaotic oscillations, we think that the hidden dynamics of imperfect transmission lines with parasitic effects and nonidealities inside real integrated devices can be unveiled on the basis of an analogy with the transmission line circuit of Equations (2)–(6) with formal chaos and that the parameters of the hidden dynamics can also be estimated by synchronizing a transmission line circuit with the chaotic oscillations acquired from the experimental circuit.
- We will report bifurcation processes with each of bifurcation parameters, Z or R, because nonlinear phenomena such as intermittency of chaos or blue sky bifurcation are observed in simulations.
- We will establish a method to find the bifurcation parameter ranges such that formal chaos exists for applications relative to several digital communication systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Theorems and Corollaries
- 1.
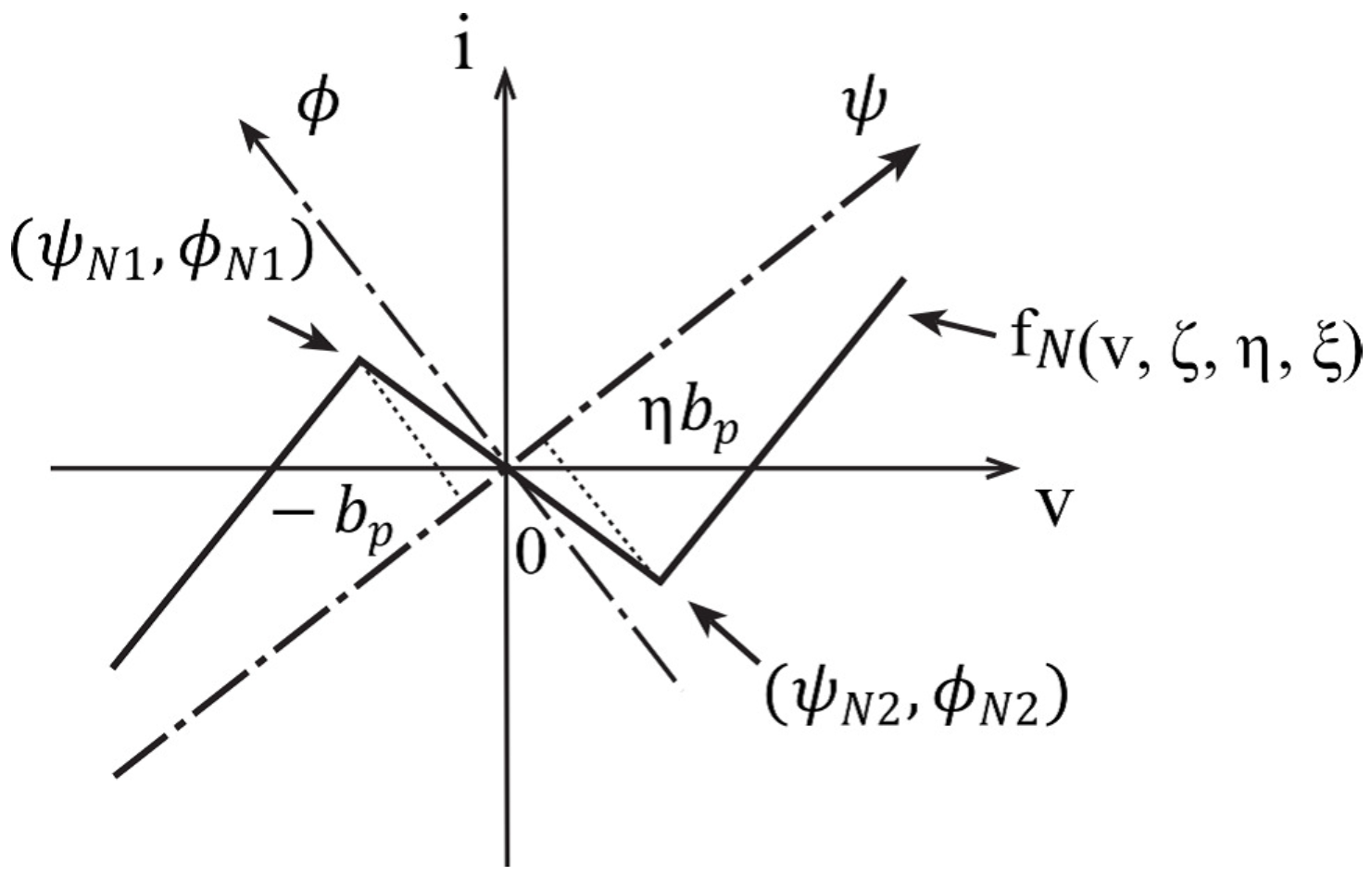
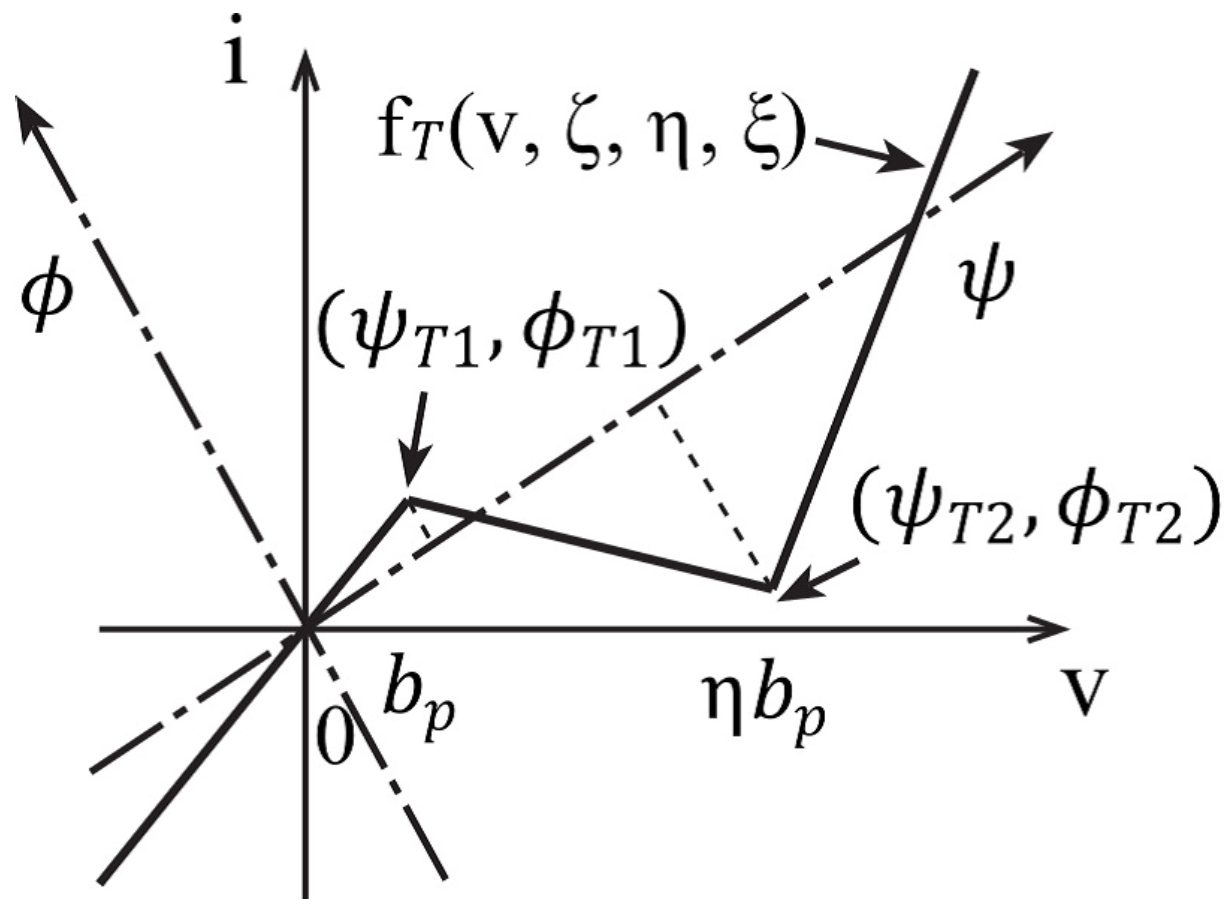
- In the case of : By using Equations (5) and (8), the break points and are transformed into and , respectively, such that the following is the case.and hold because and , respectively. Since -coordinate system is identical with the rotation of -coordinate system and and , as shown in Figure A1, is explicitly described by a three-segment piecewise linear function of Equation (16). , , , and hold because of the conditions such that and . Therefore, , , and hold.
- 2.
- In the case of : By using Equations (6) and (8), the break points and are transformed into and , respectively, such that the following is the case:and hold because and , respectively. Since the -coordinate system is identical with the rotation of -coordinate system and and , as shown in Figure A2, is explicitly described by a three-segment piecewise linear function of Equation (16). , , , , , and hold because of the conditions such that and . Therefore, , , and hold.
References
- Saito, T. A Chaos Generator Based on a Quasi-Harmonic Oscillator. IEEE Trans. Circuits Syst. 1985, 32, 320–331. [Google Scholar] [CrossRef]
- Saito, T.; Nakagawa, S. Chaos from a hysteresis and switched circuit. Philos. Trans. R. Soc. Lond. Math Phys. Sci. 1995, 352, 47–57. [Google Scholar]
- Miyoshi, T.; Saito, T.; Inaba, N. Chaotic Phenomena in a Iron Resonant Circuit Including an Inductor with Complete Saturation Characteristic. IEICE Trans. 1997, 80, 346–354. (In Japanese) [Google Scholar]
- Kennedy, M.P.; Rovatti, R.; Setti, G. (Eds.) Chaotic Electronics in Telecommunications; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Nagumo, J.; Shimura, M. Self-oscillation in a transmission line with a tunnel diode. Proc. IRE. 1961, 49, 1281–1291. [Google Scholar] [CrossRef]
- Nagumo, J.; Sato, S. On a Response Characteristic of a Mathematical Neuron Model. Kybernetik 1972, 10, 155–164. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Nakano, H.; Okazaki, H. Bifurcation Phenomena of a Distributed parameter System with a Nonlinear Element Having Negative Resistance. IEICE Trans. Fundam. 1992, 75, 339–346. [Google Scholar]
- Sharkovsky, A.N.; Maistrenko, Y.U.; Deregel, P.H.; Chua, L.O. Dry Turbulence a Time-Delayed Chua’s Circuit. J. Circuits Syst. Comput. 1993, 3, 645–668. [Google Scholar] [CrossRef]
- Sharkovsky, A.N. Chaos from a Time-Delayed Chua’s Circuit. IEEE Trans. Circuits Syst. 1993, 40, 781–783. [Google Scholar] [CrossRef]
- Sharkovsky, A.N.; Romanenko, E.; Berezovsky, S. Ideal turbulence: Definition and models. In Proceedings of the 2003 IEEE International Workshop on Workload Characterization (IEEE Cat. No.03EX775), St. Petersburg, Russia, 20–22 August 2003; Volume 1, pp. 23–30. [Google Scholar]
- Miyabayashi, N.; Moro, S.; Mori, S. Spatio-temporal dynamics in an array of time delayed Van der Pol oscillators. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems (ISCAS ’97), Hong Kong, China, 12 June 1997; Volume 2, pp. 917–920. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Gagliano, S. Imperfections in Integrated Devices Allow the Emergence of Unexpected Strange Attractors in Electronic Circuits. IEEE Access 2021, 9, 29573–29583. [Google Scholar] [CrossRef]
- Kohda, T. Discrete Dynamics and Chaos; Corona Publishing: Tokyo, Japan, 1998. (In Japanese) [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations Dynamical Systems, and Bifurcation of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; The Benjamin/Cummings Publishing: San Francisco, CA, USA, 1986. [Google Scholar]
- Robinson, C. Dynamical Systems, Stability, Symbolic Dynamics, and Chaos, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Kokubu, H. Foundation of Dynamical Systems; Asakura Publishing: Tokyo, Japan, 2000. (In Japanese) [Google Scholar]
- Thunberg, H. Periodicity versus Chaos in One-Dimensional Dynamics. SIAM Rev. 2001, 43, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Moser, J. Stable and Random Motions in Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Oono, Y.; Oshikawa, M. Chaos in Nonlinear Difference Equations I. Prog. Theor. Phys. 1980, 64, 54–67. [Google Scholar] [CrossRef] [Green Version]
- Aoki, N. Dynamical Systems and Chaos-Geometric Construction of Nonlinear Phenomena; Kyoritsu Publishing: Tokyo, Japan, 2000. (In Japanese) [Google Scholar]
- Okazaki, H.; Okazaki, C.; Honda, H.; Nakano, H. Rigorous verification of formal chaos produced by one-dimensional discrete dynamical system with use of interval arithmetic. In Proceedings of the 2005 IEEE 48th Midwest Symposium on Circuits and Systems (The IEEE MWSCAS 2005), Covington, KY, USA, 7–10 August 2005; pp. 1597–1660. [Google Scholar]
- Lynch, S. Dynamical Systems with Applications Using MAPLE; Birkhäuser: Basel, Switzerland, 2010. [Google Scholar]
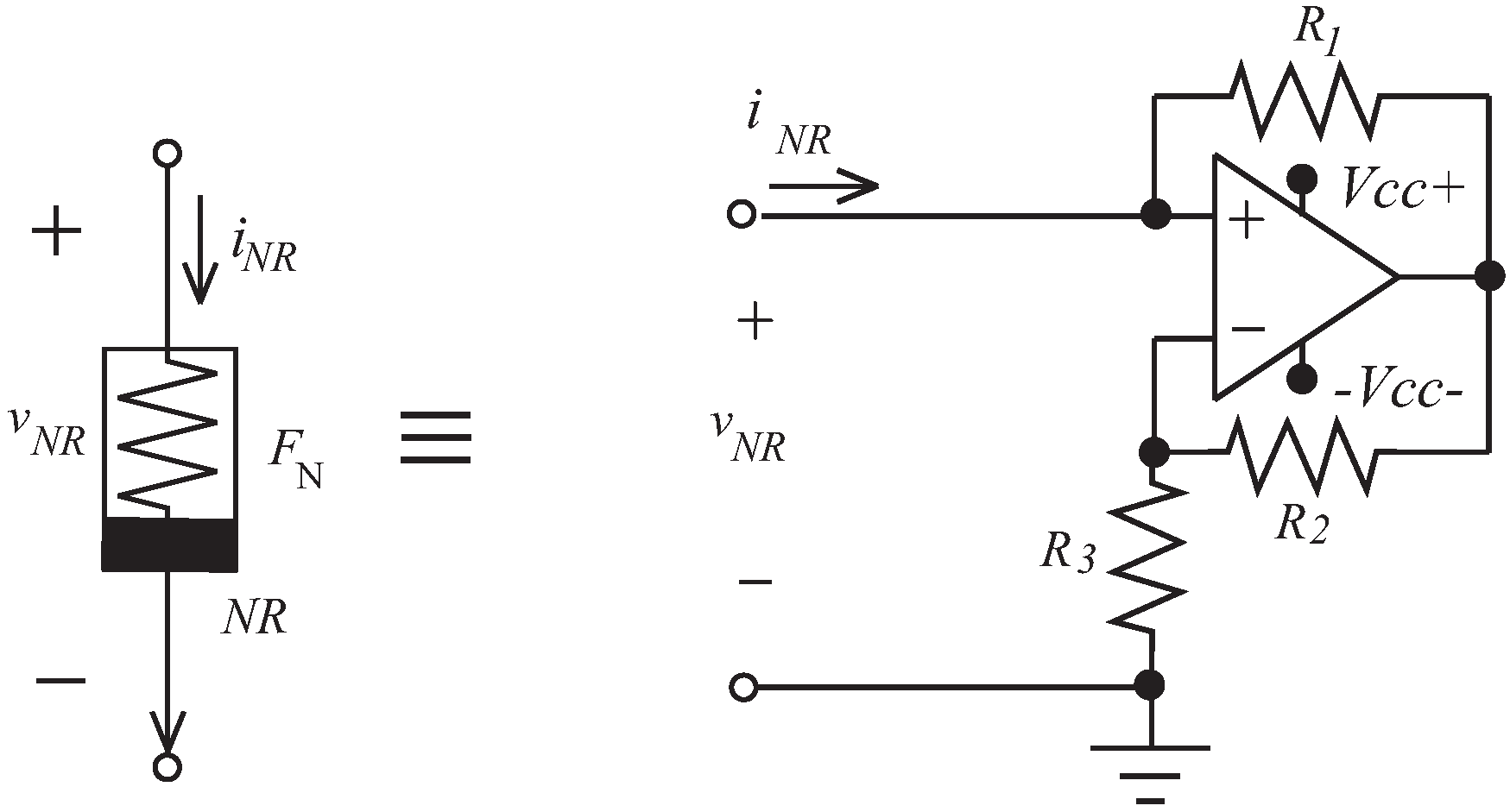


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozawa, K.; Isogai, K.; Nakano, H.; Okazaki, H. Formal Chaos Existing Conditions on a Transmission Line Circuit with a Piecewise Linear Resistor. Appl. Sci. 2021, 11, 9672. https://doi.org/10.3390/app11209672
Ozawa K, Isogai K, Nakano H, Okazaki H. Formal Chaos Existing Conditions on a Transmission Line Circuit with a Piecewise Linear Resistor. Applied Sciences. 2021; 11(20):9672. https://doi.org/10.3390/app11209672
Chicago/Turabian StyleOzawa, Kazuya, Kaito Isogai, Hideo Nakano, and Hideaki Okazaki. 2021. "Formal Chaos Existing Conditions on a Transmission Line Circuit with a Piecewise Linear Resistor" Applied Sciences 11, no. 20: 9672. https://doi.org/10.3390/app11209672
APA StyleOzawa, K., Isogai, K., Nakano, H., & Okazaki, H. (2021). Formal Chaos Existing Conditions on a Transmission Line Circuit with a Piecewise Linear Resistor. Applied Sciences, 11(20), 9672. https://doi.org/10.3390/app11209672





