DEA-Based PROMETHEE II Distribution-Center Productivity Model: Evaluation and Location Strategies Formulation
Abstract
1. Introduction
2. Relevant Literature
3. Methods
3.1. PROMETHEE II
3.2. DEA
4. Application
4.1. Background
4.2. DEA-Based PROMETHEE II Model Development
- Vehicle Off Road (VOR)
- Number of Employees (NE)
- Stock Efficiency (SE)
- Stock Month (SM)
- Immediate Supply Job Card Fill Rate (JCFR) Task Achievement
- Service Rate (SR)
- Guest Delight Index (GDI)
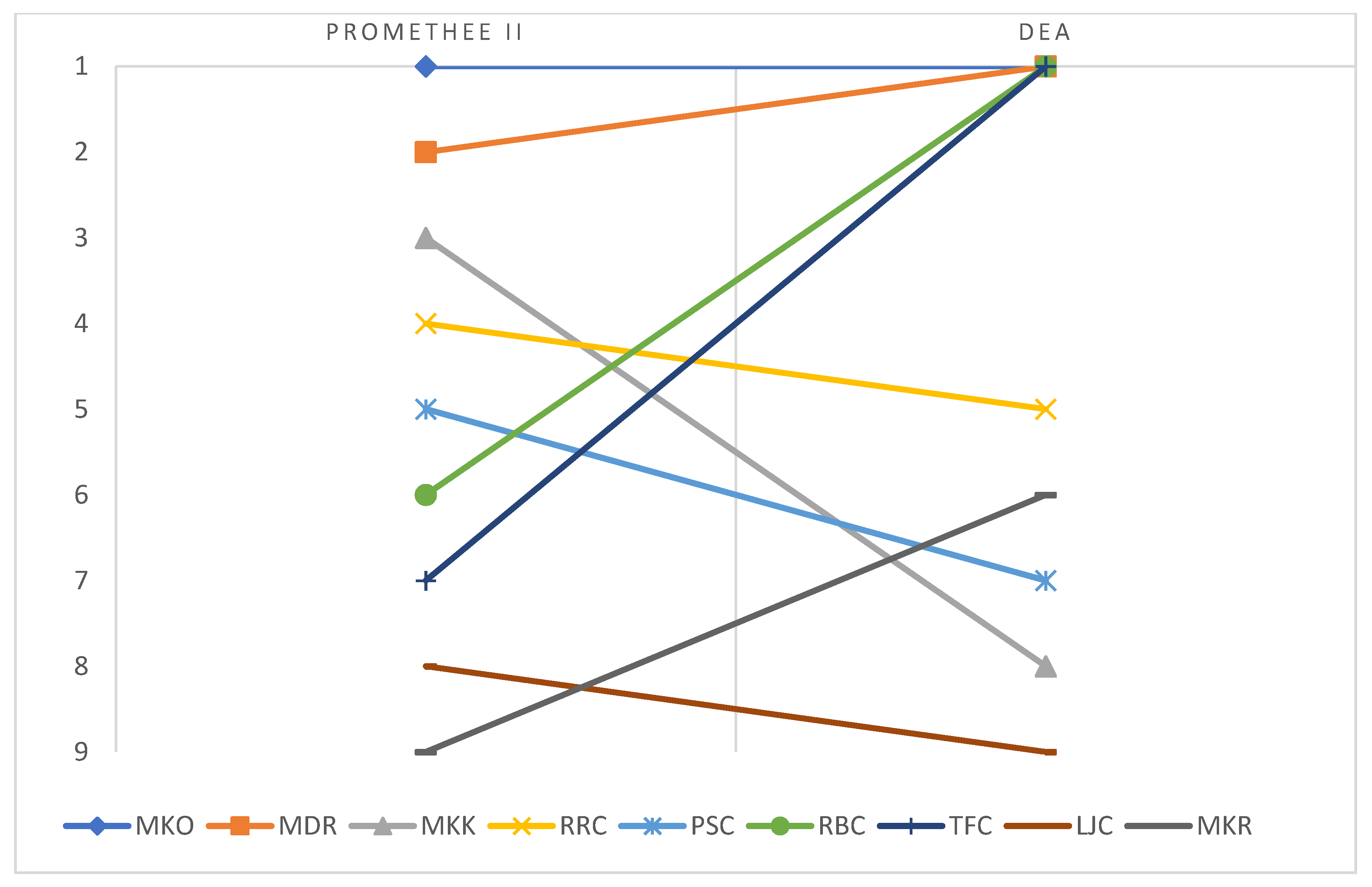
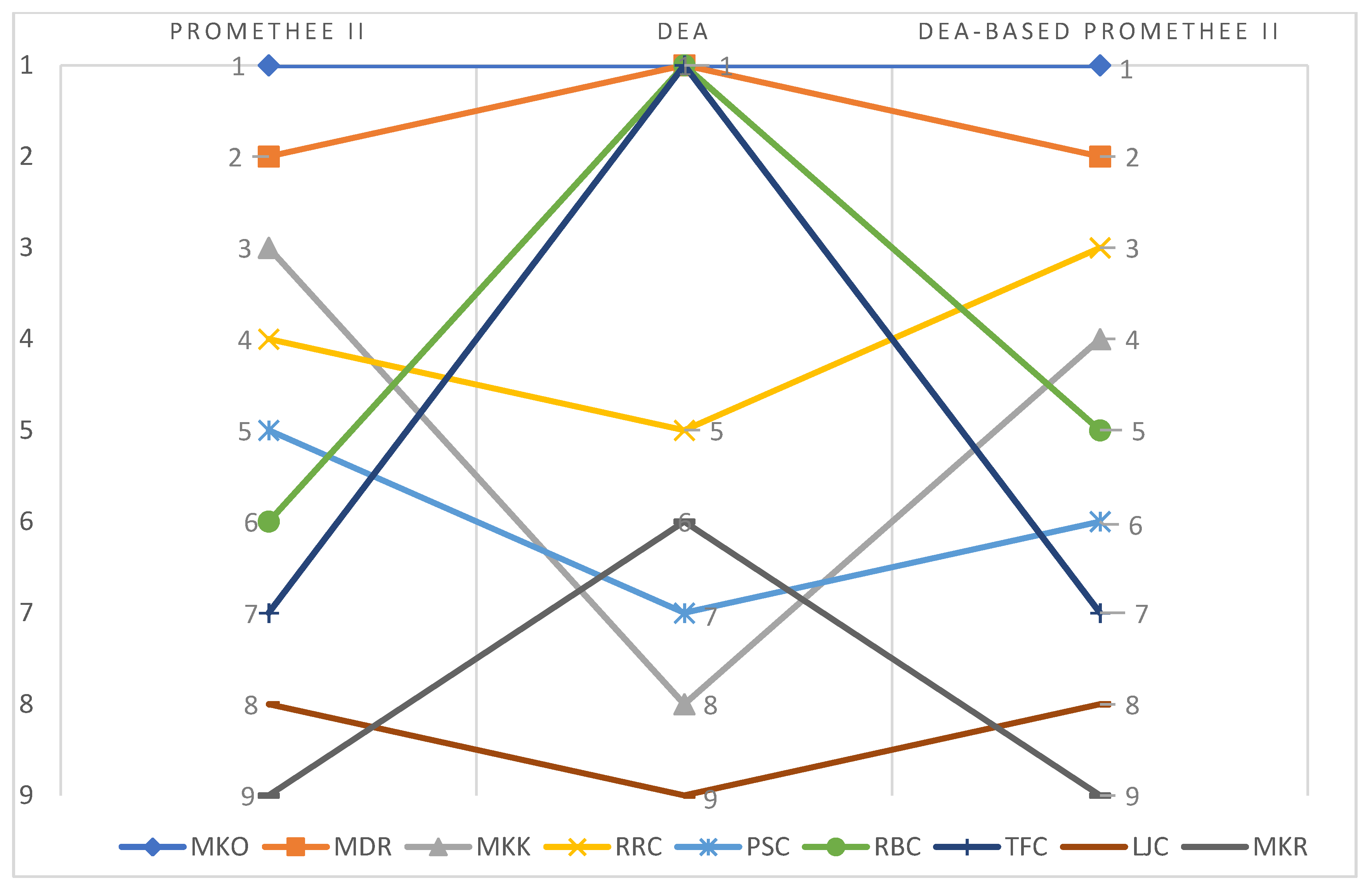
5. Results and Discussion
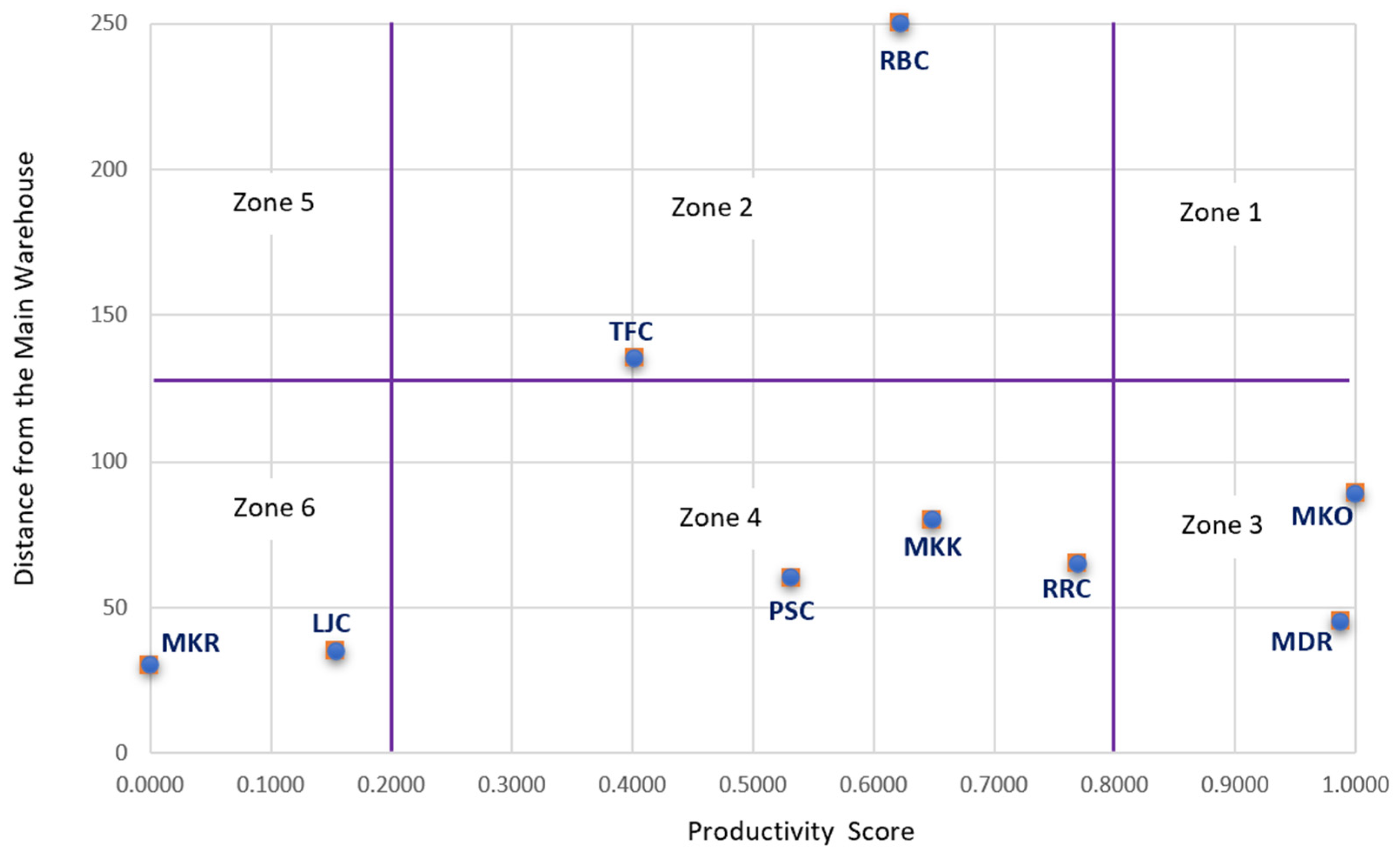
6. Implications of DCs Locations
- Strategy 1
- Strategy 2
- Strategy 3
- Strategy 4
- Strategy 5
- Strategy 6
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sumanth, D.J. Productivity Engineering and Management: Productivity Measurement, Evaluation, Planning, and Improvement in Manufacturing and Service Organizations; McGraw-Hill College: New York, NY, USA, 1984. [Google Scholar]
- Dey, B.; Bairagi, B.; Sarkar, B.; Sanyal, S.K. Group heterogeneity in multi member decision making model with an application to warehouse location selection in a supply chain. Comput. Ind. Eng. 2017, 105, 101–122. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K. A new fuzzy additive ratio assessment method (ARAS-F). Case study: The analysis of fuzzy multiple criteria in order to select the logistic centers location. Transport 2010, 25, 423–432. [Google Scholar] [CrossRef]
- Özcan, T.; Çelebi, N.; Esnaf, Ş. Comparative analysis of multi-criteria decision making methodologies and implementation of a warehouse location selection problem. Expert Syst. Appl. 2011, 38, 9773–9779. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection. Expert Syst. Appl. 2014, 41, 8112–8128. [Google Scholar] [CrossRef]
- Komchornrit, K. The selection of dry port location by a hybrid CFA-MACBETH-PROMETHEE method: A case study of Southern Thailand. Asian J. Shipp. Logist. 2017, 33, 141–153. [Google Scholar] [CrossRef]
- Stević, Ž.; Vesković, S.; Vasiljević, M.; Tepić, G. The selection of the logistics center location using AHP method. In Proceedings of the 2nd Logistics International Conference, Belgrade, Serbia, 21–23 May 2015; Vidovic, M., Kilibarda, M., Zecevic, S., Miljus, M., Radivojevic, G., Eds.; pp. 86–91. [Google Scholar]
- Pham, T.Y.; Ma, H.M.; Yeo, G.T. Application of Fuzzy Delphi TOPSIS to locate logistics centers in Vietnam: The logisticians’ perspective. Asian J. Shipp. Logist. 2017, 33, 211–219. [Google Scholar] [CrossRef]
- Cristea, M.; Cristea, C. A multicriteria decision-making approach used for the selection of a logistics center location. Ann. Univ. Oradea. 2016, 25, 2011–2016. [Google Scholar] [CrossRef]
- Elevli, B. Logistics freight center locations decision by using Fuzzy-PROMETHEE. Transport 2014, 29, 412–418. [Google Scholar] [CrossRef]
- Rimienė, K.; Grundey, D. Logistics centre concept through evolution and definition. Eng. Econ. 2007, 54, 87–95. [Google Scholar]
- Rushton, A.; Croucher, P.; Baker, P. The Handbook of Logistics and Distribution Management: Understanding the Supply Chain; Kogan Page Publishers: New York, NY, USA, 2014; ISBN 0749466286. [Google Scholar]
- Korpela, J.; Lehmusvaara, A.; Nisonen, J. Warehouse operator selection by combining AHP and DEA methodologies. Int. J. Prod. Econ. 2007, 108, 135–142. [Google Scholar] [CrossRef]
- Uysal, H.; Yavuz, K. Selection of logistics centre location via ELECTRE method: A case study in Turkey. Int. J. Bus. Soc. Sci. 2014, 5, 9. [Google Scholar]
- Yıldırım, B.F.; Önder, E. Evaluating potential freight villages in Istanbul using multi criteria decision making techniques. J. Logist. Manag. 2014, 3, 1–10. [Google Scholar]
- Żak, J.; Węgliński, S. The selection of the logistics center location based on MCDM/A methodology. Transp. Res. Procedia 2014, 3, 555–564. [Google Scholar] [CrossRef]
- Özceylan, E.; Erbaş, M.; Tolon, M.; Kabak, M.; Durğut, T. Evaluation of freight villages: A GIS-based multi-criteria decision analysis. Comput. Ind. 2016, 76, 38–52. [Google Scholar] [CrossRef]
- Zarali, F.; Yazgan, H.R.; Delice, Y. AHP ve VIKOR Bütünleşik yaklaşımıyla Lojistik Merkez Yer Seçimi: Kayseri ili örneği. Erciyes Üniversitesi Fen Bilimleri Enstitüsü Derg. 2018, 34, 1–9. [Google Scholar]
- Ghoseiri, K.; Lessan, J. Location selection for logistic centres using a two-step fuzzy AHP and ELECTE method. In Proceedings of the 9th Asia Pasific Industrial Engineering & Management Systems Conference, Bali, Indonesia, 3–5 December 2008; pp. 434–440. [Google Scholar]
- Li, Y.; Liu, X.; Chen, Y. Selection of logistics center location using Axiomatic Fuzzy Set and TOPSIS methodology in logistics management. Expert Syst. Appl. 2011, 38, 7901–7908. [Google Scholar] [CrossRef]
- Chen, K.-H.; Liao, C.-N.; Wu, L.-C. A selection model to logistic centers based on TOPSIS and MCGP methods: The case of airline industry. J. Appl. Math. 2014, 2014, 470128. [Google Scholar] [CrossRef]
- Chen, C.-T. A fuzzy approach to select the location of the distribution center. Fuzzy Sets Syst. 2001, 118, 65–73. [Google Scholar] [CrossRef]
- Amiri, M.; Kazemi, A.; Sadaghiani, J.S.; Yaghoubi, A.; Mashatzade, H. Developing and solving a new model for the location problems: Fuzzy-goal programming approach. J. Appl. Sci. 2009, 9, 1344–1349. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S.; Goyal, S.K. A multi-criteria decision making approach for location planning for urban distribution centers under uncertainty. Math. Comput. Model. 2011, 53, 98–109. [Google Scholar] [CrossRef]
- Chu, T.-C.; Hsu, W.-C. Evaluating distribution centers via a maximizing set and minimizing set based Fuzzy MCDM approach. J. Bus. Econ. 2016, 7, 81–93. [Google Scholar]
- Li, S.; Wei, Z. A hybrid approach based on the analytic hierarchy process and 2-tuple hybrid ordered weighted averaging for location selection of distribution centers. PLoS ONE 2018, 13, e0206966. [Google Scholar] [CrossRef]
- Quynh, M.; Thu, T.; Huong, Q.; Van, A.; Van, H.; Van, D. Distribution center location selection using a novel multi criteria decision-making approach under interval neutrosophic complex sets. Decis. Sci. Lett. 2020, 9, 501–510. [Google Scholar] [CrossRef]
- Waters, C.D.J. Logistics: An Introduction to Supply Chain Management; Red Globe Press: New York, NY, USA, 2019; ISBN 1137262346. [Google Scholar]
- Ross, A.; Droge, C. An integrated benchmarking approach to distribution center performance using DEA modeling. J. Oper. Manag. 2002, 20, 19–32. [Google Scholar] [CrossRef]
- Ballis, A.; Mavrotas, G. Freight village design using the multicriteria method PROMETHEE. Oper. Res. 2007, 7, 213–231. [Google Scholar] [CrossRef]
- Jiang, C.; Fu, P. Evaluating efficiency and effectiveness of logistics infrastructure based on PCA-DEA approach in China. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 3, pp. 62–66. [Google Scholar]
- Vijay, M.A.; Shankar, C. Facility Location Selection using PROMETHEE II Method. In Proceedings of the 2010 International Conference on Industrial Engineering and Operations Management, Dhaka, Bangladesh, 9–10 January 2010; pp. 59–64. [Google Scholar]
- Alp, Ö.N.; Demirtaş, N.; Baraçli, H.; Tuzkaya, U.R. Fuzzy AHP-PROMETHEE methodology to select bus garage location: A case study for a firm in the urban passenger transport sector in Istanbul. In Proceedings of the 15th International Research/Expert Conference, Prague, Czech Republic, 12–18 September 2011; Citeseer: Prague, Czech Republic, 2011. [Google Scholar]
- Fontana, M.E.; Cavalcante, C.A.V. Use of Promethee method to determine the best alternative for warehouse storage location assignment. Int. J. Adv. Manuf. Technol. 2014, 70, 1615–1624. [Google Scholar] [CrossRef]
- Andrejić, M.; Bojović, N.; Kilibarda, M. A framework for measuring transport efficiency in distribution centers. Transp. Policy 2016, 45, 99–106. [Google Scholar] [CrossRef]
- Ishizaka, A.; Resce, G.; Mareschal, B. Visual management of performance with PROMETHEE productivity analysis. Soft Comput. 2018, 22, 7325–7338. [Google Scholar] [CrossRef]
- Dixit, A.; Routroy, S.; Dubey, S.K. Measuring performance of government-supported drug warehouses using DEA to improve quality of drug distribution. J. Adv. Manag. Res. 2020, 17, 567–581. [Google Scholar] [CrossRef]
- Zapletal, F. A novel hybrid fuzzy PROMETHEE-IDEA approach to efficiency evaluation. Soft Comput. 2021, 25, 3913–3929. [Google Scholar] [CrossRef]
- Brans, J.P. L’ingenierie de la decision, l’laboration d’instruments d’aidea la decision. In Proceedings of the Colloque sur l’Aidea la Decision, Faculte des Sciences de l’Administration, Universite Laval, Québec, QC, Canada, 1982. [Google Scholar]
- Vincke, J.P.; Brans, P. A preference ranking organization method. The PROMETHEE method for MCDM. Manag. Sci. 1985, 31, 647–656. [Google Scholar]
- Doumpos, M.; Zopounidis, C. A multicriteria classification approach based on pairwise comparisons. Eur. J. Operat. Res. 2004, 158, 378–389. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Operat. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Alidrisi, H.; Aydin, M.E.; Bafail, A.O.; Abdulal, R.; Karuvatt, S.A. Monitoring the performance of petrochemical organizations in Saudi Arabia using data envelopment analysis. Mathematics 2019, 7, 519. [Google Scholar] [CrossRef]
- Taylan, O.; Alidrisi, H.; Kabli, M. A multi-criteria decision-making approach that combines fuzzy topsis and DEA methodologies. S. Afr. J. Ind. Eng. 2014, 25, 39–56. [Google Scholar] [CrossRef][Green Version]
- Saputri, V.H.L.; Sutopo, W.; Hisjam, M.; Ma’aram, A. Sustainable agri-food supply chain performance measurement model for GMO and Non-GMO using data envelopment analysis method. Appl. Sci. 2019, 9, 1199. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Operat. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Taylan, O.; Alamoudi, R.; Kabli, M.; AlJifri, A.; Ramzi, F.; Herrera-Viedma, E. Assessment of energy systems using extended fuzzy AHP, fuzzy VIKOR, and TOPSIS approaches to manage non-cooperative opinions. Sustainability 2020, 12, 2745. [Google Scholar] [CrossRef]
- Alidrisi, H.; Mohamed, S. Resource allocation for strategic quality management: A goal programming approach. Int. J. Qual. Reliab. Manag. 2012, 29, 265–283. [Google Scholar] [CrossRef]
- Alidrisi, H. Measuring the environmental maturity of the supply chain finance: A big data-based multi-criteria perspective. Logistics 2021, 5, 22. [Google Scholar] [CrossRef]
| DC | NE | SE | GDI | SR | SM | JCFR | VOR |
|---|---|---|---|---|---|---|---|
| LJC | 7 | 51.7 | 98.1 | 75.17 | 1.1 | 91.9 | 0.03731 |
| MKK | 9 | 48.4 | 98 | 99.10 | 1.1 | 89.5 | 0.02173 |
| PSC | 6 | 62.2 | 94.5 | 92.40 | 1.8 | 79.3 | 0.03021 |
| MKO | 6 | 40.8 | 94.1 | 92.50 | 2.7 | 80.1 | 0.01655 |
| MDR | 11 | 66.9 | 93.6 | 93.30 | 1.5 | 95.2 | 0.01485 |
| RRC | 8 | 59.1 | 93.5 | 96.50 | 1.1 | 91.7 | 0.01934 |
| RBC | 2 | 9.6 | 90.6 | 91.30 | 2.4 | 77 | 0.01165 |
| TFC | 3 | 38.1 | 89.9 | 94.30 | 1.5 | 73 | 0.01552 |
| MKR | 13 | 21.9 | 89 | 96.30 | 1.1 | 87.2 | 0.01508 |
| DC | Rank | |||
|---|---|---|---|---|
| LJC | 0.1867 | 0.3023 | −0.1156 | 8 |
| MKK | 0.2192 | 0.1339 | 0.0853 | 3 |
| PSC | 0.1765 | 0.1722 | 0.0043 | 5 |
| MKO | 0.2370 | 0.1173 | 0.1197 | 1 |
| MDR | 0.2333 | 0.1175 | 0.1159 | 2 |
| RRC | 0.1846 | 0.1207 | 0.0639 | 4 |
| RBC | 0.2350 | 0.2362 | −0.0012 | 6 |
| TFC | 0.1501 | 0.2219 | −0.0718 | 7 |
| MKR | 0.0995 | 0.3000 | −0.2005 | 9 |
| Potential Improvements for Output and Input Measures | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| DC | Efficiency Score | Rank | SE | GDI | SR | SM | JCFR | NE | VOR |
| LJC | 0.582 | 9 | +71% | +113% | +192% | +218% | +85% | … | −2% |
| MKK | 0.727 | 8 | +37% | +39% | +40% | +124% | +37% | … | … |
| PSC | 0.832 | 7 | +20% | +85% | +98% | +62% | +79% | … | … |
| MKO | 1 | 1 | … | … | … | … | … | … | … |
| MDR | 1 | 1 | … | … | … | … | … | … | … |
| RRC | 0.932 | 5 | +7% | +24% | +23% | +73% | +13% | … | … |
| RBC | 1 | 1 | … | … | … | … | … | … | … |
| TFC | 1 | 1 | … | … | … | … | … | … | … |
| MKR | 0.881 | 6 | +13% | +26% | +17% | +150% | +13% | −65% | … |
| DC | DEA Efficiency Score | DEA-Based PROMETHEE II Score | ||||
|---|---|---|---|---|---|---|
| MKO | 0.1197 | 0.119747 | 1.0000 | 1 | 1.0000 | |
| MDR | 0.1159 | … | 0.9879 | 1 | 0.9879 | |
| MKK | 0.0853 | 0.8924 | 0.727 | 0.6488 | ||
| RRC | 0.0639 | 0.8255 | 0.932 | 0.7693 | ||
| PSC | 0.0043 | 0.6395 | 0.832 | 0.5321 | ||
| RBC | −0.0012 | 0.6223 | 1 | 0.6223 | ||
| TFC | −0.0718 | 0.4020 | 1 | 0.4020 | ||
| LJC | −0.1156 | 0.2652 | 0.582 | 0.1543 | ||
| MKR | −0.2005 | −0.20051 | 0.0000 | 0.881 | 0.0000 |
| Title of Previous Studies | Publication Date | MCDM Theoretical Base & Assumptions (Context, Criteria, Alternatives, Decision Making Units (DMU), … etc.) | Methodology (MCDM Tools and Techniques) | Dissimilarities in the Contribution Compared to the Current Study (Including Any Potential Improvements to Be Handled in Further/Future Studies, Gaps/Aspects not Covered, or Motives for Further Investigations) |
|---|---|---|---|---|
| An integrated benchmarking approach to distribution center performance using DEA modelling [29]. | 2002 | Context: Distribution Center Performance; Criteria: 3 inputs (fleet size, experience, and the mean order throughput time in days (MOT)); and 4 outputs (sales volume of 4 different products); Alternatives: Distribution Centers. | DEA | Use of DEA alone (i.e., efficiency focused model) All outputs focused on sales volumes |
| Freight village design using the multicriteria method PROMETHEE [30]. | 2007 | Context: Freight village design; Criteria: freight village layout, the cross-docking options of the modules and direct railway access, and the circulation conditions; Alternatives: three alternative designs of the freight village layout are compared by means of multicriteria analysis | PROMETHEE | The context of the “freight village” is more generic and comprehensive compared to the context of the “distribution centers” Based on a single technique (PROMETHEE) |
| Evaluating Efficiency and Effectiveness of Logistics Infrastructure Based on PCA-DEA Approach in China [31]. | 2009 | Context: Logistics Infrastructure; Criteria: 6 inputs (number of staff and employed workers in transport, possession of civil motor vehicles, possession of watercraft, railway density, waterway density, highway density) and 2 outputs (freight traffic, and turnover volume of freight traffic); Alternatives: logistics infrastructure for 31 major regions (23 provinces, 4 municipalities, and 4 autonomous regions) in China | Principal Component Analysis (PCA) and DEA | Logistics infrastructure and location oriented, not performance oriented. Not clarified—how the effectiveness has been measured (as DEA is commonly, and scientifically, known to be employed to measure the efficiency (i.e., not effectiveness) |
| Facility Location Selection using PROMETHEE II Method [32]. | 2010 | Context: Facility Location Selection Problem; Criteria: (closeness of market, closeness to raw material, land transportation, air transportation, cost of labor, availability of labor, community education, and business climate); Alternatives: 3 locations | PROMETHEE | The criteria are suitable for a selection model, not for performance evaluation. Based on a single technique (PROMETHEE) Efficiency not considered |
| Fuzzy AHP-PROMETHEE methodology to select bus garage location: a case study for a firm in the urban passenger transport sector in Istanbul [33]. | 2011 | Context: Garage Location Selection Problem (busses); 6 main Criteria: (cost, infrastructure, accessibility, social and economic structure, macro factors, and environmental factors); Alternatives: 3 garage locations | Fuzzy AHP and PROMETHEE | Irrelevant context Selection focused (i.e., not evaluation) Efficiency not considered |
| Use of Promethee method to determine the best alternative for warehouse storage location assignment [34]. | 2014 | Context: warehouse storage location assignment; Criteria: space, picking (the total distance travelled when the pick is issued from a single command), total cost of picking a single command, time to products (the round trip), the average time it takes to serve a client, and the average time it takes to serve a group; Alternatives: Warehouses | PROMETHEE | Warehouse functions focus on storing, which is limited compared to the distribution centers functions Location oriented, not performance oriented Use of PROMETHEE alone |
| A framework for measuring transport efficiency in distribution centers [35]. | 2016 | Context: transport efficiency in distribution centers; Criteria: 3 inputs (number of vehicles, fuel costs and total vehicle time in operation) and 3 outputs (total distance driven, tons shipped, and vehicle utilization); Alternatives: Distribution Centers | DEA | Concentration on transportation (i.e., other productivity aspects were not considered due to the scope of the study) Use of DEA alone (i.e., efficiency focused model) |
| Visual management of performance with PROMETHEE productivity analysis [36]. | 2018 | Context: Facility Productivity of British Universities; Criteria: 2 inputs (Staff and Facilities spent) and 7 outputs (student satisfaction, research quality, admissions service, graduate prospects, graduates’ achievement, completion rate, and the total number of students); Alternatives: The British Universities | PROMETHEE Productivity Analysis (PPA) | Irrelevant application to the “distribution centers”. Although a graphical representation was provided in order to “distinguish between efficient, effective, frugal and ineffective actions” in the proposed approach [36], it focused mainly on the efficiency (outputs/inputs) rather than the effectiveness (i.e., not well linked with the simple definition of productivity that considers both efficiency and effectiveness). |
| Measuring performance of government-supported drug warehouses using DEA to improve quality of drug distribution [37]. | 2020 | Context: Drug warehouses; Criteria: 4 inputs (warehouse storage capacity, temperature-controlled storage capacity, number of skilled employees and operational cost) and 6 outputs (fill rate, number of generic drugs, volume of drugs, consumption points, inventory turns ratio and time efficiency); Alternatives: Warehouses. | DEA | Warehousing orientation (for drugs), which is relatively different from the distributing orientation (automotive spare parts industry) Focusing on efficiency only via the utilization of DEA alone |
| A novel hybrid fuzzy PROMETHEE-IDEA approach to efficiency evaluation [38]. | 2021 | Context: Facility EU national steel sectors; Criteria: 3 inputs (number of employees, cost of labor, electricity consumption) and 3 outputs (production value, cost of emissions trading, and net export of the final products); Alternatives: 6 selected sectors (6 EU Countries) | DEA and PROMETHEE | The application was built based on an example that considers 6 different EU steel sectors, which is relatively irrelevant application. Although both DEA & PROMETHEE were employed, the focus was on efficiency (the consideration of outputs/inputs), not on the effectiveness (the achievement with respect to each criterion) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alidrisi, H. DEA-Based PROMETHEE II Distribution-Center Productivity Model: Evaluation and Location Strategies Formulation. Appl. Sci. 2021, 11, 9567. https://doi.org/10.3390/app11209567
Alidrisi H. DEA-Based PROMETHEE II Distribution-Center Productivity Model: Evaluation and Location Strategies Formulation. Applied Sciences. 2021; 11(20):9567. https://doi.org/10.3390/app11209567
Chicago/Turabian StyleAlidrisi, Hisham. 2021. "DEA-Based PROMETHEE II Distribution-Center Productivity Model: Evaluation and Location Strategies Formulation" Applied Sciences 11, no. 20: 9567. https://doi.org/10.3390/app11209567
APA StyleAlidrisi, H. (2021). DEA-Based PROMETHEE II Distribution-Center Productivity Model: Evaluation and Location Strategies Formulation. Applied Sciences, 11(20), 9567. https://doi.org/10.3390/app11209567






