A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors
Abstract
:1. Introduction
2. Materials and Methods
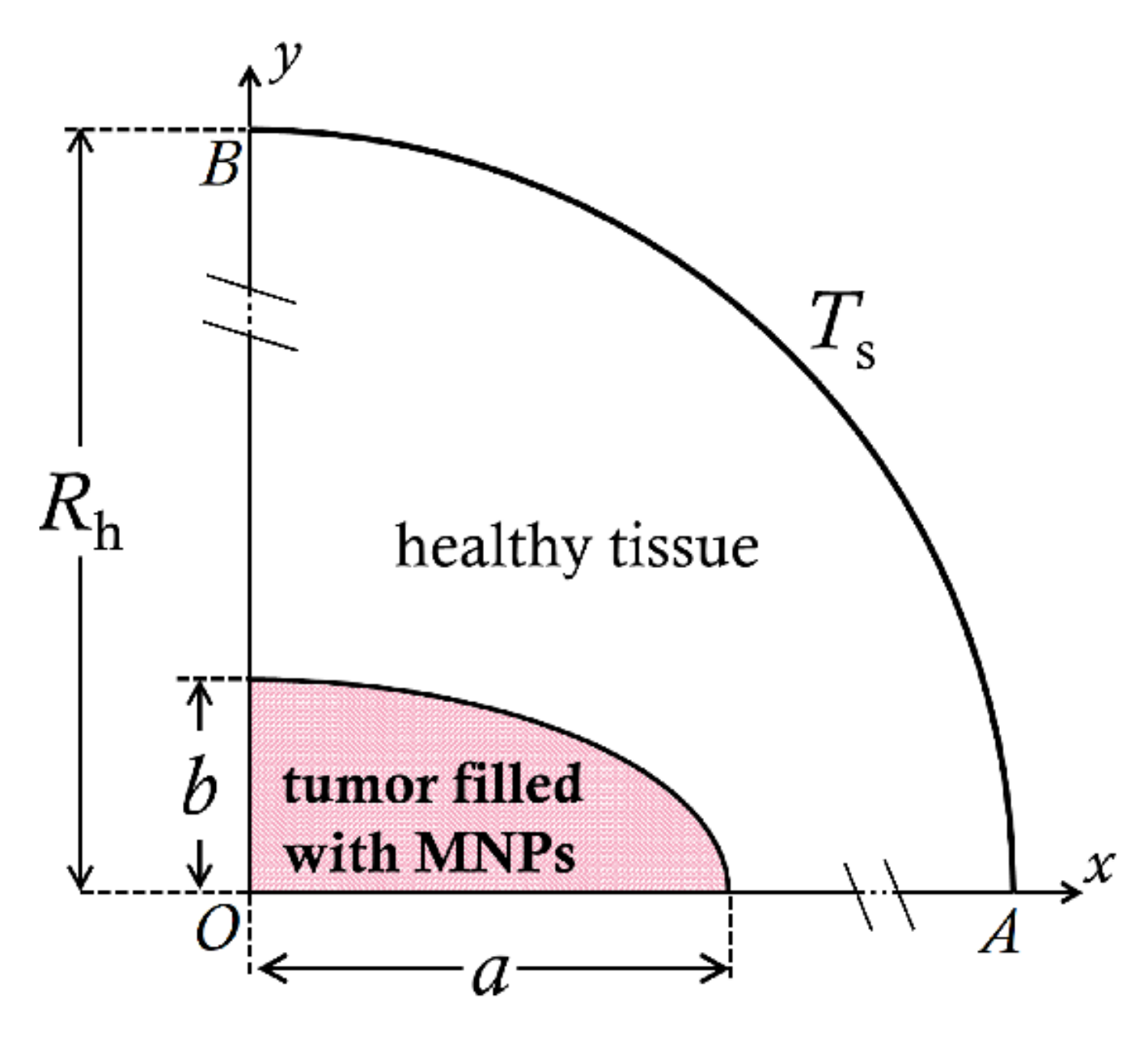
2.1. Geometrical Description
- (i)
- oblate spheroids with semi-axis a > b
- (ii)
- prolate spheroids with semi-axis a < b
2.2. Bio-Heat Transfer Analysis
2.3. Heat Generation by the Magnetic Nanoparticles
2.4. Tissue Thermal Damage
2.5. Mesh and Timestep Sensitivity Analysis
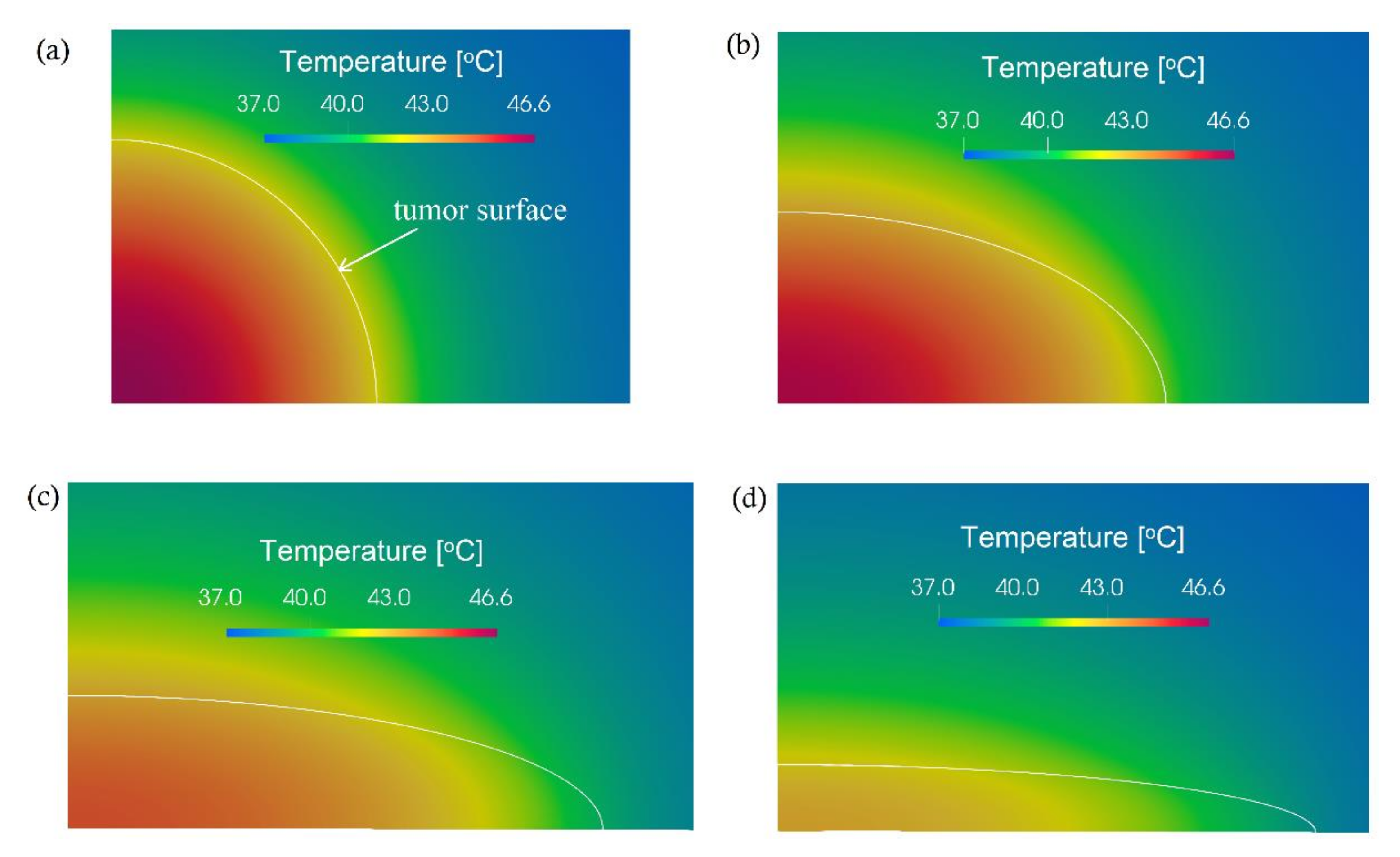
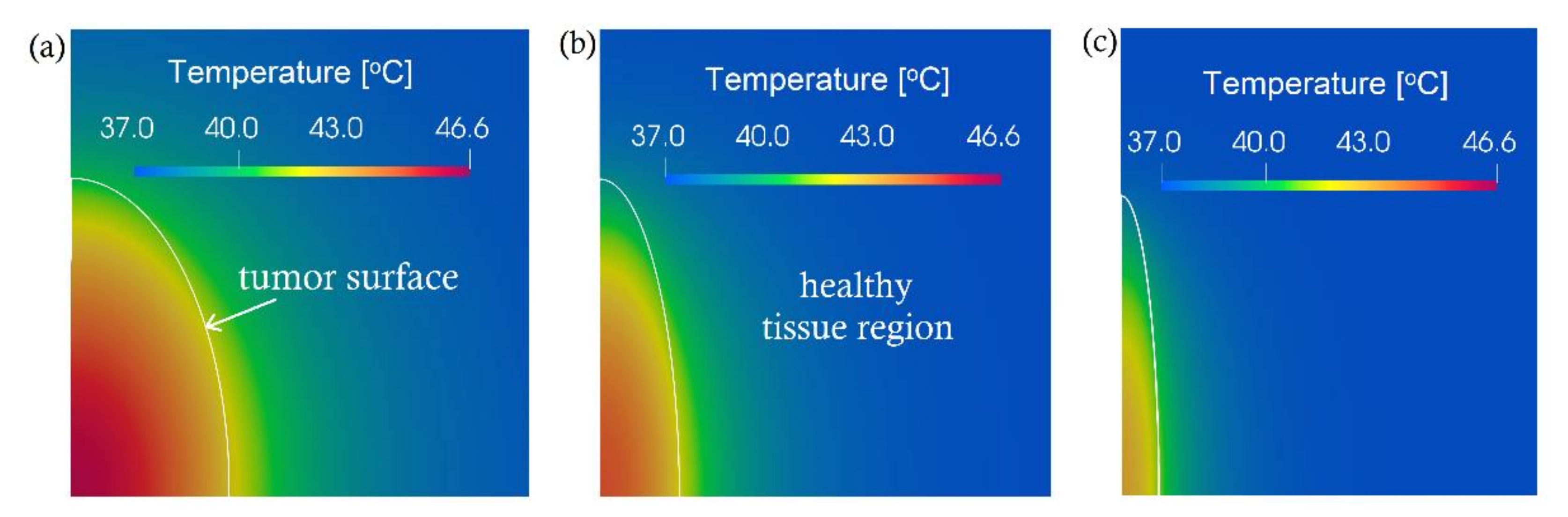
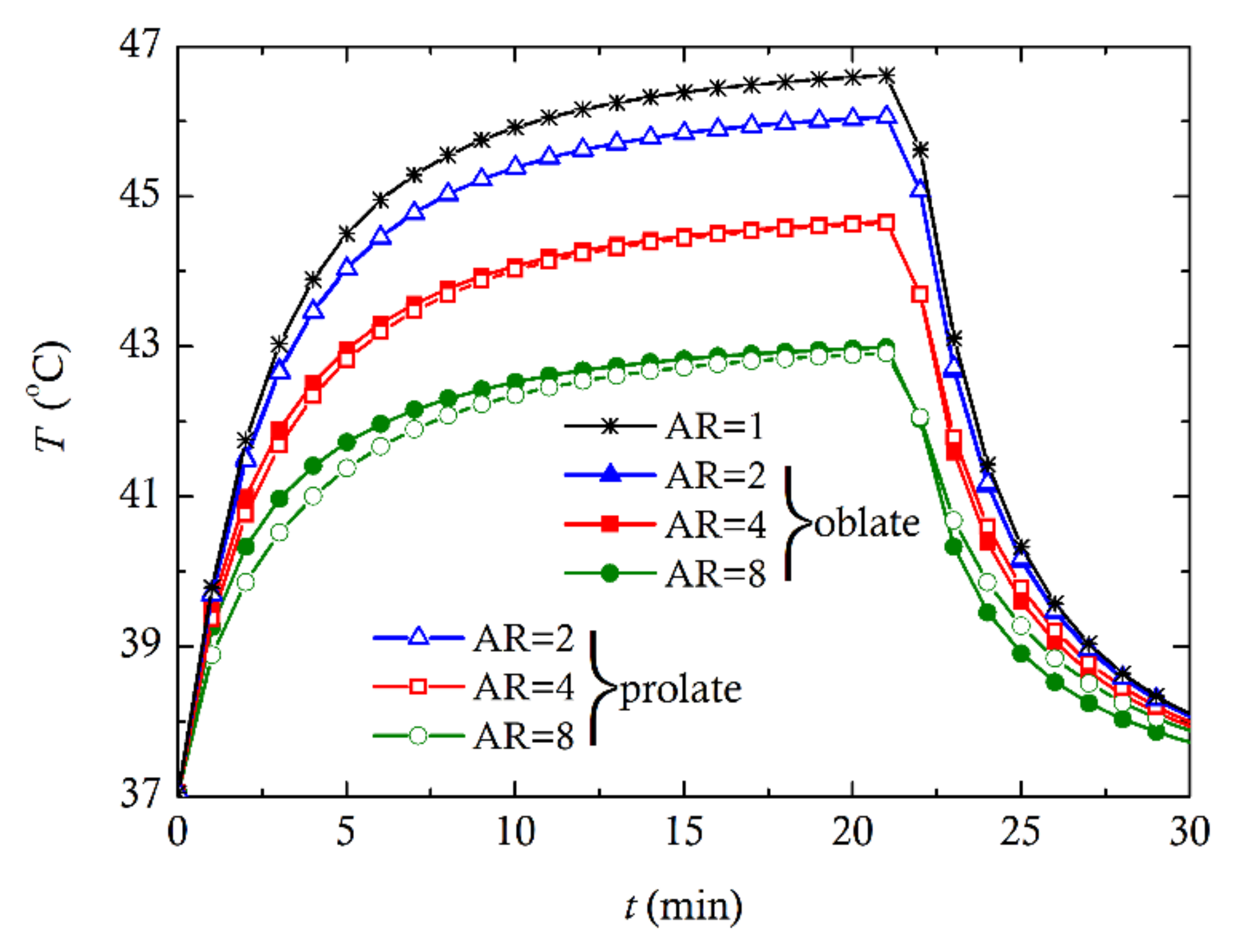
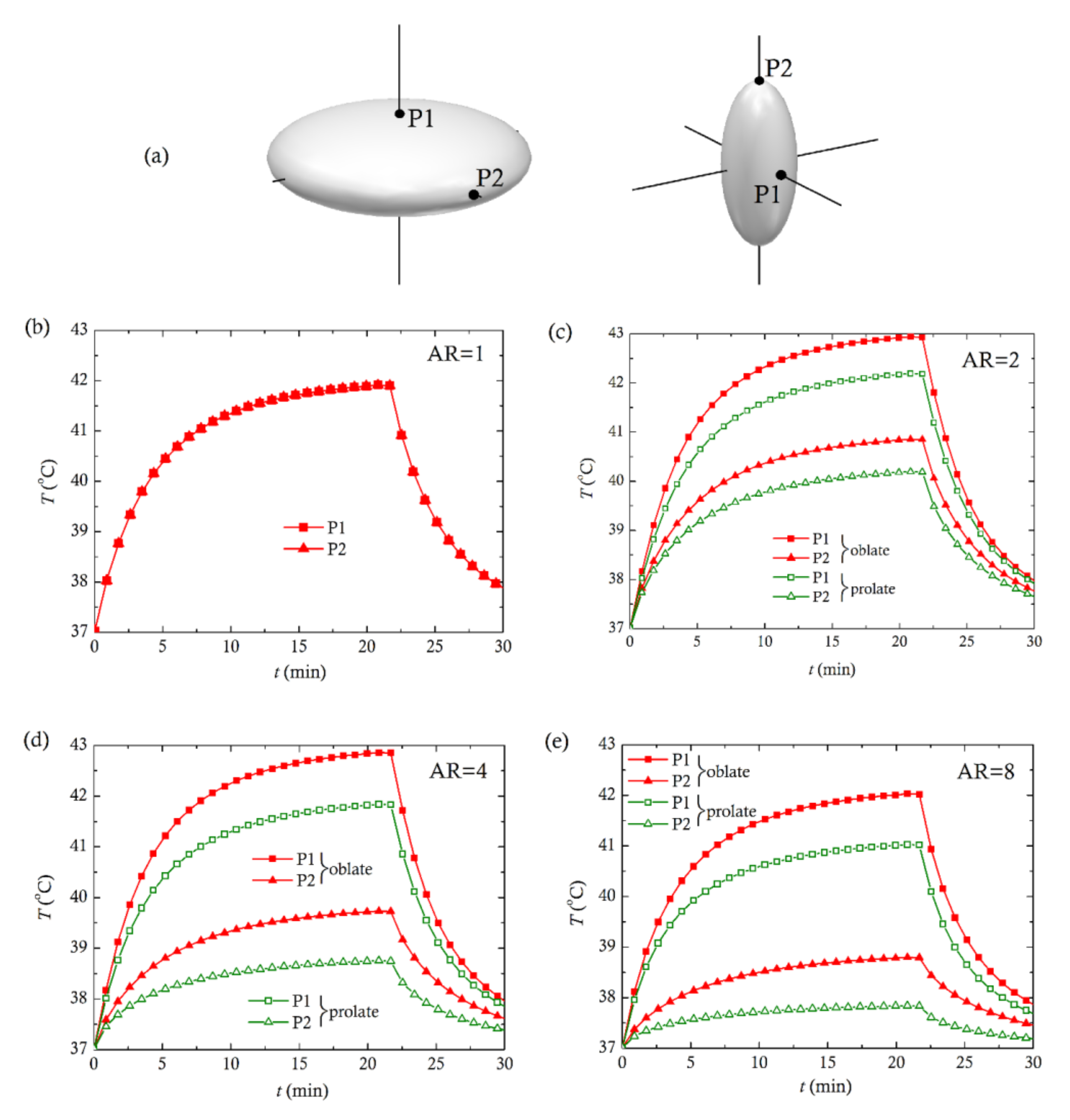
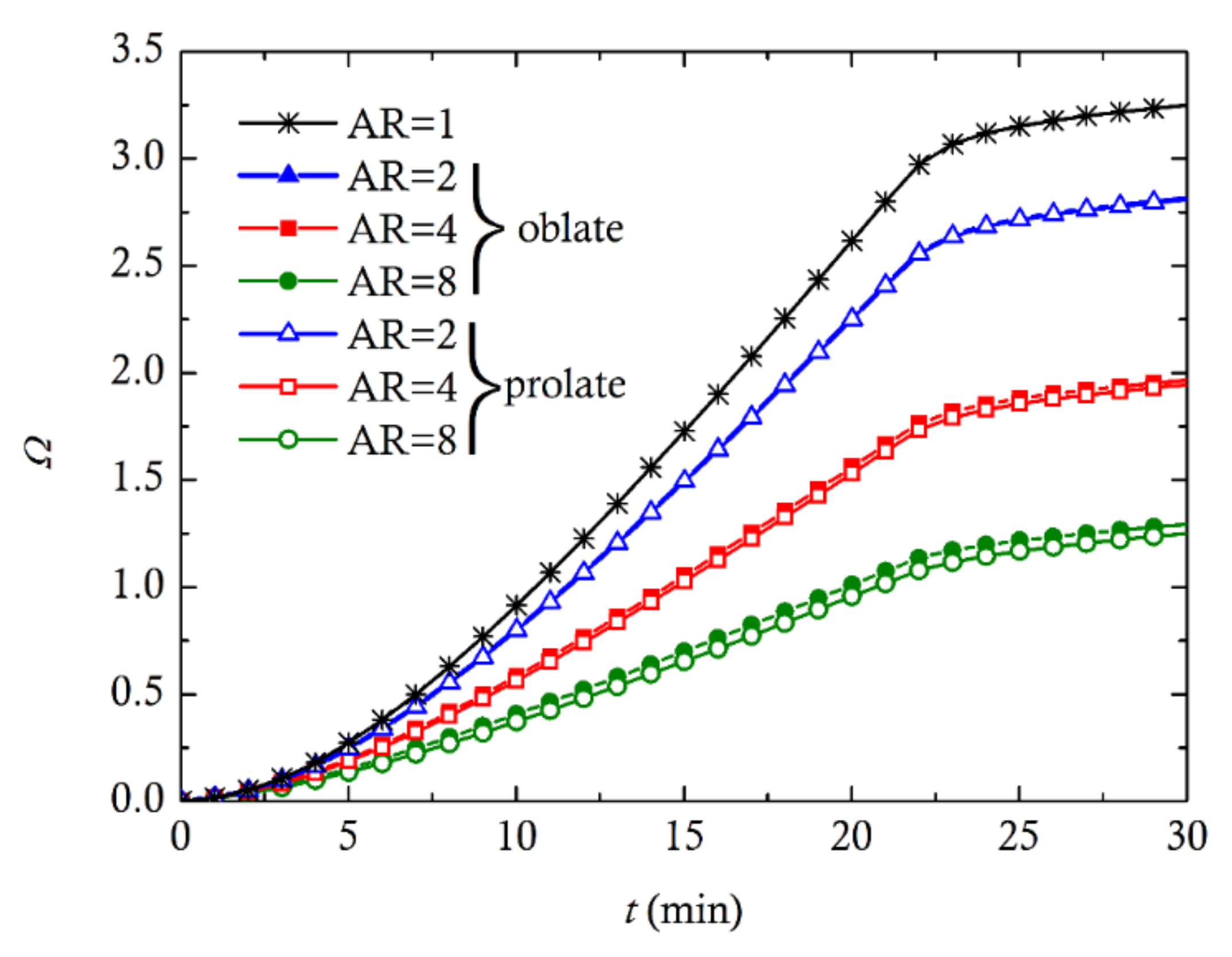
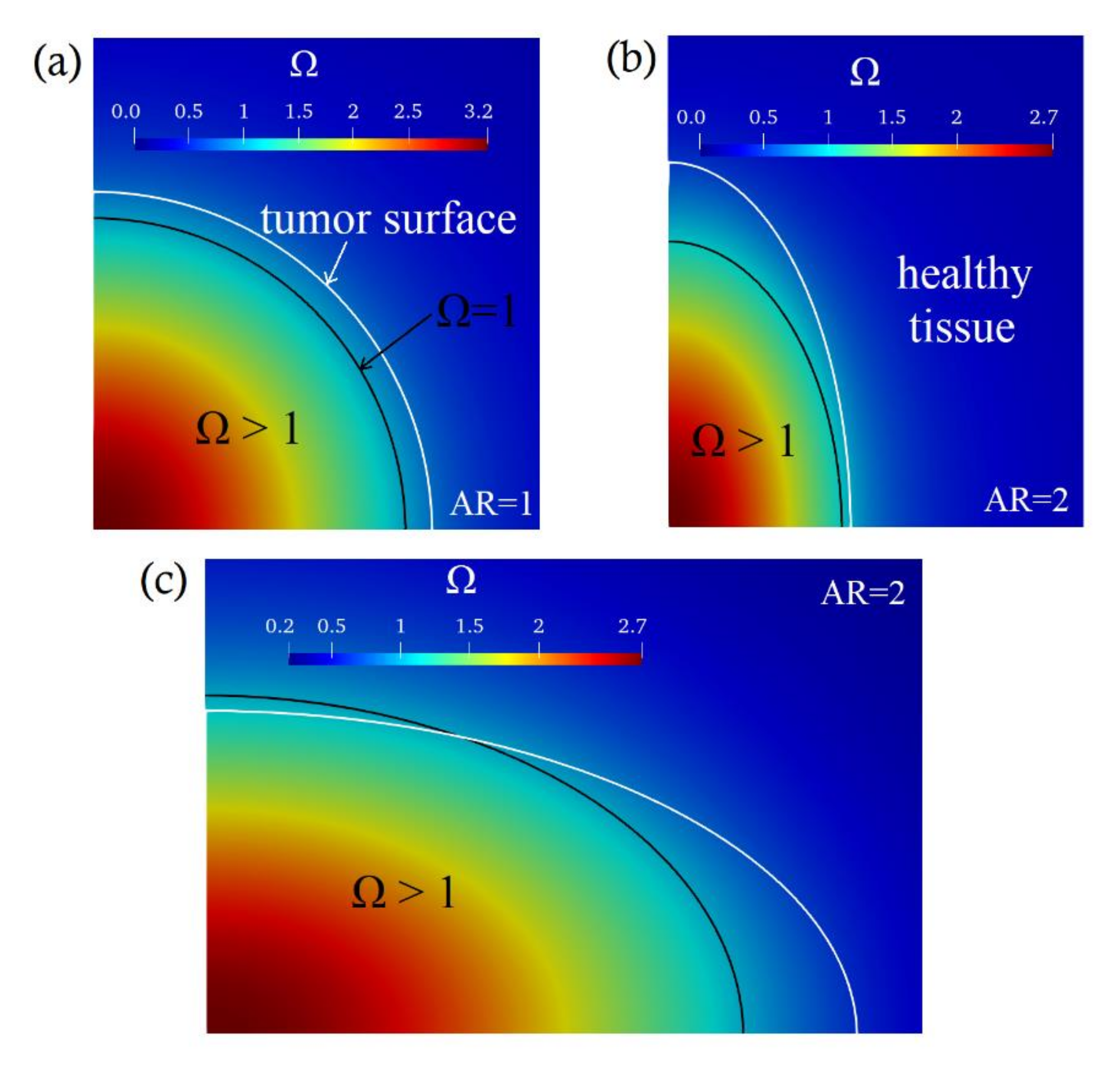
3. Computational Results and Discussion
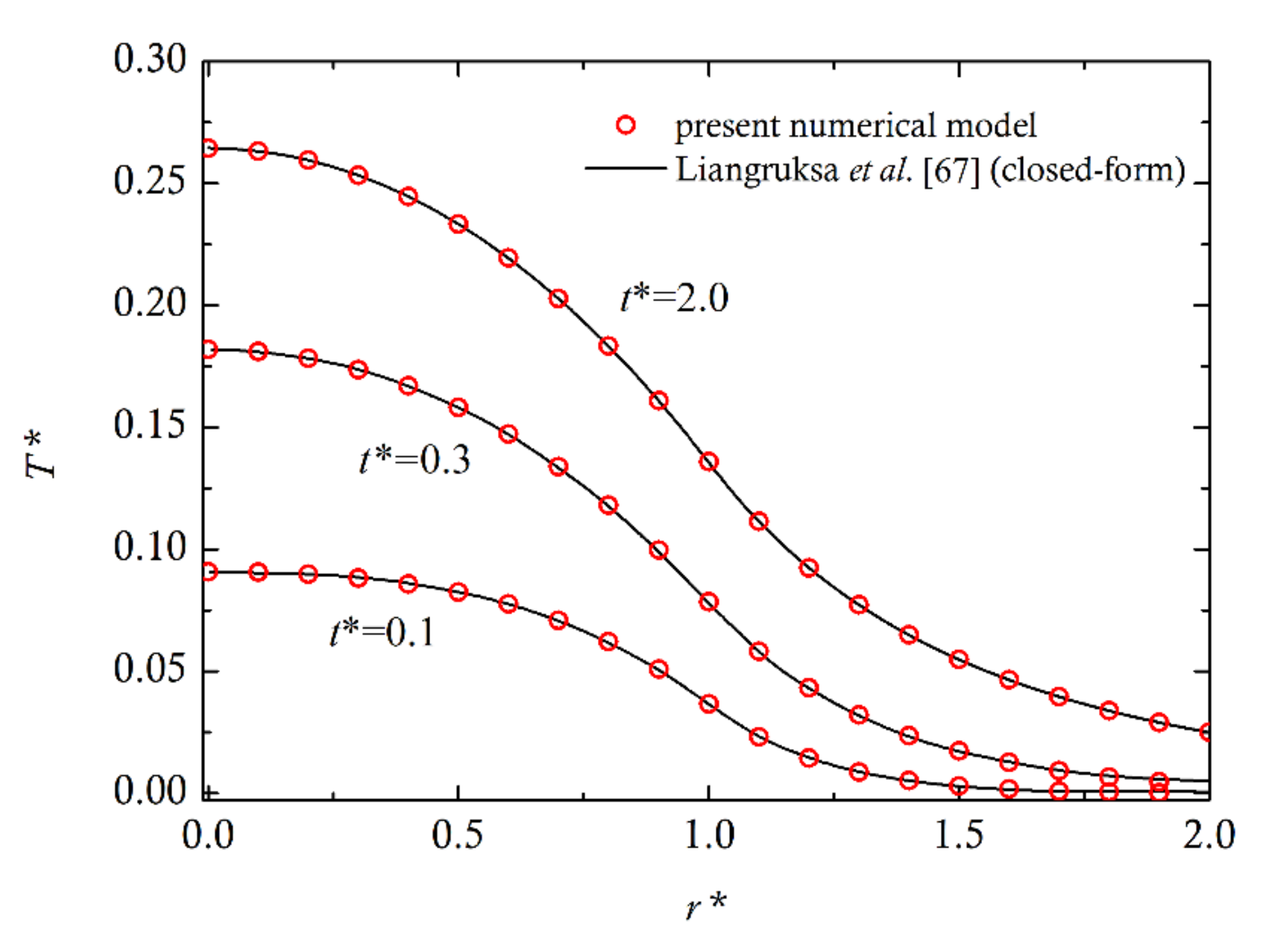
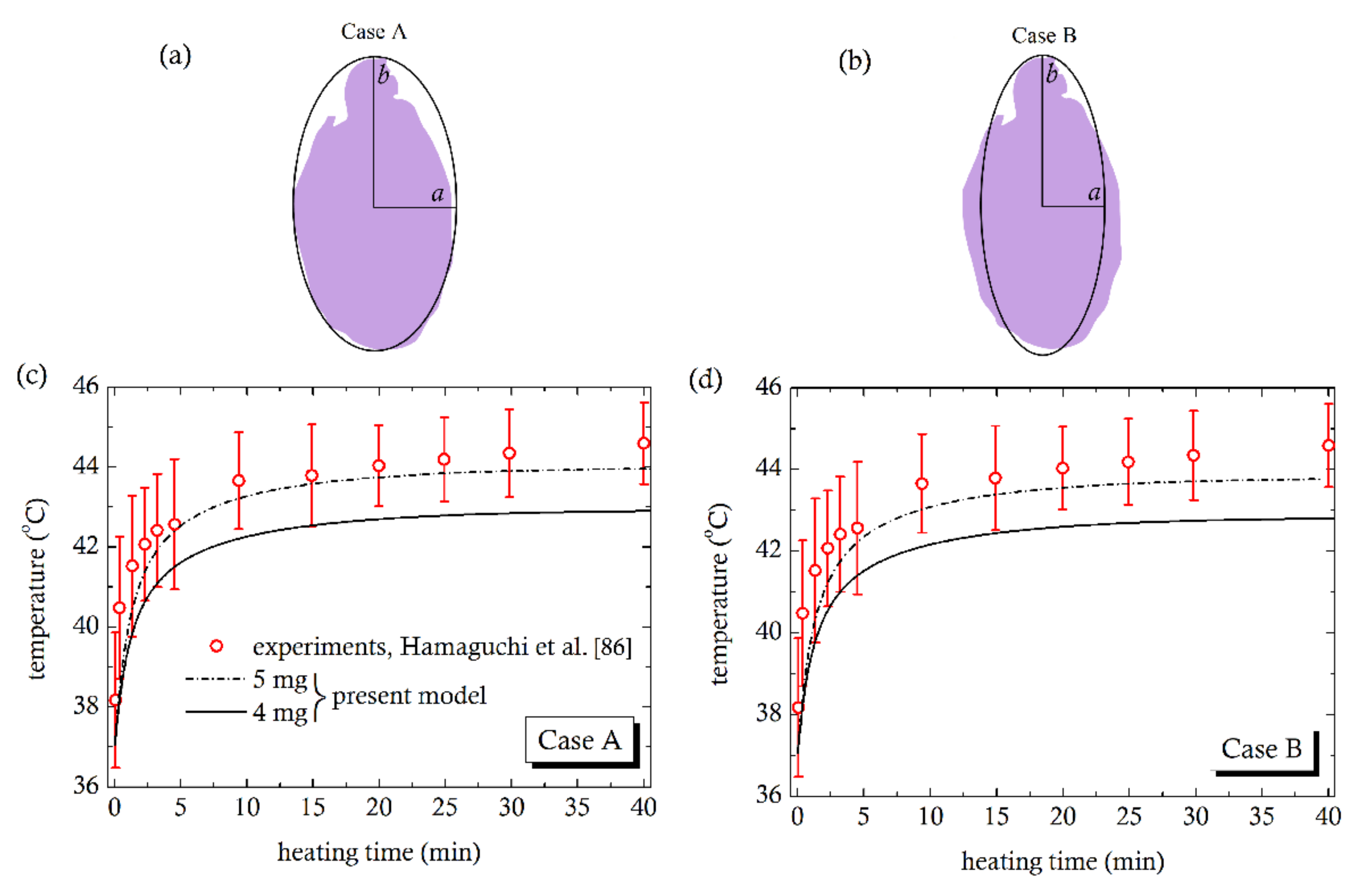
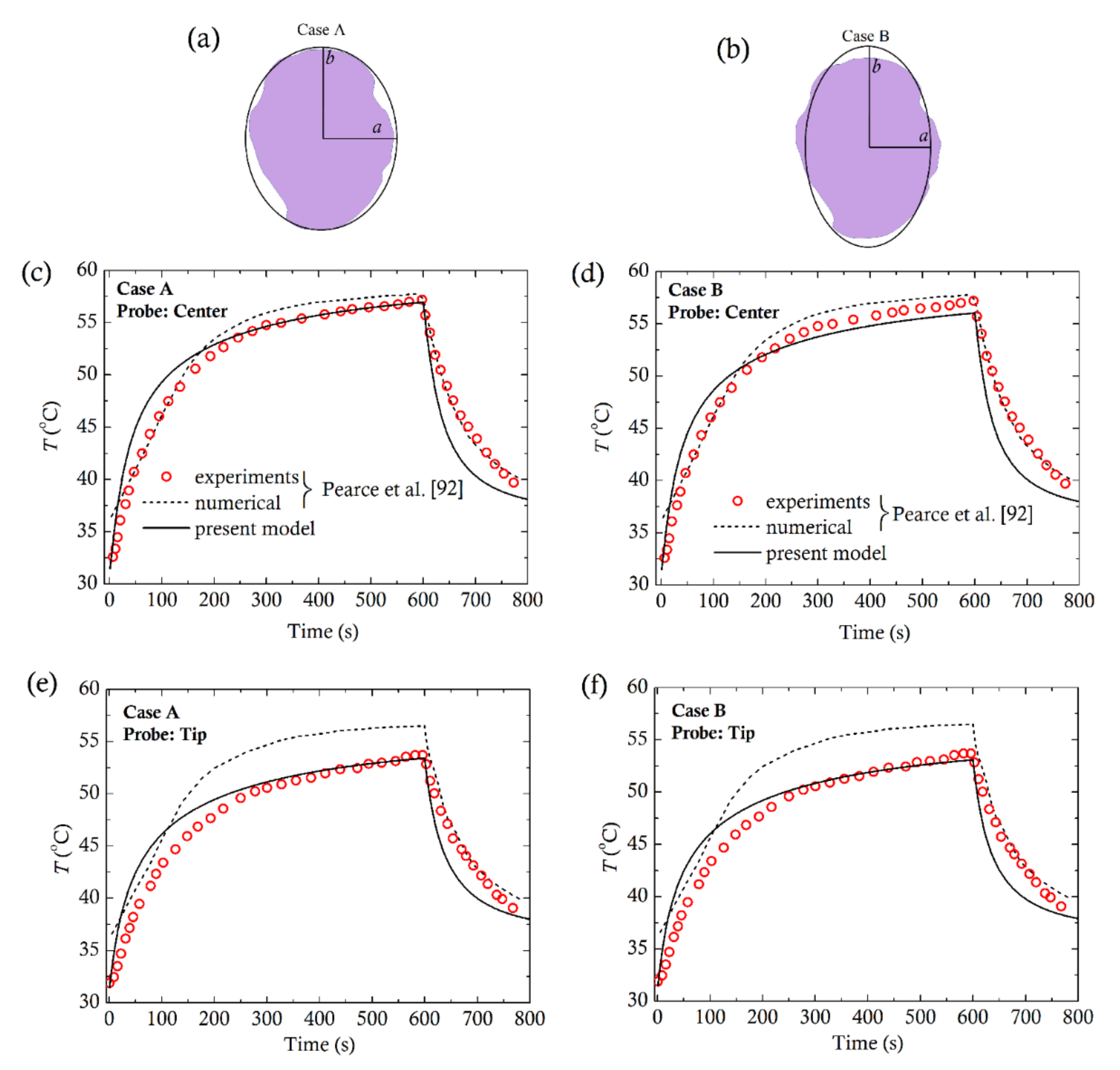
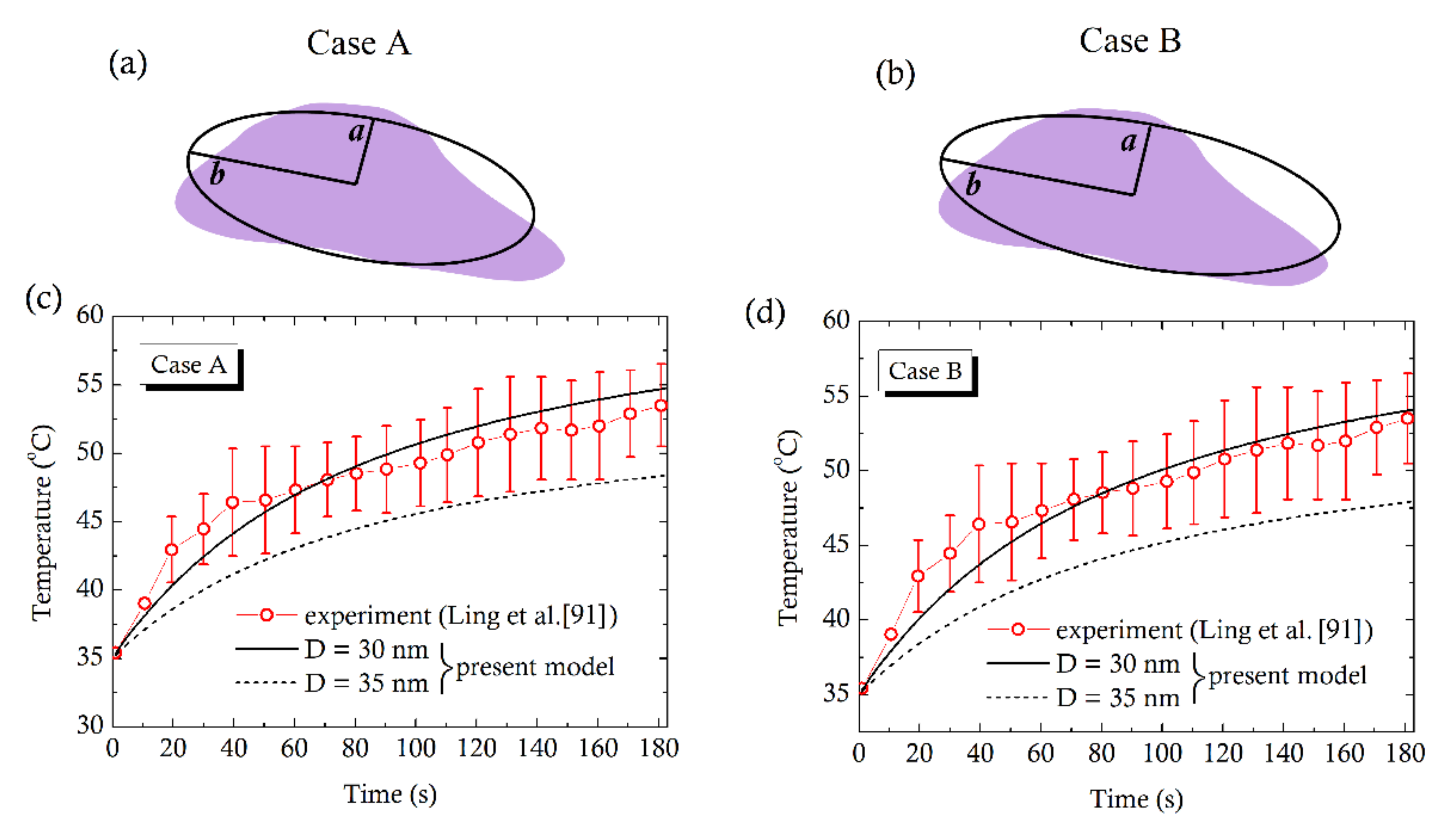
4. Comparison with Experiments
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Piroth, M.D.; Gagel, B.; Pinkawa, M.; Stanzel, L.; Asadpour, B.; Eble, M.J. Postoperative radiotherapy of glioblastoma multiforme: Analysis and critical assessment of different treatment strategies and predictive factors. Strahlenther. Onkol. 2007, 183, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Stupp, R.; Mason, W.P.; van den Bent, M.J.; Weller, M.; Fisher, B.; Taphoorn, M.J.B.; Belanger, K.; Brandes, A.A.; Marosi, C.; Bogdahn, U.; et al. Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. N. Engl. J. Med. 2005, 352, 987–996. [Google Scholar] [CrossRef]
- Verma, J.; Lal, S.; Van Noorden, C.J.F. Nanoparticles for hyperthermic therapy: Synthesis strategies and applications in glioblastoma. Int. J. Nanomed. 2014, 9, 2863–2877. [Google Scholar] [CrossRef] [Green Version]
- González-Suárez, A.; Berjano, E. Comparative analysis of different methods of modeling the thermal effect of circulating blood flow during RF cardiac ablation. IEEE Trans. Biomed. Eng. 2016, 63, 250–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iasiello, M.; Andreozzi, A.; Bianco, N.; Vafai, K. The Porous Media Theory Applied to Radiofrequency Catheter Ablation. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 2669–2681. [Google Scholar] [CrossRef]
- Chung, S.; Vafai, K. Mechanobiology of low-density lipoprotein transport within an arterial wall–impact of hyperthermia and coupling effects. J. Biomech. 2014, 47, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Hypo- and Hyperthermia effects on LDL deposition in a curved artery. Comput. Therm. Sci. 2019, 11, 95–103. [Google Scholar] [CrossRef]
- You, J.O.; Guo, P.; Auguste, D.T. A drug-delivery vehicle combining the targeting and thermal ablation of HER2+ breast-cancer cells with triggered drug release. Angew. Chem. Int. Ed. 2013, 52, 4141–4146. [Google Scholar] [CrossRef] [Green Version]
- Andreozzi, A.; Iasiello, M.; Netti, P.A. Effects of pulsating heat source on interstitial fluid transport in tumour tissues. J. R. Soc. Interface 2020, 17, 20200612. [Google Scholar] [CrossRef]
- Faridi, P.; Keselman, P.; Fallahi, H.; Prakash, P. Experimental assessment of microwave ablation computational modeling with MR thermometry. Med. Phys. 2020, 47, 3777–3788. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Abbosh, A.M.; Crozier, S. 3D-focused microwave hyperthermia for breast cancer treatment with experimental validation. IEEE Trans. Antennas Propag. 2017, 65, 3489–3500. [Google Scholar] [CrossRef]
- Gas, P.; Miaskowski, A.; Subramanian, M. In silico Study on Tumor-sized-dependent Thermal Profiles inside Anthropomorphic Female Breast Phantom Subjected to Multi-dipole Antenna Array. Int. J. Mol. Sci. 2020, 21, 8597. [Google Scholar] [CrossRef]
- Laurent, S.; Dutz, S.; Häfeli, U.O.; Mahmoudi, M. Magnetic fluid hyperthermia: Focus on superparamagnetic iron oxide nanoparticles. Adv. Colloid Interface Sci. 2011, 166, 8–23. [Google Scholar] [CrossRef]
- Kumar, C.S.S.R.; Mohammad, F. Magnetic nanomaterials for hyperthermia-based therapy and controlled drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 789–808. [Google Scholar] [CrossRef] [Green Version]
- Raouf, I.; Gas, P.; Kim, H.S. Numerical Investigation of Ferrofluid Preparation during In-vitro Culture of Cancer Therapy for Magnetic Nanoparticle Hyperthermia. Sensors 2021, 21, 5545. [Google Scholar] [CrossRef] [PubMed]
- Cascinu, S.; Catalano, V.; Baldelli, A.M.; Scartozzi, M.; Battelli, N.; Graziano, F.; Cellerino, R. Locoregional treatments of unresectable liver metastases from colorectal cancer. Cancer Treat. Rev. 1998, 24, 3–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Calderwood, S.K. Autophagy, protein aggregation and hyperthermia: A mini-review. Int. J. Hyperther. 2011, 27, 409–414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khandhar, A.P.; Ferguson, R.M.; Simon, J.A.; Krishnan, K.M. Enhancing cancer therapeutics using size-optimized magnetic fluidhyperthermia. J. Appl. Phys. 2012, 111, 7B306. [Google Scholar] [CrossRef] [Green Version]
- Chicheł, A.; Skowronek, J.; Kubaszewska, M.; Kanilowski, M. Hyperthermia—Description of a method and a review of clinical applications. Rep. Pract. Oncol. Radiother. 2007, 12, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Kho, A.S.K.; Foo, J.J.; Ooi, E.T.; Ooi, E.H. Shape-shifting thermal coagulation zone during saline-infused radiofrequency ablation: A computational study on the effects of different infusion location. Comput. Methods Progr. Biomed. 2020, 184, 105289. [Google Scholar] [CrossRef]
- Gas, P.; Wyszkowska, J. Influence of multi-tine electrode configuration in realistic hepatic RF ablative heating. Arch. Electr. Eng. 2019, 68, 521–533. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Sabo, M.; Prnova, M.; Šoltes, L.; Radjenović, B. Finite element analysis of the microwave ablation method for enhanced lung cancer treatment. Cancers 2021, 13, 3500. [Google Scholar] [CrossRef] [PubMed]
- Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water 2019, 11, 1135. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Villarejo, R.; Estellé, P.; Navas, J. Boron nitride nanotubes-based nanofluids with enhanced thermal properties for use as heat transfer fluids in solar thermal applications. Sol. Energy Mater. Sol. Cells 2020, 205, 110266. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Salloum, M.; Ma, R.; Zhu, R. An in-vivo experimental study of temperature elevations in animal tissue during magnetic nanoparticle hyperthermia. Int. J. Hyperther. 2008, 24, 589–601. [Google Scholar] [CrossRef]
- Gilchrist, R.K.; Medal, R.; Shorey, W.D.; Hanselman, R.C.; Parrott, J.C.; Taylor, C.B. Selective inductive heating of lymph nodes. Ann. Surg. 1957, 146, 596–606. [Google Scholar] [CrossRef] [PubMed]
- Jordan, A.; Scholz, R.; Wust, P.; Fähling, H.; Felix, R. Magnetic fluid hyperthermia (MFH): Cancer treatment with AC magnetic field induced excitation of biocompatible superparamagnetic nanoparticles. J. Magn. Magn. Mater. 1999, 201, 413–419. [Google Scholar] [CrossRef]
- Dutz, S.; Hergt, R. Magnetic nanoparticle heating and transfer on a microscale: Basic principles, realities and physical limitations of hyperthermia for tumour therapy. Int. J. Hyperther. 2013, 29, 790–800. [Google Scholar] [CrossRef]
- Ferrero, R.; Barrera, G.; Celegato, F.; Vicentini, M.; Sözeri, H.; Yildiz, N.; Dinҫer, C.A.; Coïsson, M.; Manzin, A.; Tiberto, P. Experimental and Modelling Analysis of the Hyperthermia Properties of Iron Oxide Nanocubes. Nanomaterials 2021, 11, 2179. [Google Scholar] [CrossRef] [PubMed]
- Karvelas, E.G.; Lampropoulos, N.K.; Sarris, I.E. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM. Comput. Methods Progr. Biomed. 2017, 142, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Karvelas, E.G.; Lampropoulos, N.K.; Benos, L.T.; Karakasidis, T.; Sarris, I.E. On the magnetic aggregation of Fe3O4 nanoparticles. Comput. Methods Progr. Biomed. 2021, 198, 105778. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Bordelon, D.E.; Cornejo, C.; Grüttner, C.; Westphal, F.; DeWeese, T.; Ivkov, R. Magnetic nanoparticle heating efficiency reveals magneto-structural differences when characterized with wide ranging and high amplitude alternating magnetic fields. J. Appl. Phys. 2011, 109, 124904. [Google Scholar] [CrossRef]
- Espinosa, A.; Di Corato, R.; Kolosnjaj-Tabi, J.; Flaud, P.; Pellegrino, T.; Wilhelm, C. Duality of iron oxide nanoparticles in cancer therapy: Amplification of heating efficiency by magnetic hyperthermia and photothermal bimodal treatment. ACS Nano 2016, 10, 2436–2446. [Google Scholar] [CrossRef] [PubMed]
- Kappiyoor, R.; Liangruksa, M.; Ganguly, R.; Puri, I.K. The effects of magnetic nanoparticle properties on magnetic fluid hyperthermia. J. Appl. Phys. 2010, 108, 94702. [Google Scholar] [CrossRef]
- Nemec, S.; Kralj, S.; Wilhelm, C.; Abou-Hassan, A.; Rols, M.P.; Kolosnjaj-Tabi, J. Comparison of Iron Oxide Nanoparticles in Photothermia and Magnetic Hyperthermia: Effects of Clustering and Silica Encapsulation on Nanoparticles’ Heating Yield. Appl. Sci. 2020, 10, 7322. [Google Scholar] [CrossRef]
- Moroz, P.; Jones, S.K.; Gray, B.N. Magnetically mediated hyperthermia: Current status and future directions. Int. J. Hyperther. 2002, 18, 267–284. [Google Scholar] [CrossRef]
- Hedayatnasab, Z.; Abnisa, F.; Daud, W.M.W.A. Review on magnetic nanoparticles for magnetic nanofluid hyperthermia application. Mater. Design 2017, 123, 174–196. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, D.; Huang, J.; Zhang, J.; Xiao, W.; Yu, H.; Zhang, L.; Ye, J. The anti-hepatoma effect of nanosized Mn-Zn ferrite magnetic fluid hyperthermia associated with radiation in vitro and in vivo. Nanotechnology 2013, 24, 255101. [Google Scholar] [CrossRef] [PubMed]
- Benos, L.; Spyrou, L.A.; Sarris, I.E. Development of a new theoretical model for blood-CNTs effective thermal conductivity pertaining to hyperthermia therapy of glioblastoma multiform. Comput. Methods Programs Biomed. 2019, 172, 79–85. [Google Scholar] [CrossRef]
- Attaluri, A.; Kandala, S.K.; Wabler, M.; Zhou, H.; Cornejo, C.; Armour, M.; Hedayati, M.; Zhang, Y.; DeWeese, T.L.; Herman, C.; et al. Magnetic nanoparticle hyperthermia enhances radiation therapy: A study in mouse models of human prostate cancer. Int. J. Hyperther. 2015, 31, 359–374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Attaluri, A.; Ma, R.; Qiu, Y.; Li, W.; Zhu, L. Nanoparticle distribution and temperature elevations in prostatic tumors in mice during magnetic nanoparticle hyperthermia. Int. J. Hyperther. 2011, 27, 491–502. [Google Scholar] [CrossRef]
- Shojaee, P.; Niroomand-Oscuii, H.; Sefidgar, M.; Alinezhad, L. Effect of nanoparticle size, magnetic intensity, and tumor distance on the distribution of the magnetic nanoparticles in a heterogeneous tumor microenvironment. J. Magn. Magn. Mater. 2020, 498, 166089. [Google Scholar] [CrossRef]
- Soetaert, F.; Korangath, P.; Serantes, D.; Fiering, S.; Ivkov, R. Cancer therapy with iron oxide nanoparticles: Agents of thermal and immune therapies. Adv. Drug Deliv. Rev. 2020, 163, 65–83. [Google Scholar] [CrossRef]
- Salloum, M.; Ma, R.H.; Weeks, D.; Zhu, L. Controlling nanoparticle delivery in magnetic nanoparticle hyperthermia for cancer treatment: Experimental study in agarose gel. Int. J. Hyperther. 2008, 24, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.F.; Capistrano, G.; Bakuzis, A.F. In vivo magnetic nanoparticle hyperthermia: A review on preclinical studies, low-field nano-heaters, noninvasive thermometry and computer simulations for temperature planning. Int. J. Hyperther. 2020, 37, 76–99. [Google Scholar] [CrossRef]
- Capistrano, G.; Rodrigues, H.F.; Zufelato, N.; Gonçalves, C.; Cardoso, C.G.; Silveira-Lacerda, E.P.; Bakuzis, A.F. Noninvasive intratumoral thermal dose determination during in vivo magnetic nanoparticle hyperthermia: Combining surface temperature measurements and computer simulations. Int. J. Hyperther. 2020, 37, 120–140. [Google Scholar] [CrossRef]
- Miaskowski, A.; Sawicki, B. Magnetic fluid hyperthermia modeling based on phantom measurements and realistic breast model. IEEE. Trans. Biomed. Eng. 2013, 60, 1806–1813. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Keangin, P.; Rattanadecho, P. Analysis of heat transport on local thermal non-equilibrium in porous liver during microwave ablation. Int. J. Heat Mass Transf. 2013, 67, 46–60. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef]
- Pearce, J.A. Models for thermal damage in tissues: Processes and applications. Crit. Rev. Biomed. Eng. 2010, 38, 1–20. [Google Scholar] [CrossRef]
- Pearce, J.A. Comparative analysis of mathematical models of cell death and thermal damage processes. Int. J. Hyperther. 2013, 29, 262–280. [Google Scholar] [CrossRef]
- Selmi, M.; Bin Dukhyil, A.A.; Belmabrouk, H. Numerical Analysis of Human Cancer Therapy Using Microwave Ablation. Appl. Sci. 2020, 10, 211. [Google Scholar] [CrossRef] [Green Version]
- Tan, Q.; Zou, X.; Ding, X.; Zhao, X.; Qian, S. The Influence of Dynamic Tissue Properties on HIFU Hyperthermia: A Numerical Simulation Study. Appl. Sci. 2018, 8, 1933. [Google Scholar] [CrossRef] [Green Version]
- Pearce, J.A. Improving accuracy in Arrhenius models of cell death: Adding a temperature dependent time delay. J. Biomech. Eng. 2015, 137, 121006. [Google Scholar] [CrossRef] [PubMed]
- Lim, D.; Namgung, B.; Woo, D.G.; Choi, J.S.; Kim, H.S.; Tack, G.R. Effect of Input Waveform Pattern and Large Blood Vessel Existence on Destruction of Liver Tumor Using Radiofrequency Ablation: Finite Element Analysis. J. Biomech. Eng. 2010, 132, 61003. [Google Scholar] [CrossRef]
- Chen, C.; Yu, M.-A.; Qiu, L.; Chen, H.-Y.; Zhao, Z.-L.; Wu, J.; Peng, L.-L.; Wang, Z.-L.; Xiao, R.-X. Theoretical Evaluation of Microwave Ablation Applied on Muscle, Fat and Bone: A Numerical Study. Appl. Sci. 2021, 11, 8271. [Google Scholar] [CrossRef]
- O’Neill, D.P.; Peng, T.; Stiegler, P.; Mayrhauser, U.; Koestenbauer, S.; Tscheliessnigg, K.; Payne, S.J. A three-state mathematical model of hyperthermic cell death. Ann. Biomed. Eng. 2011, 39, 570–579. [Google Scholar] [CrossRef]
- Feng, Y.; Oden, J.T.; Rylander, M.N. A two-state cell damage model under hyperthermic conditions: Theory and in vivo experiments. J. Biomech. Eng. 2008, 130, 41016. [Google Scholar] [CrossRef]
- Andrä, W.; d’Ambly, C.G.; Hergt, R.; Higler, I.; Kaiser, W.A. Temperature distribution as a function of time around a small spherical heat source of local magnetic hyperthermia. J. Magn. Magn. Mater. 1999, 194, 197–203. [Google Scholar] [CrossRef]
- Bagaria, H.G.; Johnson, D.T. Transient solution to the bioheat equation and optimization for magnetic fluid hyperthermia treatment. Int. J. Hyperther. 2005, 21, 57–75. [Google Scholar] [CrossRef]
- Lin, C.-T.; Liu, K.-C. Estimation for the heating effect of magnetic nanoparticles in perfused tissues. Int. Commun. Heat Mass Transf. 2009, 36, 241–244. [Google Scholar] [CrossRef]
- Giordano, M.A.; Gutierrez, G.; Rinaldi, C. Fundamental solutions to the bioheat equation and their application to magnetic fluid hyperthermia. Int. J. Hyperther. 2010, 26, 475–484. [Google Scholar] [CrossRef] [PubMed]
- Purusotham, S.; Ramanujan, R.V. Modeling the performance of magnetic nanoparticles in multimodal cancer therapy. J. Appl. Phys. 2010, 107, 114701. [Google Scholar] [CrossRef]
- Liangruksa, M.; Ganguly, R.; Puri, I.K. Parametric investigation of heating due to magnetic fluid hyperthermia in a tumor with blood perfusion. J. Magn. Magn. Mater. 2011, 323, 708–716. [Google Scholar] [CrossRef]
- Attar, M.M.; Haghpanahi, M.; Amanpour, S.; Mohaqeq, M. Analysis of bioheat transfer equation for hyperthermia cancer treatment. J. Mech. Sci. Technol. 2014, 28, 763–771. [Google Scholar] [CrossRef]
- Atsarkin, V.A.; Levkin, L.V.; Posvyanskiy, V.S.; Melnikov, O.V.; Markelova, M.N.; Gorbenko, O.Y.; Kaul, A.R. Solution to the bioheat equation for hyperthermia with La1-xAgyMnO3-δ nanoparticles: The effect of temperature autostabilization. Int. J. Hyperther. 2009, 25, 240–247. [Google Scholar] [CrossRef]
- Lahonian, M.; Golneshan, A.A. Numerical study of temperature distribution in a spherical tissue in magnetic fluid hyperthermia using Lattice Boltzmann Method. IEEE Trans. Nanobiosci. 2011, 10, 262–268. [Google Scholar] [CrossRef]
- Golneshan, A.A.; Lahonian, M. The effect of magnetic nanoparticle dispersion on temperature distribution in a spherical tissue in magnetic fluid hyperthermia using the lattice Boltzmann Method. Int. J. Hyperther. 2011, 27, 266–274. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Cheng, J.; Liu, W.; Chen, X. Numerical analysis of electromagnetically induced heating and bioheat transfer for magnetic fluid hyperthermia. IEEE Trans. Magn. 2015, 51, 4600204. [Google Scholar] [CrossRef]
- Tang, Y.; Jin, T.; Flesch, R.C.C. Numerical temperature analysis of magnetic hyperthermia considering nanoparticle clustering and blood vessels. IEEE Trans. Magn. 2017, 53, 5400106. [Google Scholar] [CrossRef]
- Tang, Y.; Flesch, R.C.C.; Jin, T. Numerical investigation of temperature field in magnetic hyperthermia considering mass transfer and diffusion in interstitial tissue. J. Phys. D Appl. Phys. 2018, 51, 035401. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Hou, H.; Shao, J. Simulation analysis of coupled magnetic-temperature fields in magnetic fluid hyperthermia. AIP Adv. 2019, 9, 105317. [Google Scholar] [CrossRef]
- Tang, Y.; Flesch, R.C.C.; Jin, T. Numerical method to evaluate the survival rate of malignant cells considering the distribution of treatment temperature field for magnetic hyperthermia. J. Magn. Magn. Mater. 2019, 490, 165458. [Google Scholar] [CrossRef]
- Zomordikhani, Z.; Attar, M.; Jahangiri, A.; Barati, F. Analysis of nonlinear bioheat transfer equation in magnetic fluid hyperthermia. J. Mech. Sci. Technol. 2020, 34, 3911–3918. [Google Scholar] [CrossRef]
- Suleman, M.; Riaz, S. 3D in silico study of magnetic fluid hyperthermia of breast tumor using Fe3O4 magnetic nanoparticles. J. Therm. Biol. 2020, 91, 102635. [Google Scholar] [CrossRef]
- Tang, Y.; Jin, T.; Flesch, R.C.C.; Gao, Y.; He, M. Effect of nanofluid distribution on therapeutic effect considering transient bio-tissue temperature during magnetic hyperthemia. J. Magn. Magn. Mater. 2021, 517, 167391. [Google Scholar] [CrossRef]
- Mills, K.L.; Kemkemer, R.; Rudraraju, S.; Garikipati, K. Elastic free energy drives the shape of prevascular solid tumors. PLoS ONE 2014, 9, e103245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulwanto, J.; Gearhart, J.; Gong, X.; Herzog, N.; Getzin, M.; Skobe, M.; Mills, K.L. Growth of tumor emboli within a vessel model reveals dependence on the magnitude of mechanical constrain. Integr. Biol. 2021, 13, 1–16. [Google Scholar] [CrossRef]
- Byrd, B.K.; Krishnaswamy, V.; Gui, J.; Rooney, T.; Zuurbier, R.; Rosenkranz, K.; Paulsen, K.; Barth, R.J., Jr. The shape of breast cancer. Breast Cancer Res. Treat. 2020, 183, 403–410. [Google Scholar] [CrossRef] [PubMed]
- Tirumani, S.H.; Shinagare, A.B.; O’Neill, A.C.; Nishino, M.; Hosenthal, M.H.; Ramaiya, N.H. Accuracy and feasibility of estimated tumor volumetry in primary gastric gastrointestinal stromal tumours: Validation using semiautomated technique in 127 patients. Eur. Radiol. 2016, 26, 286–295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanghani, P.; Ang, B.T.; King, N.K.K.; Ren, H. Overall survival prediction in glioblastoma multiforme patients from volumetric, shape and texture features using machine learning. Surg. Oncol. 2018, 27, 709–714. [Google Scholar] [CrossRef] [PubMed]
- Ohno, T.; Wakabayashi, T.; Takemura, A.; Yoshida, J.; Ito, A.; Shinkai, M.; Honda, H.; Kobayashi, T. Effective solitary hyperthermia treatment of malignant glioma using stick type CMC-magnetite. In vivo study. J. Neurooncol. 2002, 56, 233–239. [Google Scholar] [CrossRef]
- Hamaguchi, S.; Tohnai, I.; Ito, A.; Mitsudo, K.; Shigetomi, T.; Ito, M.; Honda, H.; Kobayashi, T.; Ueda, M. Selective hyperthermia using magneto liposomes to target cervical lymph node metastasis in a rabbit tongue tumor model. Cancer Sci. 2003, 94, 834–839. [Google Scholar] [CrossRef]
- Jordan, A.; Scholz, R.; Maier-Hauff, K.; van Landeghem, F.K.H.; Waldoefner, N.; Teichgraeber, U.; Pinkernelle, J.; Bruhn, H.; Neumann, F.; Thiesen, B.; et al. The effect of thermotherapy using magnetic nanoparticles on rat malignant glioma. J. Neurooncol. 2006, 78, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Petryk, A.A.; Giustini, A.J.; Gottesman, R.E.; Trembly, B.S.; Hoopes, P.J. Comparison of magnetic nanoparticle and microwave hyperthermia cancer treatment methodology and treatment effect in a rodent breast cancer model. Int. J. Hyperther. 2013, 29, 819–827. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, H.F.; Mello, F.M.; Branquinho, L.C.; Zufelato, N.; Silveira-Lacerda, E.P.; Bakuzis, A.F. Real-time infrared thermography detection of magnetic nanoparticle hyperthermia in a murine model under a non-uniform field configuration. Int. J. Hyperther. 2013, 29, 752–767. [Google Scholar] [CrossRef]
- Alphandéry, E.; Idbaih, A.; Adam, C.; Delattre, J.-Y.; Schmitt, C.; Guyot, F.; Chebbi, I. Development of non-pyrogenic magnetosome minerals coated with poly-l-lysine leading to a full disappearance of intracranial U87-Luc glioblastoma in 100% of treated mice using magnetic hyperthermia. Biomaterials 2017, 141, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Ling, Y.; Tang, X.; Wang, F.; Zhou, X.; Wang, R.; Deng, L.; Shang, T.; Liang, B.; Li, P.; Ran, H.; et al. Highly efficient magnetic hyperthermia ablation of tumors using injectable polymethylmethacrylate-Fe3O4. RSC Adv. 2017, 7, 2913–2918. [Google Scholar] [CrossRef] [Green Version]
- Pearce, J.A.; Petryk, A.A.; Hoopes, P.J. Numerical model study of in vivo magnetic nanoparticle tumor heating. IEEE. Trans. Biomed. Eng. 2017, 64, 2813–2823. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.F.; Capistrano, G.; Mello, F.M.; Zufelato, N.; Silveira-Lacerda, E.; Bakuzis, A.F. Precise determination of the heat delivery during in vivo magnetic nanoparticle hyperthermia with infrared thermography. Phys. Med. Biol. 2017, 62, 4062. [Google Scholar] [CrossRef] [PubMed]
- Kandala, S.K.; Liapi, E.; Whitcomb, L.L.; Attaluri, A.; Ivkov, R. Temperature-controlled power modulation compensates for heterogeneous nanoparticle distributions: A computational optimization analysis for magnetic hyperthermia. Int. J. Hyperther. 2019, 36, 115–129. [Google Scholar] [CrossRef] [PubMed]
- Egolf, P.W.; Shamsudhin, N.; Pané, S.; Vuarnoz, D.; Pokki, J.; Pawlowski, A.-G.; Tsague, P.; De Marco, B.; Bovy, W.; Tucev, S.; et al. Hyperthermia with rotating magnetic nanowires inducing heat into tumor by fluid friction. J. Appl. Phys. 2016, 120, 64304. [Google Scholar] [CrossRef]
- Tehrani, M.H.H.; Soltani, M.; Kashkooli, F.M.; Raahemifar, K. Use of microwave ablation for thermal treatment of solid tumors with different shapes and sizes-A computational approach. PLoS ONE 2020, 15, e0233219. [Google Scholar] [CrossRef]
- Grimes, D.R.; Currell, F.J. Oxygen diffusion in ellipsoidal tumour spheroids. J. R. Soc. Interface. 2018, 15, 20180256. [Google Scholar] [CrossRef] [Green Version]
- Zwillinger, D. CRC Standard Mathematical Tables and Formulas, 33th ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Polychronopoulos, N.D.; Gkountas, A.A.; Sarris, I.E.; Spyrou, L.A. Numerical analysis of temperature distribution in ellipsoidal tumors in magnetic fluid hyperthermia. In Proceedings of the 2020 IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE), Cincinatti, OH, USA, 26–28 October 2020; pp. 354–357. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Wang, J. Simulation of Magnetic Nanoparticle Hyperthermia in Prostate Tumors. Ph.D. Thesis, Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD, USA, 2014. [Google Scholar]
- Spyrou, L.A.; Aravas, N. Thermomechanical modeling of laser spot welded solar absorbers. J. Manuf. Sci. Eng. 2015, 137, 11016. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Polychronopoulos, N.D.; Vlachopoulos, J. Computer Flow Simulations of Moffatt Eddies in Single Screw Extrusion. Int. Polym. Proc. 2018, 33, 662–668. [Google Scholar] [CrossRef]
- Eltejaei, I.; Balavand, M.; Mojra, A. Numerical analysis of non-Fourier thermal response of lung tissue based on experimental data with application in laser therapy. Comput. Methods Progr. Biomed. 2021, 199, 105905. [Google Scholar] [CrossRef] [PubMed]
- Henriques, F.C. Studies of thermal injury: V. The predictability and significance of thermally induced rate processes leading to irreversible epidermal injury. Arch. Pathol. 1947, 43, 489–502. [Google Scholar]
- Henriques, F.C.; Moritz, A.R. Studies of thermal injury: I. The conduction of heat to and through skin and the temperatures attained therein: A theoretical and experimental investigation. Am. J. Pathol. 1947, 23, 531–541. [Google Scholar]
- Van Rhoon, G.C. Is CEM43 still a relevant thermal dose parameter for hyperthermia treatment monitoring? Int. J. Hyperther. 2016, 32, 50–62. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Numerical analysis of the pulsating heat source effects in a tumor tissue. Comput. Methods Progr. Biomed. 2021, 200, 105887. [Google Scholar] [CrossRef]
- Rumble, J. CRC Handbook of Chemistry and Physics, 102nd ed.; CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Wypych, G. Handbook of Polymers, 2nd ed.; ChemTec Publishing: Scarborough, ON, Canada, 2012. [Google Scholar]
- Giustini, A.J.; Petryk, A.A.; Cassim, S.M.; Tate, J.A.; Baker, I.; Hoopes, P.J. Magnetic nanoparticle hyperthermia in cancer treatment. Nano Life 2010, 1, 17–32. [Google Scholar] [CrossRef]

| Prolate Tumors | ||
|---|---|---|
| Aspect ratio (AR) | a (mm) | b (mm) |
| 2 | 7.93 | 15.87 |
| 4 | 6.29 | 25.19 |
| 8 | 5.0 | 40.0 |
| Oblate Tumors | ||
| Aspect ratio (AR) | a (mm) | b (mm) |
| 1 | 10.0 | 10.0 |
| 2 | 12.5 | 6.29 |
| 4 | 15.87 | 3.96 |
| 8 | 20.0 | 2.50 |
| Tissue | ρ (kg/m3) | c (J/kg∙K) | k (W/m∙K) | wb (s−1) | Qmet (W/m3) |
|---|---|---|---|---|---|
| Tumor | 1045 | 3760 | 0.5 | 1.3 × 10−3 | 540 |
| Healthy tissue | 1045 | 3760 | 0.5 | 1.3 × 10−3 | 540 |
| Blood | 1060 | 3770 | – | – | – |
| Mesh Number | Number of Cells | Temperature Location 2 mm above Tumor Center (°C) |
|---|---|---|
| 1 | 9500 | 41.581 |
| 2 | 15,740 | 41.852 |
| 3 | 32,781 | 41.911 |
| 4 | 57,468 | 41.915 |
| Parameter | Value |
|---|---|
| Md (kA∙m−1) | 446 |
| (kJ∙m−3) | 41 |
| ρnano (kg∙m−3) | 5180 |
| R (nm) | 9.5 |
| η (Pa∙s) | 6.53 × 10−4 |
| φ | 4.8 × 10−4 |
| f (kHz) | 220 |
| H0 (A∙m−1) | 6800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polychronopoulos, N.D.; Gkountas, A.A.; Sarris, I.E.; Spyrou, L.A. A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors. Appl. Sci. 2021, 11, 9526. https://doi.org/10.3390/app11209526
Polychronopoulos ND, Gkountas AA, Sarris IE, Spyrou LA. A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors. Applied Sciences. 2021; 11(20):9526. https://doi.org/10.3390/app11209526
Chicago/Turabian StylePolychronopoulos, Nickolas D., Apostolos A. Gkountas, Ioannis E. Sarris, and Leonidas A. Spyrou. 2021. "A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors" Applied Sciences 11, no. 20: 9526. https://doi.org/10.3390/app11209526
APA StylePolychronopoulos, N. D., Gkountas, A. A., Sarris, I. E., & Spyrou, L. A. (2021). A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors. Applied Sciences, 11(20), 9526. https://doi.org/10.3390/app11209526








