Abstract
The nonlinear dynamic features of compression roller batteries were investigated together with their nonlinear response to primary resonance excitation and to internal interactions between modes. Starting from a parametric nonlinear model based on a previously developed Lagrangian formulation, asymptotic treatment of the equations of motion was first performed to characterize the nonlinearity of the lowest nonlinear normal modes of the system. They were found to be characterized by a softening nonlinearity associated with the stiffness terms. Subsequently, a direct time integration of the equations of motion was performed to compute the frequency response curves (FRCs) when the system is subjected to direct harmonic excitations causing the primary resonance of the lowest skew-symmetric mode shape. The method of multiple scales was then employed to study the bifurcation behavior and deliver closed-form expressions of the FRCs and of the loci of the fold bifurcation points, which provide the stability regions of the system. Furthermore, conditions for the onset of internal resonances between the lowest roller battery modes were found, and a 2:1 resonance between the third and first modes of the system was investigated in the case of harmonic excitation having a frequency close to the first mode and the third mode, respectively.
1. Introduction
Aerial ropeways are transportation systems which are becoming increasingly popular in recent years, not only in mountain regions with ski resorts and in sightseeing areas, but also in urban environments [1]. Two criteria can be used to classify ropeway systems, namely, the number of cables, and the operating mode. In this work, attention is focused on monocable ropeways, in which the vehicles are fixed on a single propelling cable. The cable travels continuously in a loop at a uniform speed and passes across the supporting towers, equipped with an ensemble of rollers, which facilitate a smooth cable transit across the tower where a change of slope occurs. Investigating the static and dynamic response of these multibody systems is challenging, and the literature on this topic is limited and mainly focused on the dynamic response of the vehicles under the ropeway operating condition [2,3]. Some works [4,5,6] investigated the dynamic behavior of carrying hauling ropes, dealing with the study of the effects of moving loads in an existing ropeway system, while [7] investigated the nonlinear coupling between the motion of the hauling cable and the swaying dynamics of the cabins in bi-cable circulating gondola ropeway systems. They show that these systems depend on the track inclination. A recent work [8] presented a computational approach for determining the initial tension of the carrying cable of a bi-cable ropeway under an in-service moving load, and to investigate the influence of nonlinear effects on the displacement state and axial forces. Furthermore, a theoretical model that solves the minimization of aerial ropeway vehicle oscillations, induced as the vehicle passes over a support, was proposed in [9], and then experimentally validated by the same authors in [10].
On the other hand, little attention was paid to the study of the local dynamic interactions taking place between the vehicle, the cable, the roller battery, and the supporting tower; few works have investigated these aspects [11]. A nonlinear model of compression roller batteries, used as a starting point for the studies proposed in the present work, was first developed in [12,13]. In such works, experimental tests were also carried out on an operating ropeway, so as to identify the modal characteristics of the system by adopting the Enhanced Frequency Domain Decomposition method, and to validate the analytical model by comparing the experimental dynamic responses with the numerical simulations. The model was further extended in [14,15] to include a passive vibration control system made by a group of linear or hysteretic vibration absorbers to mitigate the accelerations of roller batteries in cableways caused by vehicle transit.
To the best of the author’s knowledge, there are no publications dealing with the characterization of the nonlinear dynamic behavior of the ropeways roller batteries or aimed at investigating their dynamic response to periodic excitations. The present work aims at filling the lack of knowledge regarding the characterization of the nonlinear dynamic features of roller battery systems and to investigate the effects of the periodic excitations induced by the moving cable that may give rise to resonance phenomena and nonlinear modal interactions. These phenomena were studied in the past in different mechanical systems, such as cranes [16,17,18,19], tethering [20], pendulum systems [21,22], piezoelectric beams [23,24], and plates [25,26], or, more generally, in slender structures possessing strong geometric nonlinearities [27,28,29]. Such nonlinearities can affect the dynamic response of highly deformable structural elements and can be suitably exploited for practical applications, as it was largely demonstrated in the literature [30,31,32,33]. Within this context, the asymptotic approach proved to be a suitable method to investigate the dynamics of nonlinear mechanical systems. This approach allows us to perform sensitivity analyses on the effect of the system parameters on the nonlinear dynamic response by determining closed-form expressions of the bifurcation response.
By employing the method of multiple scales [34,35,36], the asymptotic frequency response analyses were conducted in the present work, together with a deep discussion of the meticulously derived analytical treatment to highlight the scenarios of nonlinear interactions between the external excitation and the modes of the system. Furthermore, a thorough bifurcation analysis, carried out via path-following of the fixed points of the modulation equations shed light onto several interesting features of the roller battery single- and coupled-mode responses.
2. Nonlinear Dynamic Characterization
The proposed mechanical model of compression roller batteries is based on the formulation proposed, for the first time, in [13], which includes finite kinematics, for the description of the rollers and the vehicle motions, and obtains the nonlinear equations of motion via an energetic approach. In such a model, the mechanical system is represented by an assembly of four mechanical subsystems, namely, the hoisting beam supporting the roller battery, the roller battery, the elastic cable traveling across the ropeway and, finally, the cabin attached to the cable. The cable is modeled as a one-dimensional pre-stressed string. On the other hand, the roller battery is a mechanism made of eight rollers rigidly connected to each other by means of hierarchical balancers rotating around moving hinges and positioned symmetrically with respect to a connection point with the hoisting beam. The latter is modeled as an equivalent one-dimensional Euler-Bernoulli beam, while the cabin behaves like a pendulum with the support point fixed to the moving cable.
The whole modeling procedure, including all relevant details of the underlying complex mechanical behavior, such as the effects of the vehicle grip on the rollers or the periodic forcing caused by the interwire spacing on the outer layer of the monocable rope, was derived and extensively discussed in [13]. Therefore, the author of the present work will refer to the equations and mechanical parameters of the case-study roller battery reported in the above mentioned work. Since, in this paper, only the nonlinear dynamic behavior of the roller battery system is investigated and characterized, the presence of the cabin is neglected. Therefore, the mechanical formulation, reduced to the dynamic configuration considered in this work, is briefly summarized, and all the relevant equations are reported in the next sections.
2.1. Kinematic Descriptors
The kinematics are described in the plane containing the direction collinear with the cable configuration as well as the vertical direction. In particular, two fixed frames are introduced, namely, the frame with origin in C and oriented as the horizontal and vertical directions, respectively. The frame , centered in C and oriented along the roller battery in the inclined direction, thus rotated with respect to the fixed (global) frame by (see Figure 1). The geometric parameters characterizing the reference configuration of the roller battery, the cable, the cabin, and the grip are shown in Figure 1. In particular, along the direction , denotes the distance between C and (), is the distance between and , and represents the distance between and each of the two corresponding roller-cable contact points . Similarly, the distances , , and represent the distances along between the mentioned hinges. The parameters characterizing the reference geometry of the cable are the side lengths and (i.e., the distances of the two supports from the first and last rollers and , respectively).
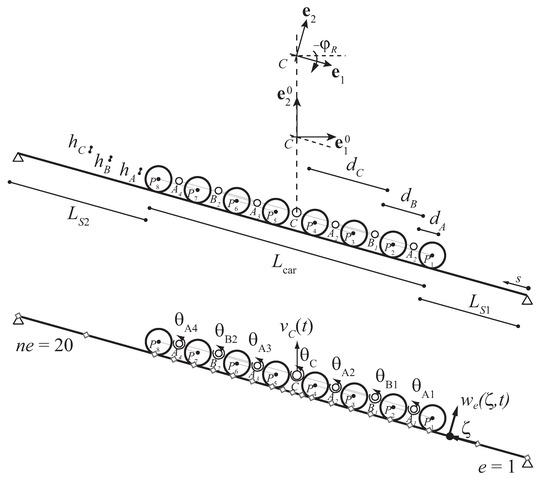
Figure 1.
(Top) Geometric characteristics of the roller battery system in compression towers. (Bottom) Degrees-of-freedom and FE discretization (i.e., diamonds symbols).
The roller battery degrees of freedom (DOFs) are the rotations , , and , about the hinges , , and C, respectively. Therefore, the current configuration of the roller battery can be described by the vectors , , , and which provide, at time t, the positions of the cable contact points () and of the hinges (), () and C, respectively, or by the displacement vectors of the above mentioned points, that is, , , and , respectively.
To discretize the time- and space-dependent function representing the vertical displacement of the centerline hoisting cantilever beam, having length , the Galerkin method is adopted by considering a suitable number of trial functions to approximate the dynamics of the beam-like subsystem. In particular, the lowest mode shapes the of the cantilever beam, which are employed to discretize the beam deflection in space, while () represent the time-dependent generalized coordinates, hence, the beam deflection can be written as , and the vertical displacement of point C turns out to be .
On the other hand, due to the multiple contact points () between the cable and roller battery, the cable discretization is carried out according to the finite element (FE) technique. In particular, finite elements are used to discretize the cable length such that each contact point coincides with a finite element node while the cable support points are the boundary nodes. First-order Lagrangian polynomials are employed to approximate the cable transversal displacement and to describe the kinematic function in the eth element. The latter can be written as , where the subscript e indicates the element, is the local arclength, is the vector collecting the shape functions of each element, is the vector of the nodal degrees of freedom, having size , and is the extraction matrix. Finally, due to the cable fixed boundary conditions, it turns out that .
The unilateral contacts at points () between the rollers and the cable are modeled by introducing fictitious springs collocated at each point . These springs behave as internal elastic constraints whose stiffness is suitably tuned in order to simulate a quasi-rigid behavior.
2.2. Nonlinear Equations of Motion
The equations governing the motion of the roller battery system, including the interaction between the hoisting beam and the cable are derived via the Euler-Lagrange approach. To this end, the potential and kinetic energies of the beam and cable are first calculated together with the potential energy of the fictitious springs and the kinetic energy of the rollers to calculate the Lagrangian of the system, from which the nonlinear equations of motion of the roller battery are obtained. In particular, the potential energy of the hoisting beam and the cable can be expressed as:
respectively, where represents the partial differentiation with respect to the beam arclength s (with origin at the beam clamped cross section), is the hoisting beam flexural stiffness, while , incorporating the cable pretension , is the global stiffness matrix of the cable. The energy stored by the fictitious springs connecting the cable and the rollers is computed as follows:
where is the relative displacement along the roller local direction (corresponding to the transverse direction of the cable) and is the cable displacement at the node corresponding to the ith roller.
On the other hand, the hoisting beam and the cable kinetic energy contributions to the dynamics of the system are given by:
respectively, where and the overdot represent partial and total differentiation with respect to time t, respectively. is the hoisting beam mass per unit length, while , includes the cable mass per unit length , is the global mass matrix of the cable. Finally, the kinetic energy possessed by the rollers can be calculated as:
where , , and are the equivalent masses of the roller battery lumped at , , , respectively, and is part of the mass of the roller battery, acting at C. Finally, the stored and the kinetic energies of the overall system are given by:
The simplifications made in the model formulation proposed in [13] include the assumption of considering the cable as a straight, prestressed string. Nevertheless, when crossing the roller battery system, the cable is subject to a small curvature due to the slight change in slop of the cable passing from the first to the last roller. Although this simplification does not imply relevant errors in the description of the dynamic behavior of this system (as demonstrated by the comparison with experimental results in [13]), the actual cable curvature generates a force acting on each roller transversally to the cable direction. Moreover, since the cable is made by an assembly of wires wound around its axis to study the effects of the interwire periodicity when the cable travels at the speed , harmonic forces orthogonal to the cable are considered to act on each roller. In particular, by denoting with the interwire distance of the outer cable layer, the periodic forces arising from the cable curvature will exhibit a circular frequency given by and can be expressed as (), assuming that the maximum amplitude F of the force is the same at each roller.
The motion equations are then obtained via a Lagrangian approach. In particular, by introducing the Rayleigh dissipation function, and by calculating the Lagrangian of the system , the equations of motion can be written as:
where and is the total number of DOFs of the system, is the linear viscous damping coefficient associated with the lth DOF, represents total differentiation with respect to time t, and is the lth generalized coordinate extracted out of the vector collecting the system degrees of freedom, namely, …… (see [13,14] for further details). Finally, in Equation (6), represents the lth Lagrangian component of the periodic excitation acting at the ith roller () and is calculated as: .
2.3. Nondimensional Vector Form of the Equations of Motion
The equations of motion are then nondimensionalized by adopting the characteristic time and the equivalent beam span as the characteristic length, respectively. The latter can be used for the nondimensionalization of the systems geometric parameters, and for the unknown generalized coordinates corresponding to and , respectively. Furthermore, it turns out that can be used to nondimensionalize the forces acting in the system: in this case, the nondimensional maximum force acting on each roller can be calculated as . The numerical simulations are then carried out considering finite elements for the cable discretization and trial functions for the hoisting beam discretization; therefore, the system dynamics are described by DOFs. The geometric and mechanical properties of the roller battery considered in this work are taken in consonance with the data reported in [13].
The equations of motion reported in Equation (6) involve strongly nonlinear functions of the system DOFs (i.e., nonlinear combinations of trigonometric functions); nevertheless, their time integration can be quite easily performed by using well-established numerical integration schemes. On the other hand, their analytical treatment requires an asymptotic expansion of the nonlinear functions present in Equation (6). Since the system investigated includes only geometric nonlinearities, the most relevant effects of these nonlinearities are given by the approximating second- and third-order polynomial terms. Therefore, a third-order Taylor expansion of Equation (6) was performed, and the obtained system of nondimensional nonlinear equations of motion can be conveniently recast in vector form as:
where is the vector collecting the generalized coordinates, while , , and are the mass, viscous damping, and stiffness matrices of the system, respectively. Moreover, is the vector of the nondimensional amplitudes of the external excitation, while , , and (), are the inertial, velocity-proportional, and stiffness nonlinear operators of oth order, respectively, arising from the system geometric nonlinearities. Finally, is the null vector and the natural initial conditions are considered (i.e., , and , respectively).
3. Modal Characterization
Eigenvalue analysis is first performed to characterize the fundamental modes of the system. By linearizing Equation (7), i.e., setting (), neglecting the forcing term and the linear viscous damping force (i.e., setting and , being the null matrix), the homogeneous system of linear equations governing the free undamped oscillations of the system assumes the classical form:
The eigenvalues of Equation (8) provide the natural frequencies () of the system and the corresponding eigenvectors, conveniently normalized, deliver the mode shapes of the roller battery. In particular, by referring to the vectors and natural frequencies of the mth and nth modes of the system, i.e., (, ) and (, ), respectively, the following relationships are satisfied: and , being the Kronecker delta. The lowest eight nondimensional circular frequencies of the system are reported in Table 1 and the corresponding mode shapes of the roller battery are displayed in Figure 2.

Table 1.
Lowest eight nondimensional circular frequencies.
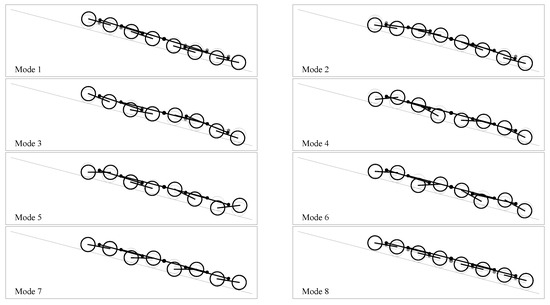
Figure 2.
Shapes of the lowest eight linear normal modes of the roller battery system.
Interesting considerations emerge from the analysis of the ratios between the lowest frequencies of the system. Figure 3 reports the ratios between the frequencies of modes with respect to the lowest frequency (Figure 3a) and of the modes with respect to the second frequency (Figure 3b), respectively. As shown in Figure 3a, the frequency of the third roller battery mode is close to twice the frequency of the lowest mode while the sixth and seventh modes have frequency three times . The same integer ratios occur between the frequency of the seventh and eighth modes with respect to the frequency of the second mode, i.e., 2:1 and 3:1 ratio, respectively, as shown in Figure 3b. When in a nonlinear dynamical system, the frequencies of two modes are in an integer ratio with each other, then the internal exchange of energy between the modes involved may occur, leading the system to dynamic interactions, i.e., the so-called internal resonances [34,35,36].
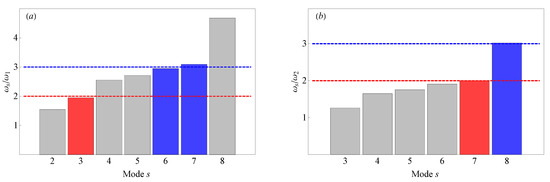
Figure 3.
Ratios of the lowest eight frequencies of the system with respect to (a) the lowest frequency and (b) the second frequency . Red and blue bars and dashed lines indicate 2:1 and 3:1 ratios, respectively.
It is a matter of fact that the internal resonances may more easily be activated between modes having lower frequencies, such as in the case of the mechanical system investigated, shown by the first and third mode of the roller battery (see red bar and red line in Figure 3a). Therefore, when the frequency of the cable-induced harmonic excitation is close to the frequency of the system, primary resonance may occur; furthermore, if the latter is a multiple or an integer ratio of the frequency of a different mode then internal resonance may also take place.
In the system investigated in this work, the cable-induced periodic excitation has a frequency dependent on the cable speed which never exceeds the nondimensional value of in the ropeway studied here; this value corresponds to a maximum nondimensional excitation frequency . This means that low cable speeds may generate periodic excitations inducing primary resonance in all of the lowest eight modes investigated. After characterizing the nonlinearity of the lowest modes of the system, the focus will be devoted to the analysis of the primary resonance of the lowest mode (i.e., ). Moreover, it will be shown that when , then 2:1 internal resonance with mode three may take place only for very high excitation amplitudes. On the other hand, the threshold for the activation of two-to-one internal resonance between mode three and mode one when the periodic excitation has frequency is calculated, and the nonlinear frequency response curves of the resonating modes are determined for a selected value of the excitation amplitude.
4. Asymptotic Solution of the Equations of Motion
The method of multiple scales [34,35,36] is adopted to first characterize the nonlinearity of the system modes and then to study the bifurcation scenarios due to direct harmonic excitations to obtain closed-form expressions of the stable and unstable branches of the FRCs, together with the continuation of the fold bifurcation points.
By letting denote a small nondimensional parameter representing the norm of the deviation of the current roller battery configuration from its reference state, a third-order expansion of the solutions of Equation (7) is sought in the form:
where is the nondimensional fast time scale and is the slow time scale in which the nondimensional time derivative can be written as , with and , respectively, while , with , , and , respectively.
The perturbation treatment requires a preliminary rescaling of the viscous damping force and of the excitation term; therefore, since the nonlinearities of the system are such that resonant terms are generated at the cubic order. The linear viscous damping force is assumed to appear at the third order; this, analytically implies a re-scaling of the viscous damping matrix as , while the forcing term is rescaled so that . Substituting Equation (9) into Equation (7), and retaining only the terms up to order , the following hierarchy of linear problems is obtained by equating to zero the coefficients of like powers of :
order
order
order
where is a matrix of constant terms, while , , , and are stiffness, velocity-proportional, and inertial third-order operators, respectively; which, in turn, are functions of the first- and second-order solutions.
4.1. Nonlinearity of the Lowest Normal Modes
By setting and in Equation (12), it is possible to study the nonlinearity of the roller battery nonlinear normal modes by solving, in cascade, the hierarchy of perturbation problems given by Equations (10)–(12). In particular, to study the nonlinearity of the mth mode, the general solution of the -order problem, Equation (10), can be written as:
where and are the complex and complex-conjugate amplitudes of the mth mode, respectively. The non-resonant terms are present in the second-order problem; therefore, after substituting the first-order solution (13) into Equation (11), the solution of the inhomogeneous -order problem can be expressed in the form:
where the vector () is the linear combination of the modes of the system, that is: . The solution given by Equation (14) is substituted into the -order problem and Equation (11) is then projected into the modal space through the -by- modal matrix , whose sth column is the vector (i.e., the sth mode), as:
where is the vector collecting the second-order inhomogeneous terms. By then equating the coefficients of terms having the same frequency in Equation (15), it is possible to calculate the coefficients and find the second-order solution .
First- and second-order solutions given by Equations (13) and (14), respectively, are then substituted into the -order problem. The singularity generated by the secular terms exhibited in the third-order problem can be removed by enforcing solvability conditions [35]. To this end, by now introducing the general solution of the adjoint homogeneous problem of Equation (12):
where stands for complex-conjugate, the solvability condition is enforced by requiring the orthogonality between (16) and the inhomogeneous term (right-hand side) in Equation (12) as:
where:
Equation (17), which annihilates the secular terms arising in , governs the modulation in time of the amplitudes and through to the following equations:
where is a strongly nonlinear function of the frequency of the mth mode and of the systems mechanical parameters.
After removing the secular terms, the solution of the inhomogeneous third-order problem can be calculated as:
where the vector () is expressed, again, as a linear combination of the modes of the system, that is: . The solution given by Equation (20) is substituted into the -order problem and Equation (12) is then projected into the modal space as: . By then equating the coefficients of terms having the same frequency, it is possible to calculate the coefficients and find the second-order solution .
To study the nonlinearity of the mth normal mode, the complex amplitudes are expressed in polar form as and , respectively, where is the real amplitude and is the phase of the mth nonlinear normal mode. The polar form is then substituted into the modulation equations (19). Furthermore, the separation of the real and imaginary parts yields the following differential relationships in terms of the real amplitude and the phase of the mth mode:
By defining the relative phase , with being a detuning parameter, it turns out that the fixed points of the dynamic system are obtained when and ; therefore, the detuning can be calculated from Equation (21) as and the frequency of the mth nonlinear normal mode can be expressed in terms of the real modal amplitude as:
The function is also known as the effective nonlinearity coefficient of the mth mode: when , the nonlinearity is hardening, while, when , it is softening.
One-Mode Projection of the Nonlinear Equations of Motion
The nonlinearity of the mth normal mode can be qualitatively investigated by neglecting the contribution of the remaining modes in the reconstruction of the second- and third-order solutions given by Equations (14) and (20). This approach, although simplified, creates a better understanding of the role of the system mechanical parameters into the effects of the geometric nonlinearity of the system. To this end, the solution of Equation (7) is expressed as , where is the mth generalized coordinate. Equation (7) is then projected into the mth mode by pre-multiplying it by to obtain the mth nonlinear modal equation in the form:
where is the modal damping coefficient, is the modal component of the excitation term, and:
are the second- and third-order inertial, velocity-proportional, and stiffness modal coefficients, respectively.
The same asymptotic procedure, based on the method of multiple scales, can be used to investigate the nonlinearity of the mth mode through the nonlinear equation of motion (23), whose solution is sought in the form . Therefore, after rescaling the excitation term as and the modal viscous damping force as , the lowest three perturbation problems can be written as:
To study the nonlinearity of the mth mode the excitation term is set to zero, i.e., , and the modal viscous damping is neglected, i.e., .
The solution of the first-order problem can be written as , while the solution of the second-order problem, which does not show resonant terms, is given in the form:
At the third order, the singularity generated by the resonant terms is removed when the modulation equations, having the same form of Equation (19), hold; although, in this case, the nonlinearity coefficient of the mth mode has the simpler expression:
After removing the secular terms by superimposing Equation (19), the solution of the inhomogeneous third-order problem can be written as:
and can be substituted into the inhomogeneous third-order problem; then, by equating the coefficients of terms having the same frequency, it is possible to calculate the unknown coefficients of Equation (28), which turn out to be , where:
To study the nonlinearity of the mth normal mode and express the complex amplitudes in polar form, substitute their expressions into the modulation equations and separate the real and imaginary parts; this furnishes differential relationships in terms of the real amplitude and the phase of the mth mode in the same form of Equation (21). By introducing the relative phase , the fixed points are obtained when and ; hence, the frequency of the mth nonlinear normal mode can be expressed in terms of the real modal amplitude and through the effective nonlinearity coefficient given by Equation (27) as: .
The backbone curves of the lowest four nonlinear normal modes, that is, the nonlinear relationships between the modal amplitude and the detuning (where ), are shown in Figure 4a. The dashed lines in Figure 4a indicate the backbones calculated by adopting the one-mode projection, while solid lines refer to the solution obtained by using the full modal basis discretization. As shown in the figure, the differences between the curves obtained with the two approaches are more evident for the lowest skewsymmetric mode (red lines) and the lowest symmetric mode (blue lines). Nevertheless, as shown in Figure 4b,c, the shapes of the corresponding modes are less influenced by the modal discretization.
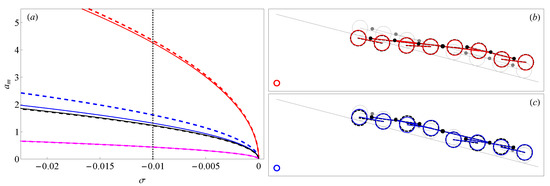
Figure 4.
(a) Backbones of the lowest four nonlinear normal modes. (b) Shape of the first and (c) second normal modes at ; one-mode projection (dashed lines) vs. full modal basis discretization (solid lines).
Figure 5 reports the values of the coefficients of the nonlinear terms of Equation (23) for the lowest four modes. It is shown that all coefficients of the quadratic terms are negative. On the other hand, the inertial and velocity-proportional coefficients of the cubic terms are positive for all modes, while the coefficient of the stiffness cubic term is always negative. Moreover, the coefficients of the stiffness terms are orders of magnitude higher than the inertial and velocity-proportional coefficients. This indicates that the nonlinearity of the roller battery is mainly governed by the stiffness terms while the nonlinear effects provided by the inertial and velocity-proportional terms are negligible. This is further confirmed by the values of the nonlinearity coefficients reported in Table 2. In the latter are the values of of the lowest four modes calculated by considering the contribution of: (i) all types of nonlinearity, (ii) the inertia-associated nonlinearity (i.e., by setting ), (iii) the velocity-associated nonlinearity (i.e., by setting ), (iv) the stiffness-associated nonlinearity (i.e., by setting ), respectively.
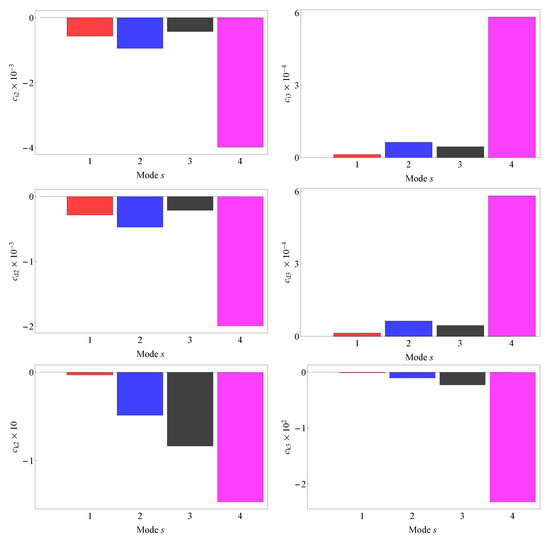
Figure 5.
Coefficients of the inertial ( and ), velocity-proportional ( and ), and stiffness nonlinear terms ( and ), of the lowest four modes.

Table 2.
Nonlinearity coefficient of the lowest four nonlinear normal modes (): effect of the nonlinearity type.
The results reported in Table 2, clearly show that the stiffness-related nonlinearity is predominant since the effective nonlinearity coefficient is an order of magnitude higher with respect to the associated nonlinearity of the inertia and velocity-proportional terms. On the other hand, it is shown that the velocity-proportional nonlinear terms confer to the system a hardening nonlinear behavior (i.e., ).
5. Cable Motion-Induced Resonances
In this section the nonlinear dynamic response of roller batteries subjected to periodic excitation provided by the forces induced by the moving cable will be investigated. In particular, the focus is first devoted to the analysis of the primary resonance of the lowest mode (i.e., when ); then, the two-to-one internal resonance between the first and third mode will be investigated when and when , respectively. To this end, the asymptotic approach presented in Section 4 based on the full modal discretization for the evaluation of the second- and third-order solutions (see Section 4.1), is adopted to calculate the nonlinear frequency response curves and the stability regions of the dynamic responses.
5.1. Primary Resonance
First- and second-order solutions of the hierarchical systems of equations, Equations (10) to (12), are given by Equations (13) and (14), respectively. The latter are then substituted into the -order problem Equation (12) and the singularity generated by the secular terms can be removed by enforcing the solvability condition. To this end, after introducing the general solution of the adjoint homogeneous problem (i.e., Equation (16)), the orthogonality between (16) and the inhomogeneous term (right-end side) in Equation (12) is enforced as: , where:
To investigate the primary resonance of the mth mode, the frequency of the excitation term is expressed as , with as a detuning parameter. Moreover, to make use of complex algebra, ; then, at the third order, the singularity generated by the resonant terms is removed when the following modulation equations hold:
where, and are strongly nonlinear functions of the linear frequency of the mth mode. Note that, in case of the one-mode projection of the equations of motion, it turns out that , , and is given by Equation (27).
By expressing the complex amplitudes in polar form and separating the real and imaginary parts, the modulation equations in terms of the real amplitude and phase read:
By solving Equation (32) for and and introducing the relative phase , the fixed points can be sought to impose and , respectively. By solving the ensuing equations in terms of and , and enforcing the trigonometric identity, the frequency-response function providing the nonlinear relationship between the real amplitude and frequency detuning can be obtained in its implicit form as:
The equation that allows for describing the bifurcation behavior of the system is given by ; moreover, from the stationarity of with respect to it is possible to calculate the loci of the fold bifurcation points as the four non-trivial solutions of the equation , that is:
with being the trivial solution (i.e., ).
Finally, after removing the secular terms by means of Equation (31), the solution of the inhomogeneous third-order problem can be calculated as , where the vectors () are expressed, again, as a linear combination of the modes of the system, that is: . The third-order solution is then substituted into the -order problem and it is then projected into the modal space as: . By then equating the coefficients of terms having the same frequency, it is possible to calculate the coefficients and find the second-order solution .
Thereafter, the nonlinear equations of motion of the system expressed by Equation (6) are numerically integrated in time by using the built-in NDSolve algorithm present in the software Mathematica [37]. For each simulation, at a selected excitation frequency , the maximum integration time was set to , where is the excitation period, while the time step was . At steady-state, the state vector (, ) was saved and assigned as the initial condition for the time integration run with the subsequent . Finally, backward and forward frequency sweeps were performed so as to calculate the numerical FRCs.
Figure 6 shows the frequency response curves in terms of the vertical component (i.e., along the direction ) of the nondimensional displacement vectors of points , , , and C, respectively, when . The comparison between numerical time integration (gray dots) and the third-order asymptotic solution obtained via the method of multiple scales (solid and dashed lines) shows a very good agreement in most of the range of stable solutions. The asymptotic analysis allowed us to investigate the unstable solutions (dashed lines) and calculate the threshold values of amplitude and frequency, where fold bifurcation occurs (i.e., at the boundary between solid and dashed lines). The analysis was performed for a value of the nondimensional maximum amplitude of the periodic force , so as to show the softnening nonlinearity of the dynamic response. The value of the forcing amplitude is almost two orders of magnitude lower than the characteristic force of the system. This means that moderately high values of the forcing term can also induce a nonlinear resonance response of the system.
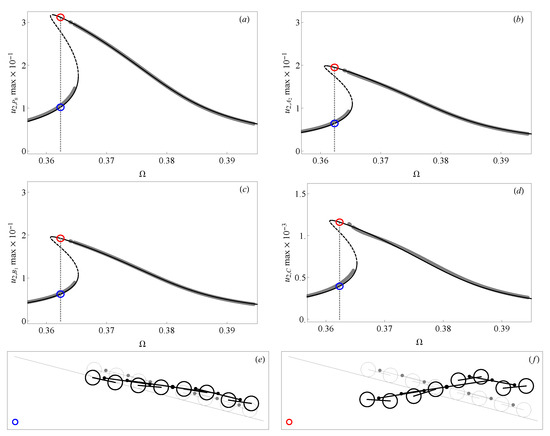
Figure 6.
Primary resonance: frequency response curves of the vertical displacements of points (a) , (b) , (c) , and (d) C. Solid and dashed lines refer to the stable and unstable branches, respectively, evaluated via asymptotic approaches, while dots indicate the results of the numerical time integration. Configurations at in the multistability range: (e) low-amplitude response, (f) high-amplitude response.
Figure 7a shows the FRCs in terms of the modal amplitude for two values of the modal damping coefficient for the case . In particular, was rescaled through a nondimensional coefficient as and the cases of and are considered. This rescaling allowed us to perform a parametric study on the effect of damping on the nonlinear resonance response. In Figure 7a we report the regions collecting the unstable solutions in the plane (i.e., blue and black shaded surfaces). The latter are bounded by the curves enveloping the fold bifurcation points and provided by Equation (34). The loci of the fold bifurcation points are then plotted in Figure 7b for several values of the modal damping coefficient by varying the rescaling coefficient in the range , showing how instable regions reduce large values of and demonstrating the stability effect of damping in the nonlinear dynamic response of the roller battery.
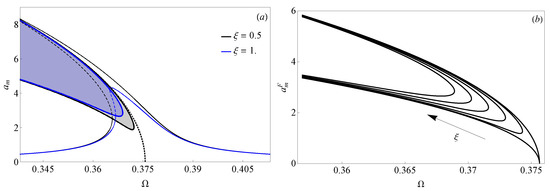
Figure 7.
(a) FRCs of the modal amplitude (case ) and stability regions for two different values of the coefficient which rescales the damping; the dotted line indicates the backbone of the mode . (b) Loci of the fold bifurcation points for .
5.2. Two-to-One Internal Resonance
In this section, we investigate the phenomenon of the two-to-one internal resonance between two modes of the roller battery occurring when one mode of the system undergoes primary resonance due to the periodic excitation of the moving cable.
Without loss of generalization, the two resonant modes are indicated as mode m and mode n, respectively, and the corresponding frequencies have a ratio close to two (i.e., ). Two case-studies are investigated, namely, the case when the frequency of the periodic excitation is near the frequency of the mode m (i.e., primary resonance of mode m, with ), and the case when (i.e., primary resonance of mode n), respectively. As mentioned in Section 3, 2:1 internal resonance is possible in the mechanical system studied in this work since the frequencies of the third and first mode have a ratio close to two.
The two-to-one internal resonance is caused by the quadratic nonlinearities of the system; therefore, the asymptotic treatment of Equation (7) starts by seeking its solution in the form:
where is the nondimensional fast time scale and is the slow time scale in which the nondimensional time derivative can be written as , with and , respectively, while , with , , and , respectively.
In this case, the resonant terms are generated at the quadratic order, therefore, the viscous damping force and excitation need to be rescaled so as to appear at the second perturbation order; hence, we set and , respectively. By now substituting Equation (35) into Equation (7), and retaining only terms up to order , the following hierarchy of linear problems is obtained by equating to zero the coefficients of like powers of :
order
order
In the case of two interacting modes (i.e., mode m and mode n), the general solution of the -order problem (36) can be written as:
where and are the complex amplitudes of the mth and the nth mode, respectively, while stands for complex conjugate. The first-order solution to Equation (38) is then substituted into the -order problem. The singularity generated by the secular terms exhibited in the second-order problem can be removed by enforcing solvability conditions. By introducing the mth and nth general solutions of the adjoint homogeneous problem of Equation (37) we get:
the solvability condition is enforced by requiring the orthogonality between (39) and (40) and the inhomogeneous term (right-end side) in Equation (37) as:
where
To express the closeness of the two interacting frequencies, the detuning parameter is introduced so that . On the other hand, the primary resonance condition between the periodic force and the modes m and n is achieved when and , respectively, with being a further detuning parameter. Thus, substituting the external and internal resonance conditions into Equation (41), it is possible to obtain the modulation equations for the amplitudes and (and their complex conjugates) for both cases of and , respectively.
Finally, after removing the secular terms, the solution of the second-order inhomogeneous problem can be calculated as:
where the vector is expressed as a linear combination of the modes of the system, that is: . Note that, the terms proportional to , , , , and their complex conjugates, respectively, are orthogonal to the general solutions (39) and (40) of the adjoint homogeneous problem of Equation (37). Therefore, although present in , these terms vanish when the solvability condition given by Equation (41) is enforced. The second-order solution is substituted into the -order problem which is then projected into the modal space as: . Finally, by equating the coefficients of terms having the same frequency, it is possible to calculate the coefficients of the second-order solution.
5.2.1. The Case of
In the case of primary resonance on mode m (i.e., ), the modulation equations of the amplitudes and have the following form:
where and are positive coefficients, while , are the components of the damping coefficients in the modulation equation of and , respectively, while is the component of the excitation amplitude in the modulation equation of . By expressing the complex amplitudes in polar form as , , introducing the relative phases and , and substituting the polar form into Equation (43). Separating the real and imaginary parts yields the four differential equations governing the slow modulation of the real amplitudes and the relative phases. Then, the fixed points can be calculated by setting and , respectively, and the bifurcation equations can be written as:
The system of four nonlinear algebraic equations (44) can be solved for selected values of the detuning parameters, and , and in terms of the nondimensional forcing amplitude (embedded in the coefficient ) to obtain the force response curves shown in Figure 8a. It is interesting to note that, in the case of primary resonance on mode m (i.e., ), a 2:1 internal resonance involving large amplitude oscillations of mode n arises for values of the nondimensional excitation amplitude orders of magnitude higher with respect to the value of the amplitude used in Section 5.1 (i.e., ), to investigate the primary resonance of the mth mode. As shown in Figure 8b, only at very large values of is it possible to obtain frequency response curves involving comparable amplitudes of oscillation of the two resonating modes, and , respectively (i.e., coupled-mode oscillations). In this circumstance, the modal amplitudes are two orders of magnitude higher, with respect to the case of primary resonance of mode m with no internal resonance. In the case considered (i.e., ), the FRCs of amplitudes and have a specular behavior with respect to the detuning (i.e., the curves are symmetric with respect to the axis ). Moreover, stable (solid lines) and unstable (dashed lines) responses are obtained in a short range of the detuning parameter around the value , while, in a larger range of positive and negative values of the detuning parameter , multistable responses are found. Here the stability of the dynamic response is ascertained by the study of the eigenvalues of the Jacobian matrix of Equation (44).
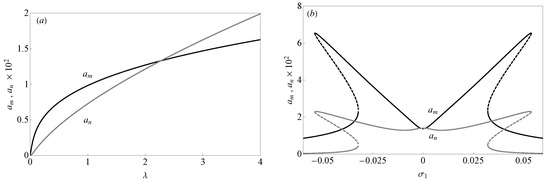
Figure 8.
(a) Force response curves of the amplitude (black line) and (gray line) when and . (b) Frequency response curves of the amplitude (black line) and (gray line) when and . Solid lines indicate stable responses while dashed lines indicate unstable responses.
On the other hand, in the range of low values of the excitation amplitude , internal resonance induces negligible oscillation amplitudes of mode n, as shown in Figure 9a. In particular, at (dashed vertical line) is more than one order of magnitude lower than , as shown in Figure 9b where it is reported that the ratio between the amplitude of the mode directly excited, and the amplitude of the internally resonant mode. The study conducted allows the claim that, although the third and first mode of the roller battery investigated are internally resonant, in the case of periodic excitation of the first mode, the amplitude of the forcing term must be enormously high to activate appreciable oscillations of the third mode.
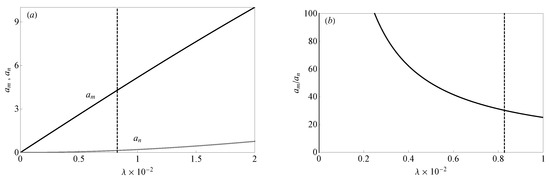
Figure 9.
(a) Force response curves of the amplitude (black line) and (gray line), when and in a lower range of force amplitudes . (b) Ratio between the amplitudes and varying . The dashed vertical line indicates the value of adopted in Section 5.1.
For the sake of rigor, it is worth noting that the ratio between the frequency of the third and first mode of the roller battery is not exactly equal to two. In particular, and ; this implies that, in the case-study investigated (i.e., ). Therefore, the force response curves and the FRCs are slightly different with respect to the perfectly resonant case (), although the dynamic behavior does not change appreciably. As shown in Figure 10a, the range of , inducing comparable amplitudes and in the coupled-mode oscillations, is the same of the case when , while in Figure 10b it is shown how the nontrivial detuning implies a loss of symmetry in the FRCs, although the nonlinear behavior is qualitatively the same as the case when .
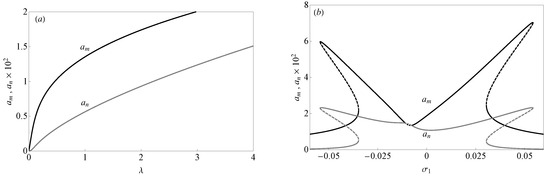
Figure 10.
(a) Force response curves of the amplitude (black line) and (gray line) when and . (b) Frequency response curves of the amplitude (black line) and (gray line) when and . Solid lines indicate stable responses while dashed lines indicate unstable responses.
5.2.2. The Case of
In the case of the primary resonance on mode n (i.e., ), the modulation equations of the amplitudes and have the following form:
where is the component in the modulation equation of of the amplitude of the periodic excitation. By introducing the polar form, the relative phases and , substituting the polar form into Equation (45), and separating the real and imaginary parts yields the four differential equations governing the slow modulation of the real amplitudes and relative phases. Finally, the fixed points can be calculated by setting and , respectively, and the bifurcation equations can be written as:
The force response curves shown in Figure 11a can be calculated by solving the system of four nonlinear algebraic equations (46) for selected values of the detuning parameters and and in terms of the nondimensional forcing amplitude (embedded in the coefficient ). Solid and dashed lines indicate stable and unstable responses, respectively, and the stability is ascertained by monitoring the eigenvalues of the Jacobian matrix of the Equation (46). Figure 11a displays a paradigmatic behaviour in the context of 2:1 internal resonances for a variety of nonlinear systems, the so-called saturation phenomenon. The response of the directly excited mode grows linearly up to a threshold excitation amplitude past which the single-mode response becomes unstable in favour of a two-mode response. The directly excited response (i.e., the amplitude ) saturates at a constant value, while the amplitude of the internally resonant mode (i.e., the amplitude ) grows nonlinearly with the excitation amplitude. In Figure 11b,c the bifurcation scenarios are shown through the FRCs calculated at two different values of the excitation amplitude (i.e., at and , respectively). These are obtained by path-following the fixed points of the modulation equations (46) and the stability of the system is monitored by checking the eigenvalues of the Jacobian matrix. Figure 11c, obtained for the value of , shows the FRC of the single-mode response (i.e., , ) in which the only nontrivial amplitude is that of the mode directly excited by the periodic force (gray line).
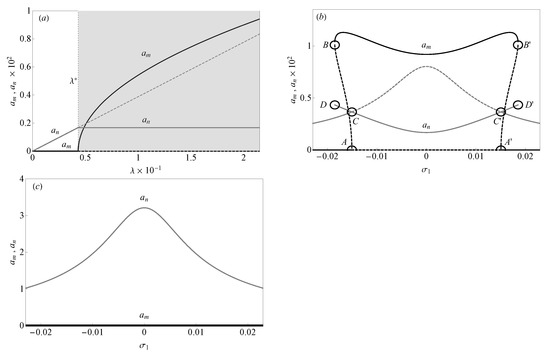
Figure 11.
(a) Force response curves of the amplitude (black line) and (gray line) when and . Frequency response curves of the amplitude (black line) and (gray line) when and (b) at high excitation amplitude (c) at a low excitation amplitude .
The force response curves and the frequency response curves depicted in Figure 11 are obtained for and for a perfect tuning among the frequencies of the resonant modes, i.e., , while Figure 12a shows the force response curves in the case of negative detuning (i.e., ), which characterizes the system investigated in this work. As seen in the case illustrated in the previous section (i.e., ), when the primary resonance involves the higher frequency mode (i.e., ), the frequency response curves are symmetric with respect to the detuning parameter , while losing their symmetry when (as shown in Figure 12b). From the bifurcation analyses conducted for both cases ( and , respectively) it turns out that, as expected [34], at point A and C ( and ), the single-mode response (, ) becomes unstable. Fold bifurcation occurs at points B and , respectively; between those two points, the two-mode response (, ) shows multistability. Finally, points D and represent the boundaries of the detuning parameter , outside which, the response is always a single-mode stable solution.
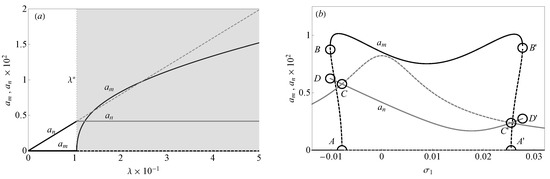
Figure 12.
(a) Force response curves of the amplitude (black line) and (gray line) when and . (b) Frequency response curves of the amplitude (black line) and (gray line) when and at high excitation amplitude .
6. Conclusions
In this work, the nonlinear dynamic behavior of roller batteries was characterized, investigated, and discussed for the first time in the literature. An accurate analytical treatment of the equations of motion was proposed to highlight the nonlinearities of the system and the method of multiple scales was employed to deliver closed-form expressions of the roller battery nonlinear dynamic responses. The nonlinearity of the lowest normal modes of the system was clearly identified and showed to be of the softening type. The simplification of the asymptotic treatment, obtained through the one-mode projection of the equations of motion, shed light onto the effects of the system nonlinearities and to prove that the stiffness nonlinearities govern the dynamic behavior of the roller battery.
The effects of the periodic direct excitation deriving from the cable motion were investigated by studying the primary resonance of the lowest normal mode of the roller battery. It was shown that, for moderately high values of the excitation, the nonlinear response was multistable in a wide range of excitation frequencies. The analytical results were also validated through numerical time integration of the nonlinear equations of motion. Moreover, the instability regions, whose boundaries were analytically obtained in closed form, were parametrically investigated so as to discuss the role of the structural damping, and for demonstrating that higher values of the damping coefficient reduce the region where unstable responses occur.
Furthermore, the modal characterization of the system allowed us to discover the potential scenarios of modal interactions and to investigate the phenomenon of internal resonance between two modes having frequency ratios close to two (i.e., the third and first mode) both in the case of primary resonance of the lowest mode and of the higher mode, respectively. A stability analysis of the fixed points of the modulation equations for the two mode amplitudes and phases allowed us to describe the bifurcation scenarios both for the single-mode and the coupled-mode responses. It was shown that, although internal resonances were possible in the system, in order to cause large-amplitude coupled-mode oscillations, the amplitude of the periodic excitation must be orders of magnitude higher and sufficient to induce large oscillations in the primary resonance of the lowest mode.
Funding
This research received no external funding.
Acknowledgments
A.A. gratefully acknowledges partial support through the Assistant Professor Sapienza Fellowship program. The project ”Dynamics of towers-feasibility of vibration absorbers” supported by POMA is gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
References
- Alshalalfah, B.W.; Shalaby, A.S.; Dale, S.; Othman, F.M. Feasibility Study of Aerial Ropeway Transit in the Holy City of Makkah. Transp. Plan. Technol. 2015, 38, 392–408. [Google Scholar] [CrossRef]
- Hoffmann, K.; Liehl, R. Cable-drawn urban transport systems. WIT Trans. Built Environ. 2005, 77, 25–36. [Google Scholar]
- Hoffmann, K.; Gabmayer, T.; Huber, G. Measurement of Oscillation Effects on Ropeways and Chairlifts. ÖIAZ 2008, 153, 435–438. [Google Scholar]
- Portier, B. Dynamic Phenomena in Ropeway after a Haul Rope Rapture. Earthq. Eng. Struct. Dyn. 1984, 12, 433–449. [Google Scholar] [CrossRef]
- Brownjohn, J.W. Dynamics of Aerial Cableway System. Eng. Struct. 1998, 20, 826–836. [Google Scholar] [CrossRef]
- Renezeder, H.; Steindl, A.; Troger, H. On the Dynamics of Circulating Monocable Aerial Ropeways. Proc. Appl. Math. Mech. 2005, 5, 123–124. [Google Scholar] [CrossRef]
- Bryja, D.; Knawa, M. Computational Model of an Inclined Aerial Ropeway and Numerical Method for Analyzing Nonlinear Cable-car Interaction. Comput. Struct. 2011, 89, 1895–1905. [Google Scholar] [CrossRef]
- Knawa-Hawryszków, M. Determining initial tension of carrying cable in nonlinear analysis of bi-cable ropeway—Case study. Eng. Struct. 2021, 244, 1–13. [Google Scholar] [CrossRef]
- Wenin, M.; Windisch, A.; Ladurner, S.; Bertotti, M.L.; Modanese, G. Optimal velocity profile for a cable car passing over a support. Eur. J. Mech./A Solids 2019, 73, 366–372. [Google Scholar] [CrossRef]
- Wenin, M.; Ladurner, S.; Reiterer, D.; Bertotti, M.L.; Modanese, G. Validation of the Velocity Optimization for a Ropeway Passingover a Support. Sustainability 2021, 13, 2986. [Google Scholar] [CrossRef]
- Nan, C.; Meyer-Piening, H.R.; Decking, C. Dynamic Behaviour of Cable Supporting Roller Batteries: Basic Model. Comput. Struct. 1998, 69, 95–104. [Google Scholar] [CrossRef]
- Arena, A.; Carboni, B.; Lacarbonara, W.; Babaz, M. Dynamic response and identification of tower-cable-roller battery interactions in ropeways. In Proceedings of the ASME Design Engineering Technical Conference, IDETC/CIE 2017, Cleveland, OH, USA, 6–9 August 2017; ASME: New York, NY, USA, 2017; Volume 6. [Google Scholar]
- Arena, A.; Carboni, B.; Lacarbonara, W.; Babaz, M. Ropeway roller batteries dynamics: Modeling, identification, and full-scalevalidation. Eng. Struct. 2019, 180, 793–808. [Google Scholar] [CrossRef]
- Carboni, B.; Arena, A.; Lacarbonara, W. Passive vibration control of roller batteries in cableways. In Proceedings of the ASME Design Engineering Technical Conference, IDETC/CIE 2018, Quebec City, QC, Canada, 26–29 August 2018; ASME: New York, NY, USA, 2018; Volume 6. [Google Scholar]
- Carboni, B.; Arena, A.; Lacarbonara, W. Nonlinear vibration absorbers for ropeway roller batteries control. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 1–15. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z. Dynamics and control of cranes: A review. J. Vib. Control 2001, 9, 863–908. [Google Scholar] [CrossRef]
- Cartmell, M.P. On the need for control of nonlinear oscillations in machine systems. Meccanica 2003, 38, 185–212. [Google Scholar] [CrossRef]
- Ellermann, K.; Kreuzer, E.; Markiewicz, M. Nonlinear primary resonances of a floating crane. Meccanica 2003, 38, 4–17. [Google Scholar] [CrossRef]
- Arena, A.; Lacarbonara, W.; Cartmell, M.P. Nonlinear Interactions in Deformable Container Cranes. Proc IMechE Part C J. Mech. Eng. Sci. 2016, 230, 5–20. [Google Scholar] [CrossRef] [Green Version]
- Zukovic, M.; Kovacic, I.; Cartmell, M.P. On the dynamics of a parametrically excited planar tether. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 250–264. [Google Scholar] [CrossRef]
- Cartmell, M.P.; Kovacic, I.; Zukovic, M. Autoparametric interaction in a double pendulum system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 1971–1986. [Google Scholar] [CrossRef]
- Kovacic, I.; Zukovic, M.; Cartmell, M.P. On the oscillation death phenomenon in a double pendulum system with autoparametric interaction. J. Phys. Conf. Ser. 2012, 382, 012055. [Google Scholar] [CrossRef] [Green Version]
- Moura, A.G.; Erturk, A. Combined piezoelectric and flexoelectric effects in resonant dynamics of nanocantilevers. J. Intell. Mater. Syst. Struct. 2018, 24, 266–273. [Google Scholar] [CrossRef]
- Arena, A.; Lacarbonara, W. Piezoelectrically induced nonlinear resonances for dynamic morphing of lightweight panels. J. Sound Vib. 2021, 498, 115951. [Google Scholar] [CrossRef]
- Yuda, H.; Jing, L. The magneto-elastic subharmonic resonance of current-conducting thin plate in magnetic filed. J. Sound Vib. 2009, 319, 1107–1120. [Google Scholar] [CrossRef]
- Givois, A.; Giraud-Audine, C.; Deü, J.F.; Thomas, O. Experimental analysis of nonlinear resonances in piezoelectric plates with geometric nonlinearities. Nonlinear Dyn. 2020, 102, 1451–1462. [Google Scholar] [CrossRef]
- Luongo, A.; Rega, G.; Vestroni, F. On Nonlinear Dynamics of Planar Shear Indeformabie Beams. J. Appl. Mech. 1986, 53, 619–624. [Google Scholar] [CrossRef]
- Rahman, Z.; Burton, T.D. Large amplitude primary and superharmonic resonances in the duffing oscillator. J. Sound Vib. 1986, 110, 363–380. [Google Scholar] [CrossRef]
- Rahman, Z.; Burton, T.D. On higher order methods of multiple scales in non-linear oscillations-periodic steady state response. J. Sound Vib. 1989, 133, 369–379. [Google Scholar] [CrossRef]
- Wojnowsky Krieger, S. The Effect of an Axial Force on the Vibration of Hinged Bars. J. Appl. Mech. 1950, 17, 35–36. [Google Scholar] [CrossRef]
- Eisley, J.G. Nonlinear vibration of beams and rectangular plates. J. Appl. Math. Phys. (ZAMP) 1964, 15, 167–175. [Google Scholar] [CrossRef] [Green Version]
- Evensen, D.A. Nonlinear Vibrations of Beams with Various Boundary Conditions. Am. Inst. Aeronaut. Astronaut. J. 1968, 6, 370–372. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T.; Lobitz, D.W. Numerical-Perturbation Method for the Nonlinear Analysis of Structural Vibrations. Am. Inst. Aeronaut. Astronaut. J. 1974, 12, 1222–1228. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley-Interscience: New York, NY, USA, 1979. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Nayfeh, A.H. Nonlinear Interactions: Analytical Computational and Experimental Methods; John Wiley and Sons Ltd.: New York, NY, USA, 2000. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 11.0; Wolfram Research, Inc.: Champaign, IL, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).